From batch to continuous free-radical solution polymerization of acrylic acid using a stirred tank reactor†
Abstract
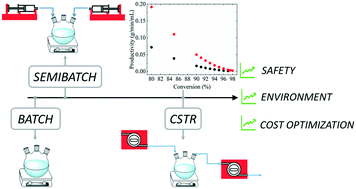
Nowadays, the majority of the world polymer production is obtained through discontinuous or semi-continuous processes. In the specific case of free-radical polymerization (FRP), discontinuous processes suffer from many limitations with respect to safety, productivity, product quality and cost. In this work, we report a model-assisted strategy for transition of the solution FRP of non-ionized acrylic acid (AA) from batch to continuous with the aim of preserving the product quality in terms of weight-average molecular weight. A basic kinetic model is developed and validated by comparison with experimental results for three reactor configurations, batch, semibatch and continuous stirred tank reactor (CSTR). Then, examples of transitioning from a semibatch to a continuous process, using a stirred tank reactor, are analysed. Taking advantage of the validated model, a successful transition is designed through an optimization procedure. Based on a minimum acceptable monomer conversion of 98%, an increase in the polymer productivity up to 88% is achieved.


 Please wait while we load your content...
Please wait while we load your content...