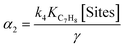Photocatalytic toluene degradation: braiding physico-chemical and intrinsic kinetic analyses

Abstract

In this study, we analyzed the photocatalytic degradation of toluene using composite systems consisting of a tungsten oxide component supported on a pure anatase phase. To scrutinize the photocatalytic process, herein we presented a new method with combined spectroscopic and kinetic tools to provide novel and quantitative information mostly obtained in situ under reaction conditions. First, it allows us to extract information quantitatively, regarding charge recombination and the fraction of kinetically relevant charge species reaching the surface of the material and used in chemical steps. In addition, the method allows us to detail how efficiently such kinetically relevant charge carrier species interact with key reactant and intermediate molecules. The application of such procedure to the elimination of toluene shows how the composite system improves the activity with respect to the relevant pure-anatase reference catalyst. This appears to be a complex phenomenon, with implication in several elemental steps of the reaction. The new method can be easily generalized to any photocatalytic reaction and would pave the way to progress in the quantitative understanding of the photocatalytic process.

---

1. Introduction

Pollution-related problems coming from human activities have raised public awareness about the need for creating efficient ways of controlling pollutants originating from industrial and mobility activities. In this context, much attention has been paid to novel advanced oxidation processes. Heterogeneous photocatalysis is one advanced oxidation process that uses semiconductors and light to control and reduce pollution. Its main field of application corresponds to the degradation and/or transformation of organic and inorganic pollutants as well as biological microorganisms.^1–5 Photocatalysis has the most significant advantage when compared with other remediation technologies, which could be the use of rather mild and economically viable conditions, as it works at ambient pressure and temperature and using air as an oxidant of the process.

Although TiO₂ is the most widely used photocatalyst, it has certain limitations in the efficient depollution processes of specific molecules.^1,3,6 This is the case of toluene, a typical urban contaminant corresponding to a though still frequently used testing molecule to calibrate the photo-elimination power of catalytic materials.^7–9 Whether for toluene or, in general, for the elimination of all kinds of pollutants, there is an urgent need for developing materials capable of increasing the activity of titania. The use of other active semiconductors within a titania-based composite system is one of the successful ways to approach this task. The combination of tungsten and titanium oxides has been shown to be particularly effective in the photo-elimination of pollutants irrespective of the illumination characteristics (UV, visible, solar) or other (reactant chemical nature) reaction conditions.^10–17

Herein, we started the study with an exhaustive kinetic analysis of the gas-phase toluene photo-elimination using tungstenia–titania composite systems.¹⁷ To approach the analysis of the photo-elimination from a novel perspective, we carried out a kinetic analysis of the reaction, exploring the response of the catalytic solids to the most significant experimental variables affecting photoactivity within a Box–Behnken experimental design.¹⁸ The mechanistically derived formalism utilized here includes an intrinsic expression to introduce light into the chemical reaction mechanism and utilizes the IUPAC rules to calculate the light-matter interaction taking place in the photo-catalytic films.¹⁹ Such an intrinsic kinetic approach is critical to ensure the transferability (for other studies) as well as the meaningfulness of the study. Although numerically and computationally complex, intrinsic kinetic formalisms have been previously utilized to study photo-catalytic processes.^20–22 However, only few works tested the results coming from kinetic studies with parallel physico-chemical studies coming from independent spectroscopic^23,24 or adsorption²⁵ studies. Here, we wish to go a step forward in order to braid chemical and chemical engineering information into a kinetic procedure that takes into account initial and independently obtained physico-chemical information to test the results of the kinetic formalism and, at the same time, fixing numerical details of such procedures to ensure that the kinetic formalism by itself can provide useful physico-chemical information.

To show the consistency of our novel approach, we will subject to analysis both activity and selectivity of the toluene photo-elimination from both (relevant) physico-chemical and kinetic perspectives and get novel information about the way the catalysts interact with the catalytically relevant molecules. Such an information cannot be achieved by physico-chemical or kinetic methods alone and thus opens a way to extract otherwise “inaccessible” chemical knowledge. This approach is here utilized to interpret the photo-chemical and photo-physical effects coming from addition of tungsten oxide to the (parent) anatase single-phase reference in composite systems. Such an approach provides novel information in a quantitative way, opening a path for the understanding of complex catalytic reactions and composite catalysts.

2. Materials and methods

2.1. Sample preparation and characterization

Titania (called here Ti) was synthesized by a microemulsion method in a single pot for both single titania and composite samples. The microemulsion involved an aqueous phase dispersed in n-heptane, using Triton X-100 (Aldrich) as a surfactant and hexane as a cosurfactant.²⁶ Titanium tetraisopropoxide (Aldrich) and ammonium tungsten oxide (Alfa Caesar) were used in all synthesis procedures. The total cation content of the aqueous solution is 0.5 M. Water/(Ti + W) and water/surfactant molar ratios were, respectively, 18 and 110 for all samples. In the case of composite samples (called TiW, having a 0.25 mol% of WO₃, selected based on a previous study¹⁷), the aqueous solution of the tungsten precursor (ammonium tungsten oxide from Alfa Cesar) was agitated for 30 min. Subsequently, a stoichiometric (to obtain the corresponding W(VI) hydroxide) quantity of tetramethylammonium-hydroxide (TMAH) was introduced from the aqueous phase of a similar microemulsion. After 5 min of contact, titanium tetraisopropoxide (a mixture with isopropanol (2 : 3)) was added drop by drop into the previously resulting microemulsion. In the case of doped samples, we added titanium tetraisopropoxide (mixed with isopropanol as described before) to an inverse emulsion containing an aqueous solution of the tungsten precursor (previously agitated for 30 minutes). In both samples, the resulting mixtures were stirred for 24 h, centrifuged, decanted, rinsed with methanol and dried at 300 K for 6 h. Following the microemulsion preparation method, the amorphous powders were calcined at 723 K under air for 2 h.

The BET surface areas and average pore volumes and sizes were measured by nitrogen physisorption (Micromeritics ASAP 2010). XRD profiles were obtained using a Seifert D-500 diffractometer with Ni-filtered Cu Kα radiation in a 0.02° step. The particle sizes were estimated by XRD using the Williamson–Hall formalism.²⁷ UV-vis diffuse-reflectance spectroscopic experiments were performed using a Shimadzu UV2100 apparatus with nylon as a reference and the results presented as the Kubelka–Munk transform.²⁸

Electron paramagnetic resonance (EPR) measurements were done using a Bruker ER200D spectrometer operating in the X-band. The sample suspensions (0.5 mg mL⁻¹) were prepared in redistilled water (Milli Q) or methanol (HPLC grade, Scharlab) and sonicated for 4 min before the experiment. In this experiment, 5,5-dimethyl-1-pyrroline-N-oxide (DMPO, Sigma-Aldrich) was used as a spin trapping agent. The solutions of DMPO (0.01 M) were prepared in water and kept on ice during the whole set of experiments. Then, 100 μL of the solid suspension and 100 μL of the corresponding DMPO solution were mixed into an EPR flat quartz cell under atmospheric air. Then the cell containing the experimental mixture (sample/DMPO/water) was irradiated for different time periods (from 0.5 to 10 min) with the identical light excitation source to that employed for the photoreactor (see below), being then immediately transferred to the spectrometer cavity for EPR analysis. In some cases, decay of a small radical concentration (below 3% on average) was observed in the darkness during the course of spectrum recording. Typical EPR spectrometer settings in a standard experiment were: ca. 9.75 GHz microwave frequency, 19.5 mW microwave power, 100 kHz modulation frequency, 1 G modulation amplitude and 2 × 10⁵ spectrometer gain. All spectra were recorded at room temperature. No significant signal saturation was observed in those conditions. Blank experiments (without sample) were also performed to check the absence of radical formation in DMPO solutions (water or methanol) under irradiation and in the absence of solid. The g-values (±0.0001) were determined using 2,2-diphenyl-1-picrylhydrazyl (DPPH, Sigma-Aldrich) as an internal standard. The EPR spectra were recorded and analyzed using the Bruker software WinEPR.

2.2. Adsorption and photo-catalytic experimental details

Adsorption of toluene and benzaldehyde in the ppm range was followed by mass spectrometry (Onmistart 300) and gas chromatography (FID, HP-Innowax 0.32 mm I.D. × 30 m) using a gas mixture prepared by injected toluene or benzaldehyde with a syringe pump (Cole-Parmer 74900) in a N₂ flow (Bronkhorst mass flow controller) under illumination conditions. In situ light excitation was carried out using 365 nm radiation. A Hg–Xe 500 W lamp with a 280–400 nm dichroic filter coupled with a 365 nm (25 nm half-width) filter (LOT-Oriel) were used to select the light excitation. The intensity was nearly identical (ca. 8.5 mW cm⁻²) to photo-catalytic experiments as measured using a HD2303 Delta Ohm radiometer.

Gas-phase photo degradation of toluene (≥99% Aldrich) was carried out in a continuous-flow annular photoreactor containing ca. 0.4 mg cm⁻² of photocatalyst as a thin layer coating on a Pyrex tube (the loading is fixed to maximize the activity of the samples, see ref. 16). The reactor details are fully described in a previous work and a scheme of it is presented in Fig. S1.†²⁹ The reacting mixture (100 mL min⁻¹) was prepared by injecting toluene into a wet (ca. 15–90% relative humidity) 20 vol% O₂/N₂ flow before entering to the photoreactor, yielding an organic inlet concentration of ca. 200–400 ppmv. Fluorescent UV (Sylvania F6WBLT-65; 6 W) was used for the photoreaction experiment. Reaction rates and selectivity were evaluated under steady-state conditions, typically achieved after ca. 3 h from the irradiation starting time. Selectivity is presented as molar percentage of carbon-containing products. Carbon balance is better than 95.8% in all cases. The concentrations of toluene and the reaction products were analyzed using an on-line gas chromatograph (Agilent GC 6890) equipped with a TCD (for CO₂ measurement) and an FID (organics measurement) detector.

3. Results and discussion

3.1. General formalism

According to the reactor geometry presented in Fig. S1† and under kinetic control regime (see “external and internal mass-heat transfer” analysis in the ESI† section), the differential mass balance equation for toluene photo degradation can be expressed as:In eqn (1), v_z, a, C_C7H8 and r_C7H8 are, respectively, the axial velocity, the external catalytic surface area per unit volume, the toluene concentration and the average reaction rate. To solve eqn (1), one boundary condition is necessary:

C_C7H8(z = 0) = C_C7H8,in (2)

Eqn (1) and (2) take into consideration only the convective flow through the axial coordinate z, which is a typical approach for this configuration reactor. Besides, the following assumptions were considered: (i) the reactor operates under steady state conditions, (ii) negligible axial diffusion when compared to the convective flux in that direction, and (iii) negligible homogeneous photo-chemical reactions.^29,30 More details about the mass balance equation deduction are presented in the ESI† (section 2, “mass balance”).

Similarly, we can establish the corresponding differential mass balance for the products generated under reaction. In this case, we only detected production of benzaldehyde (C₇H₆O) as an intermediate and CO₂ as a final oxidation product. The one corresponding to benzaldehyde (eqn (3) and (4)) will be utilized here in combination with those of toluene (eqn (1) and (2)) to describe the evolution through the reactor of the two linearly independent chemical species of the reaction:

The boundary condition is:

C_C7H6O(z = 0) = 0 (4)

The two differential equations (eqn (1) and (3)) will be solved simultaneously using as input the experimental results presented in Table 1. This table summarized the results for 15 experiments (with repetition of the central point 3 times) per sample, defined following the Box–Behnken scheme of three factors (water inlet content, illumination level and toluene inlet concentration) and three levels.¹⁸

Table 1 Details of the Box–Behnken factors used as well as catalytic responses measured through the toluene (Tol) reaction rate and benzaldehyde (Bz) yields

Experimental variables			RateTol (10^11 mol m^−2 s^−1)		YieldBz (10^11 mol m^−2 s^−1)
HR/%	Light^a/%	Toluene Conc. (10^3 mol m^−3)	Ti	TiW	Ti	TiW
a Lamp intensity. Full illumination conditions: 1.55 × 10^−8 Einstein cm^−2 s^−1.
90	50	4.46	3.75	9.28	0.60	7.45
15	50	4.46	3.97	9.83	1.07	8.53
45	100	4.46	4.30	10.64	1.07	9.57
45	25	4.46	2.80	6.92	0.42	5.51
45	50	6.69	4.52	11.19	1.09	8.84
90	25	6.69	2.75	7.17	0.63	5.07
90	100	6.69	6.53	16.29	1.11	11.40
15	25	6.69	3.47	8.66	0.99	7.11
15	50	8.92	4.92	12.36	1.72	10.46
45	25	8.92	2.93	7.28	1.05	6.56
45	100	8.92	4.08	10.27	1.97	9.76
90	50	8.92	3.45	8.64	1.21	8.56
15	100	6.69	5.37	13.69	2.12	12.59
45	50	6.69	4.52	11.19	1.09	8.84
45	50	6.69	4.52	1.19	1.09	8.84

---

The solving of eqn (1) and (3) requires deriving the expression of the reaction rate as a function of the experimental variables presented in Table 1. To reach this objective, first we need to fix a formalism to obtain the reaction rate from a reaction scheme summarized in Table 2. The reaction mechanism can be simplified considering the well-established initial steps of any photocatalytic processes: (i) the photo-excited sample generates electrons and holes, (ii) holes may react with adsorbed water and superficial OH⁻ ions to generate hydroxyl radicals, and (iii) molecular oxygen acts as an acceptor species in the electron-transfer reaction, partly reducing the recombination processes and the resulting loss of energy as heat.^{20,23,25,30,31} For toluene, the main charge carrier species interacting with the organics is known to be the hydroxyl radical.^7,20,32 For the hydroxyl-type mechanism, the benzaldehyde is the main intermediate and is produced by the OH-radical attack to the methyl moiety of toluene.^20,33,34 From this intermediate, the mechanism is complex but the corresponding carbon-containing species evolve via hydroxyl-radical attack.^{7,20,23,25,32–34}Table 2 summarizes all these elemental steps as well as termination steps for hydroxyl radical species.

Table 2 Hydroxyl-mediated mechanism for toluene photo-oxidation

Reaction step							Const.
Activation
Photocatalyst	+	hν	→	h^+	+	e^−	r g

---

Adsorption
Site	+	C7H8	↔	C7H8ads			K C7H8
Site	+	C7H6O	↔	C7H6Oads			K C7H6O
Site	+	H2O	↔	H2Oads			K H2O
SiteO2	+	O2	↔	O2ads			K O2

---

Electron capture
O2ads	+	e^−	→	O2ads˙^−			k 1

---

Hole trap
H2Oads	+	h^+	→	HO˙	+	H^+	k 2

---

Recombination
h^+	+	e^−	→	Heat			k 3

---

Toluene oxidation
C7H8ads	+	HO˙	→	C7H6Oads			k 4

---

Benzaldehyde oxidation
C7H6Oiads	+	HO˙	→	Productsi,ads			k 5

---

Radical termination
HO˙	+	HO^−	→	O2˙^−	+	H2O	k 6

---

According to Table 2, the reaction rate of toluene consumption and benzaldehyde generation are described by eqn (5) and (6) (presented in Table 3), respectively. As outlined in ref. 19, to obtain these equations we need to consider: i) the application of the steady-state approximation to holes and hydroxyl radical species; ii) that charge recombination in semiconductors is expected to be much faster than any chemically related charge transfer step (k₃[h⁺][e⁻] ≫ k₂ [H₂O]_ads[h⁺] in Table 2); iii) the solving of the balance of sites where the adsorption of molecules are defined by Langmuir–Hinshelwood-type formulae, taking into account that organic molecules (but not oxygen) compete with water; and iv) the local superficial rate of electron–hole pair generation r_g (see first row in Table 2) has been substituted by .

Table 3 Summary of the kinetic formalism

Kinetic equations	Kinetic constants	Physical interpretation and constrains	Parameters measured with EPR
(5)
(6)

---

In eqn (5) and (6), the concentrations are described by C_chemical, k_i are rate constants defined in Table 2, K_chemical are adsorption constants (also defined in Table 2), and [sites] are the available surface sites for adsorption. Thus, eqn (5) and (6) include the effect of the reactant and water content of the reaction feed as well as light trough the local superficial rate of photon absorption (e^a,s), as defined by eqn (7).^19,29 In this equation F_AS is the fraction of light absorbed by the sample and q_sup the radiation flux at each position (x̲ [triple bond, length half m-dash] X_S, Y_S, Z_S) of the catalytic film (see Fig. S1†).

e^a,s(x̲) = q_sup(x̲)F_AS (7)

To obtain the radiation flux on the surface of the samples, we first calculated the impinging radiation flux from the lamps (q_n in Fig. S1†). Considering the coordinate system presented in Fig. S1† and the geometry of the reactor (annular multilamp), q_n can be determined by eqn (8).²⁹In eqn (8), X_S, Y_S, Z_S and R are the coordinates of the points located on the surface of the catalytic films and the radius of the cylinder supporting the sample (Fig. S1†). Angle variables (θ, φ) are defined as described in Fig. S1† and section 1 of the ESI† section. The integration limits can be evaluated using the ray tracing method²⁹ and are presented in the ESI† section. Finally, the q_supx/y components (see Fig. S1;†eqn (9)) can be determined using q_n and a radiation balance, which considers the main optical (transmittance, F_i, and reflectance, R_i) events occurring in all components of the reactor placed between the emission source and catalyst, i.e. glass and reaction media, as well as the catalytic film.

q^x,y_sup = f(q_n, F_i, R_i); i = catalyst, glass, reaction media (9)

A detailed description of the mathematical formulation to provide q_sup as a function of q_n (eqn (8)) and the transmittance/reflectance optical measurements for each component of our reactor system can be found elsewhere.^29,31

Eqn (5) and (6) are the rate equations to be introduced in partial differential eqn (1) and (3). The rate equations contain four constants (presented as α_i constants in Table 3). To obtain physico-chemical information from the kinetic analysis, we defined the β constants presented in Table 3. In fact, β₁ informs about the ratio between the rates for generation (“activation row” in Table 2) and recombination of charge (“recombination row” in Table 2), and thus, it is a measure of the number of charge carriers accessing the surface of the material. Note that this measurement is carried out under relevant reaction conditions, thus providing much better information than luminescence, photoelectrochemical or any other physico-chemical characterization procedure. Additionally, β₂ informs about the combination of rates of adsorption and hydroxyl attack of toluene vs. the intermediate, benzaldehyde (see the corresponding constants for “toluene and benzaldehyde adsorption and oxidation” rows in Table 2). Therefore, from the kinetic approach just presented, we can obtain information about the charge carrier handling of a catalyst (β₁) as well as the combined effect of surface adsorption and hydroxyl attack for the reactant and stable intermediates (β₂). The two-way feedback between physico-chemical techniques and the kinetic approach considers, in first place, the analysis of the reliability of the β₁ parameter using the measurement of radical species with EPR. Using the formalism presented in section 4 of the ESI,† we can show that the δ parameter presented in Table 3 is closely connected with the β₁ parameter. Moreover, measuring experimentally the absorption constants of toluene and benzaldehyde and using the β₂ parameter we can derive the ratio between the kinetic constants of the two organic molecules involved in the mechanism.

A big issue in solving eqn (1) and (3) is to obtain a result with physical meaning. We note that the formalism summarized in Table 3 for the β parameters indicates that there is a relationship between the values of the alpha parameters that must be satisfied. This provides a strong guidance to the fitting procedure. Otherwise the solution can have some uncertainly due to the complex surface of hyperpotential of the fitting problem.³⁵

A MATLAB® R2018b algorithm was build up to obtain the kinetic parameters using a subroutine to solve (simultaneously) the differential eqn (1) and (3) (subroutine ode45 based in a Runge–Kutta formalism) subjected to boundary conditions (eqn (2) and (4)), coupled with a nonlinear least-squares fitting algorithm (lsqnonlin, algorithm: trust-region-reflective optimization) to obtain the parameters of eqn (5) and (6). To provide an insightful analysis of the fitting procedure, we used the “MultiStart” MATLAB formalism³⁶ in order to obtain a global minimum (mathematical) of the fitting procedure and compare it with the result obtained using the additional constrains (with physical meaning) coming from introducing the relationship between alpha parameters used to define the beta parameters (Table 3). Hereafter, the first result is called “math” (representing the mathematical solution yielding a global minimum) result and the second “phys” (a local minimum with physical meaning). In both cases, we tested 10⁵ starting sets of parameters to run the calculations. The analysis of errors in the kinetic parameters was carried out using the MatLab “nlparci” subroutine. The “nlparci” subroutine returns the 95% confidence intervals for the nonlinear least squares parameter estimates using the Jacobian matrix associated with eqn (5) and (6) as well as the experimentally measured errors obtained for the reaction rate. As mentioned, experimental data to carry out the process are compiled in Table 1.

3.2. Braiding physico-chemical and kinetic information

Our main objective is to set up a procedure which would provide an effective two-way interaction procedure linking physico-chemical and kinetic information as well as to provide new information, currently non-accessible by the isolated application of each type of study to photo-catalytic materials. The utility of this objective is exemplified through the new clues offered towards the understanding of the catalytic effects coming from the addition of tungsten oxide to a single-phase anatase powder. The main physico-chemical properties of the single-phase Ti and composite TiW materials are presented in Table S2 of the ESI† section. Titania presents the anatase structure (PDF 21-1272; space group I4₁/amd), while tungsten oxide shows the monoclinic structure (PDF 83-0951; space group P2₁/n) with the particle size in the 10–15 nm range and ca. 23 nm, as detailed in Table S2.†

The catalytic results for the two samples are presented in Table 1. We note that the tungsten oxide reference is not presented, as it displays more than one order of magnitude inferior activity than the Ti reference, thus giving a rather limited contribution by itself to the composite system. The higher activity of the TiW sample with respect to the Ti reference as well as a significant variation in selectivity (benzaldehyde formation is enhanced in the presence of tungsten oxide) between the two catalysts are evident from this table. A first analysis of the Box–Behnken catalytic results is carried out using the Pareto plots present in Fig. 1. Pareto charts of standardized effects and main effects are powerful visualization tools that summarize the results of the factorial design carried out. They indicate the statistically significant parameters as those that are above the established threshold. To model the catalytic response of the solids, we utilized linear, quadratic and crossed terms between the three factors studied. For a parameter to be statistically significant, the null hypothesis of the parameter's coefficient being equal to zero is tested by comparing the calculated ANOVA p-value with a significance test level here set at α = 0.05 (95% of probability). This value is shown by a vertical line in the charts presented in Fig. 1. If the p-value is less than α, the hypothesis that the coefficient is equal to zero is rejected and deemed to be statistically significant. The weight of the parameters is indicated by the length of the plotted bar.³⁷

Fig. 1 Pareto plots for experimental design variables (A, relative humidity, %; B, light intensity, %; C, Cⁱⁿ_Toluene, mol cm⁻³) on toluene photo-oxidation and benzaldehyde photo-production. Catalytic rates (mmol g⁻¹ h⁻¹), α (vertical blue line): 0.05.

Some differences in the functional response of the TiW and the Ti materials to changes in the experimental variables (relative humidity, irradiation intensity and toluene inlet concentration) can be inferred from Fig. 1. More concretely, for toluene we see essentially the same behavior (except in the exact values of the weight of the parameters) with dominance in both cases of toluene concentration inlet-related variables. Contrarily, the important differences in the generation of benzaldehyde are highlighted by the analysis of Fig. 1. Such figure provides conclusive evidence that selectivity differences between the TiW and Ti samples are strongly dependent on the reaction conditions, allowing us to conclude that the analysis of selectivity using a single reaction condition can provide rather poor information. In addition, the benzaldehyde production of the TiW sample shows significant sensitivity to the relative humidity of the inlet stream (and to lower extent light intensity), while in the case of the Ti sample, the three factors (and their interactions) strongly affect benzaldehyde production.

Eqn (5) and (6) provide a mathematical model, all these factors and their interaction effects in the reaction rate of toluene disappearance and the generation of benzaldehyde production. The goodness of the fitting process considering the “math” and “phys” procedures is summarized in Fig. 2. The goodness of the fittings is analyzed using the linear fitting R² parameter between experimental and modeled toluene/benzaldehyde outlet concentrations as well as the root mean square error (RMSE) differences between these two concentrations and two molecules. In the case of toluene, the two fitting procedures are essentially indistinguishable for both samples Ti and TiW. For benzaldehyde production differences between the two fitting procedures are visible between the Ti and TiW samples but according to both R² and RMSE parameters are of limited significance. We further analyze the adequacy of the kinetic model in Fig. 3 and 4. Fig. 3 displays the results of the fitting model (full lines constituting the mesh) for the Ti sample, while Fig. 4 does the same for the TiW sample. Both figures also contain the experimental points corresponding to fix to the middle-level value(s) one of the three factors (and scanning all other values for the two remaining factors) used in the Box–Behnken design. The surfaces provide clear evidence of the “flat” and/or “planar-type” response of toluene to the factors in comparison to the one of benzaldehyde in the two samples. We can see that benzaldehyde shows a more complex response to the three factors in both samples. Moreover, the figures allow us to visualize the complex interaction between factors described by a simple number in the Pareto plots of Fig. 1. In particular, we can see the different interplays observed between the relative humidity and light in both samples (corresponding benzaldehyde top panel of Fig. 3 and 4). A larger response of benzaldehyde and thus a stronger interaction between these two factors are observed in the case of the Ti sample. Moreover, a different response between the samples is evident when analyzing the interplay between relative humidity and toluene inlet concentration (lower panel of Fig. 3 and 4). Such a rich response is reproduced adequately by our model according to fitting goodness parameters summarized in Fig. 2.

Fig. 2 Correlation plot between experimental values and model (simulated) prediction values of toluene and benzaldehyde concentrations using Ti and TiW catalysts and different fitting models (Math and Phys).

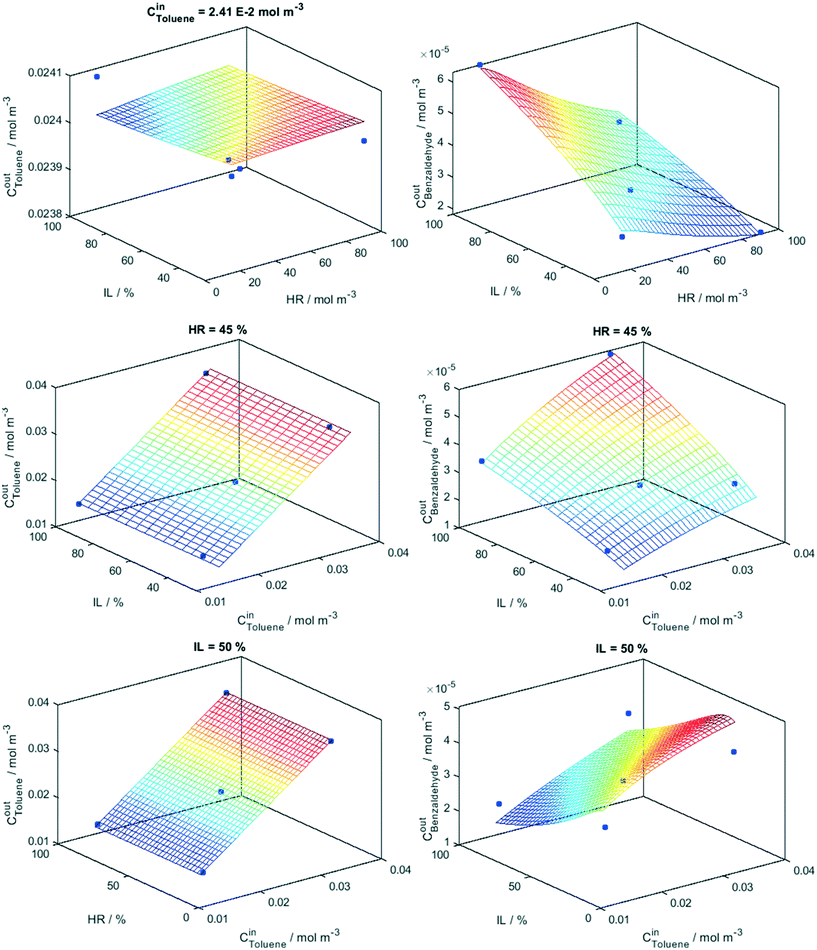Fig. 3 Model (net) and experimental values (points) at constant initial concentration (Cⁱⁿ), humidity (HR) and irradiation (IL) levels indicated in the panels. Sample: Ti.

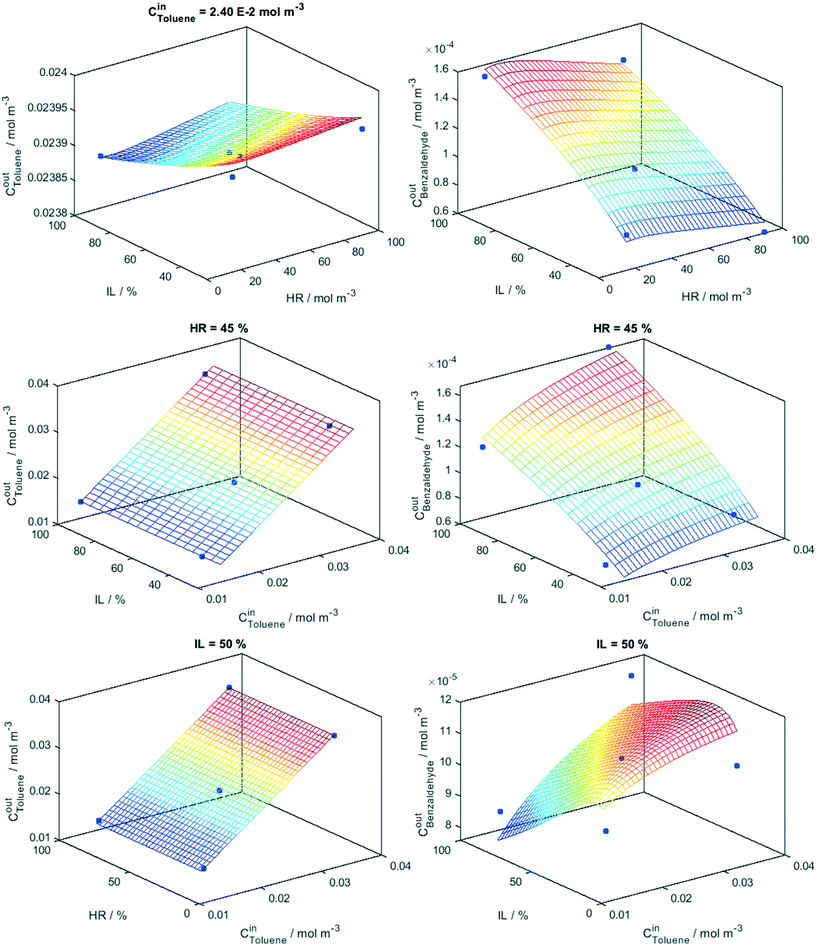Fig. 4 Model (net) and experimental values (points) at constant initial concentration (Cⁱⁿ), humidity (HR) and irradiation (IL) levels indicated in the panels. Sample: TiW.

To introduce physico-chemical information in the analysis procedure, we calculated the rate of formation of OH radicals using EPR and optical measurements (see section 4 of the ESI† section) and measured the adsorption constants of toluene and benzaldehyde. The inset in panel A of Fig. 5 shows a typical 4-peak signal attributed to the formation of a ˙DMPO–OH adduct, only formed after the irradiation of the sample. This EPR signal displays (peak) intensities of 1 : 2 : 2 : 1 and spin Hamiltonian parameters: a_NO = 14.9 G, a_H = 14.9 G; g = 2.0056. For all samples, the intensity of the signal vs. time displays a characteristic behavior, with an initial growth period followed by a saturation plateau. This is a well-known behavior coming from the growth of the radical formation species until the interaction between radicals leads to the formation of diamagnetic species. The formation of hydroxyl-type radical species is thus measured through the initial rate of radical formation.^38–40 After normalization using the optical properties (see section 4 of the ESI†), we obtained a spectroscopic parameter, the so-called δ parameter in Table 3, paralleling the β₁ parameter. In panel B of Fig. 5, we can observe a comparison between the EPR and kinetic β₁-type parameters for Ti and TiW samples. Important differences are observed between the β₁-type parameters obtained for the samples and coming from the “math” and “phys” kinetic analyses. Although these fitting results are essentially indistinguishable from a statistical point of view (Fig. 2), a confrontation with the spectroscopic measurement indicates that introducing physical restrictions to the mathematical fitting procedure leads to a consistent picture between the independent physico-chemical and kinetic ways of obtaining the observable. Note that this indicates that the kinetic information can be carefully obtained in order to have physical meaning and that, however, kinetics can provide information obtained under real (reaction) conditions about a key point of the catalytic process, the number of kinetically-relevant charge carrier species reaching the surface of the solids. The latter indicates that the TiW sample overperforms the Ti reference in a factor near 2.5–2.7 times. Therefore, the charge separation taking place after light excitation and physically separating charge between the two semiconductors^12,13,17 make a significant contribution to the rate of the hydroxyl-mediated photo degradation of all carbon-containing molecules present at the surface of the catalysts.

Fig. 5 Interpretation of the analytical procedure. (A) EPR measurement of OH radical species vs. time. Inset: EPR signal obtained for TiW at 1 minute. (B) Correlation plot between the reaction rate and the β₁ and δ factors (see Table 3). (C) Parity plot of the β₂ factor values obtained using the two possible procedures presented in Table 3. (D) Adsorption isotherms for toluene. (E) Adsorption isotherms for benzaldehyde. (F) Ratio between toluene and benzaldehyde kinetic and adsorption constants (constants defined in Table 2).

The study will be completed with the analysis of the β₂ parameter. This parameter is presented in panel C of Fig. 5. Again, the difference between the “math” and “phys” procedures becomes evident. The reliability of the two procedures is tested by comparing the estimation of the β₂ parameter using the two procedures possible to calculate this observable for each fitting presented in Table 3. Inherent to the “phys” procedure is to render the same value (within error) for the two estimations, while it is clear that this does not occur in the case of the “math” procedure. To have physical insights from the β₂ parameter, we first carried out an adsorption study of benzaldehyde and toluene to obtain the adsorption constants. The experimental data of the absorption curves is presented in panels D and E of Fig. 5 for, respectively, toluene and benzaldehyde. The fitting of the data using a Langmuir–Hinshelwood isotherm formalism is presented as a solid line in the plots and was utilized to obtain the adsorption constants. The ratios between toluene and benzaldehyde adsorption and kinetic constants define the β₂ parameter (Table 3) and are displayed in panel F of Fig. 5. For our purposes, the key information is enclosed in the corresponding kinetic constant ratio for Ti and TiW. As can be seen in the figure, this ratio suffers a strong increase in going from the Ti reference to the composite TiW sample. This increase takes a value of ca. 29 times. This demonstrates that the high activity of the system is not only achieved by increasing the available hydroxyl radical species at the surface of the materials by decreasing charge recombination, but also by altering the transformation of the benzaldehyde vs. toluene radical attack. Obviously, this would have implications in the selectivity of the photo degradation reaction. In this case, this is the origin of the significantly higher selectivity towards benzaldehyde presented by the TiW sample with respect to the Ti reference. This occurs by accumulation of benzaldehyde at the surface of the TiW catalyst. In short, we highlight the fact that the procedure outlined quantitatively measured several relevant physical phenomena, providing a tool to quantitatively analyze the effects of controlling activity and selectivity in a series of samples.

4. Conclusion

Braiding spectroscopic and kinetic information taken under relevant reaction conditions is a must in order to progress in the photocatalytic research field. Herein, we presented a two-way interaction scheme between physico-chemical and kinetic approaches for analyzing activity and selectivity. Such a procedure was used to analyze the physical origin of the activity enhancement taking place by the addition of tungsten oxide onto the surface of a highly active anatase powder. We stress the fact that such analysis is carried out quantitatively. The first information revealed by the method is the number of kinetically relevant charge species reaching the surface and able to interact with the organic molecules. Second, we can detail, through the corresponding kinetic constants, how such surface charge carrier species interact with each one of the relevant organic molecules generated via the attack of the radical species.

This procedure unveils that the photo-physical effects directly related to the formation of hydroxyl radicals able to reach the surface of the catalysts increase by a factor of ca. 2.5 times in the composite TiW system with respect to the pure anatase Ti reference. It also shows drastic changes in the kinetic constant of key benzaldehyde intermediate with respect to the one of the toluene reactant when comparing the single-phase and composite systems. The study shows that tungsten oxide presence promotes the radical attack to the toluene molecule in ca. 30 times with respect to benzaldehyde. This shows that the selectivity is not based in favoring the interaction of the catalyst surface with polar (benzaldehyde) vs. non-polar (toluene) molecules. Although there are changes in the adsorption of these molecules, they do not command the main effects controlling the corresponding disappearance (toluene) and formation (benzaldehyde) rates, which do respond dominantly to kinetic effects. Such kinetic effects command the selectivity of toluene photo-elimination.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Authors thank the “Ministerio de Ciencia e Innovación” for the ENE2016-77798-C4-1-R and PID2019-105490RB-C31 grants. M. F. G. is fully indebted to Prof. F. Fernández-Martín for general discussions. The support by Secretaria de Educación, Ciencia, Tecnología e Innovación of CDMX (SECTEI, México. U. Caudillo-Flores) is also acknowledged.-

References

1. A. Kubacka, M. Fernández-García and G. Colón, Chem. Rev., 2012, 112, 1555–1614.
2. J. C. Colmenares and R. Luque, Chem. Soc. Rev., 2014, 43, 765–778.
3. L. Jing, W. Zhou, G. Tian and H. Fu, Chem. Soc. Rev., 2013, 42, 9509–9549.
4. X. Li, J. Yu, J. Low, Y. Fang, J. Xiao and X. Chen, J. Mater. Chem. A, 2015, 3, 2485–2534.
5. L. Yuan, N. Zhang, Y.-J. Xu and J. C. Colmenares, in Heterogeneous Photocatalysis: From Fundamentals to Green Applications, ed. J. C. Colmenares and Y.-J. Xu, Springer Berlin Heidelberg, Berlin, Heidelberg, 2016, pp. 249–282.
6. A. H. Mamaghani, F. Haghighat and C.-S. Lee, Chemosphere, 2019, 219, 804–825.
7. O. d'Hennezel, P. Pichat and D. F. Ollis, J. Photochem. Photobiol., A, 1998, 118, 197–204.
8. A. Kubacka, M. Fernández-García and G. Colón, J. Catal., 2008, 254, 272–284.
9. J. Qu, D. Chen, N. Li, Q. Xu, H. Li, J. He and J. Lu, Appl. Catal., B, 2019, 256, 117877.
10. A. Fuerte, M. D. Hernández-Alonso, A. J. Maira, A. Martinez-Arias, M. Fernandez-Garcia, J. C. Conesa and J. Soria, Chem. Commun., 2001, 2718–2719.
11. J. H. Pan and W. I. Lee, Chem. Mater., 2006, 18, 847–853.
12. K. K. Akurati, A. Vital, J.-P. Dellemann, K. Michalow, T. Graule, D. Ferri and A. Baiker, Appl. Catal., B, 2008, 79, 53–62.
13. M. J. Muñoz-Batista, A. Kubacka, R. Rachwalik, B. Bachiller-Baeza and M. Fernández-García, J. Catal., 2014, 309, 428–438.
14. A. K. L. Sajjad, S. Shamaila, B. Tian, F. Chen and J. Zhang, Appl. Catal., B, 2009, 91, 397–405.
15. L. Zhang, M. Qin, W. Yu, Q. Zhang, H. Xie, Z. Sun, Q. Shao, X. Guo, L. Hao and Y. Zheng, J. Electrochem. Soc., 2017, 164, H1086.
16. A. Bojinova, N. Kaneva, K. Papazova, A. Eliyas, E. Stoyanova-Eliyas and D. Dimitrov, React. Kinet., Mech. Catal., 2017, 120, 821–832.
17. U. Caudillo-Flores, M. J. Muñoz-Batista, A. B. Hungría, M. L. Haro, M. Fernández-García and A. Kubacka, Appl. Catal., B, 2019, 245, 49–61.
18. G. E. P. Box and D. W. Behnken, Technometrics, 1960, 2, 455–475.
19. S. E. Braslavsky, A. M. Braun, A. E. Cassano, A. V. Emeline, M. I. Litter, L. Palmisano, V. N. Parmon and N. Serpone, Pure Appl. Chem., 2011, 83, 931–1014.
20. M. J. Muñoz-Batista, M. M. Ballari, A. Kubacka, O. M. Alfano and M. Fernández-García, Chem. Soc. Rev., 2019, 48, 637–682.
21. M. R. Karimi Estahbanati, M. Feilizadeh and M. C. Iliuta, AIChE J., 2019, 65, e16724.
22. F. Salvadores, O. M. Alfano and M. M. Ballari, Appl. Catal., B, 2020, 268, 118694.
23. M. J. Muñoz-Batista, A. Kubacka, M. N. Gómez-Cerezo, D. Tudela and M. Fernández-García, Appl. Catal., B, 2013, 140–141, 626–635.
24. M. J. Muñoz-Batista, M. N. Gómez-Cerezo, A. Kubacka, D. Tudela and M. Fernández-García, ACS Catal., 2014, 4, 63–72.
25. U. Caudillo-Flores, M. J. Muñoz-Batista, R. Luque, M. Fernández-García and A. Kubacka, Chem. Eng. J., 2019, 378, 122228.
26. A. Kubacka, G. Colón and M. Fernández-García, Catal. Today, 2009, 143, 286–292.
27. G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22–31.
28. P. Kubelka, J. Opt. Soc. Am., 1948, 38, 448–457.
29. M. J. Muñoz-Batista, A. Kubacka, A. B. Hungría and M. Fernández-García, J. Catal., 2015, 330, 154–166.
30. G. E. Imoberdorf, A. E. Cassano, H. A. Irazoqui and O. M. Alfano, Chem. Eng. Sci., 2007, 62, 1138–1154.
31. G. E. Imoberdorf, H. A. Irazoqui, A. E. Cassano and O. M. Alfano, Ind. Eng. Chem. Res., 2005, 44, 6075–6085.
32. M. J. Muñoz-Batista, A. Kubacka and M. Fernández-García, ACS Catal., 2014, 4, 4277–4288.
33. N. Masunga, G. S. Tito and R. Meijboom, Appl. Catal., A, 2018, 552, 154–167.
34. D. W. Bahnemann, M. Hilgendorff and R. Memming, J. Phys. Chem. B, 1997, 101, 4265–4275.
35. W. A. Thompson, E. S. Fernandez and M. M. Maroto-Valer, ACS Sustainable Chem. Eng., 2020, 8, 4677–4692.
36. Z. Ugray, L. Lasdon, J. Plummer, F. Glover, J. Kelly and R. Martí, INFORMS J. Comput., 2007, 19, 328–340.
37. J. Antony, Design of Experiments for Engineers and Scientists, Elsevier Science, Amsterdam, 2nd edn, 2014.
38. M. A. Grela, M. E. J. Coronel and A. J. Colussi, J. Phys. Chem., 1996, 100, 16940–16946.
39. E. G. Janzen, N. Sankuratri and Y. Kotake, J. Magn. Reson., Ser. B, 1996, 111, 254–261.
40. A. Kubacka, M. J. Munoz-Batista, M. Ferrer and M. Fernández-García, Appl. Catal., B, 2013, 140, 680–690.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0re00211a

---