Advanced temperature sensing with Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors through upconversion luminescence
Ikhlas
Kachou
 a,
Kamel
Saidi
a,
Kamel
Saidi
 a,
Utku
Ekim
a,
Utku
Ekim
 b,
Mohamed
Dammak
b,
Mohamed
Dammak
 *a,
Miray
Çelikbilek Ersundu
*a,
Miray
Çelikbilek Ersundu
 b and
Ali Erçin
Ersundu
b and
Ali Erçin
Ersundu
 *b
*b
aLaboratoire de Physique Appliquée, Groupe de Physique des Matériaux Luminescents, Faculté des Sciences de Sfax, Département de Physique, Université de Sfax, BP 1171, Sfax, Tunisia. E-mail: madidammak@yahoo.fr
bYildiz Technical University, Faculty of Chemical and Metallurgical Engineering, Department of Metallurgical and Materials Engineering, Glass Research and Development Laboratory, Istanbul, 34220, Turkiye. E-mail: ersundu@yildiz.edu.tr
First published on 8th January 2024
Abstract
Optical thermometry is a non-contact temperature sensing technique with widespread applications. It offers precise measurements without physical contact, making it ideal for situations where contact-based methods are impractical. However, improving the accuracy of optical thermometry remains an ongoing challenge. Herein, enhancing the thermometric properties of luminescent thermometers through novel materials or strategies is crucial for developing more precise sensors. Hence, the present study focuses on the application of four-mode luminescence thermometric techniques in sol–gel synthesized Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors for optical temperature sensing in the temperature range of 298–573 K. The upconversion (UC) luminescence is achieved under excitations of 980 nm or 1550 nm, resulting in bright yellow-green emission in the visible spectral range. Temperature sensing is realized by exploiting the UC emissions of 4S3/2, 2H11/2 and 4F7/2 bands, which represent intensity ratios of thermally coupled levels (TCELs) and non-thermally coupled levels (NTCELs) of Er3+/Yb3+, along with the emission lifetimes at 4S3/2. The relative sensitivity (Sr) values for TCELs exhibit a gradual decrease with rising temperature, reaching a maximum of 1.1% K−1 for 980 nm excitation and 0.86% K−1 for 1550 nm excitation at 298 K. Conversely, for NTCELs, the highest Sr value observed is 0.9% K−1 at 298 K for 1550 nm excitation. Moreover, the emission lifetimes at 4S3/2 yield notably high Sr values of up to 5.0% μs K−1 (at 425 K). Furthermore, the studied phosphors have a sub-degree thermal resolution, making them excellent materials for accurate temperature sensing. Overall, this study provides a promising new direction for the development of more precise and reliable optical thermometry techniques, which could have important implications for a range of scientific and industrial optical temperature sensing applications.
1. Introduction
Nanoscale temperature measurement is crucial for applications where precise detection of the local temperature changes is required especially related to biochemical processes like living cells and nanomedicine, microelectronics, optics, microfluidics, and chemical reactions.1–6 Herein, optical thermometry has emerged as a promising approach due to its exclusive advantages such as contactless operation, rapid response time, excellent spatial resolution, and wide detection range. Optical temperature sensing is a technique that utilizes temperature-responsive optical parameters such as emission intensity, luminescence peak position, spectral bandwidth, fluorescence decay lifetime (FL), and fluorescence intensity ratio (FIR) for the non-invasive and rapid detection of local temperature values in inspected systems. The fluorescence intensity ratio (FIR) technique, which relies on the temperature-dependent alteration of luminescence intensities of two closely spaced thermally coupled levels (TCELs) or non-thermally coupled levels (NTCELs) of activators, along with fluorescence lifetime (FL) technology, which is based on the temperature-dependent lifetimes, have been recognized as the most viable methods for temperature sensing due to their insensitivity to external interference and measurement conditions.7 Therefore, the technique which exploits the change of the spectroscopic properties of the phosphor materials for remote temperature determination, called luminescent thermometry, is a subject of intensive studies in recent years.8–11In order to enhance the luminescence properties of phosphors, they are usually coupled with lanthanide ions since lanthanide ions are known to exhibit efficient and superior spectroscopic properties due to their diverse energy transfer mechanisms, higher luminescence intensities and efficiencies. Therefore, lanthanide-doped phosphor nanoparticles seem to be the best candidates as luminescence nanothermometers, because they can benefit from temperature-dependent emission lifetimes, as well as band ratios of alike TCELs and NTCELs.12–23
Single-mode detection is the foundation of many modern luminescent thermometers. However, they are always susceptible to the error caused by the temperature's insensitivity in a certain range. To overcome this limitation, dual- or three-mode optical thermometers have been developed continuously in recent years since the combination of multiple optical thermometer modes can leverage their individual advantages to attain greater accuracy and expanded temperature measurement capabilities.24–34 There are four main categories for dual- or three-mode optical thermometers. The first category is the combination of TCELs and NTCELs, known as the FIR technique.27,29–31 Another category involves the integration of FL with FIR, specifically from TCELs.26 A third category involves coupling FL with FIR from NTCELs,27,35,36 while the last category combines FL with FIR from both TCELs and NTCELs.32,34
The ability to convert light from the near-infrared (NIR) to the visible spectral region, resulting from the upconversion (UC) energy transfer mechanism, opens new possibilities to overcome current limitations in solar energy,37,38 autofluorescence-free biosensing and -imaging,39–41 nanoscale electric field sensing,42 and temperature sensing.22 It is quite common to use a 980 nm laser diode as the excitation source and, the UC luminescence usually takes place in different lanthanide ions co-doped systems, including Yb3+/Er3+, Yb3+/Ho3+, or Yb3+/Tm3+, where Yb3+ acts as a sensitizer and transfers the absorbed excitation energy to emitting ions, i.e. Er3+, Ho3+, or Tm3+.12,43–48 However, excitation by 980 nm laser source is not suitable for biological applications. It tends to arouse overheating and lower the penetration depth due to the strong absorption of water molecules in human tissue.49 Therefore, excitation and/or emission wavelengths falling in the so-called biological windows (1st 650–950 nm, 2nd 1000–1400 nm, 3rd 1500–1800 nm) have been developed.50–53 Herein, 1550 nm laser excitation has obtained considerable attention due to its wide applications in optical communication and solar cells; meanwhile, it is also an effective excitation source to investigate the UC luminescence properties of some lanthanide-doped materials.54–56 Er3+ ions are in particular the material of choice for UC energy transfer mechanism with 1550 nm excitation; however, one limitation of Er3+ ions is their relatively low absorption cross-section and brightness.57–60
The development of a multimode temperature sensor relies heavily on the use of an appropriate host material, as the host has a significant impact on the UC emission efficiency. Particularly, a host with lower phonon energy can improve the UC efficiency by inhibiting the multi-phonon relaxation. In order to limit the undesired multi-phonon relaxation processes, the UC materials are usually doped in inorganic matrices having low phonon energy, such as fluorides, oxides, vanadates, phosphates, and borates.10,43,44,61–64 These matrices can be utilized to make extremely effective phosphors that have a strong photoluminescence signal because they are thermally stable and have low phonon energies.65 Herein, Er3+ and Yb3+ co-doped Ba2GdV3O11 holds significant importance for thermometry applications. Ba2GdV3O11 is widely acknowledged as a favorable host material due to its capacity for enduring high-temperature processing, versatility for co-doping with various lanthanide ions, facile synthesis under elevated temperatures, and its characteristic self-activated luminescence. This luminescence stems from a broad visible emission band resulting from electronic charge transfer from the oxygen (2p orbital) to the V5+ ion. Notably, Ba2GdV3O11 has been extensively investigated for its doping versatility with several lanthanide ions, including Er3+ and Yb3+.66–70 In particular, Er3+ and Yb3+ ions are strategically employed as the activator and sensitizer, respectively, in UC materials due to their abundant ladder-like energy levels and robust absorption cross-section in the near-infrared (NIR) range. This co-doped system presents a promising avenue for precise and efficient thermometry applications, leveraging the unique properties of Er3+ and Yb3+ ions in the Ba2GdV3O11 host matrix. However, to the best of our knowledge, no prior work has been reported on the thermometric properties and UC luminescence characteristics of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors.
The development of a novel four-mode thermometer with reliable and outstanding modes has been a significant challenge in the field. To address this need, in this work, we present a pioneering investigation of four-mode UC luminescence for high precision optical temperature sensing in Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors. The characteristic luminescence properties, chromaticity diagrams and thermometric parameters are investigated under 980 nm and 1550 nm excitations. The analysis of UC mechanism processes is followed by an investigation of optical temperature sensing characteristics based on TCEL and NTCELs, as well as kinetic-based luminescence. A bright yellow-green UC luminescence is used for multimode optical temperature sensing in the temperature range of 298–573 K in the visible spectral range and ultimately advanced luminescence thermometric techniques are constructed.
2. Experimental studies
2.1 Synthesis of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors
Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors are synthesized using the sol–gel method with citric acid as the complexing agent. All chemicals employed in the synthesis, including barium nitrate [Ba(NO3)2 (99.0%)], gadolinium nitrate hexahydrate [Gd(NO3)3·6H2O (99.9%)], ammonium metavanadate [NH4VO3 (99.96%)], erbium nitrate pentahydrate [Er(NO3)3·5H2O (99.9%)], ytterbium nitrate pentahydrate [Yb(NO3)3·5H2O (99.9%)], and citric acid [C6H8O7 (99.0%)], are purchased from Sigma-Aldrich and utilized without further purification.The synthesis procedure initiates with the magnetic stirring of all precursors in an Erlenmeyer flask at 70 °C. Subsequently, citric acid is added, inducing a color change in the solution from green to blue. The solution is subjected to swirling and heating at 80 °C until it undergoes hydrolysis, transitioning into a sol and then a gel. The resulting xerogel is annealed at 400 °C for 3 hours, yielding black-colored flakes. Finally, the gel undergoes calcination at 700 °C for approximately 4 hours to achieve pure-phase crystals. Using this method, Ba2GdV3O11 phosphors are doped with Yb3+ (10 mol%) and Er3+ (2 mol%). These specific concentrations are strategically chosen to prevent UC luminescence extinction, informed by our previous experience, and supported by both theoretical knowledge and empirical evidence. Notably, the literature commonly adopts a higher quantity of sensitizer (Yb3+) along with lower concentrations of emitters (Er3+) in UC systems, as it has proven effective in generating a robust emission.69,71 The synthesis details of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors are illustrated in Fig. 1.
 | ||
| Fig. 1 Schematic illustration of applied synthesis procedure of 2 mol% Er3+/10 mol% Yb3+ co-doped Ba2GdV3O11 phosphors. | ||
2.2 Experimental methods for the characterization of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors
The X-ray diffraction (XRD) measurements are performed with a Bruker AXS D8 Advance diffractometer in a scanning mode with Cu Kα radiation (λ = 1.5406 Å) at a step size of 0.015° from 20° to 80°. The XRD peak positions and intensities of crystallized phases are compared with the JCPDS card files. The morphology of the materials is examined using a Thermo Scientifıc Apreo 2 S LoVac field emission scanning electron microscopy (FE-SEM). A Horiba Labram HR 800 monochromator is employed to conduct Raman spectroscopy studies. The spectrometer features a wave number resolution exceeding 3 cm−1 and is outfitted with an Olympus BX41 microscope, a 633 nm He–Ne laser emitting with a power output of less than 5 mW, and a CDD detector. The laser beam is precisely focused on the sample through a 50× microscope objective. Diffuse reflectance spectrum is collected by the use of a PerkinElmer Lambda 365 UV–Vis spectrometer.The steady-state and time-resolved photoluminescence (PL) properties of the samples are investigated using an Edinburgh Instruments FS5 spectrofluorometer. PL spectra are recorded using laser diodes emitting at 980 and 1550 nm with a signal to noise ratio of water Raman signal greater than 6000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 0.5 nm spectral resolution using an excitation power of 0.5 W. The temperature dependence of the PL properties is studied using a Pike Technologies heated solid transmission attachment fitted in the spectrofluorometer to perform measurements over a temperature range of 298–573 K. To avoid biased temperature readings and ensure accurate measurements, a calibration curve relating the optical signal (e.g., fluorescence intensity or lifetime) to temperature is initially established, with the lowest laser power permitting reliable signal detection being employed. A stable and controlled measurement environment is maintained, and baseline measurements are taken without laser excitation to determine the intrinsic temperature of the sample under experimental conditions. During temperature measurements, the laser power and sample temperature are continuously monitored, and the calibration curve is periodically verified by measuring known temperatures using an independent reference thermometer to ensure measurement accuracy and reliability. In the data analysis, the laser heating effect is considered and corrected, if necessary, by subtracting the baseline temperature from the measured temperature to obtain the true temperature change induced by the laser. Subsequently, the temperature measurement protocol is validated under various conditions and sample types to ensure its applicability and accuracy across different scenarios. To obtain time-resolved PL spectra, a 980 nm pulsed laser operating at a frequency of 1 kHz is used to monitor the characteristic wavelength of Er3+ at 555 nm over time.
1 and 0.5 nm spectral resolution using an excitation power of 0.5 W. The temperature dependence of the PL properties is studied using a Pike Technologies heated solid transmission attachment fitted in the spectrofluorometer to perform measurements over a temperature range of 298–573 K. To avoid biased temperature readings and ensure accurate measurements, a calibration curve relating the optical signal (e.g., fluorescence intensity or lifetime) to temperature is initially established, with the lowest laser power permitting reliable signal detection being employed. A stable and controlled measurement environment is maintained, and baseline measurements are taken without laser excitation to determine the intrinsic temperature of the sample under experimental conditions. During temperature measurements, the laser power and sample temperature are continuously monitored, and the calibration curve is periodically verified by measuring known temperatures using an independent reference thermometer to ensure measurement accuracy and reliability. In the data analysis, the laser heating effect is considered and corrected, if necessary, by subtracting the baseline temperature from the measured temperature to obtain the true temperature change induced by the laser. Subsequently, the temperature measurement protocol is validated under various conditions and sample types to ensure its applicability and accuracy across different scenarios. To obtain time-resolved PL spectra, a 980 nm pulsed laser operating at a frequency of 1 kHz is used to monitor the characteristic wavelength of Er3+ at 555 nm over time.
3. Results and discussion
3.1 Physical, thermal, and structural properties
Powder XRD technique is used to determine the crystal structure of synthesized 2 mol% Er3+/10 mol% Yb3+ co-doped Ba2GdV3O11 phosphors. The diffraction peak patterns correspond to the JCPDS card number 45-0097 (see Fig. 2), indicating that the insertion of Er3+/Yb3+ does not affect the phase pattern.67 The Rietveld refinement procedure, performed using the FullProf_Suite program, shows that the synthesized phosphors crystallized into a monoclinic crystal structure with P21/c space group symmetry (14).70 The unit cell parameters are calculated to be a = 12.374692 Å, b = 7.731662 Å, c = 11.178051 Å, β = 103.56582°, and V = 1029.88 Å3.Fig. 3 shows the representative FE-SEM images revealing surface morphologies, and grain size distribution of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors. The images clearly demonstrate the successful synthesis of Er3+/Yb3+ co-doped Ba2GdV3O11 particles at the micro scale. However, the synthesis process employing the sol–gel method leads to particle agglomeration, resulting in tightly packed, irregularly shaped particles due to their high surface energy. Usually, the tightly packed particles contribute to a decrease in scattering of light, producing to excellent luminous intensity.72 As a result, the resulting 2 mol% Er3+/10 mol% Yb3+ co-doped Ba2GdV3O11 phosphors is a well-crystallized, micro-sized material with strong and vibrant luminescence properties.
 | ||
| Fig. 3 FE-SEM images of 2 mol% Er3+/10 mol% Yb3+ co-doped Ba2GdV3O11 phosphors with different magnifications, (a) 50k×, and (b) 100k×. | ||
The room temperature Raman spectrum of the Er3+/Yb3+ co-doped Ba2GdV3O11 phosphor is displayed in Fig. 4. The observed Raman bands can be attributed to various vibrational modes, including asymmetric stretching (νas) and symmetric stretching (νs) modes of O–V–O, νs and νas modes of V–O–V vibrations, as well as lattice (L′) vibrations.73,74 The Raman bands observed between 880 to 953 cm−1 are linked to the νs vibrations of vanadium groups, while the vibrations associated with the νas modes of vanadium groups are found in the region of 800 to 878 cm−1. In the range of 410 to 520 cm−1, the observed Raman modes are attributed to both symmetric stretching and asymmetric stretching vibrations of the V–O–V bridge. Terminal bending vibrations are discerned within the region of 318 to 400 cm−1, while the bending vibrations of V–O–V bridges are noted in the range of 206 to 265 cm−1.
Fig. 5(a) depicts the diffuse reflectance spectrum of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors in the UV-Vis-NIR spectral range (200–1100 nm). The O2−–V5+ entity is responsible for the high broad bands peaking at 280 and 315 nm. The absorption peaks at 480, 525, and 655 nm are related to Er3+ transitions from 4I15/2 to 4F7/2, 2H11/2, and 4F9/2, respectively. Additional absorption peaks appear in the 900 nm–1050 nm range which correspond to 4I15/2 → 4I11/2, 2F7/2 → 2F5/2 transitions of Er3+ and Yb3+ ions, respectively. Employing diffuse reflectance spectrum, the band gap (Eg) of Ba2GdV3O11 phosphors is measured according to the Kubelka–Munk (KM) theory.75–77 The relation between the diffuse reflectance of the sample R, absorption coefficient (k), scattering coefficient (S), and absorption coefficient of the material (α) are related by the KM remission function F(R):67
 | (1) |
 | ||
| Fig. 5 (a) Diffuse reflectance spectra for Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors, (b) the plot of [F(R∞)hν]2versus hν. | ||
The well-known Tauc equation relates the Eg and absorption coefficient α of a direct band gap semiconductor in the parabolic band structure:
| ((F(R)hν)n) = B(hν − Eg) | (2) |
In this equation, hν represents the photon energy, B is a proportional constant, and Eg is the band gap energy. The nature of optical transitions in a material is determined by a constant (n), which varies depending on the type of transition. For instance, an indirect allowed transition corresponds to n = 2, an indirect forbidden transition corresponds to n = 3, a direct allowed transition corresponds to n = 1/2, and a direct forbidden transition corresponds to n = 3/2. Direct allowed transition is characterized by nonlinear and linear parts in the plot of [F(R∞) hν]2versus hν. The fundamental absorption is characterized by the linear portion, whereas the residual absorption involving impurity states is represented by the nonlinear portion. Furthermore, the band gap of 3.06 eV for Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors is determined by extrapolating the line for [F(R∞)hν]2 = 0, as shown in Fig. 5(b).
3.2 Power-dependent luminescence properties, and UC mechanism
To gain a better understanding of the UC process, laser pump power-dependent UC spectra of Er3+/Yb3+ co-doped Ba2GdV3O11 nanophosphors are recorded. As shown in Fig. 6(a) and (b), the emission intensity of Er3+ increases with increasing pump power. The relationship between laser pump power (P) and UC emission intensity (I) is commonly expressed using the following formula:65,78| I = K × Pn | (3) |
To calculate the quantity of infrared photons, the peaks at 555 nm and 665 nm are selected due to their high intensity and variation with laser pump power. It can be observed that the plots of log intensity versus log laser power show a clear linear relationship in the experimental data. The slopes of the 555 nm and 665 nm emission peaks are found to be 2.03 and 1.91, respectively under 980 nm excitation, indicating that the UC processes involve in the phosphors are two-photon processes.79,80 Furthermore, under 1550 nm excitation, the green and red emissions can be a three-photon process (n = 3.03 and n = 3.05, respectively) as determined by the double-logarithmic fitting of UC luminescence intensity to excitation power. The slight differences in the n values may be attributed to the calculation error of the integrated intensity and the fitting process.
Fig. 7 shows the energy levels and UC mechanism of Yb3+ and Er3+ in the Ba2GdV3O11 phosphors under 980 nm and 1550 nm excitation. Upon excitation by a 980 nm laser, Yb3+ ions are excited from the 2F7/2 state to the 2F5/2 state and serve as sensitizers, transferring the absorbed excitation energy to nearby Er3+ ions. The Er3+ ions are then excited from their initial 4I15/2 state to the 4I11/2 and 4F7/2 states, followed by non-radiative relaxation to the 2H11/2, 4S3/2, and 4F9/2 states. The excess energy is released through the emission of green light at 525 nm and 555 nm wavelengths. As, Er3+ions undergo non-radiative de-excitation from the 4I11/2 to 4I13/2 state, an excitation photon from Yb3+ ion transfers its energy, elevating the population from the 4I13/2 to the 4F9/2 level. Subsequently, a radiative transition from the 4F9/2 to the 4I15/2 state results in the emission of a 665 nm photon, as illustrated in Fig. 7(a).81
 | ||
| Fig. 7 Energy level diagrams of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors upon (a) 980 nm, (b) and (c) 1550 nm excitations. | ||
Fig. 7(b) and (c) present the UC luminescence of Er3+ ions in Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors upon 1550 nm excitation obtained via energy transfer processes. Four possible basic population mechanisms are involved in these UC luminescence processes, including energy transfer UC (ETU or ET), ground state absorption (GSA), excited state absorption (ESA) and back energy transfer (BET) mechanisms.82
The UC luminescence of Er3+ under 1550 nm excitation shown in Fig. 7(b and c) can be obtained by both direct light absorption of Er3+ ions or energy transfer (ET) from Er3+ ions to Yb3+ ions. By considering only Er3+ ions, the population of 2H11/2 and 4S3/2 levels upon excitation can be achieved by successive absorbing three 1550 nm photons via one GSA and two ESA or ET processes, and then yielding the green UC emissions.47,83
The proposed UC mechanisms for the absorption of 1550 nm photons exclusively involve Er3+ ions, as depicted in Fig. 7(b). Initially, Er3+ ions absorb the first 1550 nm photons, raising them to the 4I13/2 level through ground-state absorption (GSA). Subsequently, the absorption of a second photon propels the excited ions to the higher 4I9/2 energy level. Additionally, the 4I9/2 excited level can be populated through a cross-relaxation (CR) process. The third photon is absorbed from the 4I9/2 energy level, promoting the 4F7/2 excited level, which then undergoes non-radiative decay to the lower 2H11/2 and 4S3/2 levels. These latter excited levels contribute to the green emissions from Er3+. Another UC mechanism associated with the absorption of 1550 nm photon involves non-radiative depopulation from the 4I9/2 excited level to the 4I11/2 level, followed by the absorption of a third photon to the 4F9/2 level. From this level, Er3+ ions radiatively decay to the 4I15/2 ground level, emitting red radiation.83–87
By considering Yb3+ as a sensitizer ion (see Fig. 7(c)), the UC luminescence process of Er3+ can occur through an energy transfer (ET) process, since Yb3+ cannot directly absorb the energy of 1550 nm photons. The ET process from Er3+ to Yb3+ ions is an important mechanism for the UC luminescence of Er3+ under 1550 nm excitation.47,88,89 Er3+ initially absorbs two 1550 nm photons, populating the 4I9/2 level, and achieves the population of 4I13/2 level via a subsequent non-radiative relaxation process. The energy is then transferred from Er3+ to an adjacent Yb3+ ion through the BET (back energy transfer) process, exciting Yb3+ to the 2F5/2 level. The excited Yb3+ ion transfers energy to a neighboring Er3+ ion, achieving population of 2H11/2 and 4S3/2 levels of Er3+via ET2 process, and population of the 4F9/2 level via the ET1 process. Finally, green and the red UC emissions can be achieved. The green UC emissions involve the absorption of a 1550 nm photon by an Er3+ ion, which excites it to the 4I11/2 level from the ground state with GSA. Then, the BET process occurs and transfers the excess energy to the 2F5/2 level of a neighboring Yb3+ ion through ET1. From there, the energy is again transferred to the 2H11/2 and 4S3/2 states of an adjacent Er3+ ion through ET2, and the excited ions relax to ground state by emitting green light at 525 and 555 nm wavelengths, respectively. The green UC emission requires four 1550 nm photons when Yb3+ acts as the sensitizer for Er3+. On the other hand, the red UC emission involves a similar GSA and BET process, followed by the transfer of excess energy to an Er3+ ion through only one ET step from 4F9/2 to the ground state.86
3.3 Temperature-dependent UC emission, and optical temperature-sensing behavior
Temperature-responsive UC spectra are recorded upon excitation by a 980 nm and 1550 nm laser to assess the suitability of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors for temperature sensing applications, and the excitation power is held at 0.5 W through the measurements in order to avoid the compound heating under the effect of excitation. As shown in Fig. 8(a), two different green emissions peaks are investigated to illustrate the variation tendency of the intensity ratio as the temperature rises from 298 to 573 K under 980 nm excitation. Temperature dependent PL intensity of the 4S3/2 → 4I15/2 (555 nm) transition decreases gradually with increasing temperature. However, the intensity of the 2H11/2→ 4I15/2 (525 nm) transition also decreases with temperature, but to a lesser extent than the 555 nm transition. Therefore, the 555 nm transition is more affected by temperature compared to the 525 nm transition. The red emission obtained upon 980 nm excitation exhibits very low intensity. Notably, the intensity of the red emission at 665 nm shows no significant correlation with temperature (refer to the inset of Fig. 8(a)), which makes it a suitable reference for optical temperature measurement. Fig. 8(b) shows the CIE chromaticity diagram of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors upon 980 nm laser excitation, indicating a shift in PL emission color from green to yellow/orange region with increasing temperature. Except for one instance where the color coordinates of the 573 K PL emission are detected beyond those of the 523 K PL emission, PL results show a consistent decrease in the color coordinate values of the emissions with increasing temperature. However, the rates of decrease are different for the two emissions, i.e., 525 nm and 555 nm, which may contribute to the observed exception. Notably, the combined output of the two emissions could influence this result, particularly in the case of the 573 K PL emission, where the difference is more pronounced. Fig. 8(c) shows the temperature-dependent UC luminescence spectra from 298 to 573 K under 1550 nm excitation. The green emission intensities of the 4S3/2 → 4I15/2 (555 nm) and 2H11/2 → 4I15/2 (525 nm) transitions decrease with increasing temperature. Similar to 980 nm excitation, the intensity of the 555 nm emission decreases more significantly than the 525 nm transition. Moreover, the red emission at the transition of 4F9/2 → 4I15/2 (665 nm) is discernable, and it displays a decrease in intensity as the temperature rises. The corresponding CIE chromaticity diagram of the Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors under 1550 nm laser excitation is presented in Fig. 8(d). As shown in the CIE chromaticity diagram, PL emission color shifts from greenish to the pure green region as the temperature increases.To evaluate the thermochromic performance of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors under both 980 nm and 1550 nm excitations, thermo-induced chromaticity shift (ΔE) values are computed as previously reported elsewhere.7 The resulting ΔE value is 0.052 for 980 nm excitation and 0.42 for 1550 nm excitation. Despite the seemingly proximity of these chromaticity shift values, the shift in PL emission color from green to yellow/orange under 980 nm excitation, in contrast to the shift from greenish to pure green under 1550 nm excitation, renders the former much more discernible to the naked eye or through digital imaging. This heightened visibility under 980 nm excitation underscores the potential of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors, not only in luminescent thermometry, but also as effective safety indicators in high-temperature environments.
Er3+ (2H11/2, 4S3/2) TCELs can be used for optical thermometry. According to previous reports, the FIR for the thermally coupled 2H11/2 and 4S3/2 levels follow the Boltzmann distribution and is defined as follows:
 | (4) |
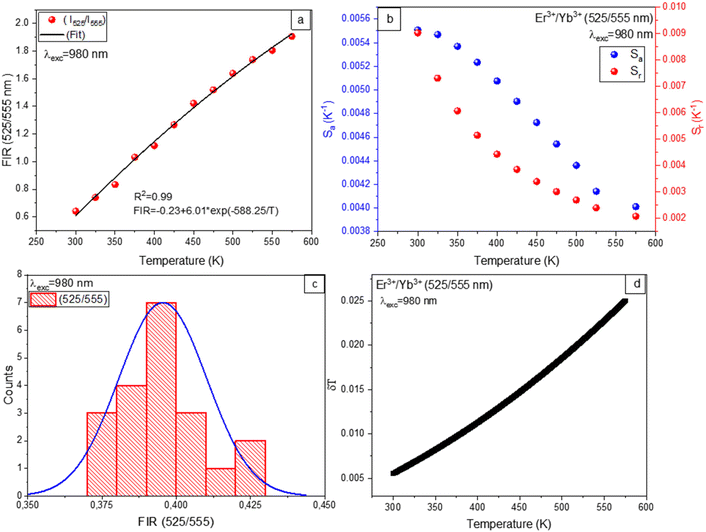
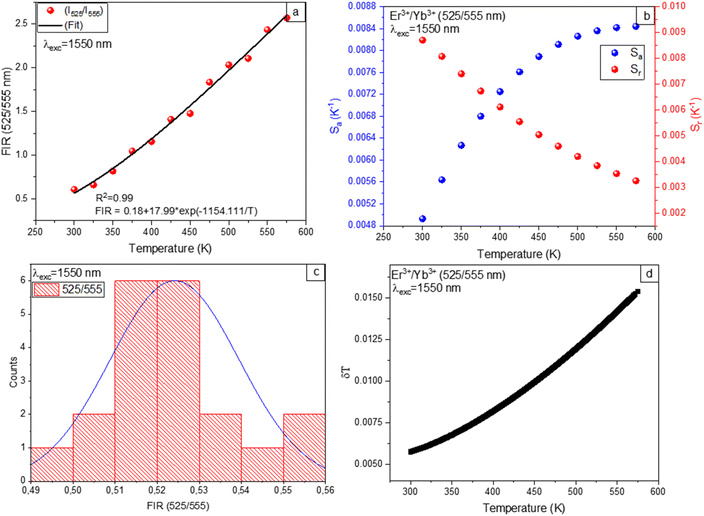
Temperature dependence of the FIR is calculated by PL with variations in temperature for the 525/555 nm bands of the Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors under 980 nm and 1550 nm excitation. The fitting results of temperature dependence of the FIR are depicted in Fig. 9(a) and 10(a), revealing correlation R2 values greater than 99%. The experimental data can be well fitting of FIR = 0.05 + 15.93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1150.52/T) for 980 nm excitation and FIR = 17.99
exp(−1150.52/T) for 980 nm excitation and FIR = 17.99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1154.11.05/T) for 1550 nm excitation. The corresponding energy gap ΔE of the thermally coupled energy levels (2H11/2 and 4S3/2) are calculated to be 799.61 cm−1 and 802.03 cm−1 for 980 nm and 1550 nm excitation, respectively. The results show that, the excitation almost has no impact on thermally coupled energy levels.
exp(−1154.11.05/T) for 1550 nm excitation. The corresponding energy gap ΔE of the thermally coupled energy levels (2H11/2 and 4S3/2) are calculated to be 799.61 cm−1 and 802.03 cm−1 for 980 nm and 1550 nm excitation, respectively. The results show that, the excitation almost has no impact on thermally coupled energy levels.
In general, monitoring the temperature-dependent sensitivities of resulting compounds is critical for determining their suitability for noninvasive thermometry. Therefore, absolute sensitivity (Sa) and relative sensitivity (Sr) parameters are interesting in order to compare with other sensors. The absolute sensitivity (Sa) and relative sensitivity (Sr) values are given by:
 | (5) |
 | (6) |
As depicted in Fig. 9(b), and 10(b) the trends observed in the calculated Sr values show a gradual decrease with increasing temperature, with a maximum of 1.1% K−1 at 298 K for 980 nm excitation and 0.86% K−1 at 298 K for 1550 nm excitation. On the other hand, the Sa values exhibit an increase for 980 nm and 1550 nm excitation with temperature. The maximum value of Sa is 75 × 10−4 K−1 at 573 K for 980 nm excitation and 84 × 10−4 K−1 at 573 K for 1550 nm excitation.
Furthermore, the temperature uncertainty (temperature resolution) (δT), a crucial indicator of the effectiveness of a thermometer, describes the smallest change in temperature that corresponds to a significant variation in the parameter under consideration. The formula below is used to estimate δT using the following equation:
 | (7) |
As a result, implementing enhanced acquisition methods as well as increasing measurement performance, which includes improving integration time and using the average of subsequent measurements to decrease experimental noise, can represent one option for increasing the resolution limit. To evaluate the limit of detection, 20 measurements are conducted at room temperature under comparable conditions for Er3+/Yb3+ co-doped Ba2GdV3O11.
Thermometric parameter's resolution limit or relative uncertainty (δFIR/FIR) is calculated as the standard deviation of each method's statistical distribution, with values of 0.014, and 0.015 upon 980 nm and 1550 nm excitations, respectively (see Fig. 9(c) and 10(c)). The minimum temperature uncertainties are calculated to be 0.013 K (at 298 K) and 0.017 K (at 298 K) upon 980 nm and 1550 nm excitations, respectively (see Fig. 9(d) and 10(d)). Using eqn (7), the obtained results are less than 0.5 K, suggesting that FIR methods offer great accuracy throughout this whole temperature range.
Since the red emission is prominent even at low power excitation under 1550 nm, it can be utilized for thermometry applications in the case of NTCELs. Additionally, the intensity of the red emission makes it a suitable reference for optical temperature measurement. Therefore, optical thermometric characteristics of Er3+ ions at 2H11/2 and 4F9/2 levels are investigated under 1550 nm excitation (see Fig. 11), where IF and IH refer to the integrated intensities of the transitions from 4F9/2 to 4I15/2 (650–680 nm) and 2H11/2 to 4I15/2 (524–537 nm), respectively. The large energy gaps of NTCELs make it challenging to populate them via thermal excitation. Therefore, traditional FIR is not suitable for NTCEL. In the absence of a well-defined physical model that accurately describes the temperature dependencies of FIR values for NTCELs of Ln3+, an empirical approach becomes crucial for capturing the intricate variations observed in experimental data. The choice of a polynomial function over commonly used physical models, such as exponentials, is grounded in its inherent flexibility and general applicability. Polynomial functions provide a versatile framework capable of accommodating diverse trends and behaviors exhibited by the NTCEL under varying temperatures. This empirical approach prioritizes the accurate representation of experimental data, acknowledging the dynamic and complex nature of the observed phenomena. Moreover, the acceptance of empirical functions in similar fields underscores the appropriateness of this approach in the absence of a precise theoretical framework. The experimental FIR can be well fitted by a polynomial function.91,92
| FIR = A + BT + CT2 + DT3 | (8) |
The sensitivity of a sensor is a crucial parameter to verify its ability to detect temperature changes. The sensitivity of the temperature sensing performance of the synthesized phosphors is evaluated by calculating the absolute sensitivity (Sa) and relative sensitivity (Sr) using the following equations:
 | (9) |
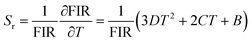 | (10) |
The Sa and Sr values obtained using eqn (9) and (10) are presented in Fig. 10(b). The maximum Sr value is 0.9% K−1 at 298 K, while the maximum Sa value is 143 × 10−4 K−1 at 298 K. Thermometric parameter's resolution limit or relative uncertainty (δFIR/FIR), is calculated as the standard deviation of each method's statistical distribution, with a value of 0.017 (see Fig. 11(c)). Additionally, the minimum temperature uncertainties are calculated to be 0.019 K at 298 K (see Fig. 11(d)). In conclusion, the thermometric sensors perform better in the NTCEL case compared to the TCEL case when excited at 1550 nm.
3.4 Temperature dependent lifetime analysis
In addition to FIR techniques from TCEL and NTCEL, the FL technique is a crucial optical thermometry method. FL-based sensitivity presents advantages over FIR methods, offering a broader temperature range, heightened sensitivity to subtle changes, and greater resilience to experimental variations and quenching effects. The suitability of FL-based techniques for complex, multicomponent systems further enhance their appeal. The time-resolved nature of decay measurements allows for precise temporal analysis, providing valuable insights into dynamic processes and lifetimes.The FL of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors is highly sensitive to changes in temperature. The average lifetime of Er3+ ions in the 4S3/2 state is calculated according to the following equation:93
 | (11) |
The variation of the average lifetime with temperature is fitted according to the following equation:7
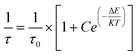 | (12) |
Absolute (Sa) and relative sensitivity (Sr) values of an optical temperature sensor is determined using FL according to the following equations:
 | (13) |
 | (14) |
As illustrated in Fig. 12, an increase in temperature leads to a noticeable decrease in the Er3+ UC lifetime of the 555 nm green emission, likely due to the increased non-radiative transitions and phonon energies. Consequently, the average lifetime Er3+ ions in the 4S3/2 state experiences a decline from 27.69 μs to 15.80 μs with an increase in temperature from 298 to 573 K.
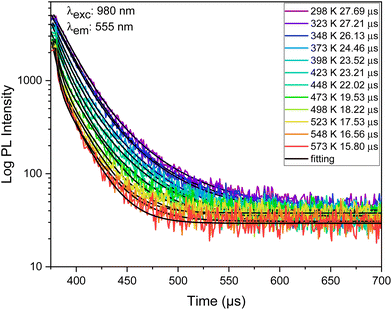 | ||
| Fig. 12 Decay curves of 555 nm (4S3/2 level) emissions of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors at different temperatures (λexc = 980 nm). | ||
Based on 4S3/2 energy levels of Er3+ FL temperature measurement schemes, Sa and Sr are calculated and shown in Fig. 13.
The maximum value of Sr, calculated from the Er3+ (4S3/2) energy level fluorescence in Er3+/Yb3+ co-doped Ba2GdV3O11, is 2.4 × 10−3 K−1 (at 510 K), while the highest value of Sa is 5.0% μs K−1 (at 425 K). The minimum temperature uncertainties are calculated to be 0.3 K (at 573 K).
Table 1 demonstrates the comparison of thermometric parameters of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors with some other previously reported studies including Er3+ or Er3+/Yb3+ doped materials in various hosts and employing different strategies.
| Material | Temperature range | S r-max | S a-max | Method used | Ref. |
|---|---|---|---|---|---|
| Na3Gd(VO4)2:Er3+/Yb3+ | 300–600 K | 0.83% K−1 | 48 × 10−4 K−1 | FIR = IF/IH | 65 |
| YPVO4:Er3+/Yb3+ | 20–440 K | 6.58% K−1 | 40 × 10−4 K−1 | FIR = IH/IS | 93 |
| Na2GdMg2(VO4)3:Yb3+,Er3+ | 303–573 K | 9.76% K−1 | 74.9 × 10−4 K−1 | FIR = IH/IS | 94 |
| La2O3:Er3+,Yb3+,Bi3+ | 300–625 K | — | 71 × 10−4 K−1 | FIR = IH/IS | 95 |
| Y2Ti2O7:Er3+,Yb3+,Li+ | 298–673 K | — | 67 × 10−4 K−1 | FIR = IH/IS | 96 |
| NaY(WO4)2:Yb3+/Er3+ | 293–503K | 1.2% K−1 | 80 × 10−4 K−1 | FIR = IH/IS | 97 |
| BaMoO4:Yb3+/Er3+ | 293–573 K | 0.47% K−1 | 8.3 × 10−4 K−1 | FIR = IF/IH | 98 |
| Na3Gd(PO4)2:Er3+/Yb3+ | 300–440K | 1.45% K−1 | 14 × 10−4 K−1 | FIR = IF/IH | 99 |
| Cs3GdGe3O9:Er3+ | 300–550 K | 0.49% K−1 | 16.34% μs K−1 | PL lifetime 4S3/2 | 7 |
| Ca2MgWO6:Er3+/Yb3+ | 303–575 K | 0.11% K−1 | 12.6% μs K−1 | PL lifetime 4S3/2 | 91 |
| Ba2GdV3O11:Er3+/Yb3+ | 298–573 K | 1.1% K−1 | 75 × 10−4 K−1 | FIR = IH/IS (980 nm) | This work |
| 298–573 K | 0.86% K−1 | 84 × 10−4 K−1 | FIR = IH/IS (1550 nm) | ||
| 298–573 K | 0.9% K−1 | 143 × 10−4 K−1 | FIR = IF/IH (1550 nm) | ||
| — | 5.0% μs K−1 | 2.4 × 10−3 K−1 | PL lifetime 4S3/2 |
As can be clearly seen, compared to previously reported studies, Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors show improved Sr and Sa thermometric values. Therefore, building upon this comparison, our findings reveal that Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors exhibit remarkable UC emission properties and robust multi-mode temperature sensitivity based on FIR (TCEL and NTCEL) and FL. Moreover, the integration of four optical thermometry technologies allows for self-calibration temperature determination, resulting in enhanced accuracy in temperature measurement. These findings suggest that the incorporation of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors into the existing collection of temperature sensors is a valuable expansion.
4. Conclusions
In conclusion, investigation of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors synthesized through a sol–gel method has revealed promising results for optical temperature sensing applications. The phase purity, morphology, and luminescence characteristics are thoroughly evaluated using X-ray diffraction (XRD), scanning electron microscopy (FE-SEM), and photoluminescence spectroscopy (PL) analysis, respectively. Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors exhibit remarkable thermochromic behavior, with the emission color changing from green to yellow/orange (980 nm excitation) and greenish to pure green (1550 nm excitation) with an increase in temperature. This change is due to the distinct temperature-dependent effects of Er3+'s green and red luminescence and is easily discernible to the naked eye. By utilizing the distinct thermo-response of luminescence at 525, 555 and 665 nm, the fluorescence intensity ratio (and 2H11/2/4F9/2) and fluorescence decay lifetime (4S3/2) of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors under 980 nm and 1550 nm excitation are exploited to achieve excellent sensitivities. This enables the realization of a four-mode temperature sensor in a single luminous center (Er3+) within Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors, which is temperature dependent on FIR from 2H11/2/4S3/2 TCEL, FIR from 2H11/2/4F9/2 NTCEL upon the 980 nm and 1550 nm excitations, as well as the fluorescence decay lifetime (4S3/2). The maximal relative sensitivities achieved are 1.1% K−1, 0.86% K−1 for the TCEL upon 980 nm and 1550 nm respectively, and 0.9% K−1% for the NTCEL upon 1550 nm. Additionally, the fluorescence decay lifetime (4S3/2) of Er3+/Yb3+ co-doped Ba2GdV3O11 under 980 nm excitation gives a high relative sensitivity with 5.0% μs K−1 (at 425 K). The obtained results highlight the potential of Er3+/Yb3+ co-doped Ba2GdV3O11 phosphors for applications such as temperature visualization and smart high-temperature alarms. Furthermore, this work serves as a platform for the design and exploration of multi-mode self-reference optical temperature sensors, opening new avenues for future research in this field.Author contributions
Ikhlas Kachou: investigation, writing – original draft. Kamel Saidi: investigation, writing – original draft. Utku Ekim: writing – original draft, investigation, visualization. Mohamed Dammak: conceptualization, validation, investigation, supervision, writing – original draft, writing – review & editing. Miray Çelikbilek Ersundu: writing – original draft, writing – review &editing, visualization, validation, supervision, project administration, funding acquisition. Ali Erçin Ersundu: writing – original draft, writing – review & editing, validation, supervision, project administration, funding acquisition.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by Yildiz Technical University Scientific Research Projects Coordination Unit under project number FBG-2023-5493.References
- I. E. Kolesnikov, D. V. Mamonova, A. A. Kalinichev, M. A. Kurochkin, V. A. Medvedev, E. Y. Kolesnikov, E. Lähderanta and A. A. Manshina, Nanoscale, 2020, 12(10), 5953–5960 RSC
.
- A. Bednarkiewicz, L. Marciniak, L. D. Carlos and D. Jaque, Nanoscale, 2020, 12, 14405–14421 RSC
.
- J. Zhou, S. Wen, J. Liao, C. Clarke, S. A. Tawfik, W. Ren, C. Mi, F. Wang and D. Jin, Nat. Photonics, 2018, 12(3), 154–158 CrossRef CAS
.
- Z. Meng, S. Wu and S. Zhang, J. Mater. Chem. C, 2018, 6(48), 13101–13107 RSC
.
- J. Zhong, D. Chen, Y. Peng, Y. Lu, X. Chen, X. Li and Z. Ji, J. Alloys Compd., 2018, 763, 34–48 CrossRef CAS
.
- H. Huang, J. Chen, Y. Liu, J. Lin, S. Wang, F. Huang and D. Chen, Small, 2020, 16(19), 2000708 CrossRef CAS PubMed
.
- R. Wei, F. Lu, L. Wang, F. Hu, X. Tian and H. Guo, J. Mater. Chem. C, 2022, 10(25), 9492–9498 RSC
.
- M. Suta and A. A. Meijerink, Adv. Theory Simul., 2020, 3(12), 2000176 CrossRef CAS
.
- M. Back, J. Ueda, J. Xu, K. Asami, M. G. Brik and S. Tanabe, Adv. Opt. Mater., 2020, 8(11), 2000124 CrossRef CAS
.
- L. Marciniak and A. Bednarkiewicz, Sens. Actuators, B, 2017, 243, 388–393 CrossRef CAS
.
- L. Marciniak, A. Bednarkiewicz, J. Drabik, K. Trejgis and W. Strek, Phys. Chem. Chem. Phys., 2017, 19(10), 7343–7351 RSC
.
- M. Runowski, P. Woźny, S. Lis, V. Lavín and I. R. Martín, Adv. Mater. Technol., 2020, 5(4), 1901091 CrossRef CAS
.
-
C. D. S. Brites, A. Millán and L. D. Carlos, Lanthanides in Luminescent Thermometry, in Handbook on the Physics and Chemistry of Rare Earths, 2016, Vol. 49, pp. 339–427 Search PubMed
.
- O. A. Savchuk, P. Haro-González, J. J. Carvajal, D. Jaque, J. Massons, M. Aguiló and F. Díaz, Nanoscale, 2014, 6(16), 9727 RSC
.
- E. Carrasco, B. del Rosal, F. Sanz-Rodríguez, A. J. de la Fuente, P. H. Gonzalez, U. Rocha, K. U. Kumar, C. Jacinto, J. G. Solé and D. Jaque, Adv. Funct. Mater., 2015, 25(4), 615–626 CrossRef CAS
.
- Z. Cao, S. Zhou, G. Jiang, Y. Chen, C. Duan and M. Yin, Curr. Appl. Phys., 2014, 14(8), 1067–1071 CrossRef
.
- S. Balabhadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Phys. Chem. C, 2017, 121(25), 13962–13968 CrossRef CAS
.
- K. Trejgis and L. Marciniak, Phys. Chem. Chem. Phys., 2018, 20(14), 9574–9581 RSC
.
- M. A. Hernández-Rodríguez, A. D. Lozano-Gorrín, I. R. Martín, U. R. Rodríguez-Mendoza and V. Lavín, Sens. Actuators, B, 2018, 255, 970–976 CrossRef
.
- M. Runowski, P. Woźny, I. R. Martín, V. Lavín and S. Lis, J. Lumin., 2019, 214, 116571 CrossRef CAS
.
- D. Wawrzynczyk, A. Bednarkiewicz, M. Nyk, W. Strek and M. Samoc, Nanoscale, 2012, 4, 6959 RSC
.
- R. G. Geitenbeek, P. T. Prins, W. Albrecht, A. van Blaaderen, B. M. Weckhuysen and A. Meijerink, J. Phys. Chem. C, 2017, 121(6), 3503–3510 CrossRef CAS PubMed
.
- M. G. Nikolić, Z. Antić, S. Ćulubrk, J. M. Nedeljković and M. D. Dramićanin, Sens. Actuators, B, 2014, 201, 46–50 CrossRef
.
- I. E. Kolesnikov, M. A. Kurochkin, E. V. Golyeva, D. V. Mamonova, A. A. Kalinichev, E. Yu. Kolesnikov and E. Lähderanta, Phys. Chem. Chem. Phys., 2020, 22, 28183–28190 RSC
.
- Z. Cai, S. Kang, X. Huang, X. Song, X. Xiao, J. Qiu and G. Dong, J. Mater. Chem. C, 2018, 6(37), 9932–9940 RSC
.
- D. Chen, Z. Wan, Y. Zhou, X. Zhou, Y. Yu, J. Zhong, M. Ding and Z. Ji, ACS Appl. Mater. Interfaces, 2015, 7(34), 19484–19493 CrossRef CAS PubMed
.
- H. Zhang, Y. Liang, H. Yang, S. Liu, H. Li, Y. Gong, Y. Chen and G. Li, Inorg. Chem., 2020, 59(19), 14337–14346 CrossRef CAS PubMed
.
- J. Xue, Z. Yu, H. Mi Noh, B. R. Lee, B. C. Choi, S. H. Park, J. H. Jeong, P. Du and M. Song, Chem. Eng. J., 2021, 415, 128977 CrossRef CAS
.
- G. Xiang, X. Liu, J. Zhang, Z. Liu, W. Liu, Y. Ma, S. Jiang, X. Tang, X. Zhou, L. Li and Y. Jin, Inorg. Chem., 2019, 58(12), 8245–8252 CrossRef CAS PubMed
.
- H. Xu, J. Yu, Q. Hu, Q. Han and W. Wu, J. Phys. Chem. Lett., 2022, 13(4), 962–968 CrossRef CAS PubMed
.
- H. L. Gong, H. S. Peng, G. A. Ashraf, F. F. Hu, R. F. Wei and R. Guo, Ceram. Int., 2022, 48, 4023–4030 CrossRef CAS
.
- X. Li, Y. Chen, T. Yang, Y. Zhu, Q. Mao, J. Zhong and S. Li, Dalton Trans., 2021, 50, 16223–16232 RSC
.
- D. Chen, W. Xu, S. Yuan, X. Li and J. Zhong, J. Mater. Chem. C, 2017, 5(37), 9619–9628 RSC
.
- Y. Jiang, Y. Tong, S. Chen, W. Zhang, F. Hu, R. Wei and H. A. Guo, Chem. Eng. J., 2021, 413, 127470 CrossRef CAS
.
- Y. Gao, Y. Cheng, T. Hu, Z. Ji, H. Lin, J. Xu and Y. Wang, J. Mater. Chem. C, 2018, 6(41), 11178–11183 RSC
.
- D. Chen, X. Wei, S. Yuan, X. Lia and J. Zhong, J. Mater. Chem. C, 2017, 5, 9619–9628 RSC
.
- A. Shalav, B. S. Richards, T. Trupke, K. W. Krämer and H. U. Güdel, Appl. Phys. Lett., 2005, 86(1), 013505 CrossRef
.
- S. Fischer, J. C. Goldschmidt, P. Löper, G. H. Bauer, R. Brüggemann, K. Krämer, D. Biner, M. Hermle and S. W. Glunz, J. Appl. Phys., 2010, 108(4), 044912 CrossRef
.
- Q. Liu, Y. Sun, T. Yang, W. Feng, C. Li and F. Li, J. Am. Chem. Soc., 2011, 133(43), 17122–17125 CrossRef CAS PubMed
.
- Z. Qiu, J. Shu and D. Tang, Anal. Chem., 2018, 90(20), 12214–12220 CrossRef CAS PubMed
.
- L. Wang and Y. Li, Chem. Commun., 2006, 24, 2557 RSC
.
- C. Würth, P. Manley, R. Voigt, D. Ahiboz, C. Becker and U. Resch-Genger, Nano Lett., 2020, 20(9), 6682–6689 CrossRef PubMed
.
- Q. Liu, Y. Zhang, C. S. Peng, T. Yang, L. M. Joubert and S. Chu, Nat. Photonics, 2018, 12(9), 548–553 CrossRef CAS PubMed
.
- A. Nadort, J. Zhao and E. M. Goldys, Nanoscale, 2016, 8(27), 13099–13130 RSC
.
- D. J. Garfield, N. J. Borys, S. M. Hamed, N. A. Torquato, C. A. Tajon, B. Tian, B. Shevitski, E. S. Barnard, Y. D. Suh, S. Aloni, J. B. Neaton, E. M. Chan, B. E. Cohen and P. J. Schuck, Nat. Photonics, 2018, 12(7), 402–407 CrossRef CAS
.
- A. Gnach and A. Bednarkiewicz, Nano Today, 2012, 7(6), 532–563 CrossRef CAS
.
- W. Zheng, P. Huang, D. Tu, E. Ma, H. Zhu and X. Chen, Chem. Soc. Rev., 2015, 44(6), 1379–1415 RSC
.
- Y. Liu, Y. Lu, X. Yang, X. Zheng, S. Wen, F. Wang, X. Vidal, J. Zhao, D. Liu, Z. Zhou, C. Ma, J. Zhou, J. A. Piper, P. Xi and D. Jin, Nature, 2017, 543(7644), 229–233 CrossRef CAS PubMed
.
- Q. Zhan, J. Qian, H. Liang, G. Somesfalean, D. Wang, S. He, Z. Zhang and S. Andersson-Engels, ACS Nano, 2011, 5(5), 3744–3757 CrossRef CAS PubMed
.
- E. Hemmer, N. Venkatachalam, H. Hyodo, A. Hattori, Y. Ebina, H. Kishimoto and K. Soga, Nanoscale, 2013, 5(23), 11339–11361 RSC
.
- U. Rocha, C. J. Silva, W. F. Silva, I. Guedes, A. Benayas, L. M. Maestro, M. A. Elias, E. Bovero, F. C. J. M. van Veggel, J. A. G. Solé and D. Jaque, ACS Nano, 2013, 7(2), 1188–1199 CrossRef CAS PubMed
.
- C. M. Hessel, V. P. Pattani, M. Rasch, M. G. Panthani, B. Koo, J. W. Tunnell and B. A. Korgel, Nano Lett., 2011, 11(6), 2560–2566 CrossRef CAS PubMed
.
- X. Zhu, W. Feng, J. Chang, Y. W. Tan, J. Li, M. Chen, Y. Sun and F. Li, Nat. Commun., 2016, 7, 10437 CrossRef CAS PubMed
.
- L. Tong, X. Li, J. Zhang, S. Xu, J. Sun, L. Cheng, H. Zheng, Y. Zhang, X. Zhang, R. Hua, H. Xia and B. Chen, Sens. Actuators, B, 2017, 246, 175–180 CrossRef CAS
.
- F. Huang, Y. Tian, H. Li, S. Xu and J. Zhang, Opt. Lett., 2015, 40(18), 4297 CrossRef CAS PubMed
.
- R. Martín-Rodríguez, S. Fischer, A. Ivaturi, B. Froehlich, K. W. Krämer, J. C. Goldschmidt and B. S. Richards, Chem. Mater., 2013, 25(9), 1912–1921 CrossRef
.
- G. E. Arnaoutakis, J. Marques-Hueso, A. Ivaturi, S. Fischer, J. C. Goldschmidt, K. W. Krämer and B. S. Richards, Sol. Energy Mater. Sol. Cells, 2015, 140, 217–223 CrossRef CAS
.
- H. Lakhotiya, S. P. Madsen, S. Roesgaard, J. Vester-Petersen, B. B. Iversen, P. Balling and B. Julsgaard, J. Phys. Chem. C, 2020, 124(41), 22357–22365 CrossRef CAS
.
- P. Manley, M. Segantini, D. Ahiboz, M. Hammerschmidt, G. Arnaoutakis, R. W. MacQueen, S. Burger and C. Becker, APL Photonics, 2021, 6(3), 036103 CrossRef CAS
.
- D. Ahiboz, E. Andresen, P. Manley, U. Resch-Genger, C. Würth and C. Becker, Adv. Opt. Mater., 2021, 9(24), 2101285 CrossRef CAS
.
- M. Runowski, N. Stopikowska, D. Szeremeta, S. Goderski, M. Skwierczyńska and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11(14), 13389–13396 CrossRef CAS PubMed
.
- F. Wang, Y. Han, C. S. Lim, Y. Lu, J. Wang, J. Xu, H. Chen, C. Zhang, M. Hong and X. Liu, Nature, 2010, 463(7284), 1061–1065 CrossRef CAS PubMed
.
- T. Grzyb and D. Przybylska, Inorg. Chem., 2018, 57(11), 6410–6420 CrossRef CAS PubMed
.
- Y. Que, C. Feng, G. Lu and X. Huang, ACS Appl. Mater. Interfaces, 2017, 9(17), 14647–14655 CrossRef CAS PubMed
.
- K. Saidi, M. Dammak, K. Soler-Carracedo and I. R. Martín, J. Alloys Compd., 2022, 891, 161993 CrossRef CAS
.
- P. Phogat, V. B. Taxak, S. P. Khatkar and R. K. Malik, Chem. Phys., 2022, 561, 111623 CrossRef CAS
.
- J. Dalal, M. Dalal, S. Devi, P. Dhankhar, A. Hooda, A. Khatkar, V. B. Taxak and S. P. Khatkar, Mater. Chem. Phys., 2020, 243, 122631 CrossRef CAS
.
- P. Phogat, V. B. Taxak and R. K. Malik, J. Electron. Mater., 2022, 51(8), 4541–4554 CrossRef CAS
.
- N. Kaczorowska, A. Szczeszak and S. Lis, J. Lumin., 2018, 200, 59–65 CrossRef CAS
.
- P. Phogat, V. B. Taxak and R. K. Malik, Solid State Sci., 2022, 133, 107013 CrossRef CAS
.
- M. Runowski, P. Woźny and I. R. Martín, J. Mater. Chem. C, 2021, 9, 4643–4651 RSC
.
- E. Pavitra, G. Seeta Rama Raju, W. Park and J. S. Yu, New J. Chem., 2014, 38(1), 163–169 RSC
.
- R. Naveenraj, E. K. Suresh, J. Dhanya and R. Ratheesh, Eur. J. Inorg. Chem., 2019, 7, 949–955 CrossRef
.
- K. Cheng, C. Li, C. Yin, Y. Tang, Y. Sun and L. Fang, J. Eur. Ceram. Soc., 2019, 39(13), 3738–3743 CrossRef CAS
.
- J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637 CrossRef CAS
.
- Y. Liu, J. Silver, R.-J. Xie, J. Zhang, H. Xu, H. Shao, J. Jiang and H. Jiang, J. Mater. Chem. C, 2017, 5, 12365–12377 RSC
.
- G. D. Gesesse, A. Gomis-Berenguer, M. Barthe and C. O. Ania, J. Photochem. Photobiol., A, 2020, 398, 112622 CrossRef CAS
.
- L. Li, Y. Tong, J. Chen, Y. Chen, G. Abbas Ashraf, L. Chen, T. Pang and H. Guo, J. Am. Ceram. Soc., 2022, 105(1), 384–391 CrossRef CAS
.
- Y. Tong, W. Zhang, R. Wei, L. Chen and H. Guo, Ceram. Int., 2021, 47(2), 2600–2606 CrossRef CAS
.
- O. A. Savchuk, J. J. Carvajal, C. Cascales, M. Aguiló and F. Díaz, ACS Appl. Mater. Interfaces, 2016, 8(11), 7266–7273 CrossRef CAS PubMed
.
- Y. Zhao, X. Wang, R. Hu, Y. Zhang, Y. Li and X. Yao, Mater. Res. Bull., 2020, 131, 110959 CrossRef CAS
.
- F. Auzel, Chem. Rev., 2004, 104(1), 139–174 CrossRef CAS PubMed
.
- Y. Fu, Y. Shi, N. Zhang, Y. Tian, M. Xing and X. Luo, Mater. Res. Bull., 2016, 84, 346–349 CrossRef CAS
.
- K. O. Lima, L. F. dos Santos, R. Galvão, A. C. Tedesco, L. S. Menezes and R. R. Gonçalves, Front. Chem., 2021, 9, 712659 CrossRef PubMed
.
- R. V. Perrella, I. C. Ribeiro, P. H. A. Campos-Junior, M. A. Schiavon, E. Pecoraro, S. J. L. Ribeiro and J. L. Ferrari, Mater. Chem. Phys., 2019, 223, 391–397 CrossRef CAS
.
- X. Wang, X. Li, H. Zhong, S. Xu, L. Cheng, J. Sun, J. Zhang, L. Li and B. Chen, Sci. Rep., 2018, 8(1), 5736 CrossRef PubMed
.
- K. Soler-Carracedo, I. R. Martín, F. Lahoz, H. C. Vasconcelos, A. D. Lozano-Gorrín, L. L. Martín and F. Paz-Buclatin, J. Alloys Compd., 2020, 847, 156541 CrossRef CAS
.
- M. Haase and H. Schäfer, Angew. Chem., Int. Ed., 2011, 50, 5808–5829 CrossRef CAS PubMed
.
- R. Martín-Rodríguez, F. T. Rabouw, M. Trevisani, M. Bettinelli and A. Meijerink, Adv. Opt. Mater., 2015, 3(4), 558–567 CrossRef
.
- K. Saidi, M. Dammak, K. Soler-Carracedo and I. R. Martín, Dalton Trans., 2022, 51, 5108–5117 RSC
.
- Y. Jiang, Y. Tong, S. Chen, W. Zhang, F. Hu, R. Wei and H. A. Guo, Chem. Eng. J., 2021, 413, 127470 CrossRef CAS
.
- D. Avram, I. Porosnicu, A. Patrascu and C. Tiseanu, Adv. Photonics Res., 2022, 3(6), 2100208 CrossRef CAS
.
- F. Ayachi, K. Saidi, W. Chaabani and M. Dammak, J. Lumin., 2021, 240, 118451 CrossRef CAS
.
- L. Li, Y. Tong, J. Chen, Y. Chen, G. A. Ashraf, L. Chen, T. Pang and H. Guo, J. Am. Ceram. Soc., 2021, 105, 384–391 CrossRef
.
- R. S. Yadav, D. Kumar, A. K. Singh, E. Rai and S. B. Rai, RSC Adv., 2018, 8(60), 34699–34711 RSC
.
- B. P. Singh, A. K. Parchur, R. S. Ningthoujam, P. V. Ramakrishna, S. Singh, P. Singh, S. B. Rai and R. Maalej, Phys. Chem. Chem. Phys., 2014, 16(41), 22665–22676 RSC
.
- M. Lin, L. Xie, Z. Wang, B. S. Richards, G. Gao and J. Zhong, J. Mater. Chem. C, 2019, 7(10), 2971–2977 RSC
.
- X. Liu, R. Lei, F. Huang, D. Deng, H. Wang, S. Zhao and S. Xu, J. Lumin., 2019, 210, 119–127 CrossRef CAS
.
- K. Saidi and M. Dammak, J. Solid State Chem., 2021, 300, 122214 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2024 |