Open Access Article
Open Access ArticleNew accurate molecular dynamics potential function to model the phase transformation of cesium lead triiodide perovskite (CsPbI3)
Saeed S. I. Almishal and
Ola Rashwan
and
Ola Rashwan *
*
Penn State Harrisburg, USA. E-mail: ola.rashwan@psu.edu
First published on 17th December 2020
Abstract
Inorganic metallic halide perovskites and cesium lead triiodide, CsPbI3, in particular, have gained enormous attention recently due to their unique photovoltaic properties and low processing temperatures. However, their structural stability and phase transition still need an in-depth investigation to better optimize their optoelectronic properties. For sake of time and cost, Classical Molecular Dynamics (CMD) and first principles calculations are being used to predict the structure stability and phase transition of CsPbI3. The major challenge of CMD is the choice of proper interatomic potential functions. In this paper, a new hybrid force field is being introduced, which integrates the embedded atomic potentials of Cs–Cs and Pb–Pb with Buckingham–Coulomb potentials. The Buckingham–Coulomb interatomic potential was solely employed as well. The outputs from both force fields were reported and compared to the experimental values. In fact, the new Hybrid Embedded Atomic Buckingham–Coulomb (EABC) potential reproduces, with a great degree of accuracy (within 2.5%), the structural properties, such as the radial distribution functions, interatomic separation distances, and the density. Also, it detects the phase transformation from an orthorhombic into a cubic crystal structure and the melting temperature at 594 K and 750 K respectively which agrees with the experimental values to within 1%. The new proposed hybrid potential proved to be accurate so it could potentially be used to infer the structure stability and the mechanical and thermal properties of the pure inorganic halide perovskites and the mixed halide perovskites as well which are used in various applications.
Introduction
Halide perovskites are gaining huge attention for being very promising not only for photovoltaic applications1 but for other applications as well. They offer various new structures with superior properties that can be used in high-pressure applications2 and low-cost and flexible memory devices.3 Halide perovskite solar cell efficiency has rapidly increased through the recent years from 2.2% in 2006 to 25.2% which has been reported recently.4Halide perovskites have an ABX3 chemical formula, where A is a monovalent cation, B is a metal divalent cation and X is a halide anion. The archetypal perovskite of this family is methylammonium lead triiodide (MAPbI3) which has been studied intensively. Solar cells based on MAPbX3 are highly attractive for their high absorption coefficient, tunable bandgap, low carrier recombination, and easy fabrication.5 The methylammonium (MA) cations cause complex dynamics because of their molecular orientation, molecular entropy and loss of stability.6 The choice of the A cations is important as it significantly influences the light absorption in the visible spectrum.7 Therefore, the MA cations could be substituted with larger cations, such as Cs+ or Rb+ for higher stability without sacrificing the optoelectronic properties as the lead halide sublattice is responsible for the direct bandgap.6,7
Recently, cesium lead triiodide (CsPbI3) has been getting attention along with the family of mixed halides of CsPb(IxBr1−x)3.8 CsPbI3 is an inorganic halide perovskite where a cesium cation (Cs+) replaces the methylammonium cation (MA+) of MAPbI3. It has a more stable structure and unique photovoltaic properties. The black cubic polymorph of CsPbI3 (α-CsPbI3) with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure and 1.73 eV bandgap, is the one used for the photovoltaic applications and was reported experimentally to be stable at a temperature higher than 593.15 K.9
m structure and 1.73 eV bandgap, is the one used for the photovoltaic applications and was reported experimentally to be stable at a temperature higher than 593.15 K.9
To better understand the effect of the temperature on the stability of the structure and the phase transition of inorganic halide perovskites over a relatively long-time, Classical Molecular Dynamics (CMD) is more favorable compared to the Density Functional Theory (DFT). Although there were numerous studies that used various first principles methods to understand the stability and electronic properties of halide perovskites,10–12 these methods are computationally expensive and unsuitable for large systems. Additionally, the stability of the structure over a relatively long time and various temperatures could not be effectively predicted by these methods. Classical Molecular Dynamics (CMD) offers a solution to model such large systems by treating the atomic movement classically through Newtons' laws.13–15 The availability and transferability of force fields, that describe the interatomic interactions among the compound constituents, pose a challenge in using CMD. Force fields are usually obtained by finding the proper fitting parameters that could reproduce the experimental structural properties, such as density and interatomic distances. These parameters are usually generated by first principle quantum mechanics calculations or empirical methods.13
In classical molecular dynamics, the total energy Etotal of the system is represented as the sum of all interactions between all the atoms in the system as shown in eqn (1)
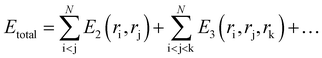 | (1) |
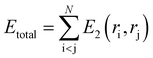 | (2) |
The first hybrid potential to model MA+ based perovskites was developed by Mattoni et al.,16 ‘MYP’, by fitting on data from ab initio models. In MYP model, the inorganic–inorganic potential parameters were rescaled to Matusi MgSiO3 parameters.17 MA+ (CH3NH3+) was represented by the standard GAFF force field that includes bonded interactions. (Pb–I) and (C–N) interactions were modelled by Buckingham–Coulomb-potential while (H–Pb) and (H–N) interactions were modelled by Coulomb–LJ potential. They also assumed that the interaction between C–Pb is the same as N–Pb and they both resemble Cs–Pb in CsPbI3, and the same applies to C–I and N–I for Cs–I. The MYP fitting parameters were further enhanced by refining the MA+ atomic partial charges and the interactions of Pb–I to reproduce the density functional theory DFT calculations of the cohesive energy, Pb–I distortion energy, molecules reorientation energy and bulk modulus of a hydrostatic deformed cubic crystal. Further, the N–I interaction was refined to ensure the orthorhombic-to-tetragonal transition.16,18
Mattoni et al.16 proved that the MYP calculations meet the experiments and DFT results on the important structural and vibrational properties of the material, such as energy as a function of lattice spacing.16 In studying the phase transition, the potential produced the general features of the transition from the orthorhombic crystal structure to the tetragonal structure and to the cubic crystal structure. Nevertheless, MYP was also used to determine the sources of phase transition in MAPbI3 which are mainly attributed to the dynamic behavior of organic cations in the lead iodide lattice.19 The MYP was further employed in studying the diffusion of point defects and it showed that the dominant mechanism of ionic transport in MAPbI3 is iodine diffusion.20
For its acceptable accuracy, the MYP force field was used to study the behavior of different phases of MAPbI3 under various conditions. It was used to model the nucleation and interfacial mismatch during the vapor deposition of MAPbI3 on the TiO2 substrate.21 It was also used to study phonon scattering,22 carrier mobility,23 polaronic strain,24 and the qualitative characterization of the nature and the relaxation properties of the dielectric polarization.25 The use of MYP was not limited to 3D structures, it was also used to study the thermal conductivity of 2D MAPbI3 thin films.26 However, the resulted volume as a function of temperature curve from the MYP has discrepancies when compared to the experimental results because of the fact that the model ignored the charge redistribution and the covalent nature of lead iodide interactions.16
Hata et al.6 studied MAPbBr3 using the same MYP potential developed by Mattoni et al.16 They used the same Pb–Pb, Pb–MA, and MA internal interactions as in MAPbI3. They calibrated the newly introduced parameters based on five scaling factors for developing a force-field for MAPbBr3. Three of which were for scaling; namely: α for coulomb–Buckingham parameters, β for the charges and γ for organic–inorganic interactions. Two additional factors resulted from the dynamics of phase transition which are AOI and ρOI of Br− (C, N). Although the developed model is simple, it reproduces, to a certain extent, the main static, and thermodynamic properties of MAPbBr3.6,16 MAPbBr3 has almost the same molecular dynamic behavior as MAPbI3. However, the volume of MAPbBr3 is consistently smaller than that of MAPbI3. The change of volume–temperature curve slope for MAPbBr3 is at 140–170 K compared to 150–200 K for MAPbI3. This is attributed to the orthorhombic-to-tetragonal phase transition as mentioned by Mattoni et al.16 Moreover, the anisotropy in the orthorhombic phase, longest to shortest lattice parameter ratio, of MAPbBr3 is slightly higher than that of MAPbI3 but still is underestimated relative to the experimental value. However, it is overestimated for MAPbI3. In fact, for both MAPbBr3 and MAPbI3, the calculated anisotropy does not change upon the phase transition from tetragonal to cubic which can be understood from the limitations of the two-body potentials for inorganic lattices. Still, by calibrating mixed I–Br interactions, it would be possible to model the large class of mixed systems MAPb(IxBr1−x)3.6
Molecular dynamics simulations were used to study the effect of moisture on MAPI3 which is highly hydrophilic. A MYP-based force field (MYP1) for water–MAPI systems was developed to study the dissolution of MAPbI3 crystals in water.27 It was further used to clarify that the apparent hydrophobic experimental contact angle resulted from the surface degradation during measurement.28 Despite the accuracy of the models developed by Mattoni et al.16 and Hata et al.,6 these models cannot predict the complex crystal structure transitions and they are not transferrable to mixed halides perovskites MAPb(I1−xBrx)3.
Handley and Freeman29 also presented a set of interatomic potentials for modelling MAPbI3 that included short-range interactions for the lead and iodide interactions to improve the degree of transferability. Artificial intelligence algorithms, such as artificial neural networks (ANNs) and genetic algorithms (GAs) were employed to develop force fields that represented the mixed halide perovskites. Chen and Pao30 used artificial neural networks (ANN) to model complex structures and transitions. They demonstrated that by developing an ANN potential for MAPbI3 as an example. Marchenko et al.31 developed a semi-empirical model that represents the mixed halides hybrid perovskites and they used it to calculate Gibbs free energy and thermodynamic properties. Balestra et al.32 used genetic algorithms to adjust the Coulomb–Buckingham pair atomic potentials to model the mixed halide systems of CsPb(IxBr1−x)3. They used their modified potential values to reproduce the DFT calculations of the lattice geometric distortions energies. However, their modified force field was fitted only to cubic structures of CsPbI3, CsPbBr3, and mixed CsPbI3Br with the aim to be transferable between them. The radial distribution function of the cubic CsPbI3 was successfully obtained and matched the experimental results.32 However, the new derived force field acceptably agreed with experiments and previous theoretical studies of structural and dynamic properties, particularly, for the pure structures, i.e., the non-mixed, in their cubic crystalline structure form.
Although, the inorganic metal halide perovskites, particularly CsPbI3, have unique properties and better stability than MAPbI3, their structural properties, and phase transitions are not well-characterized and further investigation is needed. Therefore, the objective of this work is to apply molecular dynamics to investigate the structural properties and phase transformation of CsPbI3 by applying the proper force field. We achieved this by introducing a novel hybrid force field which is referred to as “Hybrid EABC”, where EABC stands for Embedded-Atomic-Method and Buckingham–Coulomb potential. We compared the outcomes of using both Coulomb–Buckingham potential and Hybrid EABC in reproducing the experimentally reported and the ab initio structure's radial distribution functions and phase transitions of CsPbI3 with an ultimate aim to gain in-depth understanding of the CsPbI3 to further enhance its properties.
Methodology
Molecular dynamics simulations require the initial positions of atoms, which we obtained from our DFT calculations and the force field as inputs. We discuss the application of two force fields. The first force field follows the Buckingham–Coulomb representation which is an interatomic pair potential. The second force field is Hybrid EABC, which is based on the application of interatomic pair potentials combined with the Embedded Atomic Method (EAM). We also present the simulation details and discuss the outputs.The orthorhombic structure from DFT simulation
The input structures for the classical MD were obtained from the DFT electronic and ionic energy minimization using PAW-GGA with a cutoff energy of 520 eV using Vienna Ab initio Simulation Package VASP.33,34 The FAST algorithm was employed for the electronic minimization with a stopping criterion of 1 × 10−4 eV. The ionic relaxation was set to stop if all forces are smaller than 0.02 eV Å−1. The resulting orthorhombic structure of CsPbI3 is composed of 20 atoms and has lattice parameters of 4.902, 10.771, and 18.211 Å as illustrated using VESTA35 in Fig. 1.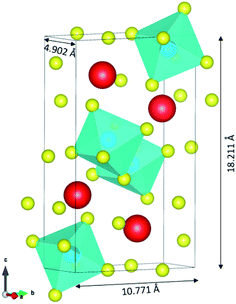 | ||
| Fig. 1 The resulting orthorhombic structure of CsPbI3 from DFT. The structure is composed of 4 Cs atoms (in red color), 4 Pb atoms (in blue color) and 12 I atoms (in yellow color). | ||
Buckingham–Coulomb pair potential
We used Buckingham–Coulomb potential (UBC) to model the pair atomic interactions due to the inorganic nature of CsPbI3 bonds. This potential is used effectively in studying inorganic and ionic crystals.17 The general schematic of Buckingham–Coulomb interactions is shown in Fig. 2.Buckingham–Coulomb potential (UBC) is numerically more stable than the Lennard-Jones potential.36 In Buckingham–Coulomb potential (UBC), the long-term coulomb interaction is added to Buckingham potential as shown in eqn (3).
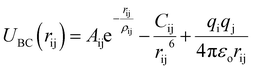 | (3) |
The potential parameters for the six interactions are required to completely define the force field between the constituent ions of CsPbI3 perovskite. For the parameters of Cs–Cs and Cs–I Interactions, the Buckingham parameters were obtained from Sangster and Atwood.38 For Cs–Pb, interaction, we used Mirskaya technique which is based on the geometric mean combining rule for the total interaction energy of two non-bonded atoms for the Buckingham potential and shown in eqn (4) and (5).39
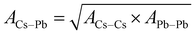 | (4) |
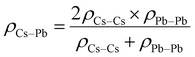 | (5) |
For CCs–Pb, an iterative algorithm was developed to find the ideal value. This value was approximately the same value for CCs–Pb that was obtained by Mirskaya39 method from CCs–Cs and CPb–Pb by Balestra et al.32 For the parameters of Pb–Pb, Pb–I, and I–I interactions, they were set to be equal to the ones in MYP.16,18 The effective charge of Cs+ was assumed to be the same charge of MA+ as in MAPbI3.18 These interactions along with the effective charges are summarized in Table 1.
| Interaction | A (eV) | ρ (Å) | C (eV Å6) | Ion | Effective charge |
|---|---|---|---|---|---|
| Cs–Cs | 3.584 × 1016 | 0.0843 | 240.34 | Cs | 1.36 |
| Cs–Pb | 3.3068 × 1011 | 0.10519 | 480.0 | ||
| Cs–I | 4913.000 | 0.3814 | 480.06 | Pb | 2.03 |
| Pb–Pb | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051 051![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120.5 120.5 |
0.131258 | 0.0 | ||
| Pb–I | 4488.05 | 0.321737 | 0.0 | I | −1.13 |
| I–I | 988.42 | 0.482217 | 30.22285 |
Hybrid EABC potential
Although pair interatomic potentials are simple and adequately model the material behavior, they do not reflect the true nature of bonds. They overestimate the vacancy formation and fail in predicting the crystal structure of metals and modelling surface relaxation behavior.40 This is expected as all the higher terms of atomic interactions are neglected.13,40Therefore, in this work, we developed a new potential of CsPbI3 by superimposing the Embedded Atomic Method (EAM) to BC pair potential to model both Cs–Cs and Pb–Pb interactions to reflect the metallic nature of these bonds. The EAM potential was first developed in 1984 by Daw and Baskes to study the hydrogen embrittlement in metals.41 EAM potential (UEAM) adds the embedding energy, which simply represents the energy required to embed positively charged atomic cores into the electron density, to the pair atomic potential. The EAM is presented schematically in Fig. 3.
The EAM potential can successfully model the cohesion, defects, surface relaxation, and ground-state impurity energies resulting in overcoming the limitations of pair potentials.13,40,42 In general, it improves the potential performance dramatically and still could be applied to large systems. The EAM potential (UEAM) is estimated using eqn (6) and (7) in terms of the pair potential and embedding energy as a function of electron density.
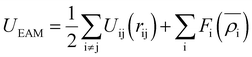 | (6) |
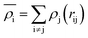 | (7) |
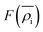 is the energy required to insert the ionic cores into the electron density and represents the many-body behavior. The
is the energy required to insert the ionic cores into the electron density and represents the many-body behavior. The 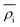 is the average total contribution from all atoms to the electron density at the position of atom i, and the ρj is the electron density contribution of atom j.13,40,42
is the average total contribution from all atoms to the electron density at the position of atom i, and the ρj is the electron density contribution of atom j.13,40,42
In our new proposed Hybrid EABC potential, for the interactions between Cs–Cs and Pb–Pb, the Buckingham part of the potential shown in eqn (3) is replaced by the EAM potential shown in eqn (6)43,44 while the Coulomb potential is still imposed. The new Hybrid EABC potential parameters are summarized in Table 2.
Molecular dynamics simulations
All classical molecular dynamics calculations were carried by Linear Atomic/Molecular Massive Parallel Simulator (LAMMPS).45 The bulk elements of 1920 atoms were generated by duplicating the unit cell 6 × 4 × 4 by ATOMSK code46 and periodic boundary conditions were applied. The supercell visualization was carried out by OVITO.47 For both force fields (BC and Hybrid EABC), the cutoff radii were set to be 12 Å based on iterations to produce the most stable structure at room temperature. First, the system was equilibrated at ambient conditions (300 K and 1 atm), with a time step of 0.5 femtoseconds (fs) for 30 picoseconds (ps) to study the density and structural properties at ambient conditions. Then, temperature was increased to study the phase transition. This was achieved by the isobaric–isothermal NPT ensemble which applied Nose–Hoover thermostat and barostat.48 In the case of the Buckingham–Coulomb potential, the temperature was raised at a rate of 100 K every 16 ps. However, in the case of the new proposed Hybrid EABC, the temperature was increased at a rate of 100 K every 48 ps to ensure proper equilibration and temperature control. For every 100 timesteps, the temperature, density, and simulation box edges were reported.The CMD simulations outputs were the radial pair distribution function, gαβ(r), and the change of density with the temperature. The gαβ(r) was calculated after the relaxation at room temperature conditions using eqn (8).
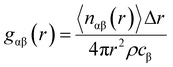 | (8) |
The radial distribution function is a structural descriptor that represents the probability distribution of β particles surrounding another specific α particle. The radial distribution function exhibits a series of discrete peaks in the case of a single crystal. In general, the magnitude and the location of the peaks depend on the exact crystal structure.49
Results and discussion
The orthorhombic structure of a supercell that includes 1920 atoms of CsPbI3, was modeled and analyzed using the classical molecular dynamic LAMMPS software. Two force fields, Buckingham–Coulomb and the new proposed Hybrid EABC force were employed and their outputs are analyzed in this section. Among the outputs of the CMD simulations were the structure descriptors, such as the radial distribution functions, the interatomic distances, and the density. But, most importantly is the accurate description of the phase transformation and the melting of CsPbI3.Structure descriptors of CsPbI3 at ambient conditions
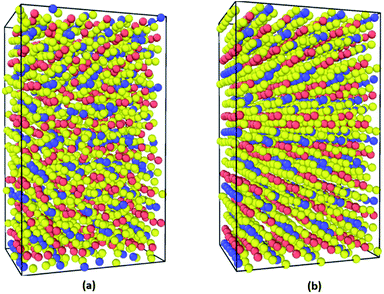
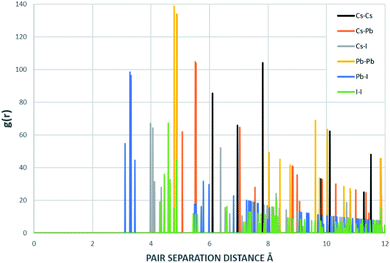
The supercells of CsPbI3 at the ambient condition from the CMD simulations using the Buckingham–Coulomb and the new proposed Hybrid EABC forces fields are illustrated in Fig. 4. It can be observed that the structure resulting from the Hybrid EABC potential (Fig. 4b) is more ordered than the outcome of the Buckingham–Coulomb potential (Fig. 4a).The radial distribution functions of bulk CsPbI3 at 300 K using the Buckingham–Coulomb potential and Hybrid EABC potential were obtained using 100 bins and illustrated in Fig. 5 and 6 respectively. One significant difference between the outcomes of using the two potentials occurs in the Pb–I interaction, where the Buckingham–Coulomb peak is shifted to the right with ∼0.15 Å compared to the Hybrid EABC peak. Moreover, both peaks of Cs–Pb and Pb–I from the Hybrid EABC potential agree with the radial distribution functions resulted from the DFT calculations shown in Fig. 7, which implies that the inclusion of EAM potential in the Hybrid EABC helps to maintain the integrity of the initial orthorhombic structure. Moreover, the peaks resulting from using the hybrid potential are closer to the peaks of the radial distributions functions which were obtained experimentally50 and are shown by the dotted red lines in Fig. 5 and 6.
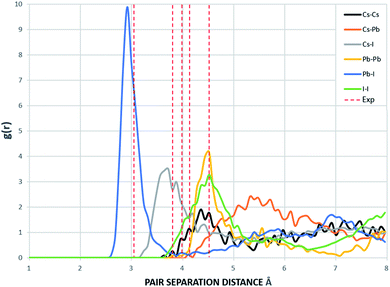 | ||
| Fig. 5 The radial distribution function of the equilibrated structure with Buckingham–Coulomb at 300 K and g(r) with 100 bins (yellow: I, red: Cs and blue: Pb). The experimental values are obtained from ref. 50. | ||
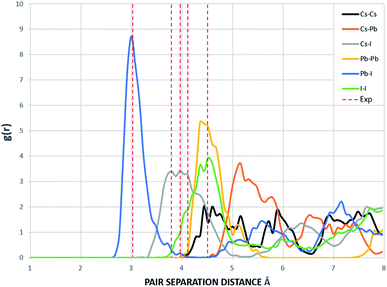 | ||
| Fig. 6 The Radial distribution function of the equilibrated structure with Hybrid EABC at 300 K and g(r) with 100 bins (yellow: I, red: Cs and blue: Pb). The experimental values are obtained from ref. 50. | ||
 | ||
| Fig. 7 Radial distribution function of the structure that resulted from DFT and inputed to MD. This RDF was generated with 1000 bins. | ||
The interatomic separation distances between the different ions using the Buckingham–Coulomb and Hybrid EABC potential functions were obtained from RDF with 1000 bins for higher accuracy and are reported in Table 3. When comparing the outcomes of the two force fields, the largest deviation occurs at the Cs–Pb interaction, where the Buckingham–Coulomb Cs–Pb peak is shifted ∼0.4 Å to the left of the Hybrid EABC peak. Whereas the least deviations occur at Cs–Cs and I–I peaks with a deviation of ∼0.01 Å.
| Interaction | Interatomic distance (Å) | |
|---|---|---|
| Coul–Buck | Hybrid EABC | |
| Cs–Cs | 4.4820 | 4.4700 |
| Cs–Pb | 5.3820 | 4.9860 |
| Cs–I | 3.6900 | 3.7500 |
| Pb–Pb | 4.4820 | 4.5180 |
| Pb–I | 2.9100 | 3.0540 |
| I–I | 4.5180 | 4.5060 |
In fact, the new proposed Hybrid EABC results in Pb–I bond lengths of ∼3.05 Å which agrees with experimental findings reported by Straus et al.50 with an error of less than 1%. Also, it proves that the change in lattice parameters with temperature must originate from tilting in the octahedra of Pb–I. The accuracy of modelling Pb–I interaction is crucial in modelling lead iodide perovskites as the electronic and optical properties are greatly dependent on this interaction.7
It is worth noting that when the structure was equilibrated with the Hybrid-EABC force field but with omitting the Cs–Cs and Pb–Pb coulomb interactions, the orthorhombic structure clustered into CsI and PbI2 as shown in Fig. 8. This demonstrates the experimental method of mixing CsI and PbI2 (ref. 9) to produce CsPbI3 but in reverse. Also, this implies the significance of coulombic interactions between Cs–Cs and Pb–Pb in stabilizing the structure.
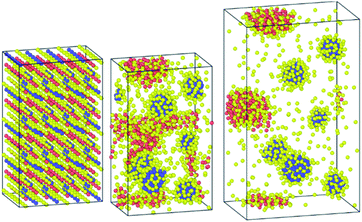 | ||
| Fig. 8 Clustering of CsPbI3 as CsI and PbI2 when the coulombic interactions are neglected between cesium ions and between lead atoms. | ||
The scatter plots of the X-positions vs. Z-positions of CsPbI3 ions within the supercell at 0 K, 300 K and 600 K are shown in Fig. 9. A clear rattling behavior appeared in the scatter plot of the X-positions vs. Z-positions of at 300 K when compared to 0 K. This behavior can be attributed to the distortion of Cs atoms and Pb–I octahedra. The highly distorted and irregular behavior of Cs ions can also be observed in our Cs–Cs interaction in the RDF results shown in Fig. 5 and 6. This agrees with the findings in ref. 50 that Cs cations become distorted, occupy two positions and rattle within the structure causing the instability of CsPbI3 at ambient conditions. At 600 K, the increase in volume which is observed from the increase in the scattered positions along the X-axis indicates the transition into a cubic crystal structure and it would be discussed in more detail in the phase transformation section.
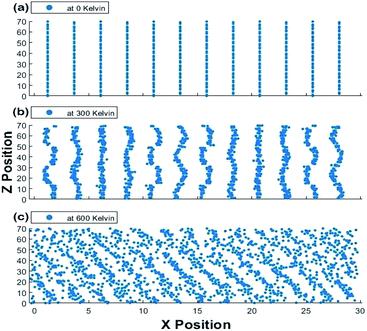 | ||
| Fig. 9 Scatter plot of X positions vs. Z positions for the 1920 atoms at (a) 0 K, (b) 300 K and (c) 600 K at one time for the Hybrid EABC model. | ||
The density of CsPbI3 orthorhombic crystal structure
The density of the orthorhombic structure, resulting from our DFT calculations was 4.983 g cm−3. After the equilibration using the Buckingham–Coulomb force field at 300 K, the structure density decreased to approximately 4.8 g cm−3. On the other hand, when the full Hybrid EABC potential was used with 0.5 fs timestep, the density was 5.2558 g cm−3, which only 2.5% lower than the experimental value of orthorhombic δ-CsPbI3 in ref. 9 and 1.9% lower than the experimental value of orthorhombic δ-CsPbI3 in ref. 51.Phase transformation of CsPbI3
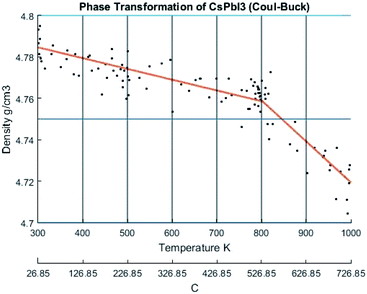
The change of density with temperature resulting from using the Buckingham–Coulomb (BC) potential is illustrated in Fig. 10. The density slowly decreases with temperature until a significant change in slope occurs at the vicinity of 800 K. This change in the slope could be attributed to the melting of CsPbI3 indicated by Sharma et al.52 However, this potential was not able to detect the transition from orthorhombic to cubic crystal structures obtained by Wang et al.9When the new hybrid EABC was employed, the density vs. temperature curve exhibits an abrupt change of density at different temperatures indicating phase transformation as shown in Fig. 11. At 300 K, CsPbI3 is stable as an orthorhombic structure with a density equal to 5.2558 g cm−3. Then, the density decreases gradually as the temperature increases to ∼560 K and an abrupt decrease in density starts at ∼610 K and it continues to decrease till it reaches 4.81 g cm−3 at 630 K. This could be attributed to the phase transformation from the orthorhombic to cubic structure, i.e. α-CsPbI3. This agrees within 1.5% with the experimental result by Trots et al.51 which stated that CsPbI3 undergoes orthorhombic-to-cubic phase transition through two stages. The first starts at 563 K where orthorhombic and cubic structures coexist and the other is at 602 K where only cubic structure is present. During this phase transition, an increase in volume by 7.5% occurs which is very comparable to the experimental value of 6.9% reported in ref. 51.
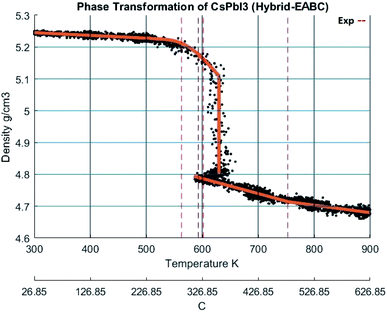 | ||
| Fig. 11 The density of CsPbI3 as a function of temperature calculated by Hybrid EABC. The scatter points represent measured points from the CMD model and the orange curve is obtained by regression fitting. The red dashed lines represent iso-temperature lines obtained from experimental values in ref. 9,51,52. | ||
At 630 K, the density drops from 5.1 to 4.81 g cm−3 while the system's Nose–Hoover thermostat was trying to maintain the system temperature at 600 K. This decrease in density along with the increase in volume was also observed in the scatter plot of the X-positions vs. Z-positions at 600 K shown previously in Fig. 9. Therefore, the system would eventually equilibrate at a density of 4.81 g cm−3 at 600 K. The resulting structure is stable from ∼593 K. The average temperature of the system from the beginning of the transformation till the end of the equilibration at the new phase is 594.6 K. These findings also perfectly match the experimental densities and the temperature reported by Wang et al.9 and Trots et al.51 and indicated by the dashed lines in Fig. 11. Further heating of the system results in a second change of slope at ∼750 K which might be attributed to melting as reported by Sharma et al.52
Conclusions
The inorganic halide perovskite cesium lead triiodide (CsPbI3) has been extensively researched for exceptional optoelectronic properties. However, an in-depth understating of its thermodynamic and structural stability was needed especially at higher temperatures when phase transformation occurs. In this paper, the molecular dynamics method was utilized to investigate the structural stability and the phase transformation of CsPbI3. The choice of the proper force fields significantly affects the accuracy of the model outputs. In this study, two force fields were tested: Buckingham–Coulomb and a newly developed force field called Hybrid EABC. Buckingham–Coulomb potential fails to reproduce the structure descriptors of CsPbI3 or to predict its phase transition. This might happen because it considers only the pair interactions. On the other hand, the new Hybrid EABC potential which combined the embedded atomic method potential with the Buckingham–Coulomb potential reproduces the main structural and thermodynamics features of CsPbI3. The phase transformation from the orthorhombic to the cubic structure occurred at an average temperature of ∼594 K with a density change from ∼5.26 to 4.81 g cm−3. Therefore, the Hybrid EABC potential could be used to predict the dynamic interactions among the CsPbI3 constituents and other properties including thermal conductivity, specific heat, and bulk modulus. This potential could also be utilized to investigate the structural stability and moisture sensitivity. Finally, the proposed Hybrid EABC potential can be extended to analyze other structures including the mixed-halides systems of CsPb(IxBr1−x)3.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Penn State Materials Research Institute (MRI) andPenn State Institutes of Energy and Environment (IEE) seed grant. Computations for this research were performed on the Pennsylvania State University's Institute for Computational and Data Sciences' Roar supercomputer.References
- A. Smets, K. Jäger, O. Isabella, R. Van Swaaij and M. Zeman, Solar Energy: the physics and engineering of photovoltaic conversion, technologies and systems, Cambridge: UIT, 2015 Search PubMed.
- Q. Li, L. Zhang, Z. Chen and Z. Quan, Metal halide perovskites under compression, J. Mater. Chem. A, 2019, 7(27), 16089–16108 Search PubMed.
- B. Li, W. Hui, X. Ran, Y. Xia, F. Xia, L. Chao, Y. Chen and W. Huang, Metal halide perovskites for resistive switching memory devices and artificial synapses, J. Mater. Chem. C, 2019, 7(25), 7476–7493 Search PubMed.
- Best Research-Cell Efficiency Chart, available, https://www.nrel.gov/pv/cell-efficiency.html Search PubMed.
- S. Patwardhan, D. H. Cao, S. Hatch, O. K. Farha, J. T. Hupp, M. G. Kanatzidis and G. C. Schatz, Introducing perovskite solar cells to undergraduates, J. Phys. Chem. Lett., 2015, 6(2), 251–255 Search PubMed.
- T. Hata, G. Giorgi, K. Yamashita, C. Caddeo and A. Mattoni, Development of a classical interatomic potential for MAPbBr3, 2017 Search PubMed.
- H. Fujiwara and R. W. Collins, Spectroscopic Ellipsometry for Photovoltaics, Springer, Switzerland, 2018 Search PubMed.
- J. Duan, H. Xu, W. E. I. Sha, Y. Zhao, Y. Wang, X. Yang and Q. Tang, Inorganic perovskite solar cells: an emerging member of the photovoltaic community, J. Mater. Chem. A, 2019, 7(37), 21036–21068 Search PubMed.
- B. Wang, N. Novendra and A. Navrotsky, Energetics, structures, and phase transitions of cubic and orthorhombic cesium lead iodide (CsPbI3) polymorphs, J. Am. Chem. Soc., 2019, 141(37), 14501–14504 Search PubMed.
- D. L. Busipalli, K. Y. Lin, S. Nachimuthu and J. C. Jiang, Enhanced moisture stability of cesium lead iodide perovskite solar cells–a first-principles molecular dynamics study, 2020 Search PubMed.
- C. Paduani and A. M. Rappe, Tuning the gap of lead-based halide perovskites by introducing superalkali species at the cationic sites of ABX3-type structure, Phys. Chem. Chem. Phys., 2017, 19(31), 20619–20626 Search PubMed.
- C. Motta, F. El-Mellouhi and S. Sanvito, Exploring the cation dynamics in lead-bromide hybrid perovskites, Phys. Rev. B, 2016, 93(23), 235412 Search PubMed.
- J. G. Lee, Computational materials science: an introduction, 2011 Search PubMed.
- F. Giustino, Materials modelling using density functional theory: properties and predictions, 2014 Search PubMed.
- D. C. Rapaport and D. C. R. Rapaport, The art of molecular dynamics simulation, Cambridge university press, 2004 Search PubMed.
- A. Mattoni, A. Filippetti, M. I. Saba and P. Delugas, Methylammonium rotational dynamics in lead halide perovskite by classical molecular dynamics: the role of temperature, 2015 Search PubMed.
- M. Matsui, Molecular dynamics study of MgSiO3 perovskite, 1988 Search PubMed.
- A. Mattoni, A. Filippetti and C. Caddeo, Modeling hybrid perovskites by molecular dynamics, 2016 Search PubMed.
- S. Maheshwari, M. B. Fridriksson, S. Seal, J. Meyer and F. C. Grozema, The Relation between Rotational Dynamics of the Organic Cation and Phase Transitions in Hybrid Halide Perovskites, J. Phys. Chem. C, 2019, 123(23), 14652–14661 Search PubMed.
- P. Delugas, C. Caddeo, A. Filippetti and A. Mattoni, Thermally activated point defect diffusion in methylammonium lead trihalide: anisotropic and ultrahigh mobility of iodine, J. Phys. Chem. Lett., 2016, 7(13), 2356–2361 Search PubMed.
- J. Wang, L. Zhao, M. Wang and S. Lin, Molecular Insights into Early Nuclei and Interfacial Mismatch during Vapor Deposition of Hybrid Perovskites on Titanium Dioxide Substrate, Cryst. Growth Des., 2017, 17(12), 6201–6211 Search PubMed.
- C. Wang, Y. Liu, S. F. Liu, B. Li and Y. Chen, Giant phonon tuning effect via pressure-manipulated polar rotation in perovskite MAPbI3, J. Phys. Chem. Lett., 2018, 9(11), 3029–3034 Search PubMed.
- J. Ma and L. W. Wang, The nature of electron mobility in hybrid perovskite CH3NH3PbI3, Nano Lett., 2017, 17(6), 3646–3654 Search PubMed.
- C. G. Bischak, A. B. Wong, E. Lin, D. T. Limmer, P. Yang and N. S. Ginsberg, Tunable polaron distortions control the extent of halide demixing in lead halide perovskites, J. Phys. Chem. Lett., 2018, 9(14), 3998–4005 Search PubMed.
- A. Mattoni and C. Caddeo, Dielectric function of hybrid perovskites at finite temperature investigated by classical molecular dynamics, J. Chem. Phys., 2020, 152(10), 104705 Search PubMed.
- A. Giri, A. Chen, A. Mattoni, K. Aryana, D. Zhang, X. Hu, S. Lee, J. Choi and P. Hopkins, Ultralow thermal conductivity of two-dimensional metal halide perovskites, Nano Lett., 2020, 20(5), 3331–3337 Search PubMed.
- C. Caddeo, M. I. Saba, S. Meloni, A. Filippetti and A. Mattoni, Collective molecular mechanisms in the CH3NH3PbI3 dissolution by liquid water, ACS Nano, 2017, 11(9), 9183–9190 Search PubMed.
- C. Caddeo, D. Marongiu, S. Meloni, A. Filippetti, F. Quochi, M. Saba and A. Mattoni, Hydrophilicity and Water Contact Angle on Methylammonium Lead Iodide, Adv. Mater. Interfaces, 2019, 6(3), 1801173 Search PubMed.
- C. M. Handley and C. L. Freeman, A new potential for methylammonium lead iodide, Phys. Chem. Chem. Phys., 2017, 19(3), 2313–2321 Search PubMed.
- H. A. Chen and C. W. Pao, Fast and Accurate Artificial Neural Network Potential Model for MAPbI3 Perovskite Materials, ACS Omega, 2019, 4(6), 10950–10959 Search PubMed.
- E. I. Marchenko, S. A. Fateev, A. A. Petrov, E. A. Goodilin, N. N. Eremin and A. B. Tarasov, Transferable Approach of Semi-Empirical Modeling of Disordered Mixed-Halide Hybrid Perovskites CH3NH3Pb (I1–x Br x)3: Prediction of Thermodynamic Properties, Phase Stability, and Deviations from Vegard’s Law, J. Phys. Chem. C, 2019, 123(42), 26036–26040 Search PubMed.
- S. R. G. Balestra, J. M. Vicent-Luna, S. Calero, S. Tao and J. A. Anta, Efficient Modelling of Ion Structure and Dynamics in Inorganic Metal Halide Perovskites, 2020 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169 Search PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59, 1758 Search PubMed.
- K. Mommda and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 Search PubMed.
- F. Jensen, Introduction to computational chemistry, John Wiley & sons, 2017 Search PubMed.
- R. A. Buckingham, The classical equation of state of gaseous helium, neon and argon, 1938 Search PubMed.
- M. J. L. Sangster and R. M. Atwood, Interionic potentials for alkali halides. II. Completely crystal independent specification of Born-Mayer potentials, J. Phys. C: Solid State Phys., 1978, 11(8), 1541 Search PubMed.
- K. Mirskaya, Combining rules for interatomic potential functions of Buckingham form, 1973 Search PubMed.
- M. S. Daw, S. M. Foiles and M. I. Baskes, The embedded-atom method: a review of theory and applications, 1993 Search PubMed.
- M. S. Daw and M. I. Baskes, Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals, Phys. Rev. B, 1984, 29(12), 6443 Search PubMed.
- R. LeSar, Introduction to computational materials science: Fundamentals to applications, 2013 Search PubMed.
- A. Nichol and G. Ackland, Property trends in simple metals: An empirical potential approach, Phys. Rev. B, 2016, 93(18), 184101, DOI:10.1103/physrevb.93.184101.
- K. Wang, W. Zhu, M. Xiang, Y. Xu, G. Li and J. Chen, Improved embedded-atom model potentials of Pb at high pressure: application to investigations of plasticity and phase transition under extreme conditions, Modell. Simul. Mater. Sci. Eng., 2018, 27(1), 015001 Search PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, 1995 Search PubMed.
- P. Hirel, Atomsk: A tool for manipulating and converting atomic data files, Comput. Phys. Commun., 2015, 197, 212–219 Search PubMed.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18(1), 015012 Search PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519 Search PubMed.
- J. G. Kirkwood and E. M. Boggs, The radial distribution function in liquids, J. Chem. Phys., 1942, 10(6), 394–402 Search PubMed.
- D. B. Straus, S. Guo, M. Abeykoon and R. J. Cava, Understanding the Instability of the Halide Perovskite CsPbI3 through Temperature-Dependent Structural Analysis, Adv. Mater., 2020, 32, 2001069 Search PubMed.
- D. M. Trots and S. V. Myagkota, High-temperature structural evolution of caesium and rubidium triiodoplumbates, J. Phys. Chem. Solid., 2008, 69(10), 2520–2526 Search PubMed.
- S. Sharma, N. Weiden and A. Weiss, Phase diagrams of quasibinary systems of the type: ABX3—A′ BX3; ABX3—AB′ X3, and ABX3—ABX′ 3; X= halogen, Z. Phys. Chem., 1992, 175(1), 63–80 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |