Open Access Article
Open Access ArticleUpper and lower bounds for tunneling splittings in a symmetric double-well potential
Miklos Rontoab and
Eli Pollak *a
*a
aChemical and Biological Physics Department, Weizmann Institute of Science, 76100 Rehovot, Israel. E-mail: eli.pollak@weizmann.ac.il
bSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK
First published on 18th September 2020
Abstract
The accurate determination of tunneling splittings in chemistry and physics is an ongoing challenge. However, the widely used variational methods only provide upper bounds for the energy levels, and thus do not give bounds on the gap between them. Here, we show how the self-consistent lower bound theory developed previously can be applied to provide upper and lower bounds for tunneling splitting between symmetric and antisymmetric doublets in a symmetric double-well potential. The tight bounds are due to the very high accuracy of the lower bounds obtained for the energy levels, using the self-consistent lower bound theory. The accuracy of the lower bounds is comparable to that of the Ritz upper bounds. This is the first time that any theory gave upper and lower bounds to tunneling splittings.
1. Introduction
The importance of tunneling splittings in physics and chemistry cannot be overstated.1–5 It is of interest in quantum field theory,6,7 statistical physics,8,9 and molecular dynamics.10,11 Recent molecular examples, and this is by no means a comprehensive list, include tunneling splittings in ammonia and phosphine,12 malonaldehyde,13,14 and ring-puckering vibrations.15The theoretical study of tunneling splittings in molecular systems has a long history. Widely used semiclassical approaches are based on the Wenzel–Kramers–Brillouin (WKB)4 and instanton methods.5 The WKB approach has been applied successfully to several model potentials, such as one- and multidimensional symmetric double-wells,16–18 one-dimensional asymmetric potentials,19 ring-puckering vibrations,15 and in combination with vibrational perturbation theory.20 A path-integral molecular dynamics method was used for double-well potentials in ref. 21. A perturbative instanton approach was used for non-rigid molecules in ref. 10. The tunneling splittings of malonaldehyde and water clusters were studied by a path-integral formulation22 and a ring-polymer implementation of instanton theory.23,24 These two systems were also studied by a wide range of approaches using accurate potential energy surfaces based on semiclassical,25 WKB,26 diffusion Monte Carlo (DMC),13,27,28 and multiconfigurational time-dependent Hartree (MCTDH) methods.29 Ab initio “on-the-fly” techniques combined with semiclassical trajectories were also employed for malonaldehyde30 and for the deep tunneling splittings in ammonia.31
Another class of theoretical methods used for the study of tunneling splittings are variational strategies, which are based on the diagonalization of the Hamiltonian matrix. For example, a calculation of tunneling splitting in phosphine was performed by exploiting symmetries in ref. 12. Malonaldehyde was studied using the Lanczos construct.14
It is then not surprising that bounding tunneling splittings is an old challenge. Simon32 worked out the leading asymptotics for an infinitely large one-dimensional potential. Kirsch and Simon33 derived lower bounds on eigenvalue splittings. Hemmen and Wreszinski34 derived an upper bound for the tunneling rate of a large quantum spin. Abramovich35 gave a lower bound comparison theorem. A workshop on the problem was held in 2006.36 More recently, Yu and Yang37 provided lower bounds for the gap between two adjacent eigenvalues. Semiclassical theories and estimates abound.38,39 However, even to date, a general theoretical framework for providing computational upper and lower bounds on tunneling splittings is lacking; this is the topic of this paper.
The main problem is that upper bounds to eigenvalues, provided by the Ritz–MacDonald variational procedure are not sufficient. It is necessary to obtain accurate lower bounds and it is the combination of the upper and lower bounds on the eigenvalues that gives upper and lower bounds on the gap between the eigenvalues. In a recent series of publications,40–43 we have developed a highly accurate Self-Consistent Lower Bound Theory (SCLBT), which can provide lower bounds to eigenvalues that are of similar and sometimes even have greater accuracy than those of the upper bounds obtained with the Ritz–MacDonald variational method.44,45 The theory generalizes and improves upon Temple's lower bound expression.46 The SCLBT is based on the application of the Lanczos algorithm47 for the tridiagonalization of matrices. Through the Lanczos transformation, explicit relations can be obtained between the overlaps of the exact and approximate wavefunctions, and these are then used extensively to derive the SCLBT expressions.
Thus far, the theory, described in detail in ref. 42 and 43, has been applied successfully to some nontrivial lattice models. The aim of this paper is to further explore the theory and apply it to the challenging problem of finding tight bounds to eigenvalue differences such as in tunneling splitting of eigenvalue energies. For many years, lower bounds were not sufficiently accurate.48–63 Especially when considering tunneling doublets, their accuracy was too poor, the gap between the lower bounds and the true energies was typically much larger than the actual energy differences between the levels. Upper and lower bounds for level differences are only meaningful if the accuracy of the upper and lower bounds is comparable and tighter than the energy splitting between the doublet states. In this paper, we demonstrate that the SCLBT is sufficiently accurate to determine tunneling splittings in a double-well potential. The lower bounds are as accurate as the Ritz–MacDonald upper bounds, allowing us to accurately bound the tunneling splitting energies.
The working expressions of the SCLBT are reviewed briefly in Section 2. The initial input required to apply the SCLBT is a not very accurate set of lower bounds for the eigenvalues of interest. Previously, we have used the Weinstein lower bound expression48 for this purpose. However, the conditions of validity of the Weinstein bound are not trivial (see Appendix A in ref. 43) and it is not always obvious how to determine without further information if the Weinstein lower bounds are truly valid. In addition, the SCLBT limits the highest state to be considered by the requirement that the corresponding Ritz eigenvalue (λj) needs to be less than the exact eigenvalue of the nearest state εj+1. The application of the method is predicated on an objective way for determining if and when these conditions hold. In previous implementations this was not a limitation; however, in the present case of a double-well potential we found that for states above the barrier the Weinstein lower bound could not be applied, as there was no way to determine when it was valid. To overcome this problem, we suggest here the application of a semiclassical estimate of the energy levels in question. The semiclassical action quantization condition (n + 1/2)h provides a reasonable estimate of the location of energy levels, especially those above the potential barrier separating between the wells. This information is then used to obtain the required initial lower bound to the energy levels as well as to determine the highest state for which the theory can be applied. This strategy is robust, since the SCLBT is not very sensitive to the accuracy of this initial input.
The application of the SCLBT to a quartic double-well potential supporting two tunneling doublets is described in Section 3. Using 11 Lanczos basis states, the lowest tunneling doublet was found to have a splitting 0.00199 ≤ ΔE ≤ 0.00224 (a.u.) while the second doublet was bounded as 0.123 ≤ ΔE ≤ 0.154. The numerically exact tunneling splittings are 0.00210 and 0.13562 for the two doublets, respectively.64 The tightness of the lower and upper bounds allows us to improve upon the estimate of the tunneling splitting value itself by taking the average of the upper and lower bounds (0.00212 and 0.13832 for the two doublets), proving highly accurate means. The paper ends with a summary of our conclusions.
2. Short review of the SCLBT
The main aim of the SCLBT is to find lower bounds to eigenvalues of the Hamiltonian operator whose eigenvalues and eigenstates are denoted as| Ĥ|φj〉 = εj|φj〉, j = 1, 2, …, | (2.1) |
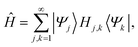 | (2.2) |
| Hj,k = 〈Ψj|Ĥ|Ψk〉. | (2.3) |
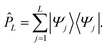 | (2.4) |
ĤL = ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) LĤ LĤ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) L L
| (2.5) |
| ĤL|Φ(L)j〉 = λ(L)j|Φ(L)j〉, j = 1, …, L, | (2.6) |
| (σ(L)j)2 = 〈Φ(L)j|Ĥ2 − (λ(L)j)2|Φ(L)j〉. | (2.7) |
The derivation of the SCLBT is described in detail in ref. 43; here, we give the final working expressions only. A key element of the theory is that the set of basis vectors |Ψj〉 is constructed using the Lanczos methodology. That is, for a chosen initial basis vector |Ψ1〉 the next vector is defined as
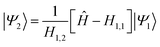 | (2.8) |
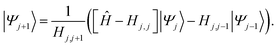 | (2.9) |
The set |Ψj〉, j = 1, …, L is by construction an orthonormal set and the resulting tridiagonal Hamiltonian is diagonalized to give the eigenvalues and eigenfunctions as defined in eqn (2.6).
As discussed in the introduction, a central restriction of the lower bound theory is that the highest state to be considered, denoted as L* has the property
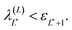 | (2.10) |
| ε(L)j,W = λ(L)j − σ(L)j ≤ εj. | (2.11) |
We assume an L-dimensional projected space, and the highest eigenvalue for which the restriction of eqn (2.10) is assured is denoted by L*. Then the lower bound expression is
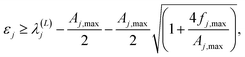 | (2.12) |
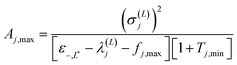 | (2.13) |
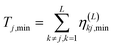 | (2.14) |
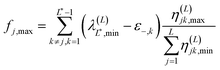 | (2.15) |
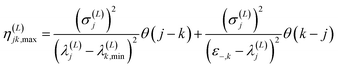 | (2.16) |
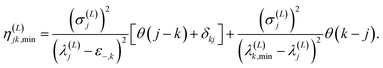 | (2.17) |
In these equations, notation ε−,j stands for a lower bound for the j-th state, λ(L)j,min represents a minimal upper bound for the j-th state, δkj is the Kronecker delta function, and θ(x) is the unit step function (defined as θ(x) = 0 if x ≤ 0 and unity otherwise). The implementation of the SCLBT is described in detail in ref. 42 and 43 and discussed again in detail in Section 3, where we present its application for obtaining upper and lower bounds for tunneling splittings.
If the maximal state is L* = 2, then fj,max = 0 (see eqn (2.15)) and the lower bound expression reduces to the simpler form of
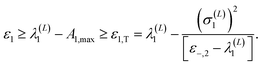 | (2.18) |
The first expression on the right-hand side is the generalization of Temple's lower bound for the ground state derived in ref. 40 and 41. The last expression is Temple's lower bound for the ground state.
3. Upper and lower bounds for tunneling splittings
3.1. Preliminary considerations
We consider a quartic double-well potential with a Hamiltonian (in atomic units)
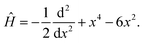 | (3.1) |
The lowest eigenvalues, reported in ref. 64, together with additional data on some higher lying states are listed in Table 1.
| Symmetry | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Sym | −6.64272703 | −2.45118605 | 0.41561275 | 3.87734184 | 8.76868217 | 14.4892323 |
| Antisym | −6.64062823 | −2.3155705 | 1.67849653 | 6.19186637 | 11.53966844 | 17.60097423 |
| Sym – scl | — | — | 0.10084667 | 3.83155489 | 8.75593471 | 14.47969607 |
| Antisym – scl | — | — | 1.75893168 | 6.18035294 | 11.52914990 | 17.59218750 |
The initial wavefunctions chosen for the symmetric and antisymmetric states are normalized double Gaussians
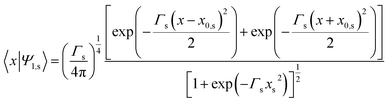 | (3.2) |
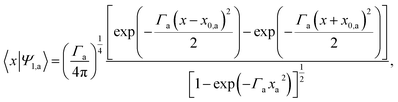 | (3.3) |
| (σ(L)j)2 = HL+1,L2〈ΨL|Φ(L)j〉2. | (3.4) |
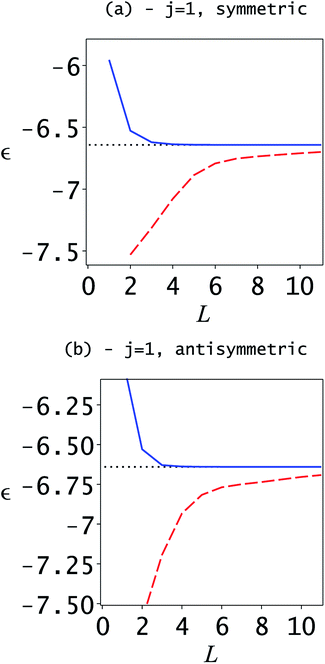
Using these results, we compared the Weinstein lower bound with the Ritz upper bound as a function of the dimensionality. The results for the ground-state doublet are shown in Fig. 1. As expected, the upper bound is a decreasing function of the dimensionality of the projected space, while the Weinstein lower bounds are increasing. The Weinstein lower bounds are low quality as compared to the upper bounds; however, they are sufficiently accurate to use as inputs to the SCLBT.
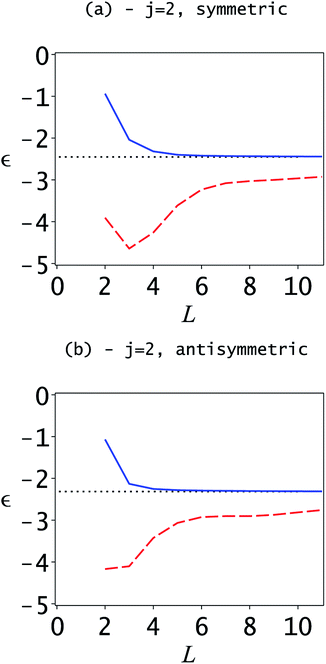
The same is true for the first excited state doublet, shown in Fig. 2. Here, initially, the symmetric Weinstein lower bound decreases with the dimensionality, which is due to the fast decrease of the Ritz eigenvalues. In this region, we cannot know without additional information if the Weinstein lower bound is valid, but the fast decrease in the Ritz eigenvalue indicates that it might be too high. However, from L = 4 onwards, the Ritz eigenvalue plot flattens out and the Weinstein lower bound increases; thus, it can be assumed that the Weinstein lower bound is correct. Although for dimensions L = 2 and 3 there is no objective way to determine if the lower bound is valid, the additional information from L ≥ 5 shows that it is actually valid in these cases.
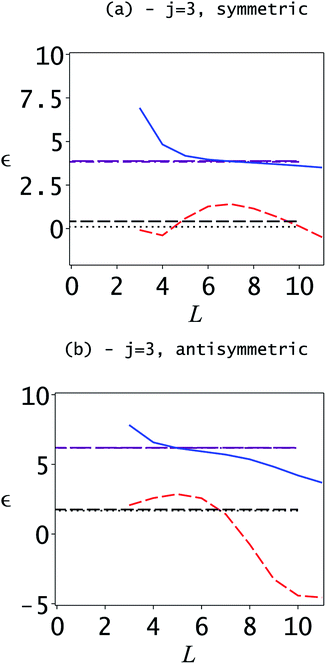
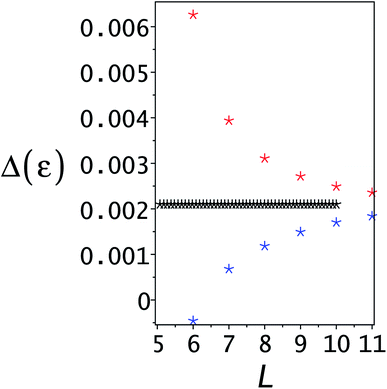
However, when considering the second excited state and higher energies difficulties arise. The Weinstein estimate for the lower bound of the second excited state (j = 3) is shown in Fig. 3. Two problems are highlighted by this figure. The first is that it is impossible to determine from the figure where the Weinstein lower bound is valid. In parts of the region it is greater than the correct second excited state energy indicated by the dotted black line. The semiclassical estimates for the third excited state energy are also shown. The second aspect is that, as highlighted in the previous section, the condition for the validity of the SCLBT is that the Ritz eigenvalue needs to be less than the adjacent higher energy. As can be seen in Fig. 3, this is only satisfied at L ≥ 10. This is the reason why we had to use L = 11 to obtain the accurate lower bounds reported below.
3.2. Case L* = 2
As can be seen in Fig. 1 and 2, the Weinstein lower bounds can be used for the two tunneling doublet states. This corresponds to the case where the lower bounds are obtained only for the ground state, given in eqn (2.18). The process is then as follows. At the first step, we have the Weinstein lower bounds for the first two states, which can be used in eqn (2.13), (2.14), and (2.17) to obtain an improved lower bound for the ground state. This improved lower bound is then used through eqn (2.17) to improve the ground-state lower bound and this is repeated until convergence. At the same time, the Weinstein lower bound for the first excited state can be used to obtain the Temple lower bound (see eqn (2.18)) to the ground state.The next step is to increase the basis set to L = 3. Again, as a first step, the Weinstein lower bound for the first two energies obtained from the L = 3 calculation can be used, then the iteration can be performed using the improved lower bound for the ground state; this is continued until convergence is achieved. In this way, one obtains the SCLBT lower bounds and the Temple lower bounds as a function of the dimensionality of the Lanczos basis set used. These, together with the upper bounds are reported in Table 2 for the symmetric and antisymmetric states.
| Type | L = 2 | L = 3 | L = 4 | L = 5 | L = 6 | L = 7 | L = 8 | L = 9 | L = 10 | L = 11 |
|---|---|---|---|---|---|---|---|---|---|---|
| ub, s | −6.5280 | −6.6209 | −6.6376 | −6.6413 | −6.6421 | −6.64238 | −6.64251 | −6.64259 | −6.64264 | −6.642663 |
| ub, a | −5.9441 | −6.6292 | −6.6380 | −6.6396 | −6.64009 | −6.64031 | −6.64044 | −6.64052 | −6.640565 | −6.640588 |
| lb, s, ST | −6.8336 | −6.7760 | −6.6876 | −6.6545 | −6.6464 | −6.64425 | −6.64355 | −6.64324 | −6.64306 | −6.642945 |
| lb, s, T | −6.9110 | −6.8633 | −6.7193 | −6.6612 | −6.6487 | −6.64584 | −6.64490 | −6.64434 | −6.64387 | −6.643536 |
| lb, a, ST | −6.9107 | −6.7232 | −6.6578 | −6.6455 | −6.6426 | −6.64170 | −6.64133 | −6.64110 | −6.64093 | −6.640822 |
| lb, a, T | −7.0180 | −6.7552 | −6.6651 | −6.6483 | −6.64454 | −6.64350 | −6.64287 | −6.64217 | −6.64160 | −6.641257 |
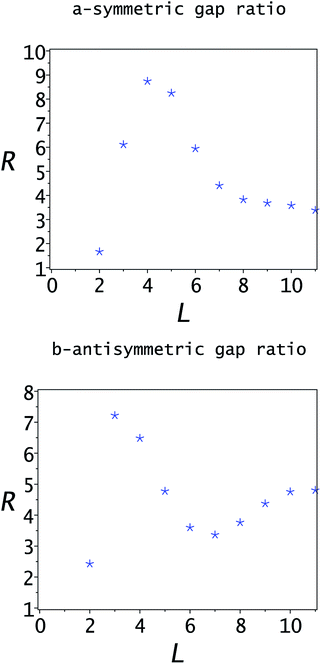
The gaps between the upper and lower bounds and the exact eigenvalue are defined as λj − εj for the upper bound and εj − ε−,j for the lower bounds. The ratio of the gaps of the lower and upper bounds using the SCLBT is plotted in Fig. 4. The typical value of the gap ratio is between 3 and 5. This is not low, but still sufficiently low to provide non-trivial bounds on the tunneling splitting as shown in Fig. 5. For L = 11 the bounds on the tunneling splitting are 0.00184 ≤ ΔE ≤ 0.00236. In comparison, using the Temple lower bounds gives 0.00141 ≤ ΔE ≤ 0.00295. The numerically exact tunneling splitting is 0.00210.
3.3. Cases L* = 3 and L* = 4
These results can be significantly improved by considering energy levels higher than L* = 2. For this, initial lower bounds are required for the higher lying states. However, as discussed above, the Lanczos basis set used here is not sufficiently good for obtaining valid Weinstein lower bounds. The initial state, which is taken as a sum of two separated Gaussians localized in the vicinity of the minima of the two wells, does not give sufficient amplitude in the relevant regions for the higher lying states. As can be seen in Fig. 3, the second excited state (j = 3) Ritz eigenvalue for both the symmetric and asymmetric manifolds is quite far from the exact value. It is also clear from the figure, that the convergence is rather slow. However, the application of the Weinstein lower bounds is only one of several different strategies for obtaining initial lower bounds. For example, the quartic double-well potential can be bound from below by a harmonic oscillator potential. However, this turns out to give insufficient estimates; the lower bounds for the symmetric and antisymmetric manifolds were in our case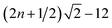 and
and 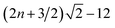 , n = 0, 1, respectively. Consequently, for n = 2, the lower bound for the third state in the symmetric manifold is approximately −5.64, which is lower than the Weinstein lower bound for the first excited state.
, n = 0, 1, respectively. Consequently, for n = 2, the lower bound for the third state in the symmetric manifold is approximately −5.64, which is lower than the Weinstein lower bound for the first excited state.
The strategy we employed was to use a semiclassical estimate for the energies, based on the action integral equal to (n + 1/2)h. This might be an inaccurate estimate for the tunneling doublets, but for the doublets this is not a problem, as we have shown that the Weinstein lower bound is appropriate. For the states above the barrier separating the two wells the two turning points for E ≥ 0 can be found directly as 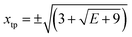 and the action integral is
and the action integral is
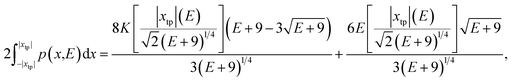 | (3.5) |
This same strategy was used to identify when the SCLBT condition expressed in eqn (2.10) was satisfied. For j = 3 the symmetric eigenvalue with L = 10 is 3.606246, which is 0.23 less than the semiclassical eigenvalue. In the antisymmetric case, the eigenvalue at L = 10 is 4.205842 while the semiclassical energy is 6.180353; thus, eqn (2.10) is satisfied and from L = 10 we can use the SCLBT with L* = 3. For L = 11 the fourth symmetric eigenvalue is 8.266892, which is less than the semiclassical energy of 8.755935 while for the antisymmetric manifold the fourth eigenvalue is 7.19180, which is much less than the semiclassical energy of 11.529150.
As a consequence, for L = 10 and L = 11 we can now obtain lower bounds also for the second tunneling doublet. First, we consider the case of L* = 3. This can be used for both the L = 10 and L = 11 dimensional Lanczos space. These results are given in the first two rows of Table 3. There is a noticeable improvement of the lower bounds as compared with those derived at L* = 2 and as the number of Lanczos vectors are increased from L = 10 to L = 11. The related gap ratios are presented in Table 4, and it is obvious that increasing L* to 3 significantly increases the quality of the lower bounds. Instead of the gap ratios in the order of ∼3–5 at L* = 2, they are in the order of ∼1–2 in this case. Obviously, the upper and lower bounds on the tunneling splittings are also improved accordingly.
| L | ε−,1,s | ε−,1,a | ε−,2,s | ε−,2,a | ΔE1 | ΔE2 |
|---|---|---|---|---|---|---|
| 10 | −6.642877 | −6.640737 | −2.469336 | −2.323896 | 0.001898 ≤ ΔE ≤ 0.002312 | — |
| 11 | −6.642826 | −6.640699 | −2.464559 | −2.322290 | 0.001963 ≤ ΔE ≤ 0.002238 | 0.119644 ≤ ΔE ≤ 0.153684 |
| 11 | −6.642836 | −6.640674 | −2.470646 | −2.318977 | 0.001989 ≤ ΔE ≤ 0.002249 | 0.122957 ≤ ΔE ≤ 0.159771 |
| L | L* | R1,s | R1,a | R2,s | R2,a |
|---|---|---|---|---|---|
| 10 | 3 | 1.628740 | 1.704331 | 1.638289 | 1.316617 |
| 11 | 3 | 1.534887 | 1.753226 | 1.445370 | 1.430994 |
| 11 | 4 | 1.696747 | 1.124009 | 2.103232 | 0.725466 |
For L* = 4, the results (last rows in Tables 3 and 4) become ambiguous. While a significant improvement can be seen for the antisymmetric lower bound energies, the symmetric case does not improve. The reason for this is that λ(11)4,s = 8.266892 is very close to the lower bound for the fifth state (8.768682). In the antisymmetric case, λ(11)4,a = 7.191803, which is substantially lower than the lower bound of 11.539668. According to eqn (2.13), when the Lanczos eigenvalue is too close to the next highest energy, the lower bound is not very accurate. This is also the reason why the L* = 4 case cannot be used to obtain lower bounds to the j = 3 state in each symmetry manifold. The resulting lower bounds are much too low.
Finally, given the high quality of the lower bounds, one can use the average of the upper and lower bounds to obtain a significantly improved estimate of the energy. For example, (λ(11)1,s + ε11,3−,1,s)/2 = −6.642745 and this can be compared with the numerically exact value of 6.642727. The mean value is nearly an order of magnitude more accurate than the estimate obtained from either the upper or lower bound separately. The same applies for the other states.
4. Discussion
In this study, we applied the self-consistent lower bound theory to obtain upper and lower bounds for tunneling splittings in a double-well potential. The results clearly show that the SCLBT provides accurate lower bounds to the relevant eigenvalues, which can be of the same quality as the upper bounds.However, the SCLBT is more complex than the upper bound theory, where only a basis set and the diagonalization of the resulting Hamiltonian matrix is required. The larger the basis set, the more accurate the eigenvalues are. For the lower bounds this is not sufficient. Some initial input is required. In this paper we showed how the Weinstein lower bounds and, if necessary, semiclassical energy estimates can be used. In addition, the SCLBT limits the energy levels for which lower bounds can be obtained according to the condition in eqn (2.10). We do note though that if the inequality does not hold, then the upper bound estimate is rather poor as well. In this sense, it can be expected that for all levels where the upper bound is relatively accurate, in the sense that its distance from the exact eigenvalue is much less than the gap between the adjacent states; the same applies for the lower bounds obtained with the SCLBT.
The system studied here is one-dimensional. A next step is to show that the SCLBT also works well for multidimensional tunneling systems, where the density of states is much higher and thus, calculations may be more challenging. The most restricting condition for application of the lower bound theory is expressed in eqn (2.10) which demands that the Ritz upper bound for the L-th state needs to be lower than the true energy of the (L + 1)-th state. Especially when the density of states is high, this condition can be challenging. We do note that typically this situation is not characteristic of the ground and lowest excited state tunneling doublets in molecules since the tunneling splittings are typically much smaller than the lowest harmonic frequency characterizing the molecule. However, further studies are needed to ascertain the extent of the challenge.
In addition, in the multidimensional case, the required basis set has to be much larger, the semiclassical estimate of levels in multidimensional systems is not always straightforward and other strategies might be needed for the initial lower bound estimates. However, we do believe that the present results are a significant step forward in the development of the lower bound theory and obtaining upper and lower bounds to energy differences.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Professor Rocco Martinazzo for helpful discussions. This work was generously supported by a grant of the Yeda-Sela Foundation of the Weizmann Institute of Science.Notes and references
- R. P. Bell, The Tunnel Effect in Chemistry, Chapman and Hall, London, 1980 Search PubMed.
- V. I. Gol'danskii, L. I. Trakhtenberg and V. N. Fleurov, Tunneling Phenomena in Chemical Physics, Gordon and Breach Sci. Publ., New York, 1991 Search PubMed.
- V. A. Benderskii, D. E. Makarov and C. A. Wight, Chemical Dynamics at Low Temperatures, Advances in Chemical Physics, John Wiley & Sons, Inc., 1994, vol. 88 Search PubMed.
- M. Razavy, Quantum Theory of Tunneling, World Scientific, 2003 Search PubMed.
- G. Mil'nikov and H. Nakamura, Tunneling Splitting and Decay of Metastable States in Polyatomic Molecules: Invariant Instanton Theory, Phys. Chem. Chem. Phys., 2008, 10, 1374–1393 RSC.
- E. M. Harrell, On the rate of asymptotic eigenvalue degeneracy, Commun. Math. Phys., 1978, 60(1), 73–95 CrossRef.
- S. Coleman, The Use of Instantons, in The Whys of Subnuclear Physics, Springer Berlin, USA, 1979, pp. 805–941 Search PubMed.
- M. Kac and C. J. Thompson, On the Mathematical Mechanisms of Phase Transition, Proc. Natl. Acad. Sci. U.S.A., 1966, 55(4), 676–683 CrossRef CAS.
- E. Brézin, G. Parisi and J. Zinn-Justin, Perturbation theory at large orders for a potential with degenerate minima, Phys. Rev. D, 1977, 16, 408–412 CrossRef.
- V. Benderskii, E. Vetoshkin, S. Grebenshchikov, L. von Laue and H. Trommsdorff, Tunneling splitting in vibrational spectra of non-rigid molecules. I. Perturbative instanton approach, Chem. Phys., 1997, 219(2), 119–142 CrossRef CAS.
- D. J. Wales, Energy Landscapes: Applications to Clusters, Biomolecules and Glasses, Cambridge University Press, Oxford, 2004 Search PubMed.
- C. Sousa-Silva, J. Tennyson and S. N. Yurchenko, Tunnelling Splitting in the Phosphine Molecule, J. Chem. Phys., 2016, 145(1–4), 091102 CrossRef.
- A. Viel, M. D. Coutinho-Neto and U. Manthe, The Ground State Tunneling Splitting and the Zero Point Energy of Malonaldehyde: A Quantum Monte Carlo Determination, J. Chem. Phys., 2007, 126(1–9), 024308 CrossRef.
- F. Wu, Y. Ren and W. Bian, The Hydrogen Tunneling Splitting in Malonaldehyde: A Full-dimensional Time-independent Quantum Mechanical Method, J. Chem. Phys., 2016, 145, 074309 CrossRef.
- A. E. Sitnitsky, Analytic Calculation of Ground State Splitting in Symmetric Double Well Potential, Comput. Theor. Chem., 2018, 1138, 15–22 CrossRef CAS.
- E. M. Harrell, Double wells, Commun. Math. Phys., 1980, 75(3), 239–261 CrossRef.
- A. Garg, Tunnel splittings for one-dimensional potential wells re-visited, Am. J. Phys., 2000, 68(5), 430–437 CrossRef.
- J. Zamastil, Multidimensional WKB approximation for particle tunneling, Phys. Rev. E, 2018, 98, 012211 CrossRef CAS.
- D.-Y. Song, Tunneling and energy splitting in an asymmetric double-well potential, Ann. Phys., 2008, 323(12), 2991–2999 CAS.
- T. A. H. Burd and D. C. Clary, Analytic Route to Tunneling Splittings Using Semiclassical Perturbation Theory, J. Chem. Theory Comput., 2020, 16(6), 3486–3493 CrossRef.
- E. Mátyus, D. J. Wales and S. C. Althorpe, Quantum tunneling splittings from path-integral molecular dynamics, J. Chem. Phys., 2016, 144(11), 114108 CrossRef.
- G. V. Mil'nikov and H. Nakamura, Practical implementation of the instanton theory for the ground-state tunneling splitting, J. Chem. Phys., 2001, 115(15), 6881–6897 CrossRef.
- J. O. Richardson and S. C. Althorpe, Ring-polymer instanton method for calculating tunneling splittings, J. Chem. Phys., 2011, 134(5), 054109 CrossRef.
- J. O. Richardson, S. C. Althorpe and D. J. Wales, Instanton calculations of tunneling splittings for water dimer and trimer, J. Chem. Phys., 2011, 135(12), 124109 CrossRef.
- C. S. Tautermann, A. F. Voegele, T. Loerting and K. R. Liedl, An accurate semiclassical method to predict ground-state tunneling splittings, J. Chem. Phys., 2002, 117(5), 1967–1974 CrossRef CAS.
- M. Takahashi, Y. Watanabe, T. Taketsugu and D. J. Wales, An ab initio study of tunneling splittings in the water trimer, J. Chem. Phys., 2005, 123(4), 044302 CrossRef.
- J. K. Gregory and D. C. Clary, Calculations of the tunneling split-tings in water dimer and trimer using diffusion Monte Carlo, J. Chem. Phys., 1995, 102(20), 7817–7829 CrossRef CAS.
- Y. Wang, B. J. Braams, J. M. Bowman, S. Carter and D. P. Tew, Full-dimensional quantum calculations of ground-state tunneling splitting of malonaldehyde using an accurate ab initio potential energy surface, J. Chem. Phys., 2008, 128(22), 224314 CrossRef.
- M. Schröder, F. Gatti and H.-D. Meyer, Theoretical studies of the tunneling splitting of malonaldehyde using the multiconfiguration time-dependent Hartree approach, J. Chem. Phys., 2011, 134(23), 234307 CrossRef.
- M. Ben-Nun and T. J. Martínez, Semiclassical Tunneling Rates from Ab Initio Molecular Dynamics, J. Phys. Chem. A, 1999, 103(31), 605–6059 CrossRef.
- R. Conte, A. Aspuru-Guzik and M. Ceotto, Reproducing Deep Tunneling Splittings, Resonances, and Quantum Frequencies in Vibrational Spectra From a Handful of Direct Ab Initio Semiclassical Trajectories, J. Phys. Chem. Lett., 2013, 4(20), 3407–3412 CrossRef CAS.
- B. Simon, Semiclassical Analysis of Low Lying Eigenvalues: II. Tunneling, Ann. Math., 1984, 120, 89–118 CrossRef.
- W. Kirsch and B. Simon, Universal Lower Bounds on Eigenvalue Splittings for one Dimensional Schrödinger Operators, Commun. Math. Phys., 1985, 97, 453–460 CrossRef.
- J. L. van Hemmen and W. F. Wreszinski, Universal Upper Bound for the Tunneling Rate of a Large Quantum Spin, Commun. Math. Phys., 1988, 119, 213–219 CrossRef.
- S. Abramovich, The Gap Between the First Two Eigenvalues of a One-dimensional Schrödinger Operator with Symmetric Potential, Proc. Am. Math. Soc., 1991, 111(2), 451–453 Search PubMed.
- M. Ashbaugh, “The Fundamental Gap”. Workshop on Low Eigenvalues of Laplace and Schrödinger Operators, Am. Inst. Math., Palo Alto, California, 2006 Search PubMed.
- X. J. Yu and C. F. Yang, The Gap Between the First Two Eigenvalues of Schrödinger Operators with Single-well Potential, Appl. Math. Comput., 2015, 268, 275–283 CrossRef.
- S. Nakamura, A Remark on Eigenvalue Splittings for One-dimensional Double-well Hamiltonians, Lett. Math. Phys., 1986, 11(4), 337–340 CrossRef.
- D.-Y. Chen and M.-J. Huang, On the Semiclassical Approximation to the Eigenvalue Gap of Schrödinger Operators, J. Math. Anal. Appl., 2012, 389, 1251–1258 CrossRef.
- E. Pollak, An Improved Lower Bound to the ground-state Energy, J. Chem. Theor. Comput., 2019, 15, 1498–1502 CrossRef CAS.
- E. Pollak, A Tight Lower Bound to the Ground-state Energy, J. Chem. Theor. Comput., 2019, 15, 4079 CrossRef CAS.
- R. Martinazzo and E. Pollak, Lower Bounds to Eigenvalues of the Schrödinger Equation by Solution of a Ninety Year Challenge, Proc. Natl. Acad. Sci. U. S. A., 2020, 202007093, DOI:10.1073/pnas.2007093117.
- E. Pollak and R. Martinazzo, Self-consistent Theory of Lower Bounds for Eigenvalues, J. Chem. Phys., 2020, 152, 244110 CrossRef CAS.
- W. Ritz and J. Reine, Über eine neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik, Ann. Math., 1908, 135, 1 Search PubMed.
- J. K. L. MacDonald, Successive Approximations by the Rayleigh-Ritz Variation Method, Phys. Rev., 1933, 43, 830–833 CrossRef.
- G. Temple, The Theory of Rayleigh's Principle as Applied to Continuous Systems, Proc. R. Soc. London, Ser. A, 1928, 119, 276 Search PubMed.
- C. Lanczos, An Iteration Method for the Solution of the Eigenvalue Problem of Linear Differential and Integral Operators, J Res Natl Bur Stand, 1950, 45, 255–282 CrossRef.
- D. H. Weinstein, Modified Ritz Method, Proc. Natl. Acad. Sci. U.S.A., 1934, 20, 529–532 CrossRef CAS.
- A. F. Stevenson, On the Lower Bounds of Weinstein and Romberg in Quantum Mechanics, Phys. Rev., 1938, 53, 199 CrossRef.
- T. Kato, On the Upper and Lower Bounds of Eigenvalues, J. Phys. Soc. Jpn., 1949, 4, 334–339 CrossRef.
- N. W. Bazley and D. W. Fox, Lower Bounds for Eigenvalues of Schrödinger's Equation, Phys. Rev., 1961, 124, 483–492 CrossRef CAS.
- P.-O. Löwdin, Studies in Perturbation Theory. XI. Lower Bounds to Energy Eigenvalues, Ground State, and Excited States, J. Chem. Phys., 1965, 43, S175 CrossRef.
- F. Weinhold, Lower Bounds to Expectation Values, J. Phys. Gen. Phys., 1970, 1, 305–313 CrossRef.
- W. H. Miller, Improved Equation for Lower Bounds to Eigenvalues; Bounds for the Second-Order Perturbation Energy, J. Chem. Phys., 1969, 50, 2758–2762 CrossRef CAS.
- M. Cohen and T. Feldmann, Lower Bounds to Eigenvalues, Can. J. Phys., 1969, 47, 1877–1879 CrossRef CAS.
- F. Weinhold, Criteria of Accuracy of Approximate Wavefunctions, J. Math. Phys., 1970, 11, 2127–2138 CrossRef.
- R. N. Hill, Tight Lower Bounds to Eigenvalues of the Schrödinger Equation, J. Math. Phys., 1980, 21, 2182–2192 CrossRef.
- A. Scrinzi, Lower Bounds to the Binding Energies of tdμ, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7787–7791 CrossRef.
- M. G. Marmorimo, Equivalence of Two Lower Bound Methods, J. Math. Chem., 2002, 31, 197–203 CrossRef.
- M. G. Marmorino and F. Gupta, Surpassing the Temple Lower Bound, J. Math. Chem., 2004, 35, 189–197 CrossRef CAS.
- M. G. Marmorino, A. Almayouf, T. Krause and D. Le, Optimization of the Temple Lower Bound, J. Math. Chem., 2012, 50, 833–842 CrossRef CAS.
- M. G. Marmorino and V. Black, Lower Bounds to the Ground-State Expectation Value of Non-negative Operators, J. Math. Chem., 2016, 54, 1973–1985 CrossRef CAS.
- M. G. Marmorino, Upper and lower bounds to atomic radial position moments, J. Math. Chem., 2020, 58, 88–113 CrossRef CAS.
- F. Rioux, Numerical solutions for a double-minimum potential well, Chemistry Libre Texts, 2019 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |