Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solar thermochemical CO2 splitting with doped perovskite LaCo0.7Zr0.3O3: thermodynamic performance and solar-to-fuel efficiency
Lei Wang ab,
Tianzeng Maab,
Shaomeng Daiab,
Ting Rena,
Zheshao Changa,
Mingkai Fu
ab,
Tianzeng Maab,
Shaomeng Daiab,
Ting Rena,
Zheshao Changa,
Mingkai Fu *a,
Xin Liab and
Yong Li
*a,
Xin Liab and
Yong Li *c
*c
aInstitute of Electrical Engineering, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: fumingkai@mail.iee.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing, 100190, China
cSchool of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China. E-mail: liyong@ustb.edu.cn
First published on 29th September 2020
Abstract
The research of thermochemical CO2 splitting based on perovskites is a promising approach to green energy development. Performance evaluation was performed towards the doped perovskite LaCo0.7Zr0.3O3 (LCZ-73) based two-step thermochemical CO2 splitting process thermodynamically based on the experimentally derived parameters for the first time. The impacts of vacuum pump and inert gas purge to reduce oxygen partial pressure and CO2 heating on the performance parameter ηsolar-to-fuel have been analyzed. The results showed that at the PO2 of 10−5 bar, non-stoichiometric oxygen δ increased by more than 3 times as the reduction temperature varied from 1000 °C to 1300 °C, however, no significant deviation of δ was observed between 1300 °C and 1400 °C. The reaction enthalpy ranged from 60 to 130 kJ mol−1 corresponding to δ = 0.05–0.40. Comparing the abovementioned two ways to reduce the oxygen partial pressure, the ηsolar-to-fuel of 0.39% and 0.1% can be achieved with 75% and without heat recovery with the CO2 flow rate of 40 sccm under experimental conditions, respectively. The energy cost for CO2 heating during the thermodynamic process as the nCO2/nLCZ-73 increases was obtained from the perspective of energy analysis. The ratio of nCO2/nLCZ-73 at lower temperature required more demanding conditions for the aim of commercialization. Finally, the ability of perovskite to split CO2 and thermochemical performance were tested under different CO2 flow rates. The results showed that high CO2 flow rate was conducive to the production of CO, but at the cost of low ηsolar-to-fuel. The maximum solar-to-fuel efficiency of 1.36% was achieved experimentally at a CO2 flow rate of 10 sccm in the oxidation step and 75% heat recovery.
1. Introduction
CO2 is the main greenhouse gas of the Earth because of its stable thermodynamic properties and large amounts of emission in a short period of time.1 Thermochemical CO2 splitting is an effective method to mitigate CO2 emissions and provide a sustainable energy development path.2 As the most abundant energy source on the Earth, solar energy is clean and pollution-free, and has received the attention of many countries in the world. Using solar energy as a source of energy for thermochemical fuel production can effectively alleviate the global energy crisis and global warming effect.3,4 Solar thermochemical CO2 splitting takes sufficient solar energy as the heat source and greenhouse gas CO2 as the carbon source, which can realize the sustainable production of carbonaceous fuel,5,6 and can be converted into liquid fuels through existing industrial facilities for long-distance transportation and storage.7 At the same time, in this process, discontinuous and low energy density solar energy is stored in the form of fuel chemical energy with high energy density.The solar two-step thermochemical fuel production with metal oxide perovskite, ABO3, as the oxygen carrier has received more and more attention from the researchers in recent years.8,9 Compared to the more studied binary oxide cerium oxide, perovskites have the advantage of being able to be reduced at lower operating temperatures, while having a greater amount of oxygen released so that more fuel can be produced in the oxidation step.10,11 In recent years, it has been reported that perovskite is used as oxygen carrier to split CO2 for CO production.12,13 Dey et al. studied the substituted La0.5Sr0.5MnO3 with trivalent metal ion at B site, and the results showed that the performance of thermochemical CO2 splitting was significantly improved by 5% Sc substitution at B position, and the yield of O2 and CO increased by 2 times and 1.7 times, respectively.14 Muhich et al. compared the performance of perovskite and ceria in thermochemical splitting of CO2, and found that perovskite has a high CO production capacity under a large CO2 flow rate, but at the same time, the solar-to-fuel efficiency is lower due to the high heating cost.15 Ezbiri et al. extensively screened the perovskite redox activity and thermochemical stability used for solar thermochemical splitting of CO2 by density functional theory, and verified the calculation results through experiments and applied them to fine-tune the oxygen exchange capacity of selected perovskite components.16 Galvez and coworkers studied the splitting of CO2 by Ca and Sr-doped LaMnO3 perovskites and found that the formation of carbonates resulted in a decrease in thermochemical efficiency due to incomplete conversion of CO2.17 Demont et al. studied the solar CO2 splitting via two-step thermochemical cycle with A- and B-site substituted Mn-perovskites, the results showed the effectiveness of the incorporation of Y in A-site and Mg in B-site in terms of CO production when compared with ceria.18 Cooper et al. studied LaMnO3 perovskite with Ca/Sr A-site and Al B-site doping for CO2 splitting, the results show that these materials could split CO2 into CO at 1240 °C and could approach complete oxidation at 1040 °C. The fuel production per unit mass was 10 times that of CeO2 under the same conditions.19 Bork and coworkers found a material, La0.6Sr0.4Cr0.8Co0.2O3−δ with efficient solar-to-fuel conversion at lower temperatures. Thermogravimetric experiments showed that the ability to decompose CO2 is more than 25 times that of CeO2 in the two-step thermochemical cycle of 800–1200 °C.20 Demont et al. studied the splitting of CO2 by two-step solar thermochemical of LaMnO3 perovskite doped with Sr, and characterized the redox thermodynamics properties. The results showed that a certain amount of Sr can tune the redox thermodynamics of the series of materials, which has a high activity for the splitting of CO2.21 Takalkar et al. studied the thermochemical CO2 splitting by PrxSr1−xMnO3 perovskites by thermogravimetry. It was found that lower Pr and higher Sr can effectively increase CO production, and two optimal perovskites were identified as promising materials for thermochemical CO2 splitting.22 Jiang et al. studied the loaded LaFeO3 perovskite with A- and B-sites doping. The CO production increased by 2–3 times, and the controlling mechanism and kinetic model of CO2 splitting process were analyzed.23
Currently, in the two-step thermochemical CO2 splitting with perovskite as the oxygen carrier, most of the researches focus on one or the perovskite series through the different contents of elemental doping. The main goal of the studies is to find a high-performance perovskite that increases fuel production and thus achieves high solar-to-fuel efficiency (ηsolar-to-fuel). The direction of efforts is mainly focused on the improvement of redox thermodynamics, kinetic properties and thermal stability of the material thermochemical cycle. Although researchers have made a lot of efforts in these areas and made great progress in some areas, the current researches in the field of thermochemical fuel research have low efficiency and cannot be commercialized. At present, the world's largest thermochemical fuel system is in pilot scale,24 and how to achieve efficient fuel production remains a major challenge. It is beneficial to explore materials that can balance the advantages of reduction and oxidation reactions, and thermodynamic analysis should be performed when conducting primary materials screening.25 However, there are few studies on the thermodynamics of perovskite thermochemical fuel production. Thermodynamic analysis was only performed theoretically in literatures. Carrillo and Scheffe established a thermodynamic model to calculate the solar-to-fuel efficiency of La1−x(Sr,Ca)xMn1−yAlyO3 perovskites, showing the potential to improve the efficiency during isothermal or near-isothermal thermochemical cycles.26 Muhich et al. implemented a thermodynamic system model of solar thermochemical fuel production based on mass and energy balances, the results showed the promising of perovskites due to the high fuel production capacities under large H2O/CO2 flow rates, but the poor solar-to-fuel efficiency due to the high heating load.15 Bork et al. performed a Calphad defect model to optimize and calculate the redox thermodynamics of Cr-doped La0.6Sr0.4MnO3 perovskite for solar-to-fuel conversion, the results revealed that both the thermochemical fuel production and the solar-to-fuel efficiency of the Cr-doped materials were improved. These predictive perspectives are expected to provide prospects for the thermodynamic engineering of perovskite thermochemical reactions towards high solar-to-fuel efficiency.27 Overall, the existing studies on thermodynamic analysis and solar-to-fuel efficiency mainly focus on theoretical analysis, but the extent to which level of this efficiency, especially the solar-to-fuel efficiency still needs more experimental proof.
To our knowledge, there are no studies addressing the thermodynamic analysis of CO2 conversion into fuels using Zr doped LaCoO3. This paper focuses on the report of a detailed thermodynamic analysis of a two-step thermochemical CO2 splitting process with perovskite LaCo0.7Zr0.3O3 (LCZ-73) as the oxygen carrier based on the obtained thermodynamic parameters experimentally. Material synthesis, characterization and thermochemical performance of CO2 splitting have been reported in the previous experimental work,28 in which studies of elements doping, doping concentration, the redox temperatures, heating rates on the performance of the doped LaCoO3 perovskites based two-step thermochemical CO2 splitting and reduction kinetics were illustrated. The results demonstrated the stability of the material before and after the thermochemical redox cycles, the activity of thermochemical CO2 splitting and better reduction kinetics than other perovskite metal oxides and cerium oxides reported in the literature. These studies focused on discussing the performance of thermochemical CO2 splitting from the perspective of experiments, but did not involve the thermodynamics of this process. Therefore, this paper discussed the thermodynamics of thermochemical CO2 splitting from the perspective of solar to fuel conversion. The thermochemical reduction enthalpy was obtained and the thermodynamic efficiency was analyzed with the consideration of gas–gas, gas–solid phase heat recuperation as well as the use of vacuum pump and vacuum pump combined with inert gas purge to reduce the oxygen partial pressure. Based on the experimental conditions, the solar-to-fuel efficiency of the solar thermochemical fuel production process was analyzed by combining the vacuum pump with the inert gas purge and directly the vacuum pump to reduce the oxygen partial pressure, respectively. The energy consumed for CO2 heating took up the bulk of energy consumption of the thermodynamic process as the nCO2/nLCZ-73 increases based on the energy analysis. Finally, the thermodynamic model was verified by experimentally testing the CO2 splitting performance under different CO2 flow rates and analyzing its solar-to-fuel efficiency. This paper revealed that one of the main problems in the field of solar thermochemical fuel production was the huge energy input caused by excessive oxidant in the oxidation step, which resulted in low efficiency.
2. Experiment and mathematical model
2.1. Experimental procedure and apparatus
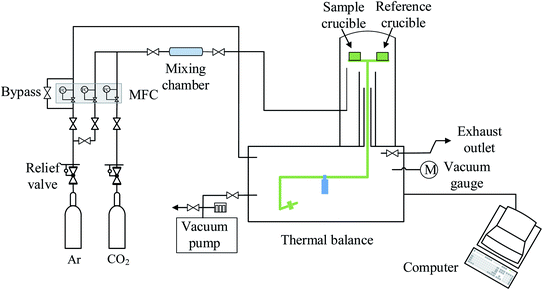
LaCo0.7Zr0.3O3 perovskite powder was prepared by citric acid sol–gel method, which was described in detail in previous studies.28 Metal nitrate precursors were obtained commercially (Aladdin and Macklin) and were specified to be >99.5% pure. XRD measurements confirmed the existence of perovskite structure LaCo0.7Zr0.3O3, SEM image showed that the sample was irregularly shaped particles with a size in the a few microns and EDS analysis verified that the synthesized sample compositions were in line with expectations. Similarly, XRD of the powder sample after reduction showed that it still maintained the perovskite phase structure. The measurements of the redox reactions were carried out with a high temperature thermogravimetric analyzer (TGA, LINSEIS STA PT 1600). To avoid the effects of thermal inertia during testing, fresh material of LaCo0.7Zr0.3O3 (LCZ-73) oxide of the same batch of synthetic sample powder was used in each test. Granular powders with an average weight of approximately 10 mg were evenly placed in an alumina crucible with a volume of about 100 μl throughout all the measurement series. Before the formal start of the redox experiments, a vacuum pump was used to vacuum the furnace chamber to 5.5 × 10−5 atm for a low oxygen environment, and then purged with high purity argon (99.999%) for one hour to provide an inert environment and further reduce the oxygen partial pressure. The inert atmosphere was always maintained throughout the reduction process and during the process of reducing from reduction temperature to the oxidation temperature to blow the released oxygen out of the furnace in time. High purity argon was used as the purge and protective gas, the same high purity carbon dioxide (99.999%) was used as the oxidant during the oxidation process. The overall gas flow rate entering the reaction chamber was maintained at 80 sccm, with the balance being protected with argon flow of 40 sccm at all times. In the reduction process, the sample was heated to 1000, 1100, 1200, 1300, 1400 °C, respectively, at a heating rate of 30 °C min−1 and maintained for 60 min with continuous and constant Ar flow. Then the temperature was lowered to 800 °C at the same rate for oxidation. In the oxidation step, the high purity Ar (40 sccm) and high purity CO2 with a flow rate of 40 sccm (PCO2 = 0.5 atm) were mixed and introduced into the furnace chamber to react with the oxygen-deficient perovskite and produce CO. The trace oxygen was blown out and diluted to further reduce the impact on CO2 splitting. This oxidation process proceeded for 60 min. The specific experimental platform was shown in the Fig. 1.Since the redox behavior analysis of perovskite in this work was mainly based on thermogravimetric analysis, the mass change in sample was induced by the release and uptake of oxygen under high temperatures and specific oxygen partial conditions, then the non-stoichiometry of the perovskite can be determined by measuring the mass change. The relationship between the mass change Δm and the nonstoichiometric oxygen δ is as follow:29
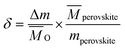 | (1) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) perovskite and
perovskite and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) O are the molar mass of the perovskite and the atomic oxygen, respectively.
O are the molar mass of the perovskite and the atomic oxygen, respectively.
Thermodynamic parameters are extracted from the Van't Hoff approach. The standard molar Gibbs free energy of the reduction reaction can be expressed as follow:8,30
ΔGΘ(T) = −![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) T T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kred = ΔHΘred − TΔSΘred Kred = ΔHΘred − TΔSΘred
| (2) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and T are the oxygen partial pressure, the standard pressure and PΘ = 1 bar, the universal gas constant and the reduction temperature, respectively. Inserting the relationship of Kred into eqn (1), for constant oxygen non-stoichiometry, δ, the above equation can be rearranged as
and T are the oxygen partial pressure, the standard pressure and PΘ = 1 bar, the universal gas constant and the reduction temperature, respectively. Inserting the relationship of Kred into eqn (1), for constant oxygen non-stoichiometry, δ, the above equation can be rearranged as
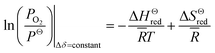 | (3) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) Θred is the standard molar enthalpy and can be determined through an Arrhenius plot for sets of temperature T and ln(PO2).
Θred is the standard molar enthalpy and can be determined through an Arrhenius plot for sets of temperature T and ln(PO2).
2.2. Mathematical model
A typical thermochemical redox cycle of CO2 splitting for a two-step process based on perovskite can be exemplified in the following reactions:
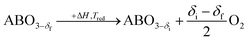 | (4) |
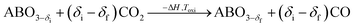 | (5) |
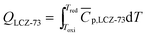 | (6) |
The energy required to drive the reduction reaction of one molar perovskite is:
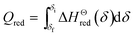 | (7) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p,LCZ-73 is the molar specific heat capacity of perovskite LCZ-73 used in the test, which can be obtained by differential scanning calorimeter. According to the thermal effect obtained by differential scanning calorimetry and the formula ΔQ = (m/
p,LCZ-73 is the molar specific heat capacity of perovskite LCZ-73 used in the test, which can be obtained by differential scanning calorimeter. According to the thermal effect obtained by differential scanning calorimetry and the formula ΔQ = (m/![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) )
)![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) pΔT, the value of
pΔT, the value of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p can be obtained. In fact, the specific heat capacity is a function of temperature, but for convenience, the average value of
p can be obtained. In fact, the specific heat capacity is a function of temperature, but for convenience, the average value of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p,LCZ-73 = 157.5 J (mol−1 K−1) is considered.
p,LCZ-73 = 157.5 J (mol−1 K−1) is considered.
Researches have shown that decreasing oxygen partial pressure in the thermal reduction process is beneficial to the increase of δ and the efficiency of thermochemical fuel production.31 There are two common ways to reduce oxygen partial pressure of the reduction process in thermochemical fuel research: vacuum pump and inert gas purge.
2.2.1.1. Pumping. A vacuum pump is needed to eliminate the residual air in the reactor to provide a lower oxygen partial pressure environment during the thermal reduction process. Qpump is the energy consumed to obtain a lower oxygen partial pressure with a vacuum pump. In this paper, the ideal pump work is used to calculate the performance of solar-to-fuel efficiency.32
Qpump = nO2![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) Tpump Tpump![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P0/PO2)/ηS→W ln(P0/PO2)/ηS→W
| (8) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is the universal gas constant, Tpump is the operating temperature of the pump. In this study, the temperature is the ambient temperature. P0 is the experimental pressure at atmospheric pressure. PO2 is the oxygen partial pressure inside the instrument after vacuuming, ηS→W is the solar energy to pump work conversion efficiency and its value is assumed to be 0.1 in this paper.32
is the universal gas constant, Tpump is the operating temperature of the pump. In this study, the temperature is the ambient temperature. P0 is the experimental pressure at atmospheric pressure. PO2 is the oxygen partial pressure inside the instrument after vacuuming, ηS→W is the solar energy to pump work conversion efficiency and its value is assumed to be 0.1 in this paper.32
2.2.1.2. Sweep gas. Argon was used as the sweep gas in the reduction step and as the shielding gas for the balance chamber throughout the thermochemical process. In our experiment, high purity Ar (99.999%) with an oxygen impurity concentration less than 10 ppm was used. Considering that the high-temperature exhaust gas in the reduction process carries a large amount of heat, it can be used to preheat Ar required for the reduction reaction. Therefore, the energy required to heat sweep gas by considering the heat recovery of exhaust gas is calculated as:
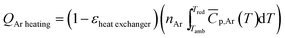 | (9) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p,Ar = 20.786 J (mol−1 K−1).34
p,Ar = 20.786 J (mol−1 K−1).34
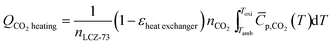 | (10) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p,CO2(T) = 20.99 + 6.768 × 10−2T − 4.960 × 10−5T2 + 1.779 × 10−8T3 − 2.495 × 10−12T4 p,CO2(T) = 20.99 + 6.768 × 10−2T − 4.960 × 10−5T2 + 1.779 × 10−8T3 − 2.495 × 10−12T4
| (11) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p,CO2 is the molar specific heat capacity of CO2 under a standard atmospheric pressure and is a function of temperature T, which can be given as a polynomial fits in J (mol−1 K−1).33
p,CO2 is the molar specific heat capacity of CO2 under a standard atmospheric pressure and is a function of temperature T, which can be given as a polynomial fits in J (mol−1 K−1).33
2.2.2.1. Heat recovery. It is difficult to realize the heat utilization of solid reactants by heating low temperature solid with high temperature solid35 and may present some other problems. In many previous studies, the heat recovery of solid reactants was not considered.33 The idea of using a heat exchanger to convert solid heat into process heat to heat the oxidant to improve efficiency33 is also used in the analysis herein.
Under the experimental conditions, in order to maintain the oxidation reaction at a constant temperature, continuous additional heating is necessary. The heat transfer for one molar LCZ-73 during the oxidation reaction is calculated:
| Qoxi = −Qred + (δi − δf)HHVCO | (12) |
The available amount of the recovered heat from the solid reactants is limited by the heat required for CO2 heating in the oxidation process,
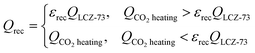 | (13) |
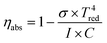 | (14) |
An energy balance equation for the entire thermochemical processes yields the following equation:33,38
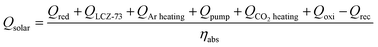 | (15) |
Here we assume that the required electrical heating energy, pumping power, energy for gas purging, CO2 heating and energy required to maintain a constant temperature for oxidation and other energy-consuming processes of the thermochemical cycle are all provided by solar energy. The available heat recovery of the system is also considered.
According to the first law of thermodynamic, ηsolar-to-fuel of the two-step thermochemical redox processes is chosen as the merit of the thermochemical cycling performance,40,41 which is defined as the ratio of the calorific value of the fuel to the total solar energy input in the system:33,38,42
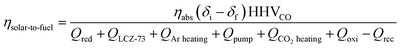 | (16) |
3. Results and discussion
3.1. Thermodynamic characteristics of LCZ-73
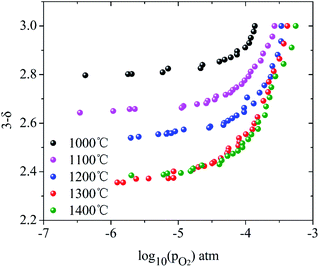
Here, the relationship between oxygen partial pressure and non-stoichiometric oxygen δ during the reduction process after reaching the target temperatures is revealed. As shown in Fig. 2, the non-stoichiometric oxygen δ in LaCo0.7Zr0.3O3−δ is highly dependent on reduction temperature and the oxygen partial pressure (PO2). As the oxygen partial pressure (PO2) decreases, the non-stoichiometric oxygen δ gradually increases, but the increase rate slows down as the reduction reaction proceeds. Under the same oxygen partial pressure environment, the high temperature is more favorable for the generation of non-stoichiometric oxygen in the reduction process. But it is not that the higher the temperature is, the better it will be. At 1300 °C and 1400 °C, the ability to produce non-stoichiometric oxygen under both conditions is nearly the same. At the oxygen partial pressure of 10−5 bar, the non-stoichiometric oxygen at the reduction temperature of 1000–1400 °C is 0.18, 0.34, 0.44, 0.60 and 0.60, respectively. The non-stoichiometric oxygen δ increases by more than 3 times when the temperature varies from 1000 °C to 1300 °C. At 1000 °C, the non-stoichiometric oxygen δ is doubled when PO2 changes from 10−4 to 10−5 bar, while, at 1300 °C, this value increases by a third. Lower oxygen partial pressure is required when the same non-stoichiometric oxygen is reached at low temperature. At δ = 0.2, the oxygen partial pressure PO2 during 1000–1400 °C varies from 10−5.75 to 10−3.55 bar.Based on the above analysis, the derived ln(PO2) versus inverse temperature for LCZ-73 is shown in Fig. 3. Considering that there is a certain error in the oxygen partial pressure at some points, the linearity is not ideal for all when performing linear fitting on the data points, especially for the δ = 0.20 and δ = 0.25. Similarly, it can be found that the non-stoichiometric oxygen increases with decreasing the oxygen partial pressure at the same temperature. In order to achieve the same δ, a lower oxygen partial pressure is required at low temperature. Fig. 3 also shows two ways to obtain larger non-stoichiometric oxygen δ: increasing temperature and decreasing oxygen partial pressure. According to the existing data with better linearity, it can be seen that ΔHΘred in eqn (3) is likely to be temperature-independent, which is confirmed in other studies.30 Simultaneously, this also shows the reliability of our experimental data. Based on this, we can get the relationship between the reduction enthalpy ΔHΘred and the different oxygen stoichiometry δ during the thermochemical reduction process, which will be discussed next.
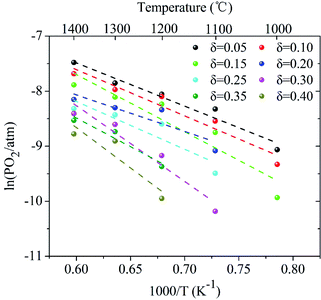 | ||
| Fig. 3 Arrhenius plots of oxygen partial pressure versus inverse temperature for LaCo0.7Zr0.3O3 (LCZ-73) corresponding to fixed δ between 0.05 and 0.40. | ||
The energy required to generate oxygen vacancies in the perovskite LCZ-73 can be obtained via the change of reduction enthalpy, ΔHΘred. Similar studies have shown that reduction enthalpy is only related to stoichiometry δ.8,43 As shown in Fig. 4, the curve for the change in standard molar reduction enthalpy is fit with a polynomial. The value of ΔHΘred is 60–130 kJ mol−1 when δ in the range of 0.05–0.40. The following thermodynamic analysis will be based on these results for discussion.
| ΔHΘred(δ) = 58.529 + 71.905δ + 905.361δ2 − 1724.966δ3 | (17) |
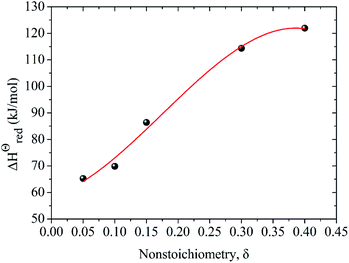 | ||
| Fig. 4 Variation of reduction enthalpy of LaCo0.7Zr0.3O3 (LCZ-73) as a function of oxygen non-stoichiometry δ. | ||
3.2. Solar-to-fuel efficiency analysis for LCZ-73 based solar CO production system
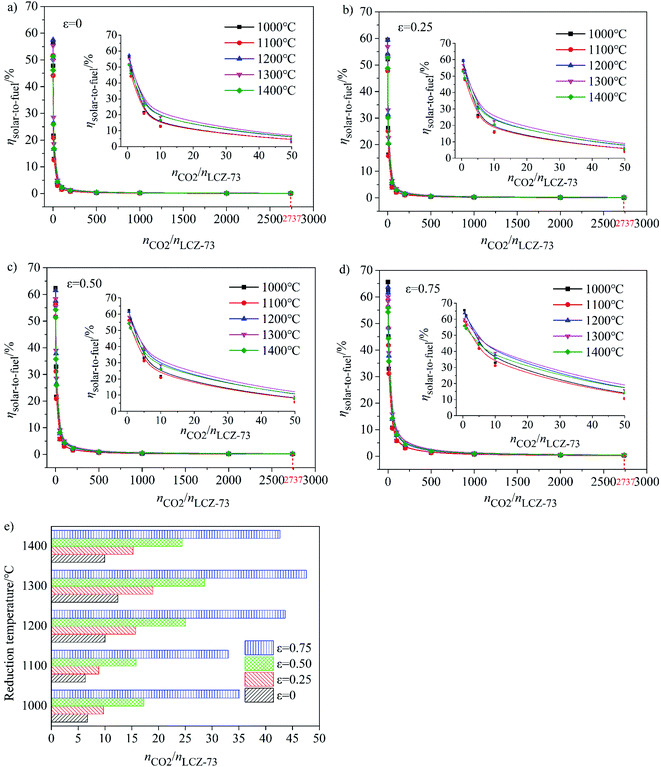
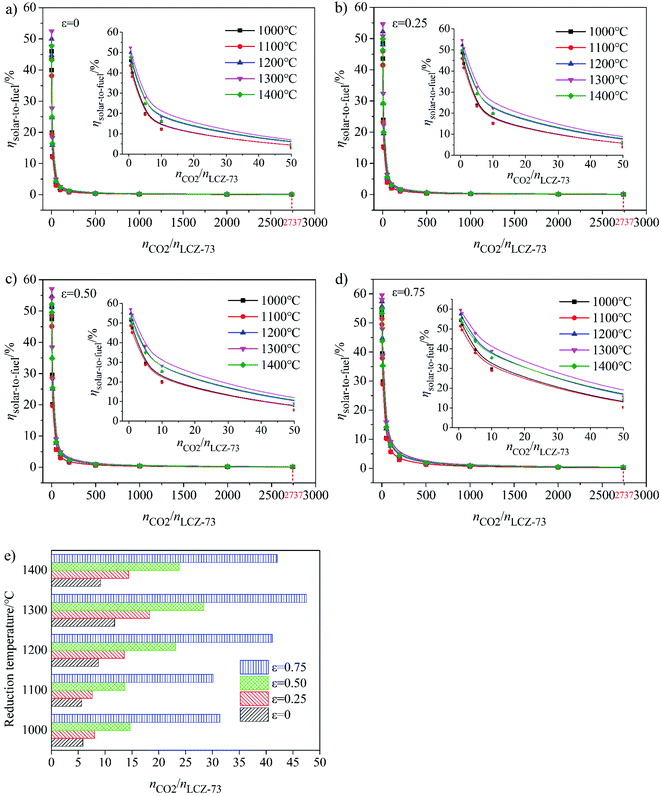
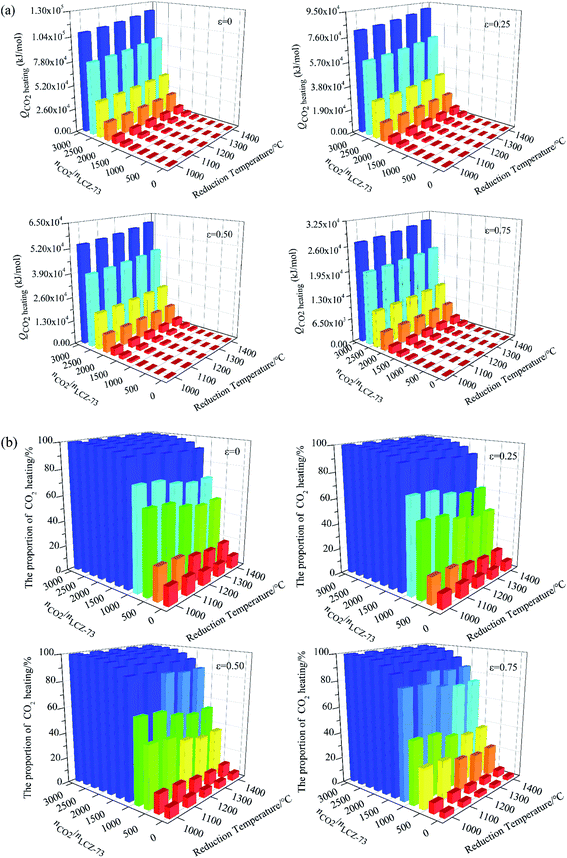
As shown in Fig. 5(a)–(d), at the molar ratio of nCO2/nLCZ-73 ≤ 500, ηsolar-to-fuel decreases rapidly with the increase of the ratio, and decreases slowly when the molar ratio is greater than 500. In Fig. 5(a)–(c), ηsolar-to-fuel ≤ 1% at nCO2/nLCZ-73 ≥ 500, the molar ratio of nCO2/nLCZ-73 is enlarged to 1000 in Fig. 5(d). This also means that higher efficiency can be achieved with higher heat recovery. This can also be found from Fig. 5(a)–(d) that with the increase of εheat exchanger, ηsolar-to-fuel increases gradually. In the current experimental situation, the molar ratio of nCO2/nLCZ-73 is 2737![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ηsolar-to-fuel = 0.39% is obtained at the reduction temperature of 1300 °C with 75% heat recovery. While, when no heat recovery is considered, this efficiency is just 0.1%.
1, ηsolar-to-fuel = 0.39% is obtained at the reduction temperature of 1300 °C with 75% heat recovery. While, when no heat recovery is considered, this efficiency is just 0.1%.
The insets are the partial enlargements with the molar ratio of less than 50. Overall, under the same conditions, the highest ηsolar-to-fuel is achieved at 1300 °C and nCO2/nLCZ-73 ≥ 5 in Fig. 5(a)–(c) and nCO2/nLCZ-73 ≥ 10 in Fig. 5(d). When the ratio of nCO2/nLCZ-73 < 10, ηsolar-to-fuel will reach 20% or more in Fig. 5(a)–(c) and for higher heat recovery in Fig. 5(d), ηsolar-to-fuel of 20% can be achieved at nCO2/nLCZ-73 < 50. This efficiency value is also proposed based on estimated qualitatively in reference and is considered as the benchmark for commercially achievable system-level annual average solar-to-fuel efficiency for a viable alternative to conventional electrolysis.44 For this competitive efficiency reference value, further analysis is shown in Fig. 5(e). When the efficiency reaches 20%, nCO2/nLCZ-73 = 47.59 at 1300 °C, and nCO2/nLCZ-73 = 35.12 at 1000 °C with 75% heat recovery. The molar ratios of nCO2/nLCZ-73 are 12.4 and 6.74 with no heat recovery, respectively. Compared with higher temperature conditions (1300 and 1400 °C), the molar ratio of nCO2/nLCZ-73 at low temperature requires more demanding conditions with the prospects of commercialization. This is still a big challenge in the current research background of thermochemical fuels. However, under the same conditions, the larger molar ratio of nCO2/nLCZ-73 is more accessible under current technical conditions.
Variation of molar ratio of nCO2/nLCZ-73 corresponding to the solar-to-fuel efficiency of 20% with heat exchange coefficient εheat exchanger at different reduction temperatures was shown in Fig. 6(e). Similarly, we find that when the efficiency reaches 20% and as the benchmark, the ratio of nCO2/nLCZ-73 is maximum at 1300 °C, reaching about 50, which is the easiest to reach in the temperature range in question. At the same time, this means that if there is a more efficient way to reduce the ratio of nCO2/nLCZ-73, then at 1300 °C, solar-to-fuel efficiency will be higher than 20%. This is a great encouragement for commercialization. However, in most of the current experimental studies of two-step solar thermochemical fuel production cycles, the far excessive amount of oxidant in oxidation step is used for a high fuel production. How to effectively reduce the amount of oxidant introduced into the oxidation step becomes the key to improve the solar-to-fuel efficiency. Another finding is that as the heat exchange coefficient increases, nCO2/nLCZ-73 at the same temperature changes monotonously, indicating that as the heat recovery increases, the conditions for commercialization are more moderate, and the solar-to-fuel efficiency is higher.
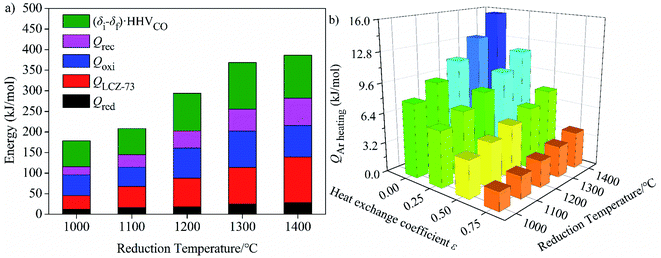
Similarly, the energy consumed for CO2 heating with heat recovery as functions of reduction temperature and molar ratio of nCO2/nLCZ-73 is given in Fig. 8(a). The molar ratio of nCO2/nLCZ-73 increases as the amount of CO2 increases, and the energy consumed for CO2 heating increases significantly. When nCO2/nLCZ-73 varies from 100 to 1000, the energy consumed increases by a corresponding multiple. Compared with the molar ratio of nCO2/nLCZ-73, the reduction temperature has much smaller impact on the energy consumed for CO2 heating. The energy increases slightly with the increase of reduction temperature, but the trend is gentle. The energy for CO2 heating is two or three orders of magnitude higher than those in Fig. 7(a) and (b).
Finally, the proportion of energy required for CO2 heating in total input energy is summarized in Fig. 8(b). It can be seen that the proportion rapidly increases with the increase of nCO2/nLCZ-73, but decreases slightly with the increase of the reduction temperature, which is mainly because the reduction temperature has little influence on the energy of CO2 heating, but has great impact on the total input energy. With the increase of heat exchanger coefficient, the proportion of energy consumption for CO2 heating gradually decreases. As the molar ratio of nCO2/nLCZ-73 increases, the proportion of energy for CO2 heating in total input energy increases rapidly, resulting in lower solar-to-fuel efficiency. At 1300 °C and εheat exchanger = 0.5, when nCO2/nLCZ-73 = 0.5, the proportion of CO2 heating is only 5.35%, while, when nCO2/nLCZ-73 = 50, the proportion reaches nearly 85.0%. When the amount of CO2 is further increased, this proportion reaches 95.8% as the ratio of nCO2/nLCZ-73 increased to 200. This also reveals the reason why the current thermochemical fuel research is less efficient.
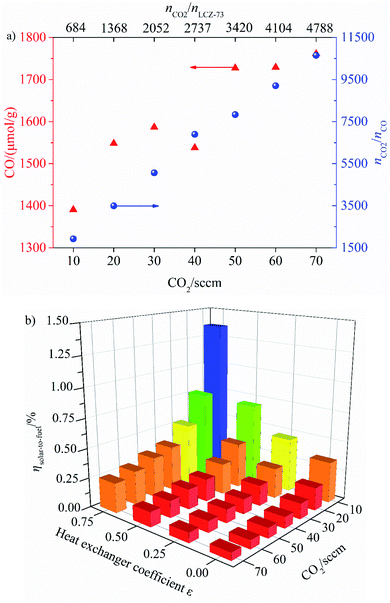
As shown, the effects of CO2 flow rate on CO yield and solar-to-fuel efficiency at various heat exchanger coefficient εheat exchanger are analyzed. It can be clearly seen from Fig. 9(a) that the yield of CO increases gradually with the increase of CO2 flow rate, and the high CO2 concentration is favorable for the oxidation reaction. At the same time, the ratio of nCO2/nCO changes monotonically with the increase of CO2 flow rate. When the CO2 flow rate in the oxidation step is 10 sccm, nCO2/nLCZ-73 = 684, nCO2/nCO = 1926, and the same value is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 when the CO2 flow rate is 70 sccm at nCO2/nLCZ-73 = 4788, the latter represents an increase of nearly 27% in CO yield over the former. However, it is also noted that solar-to-fuel efficiency is negatively correlated with the increase of CO2 flow rate in Fig. 9(b). Although CO yield is low at low CO2 flow rate, solar-to-fuel efficiency is high. In order to prove that this material can still split CO2 under the condition of lower molar ratios, further experiments would be needed for verification, such as the CO2 flow rate is less than 10 sccm (nCO2/nLCZ-73 < 684). It should be noted that an excessively low CO2 flow rate may impose higher requirements on the experimental devices in actual operation. Considering the effect of heat transfer coefficient, solar-to-fuel efficiency increases with the increase of heat transfer coefficient at the same CO2 flow rate. The maximum solar-to-fuel efficiencies of 1.36% and 0.35% are achieved with 75% heat recovery and without heat recovery with the CO2 flow rate of 10 sccm (nCO2/nLCZ-73 = 684). However, the solar-to-fuel efficiencies under the same heat exchange conditions are only 0.25% and 0.06% with the CO2 flow rate of 70 sccm.
648 when the CO2 flow rate is 70 sccm at nCO2/nLCZ-73 = 4788, the latter represents an increase of nearly 27% in CO yield over the former. However, it is also noted that solar-to-fuel efficiency is negatively correlated with the increase of CO2 flow rate in Fig. 9(b). Although CO yield is low at low CO2 flow rate, solar-to-fuel efficiency is high. In order to prove that this material can still split CO2 under the condition of lower molar ratios, further experiments would be needed for verification, such as the CO2 flow rate is less than 10 sccm (nCO2/nLCZ-73 < 684). It should be noted that an excessively low CO2 flow rate may impose higher requirements on the experimental devices in actual operation. Considering the effect of heat transfer coefficient, solar-to-fuel efficiency increases with the increase of heat transfer coefficient at the same CO2 flow rate. The maximum solar-to-fuel efficiencies of 1.36% and 0.35% are achieved with 75% heat recovery and without heat recovery with the CO2 flow rate of 10 sccm (nCO2/nLCZ-73 = 684). However, the solar-to-fuel efficiencies under the same heat exchange conditions are only 0.25% and 0.06% with the CO2 flow rate of 70 sccm.
4. Conclusions
This work performs the performance evaluation towards the doped perovskite LaCo0.7Zr0.3O3 (LCZ-73) based thermochemical CO2 splitting process thermodynamically via the experimentally derived parameters for the first time. The impacts of vacuum pump and vacuum pump combined with inert gas purge to reduce oxygen partial pressure and CO2 heating on the performance parameter ηsolar-to-fuel have been analyzed with the consideration of gas–gas, gas–solid phase heat recuperation. The energy cost of CO2 heating during the redox process is underscored. At the oxygen partial pressure of 10−5 bar, non-stoichiometric oxygen δ increases by more than 3 times as the reduction temperature increases from 1000 °C to 1300 °C. However, the deviation of δ is negligible between 1300 °C and 1400 °C. The reaction enthalpy ranges from 60 to 130 kJ mol−1 corresponding to δ = 0.05–0.40. Comparing ηsolar-to-fuel via vacuum pump with the case of vacuum pump combined with inert gas purging, the efficiencies of 0.39% and 0.1% can be achieved with 75% and without heat recovery under experimental conditions, respectively. Based on the energy analysis, the energy cost of CO2 heating took up the bulk of energy consumption of the thermodynamic process as the nCO2/nLCZ-73 increases, which is two or three orders of magnitude higher than other heating items. Compared with higher temperature conditions, nCO2/nLCZ-73 at lower temperature requires more demanding conditions for the aim of commercialization. Finally, the ability of the perovskite LCZ-73 to split CO2 and thermochemical performance were tested under different CO2 flow rates. The results show that high CO2 flow rate is conductive to the production of CO, but at the cost of low ηsolar-to-fuel. The maximum solar-to-fuel efficiencies of 1.36% and 0.35% are achieved with 75% heat recovery and without heat recovery with the CO2 flow rate of 10 sccm. However, values under the same heat exchange conditions are only 0.25% and 0.06% with the CO2 flow rate of 70 sccm. On the premise of meeting the requirements of the experimental device, further experiments are needed to verify the ability of the perovskite to split CO2 at lower CO2 flow rate (e.g., less than 10 sccm, nCO2/nLCZ-73 < 684).Nomenclature
| M | The molar mass of perovskite, g mol−1 |
| m | Mass of the matter, g |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) | Universal molar gas constant, 8.314 J mol−1 K−1 |
| T | Temperature, K |
| K | The equilibrium constant |
| P | Pressure, atm |
| Q | The energy required or recovered for each process, J mol−1 |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) p p | The specific molar heat capacity, J mol−1 K−1 |
| n | Amount of substance, mol |
| HHV | Higher heating value, J mol−1 |
| C | Solar concentration ratio, suns |
| I | 1000 W m−2 |
| nCO2/nLCZ-73 | Molar ratio of CO2 to perovskite LaCo0.7Zr0.3O3 |
Greek symbols
| Δm | Mass change, g |
| δ | Nonstoichiometric oxygen |
| ΔGΘ | Standard molar Gibbs free energy, J mol−1 |
| ΔHΘred | Standard molar enthalpy for reduction, J mol−1 |
| ΔSΘred | Standard molar entropy for reduction, J mol−1 |
| Δδ | Non-stoichiometry change |
| ΔQ | The energy change in a process, J mol−1 |
| ΔT | Temperature swing, K |
| ηS→W | Solar energy to vacuum pumping conversion efficiency |
| εheat exchanger | The heat exchange coefficient of the heat exchanger |
| εrec | The effectiveness of heat recovery, 0.6 |
| ηabs | Heat absorption efficiency of solar reactor |
| σ | Stefan–Boltzmann constant, 5.67 × 10−8 W m−2 K−4 |
| ηsolar-tio-fuel | Solar to fuel conversion efficiency |
Subscripts
| O | Oxygen atom |
| O2 | Oxygen gas |
| red | Reduction |
| oxi | Oxidation |
| i | The state of non-stoichiometric oxygen after reduction |
| f | The state of non-stoichiometric oxygen after oxidation |
| pump | Vacuum pump |
| 0 | The atmospheric pressure, 1 atm |
| Ar heating | Preheat the sweeping gas Ar |
| amb | Ambient condition |
| CO2 | Carbon dioxide |
| CO | Carbon monoxide |
| rec | Recovery |
| CO2 heating | Preheat the CO2 gas |
| abs | Absorption |
Superscripts
| Θ | Standard condition at T and Patm |
Abbreviations
| LCZ-73 | LaCo0.7Zr0.3O3 |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Key Research and Development Program of China (Grant No. 2018YFB1502005), the National Natural Science Foundation of China (Grant No. 51806209) and Institute of Electrical Engineering, Chinese Academy of Sciences (Grant No. Y770111CSC).References
- A. M. A. Hussein, K. G. Burra, G. Bassioni, R. M. Hammouda and A. K. Gupta, Appl. Energy, 2019, 235, 1183–1191 CrossRef CAS.
- R. R. Bhosale, A. Kumar, F. AlMomani, U. Ghosh, D. Dardor, Z. Bouabidi, M. Ali, S. Yousefi, A. AlNouss, M. S. Anis, M. H. Usmani, M. H. Ali, R. S. Azzam and A. Banu, Energy Convers. Manage., 2016, 112, 413–422 CrossRef CAS.
- Y. W. Zhao, Y. D. Zhang, W. J. Li, Y. Hao and H. G. Jin, J. Cleaner Prod., 2018, 176, 758–769 CrossRef CAS.
- S. Chuayboon and S. Abanades, J. Cleaner Prod., 2019, 232, 784–795 CrossRef CAS.
- J. Huang, Y. Fu, S. Li, W. Kong, J. Zhang and Y. Sun, J. CO2 Util., 2018, 27, 450–458 CrossRef CAS.
- F. A. Costa Oliveira, M. A. Barreiros, S. Abanades, A. P. F. Caetano, R. M. Novais and R. C. Pullar, J. CO2 Util., 2018, 26, 552–563 CrossRef CAS.
- S. Chuayboon, S. Abanades and S. Rodat, J. Energy Chem., 2020, 41, 60–72 CrossRef.
- M. Takacs, M. Hoes, M. Caduff, T. Cooper, J. R. Scheffe and A. Steinfeld, Acta Mater., 2016, 103, 700–710 CrossRef CAS.
- A. H. Bork, E. Povoden-Karadeniz and J. L. M. Rupp, Adv. Energy Mater., 2017, 7, 1601086 CrossRef.
- S. Dey, B. S. Naidu and C. N. Rao, Chemistry, 2015, 21, 7077–7081 CrossRef CAS.
- S. Dey, B. S. Naidu, A. Govindaraj and C. N. Rao, Phys. Chem. Chem. Phys., 2015, 17, 122–125 RSC.
- M. M. Nair and S. Abanades, Sustainable Energy Fuels, 2018, 2, 843–854 RSC.
- S. Mulmi, H. M. Chen, A. Hassan, J. F. Marco, F. J. Berry, F. Sharif, P. R. Slater, E. P. L. Roberts, S. Adams and V. Thangadurai, J. Mater. Chem. A, 2017, 5, 6874–6883 RSC.
- S. Dey, B. S. Naidu and C. N. Rao, Dalton Trans., 2016, 45, 2430–2435 RSC.
- C. L. Muhich, S. Blaser, M. C. Hoes and A. Steinfeld, Int. J. Hydrogen Energy, 2018, 43, 18814–18831 CrossRef CAS.
- M. Ezbiri, M. Takacs, B. Stolz, J. Lungthok, A. Steinfeld and R. Michalsky, J. Mater. Chem. A, 2017, 5, 15105–15115 RSC.
- M. E. Galvez, R. Jacot, J. Scheffe, T. Cooper, G. Patzke and A. Steinfeld, Phys. Chem. Chem. Phys., 2015, 17, 6629–6634 RSC.
- A. Demont and S. Abanades, J. Mater. Chem. A, 2015, 3, 3536–3546 RSC.
- T. Cooper, J. R. Scheffe, M. E. Galvez, R. Jacot, G. Patzke and A. Steinfeld, Energy Technol., 2015, 3, 1130–1142 CrossRef CAS.
- A. H. Bork, M. Kubicek, M. Struzik and J. L. M. Rupp, J. Mater. Chem. A, 2015, 3, 15546–15557 RSC.
- A. Demont and S. Abanades, RSC Adv., 2014, 4, 54885–54891 RSC.
- G. Takalkar and R. R. Bhosale, Fuel, 2019, 254, 115624 CrossRef CAS.
- Q. Jiang, J. Tong, G. Zhou, Z. Jiang, Z. Li and C. Li, Sol. Energy, 2014, 103, 425–437 CrossRef CAS.
- J. P. Säck, S. Breuer, P. Cotelli, A. Houaijia, M. Lange, M. Wullenkord, C. Spenke, M. Roeb and C. Sattler, Sol. Energy, 2016, 135, 232–241 CrossRef.
- C. N. R. Rao and S. Dey, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13385–13393 CrossRef CAS.
- R. J. Carrillo and J. R. Scheffe, Energy Fuels, 2019, 33, 12871–12884 CrossRef CAS.
- A. H. Bork, E. Povoden-Karadeniz, A. J. Carrillo and J. L. M. Rupp, Acta Mater., 2019, 178, 163–172 CrossRef CAS.
- L. Wang, T. Ma, S. Dai, T. Ren, Z. Chang, L. Dou, M. Fu and X. Li, Chem. Eng. J., 2020, 389, 124426 CrossRef CAS.
- J. Vieten, B. Bulfin, M. Senholdt, M. Roeb, C. Sattler and M. Schmücker, Solid State Ionics, 2017, 308, 149–155 CrossRef CAS.
- Y. Hao, C.-K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082 CrossRef CAS.
- I. Ermanoski, N. P. Siegel and E. B. Stechel, J. Sol. Energy Eng., 2013, 135, 10 CrossRef.
- H. Kong, Y. Hao and H. Jin, Appl. Energy, 2018, 228, 301–308 CrossRef CAS.
- B. Bulfin, F. Call, M. Lange, O. Lübben, C. Sattler, R. Pitz-Paal and I. V. Shvets, Energy Fuels, 2015, 29, 1001–1009 CrossRef CAS.
- B. J. McBride, S. Gordon and M. A. Reno, NASA Tech. Pap. 3287, 1993, p. 16 Search PubMed.
- J. E. Miller, M. D. Allendorf, R. B. Diver, L. R. Evans, N. P. Siegel and J. N. Stuecker, J. Mater. Sci., 2008, 43, 4714–4728 CrossRef CAS.
- H. Wang, M. Liu, H. Kong and Y. Hao, Appl. Therm. Eng., 2018, 152, 925–936 CrossRef.
- R. R. Bhosale, A. Kumar and P. Sutar, Energy Convers. Manage., 2017, 135, 226–235 CrossRef CAS.
- S. Li, V. M. Wheeler, P. B. Kreider, R. Bader and W. Lipiński, Energy Fuels, 2018, 32, 10848–10863 CrossRef CAS.
- B. D. Ehrhart, C. L. Muhich, I. Al-Shankiti and A. W. Weimer, Int. J. Hydrogen Energy, 2016, 41, 19881–19893 CrossRef CAS.
- S. Abanades, P. Charvin, G. Flamant and P. Neveu, Energy, 2006, 31, 2805–2822 CrossRef CAS.
- L. Wang, T. Ma, Z. Chang, H. Li, M. Fu and X. Li, Sol. Energy, 2019, 177, 772–781 CrossRef CAS.
- Y. Hao, J. Jin and H. Jin, Appl. Therm. Eng., 2019, 166, 113600 CrossRef.
- R. J. Panlener, R. N. Blumenthal and J. E. Garnier, J. Phys. Chem. Solids, 1975, 36, 1213–1222 CrossRef CAS.
- N. P. Siegel, J. E. Miller, I. Ermanoski, R. B. Diver and E. B. Stechel, Ind. Eng. Chem. Res., 2013, 52, 3276–3286 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |