DFT study of α-Keggin, lacunary Keggin, and iron^II–VI substituted Keggin polyoxometalates: the effect of oxidation state and axial ligand on geometry, electronic structures and oxygen transfer

Abstract

Herein, the geometry, electronic structure, Fe–ligand bonding nature and simulated IR spectrum of α-Keggin, lacunary Keggin, iron(II/III)-substituted and the important oxidized high-valent iron derivatives of Keggin type polyoxometalates have been studied using the density functional theory (DFT/OPTX-PBE) method and natural bond orbital (NBO) analysis. The effects of different Fe oxidation states (II–VI) and H₂O/OH⁻/O²⁻ ligand interactions have been addressed concerning their geometry and electronic structures. It has been revealed that the d-atomic orbitals of Fe and 2p orbitals of polyoxometalate's oxygen-atoms contribute in ligand binding. Compared with other high valent species, the considered polyoxometalate system of [PW₁₁O₃₉(Fe^VO)]⁴⁻, possesses a high reactivity for oxygen transfer.

---

1. Introduction

Polyoxometalates (POMs) represent a diverse class of inorganic metal-oxide anion clusters with defined structures based on MO₆ octahedra mostly containing tungsten and/or molybdenum in their highest oxidation states.^1–3 Owing to their attractive structure along with chemical and electronic versatility, they have found different applications in catalysis, medicine and materials sciences.^4–6 Among a wide variety of heteropoly compounds, Keggin type POMs, [XM₁₂O₄₀]ⁿ⁻, are the most stable and available species. Substitution of addenda atoms (W or Mo) in Keggins with other transition metals generates transition metal substituted Keggin type POMs (TMSPOMs). This type of substitution, as one of the main source of diversity, improves redox and acid/base properties of POMs in a variety of chemical processes.² Some of the TMSPOMs, such as high-valent iron–oxo species in heme enzymes (or metalloporphyrin complexes)^7,8 and nonheme reagents,⁹ are used as oxidation catalyst in different organic reactions.

Understanding the effect of various properties, such as the roles of transition metals, framework metal atoms M_FM, and type of heteroatom X and counter ions, in TMSPOMs stability and reactivity could be useful in designing efficient POM-based materials in emerging technologies. Electronic structure and reactivity of this growing class of inorganic compounds need to comprehensive experimental and theoretical investigations.

As stated above, POMs and especially TMSPOMs have been used extensively in different catalytic oxidation reactions using environmentally friendly oxidants such as hydrogen peroxide. These compounds and some of their derivatives, which could be produced in the reaction medium, with respect to stability, energy and their properties, possibly will contribute in catalytic processes.

The structural and reactivity differences in high-valent metal derivatives of TMSPOMs allow the researchers to resort the computational examinations in this field. There are a vast number of reports devoted on theoretical exploration of POMs with focus on understanding the electronic structure, redox property, magnetism, and reaction mechanisms.^10–27 For example, the essential role of [(Xⁿ⁺O₄)M^III₂(OH)₂(M_FW)₁₀O₃₂]⁽⁸⁻ⁿ⁾⁻ chemical composition – where M = Fe, Mn, Ru, M_FW = Mo and W, and X = Al^III, Si^IV, P^V, and S^VI – in the geometry, electronic structure, magnetic properties and defining lower-lying electronic state of these species were investigated. This, in turn, would possibly have an impact on their reactivity.^28,29 The molecular geometry, electronic structure, redox properties and metal-functional group bonding nature of a series of transition metal nitrido and dinitrogen derivatives of Keggin type POMs were also analyzed by density functional theory (DFT) and natural bond orbital (NBO) analysis. Their findings indicate that the electrophilic/nucleophilic reactivity and interaction between metal and functional group in these POMs is directly related to the transition metal substitution.^30–32 The systematic DFT and NBO analysis were employed to investigate the electronic structures and bonding features of the ruthenium(II) atom and SO₂ molecule in the two ruthenium–sulfur dioxide (SO₂) adducts of trans-Ru(NH₃)₄(SO₂)Cl⁺ and [(SiW₁₁O₃₉)Ru^II(SO₂)].^6–33 The DFT method has also been employed to design a new [Mo₅O₁₈Fe=O]³⁻ catalyst, which would act as selective C–H hydroxylation reagent³⁴ and adopted to identify the electronic and redox properties, protonation, and stability of five [α-PTi₂W₁₀O₄₀]⁷⁻ isomers.³⁵ All of these valuable studies shed more light on the application of POMs in different realms.

The theoretical study of TMSPOMs derivatives is difficult because of multiple lower lying electronic states, high negative charges and large sizes. In this study, high level density functional theoretical method has been applied to study a Keggin POM, α-[PW₁₂O₄₀]³⁻ (PW₁₂), lacunary Keggin POM, [PW₁₁O₃₉]⁷⁻ (PW₁₁), Fe^II/III substituted Keggin POMs, [PW₁₁O₃₉(Feⁿ⁺)]⁽⁷⁻ⁿ⁾⁻ (PWFeⁿ⁺) (n = 2, 3), Fe^II/III/IV substituted Keggin POMs with H₂O ligand, [PW₁₁O₃₉(Feⁿ⁺OH₂)]⁽⁷⁻ⁿ⁾⁻ (PWFeⁿ⁺OH₂) (n = 2, 3, 4), and other high valent Fe^IV/V/VI POMs with OH⁻ and O²⁻ ligands as potential active POM species. The significance of the work could be unravelled when the difficulties associated with theoretical studies of organometallic, owing to strong spin contamination problems would be taken into account. Fortunately, recent development in deMon2K code,³⁶ by implementing the auxiliary DFT approaches and robust algorithms made it feasible to study such heavy systems.

2. Results and discussion

2.1. Ground state geometries, charge distribution, electronic structure, and simulated infrared spectra of PW₁₂ and PW₁₁ anions

The most common Keggin heteropoly anions like PW₁₂, [SiW₁₂O₄₀]⁴⁻ and [PMo₁₂O₄₀]³⁻ are formed from simple oxoanions and required heteroatoms through a self-assembly process upon acidification in aqueous solutions.

12WO₄²⁻ + HPO₄²⁻ + 23H⁺ → [PW₁₂O₄₀]³⁻ + 12H₂O

Adding controlled amounts of hydroxide ions to the aqueous solution of these heteropoly anions could generate the lacunary (defect) POMs. These POM anions encompass one or more vacancies due to loss of addenda atom(s) from the structure. At the pH = 2, this process is expressed as follows:^37,38

[PW₁₂O₄₀]³⁻ ⇄ [PW₁₁O₃₉]⁷⁻ + WO⁴⁺

The mono lacunary Keggin POMs could act as pentadentate ligands and so frequently applied in preparing TMSPOMs. These compounds come in a big variety and are used as acid or oxidation catalysts.

In this study, attempts are made to investigate the geometry, electronic structure and simulation of IR spectra of the mentioned POMs. The process begins with study on PW₁₂ and followed by PW₁₁, where one WO⁴⁺ unit is removed, Fe substituted PW₁₁ as PWFeⁿ⁺ (n = 2 and 3) and ended by PWFeⁿ⁺OH₂ (n = 2 and 3) with H₂O as the axial ligand. Since this TMSPOMs could be used as catalyst in oxidation reactions through the interaction between oxidant and catalyst, different types of high oxidation state Fe substituted Keggin POMs along with various axial ligands have been considered.

2.1.1. Ground state geometries. To compare with X-ray crystallography information for PW₁₂ system,^21,35 the geometry optimization of PW₁₂ and PW₁₁ species have been performed in singlet, triplet and quintet spin states at DFT/OPTX-PBE/DZVP-GGA level (ESI†). Selected optimized geometry-parameters for PW₁₂ and PW₁₁ in singlet spin state are tabulated in Table 1. According to Table 1, the theoretical geometry parameters are in good agreement with the corresponding experimental values, while discrepancy appear only in the P–O_a bonds, which is underestimated by a 0.033 Å.

Table 1 Selected optimized geometry parameters (bond lengths in Å) of PW₁₂ and PW₁₁

Exp.^a	PW11		PW12
	Selected bond	Bond length	Selected bond	Bond length
a The experimental values were adapted from ref. 21 and 35.
1.530	P^1–Oa^13	1.563	P^1–Oa^14	1.597
—	P^1–Oa^14	1.563	P^1–Oa^15	1.561
2.430	W^2–Oa^13	2.428	W^2–Oa^14	2.375
—	W^6–Oa^13	2.429	W^6–Oa^14	2.516
1.900	W^2–Ob^24	1.867	W^2–Ob^25	2.061
1.900	W^6–Ob^28	1.868	W^6–Ob^29	1.912
1.910	W^2–Oc^33	1.881	W^2–Oc^34	1.893
1.910	W^6–Oc^39	1.881	W^6–Oc^40	1.902
1.690	W^2–Od^41	1.700	W^2–Od^42	1.745
1.690	W^6–Od^44	1.700	W^6–Od^45	1.741

---

Bond length is a good parameter for evaluation of interaction strength between two atoms. By removing a WO⁴⁺ moiety from PW₁₂, the system's charge is varied from −3 to −7 in PW₁₁. As a result, the P¹–O_a¹³ (1.597 Å), W⁶–O_a¹³ (2.516 Å), W⁶–O_b²⁸ (1.912 Å), W⁶–O_c³⁹ (1.902 Å) and W⁶–O_d⁴⁴ (1.741 Å) bond lengths in PW₁₁ elongate respect to P¹–O_a¹⁴ (1.563 Å), W⁶–O_a¹⁴ (2.429 Å), W⁶–O_b²⁹ (1.868 Å), W⁶–O_c⁴⁰ (1.881 Å) and W⁶–O_d⁴⁵ (1.70 Å) bond lengths in PW₁₂, respectively (see Scheme 1 for numbering). These results indicate a few weakening of binding interactions in PW₁₁ for bonds far from lacuna position and larger changes in the bond lengths around cavity (lacuna). The bond lengths of W (4, 5, 9 and 10) atoms with O (25, 19, 32 and 38) atoms in PW₁₁ respect to PW₁₂ are shortened from 1.920 to 1.730 Å. This bond length shortening could be related to the high electronic density on O (25, 19, 32 and 38) atoms after removal of WO⁴⁺. As mentioned, O atom's electronic density could be shifted to W and thus, strengthening of interactions.

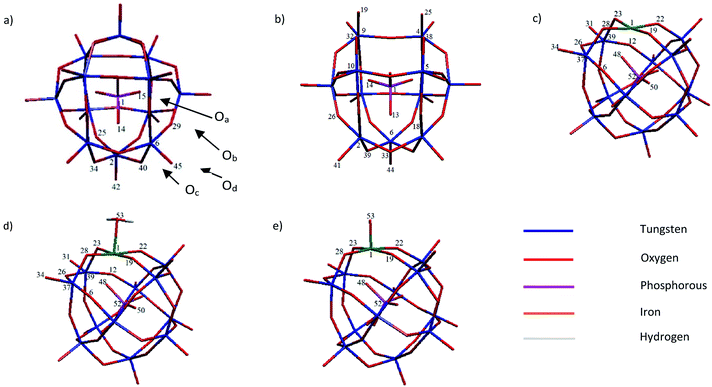Scheme 1 The relevant numbering pattern of studied systems: (a) PW₁₂, (b) PW₁₁, (c) PWFeⁿ⁺ (n = 2, 3), (d) PWFeⁿ⁺OH₂ (n = 2, 3 and 4) and (e) PWFeⁿ⁺O (n = 4, 5 and 6).

For PW₁₂, it has been predicted that the singlet spin state (S = 0) is the most stable state, while the triplet (S = 1) and quintet (S = 2) spin states are 57.30 and 125.50 kcal mol⁻¹ higher in energy than the singlet state, respectively (Table S1†). Also, in PW₁₁ the triplet spin state is 55.86 kcal mol⁻¹ higher in energy than corresponding singlet spin state.

2.1.2. Charge distribution. The local charge distributions on the PW₁₂ and PW₁₁ heteropolyanions are tabulated in Table 2.

Table 2 Calculated atomic charge distributions of PW₁₂ and PW₁₁ determined at the NBO/UOPBE/6-31G(d) theoretical level (and LANL2DZ basis set on the metal atom)

POM	PO4^3−	W	Ob	Oc	Od
PW12	−0.98	+1.98	−0.82	−0.77	−0.56
PW11	−1.06	+1.67 to +1.92	−0.70 to −0.87	−0.70 to −0.82	−0.69

---

Atomic charges of PW₁₂ and PW₁₁ were calculated at UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom). Although in computational context, the absolute Mulliken charges are not so accurate, their variations could be quite reliable.²¹ According to the theoretical studies by Courcot and Bridgeman, the Mulliken atomic charges – compared to Hirshfeld, Voronoi Deformation Density (VDD), Quantum Theory of Atoms in Molecules (QTAIM) and the Net Total Voronoi (NTV) charges – could show the best convergence during the calculation with experimental data for several polyanions and provide a good description of Coulomb potential and their chemistry properties.^39–43 For PW₁₂, an electronic charge of −0.98e is assigned for the central PO₄³⁻ moiety, which increases slightly by −0.08e for PW₁₁ (i.e. q = −1.06e, q is the net charge of central PO₄³⁻ in PW₁₁), and in turn constitutes the difference between local charge of central PO₄³⁻ in PW₁₁ and PW₁₂. High differences between the net charges for O_d in PW₁₁ (−0.69e) and PW₁₂ (−0.56e) have not changed the local charge of central PO₄³⁻. This high charge density is accumulated in the W₁₁O₃₅ framework of POM, especially in the terminal oxygen atoms, and increases the basicity of them.

Other prominent changes occur in atoms near the lacuna, which the positive charge of W (4, 5, 9 and 10) atoms in PW₁₂ decreased from 1.98e to 1.67e in PW₁₁. This is related to the charge transfer from O (19, 25, 32 and 38) atoms in PW₁₁ which bearing the high charge density after removal of WO⁴⁺ moiety (more information on Mulliken charges of PW₁₂ and PW₁₁ is presented in Table S6†).

2.1.3. Electronic structure. The electronic structure in POMs is an important subject, owing to its direct effects on all chemical characters. The valence molecular orbitals of PW₁₂ and PW₁₁ were obtained by UOPBE/6-31G(d) level calculation (Fig. S1, see ESI† for MOs). As shown in Fig. S1,† for PW₁₂ anion HOMO orbitals are distributed over O atoms and LUMO orbitals contain d-orbitals of W atoms with a large energy gap (2.81 eV) in the ground state. The predicted ΔE(HOMO–LUMO) of PW₁₁ (amount to 2.89 eV) is similar to that of PW₁₂. Also, the nature of HOMO and LUMO in PW₁₁ are similar to those of PW₁₂ moiety. Thus, it could be concluded that the removal of WO⁴⁺ moiety from the Keggin POM does not change the HOMO and LUMO nature and also energy gap between the occupied and unoccupied orbitals.

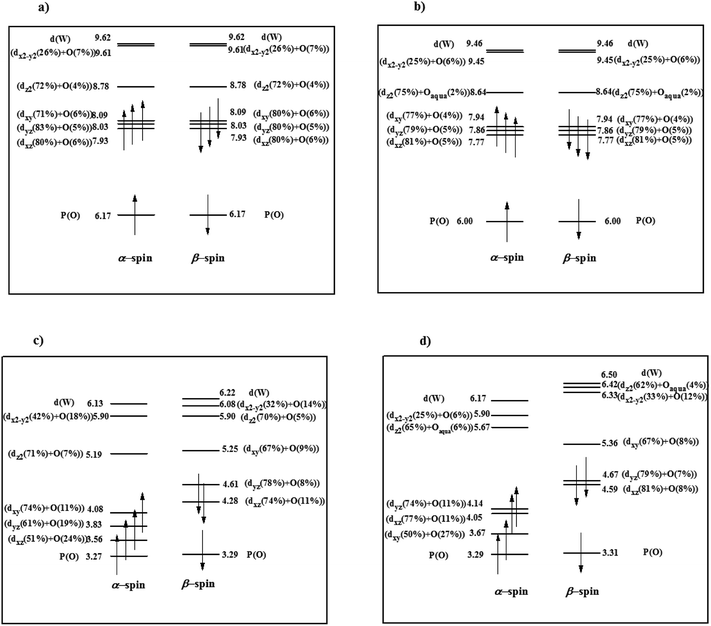
Moreover, in order to determine the effect of additional negative charge on the valence orbital energies, six valence orbitals (α and β-spin) were selected for PW₁₂ and PW₁₁ compounds (Fig. 1). From Fig. 1a, among six selected α and β orbitals for PW₁₂, there are only two orbitals with negative energy and four MOs with energy close to zero. However, for PW₁₁, all mentioned orbitals possess high positive energy (Fig. 1b). The results also indicate positive energy for the interior orbitals (up to HOMO−118; no. 127). So, it can be deduced that an additional negative charge on PW₁₁ increases the orbital energy. As a result, in PW₁₁, electrons are better available for stabilizing transition metals in different oxidation states and so PW₁₁ converts to a better electron donor ligand.

Fig. 1 Energy level expressions of frontier molecular orbitals (FMOs) for (a) PW₁₂ and (b) PW₁₁ in the ground state. The orbital energy values have been represented in eV.

Also, by removal of WO⁴⁺ moiety the molecular symmetry of PW₁₂ reduces from T_d to C₃ in PW₁₁. Decent in symmetry leads to lifting the doublet-triplet degeneracy in d_xy-like orbitals²¹ of PW₁₂ and singlet degeneracy for all orbitals performs in PW₁₁ (Fig. 1).

2.1.4. Simulated infrared spectra (IR). From the optimized geometries of PW₁₂ and PW₁₁, it is revealed that by removing one WO⁴⁺ moiety from PW₁₂ the P–O_a, W=O_d, W–O_b–W and W–O_c–W bond lengths in PW₁₁, which are far from lacuna site, would increase. IR spectroscopy being able to detect small structural differences and so, is a sufficient probe for investigation of the variation of Keggin-type POM structures. Keggin-type POMs, as metal–oxygen clusters, contain some of metal–oxygen stretching vibrational modes at 500–1100 cm⁻¹. Accordingly, based on vibrational frequency calculations, simulation of IR spectrum of PW₁₂ and PW₁₁ have been done at OPTX-PBE/DZVP-GGA level.

For PW₁₂ structure, four infrared absorption bands at 1067, 963, 863 and 790 cm⁻¹ have been assigned to P–O_a, W=O_d, W–O_b–W and W–O_c–W stretching bonds, respectively. From literature, it has been established that DFT methods generate IR vibrational frequencies with a slight shift towards low energies.⁴⁴ As to PW₁₁, the P–O_a stretching mode exhibits a splitting to two components at 1060 and 1050 cm⁻¹ which is approved by experimental data.⁴⁵ Moreover, the vibrational frequencies of P–O_a, W=O_d, W–O_b–W and W–O_c–W bonds in PW₁₁ at 1060, 1050, 871, 800 and 706 cm⁻¹, in comparison with PW₁₂, are appeared at lower frequencies. The results of IR spectrum calculations, that verify the modification in PW₁₁ geometry, are tabulated in Table 3 (and also Fig. S3 and S4†).

Table 3 Calculated vibrational frequencies (cm⁻¹) and assigned bands of PW₁₂ and PW₁₁ determined at OPTX-PBE/DZVP-GGA level

Stretching mode	Vibrational frequency/cm^−1
	PW11	PW12
ν (P–Oa)^1	1060	1067
ν (P–Oa)^2	1050	—
ν (W=Od)	871	963
ν (W–Ob–W)	800	863
ν (W–Oc–W)	706	790

---

2.2. Ground state geometries, charge distribution, electronic structure, and simulated infrared spectra of PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3)

In respect to the role of TMSPOMs in different reactions like oxidative and acid/base processes^46–50 and also the effective role of iron substituted POMs,⁵¹ various Fe oxidation states in iron substituted Keggin type POMs have been studied in this work. As stated above, truncation of PW₁₂ by removing of WO⁴⁺ moiety leaves behind a lacunary PW₁₁ which act as a ligand and in combination with Fe generates PWFeⁿ⁺ (n = 2 and 3) as iron substituted POMs. By locating a H₂O ligand at the sixth octahedral coordination position, the PWFeⁿ⁺OH₂ (n = 2 and 3) cluster would be formed.

2.2.1. Ground state geometries. It is well known that the spin state of each complex is depended on its environment and especially the nature of their ligands.^52,53 In the PWFeⁿ⁺, the ground state geometry of Fe^II/III substituted POM structures have been optimized at the spin-unrestricted OPTX-PBE/DZVP-GGA level. For POM–Fe^II, three spin states of singlet (S = 0), triplet (S = 1) and quintet (S = 2) have been considered. It was predicted that the quintet spin state (S = 2) is the most stable state, while the singlet (S = 0) and triplet (S = 1) spin states are 23.53 and 12.43 kcal mol⁻¹ less stable, respectively. Moreover, for Fe^III substituted POM, among three considered spin states (S = 1/2, 3/2, 5/2), it has been predicted that the sextet (S = 5/2) is the most stable while doublet (S = 1/2) and quartet (S = 3/2) spin states are roughly 23.03 and 8.16 kcal mol⁻¹ less stable, respectively.

Also, the structure of PWFe^IIOH₂ was optimized in three spin states singlet (S = 0), triplet (S = 1) and quintet (S = 2). From the results, it has been unravelled that quintet state (S = 2) is the most stable while singlet (S = 0) and triplet (S = 1) spin states are 23.53 and 12.49 kcal mol⁻¹ less stable, respectively. Our attempts failed in determination a local minimum for interacting of H₂O and Fe^II in triplet and quintet spin states since the weak iron–water interaction results in separation of H₂O following optimization and then their interaction with O²⁸ of POM through hydrogen bond has been exhibited. Consequently, the singlet spin state is more favourable for this Fe substituted POM in an oxidation process, because Fe interacts directly with H₂O ligand. At higher spin states, electron transfer from Fe^II d orbitals of antibonding MOs of Fe–OH₂ bond leads to weakening the interaction between H₂O and Fe, and so dissociation of H₂O following optimization of corresponding geometry. The same holds true for PWFe^IIIOH₂ at doublet, quartet and sextet spin states, where doublet spin state is more appropriate because Fe interacts directly with H₂O. As shown in Fig. 2, PWFeⁿ⁺OH₂ (n = 2 and 3) which is generated through replacing WO⁴⁺ moiety with [Fe–OH₂] in PW₁₂ is optimized at doublet, quartet and sextet spin states for Fe^III and singlet, triplet and quintet spin states for Fe^II (see ESI† for xyz coordinates of studied systems).

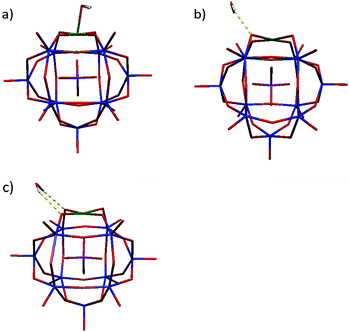Fig. 2 The optimized geometry of PWFe^IIOH₂ (a) in the singlet, (b) in the triplet and (c) in the quintet spin states obtained by OPTX-PBE/DZVP-GGA calculation.

Key geometry parameters of PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3) are tabulated in Table S2.† In PWFe^II, as the total charge reduced from −7 to −5 respect to PW₁₁, the bond lengths are also shortened, while these are still long respect to PW₁₂. This implies that by changing the electron density on atoms the whole system remained stable but some of the bond lengths are altered. The most important alterations in the bond lengths have been predicted in the bonds around lacuna region in POM. The W–O bond length nearby the lacuna, which their oxygen atoms are ligated to Fe^II, increases from 1.730 Å in PW₁₁ to 1.808 Å in PWFe^II (Table S2†). Substitution of Fe in PW₁₁ is along with significant charge distribution from oxygen atoms to Fe. The charges of Fe, W (35, 37, 39 and 44) and O donor atoms (19, 22, 23 and 28) in PWFe^II are 0.67e, 1.86e and −0.69e respectively, which in compare with charges of W (4, 5, 9 and 10) and O donor atoms (19, 25, 32 and 38) in PW₁₁ (1.70e and −0.63e respectively), the positive charge of W atoms is increased. Thus the bond length for W³⁷–O_c²⁸ (1.808 Å) is predicted to be shorter and stronger with respect to Fe¹–O_c²⁸ (1.932 Å). The difference predicted between Fe¹–O_a⁴⁸ (1.938 Å) and W³⁷–O_a⁴⁸ (2.460 Å) bond lengths shows the stronger interaction between Fe and O_a⁴⁸ (centre tetrahedral oxygen) respect to W³⁷–O_a⁴⁸, even though Fe^II and W^VI radiuses are almost equal. This is because the bond length depends on both of the M–O interaction and metal radius. Also, the stronger interaction can be related to the favourable orientation of Fe d_z² orbital with O_a⁴⁸ pz orbital and not to the charge distribution, because the charge of O_a⁴⁸ (−0.76) in PWFe^II compared with O_a¹³ (−0.74) in PW₁₁ was not changed significantly. In PWFe^III, single electron oxidation of Fe^II into Fe^III caused the shortening of all above mentioned bond lengths. This implies that bonding interaction between Fe^III atom and four oxygen atoms of POM lacuna is stronger than that of Fe^II.

Our calculation also shows small structural differences between PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3) (Table S2†). A slight structural change has been exhibited when H₂O ligated on Fe and so Fe¹–O_a⁴⁸ (see Scheme 1 for labelling) bond length become longer in PWFeⁿ⁺OH₂ (n = 2 and 3) (i.e. q = 0.044 Å) and is the difference in Fe¹–O_a⁴⁸ bond length between PWFe^II and PWFe^IIOH₂. The large Fe¹–O_a⁴⁸ length shows a weak bonding interaction which provides an unsaturated metal atom in pseudo-octahedral coordinated sphere.^19,30,31 Thus, Fe has an additional ability for binding to H₂O ligand. It is well-known that POMs have excellent structural stability while accepting or donating one or several electrons in various chemical mediums. Along with our study, the geometric parameters of POMs were checked for single electron oxidation of iron in POM (Fe^II to Fe^III). As expected, no significant structural changes were predicted and only the geometric parameters of Fe–OH₂ bond have been influenced. The Fe^II–O_aqua and Fe^III–O_aqua bond lengths were 2.113 Å and 2.060 Å respectively, and Δr(Fe^III/II–O_aqua) = 0.053 Å.

The bonding nature has also been investigated using NBO analysis. The calculated WBI (Wiberg Bond Index) values for Fe^II–OH₂ and Fe^III–OH₂ are 0.3358 and 0.3759, respectively (Table S2†). Thus, there is a single and weak bonding interaction between Fe^II and Fe^III with H₂O molecule.

2.2.2. Charge distribution. The computed atomic charge distributions for PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3) are tabulated in Table 4 and can be described as follows:

Table 4 Calculated atomic charges of PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3) determined based on the NBO/UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom)

Atom/group	PWFe^II	PWFe^IIOH2	PWFe^III	PWFe^IIIOH2
PO4	−0.96	−0.96	−0.97	−0.94
Od	−0.63	−0.63	−0.60	−0.60
O48	−0.78	−0.76	−0.76	−0.74
Ob (W2)	−0.82	−0.82	−0.83	−0.82
Ob (FeW)	−0.70	−0.70	−0.72	−0.72
Oc (W2)	−0.78	−0.78	−0.78	−0.77
Oc (FeW)	−0.67	−0.69	−0.68	−0.70
Fe	0.67	0.64	0.85	0.66
W	1.90	1.91	1.95	1.95
Oaqua	—	−0.90	—	−0.75

---

(i) The O_b(W₂) and O_c(W₂) charges in Fe-substituted systems are similar to that of PW₁₂ and PW₁₁. The higher negative charges of bridged oxygen atoms, O_b(W₂) and O_c(W₂) with values between −0.82e and −0.77e, than terminal oxygen atoms have revealed higher basicity of bridged oxygen atoms.

(ii) In these systems, because of shorter bond lengths, favourable orientations and so higher negative overlap in terminal metal–oxygen bonds are expected. Also, transfer charges from O_d (−0.63e) to tungsten are predicted to be more than those of O_b (−0.82e) and O_c (−0.78e) as bridged oxygen atoms. These results state that W=O_d bond (1.720 Å) is stronger and shorter than W–O_b (1.945 Å) and W–O_c (1.967 Å) bonds.

(iii) The negative charges on bridge and corner oxygen atoms in O_b (W₂) and O_c (W₂) are larger than those of bridge and corner oxygen atoms in O_b (FeW) and O_c (FeW). This indicates more charge transfer effect from these oxygen atoms to Fe.

(iv) For PW₁₂, the Mulliken analysis assigns an electronic charge of −0.98e on PO₄³⁻. Slightly decreasing in the negative charge on PO₄³⁻ in Fe-substituted POM indicates that Fe substitution in POM does not change the net charge on PO₄³⁻. So, additional charges from substitution of Feⁿ⁺ (n = 2 and 3) instead of WO⁴⁺ moiety in Keggin POM may be directed to W₁₁O₃₅ framework of POM and specially concentrated in terminal oxygen atoms. As it could be seen, the charges on terminal oxygen atoms in these systems are greater than those of PW₁₂. Accumulation of charge density in the terminal oxygen atoms of Keggin POMs shows a relationship between the basicity of terminal oxygen atoms and the number and type of substituted metals. Also, in electron transfer reactions of Keggin POMs, additional electron transfers to the terminal oxygen atoms and the POM structure occur without significantly deforming in the framework. For this reason, the Keggin POMs are of interest in oxidation catalysis.^21,54–56

(v) Different atoms in PWFeⁿ⁺ resemble the charges on PWFeⁿ⁺OH₂ (n = 2 and 3), except the positive charge on Fe which decreases after H₂O placing. The charge reduction for oxidation state III is more than oxidation state II. This implies a charge reorganization or transfer from O atom of H₂O ligand to Fe and reduction of positive charge on Fe atom.

2.2.3. Fe–POM interactions based on electronic structure. The energy level scheme of the MOs obtained from optimized PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3) structures is shown in Fig. 3. As shown, following substitution of Fe^II in PW₁₁ lacuna, the d orbitals of Fe^II are distributed between d(W) and p(O) orbitals of PW₁₁ (Fig. 3a). In this diagram five MOs (HOMO−2, HOMO−1, HOMO, LUMO and LUMO+1) are metal-based d orbitals and responsible for bonding interaction between Fe atom and four oxygen atoms of PW₁₁. More accurate analysis of the MOs shows that 2p orbitals of oxygen atoms (19, 22, 23 and 28) and d orbitals of Fe have the most important contribution in obtaining those valance MOs, having significant metal character (>70%). Moreover, based on the NBO analysis, the electronic structure of PWFe^II has been studied. The calculated NBO partial charges of these complexes are listed in Table 4. From the results the charge of Fe is 0.67e.

Fig. 3 The energy level expressions of frontier MOs for (a) PWFe^II, (b) PWFe^IIOH₂, (c) PWFe^III and (d) PWFe^IIIOH₂ at ground state calculated at UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom). The orbital energy values have been represented in eV.

Compared with the free metal ion, lower magnitude of positive charge on Fe indicates charge reorganization or transfer from Keggin-type POM cage to the transition metal center, which is in well agreement with the MO prediction. Increasing of the Fe oxidation state from II to III is along with an increasing in oxygen 2p-orbital contribution (19, 22, 23 and 28) in PW₁₁ indicating a stronger interaction between Fe^III and PW₁₁. This is mainly due to lower energy gaps between Fe^III d orbitals and oxygen 2p orbitals in PW₁₁ than that of Fe^II ion. By linking H₂O ligand to iron, the orbital energies and configuration of electronic structure in PWFe^IIOH₂ do not change, in respect to PWFe^II (Fig. 3b). Bonding interaction between Fe and H₂O ligand is accompanied by overlapping between σ(b₂) non-bonding orbital of H₂O ligand and 3d_z² orbital of Fe leading to a weak σ bonding interaction. A charge transfer from H₂O oxygen atom to Fe could be occurred after this σ interaction,^57,58 and so, in PWFe^III the interaction of metal center with H₂O becomes stronger. Moreover, orbital energies for PWFeⁿ⁺ and PWFeⁿ⁺OH₂ (n = 2 and 3) decrease by changing the Fe^II to Fe^III in a significant manner (Fig. 3).

2.2.4. Simulated infrared spectra. The IR spectra of selected systems (PWFeⁿ⁺ and PWFeⁿ⁺OH₂; n = 2 and 3) have also been determined. From the results in Table 5 (and Fig. S5–S8†), P–O_a asymmetric stretching vibration at 1067 cm⁻¹ in α-PW₁₂ splits into two IR bands in PW₁₁. Iron substitution at lacuna position of PW₁₁ – which contains donor oxygen atoms – and formation of PWFeⁿ⁺ (n = 2 and 3) again results in one IR single band for P–O_a. This is also observed for the most of mono transition metal substituted Keggin type POMs.^20,59 Moreover, the W–O_c–W band in PW₁₂ is splitted into W–O_c–W and W–O_c–Fe IR bands in PWFeⁿ⁺ (n = 2 and 3).²⁰ Meanwhile, in these two POMs W=O_d and W–O_b–W vibrations, compared to α-PW₁₂, shifted to lower energies. Therefore, five characteristic bands could easily be employed to identify the structure of PWFeⁿ⁺ (n = 2 and 3) POMs.⁵⁹ For simulated vibrational spectrum of PWFeⁿ⁺OH₂ compared with that of PWFeⁿ⁺ (n = 2 and 3), the IR band of P–O_a is predicted to shift by 12 cm⁻¹ upon linking to H₂O (Table 5, and Fig. S5–S8†). However, W=O_d, W–O_b–W, W–O_c–Fe and W–O_c–W vibrations are not significantly shifted which indicate that these vibrational bands are not sensitive to H₂O ligation.

Table 5 Selected vibrational frequencies (cm⁻¹) of POM complexes determined at OPTX-PBE/DZVP-GGA level

POM	2S + 1	ν (P–Oa)	ν (W=Od)	ν (W–Ob–W)	ν (W–Oc–W)	ν (W–Oc–Fe)	ν (H–O–H)	ν (H–O–H)	ν (H–O–H)
PWFe^III	2	1092	942	843	778	756	—	—	—
PWFe^IIIOH2	2	1080	941	844	777	756	1684	3636	3732
PWFe^II	1	1072	921	831	769	738	—	—	—
PWFe^IIOH2	1	1061	921	834	775	731	1689	3635	3716

---

According to the simulated IR spectrum of PWFeⁿ⁺OH₂ (n = 2 and 3), the symmetric stretching and bending vibrational frequencies of H₂O are similar in both complexes. This is mainly due to weak interaction between H₂O and iron atoms in both of Fe oxidation states. By increasing the Fe oxidation state (from +2 to +3), all vibrational frequencies of P–O_a, W=O_d, W–O_b–W and W–O_c–W bonds in simulated IR spectrum move towards higher frequencies which is compatible with corresponded bond lengths.

2.3. High-valent PWFe^IV(OH₂/OH) and PWFe^IV/V/VI(O) substituted POMs

TMSPOMs are of major importance in oxygenation of organic compounds.^3,4,60–66 In the oxidative process, high-valent TMSPOMs are usually generated by interaction of low-valent substituted transition metals with oxidant or other species available in the reaction medium and exhibited improved catalytic behaviours. Study on these high-valent TMSPOMs is essential for determining and characterizing their active species in reaction mediums. To our knowledge, rare studies on geometry, electronic structure and activity of high-valent TMSPOMs have been reported in literature. The quantum chemistry calculations based on DFT are applicable tools to shed more light on this context. A detailed DFT study on geometry, electronic structure and chemical bonding features of important high-valent species consist of [PW₁₁O₃₉(Fe^IVOH₂)]³⁻ (PWFe^IVOH₂), [PW₁₁O₃₉(Fe^IVOH)]⁴⁻ (PWFe^IVOH), [PW₁₁O₃₉(Fe^IVO)]⁵⁻ (PWFe^IVO), [PW₁₁O₃₉(Fe^VO)]⁴⁻ (PWFe^VO), and [PW₁₁O₃₉(Fe^VIO)]³⁻ (PWFe^VIO) were done at the OPTX-PBE/DZVP-GGA level. High-valent [PW₁₁O₃₉(Feⁿ⁺O)]⁽⁹⁻ⁿ⁾⁻ (PWFeⁿ⁺O; n = 4, 5, 6) species constitute important intermediates in oxidation processes. These oxidized species could have terminal Fe=O bond as an essential active site in catalytic oxygenation reactions. For terminal W=O bonds, because of π*-antibonding unoccupied orbitals, their bonding interactions lie in very high energy and so are not available for interaction with substrates.³² In this section, at first the geometry, electronic structure and chemical bonding features of seven considered species will be deliberated, and then favourable species for oxidation reactions will be addressed.

2.3.1. PWFe^IVOH₂ and PWFe^IVO species. The PWFe^IVOH₂, as one of the high-valent species generated in the oxidation process, has three possible spin states of singlet, triplet, and quintet. From the results, singlet spin state is higher in energy than triplet by 7.4 kcal mol⁻¹. As for quintet spin state, weak interaction between Fe^IV and H₂O leads to the separation of H₂O from Fe and interaction with 23 and 29 oxygen atoms of lacuna POM through H₂O hydrogen atoms. For triplet spin state of PWFe^IVOH₂, the optimized geometry revealed a 2.047 Å bond length for Fe^IV–OH₂. The calculated WBI value for Fe^IV–O_aqua bond in PWFe^IVOH₂ is 0.384 (Table S3†). Thus, Fe^IV–OH₂ is a weak single bond and consequently terminal Fe=O bond could not exist in PWFe^IVOH₂. As previously mentioned, POMs can accept or donate one or several electrons with minimal structural changes,^27,30 thus our focus was not concentrated on bond lengths in this POMs (Table S3†). To verify, similarity in the IR frequencies of high-valent TMSPOMs have been shown by calculation (Table S4 and Fig. S9–S13†).

Bond length and bonding interaction in Fe^IV–OH₂ has not much difference with those of low-oxidation state species PWFe^IIIOH₂. Thus, Fe–O_ligand bond length is decreased from 2.060 Å in PWFe^IIIOH₂ to 2.047 Å in PWFe^IVOH₂ (Δr(Fe–OH₂) = 0.013 Å) and so the electronic structures of PWFe^IIIOH₂ and PWFe^IVOH₂ are almost similar. From the orbital energies of PWFe^IVOH₂ calculated through UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom), five MOs of HOMO−2, HOMO−1, HOMO, LUMO and LUMO+1 (Fig. S2a†) are metal-based d orbitals with antibonding character. These are originated from the overlapping between d orbitals of Fe and oxygen p orbitals (19, 22, 23 and 28). From the interaction between Fe 3d_z² orbital and σ(b2) non-bonding orbital of H₂O, a σ* molecular orbital could be formed.

Also, the inspection of molecular orbital diagram in this compound indicates that the π*-antibonding orbital, which is responsible for Fe=O bond, is not formed (Fig. S2a†). This expression of electronic configuration which made by molecular orbital analysis could be confirmed by Mulliken spin population. Obviously, the spin densities contribute in determining the electronic structure in all POM compounds. The spin density of PWFe^IVOH₂ in its triplet ground state is mainly localized on Fe^IV (1.6) and partly on the four coordinated oxygen atoms of PW₁₁ (0.085). No spin density resides on O_aqua (−0.015) being in well agreement with the MO prediction (Table 6).

Table 6 Calculated atomic charges and spin density of OH₂, OH, O and Fe atoms in PWFe^II–VI species determined based on NBO/UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom)

POM	Charge of Oligand	Charge of Fe	Spin density of Oligand	Spin density of Fe
PWFe^IIOH2	−0.90	0.64	0	0
PWFe^IIIOH2	−0.75	0.66	−0.008	0.924
PWFe^IVOH2	−0.73	0.82	−0.01	1.595
PWFe^IVOH	−0.64	0.87	0.10	1.713
PWFe^IVO	−0.43	0.86	0.76	3.072
PWFe^VO	−0.37	0.96	0.81	1.986
PWFe^VIO	−0.31	1.11	0.46	1.332

---

Geometry structure of the other high oxidation state Fe substituted POMs, PWFe^IVOH, was also optimized at OPTX-PBE/DZVP-GGA level. As results show, triplet state (S = 1) is the most stable and for singlet (S = 0) and quintet (S = 2) spin states lower stabilities up to 11.1 and 4.8 kcal mol⁻¹ were obtained, respectively. From the key geometrical parameters tabulated in Table S3,† by OH ligand in place of H₂O, interaction between Fe^IV and OH in a significant manner is improved. Thus, the optimized Fe^IV–O_ligand bond length is decreased from 2.047 Å in PWFe^IVOH₂ to 1.815 Å in PWFe^IVOH (Δr(Fe–O_ligand) = 0.232 Å). The calculated WBI value for Fe^IV–OH is 0.9089 and so Fe^IV–OH bond is a strong single bond.

According to our calculations, significant change on the Fe–OH bond in PWFe^IVOH demonstrates different electronic structure from Fe^II/III/IV–OH₂ POMs (Fig. S2b†). Among five frontier molecular orbitals that are metal-based d orbitals, two are responsible for Fe–OH bonding interaction. The σ(p–d) orbital come from overlapping between 2p_z orbital of OH ligand with 3d_z² orbital of Fe.

Also, the π*-antibonding orbitals arise from the interaction among 3d_xz orbital of Fe and 2p_x from oxygen in OH. It is well known that Fe–O_ligand π*-antibonding unoccupied orbital is closely correlated to the catalytic oxygenation processes, because it provides an electronic clue for reactivity in oxygen transfer reactions. Therefore, PWFe^IVOH with unoccupied 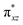-antibonding orbital may have a better reactivity for oxygen transfer reaction.^67,68

2.3.2. The effect of Fe oxidation state in defining favourable catalyst for oxygen transfer. In the next step, high-oxidation state iron substituted POMs with oxo ligand, PWFeⁿ⁺O (n = 4, 5 and 6), in various spin states optimized at DFT/OPTX-PBE/DZVP-GGA level have been investigated. According to the results, PWFe^IVO, PWFe^VO and PWFe^VIO have triplet, quartet, and triplet ground spin states respectively.

In PWFe^IVO, decreasing in Fe^IV–O_ligand bond length to 1.641 Å in the triplet ground state, compared to 1.815 Å for PWFe^IVOH, could be confirmed by calculation of WBI value for Fe^IV–O_ligand which is 1.46. Moreover, this shows a significant double bond feature for Fe^IV–O_ligand (Table S3†). Analysis of Fe^IV–O bonding interaction by electronic structure shows that HOMO and HOMO−1 orbitals are responsible for metal–oxygen binding interaction (Fig. S2c†). Both orbitals are obtained from significant contribution of oxygen 2p_x/y orbitals and 3d_xz/yz orbitals of Fe^IV. It should be noted that, these orbitals have important Fe–O_ligand π*-antibonding character. Among that, 3d_xy orbital is destabilized by antibonding interactions with p orbitals of four donor oxygen atoms at lacuna POM. As mentioned above, this important unoccupied Fe–O_ligand π*-antibonding orbitals do not exist in Fe^II/III/IV–OH₂ POMs.

In PWFe^VO, optimized structure of the low energy triplet spin state show that Fe^V–O_ligand bond length decreases to 1.635 Å from 1.641 Å in Fe^IV–O. This demonstrates minor changes in Fe^V–O_ligand compared to Fe^IV–O_ligand bond. This is mainly due to electron removing from nonbonding 3d_xy orbital (β-HOMO) in Fe^V–O respect to Fe^V–O_ligand bond. From the previous experimental studies by Rong and co-workers, [PW₁₁O₃₉(Ru^VO)]⁴⁻ possesses high capability in oxygen-transfer reaction.^69,70 It is worth mentioning that in the most of oxygen transfer reactions, at first, one electron transfers from π_c=c orbital of alkene to 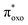orbital of M=O. This would weaken the M=O bond and then oxygen transfer from M=O group to alkene will happen.^71,72 Hence, PWFe^VO could be a favourable species in these reactions due to some of advantages that will be discussed in the following.

For optimized PWFe^VIO, the Fe^VI–O_ligand bond length decreases to 1.601 Å in the triplet ground state from 1.635 Å in PWFe^VO (Δr(Fe^V/VI–O_ligand) = 0.034 Å). Also, calculated WBI value for Fe^VI–O_ligand was 1.542 which indicates a significant double bond feature (Table S3†). In view of that, PWFe^VIO bonding interaction and subsequently their electronic structure are similar to PWFe^IV/VO.

As mentioned above, the important unoccupied Fe=O π*-antibonding orbitals are absent in PWFe^II/III/IVOH₂ while they appear in PWFe^IV/V/VIO. Mulliken spin population analysis also supports these interactions and electronic structures. Spin density in these compounds is mostly localized on Fe=O moiety and some of that on four oxygen in lacuna position of PW₁₁, while the rest of POM cage carry a small negative spin density (Table 6).

Now the question is: which of these high-oxidation states Fe substituted POMs would be favourable for oxidation process. According to frontier molecular orbital (FMO) theory, a suitable oxidation catalyst requires unoccupied orbitals with low energy and high orbital contribution of reactive atom at LUMO to achieve an appropriate overlap with the reagent FMOs.^67,68,73,74 The energy expression and participation percentage of Fe and oxygen in unoccupied Fe=O π*-antibonding orbitals are shown in Fig. 4.

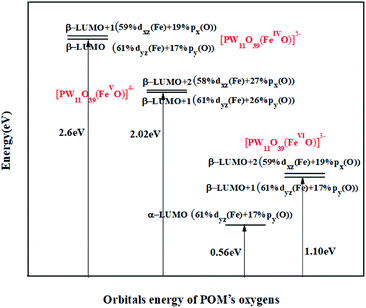Fig. 4 Unoccupied Fe=O π*-antibonding orbitals for high-oxidation states PWFe^IV/V/VIO determined based on UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom).

As it could be seen in Fig. 4, in PWFe^IV/VO species, unoccupied Fe=O π*-antibonding orbitals consist of β spin orbitals. In PWFe^VIO, unoccupied Fe=O π*-antibonding orbitals consist of α and β spin orbitals. Respect to HOMO, which contains oxygen p-orbitals, the energies of unoccupied Fe=O π*-antibonding orbitals decrease in the following order: PWFe^IVO > PWFe^VO > PWFe^VIO (Fig. 4). This order could be attributed to the POM charges reducing.^75–77 Contribution of oxygen atom orbitals in these unoccupied Fe=O π*-antibonding orbitals decreases as following: PWFe^VO > PWFe^IVO > PWFe^VIO (Fig. 4).

Calculated atomic charges and spin density values of oxygen bonded Fe in PWFe^IV/V/VIO species are tabulated in Table 6. Results in Table 6 show lower negative charge for O²⁻ ligand in these TMSPOMs than free O²⁻. Lesser negative charge on O²⁻ ligand indicates the charge transfer from oxygen to Fe. Therefore, polarization of Fe=O bond could be an important factor for determining the activity differences in these TMSPOMs. The absolute values of atomic charges decrease in the following order: PWFe^IVO (−0.43) > PWFe^VO (−0.37) > PWFe^VIO (−0.31) (Table 6). This is mainly along with increasing in the oxidation state of Fe atom. Moreover, decreasing in the spin density of O²⁻ ligand for these high-oxidation state species is as following: PWFe^VO > PWFe^IVO > PWFe^VIO (Table 6). In both of PWFe^IV/VO species, with high spin density on the O²⁻ (0.76 and 0.81 respectively), the O²⁻ ligand possess substantial radical character. In experimental reports, radical complexes are regarded as suitable catalysts for closure of the epoxide rings.²⁰ In contrary, radical character of oxygen in PWFe^VIO is weakened considerably where the calculated spin density on the O²⁻ decreased to 0.46.

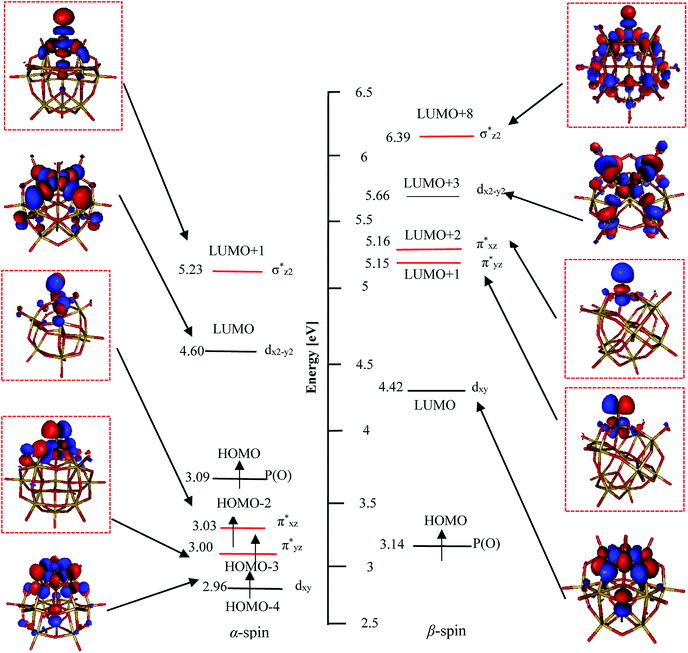
According to above mentioned points, PWFe^VO would be favorable for oxidation processes owing to unoccupied π*-antibonding orbitals (β-LUMO+1 and β-LUMO+2) with low energy and high contribution of O²⁻ respect to PWFe^II/III/IVOH₂, PWFe^IVOH and PWFe^IV/VIO. From the FMOs energy expression of PWFe^VO in Fig. 5, it could be revealed that: α and β occupied and unoccupied orbitals with π* symmetry (α-HOMO−2, α-HOMO−3, β-LUMO+1, β-LUMO+2) and α and β unoccupied orbitals with σ* symmetry (α-LUMO+1 and β-LUMO+8) are responsible for Fe=O bonding interaction in PWFe^VO. The π*-antibonding orbitals are formed from overlapping between 3d_xz/yz orbitals of Fe^V and 2p_x/y orbitals of oxygen, while the σ*-antibonding orbitals are made from combining the 3d_z² orbital of Fe^V and 2p_z orbital of O²⁻ ligand. Due to their lower energy, unoccupied π* orbitals are more important than σ* ones. According to DFT results, unoccupied Fe=O π*-antibonding orbitals comprise from β-LUMO+1 and β-LUMO+2 in which β-LUMO+1 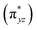contain 26% contribution of O²⁻ p_y orbital and 61% Fe^V d_yz orbital and β-LUMO+2 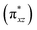contains 27% contribution of O²⁻ p_x orbital and 58% of Fe^V d_xz orbital which are mostly classified as Fe=O functional group (Fig. 4).

Fig. 5 The molecular orbitals expression of PWFe^VO calculated at UOPBE/6-31G(d) (LANL2DZ basis set on the metal atom) level. The orbital energy values have been represented in eV.

3. Computational details

All DFT computations of this work were performed with deMon2k program.³⁶ We used the OPTX exchange functional proposed by Cohen and Handy,^78,79 coupled with the Perdew–Becke–Ernzerhof (PBE) correlation functional.⁸⁰ This Generalized-Gradient-Approximation (GGA) functional has been shown adequacy for modeling iron–porphyrin and cobalt porphyrin complexes.^81–84 The Keggin type POM compounds were investigated by OPTX-PBE functional by assuming its adequacy based on previous studies.^26,34,85 The DFT energies and gradients were corrected by an empirical expression to indicate dispersion.⁸⁶ The Kohn–Sham equations were solved within the auxiliary DFT framework, where variationaly fitted auxiliary electron densities are applied in calculating both the Coulomb and the exchange-correlation (XC) potential.^87,88 An adaptive grid of fine mesh (tolerance 10⁻⁷ a.u.) was chosen for the numerical integration of the XC potential.⁸⁹ The basis set of DZVP-GGA (double-zeta-valence-polarization calibrated for generalized-gradient-approximation functional) on Fe, O, P, W and H was applied for geometry optimizations, frequency and electronic structure analyses.⁹⁰ The auxiliary electron density was expanded with the GEN-A2 auxiliary basis set on Fe, W, P, O and H.⁹¹ The self-consistent-field iterations were run with convergence criteria of 10⁻⁸ hartree on the DFT energies. The geometry optimizations were performed with 1 × 10⁻⁵ hartree per bohr tolerance criteria on the energy gradients. No molecular symmetry was applied in geometry optimizations. Vibrational frequencies were obtained at the same level in this work. Cartesian coordinates of the optimized geometries of the complexes are presented in ESI.† Natural bond orbital (NBO) analysis at the OPBE/6-31G(d) level (LANL2DZ basis set on the metal atom)^92–94 was performed to assign the atomic charges, spin densities and effective bond order/Wiberg Bond Indices (WBI). The NBO calculations were done with the Gaussian 09 package,⁹⁵ considering only the ions without either counter cations or solvent molecules.

4 Conclusion

DFT/OPTX-PBE method has been employed to investigate the geometry, electronic structure, Fe–ligand bonding nature, and simulated IR spectrum of α-Keggin, lacunary Keggin, Fe^II/III substituted and the important oxidized high-valent iron derivatives of Keggin type POMs. The most significant finding is briefed as follows:

(i) Increasing in the POM charge, like PW₁₁, results in no significant alteration of local charge at central PO₄³⁻. This high charge density is accumulated in W₁₁O₃₅ framework of the POM and specially concentrated on the terminal oxygen atoms which increase their basicity.

(ii) The electronic structures provide basis for understanding the bonding interactions between Fe^II and POM ligand. Bonding MOs result from contribution of 3d atomic orbitals of Fe^II and 2p orbitals of oxygen in POM.

(iii) The simulated IR spectra show that four characteristic peaks of PW₁₂ split into five owing to substitution of Fe atom in PWFeⁿ⁺ (n = 2 and 3).

(iv) The PWFe^II/III/IVOH₂ derivatives show the weak Fe–O_ligand single bond and PWFe^IV/V/VIO derivatives display the strong Fe=O double bond. So, it could be predicted that Fe oxidation state affect the antibonding interaction between Fe and ligand, which is the main character of these derivatives, and increase their activity in oxygen transfer processes.

(v) Relevant to other high-valent species, PWFe^VO would be favourable for oxidation process because of low energy unoccupied π*-antibonding orbitals and high contribution of oxygen.

(vi) The FMO analysis indicated that Fe=O bonding interaction mainly comes from an effective overlapping between 2p_x/y orbitals of O²⁻ ligand and 3d_xz/yz orbitals of Fe, thus an electron transfer from oxygen to Fe atom could be occurred.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are thankful of University of Isfahan for financially support of this research. We are also grateful from Prof. Aurelien de La Lande (Laboratoire de Chimie Physique, LCP, CNRS) and the University of Paris-Sud for supporting our computations at Styx.

Notes and references

1. P. Gouzerh and A. Proust, Chem. Rev., 1998, 98, 77–112.
2. J. T. Rhule, C. L. Hill, D. A. Judd and R. F. Schinazi, Chem. Rev., 1998, 98, 327–358.
3. S.-S. Wang and G.-Y. Yang, Chem. Rev., 2015, 115, 4893–4962.
4. I. V. Kozhevnikov, Chem. Rev., 1998, 98, 171–198.
5. A. Proust, R. Thouvenot and P. Gouzerh, Chem. Commun., 2008, 1837–1852.
6. T. Yamase, Chem. Rev., 1998, 98, 307–326.
7. M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841–2888.
8. C. Wang, K. V. Shalyaev, M. Bonchio, T. Carofiglio and J. T. Groves, Inorg. Chem., 2006, 45, 4769–4782.
9. J. Kaizer, E. J. Klinker, N. Y. Oh, J. U. Rohde, W. J. Song, A. Stubna, J. Kim, E. Münck, W. Nam and L. Que, J. Am. Chem. Soc., 2004, 126, 472–473.
10. N. S. Antonova, J. J. Carbó, U. Kortz, O. A. Kholdeeva and J. M. Poblet, J. Am. Chem. Soc., 2010, 132, 7488–7497.
11. S. P. de Visser, D. Kumar, R. Neumann and S. Shaik, Angew. Chem., Int. Ed., 2004, 43, 5661–5665.
12. P. Jiménez-Lozano, I. Y. Skobelev, O. A. Kholdeeva, J. M. Poblet and J. J. Carbó, Inorg. Chem., 2016, 55, 6080–6084.
13. K. Kamata, T. Hirano, S. Kuzuya and N. Mizuno, J. Am. Chem. Soc., 2009, 131, 6997–7004.
14. K. Kamata, R. Ishimoto, T. Hirano, S. Kuzuya, K. Uehara and N. Mizuno, Inorg. Chem., 2010, 49, 2471–2478.
15. K. Kamata, Y. Nakagawa, K. Yamaguchi and N. Mizuno, J. Am. Chem. Soc., 2008, 130, 15304–15310.
16. A. E. Kuznetsov, Y. V. Geletii, C. L. Hill, K. Morokuma and D. G. Musaev, Inorg. Chem., 2009, 48, 1871–1878.
17. Z. L. Lang, G. C. Yang, M. N. Ma, S. Z. Wen, L. K. Yan, W. Guan and Z. M. Su, Dalton Trans., 2013, 42, 10617–10625.
18. C. G. Liu, W. Guan, L. K. Yan and Z. M. Su, Eur. J. Inorg. Chem., 2011, 489–494.
19. C. G. Liu, W. Guan, L. K. Yan, P. Song and Z. M. Su, Dalton Trans., 2009, 6208–6213.
20. C. G Liu, X. M. Jiang and Z. M. Su, Inorg. Chem., 2017, 56, 10496–10504.
21. J. M. Maestre, X. Lopez, C. Bo, J.-M. Poblet and N. Casan-Pastor, J. Am. Chem. Soc., 2001, 123, 3749–3758.
22. D. G. Musaev, K. Morokuma, Y. V. Geletii and C. L. Hill, Inorg. Chem., 2004, 43, 7702–7708.
23. Y. Nakagawa and N. Mizuno, Inorg. Chem., 2007, 46, 1727–1736.
24. R. Prabhakar, K. Morokuma, C. L. Hill and D. G. Musaev, Inorg. Chem., 2006, 45, 5703–5709.
25. J. Wang, C. Hu, M. Jian, J. Zhang and G. Li, J. Catal., 2006, 240, 23–30.
26. H. N. Wu, J. Wang, H. Li, N. N. Ma, T. Zhang, S. Q. Shi, L. K. Yan and Z. M. Su, Comput. Theor. Chem., 2016, 1089, 28–34.
27. M. X. Jiang and C. G. Liu, J. Phys. Chem. C, 2017, 121, 12735–12744.
28. D. Quiñonero, Y. Wang, K. Morokuma, L. A. Khavrutskii, B. Botar, Y. V. Geletii, C. L. Hill and D. G. Musaev, J. Phys. Chem. B, 2006, 110, 170–173.
29. Y. Wang, G. Zheng, K. Morokuma, Y. V. Geletii, C. L. Hill and D. G. Musaev, J. Phys. Chem. B, 2006, 110, 5230–5237.
30. C.-G. Liu, S. Liu and T. Zheng, Inorg. Chem., 2015, 54, 7929–7935.
31. C. G. Liu, Z. M. Su, W. Guan and L. K. Yan, Inorg. Chem., 2009, 48, 541–548.
32. S. Romo, N. S. Antonova, J. J. Carbó and J. M. Poblet, Dalton Trans., 2008, 5166–5172.
33. B. Zhu, Z. L. Lang, M. N. Ma, L. K. Yan and Z. M. Su, Phys. Chem. Chem. Phys., 2014, 16, 18017–18022.
34. E. Derat, D. Kumar, R. Neumann and S. Shaik, Inorg. Chem., 2006, 45, 8655–8663.
35. W. Guan, L. Yan, Z. Su, S. Liu, M. Zhang and X. Wang, Inorg. Chem., 2005, 44, 100–107.
36. A. Koster, G. Geudtner, P. Calaminici, M. Casida, V. Dominguez, R. Flores-Moreno, G. Gamboa, A. Goursot, T. Heine and A. Ipatov, DeMon2k, Version 3, The deMon Developers, Cinvestav, Mexico City, Mexico, 2011.
37. R. Neumann and A. M. Khenkin, J. Mol. Catal. A: Chem., 1996, 114, 169–180.
38. P. Souchay, Polyanions et polycations, Gauthier-Villars, 1963.
39. X. Lo'pez, J. J. Carbo', C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537–7571.
40. B. Courcot and A. J. Bridgeman, Int. J. Quantum Chem., 2010, 110, 2155–2161.
41. B. Courcot and A. J. Bridgeman, J. Comput. Chem., 2011, 32, 240–247.
42. B. Courcot and A. J. Bridgeman, J. Comput. Chem., 2011, 32, 1703–1710.
43. B. Courcot and A. J. Bridgeman, J. Comput. Chem., 2011, 32, 3143–3153.
44. M. R. Farsani and B. Yadollahi, J. Mol. Catal. A: Chem., 2014, 392, 8–15.
45. I. Böschen, B. Buss and B. Krebs, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 48–56.
46. C. L. Hill and R. B. Brown, J. Am. Chem. Soc., 1986, 108, 536–538.
47. M. Colladon, A. Scarso, P. Sgarbossa, R. A. Michelin and G. Strukul, J. Am. Chem. Soc., 2007, 129, 7680–7689.
48. N. Mizuno and M. Misono, Chem. Rev., 1998, 98, 199–218.
49. N. Mizuno, K. Yamaguchi and K. Kamata, Coord. Chem. Rev., 2005, 249, 1944–1956.
50. Y. Sawada, K. Matsumoto and T. Katsuki, Angew. Chem., Int. Ed., 2007, 46, 4559–4561.
51. D. Mansuy, J. F. Bartoli, P. Battioni, D. K. Lyon and R. G. Finke, J. Am. Chem. Soc., 1991, 113, 7222–7226.
52. T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2004, 126, 6252–6254.
53. M. D. Fryzuk, S. A. Johnson, B. O. Patrick, A. Albinati, S. A. Mason and T. F. Koetzle, J. Am. Chem. Soc., 2001, 123, 3960–3973.
54. A. Hiskia and E. Papaconstantinou, Inorg. Chem., 1992, 31, 163–167.
55. L. Eberson, New J. Chem., 1992, 16, 151–156.
56. I. A. Weinstock, Chem. Rev., 1998, 98, 113–170.
57. R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Angew. Chem., Int. Ed., 2006, 45, 8038–8042.
58. H. Chen, M. Ikeda-Saito and S. Shaik, J. Am. Chem. Soc., 2008, 130, 14778–14790.
59. F. M. Santos, S. P. Magina, H. I. Nogueira and A. M. Cavaleiro, New J. Chem., 2016, 40, 945–953.
60. S. Afewerki and A. Cordova, Chem. Rev., 2016, 116, 13512–13570.
61. F. G. Gelalcha, Chem. Rev., 2007, 107, 3338–3361.
62. T. Mallat and A. Baiker, Chem. Rev., 2004, 104, 3037–3058.
63. V. C. C. Wang, S. Maji, P. P. Y. Chen, H. K. Lee, S. S. F. Yu and S. I. J. C. R. Chan, Chem. Rev., 2017, 117, 8574–8621.
64. B. Zhang, H. Asakura, J. Zhang, J. Zhang, S. De and N. Yan, Angew. Chem., Int. Ed., 2016, 55, 8319–8323.
65. C. L. Hill and C. M. Prosser-McCartha, Coord. Chem. Rev., 1995, 143, 407–455.
66. J. Roithova and D. Schroder, Chem. Rev., 2009, 110, 1170–1211.
67. S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542.
68. S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328.
69. R. Neumann and C. Abu-Gnim, J. Am. Chem. Soc., 1990, 112, 6025–6031.
70. C. Rong and M. T. Pope, J. Am. Chem. Soc., 1992, 114, 2932–2938.
71. M. T. Pope and A. Müller, Angew. Chem., Int. Ed., 1991, 30, 34–48.
72. M. Sadakane and E. Steckhan, Chem. Rev., 1998, 98, 219–238.
73. A. Decker, M. S. Chow, J. N. Kemsley, N. Lehnert and E. I. Solomon, J. Am. Chem. Soc., 2006, 128, 4719–4733.
74. A. Decker, J.-U. Rohde, L. Que and E. I. Solomon, J. Am. Chem. Soc., 2004, 126, 5378–5379.
75. J. A. Fernández, X. López, C. Bo, C. de Graaf, E. J. Baerends and J. M. Poblet, J. Am. Chem. Soc., 2007, 129, 12244–12253.
76. X. López, J. A. Fernández and J. M. Poblet, Dalton Trans., 2006, 1162–1167.
77. S. Romo, J. A. Fernández, J. M. Maestre, B. Keita, L. Nadjo, C. de Graaf and J. M. Poblet, Inorg. Chem., 2007, 46, 4022–4027.
78. N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412.
79. M. Swart, A. W. Ehlers and K. Lammertsma, Mol. Phys., 2004, 102, 2467–2474.
80. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
81. A. de la Lande, M.-H. Ha-Thi, S. Chen, B. Soep and N. Shafizadeh, Phys. Chem. Chem. Phys., 2016, 18, 16700–16708.
82. M. M. Conradie, J. Conradie and A. Ghosh, J. Inorg. Biochem., 2011, 105, 84–91.
83. M. Aarabi, R. Omidyan, S. Soorkia, G. Grégoire, M. Broquier, M.-E. Crestoni, A. de La Lande, B. Soep and N. Shafizadeh, Phys. Chem. Chem. Phys., 2019, 21, 1750–1760.
84. M. Aarabi, S. Soorkia, G. Grégoire, M. Broquier, A. de la Lande, B. Soep, R. Omidyan and N. Shafizadeh, Phys. Chem. Chem. Phys., 2019, 21, 21329–21340.
85. C. G. Liu, Mol. Phys., 2011, 109, 1851–1857.
86. A. Goursot, T. Mineva, R. Kevorkyants and D. Talbi, J. Chem. Theory Comput., 2007, 3, 755–763.
87. R. Flores-Moreno and A. M. Köster, J. Chem. Phys., 2008, 128, 134105.
88. A. Vela, V. Medel and S. Trickey, J. Chem. Phys., 2009, 130, 244103.
89. M. Krack and A. M. Köster, J. Chem. Phys., 1998, 108, 3226–3234.
90. P. Calaminici, F. Janetzko, A. M. Köster, R. Mejia-Olvera and B. Zuniga-Gutierrez, J. Chem. Phys., 2007, 126, 044108.
91. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
92. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
93. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
94. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
95. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2013.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05189f

---