Investigation of strain and doping on the electronic properties of single layers of C₆N₆ and C₆N₈: a first principles study

Abstract

In this work, by performing first-principles calculations, we explore the effects of various atom impurities on the electronic and magnetic properties of single layers of C₆N₆ and C₆N₈. Our results indicate that atom doping may significantly modify the electronic properties. Surprisingly, doping Cr into a holey site of C₆N₆ monolayer was found to exhibit a narrow band gap of 125 meV upon compression strain, considering the spin–orbit coupling effect. Also, a C atom doped in C₆N₈ monolayer shows semi-metal nature under compression strains larger than −2%. Our results propose that Mg or Ca doped into strained C₆N₆ may exhibit small band gaps in the range of 10–30 meV. In addition, a magnetic-to-nonmagnetic phase transition can occur under large tensile strains in the Ca doped C₆N₈ monolayer. Our results highlight the electronic properties and magnetism of C₆N₆ and C₆N₈ monolayers. Our results show that the electronic properties can be effectively modified by atom doping and mechanical strain, thereby offering new possibilities to tailor the electronic and magnetic properties of C₆N₆ and C₆N₈ carbon nitride monolayers.

---

1 Introduction

Recently, two-dimensional carbon nitride (2D-CN) nanomaterials have attracted remarkable attention, not only because of astonishing experimental advances concerning their synthesis but also due to their exciting physics^1–5 and promising prospects for various advanced applications, like nanoelectronics, energy storage and catalysis.^6–16 Two-dimensional carbon nitride (2D-CN) nanomaterials belong to a group of allotropes with a common chemical formula of C_nN_m, where n and m represent the number of C and N atoms in the unit cell, respectively, which can be stabilized as monolayers by taking advantage of the multifarious chemistry of C and N atoms. Depending on the composition of C and N atoms in the atomic lattice, these allotropes can show diverse electronic properties, ranging from semiconducting to half-metallic. 2D-CN monolayers exhibit considerable structural, electronic and magnetic properties^17–21 with diverse electronic properties, originating from their unique and different atomic lattices, made from strong covalent bonds.^22–25

The successful synthesis and fabrication of two-dimensional carbon nitride (2D-CN) nanomaterials, including C₂N, C₃N, C₆N₈ and C₆N₆ through bottom-up procedures, has motivated researchers to consider possible approaches for tuning the band gap and electronic response of these attractive nanosheets.^22,26–28 Some 2D-CN nanosheets have been experimentally realized using different approaches.^1,3,29–33 C₆N₆ is a 2D-CN allotrope in which two hexagonal rings are separated by a C–C bond,¹ and it has already been theoretically investigated.^34–36 Recent theoretical work showed that C₆N₆ exhibits a topologically nontrivial band gap, which can be modulated to a topological insulator by doping.¹ To search for a suitable spintronic material such as a diluted magnetic semiconductor, first-principles calculations of transition metal (TM) atoms doped in semiconducting 2D-CN sheets have been performed^2,37,38 using density functional theory (DFT) calculations.^39,40 The semiconducting nature and band alignment in this nanosheet are suitable for hydrogen generation via photo-catalytic water splitting.^41–44

First-principles calculations indicated that topologically nontrivial electronic states near the Fermi level can be characterized by a ruby model.⁴⁵ Recently, carbon nitride materials with stoichiometry of C₆N₈ have been synthesized experimentally.^12,26,46,47 C₆N₈ are the prevailing building blocks that are joined together directly or by sp²-hybridized nitrogen/carbon atoms.¹² The electronic and magnetic properties have subsequently been studied,^48,49 and theoretical studies demonstrate that C₆N₈ is not a magnetic material; however, after replacing a nitrogen atom with a carbon atom in the unit cell of C₆N₈, it displays intrinsic half-metallicity.³ Hydrogenation can also induce magnetism in carbon-based nonmagnetic materials.^50,51 It was predicted theoretically that hydrogen doping on the irradiation-induced carbon vacancy with hydrogen adsorption could induce a stronger magnetic moment than the bare vacancy.⁵² Moreover, first-principles calculations also show that semihydrogenated graphene sheets are ferromagnetic semiconductors with a small indirect gap.⁵³ On the other hand, it is well-known that the application of mechanical strain can be an effective way to adjust the electronic structure of 2DM,⁵⁴ and in previous studies strain has been proven as a common way to regulate properties. In order to enhance the application of a material in electronic and optoelectronic devices, it can be very useful to regulate the electronic properties. Atom impurities can tailor the electronic properties and can be used for a wide range of applications. Despite the fact that many 2D nanosheets have been synthesized recently, their tunable electronic properties have rarely been reported.^{55–90,108–110}

In this paper, using first-principles calculations, we systematically investigate the effect of different atom impurities in the holey sites of C₆N₆ and C₆N₈ monolayers. Our results confirm that the electronic properties can be modified by doping with Cr atoms. In addition, by applying strain, we found that the magnetic moment can be modulated and a transition from semiconductor to metal can be achieved. Our results reveal that the band gap and magnetism can be modified or induced by various atom impurities, thereby offering effective possibilities to tune the electronic and magnetic properties of C₆N₆ and C₆N₈ monolayers.

2 Methods

We report the results of our spin-polarized DFT calculations for the electronic structure as implemented in the OpenMX 3.8 package.⁹¹ Wave functions were expanded by the linear combination of multiple pseudoatomic orbitals (LCPAOs) created using a confinement scheme.^92,93 The generalized gradient approximation method proposed by Perdew–Burke–Ernzerhof (GGA-PBE)⁹⁴ was applied to deal with the exchange-correlation functionals, along with the norm-conserving pseudopotentials.⁹⁵ A quasi-Newton algorithm was employed to find the energy-minimized structures using the OpenMX package. The convergence criteria for the structural optimization were set as a force of less than 1 meV Å⁻¹ acting on each atom. After the completion of this step, we used a cutoff energy of 300 so that the total energies converge to below 1.0 meV per atom. The Brillouin zone was sampled by a k-point grid of 23 × 23 × 1 for the primitive unit cell and scaled according to the size of the supercells, on the basis of the Monkhorst–Pack scheme.⁹⁶ The monolayers are modelled as a periodic slab with a large vacuum region (20 Å) in order to prevent interactions between adjacent layers. To describe the vdW interactions we use the empirical correction method described by Grimme (DFT-D2).⁹⁷ The charge transfer was calculated using Mulliken charge analysis.⁹⁸ Scanning tunneling microscopy (STM) images were simulated using the Tersoff–Hamann theory.⁹⁹ The STM simulated images were plotted using WSxM software.¹⁰⁰

3 Results

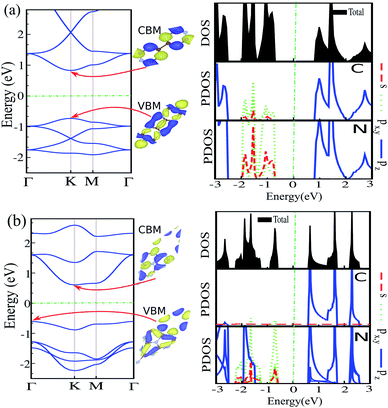
3.1 Pristine C₆N₆ and C₆N₈ monolayers

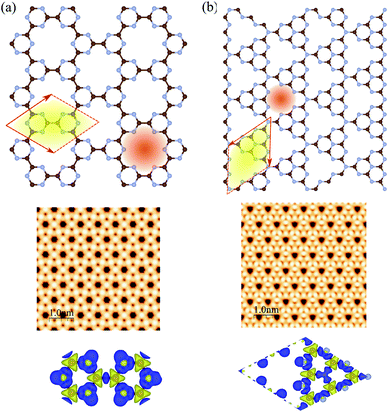
The atomic structures, simulated STM images, and charge density differences of C₆N₆ and C₆N₈ monolayers are shown in Fig. 1(a) and (b), respectively. The optimized lattice constant of C₆N₆ is calculated to be 7.11 Å and the corresponding C–C and C–N bond lengths are found to be 1.503 Å and 1.343 Å, respectively. The nanopore diameter is found to be 5.447 Å, which is equivalent to the distance from one N atom to the opposite N atom across the pore. These results are consistent with previous reports.^36,101–103 The charge density difference, in which the blue and yellow colors show the charge accumulation and depletion, respectively, reveals that the positively charged C atoms are surrounded by negatively charged N atoms. Moreover, the simulated STM image indicates that the atoms around the C atom sites show bright spots. The electronic band structure, density of states (DOS) and partial DOS (PDOS) of C₆N₆ and C₆N₈ monolayers are shown in Fig. 2(a) and (b), respectively. Apparently, the C₆N₆ monolayer is a semiconductor with a direct band gap of 1.5 eV located at the K-point, which is also supported by a previous report.³⁶ From the PDOS, we found Fermi-level sharp peaks +2 eV below the Fermi level, suggesting that there are localized wave functions in C₆N₆ and indicating that sharp double peaks (flat shallow bands) are formed from the N s and p_x,y orbitals. In the VBM, the N atoms are in the sp² configuration and their lone pairs are further exhibited in the rising band structure from the Γ to the K point near the Fermi-level. The lone pairs of N s and p_x,y lie in in-plane orbitals, suggesting the donor nature of the nanopore, although the N/C p_z antibonding delocalized orbitals form the CBM above the Fermi-level, showing the acceptor nature of C₆N₆. The filling of all the in-plane bonding orbitals implies high stability of the C₆N₆ structure.

Fig. 1 Atomic structures (top), simulated STM images (middle) and charge density differences (bottom) of (a) C₆N₆ and (b) C₆N₈ monolayers. The primitive unit cells are indicated by red parallelograms. The brown and blue atoms represent C and N atoms, respectively. The blue and yellow regions represent the charge accumulation and depletion regimes, respectively.

Fig. 2 Electronic band structure (left), density of states and partial density of states (right) of (a) C₆N₆ and (b) C₆N₈ monolayers. The insets represent the charge densities of the VBM and CBM. Zero energy is set at the Fermi level.

The optimized lattice constant of monolayer C₆N₈ is found to be 7.14 Å, with two inequivalent C–N bonds (1.414 and 1.455 Å). In addition, the ring is not a regular hexagon since the C–N–C angle is equal to 120°, while the N–C–N angles are 118° and 122°, respectively. It is clear that every six C–N hexagon rings enclose a nanopore, while the edges are surrounded by six N atoms, with a nanopore diameter of 4.773 Å (see Fig. 2(b)), which is in agreement with previous reports.^{39,101,104,105} The electronic structure of C₆N₈ exhibits an indirect semiconductor with a 1.22 eV band gap, which is in agreement with the previous result.¹⁰⁶ In addition, from the PDOS of C₆N₈ it can be clearly seen that the VBM is determined by the N s and p_x,y orbitals; however, the CBM originates from the N/C p_z orbitals.

3.2 Doping of atom into holey site

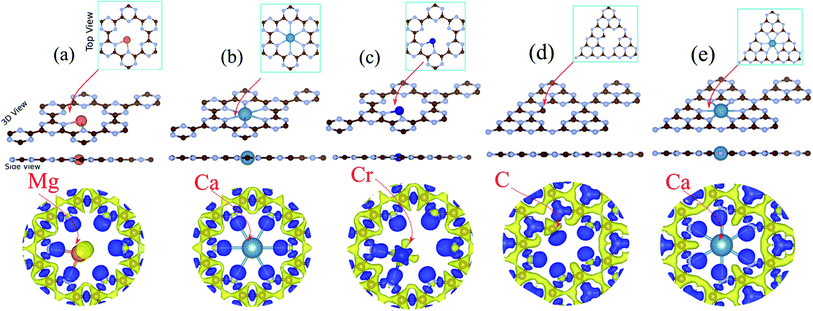
Here, we discuss the effect of atom doping on the structural and electronic properties of C₆N₆ and C₆N₈ monolayers. A 2 × 2 × 1 supercell of C₆N₆ and C₆N₈ contains 49 and 57 atoms, respectively. A schematic view of the doped atom in the holey site of the C₆N₆ and C₆N₈ monolayers is shown in the ESI, Fig. S1.† For the different atoms considered in our present study, the stable binding sites are uniformly at the nanopore. Through the rest of the study, the atom-doped C₆N₆ structure is labeled as atom@C₆N₆. For instance, Mg doped C₆N₆ is labeled Mg@C₆N₆.

The optimized structures of Mg@, Ca@ and Cr@C₆N₆ are shown in Fig. 3(a–c), respectively. The Mg and Ca atoms interact through sp²-hybridization and form two and six σ bonds with the neighboring N atoms, respectively. Our results show that the bond lengths of the Mg and Ca atoms with the nearest N atoms are 2.62 and 2.37 Å, respectively (see Table 1). The Cr atom binds to the two nearest N atoms facing the nanopore of the C₆N₆ monolayer with a bond length of 1.94 Å. Notably, upon atom doping, the planar structure of monolayer C₆N₆ is preserved. The charge density differences are presented in Fig. 3, where the bond formation, charge accumulation, and depletion regions can clearly be seen. The blue and yellow regions represent charge accumulation and depletion, respectively. For the stability of the structures, we calculate the binding energy (E_b) between the doped atoms and the C₆N₆/C₆N₈ sheets by the following formula:

E_b = E_tot − E_sheet − E_atom (1)

Here, E_tot is the total energy of the doped C₆N₆/C₆N₈ sheet, and E_sheet and E_atom are the energies of the pristine C₆N₆/C₆N₈ sheet and isolated spin-polarized atom, respectively. According to this definition, a more negative value of E_b indicates that the system has stronger binding between the atom and the C₆N₆/C₆N₈ sheet. Our results show that the binding energies for C, Mg, Ca and Cr atom doping in C₆N₆ (C₆N₈) sheets are −3.46 eV (−3.38), −3.70 eV (−3.43), −3.95 eV (−3.87) and −4.65 eV (−3.65).

Fig. 3 Optimized structures of (a) Mg, (b) Ca, and (c) Cr atom doped C₆N₆. (d and e) Optimized structures of C and Ca doped C₆N₈. Charge density differences are shown in the bottom panel. Blue and yellow regions represent charge accumulation and depletion, respectively.

Table 1 Structural, electronic and magnetic parameters of atom doped C₆N₆ and C₆N₈ monolayers. Bond length between doped atom and its nearest atom (d_AN); bond length between N–C atoms (d_NC); bond length between C–C atoms (d_CC); charge transfer (ΔQ); magnetic moment per supercell M_tot (μ_B). Electronic state (ES), specified as metal (M), half-metal (HM), ferromagnetic metal (FM), semiconductor (SC). The values outside (inside) parentheses are for C₆N₆ (C₆N₈) monolayers

Atom	dAN (Å)	dNC (Å)	dCC (Å)	ΔQ (e)	Mtot (μB)	ES
C	1.46 (1.39)	1.40 (1.44)	1.42 (1.42)	0.99 (1.38)	0 (0)	SC (SC)
Mg	2.16 (2.30)	1.39 (1.41)	1.44 (1.44)	0.99 (1.38)	0 (0)	SC (M)
Ca	2.66 (2.37)	1.38 (1.38)	1.43 (1.44)	1.17 (1.32)	0 (1)	M (FM)
Cr	1.94 (2.16)	1.41 (1.40)	1.42 (1.42)	0.56 (0.63)	2.4 (2.1)	FM (HM)

---

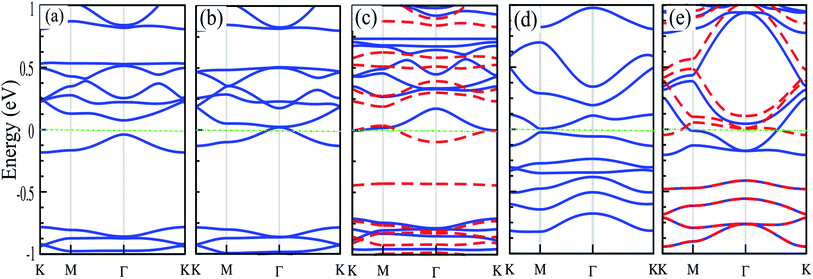
The electronic structures of Mg@, Ca@ and Cr@C₆N₆ are shown in Fig. 4(a–c), where the solid blue and dashed red lines represent ↑ and ↓ spin channels, respectively. Our results show that in comparison with pristine C₆N₆, the band structures are modified and give rise to localized mid-gap states arising from the atomic doping. Note that the doping of Mg and Cr atoms gives rise to some localized states in the band structure, which modify the electronic properties. Our results show that Mg@C₆N₆ exhibits direct band gap semiconducting behavior, with a small band gap of 100 meV where the VBM and CBM are located at the Γ point. Interestingly, we can see that the Ca@C₆N₆ monolayer exhibits metallic character. In contrast, Cr@C₆N₆ is a ferromagnetic metal with a net magnetic moment of 2.4 μ_B. Note that the energy bands of the ↑ and ↓ spin channels near the Fermi-level cross together near to the Dirac-point. On the other hand, monolayer C@C₆N₈ becomes a direct band gap semiconductor with a narrow band gap of 25 meV, with the VBM and CBM located at the M point. With Ca atom doping in C₆N₈, we see a spin-polarized ferromagnetic metal with impurity levels crossing the Fermi-level and inducing a net magnetic moment of 1 μ_B per formula unit. The atomic contributions to the electronic states can be further seen by the PDOS, which are presented in Fig. 5. It is clear that the Mg and Ca states in C₆N₆ mostly contribute to the deep valence and conduction states. On the other hand, Cr in C₆N₆ and C in C₆N₈ also contribute to the states around the Fermi-level. The optimized structures and electronic structures of C@C₆N₆, Mg@C₆N₈ and Cr@C₆N₈ are shown in Fig. S2(a–c),† respectively. We found that the C atoms interact through sp²-hybridization and form two σ bonds with the neighboring N atoms of C₆N₆. The C@C₆N₆ structure shows semiconductor behavior with an indirect band gap of 1 eV, where the VBM and CBM are located at the K and M points, respectively (see Fig. S2(a)†). Our results show that the Cr atom bonds to the N host atoms of C₆N₈ and forms six σ bonds, while the neighboring N atoms of C₆N₈ form four σ bonds with the Mg atom (see Fig. S2(a) and (b)†). From the electronic band structure, we can see that Mg@C₆N₈ turns into a metal, whereas the Cr@C₆N₈ structure becomes a half-metal and a magnetic moment of about 2.1 μ_B is induced.

Fig. 4 Electronic structures of (a) Mg@C₆N₆, (b) Ca@C₆N₆, (c) Cr@C₆N₆, (d) C@C₆N₈ and (e) Ca@C₆N₈. The energy bands of ↑ and ↓ spin channels are indicated by blue lines and red dashed lines, respectively. Zero energy is set at the Fermi-level.

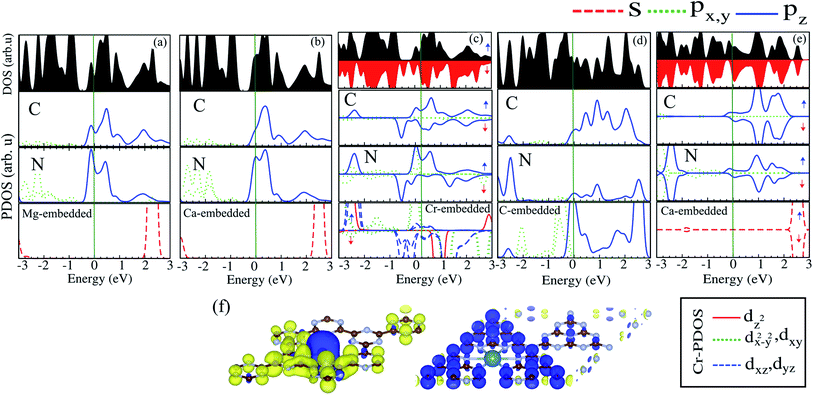Fig. 5 DOS and PDOS of (a) Mg@C₆N₆, (b) Ca@C₆N₆, (c) Cr@C₆N₆, (d) C@C₆N₈ and (e) Ca@C₆N₈. (f) Spin density difference. The blue and yellow regions represent the ↑ and ↓ spin states, respectively.

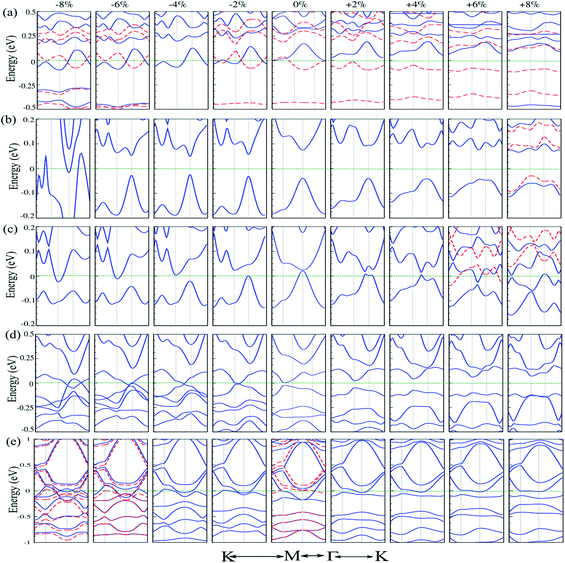
4 Effect of strain

Strain engineering is a robust method to tune the electronic properties and topological nature. In the following, we investigate the effects of uniaxial tensile and compressive strains on the electronic properties of atom doped C₆N₆ and C₆N₈ monolayers. The strain is defined as:¹⁰⁷ ε = (a ± a₀)/a₀ × 100, where a and a₀ are the strained and non-strained lattice constants, respectively, and the positive (negative) sign denotes tensile (compressive) strain. The band structures of Cr@, Mg@ and Ca@C₆N₆, and C@ and Ca@C₆N₈ as a function of the applied strain are shown in Fig. 6(a–e). Cr@C₆N₆ displays dilute magnetic semiconductor behavior under +2% tensile strain and it is preserved up to +8% strain. In addition, the magnetic moment increases from 2.8 (at −2%) to 3 μ_B (at −8%) with increasing compressive strain, while it is almost constant under tensile strain. Interestingly, when the compression strain reaches −2%, Cr@C₆N₆ exhibits spin-polarized semi-metal characteristics.

Fig. 6 Electronic band structure of (a) Cr@C₆N₆, (b) Mg@C₆N₆, (c) Ca@C₆N₆, (d) C@C₆N₈ and (e) Ca@C₆N₈ as a function of strain. The energy bands of ↑ and ↓ spin channels are indicated by blue lines and red dashed lines, respectively. Zero energy is set at the Fermi-level.

Our results show that Mg@C₆N₆ in the range of −2% to −6% exhibits a decreasing band gap from 90 meV to 70 meV, respectively, while in the strain-free case the band gap is 110 meV. This situation differs under tensile strain, such that the band gap changes in the range of 130 meV to 115 meV. Interestingly, at a tensile strain larger than +8%, the band structure of Mg@C₆N₆ in both ↑ and ↓ spin channels becomes spin-polarized, leading to the transition from nonmagnetic to magnetic states (see Fig. 6(b)). Ca@C₆N₆ is naturally a metal; surprisingly, with strains of −2% and −4% the band gaps reach 25 meV and 23 meV, respectively (see Fig. 6(c)), whereas under strain larger than −6% it transforms into a metal and we see a nontrivial band gap of 30 meV in the vicinity of the Fermi-energy. On the other hand, for monolayer Ca@C₆N₆ under +6 and +8% strain, the VBM (CBM) of the ↓ (↑) spin channel continuously shifts upward (downward) to the Fermi level, resulting in ferromagnetic metallic behavior with magnetic moments of 0.8 μ_B (+6%) and 1.8 μ_B (+8%). The electronic band structure of C@C₆N₈ under strain is shown in Fig. 6(d). C@C₆N₈ is initially a direct semiconductor with a narrow band gap of 30 meV; however, under 0% ≤ tensile strain ≤ +8%, the band gap increases monotonically from 70 meV (at +2%) to 200 meV (at +8%), while the VBM and CBM of the direct band gap are located at the M point. Our results show that the semiconducting characteristics are preserved in the range of +2% to +8%. Interestingly, C@C₆N₈ under compression strains of −2, −4 and −8% exhibits semi-metal behavior. When it reaches −6%, it transforms to a metal due to the CBM decrease and VBM increase to the Fermi-level. The electronic band structure of Ca@C₆N₈ under uniaxial strain in the ↑ and ↓ spin channels is shown in Fig. 6(e). We can see that variations in the magnetic moment occur when it is subjected to tensile and compressive strain. Ca@C₆N₈ is initially a ferromagnetic metal with a magnetic moment of 1 μ_B in the ground state. Interestingly, when a strain larger than +2% to +8% is applied, the ferromagnetic metal state is lost and both the ↑ and ↓ spin channels become non-spin-polarized, leading to a transition from a ferromagnetic metal to a nonmagnetic-metal state. Note that by increasing strain up to +2%, its magnetic moment vanishes. Also, for strains of 2–4%, Ca@C₆N₈ transforms into a nonmagnetic metal, while for larger strains (>−6%) the structure transforms into a ferromagnetic metal with magnetic moments of 0.47 μ_B (−6%) and 0.53 μ_B (−8%).

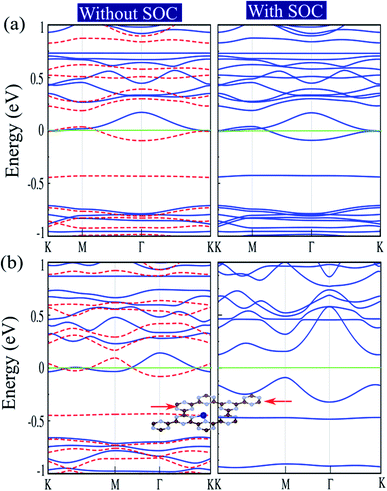
The electronic structures of Cr@C₆N₆ without strain and with −2% strain, considering spin–orbital coupling (SOC) and without SOC, are shown in Fig. 7(a) and (b). For Cr@C₆N₆ upon −2% compression strain, without considering SOC, we can see that the ↑ and ↓ spin bands cross each other at the Fermi-level, which implies a magnetic semi-metallic nature. Our results show that when the SOC effect is considered, we see a touching point along the Γ and K paths at the Fermi level, and a narrow band gap of 125 meV forms in the proximity of the Fermi level, which implies a semi-metallic character. The effect of SOC correction on the evolution of electronic structure was found to be remarkable, such that degeneracies at the VBM are removed. Due to weak screening of the Coulomb interaction in the doping of transition metal atoms, the Hubbard U energy band structure may be expected to be weak. Since the accurate value of U has not been determined, we investigate the correlation effects by the value of the Hubbard U. To confirm that semi-metallicity is not an artificial result from the GGA+U method, we perform calculations for the doping of Cr atoms. The electronic band structures of Cr@C₆N₆ without strain and with −2% strain, without (left) and with consideration of the Hubbard U effect (right) are shown in Fig. S3(a) and (b),† respectively. The correlation effects on the electronic and magnetic properties of Cr@C₆N₆ without and with strain are significant and cause changes in the spin polarization. In the Cr-doped C₆N₆ without strain and upon −2% compression strain, we can see that the ↑ and ↓ spin bands cross each other at the Fermi-level, which implies a spin-polarized semi-metallic nature, without considering Hubbard U. We can see that a nodal-line forms around the K and M points when U = 2 eV is considered. Our results show that the magnetic moment of Cr@C₆N₆ in U = 2 eV are 3.53 μ_B (without strain) and 3.63 μ_B (with −2% strain).

Fig. 7 Electronic structures of (a) Cr@C₆N₆, without and with consideration of spin–orbital coupling (SOC) effect; (b) Cr@C₆N₆ upon −2% strain, without and with SOC effect. Optimized structures under the applied strain are shown in the insets. The energy bands of ↑ and ↓ spin channels are indicated by blue lines and red dashed lines, respectively. Zero energy is set at the Fermi-level.

Here, we discuss the magnetic coupling between Cr–Cr doped in C₆N₆ monolayers. We consider two Cr atoms doped in one and two neighboring cavities for comparison. The spin density differences of Cr doped in one and two neighboring cavities of C₆N₆ are shown in Fig. S4.† The electronic band structures are indicated in the right panels. All of the possible relative positions of two Cr atoms doped in one and two cavities of C₆N₆ are considered, and only the most stable configurations are exhibited. The exchange energy E_ex, defined as E_ex = E_FM − E_AFM, is calculated to determine the most stable phase. Negative and positive E_ex indicate the FM and AFM ground states, respectively. For the case of one neighboring cavity, it is found that the Cr atoms exhibit FM coupling (with E_ex = 140 meV) in their most stable phases, and the corresponding spin density differences are shown in Fig. S4(a).† Because the distance between the two Cr atoms is small (∼1.82 Å), one may think that the two Cr atoms should show direct coupling through C/N atoms. For the case of two cavities, it is clearly seen that the case of the Cr atoms is quite different from the above findings and they show AFM coupling (E_ex = 30 meV) with corresponding spin density differences.

5 Conclusion

In summary, using first-principles calculations, we have explored the effects of atom doping on the structural, electronic, and magnetic properties of C₆N₆ and C₆N₈ monolayers. Our theoretical results indicated that with atom doping, C₆N₆ becomes a semiconductor with a narrow band gap (Mg-doped), semi-metal (Ca-doped) or ferromagnetic metal (Cr-doped). Additionally, we applied mechanical strain to both monolayers with atoms doped in their lattices. Our first-principles results revealed that the band gap and magnetism can be finely tuned by strain as well. Surprisingly, when the compressive strain reaches 2%, Cr-doped C₆N₆ displays a phase transition to a spin-polarized semi-metal without SOC; when SOC is considered, a narrow band gap of 125 meV is opened. Notably, in the case of Cr atom doped C₆N₆ upon compressive strain, considering SOC, an unusual semi-metallic character can be observed. In the C-doped C₆N₈ between applied tensile strains of 0–8%, the band gap was found to increase monotonically from 70 meV (at 2%) to 200 meV (at 8%), while it exhibits semi-metallic behavior under compressive strain larger than 2%. Our results show that a magnetic-to-nonmagnetic phase transition can occur under large tensile strain in the Ca doped C₆N₈ monolayer. In addition, Mg and Ca atom doped C₆N₆ can show topological insulator states under strain. The results provided by our extensive theoretical analysis highlight very promising electronic properties of C₆N₆ and C₆N₈ monolayers doped with various atoms and under mechanical strain, and will hopefully serve as a guide for future experimental and theoretical studies.

Conflicts of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (NRF-2017R1A2B2011989).

References

1. A. Wang, X. Zhang and M. Zhao, Nanoscale, 2014, 6, 11157–11162.
2. Y. Z. Abdullahi, T. L. Yoon, M. M. Halim, M. R. Hashim and T. L. Lim, Solid State Commun., 2016, 248, 144–150.
3. A. Du, S. Sanvito and S. C. Smith, Phys. Rev. Lett., 2012, 108, 197207.
4. G. Wang, X. Long, K. Qi, S. Dang, M. Zhong, S. Xiao and T. Zhou, Appl. Surf. Sci., 2019, 471, 162–167.
5. G. Wang, F. Zhou, B. Yuan, S. Xiao, A. Kuang, M. Zhong, S. Dang, X. Long and W. Zhang, Nanomaterials, 2019, 9, 244.
6. X. Zhao, D. Pan, X. Chen, R. Li, T. Jiang, W. Wang, G. Li and D. Y. Leung, Appl. Surf. Sci., 2019, 467–468, 658–665.
7. G.-C. Guo, R.-Z. Wang, B.-M. Ming, C. Wang, S.-W. Luo, C. Lai and M. Zhang, Appl. Surf. Sci., 2019, 475, 102–108.
8. X. Gao, Y. Shen, Y. Ma, S. Wu and Z. Zhou, Appl. Surf. Sci., 2019, 479, 1098–1104.
9. Y. Yong, H. Cui, Q. Zhou, X. Su, Y. Kuang and X. Li, Appl. Surf. Sci., 2019, 487, 488–495.
10. L.-B. Shi, M. Yang, S. Cao, Q. You, Y.-Y. Niu and Y.-Z. Wang, Appl. Surf. Sci., 2019, 492, 435–448.
11. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699.
12. X.-H. Li, X. Wang and M. Antonietti, Chem. Sci., 2012, 3, 2170–2174.
13. J. Zhang, M. Grzelczak, Y. Hou, K. Maeda, K. Domen, X. Fu, M. Antonietti and X. Wang, Chem. Sci., 2012, 3, 443–446.
14. X. Zhang, X. Xie, H. Wang, J. Zhang, B. Pan and Y. Xie, J. Am. Chem. Soc., 2013, 135, 18–21.
15. X. Zhang, H. Wang, H. Wang, Q. Zhang, J. Xie, Y. Tian, J. Wang and Y. Xie, Adv. Mater., 2014, 26, 4438–4443.
16. B. Zhu, L. Zhang, B. Cheng and J. Yu, Appl. Catal., B, 2018, 224, 983–999.
17. A. Bafekry, S. Farjami Shayesteh and F. M. Peeters, J. Phys. Chem. C, 2019, 123, 12485–12499.
18. A. Bafekry and M. Neek-Amal, Phys. Rev. B, 2020, 101, 085417.
19. A. Bafekry, S. F. Shayesteh and F. M. Peeters, Phys. Chem. Chem. Phys., 2019, 21, 21070–21083.
20. A. Bafekry, M. Ghergherehchi, S. F. Shayesteh and F. Peeters, Chem. Phys., 2019, 526, 110442.
21. A. Bafekry, C. Stampfl and S. Farjami Shayesteh, ChemPhysChem, 2020, 21, 164–174.
22. Q. Zhou, M. Wu, M. Zhang, G. Xu, B. Yao, C. Li and G. Shi, Materials Today Energy, 2017, 6, 181–188.
23. S. U. Lee, R. V. Belosludov, H. Mizuseki and Y. Kawazoe, Small, 2009, 5, 1769–1775.
24. J. Li, W. Cui, Y. Sun, Y. Chu, W. Cen and F. Dong, J. Mater. Chem. A, 2017, 5, 9358–9364.
25. Y. Zheng, J. Liu, J. Liang, M. Jaroniec and S. Z. Qiao, Energy Environ. Sci., 2012, 5, 6717–6731.
26. A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J.-O. Müller, R. Schlögl and J. M. Carlsson, J. Mater. Chem., 2008, 18, 4893–4908.
27. G. Algara-Siller, N. Severin, S. Y. Chong, T. Björkman, R. G. Palgrave, A. Laybourn, M. Antonietti, Y. Z. Khimyak, A. V. Krasheninnikov and J. P. Rabe, et al., Angew. Chem., Int. Ed., 2014, 53, 7450–7455.
28. J. Mahmood, E. K. Lee, M. Jung, D. Shin, I.-Y. Jeon, S.-M. Jung, H.-J. Choi, J.-M. Seo, S.-Y. Bae and S.-D. Sohn, et al., Nat. Commun., 2015, 6, 6486.
29. M. Groenewolt and M. Antonietti, Adv. Mater., 2005, 17, 1789–1792.
30. J. S. Lee, X. Wang, H. Luo and S. Dai, Adv. Mater., 2010, 22, 1004–1007.
31. Y. Xu and S.-P. Gao, Int. J. Hydrogen Energy, 2012, 37, 11072–11080.
32. V. N. Khabashesku, J. L. Zimmerman and J. L. Margrave, Chem. Mater., 2000, 12, 3264–3270.
33. B. Yang, H. Zhou, X. Zhang and M. Zhao, J. Mater. Chem. C, 2015, 3, 10886–10891.
34. Q. Guo, Q. Yang, C. Yi, L. Zhu and Y. Xie, Carbon, 2005, 43, 1386–1391.
35. J. Li, C. Cao, J. Hao, H. Qiu, Y. Xu and H. Zhu, Diamond Relat. Mater., 2006, 15, 1593–1600.
36. H. Qiu, Z. Wang and X. Sheng, Phys. Lett. A, 2013, 377, 347–350.
37. G.-X. Chen, D.-D. Wang, J.-Q. Wen, A.-P. Yang and J.-M. Zhang, Int. J. Quantum Chem., 2016, 116, 1000–1005.
38. D. Ghosh, G. Periyasamy, B. Pandey and S. K. Pati, J. Mater. Chem. C, 2014, 2, 7943–7951.
39. I. Choudhuri, G. Bhattacharyya, S. Kumar and B. Pathak, J. Mater. Chem. C, 2016, 4, 11530–11539.
40. I. Choudhuri, P. Garg and B. Pathak, J. Mater. Chem. C, 2016, 4, 8253–8262.
41. X. Jiang, P. Wang and J. Zhao, J. Mater. Chem. A, 2015, 3, 7750–7758.
42. S. Yang, W. Li, C. Ye, G. Wang, H. Tian, C. Zhu, P. He, G. Ding, X. Xie and Y. Liu, et al., Adv. Mater., 2017, 29, 1605625.
43. H. Li, H. Hu, C. Bao, F. Guo, X. Zhang, X. Liu, J. Hua, J. Tan, A. Wang and H. Zhou, et al., Sci. Rep., 2016, 6, 29327.
44. H. Li, H. Hu, C. Bao, Z. Feng, F. Guo, G. Tian and Y. Liu, Diamond Relat. Mater., 2018, 87, 50–55.
45. H. Li, H. Hu, C. Bao, J. Hua, H. Zhou, X. Liu, X. Liu and M. Zhao, Phys. Chem. Chem. Phys., 2015, 17, 6028–6035.
46. E. Kroke, M. Schwarz, E. Horath-Bordon, P. Kroll, B. Noll and A. D. Norman, New J. Chem., 2002, 26, 508–512.
47. J. Sehnert, K. Baerwinkel and J. Senker, J. Phys. Chem. B, 2007, 111, 10671–10680.
48. J. N. Hart, F. Claeyssens, N. L. Allan and P. W. May, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 174111.
49. A. Snis and S. F. Matar, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(15), 10855.
50. P. Esquinazi, D. Spemann, R. Höhne, A. Setzer, K.-H. Han and T. Butz, Phys. Rev. Lett., 2003, 91, 227201.
51. K. W. Lee and C. E. Lee, Phys. Rev. Lett., 2006, 97, 137206.
52. P. O. Lehtinen, A. S. Foster, Y. Ma, A. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2004, 93, 187202.
53. J. Zhou, Q. Wang, Q. Sun, X. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870.
54. Q.-F. Deng, L. Liu, X.-Z. Lin, G. Du, Y. Liu and Z.-Y. Yuan, Chem. Eng. J., 2012, 203, 63–70.
55. A. Bafekry, C. Stampfl, M. Ghergherehchi and S. F. Shayesteh, Carbon, 2020, 157, 371–384.
56. A. Bafekry, S. Farjami Shayesteh, M. Ghergherehchi and F. M. Peeters, J. Appl. Phys., 2019, 126, 144304.
57. M. M. Obeid, Appl. Surf. Sci., 2020, 508, 144824.
58. A. Bafekry, C. Stampfl, B. Akgenc and M. Ghergherehchi, Phys. Chem. Chem. Phys., 2020, 22, 2249–2261.
59. M. Yagmurcukardes, C. Sevik and F. Peeters, Phys. Rev. B, 2019, 100, 045415.
60. A. Bafekry, S. F. Shayesteh and F. M. Peeters, J. Appl. Phys., 2019, 126, 215104.
61. D. Kiymaz, M. Yagmurcukardes, A. Tomak, H. Sahin, R. T. Senger, F. M. Peeters, H. M. Zareie and C. Zafer, Nanotechnology, 2016, 27, 455604.
62. A. Bafekry, Phys. E, 2020, 118, 113850.
63. F. İyikanat, M. Yagmurcukardes, R. T. Senger and H. Sahin, J. Mater. Chem. C, 2018, 6, 2019–2025.
64. A. Bafekry, C. Stampfl, B. Akgenc, B. Mortazavi, M. Ghergherehchi and C. V. Nguyen, Phys. Chem. Chem. Phys., 2020, 22, 6418–6433.
65. A. Bafekry, B. Akgenc, S. F. Shayesteh and B. Mortazavi, Appl. Surf. Sci., 2020, 505, 144450.
66. A. Kasry, M. M. Fadlallah, N. H. Voelcker and A. A. Maarouf, Carbon, 2019, 155, 65–70.
67. M. Fadlallah, M. Shibl, T. Vlugt and U. Schwingenschlögl, J. Mater. Chem. A, 2018, 6, 24342–24349.
68. A. Bafekry and M. Neek-Amal, Phys. Rev. B, 2020, 101, 085417.
69. Z. Kahraman, A. Kandemir, M. Yagmurcukardes and H. Sahin, J. Phys. Chem. C, 2019, 123, 4549–4557.
70. A. Bafekry, C. Stampfl and F. M. Peeters, Sci. Rep., 2020, 10, 1–15.
71. M. Yagmurcukardes, S. Ozen, F. Iyikanat, F. Peeters and H. Sahin, Phys. Rev. B, 2019, 99, 205405.
72. B. Mortazavi, A. Bafekry, M. Shahrokhi, T. Rabczuk and X. Zhuang, Materials Today Energy, 2020, 16, 100392.
73. M. M. Fadlallah and U. Eckern, Phys. Status Solidi B, 2020, 257, 1900217.
74. M. M. Obeid, H. R. Jappor, K. Al-Marzoki, D. Hoat, T. V. Vu, S. J. Edrees, Z. M. Yaseen and M. M. Shukur, Comput. Mater. Sci., 2019, 170, 109201.
75. A. Bafekry, M. Ghergherehchi and S. F. Shayesteh, Phys. Chem. Chem. Phys., 2019, 21, 10552–10566.
76. H. R. Jappor, M. M. Obeid, T. V. Vu, D. Hoat, H. D. Bui, N. N. Hieu, S. J. Edrees, Y. Mogulkoc and R. Khenata, Superlattices Microstruct., 2019, 130, 545–553.
77. A. Bafekry, B. Mortazavi and S. F. Shayesteh, J. Magn. Magn. Mater., 2019, 491, 165565.
78. M. Shahrokhi and C. Leonard, J. Alloys Compd., 2017, 693, 1185–1196.
79. A. Bafekry, C. Stampfl and F. M. Peeters, Phys. Status Solidi B, 2020, 257, 2000182.
80. M. Fadlallah, Phys. E, 2017, 89, 50–56.
81. M. S. Eldeeb, M. M. Fadlallah, G. J. Martyna and A. A. Maarouf, Carbon, 2018, 133, 369–378.
82. A. Bafekry, B. Akgenc, M. Ghergherehchi and F. Peeters, J. Phys.: Condens. Matter, 2020, 32, 355504.
83. M. Shahrokhi and C. Leonard, J. Alloys Compd., 2016, 682, 254–262.
84. F. Shojaei, M. Azizi, Z. Mahdavifar, B. Wang and G. Frapper, RSC Adv., 2020, 10, 8016–8026.
85. M. Shahrokhi, Diamond Relat. Mater., 2017, 77, 35–40.
86. A. Bafekry, M. Yagmurcukardes, B. Akgenc, M. Ghergherehchi and C. V. Nguyen, J. Phys. D: Appl. Phys., 2020, 53, 355106.
87. B. Mortazavi, F. Shojaei, M. Azizi, T. Rabczuk and X. Zhuang, J. Mater. Chem. C, 2020, 8, 2400–2410.
88. A. Bafekry, C. Stampfl and M. Ghergherehchi, Nanotechnology, 2020, 31, 295202.
89. F. Shojaei, B. Mortazavi, X. Zhuang and M. Azizi, Materials Today Energy, 2020, 16, 100377.
90. A. Bafekry, M. Neek-Amal and F. Peeters, Phys. Rev. B, 2020, 101, 165407.
91. T. Ozaki, K. Nishio and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035116.
92. T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108.
93. T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195113.
94. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
95. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993.
96. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
97. T. Bucko, J. Hafner, S. Lebegue and J. G. Angyán, J. Phys. Chem. A, 2010, 114, 11814–11824.
98. R. Mulliken, J. Chem. Phys., 1955, 23, 2343–2346.
99. J. Tersoff and D. Hamann, Phys. Rev. Lett., 1983, 50, 1998.
100. I. Horcas, R. Fernández, J. Gomez-Rodriguez, J. Colchero, J. Gómez-Herrero and A. Baro, Rev. Sci. Instrum., 2007, 78, 013705.
101. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80.
102. G. Liu, P. Niu, C. Sun, S. C. Smith, Z. Chen, G. Q. Lu and H.-M. Cheng, J. Am. Chem. Soc., 2010, 132, 11642–11648.
103. K. Srinivasu, B. Modak and S. K. Ghosh, J. Phys. Chem. C, 2014, 118, 26479–26484.
104. Q. Zhang, Y. Cheng, L.-Y. Gan and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245447.
105. J. Wirth, R. Neumann, M. Antonietti and P. Saalfrank, Phys. Chem. Chem. Phys., 2014, 16, 15917–15926.
106. X. Li, Y. Dai, Y. Ma, S. Han and B. Huang, Phys. Chem. Chem. Phys., 2014, 16, 4230–4235.
107. H. Li, H. Hu, C. Bai, C. Bao, F. Guo, Z. Feng and Y. Liu, RSC Adv., 2019, 9, 7464–7468.
108. A. Bafekry, M. Yagmurcukardes, M. Shahrokhi and M. Ghergherehchi, Carbon, 2020, 168, 220–229.
109. A. Bafekry, M. M. Obeid, C. V. Nguyen, M. Ghergherehchi and M. B. Tagani, J. Mater. Chem. A, 2020, 8, 13248–13260.
110. M. Rassekh, J. He, S. F. Shayesteh and J. J. Palacios, Comput. Mater. Sci., 2020, 183, 109820.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra04463f

---