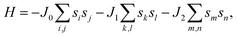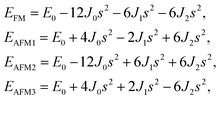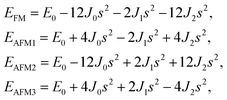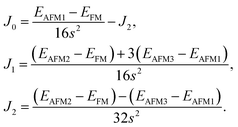DOI:
10.1039/D0RA03643A
(Paper)
RSC Adv., 2020,
10, 44430-44436
First-principles study of magnetism in some novel MXene materials†
Received
23rd April 2020
, Accepted 6th November 2020
First published on 16th December 2020
Abstract
Magnetic two-dimensional materials have gained considerable attention in recent years due to their special topologies and promising applications in electronic and spintronic devices. As a new family of two-dimensional materials, MXene materials may have unusual magnetic properties. In this work, the structural stabilities and electronic properties of 1H and 1T type pristine M2C (M = Sc, Ti, Fe, Co, Ni, Cu, Zn) MXenes with different magnetic configurations were calculated and compared. The critical temperatures of the magnetic MXenes were evaluated through Monte Carlo simulations using the spin–exchange coupling parameters. The results suggest that the ground-state 1T-Ti2C and 1T-Fe2C, 1H-Co2C MXenes are antiferromagnetic or ferromagnetic materials with high Néel or Curie temperatures. Different from the other pristine M2C MXenes with metallic properties, indirect band gaps were found for the 1T-Ti2C and 1T-Ni2C MXenes, which may be useful for their application in information storage or sensors. The findings are expected to promote the development of novel devices based on MXenes and their magnetic properties.
Introduction
Since the discovery of graphene in 2004, two-dimensional (2D) nanomaterials have been considered as prospective materials in various disciplines including electronics, optoelectronics, energy, and sensing.1,2 The exploration of new 2D nanomaterials such as h-BN3 and transition metal dichalcogenides4 has attracted attention worldwide and is still ongoing. Meanwhile, numerous theoretical and experimental works have produced rapid advances related to magnetism in 2D materials because of their potential applications in electronic and spintronic devices.5–8 However, the utilization of most known 2D materials in spintronics is limited by their intrinsically nonmagnetic (NM) properties. Therefore, several approaches such as strain engineering, doping or defect generation, and surface decoration have been adopted to introduce magnetism into 2D materials,9–12 and the effects on the magnetic properties have been discussed.13,14 Simultaneously, new magnetic 2D materials are in demand. MXenes, a unique family of metal carbides and/or nitrides with the chemical formula Mn+1Xn, where M is the transition metal that potentially generates the intrinsic magnetic moment, X can be carbon and/or nitrogen, and n varies between 1 and 3, were discovered in 2011 and have attracted extensive research interest in recent years.15–19 MXenes can be fabricated from conventional MAX phases or other layered compounds such as Zr3Al3C5 and Mo2Ga2C through chemical etching,20–22 forming the functionalized MXenes Mn+1XnTx,15 where T indicates the surface-terminating groups (–H, –F, –Cl, ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, or –OH) originating from the etching agent.23–26 Chemical vapor deposition (CVD) is another growth method for fabricating high-quality 2D MXene materials.27 Both methods are currently under development, and many attempts to improve their efficiency and purity of the products are found in the literature.
O, or –OH) originating from the etching agent.23–26 Chemical vapor deposition (CVD) is another growth method for fabricating high-quality 2D MXene materials.27 Both methods are currently under development, and many attempts to improve their efficiency and purity of the products are found in the literature.
Theoretical calculations have been widely employed to obtain insight into the relevance of the electronic structures of MXene materials and their properties to better understand and utilize MXene materials.28–31 To date, several pristine MXenes such as Ti4C3, Ti3CN, Cr2C, Cr2N, and Zr2C have been predicted to possess magnetic moments; however, synthesizing these materials and retaining the magnetic behaviors when they are exfoliated into monolayers remain challenging.31,32 He and co-workers33,34 studied the structure and magnetic properties of some V-, Cr-, and Mn-based MXenes and discussed the substrate effect of MXenes on the SiC(0001) surface. Depending on the functional group, these MXenes can be half-metals, metals, or semiconductors. Zhang et al. found that the Mn2C monolayer can transform from the antiferromagnetic (AFM) state to the ferromagnetic (FM) state under hydrogenation or oxygenation.35
At present, it is recognized that understanding the intrinsic magnetism of MXenes is a key step in promoting their application. This work focuses on the magnetism of pristine MXenes, whose geometric structures are similar to transition metal chalcogenides in two common phases (1H and 1T).36,37 Theoretical exploration via first-principles calculations was conducted on the stability, magnetism, and electronic properties of the 1H and 1T M2C MXenes with various transition metals (M = Sc, Ti, Fe, Co, Ni, Cu, Zn). The corresponding parameters, including the lattice parameters, total energies, magnetic moments, and spin exchange coupling parameters, were calculated and compared, and the critical temperatures Tc for particular magnetic MXenes were evaluated through Monte Carlo (MC) simulations. The findings provide valuable reference information toward the application of MXene materials in industry based on the magnetic characteristics.
Computational details
First-principles density functional theory (DFT) calculations were carried out based on projector augmented-wave (PAW) potentials38 in reciprocal space represented by a generalized gradient approximation (GGA).39 The Perdew–Burke–Emzerhof (PBE) exchange–correlation function was used, and the calculations were implemented in VASP code.40 Plane waves with energies of up 550 eV were employed to describe the electronic wave functions, and the Brillouin zone was sampled using a set of Γ-centered 12 × 12 × 1 k-points. Specifically, the highly accurate non-empirical density functional meta-GGA strongly constrained and appropriately normed (SCAN) + rVV10 was employed.41,42 In the structural optimization, the maximum force on each atom was 10−3 eV Å−1, and the total energies converged within 10−7 eV. A lattice parameter of 30 Å for the c-axis perpendicular to the MXene surface was set to avoid any artificial interaction between the layers and their images. The Hubbard “U” correction was also employed within the rotationally invariant DFT + U approach43 as a comparison. A correction of Ueff = U − J = 3 eV was used for Sc, Ti, Fe, Co, and Ni based on relevant previous reports33,44 on the magnetic configuration and band structure calculations. The PHONOPY software45 combined with the VASP code was utilized for phonon dispersion calculations using density functional perturbation theory46 to confirm the structural stabilities. To predict the electrical conductivity, linearized Boltzmann transport calculations based on the constant relaxation time approximation and rigid-band approximation were performed using the BoltzTraP2 code.47 For a given T and μ, the carrier concentration was obtained from the density of states, and the electrical conductivities were calculated using the transport distribution function. The relaxation time τ was variable and could be obtained by fitting the experimental data48 or using τ = 10−14 s as a general approximation to estimate the electrical conductivity.49
Results and discussion
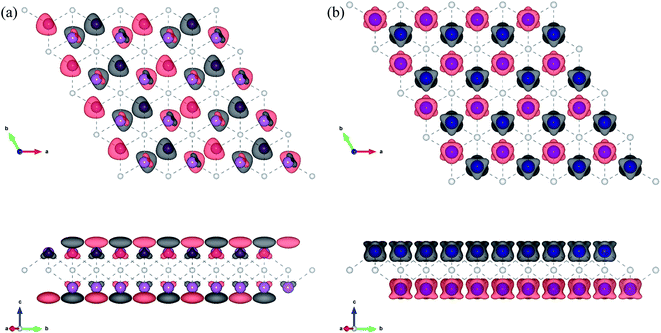
First, the geometries of the 1H and 1T pristine M2C (M = Sc, Ti, Fe, Co, Ni, Cu, Zn) MXenes shown in Fig. 1 were examined. Three possible initial magnetic configurations have been considered for the M2C MXene 1 × 1 unit cell containing two transition-metal atoms: the AFM configuration with the magnetic moments of the two metal atoms in opposite directions; the FM configuration with the magnetic moments of the two atoms in the same direction; and the NM configuration with zero atomic magnetic moment. For the M2C MXenes in the FM configuration, the spin-up and spin-down states are not symmetrical. Meanwhile, the M2C MXenes in the AFM and NM configurations exhibit zero total magnetic moments; the difference between the AFM and NM configurations is that the atomic magnetic moments for the AFM configuration are non-zero. Based on the above initial magnetic configurations, the optimized lattice constants, total energies, and magnetic properties of the M2C MXenes from the self-consistent calculations are listed in Table S1† with the most stable configurations highlighted in bold. From the table, the 1T M2C MXenes calculated in our work exhibit lower total energies than the 1H MXenes except for Co2C and Cu2C. The 1H M2C MXenes usually possess smaller lattice constants than the 1T ones, and the small differences in lattice constants vary by magnetic configuration, suggesting that the magnetic properties may have slight effects on the chemical bonds at equilibrium. From the calculations, the Ni2C, Cu2C, and Zn2C MXenes present zero atomic magnetic moments. This may be attributed to the absence of unpaired d electrons, which are necessary for atomic magnetic moments. Cu and Zn, which have 10 d electrons, cannot have unpaired electrons, and the magnetic moment for Ni is zero due to electron transfer and rearrangement in the electronic configuration.50
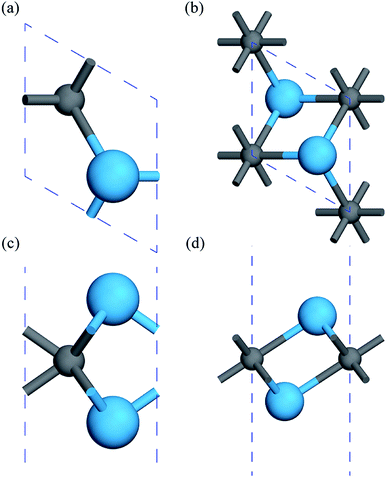 |
| | Fig. 1 Geometric structures of 1H and 1T M2C MXenes viewed from the top (a, b) and side (c, d). The blue spheres represent metal atoms, while the gray spheres represent C atoms. | |
Since phonon dispersion can be used to measure the dynamic stability of a material, the phonon dispersion plots of the lowest-energy configurations of the M2C MXenes along the high-symmetry directions in the Brillouin zone are given in Fig. S1.† According to the figure, the Sc2C (1T-FM), Ti2C (1T-AFM), Fe2C (1T-FM), Co2C (1H-FM), and Ni2C (1T-NM) MXenes are dynamically stable with all their phonon branches non-negative. Thus, these MXenes could possibly be synthesized experimentally. The structures of the Cu2C and Zn2C MXenes with imaginary phonon modes require further study. The phonon dispersions of some higher-energy configurations are also plotted in Fig. S1† for comparison. The absence of imaginary phonon modes suggests that the Sc2C (1T-AFM and NM), Ti2C (1T-FM and NM), Fe2C (1H-FM), Co2C (1H-AFM and NM), and Ni2C (1H-NM) MXenes are all dynamically stable, and the small differences in the phonon branches for the M2C MXenes with different magnetic configurations imply that the magnetic states have slight effects on the vibrational modes. This means that MXenes may exhibit different mechanical and thermal properties that do not exist in the ground magnetic states.
After investigating the basic structural and stability properties, a 2 × 1 supercell containing four metal atoms was employed to further study the magnetic properties of the 1T-Sc2C, 1T-Ti2C, 1T-Fe2C, and 1H-Co2C MXenes. Four possible magnetic configurations (three AFM and one FM) were considered; the top and side views are shown in Fig. 2(a) and (c), respectively. The spin system was typically identified by a Hamiltonian function in the 2D Ising model with the spin exchange coupling parameters J0, J1, and J2 [paths shown in Fig. 2(b) and (d)] and magnetic ordering s:51
| |
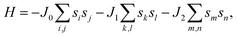 | (1) |
where
J0 is the intralayer exchange coupling interaction between nearest neighbors,
J1 and
J2 are the interlayer exchange coupling interactions between the nearest and next-nearest neighbors, respectively, and
s takes the value of ±1 for spin-up and spin-down. Correspondingly, for the 1T type, the total energies
EFM,
EAFM1,
EAFM2, and
EAFM3 can be expressed as follows:
| |
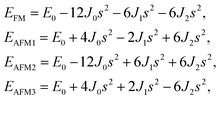 | (2) |
where
J0,
J1, and
J2 are then expressed as
| |
 | (3) |
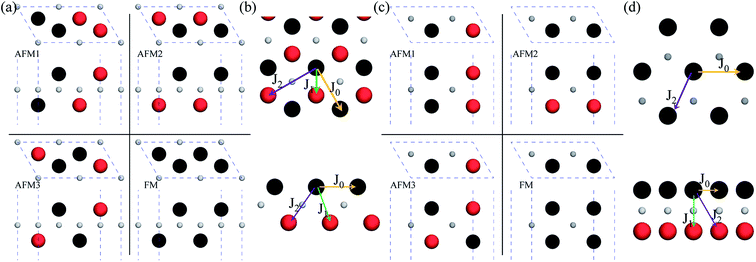 |
| | Fig. 2 Top and side views of the three AFM and one FM magnetic configurations along with the spin exchange coupling parameters J0, J1, and J2 for 1T (a, b) and 1H (c, d) M2C MXenes. Black and red represent spin-up and spin-down, respectively. | |
Similarly, for the 1H type, EFM, EAFM1, EAFM2, and EAFM3 can be expressed as follows:
| |
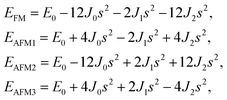 | (4) |
with
J0,
J1 and
J2 expressed as:
| |
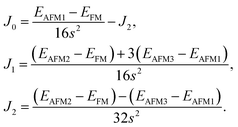 | (5) |
From the obtained relative energies listed in Table 1, Sc2C and Ti2C are predicted to possess antiferromagnetism with the magnetic configurations AFM3 and AFM2, as shown in Fig. 2, and the spin charge density distributions are plotted in Fig. 3(a) and (b), respectively. Fe2C and Co2C MXenes are predicted to be ferromagnetic, and the spin charge density distributions are shown in Fig. S2.† The spin exchange coupling parameters J0, J1, and J2 were calculated with formulas (3) and (5). We note that the absolute value of parameter J1 for the Sc2C MXene with a small interaction distance is abnormally less than J2. This may be due to the fact that every spin-polarized charge center for Sc2C is actually located on the top of the Sc atomic layer at the center of the three Sc atoms arranged in an equilateral triangle [Fig. 2(a)], different from Ti2C, Fe2C, and Co2C, in which the spin charges are around the metal atoms. The spin charge shielding effects of the metal atoms and superexchange interaction may affect the relative magnitude of the interlayer coupling parameters J1 and J2. The spin exchange interactions for 1H type Co2C are mainly dominated by the interlayer exchange coupling parameter J1. MC simulations were then performed on a NVIDIA Tesla K80 Graphics Processing Unit with the Metropolis algorithm using the coupling parameters to evaluate the critical temperature Tc. In the MC simulations, 1024 × 1024 supercells were adopted. For every spin flip operation, the change in exchange interactions before and after the trial switch of the selected si spin ΔH = Ha − Ho was calculated, and the acceptance probability was determined as Wm = exp(−ΔH/kBT), where kB is the Boltzmann constant, and T is the temperature. A random number R (0 < R < 1) was generated. If R was less than Wm, the selected spin was flipped; otherwise, the spin remained unchanged. The average magnetization orientation as a function of temperature is shown in Fig. S3.† The predicted Tc values are 110, 875, 965, and 1497 K for 1T-Sc2C, 1T-Ti2C, 1T-Fe2C, and 1H-Co2C MXenes, respectively. Consequently, the ground-state Ti2C or Fe2C, Co2C MXenes are AFM or FM materials with Néel or Curie points above room temperature.
Table 1 Calculated magnetic characteristics of the 1T-Sc2C, 1T-Ti2C, 1T-Fe2C, and 1H-Co2C MXenes. For relative energy, the ground-state are set as zero and indicated in bold
| ΔE (meV) |
Relative energy |
Exchange interaction |
Tc (K) |
| AFM1 |
AFM2 |
AFM3 |
FM |
NM |
J0 |
J1 |
J2 |
| 1T-Sc2C |
42.1 |
112.2 |
0.0 |
54.5 |
308.6 |
−3.89 |
0.97 |
3.83 |
110 |
| 1T-Ti2C |
273.7 |
0.0 |
264.0 |
97.9 |
624.9 |
13.74 |
−6.73 |
−1.43 |
875 |
| 1T-Fe2C |
268.7 |
115.0 |
343.6 |
0.0 |
3280.1 |
15.54 |
11.87 |
−2.29 |
965 |
| 1H-Co2C |
370.6 |
230.2 |
600.4 |
0.0 |
1490.7 |
23.15 |
57.48 |
0.01 |
1497 |
 |
| | Fig. 3 Top and side views of the spin charge density distribution of the AFM3 magnetic configuration 1T-Sc2C (a) and AFM2 magnetic configuration 1T-Ti2C (b). | |
To further understand the magnetic and electronic properties of the ground-state Sc2C, Ti2C, Fe2C, Co2C, and Ni2C MXenes, their band structures were calculated and are plotted in Fig. 4. The Fe2C and Co2C MXenes show observable spin splitting around the Fermi level with a metallic feature; meanwhile, the spin-up and spin-down bands of the Sc2C and Ti2C MXenes with AFM configurations are entirely coincident. In addition, the Ti2C MXene presents a band gap of 0.17 eV, and the 1T type Ni2C MXene also shows an indirect band gap. The band structures with DFT + U correction are provided in Fig. 4(f)–(j) for comparison. The similarities in band structures with the exceptions of shifts in some bands indicate the validity of the SCAN meta-GGA calculations. The transport coefficients σxx/τ at 300 K versus the chemical potential μ for magnetic Ti2C, Fe2C, and Co2C with critical temperature above 300 K and Ni2C MXenes were calculated and are plotted in Fig. 5. For the Ti2C MXene, the σxx/τ at zero chemical potential approaches zero because of the band gap near their Fermi level, and doping with electrons and holes within a certain range can both lead to a significant increase in the transport coefficient σxx/τ. Owning a special ground spin configuration, high Néel temperature, and adjustable transport coefficient, the AFM Ti2C MXene is a promising material for 2D spintronics. Moreover, a nearly zero σxx/τ value at zero chemical potential and increase in σxx/τ with doping content are found for the Ni2C MXene. The 1H Co2C MXene shows a higher transport coefficient than the MXenes. Due to their diversity, more members of the MXene and 2D material family with magnetism and potential for application in spintronic devices require further study.
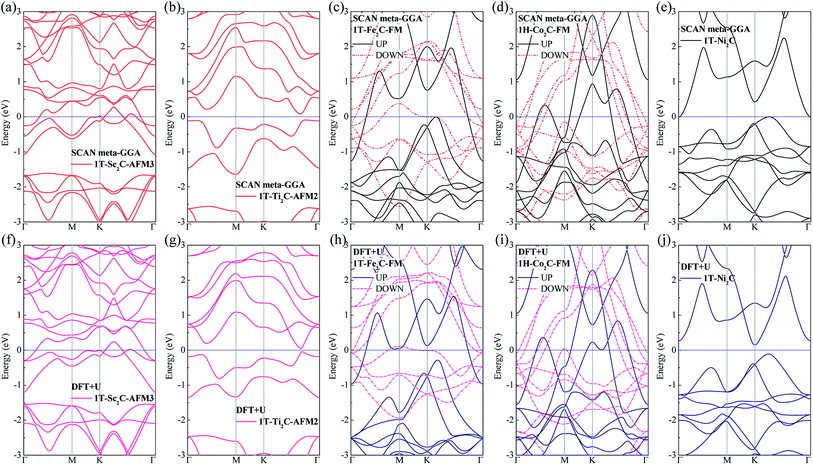 |
| | Fig. 4 Band structure plots based on SCAN meta-GGA and DFT + U calculations for 1T-Sc2C (a, f), 1T-Ti2C (b, g), 1T-Fe2C (c, h), 1H-Co2C (d, i), and 1T-Ni2C (e, j) MXenes. | |
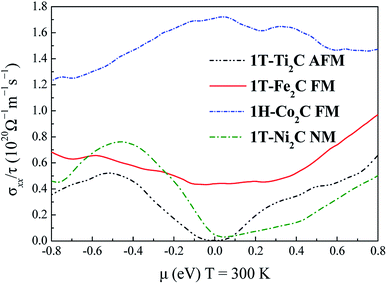 |
| | Fig. 5 Relationship between the chemical potential μ and transport coefficient σxx/τ at 300 K for 1T-Ti2C, 1T-Fe2C, 1H-Co2C, and 1T-Ni2C MXenes. | |
Conclusions
In summary, the structures, magnetic and electronic properties, and total energies for 1H and 1T pristine M2C (M = Sc, Ti, Fe, Co, Ni, Cu, Zn) MXenes with different magnetic configurations were calculated and compared. Most MXenes studied herein are stable in the 1T type, while Co2C is unique in that it possesses a 1H FM ground configuration. The spin exchange coupling parameters were calculated to predict the critical temperature Tc. The 1T-Ti2C, 1T-Fe2C, and 1H-Co2C MXenes show relatively high Néel or Curie temperatures of 875, 965, and 1497 K, respectively. Different from the other pristine M2C MXenes with metal properties, the 1T AFM ground configuration of the Ti2C MXene presents a band gap of 0.17 eV, indicating great potential for high-efficiency spintronic devices. The results provide new insights into the application of magnetic MXene materials in electronic and spintronic devices.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge the financial support from the National Key Research and Development Program of China (Grant No. 2016YFB0700100), Zhejiang Province Key Research and Development Program (Grant No. 2019C01060), National Natural Science Foundation of China (Grant No. 21875271), Zhejiang Provincial Natural Science Foundation of China (Grant No. LR16B030001 and LY19B030003), the project of the key technology for virtue reactors from NPIC, Key Research Program of Frontier Sciences, CAS (Grant No. QYZDB-SSW-JSC037), K. C. Wong Education Foundation (rczx0800), and the Foundation of State Key Laboratory of Coal Conversion (Grant No. J18-19-301).
References
- C. Tan, X. Cao, X. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225–6331 Search PubMed.
- S. Zhao, W. Kang and J. Xue, Appl. Phys. Lett., 2014, 104, 133106 Search PubMed.
- L. Ci, L. Song, C. Jin, D. Jariwala, D. Wu, Y. Li, A. Srivastava, Z. F. Wang, K. Storr, L. Balicas, F. Liu and P. M. Ajayan, Nat. Mater., 2010, 9, 430–435 Search PubMed.
- A. Kuc, N. Zibouche and T. Heine, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245213 Search PubMed.
- K. S. Burch, D. Mandrus and J. Park, Nature, 2018, 563, 47–52 Search PubMed.
- B. Zhou, S. Ji, Z. Tian, W. Cheng, X. Wang and W. Mi, Carbon, 2018, 132, 25–31 Search PubMed.
- M. Je, Y. Lee and Y. Chung, Thin Solid Films, 2016, 619, 131–136 Search PubMed.
- C. Si, J. Zhou and Z. Sun, ACS Appl. Mater. Interfaces, 2015, 7, 17510–17515 Search PubMed.
- Y. Zhou, Z. Wang, P. Yang, X. Zu, L. Yang, X. Sun and F. Gao, ACS Nano, 2012, 6, 9727–9736 Search PubMed.
- H. Shi, H. Pan, Y. Zhang and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 205305 Search PubMed.
- L. Seixas, A. Carvalho and A. H. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155138 Search PubMed.
- H. Li, M. Huang and G. Cao, J. Mater. Chem. C, 2017, 5, 4557–4564 Search PubMed.
- R. Hu, Y. H. Li, Z. H. Zhang, Z. Q. Fan and L. Sun, J. Mater. Chem. C, 2019, 7, 7745–7759 Search PubMed.
- W. Kuang, R. Hu, Z. Q. Fan and Z. H. Zhang, Nanotechnology, 2019, 30, 145201 Search PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 982 Search PubMed.
- Q. Hu, D. Sun, Q. Wu, H. Wang, L. Wang, B. Liu, A. Zhou and J. He, J. Phys. Chem. A, 2013, 117, 14253–14260 Search PubMed.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098 Search PubMed.
- V. M. Hong Ng, H. Huang, K. Zhou, P. S. Lee, W. Que, J. Z. Xu and L. B. Kong, J. Mater. Chem. A, 2017, 5, 3039–3068 Search PubMed.
- M. Khazaei, A. Ranjbar, M. Arai, T. Sasaki and S. Yunoki, J. Mater. Chem. C, 2017, 5, 2488–2503 Search PubMed.
- P. Eklund, J. Rosen and P. O. Å. Persson, J. Phys. D: Appl. Phys., 2017, 50, 113001 Search PubMed.
- J. Zhou, X. Zha, F. Y. Chen, Q. Ye, P. Eklund, S. Du and Q. Huang, Angew. Chem., Int. Ed., 2016, 55, 5008–5013 Search PubMed.
- M. A. Hadi, Comput. Mater. Sci., 2016, 117, 422–427 Search PubMed.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 Search PubMed.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 Search PubMed.
- Y. Qin, X. Zha, X. Bai, K. Luo, Q. Huang, Y. Wang and S. Du, J. Phys.: Condens. Matter, 2020, 32, 135302 Search PubMed.
- M. Li, J. Lu, K. Luo, Y. Li, K. Chang, K. Chen, J. Zhou, J. Rosen, L. Hultman, P. Eklund, P. O. Å. Persson, S. Du, Z. Chai, Z. Huang and Q. Huang, J. Am. Chem. Soc., 2019, 141, 4730–4737 Search PubMed.
- C. Xu, L. Wang, Z. Liu, L. Chen, J. Guo, N. Kang, X. Ma, H. Cheng and W. Ren, Nat. Mater., 2015, 14, 1135–1141 Search PubMed.
- X. Zha, K. Luo, Q. Li, Q. Huang, J. He, X. Wen and S. Du, Europhys. Lett., 2015, 111, 26007 Search PubMed.
- U. Yorulmaz, A. Özden, N. K. Perkgöz, F. Ay and C. Sevik, Nanotechnology, 2016, 27, 335702 Search PubMed.
- K. Luo, X. Zha, Y. Zhou, Z. Guo, C. Lin, Q. Huang, S. Zhou, R. Zhang and S. Du, RSC Adv., 2018, 8, 22452–22459 Search PubMed.
- R. M. Ronchi, J. T. Arantes and S. F. Santos, Ceram. Int., 2019, 45, 18167–18188 Search PubMed.
- G. Wang, J. Phys. Chem. C, 2016, 120, 18850–18857 Search PubMed.
- J. He, P. Lyu, L. Z. Sun, Á. Morales García and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 6500–6509 Search PubMed.
- J. He, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 11143–11149 Search PubMed.
- X. Zhang, T. He, W. Meng, L. Jin, Y. Li, X. Dai and G. Liu, J. Phys. Chem. C, 2019, 123, 16388–16392 Search PubMed.
- X. Qian, J. Liu, L. Fu and J. Li, Science, 2014, 346, 1344–1347 Search PubMed.
- C. Chen, X. Ji, K. Xu, B. Zhang, L. Miao and J. Jiang, ChemPhysChem, 2017, 18, 1897–1902 Search PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 Search PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 Search PubMed.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 Search PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 36402 Search PubMed.
- H. Peng, Z. Yang, J. P. Perdew and J. Sun, Phys. Rev. X, 2016, 6, 41005 Search PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 Search PubMed.
- J. He, G. Ding, C. Zhong, S. Li, D. Li and G. Zhang, Nanoscale, 2019, 11, 356–364 Search PubMed.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 Search PubMed.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 Search PubMed.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 Search PubMed.
- D. Guo, C. Hu, Y. Xi and K. Zhang, J. Phys. Chem. C, 2013, 117, 21597–21602 Search PubMed.
- T. P. Kaloni, N. Onder, J. Pencer and E. Torres, Ann. Nucl. Energy, 2020, 144, 107511 Search PubMed.
- J. Yang, Z. Xiao, Z. Li, Q. Wen and F. Yang, Comput. Condens. Matter, 2014, 1, 51–57 Search PubMed.
- J. Romero, M. Bisson, M. Fatica and M. Bernaschi, arXiv:1906.06297, 2019.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03643a |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Xian-Hu Zha
ab,
Xian-Hu Zha c,
Qing Huang
c,
Qing Huang b,
Cheng-Te Lin
b,
Cheng-Te Lin d,
Minghui Yangb,
Shenghu Zhou*a and
Shiyu Du
d,
Minghui Yangb,
Shenghu Zhou*a and
Shiyu Du *b
*b
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, or –OH) originating from the etching agent.23–26 Chemical vapor deposition (CVD) is another growth method for fabricating high-quality 2D MXene materials.27 Both methods are currently under development, and many attempts to improve their efficiency and purity of the products are found in the literature.
O, or –OH) originating from the etching agent.23–26 Chemical vapor deposition (CVD) is another growth method for fabricating high-quality 2D MXene materials.27 Both methods are currently under development, and many attempts to improve their efficiency and purity of the products are found in the literature.