Reconsideration of the conformation of methyl cellulose and hydroxypropyl methyl cellulose ethers in aqueous solution

Abstract

The structure and conformation of methyl cellulose (MC) and hydroxypropyl methyl cellulose (HpMC) ether samples dissolved in dilute aqueous (D₂O) solutions at a temperature of 25 °C were reconsidered in detail based on the experimental results obtained using small- and wide-angle neutron scattering (S-WANS) techniques in a range of scattering vectors (q) from 0.05 to 100 nm⁻¹. MC samples exhibited an average degree of substitution (DS) by methyl groups per glucose unit of DS = 1.8 and the weight average molar mass of M_w = 37 × 10³ and 79 × 10³ g mol⁻¹. On the other hand, HpMC samples possessed the average molar substitution number (MS) by hydroxypropyl groups per glucose unit of MS = 0.25, DS = 1.9, and M_w = 50 × 10³ and 71 × 10³ g mol⁻¹. The concentration-reduced scattering intensity data gathered into a curve for the solutions of identical sample species clearly demonstrated the relationship I(q)c⁻¹ ∝ q⁻¹ in a q range from 0.05 to 2.0 nm⁻¹, and small interference peaks were found at q ∼ 7 and 17 nm⁻¹ for all examined sample solutions. These observations strongly revealed that form factors for both the MC and HpMC samples were perfectly described with that for long, rigid rod particles with average diameters of 0.8 and 0.9 nm, respectively, and with an inner structure with characteristic mean spacing distances of ca. 0.9 and 0.37 nm, respectively, regardless of the chemically modified conditions and molar masses. A rationally speculated structure model for the MC and HpMC samples dissolved in aqueous solution was proposed.

---

Introduction

Cellulose is constantly generated by many kinds of plants. Cellulose is the most abundant steadily supplied natural organic “biomass” resource worldwide.¹ Native cellulose, such as cotton, is insoluble in most common solvents due to its highly developed inter- and intramolecular hydrogen bonds between hydroxy groups and hydroxy and ether groups, which are responsible for the formation of stable crystalline structures, cellulose-Iα and Iβ.^1–4 In the case of aqueous systems widely applied in our usual daily life, the water insolubility of cellulose is, of course, quite an important property for its application in textile products. However, although cellulose is a naturally eco-friendly material, its insolubility in common solvents, including water, has limited its wider application in chemical industries. To improve such a situation, many kinds of chemically modified celluloses that are easily soluble in various solvents have been synthesized from natural cellulose.⁵ A series of water-soluble chemically modified cellulose derivatives, such as methyl cellulose (MC), hydroxypropyl cellulose (HpC), hydroxypropyl methyl cellulose (HpMC), hydroxyethyl cellulose (HeC), and sodium carboxymethyl cellulose (NaCMC) ethers, have been developed and supplied by several chemical companies.^5–7 Organic solvent soluble chemically modified celluloses, such as ethyl cellulose (EC) and acetyl cellulose (AC) ethers, have also been supplied by some chemical companies.^5,6,8,9

In this study, we focused on the fundamental solution properties of MC and HpMC samples in aqueous solutions, such as their characteristic structures and conformations. Many commercially available and commonly used water-soluble MC and HpMC samples possess the degree of substitution (DS) of 3 hydroxy groups by methyl groups per glucose unit set at 1.8–1.9; on the other hand, the molar substitution number (MS) of hydroxypropyl groups per glucose unit is set to be lower than ca. 0.25.¹⁰ Thus, the chemically modified condition with these DS and MS values gives stable, high water solubility at temperatures lower than ca. 40 °C for MC and HpMC samples regardless of their molar masses and distribution.¹¹ Therefore, we evaluated the structure and conformation of MC and HpMC molecules in aqueous solutions at room temperature, 25 °C, in this study. In most cases, the structure and conformation of polymeric molecules in solution have been investigated by use of the weight average molar mass (M_w) dependencies of solution properties, such as the intrinsic or inherent viscosity ([η]) and mean rotational radius or radius of gyration (〈R_g²〉^1/2).¹² In the case of MC and HpMC, the Mark–Houwink–Sakurada equation, [η] ∝ M_w^α, has been widely examined for more than 3 decades by many researchers.^13–15 A contemporary analytical method using a triple-detection system consisting of light scattering (LS), viscometric and refractometeric measuring devices after a gel permeation chromatography (GPC) separation process provided the average α value of 0.81 for MC with DS = 1.8 over the M_w range from 46 × 10³ to 300 × 10³ g mol⁻¹ and 0.85 for HpMC with DS = 1.8 and MS = 0.13 over the M_w range from 20 × 10³ to 420 × 10³ g mol⁻¹.¹⁵ It is well known that the α value ranges from 0.5 for polymer chains in the θ state and 0.65 for flexible random coils, such as pullulan¹⁶ and amylose,^17,18 in aqueous solutions to a value greater than unity, such as 1.7 for stiff rods-like polysaccharides and shizophyllan,¹⁹ which form rigid triple helices in water. Since the reported value of α = 0.8–0.85 for MC and HpMC samples was not obviously larger than unity, as found for shizophyllan, but an intermediate value between 0.65 and 1.0, it has not been strongly indicated that MC and HpMC molecules behave as stiff rod-like particles in aqueous solutions. Many researchers working in the field of chemically modified cellulose science have believed, thus far, that MC and HpMC molecules do not possess stiff or rigid rod-like conformations but possess rather flexible coil-like conformations in aqueous solutions.

Recently, Bodvik et al.²⁰ first discovered that MC molecules with DS = 1.8 and M_w ∼ 160 × 10³ g mol⁻¹ and HpMC molecules with DS = 1.8, MS = 0.13 and M_w ∼ 27 × 10³ g mol⁻¹ possess rather stiff rigid rod-like conformations in aqueous solutions at 25 °C using small-angle X-ray scattering (SAXS) techniques, and they roughly evaluated the persistence length (l_p) of the molecules to be 5.8 nm. Moreover, Chatterjee et al.²¹ also observed rather stiff rod-like behaviour for MC molecules in aqueous solutions at temperatures lower than the gelation temperature of the sample solution by use of small-angle neutron scattering (SANS) techniques. Furthermore, Lodge et al.²² also reported stiff rod-like behaviour of HpMC molecules in aqueous solutions at temperatures lower than the gelation point of the sample solution by use of SANS and SAXS techniques. These pioneering experimental studies using scattering techniques, which originally focused on the gelation mechanism of the aqueous MC and HpMC systems and contradict conventional prejudice on the nonrigid conformation of the molecules in aqueous solutions at relatively low temperatures, strongly encouraged us to reconsider the structure and conformation of isolated MC and HpMC molecules in dilute aqueous solutions.

In this study, we precisely determined the size, shape and distinctive conformation of MC and HpMC molecules dissolved in dilute aqueous solutions with the standard DS ∼ 1.8 and MS ∼ 0.25 values and the relatively low M_w values less than 100 × 10³ g mol⁻¹ employing small- and wide-angle neutron scattering (S-WANS) techniques. Then, we subsequently propose a rational speculated model to describe the determined structure and conformation for isolated MC and HpMC molecules in dilute aqueous solutions, which was directly related to the essential characteristics of native cellulose molecules forming many strong inter- and intramolecular hydrogen bonds.

Experimental

Materials

Methyl cellulose, MC, and hydroxypropyl methyl cellulose HpMC, ether samples were kindly supplied by Shin-Etsu Chemical Co. Ltd. (Tokyo). Although the codes of the samples given by the company were SM15, SM100, 60SH15 and 60SH50, we recoded the samples as summarized in Table 1. The two numerical numbers found in the code parentheses for the MC samples indicated the degree of substitution, DS, of methyl groups per glucose unit and the weight average molar mass, M_w/10³, determined by use of multi-angle LS measurements after a GPC separation process (GPC-MALS) from left to right. In the case of HpMC samples, the first numerical number was added in the code parenthesis to represent the molar substitution number of hydroxypropyl groups per glucose unit, MS. All of the MC and HpMC samples were used as received without any purification procedures. High-quality (>99.9%) deuterium oxide (D₂O) was purchased from Eurisotop (Saint-Aubin) and was used as a solvent for S-WANS measurement solutions. Aqueous sodium chloride solution at a concentration of 0.1 mol L⁻¹ (M) was used as the eluent for GPC-MALS measurements.

Table 1 Characteristic parameters for the examined MC and HpMC molecules, such as the degree of substitution by methyl groups, DS, molar substitution number by hydroxypropyl groups, MS, weight average molar mass, M_w, number average molar mass, M_n, rotational radius, 〈R_g²〉^1/2, rod length, L, concentration reduced scattering intensity at q = 0, I(0)c⁻¹, contour length, L_c, and the ratio of L_c/L

Code	MS	DS	Mw/10^3 g mol^−1	Mn/10^3 g mol^−1	〈Rg^2〉^1/2/nm	L/nm^a	I(0)c^−1/cm^−1	Lc/nm	Lc/L
a Calculated from the 〈Rg^2〉^1/2 value assuming a rigid rod particle.
MC (1.8-37)	—	1.8	37	24	15	52	35	99	1.9
MC (1.8-79)	—	1.8	79	32	25	87	58	211	2.4
HpMC (0.25-1.9-50)	0.25	1.9	50	25	16	55	49	121	2.2
HpMC (0.25-1.9-71)	0.25	1.9	71	42	22	76	65	172	2.3

---

The concentrations of MC and HpMC samples in D₂O solutions for S-WANS measurements ranged from 0.2 to 1.0 wt%. The concentration of polymer samples in the eluent for GPC-MALS was 0.2 wt%.

Methods

S-WANS experiments were carried out using a system called “TAIKAN” specially designed for S-WANS measurements installed at beam line BL-15 of the Materials and Life Science Experimental Facility at J-PARC (Tokai). The used neutron source wavelength (λ) ranged from 0.07 to 0.78 nm, and the covered scattering vector (q = 4πλ⁻¹ × sin(θ/2), where θ means a scattering angle) range was from 0.05 to 100 nm⁻¹. The neutron beam source aperture size exposed to samples was 10 mm in diameter. Square-type quartz sample cells with a neutron beam path length of 4.0 mm were used for all the experiments, and the sample temperature was kept at 25 °C during the experiments. The neutron beam exposure time was 30 minutes for the solvent, D₂O, and a total of 4 hours for each sample solution. All obtained scattering data were corrected according to the standard procedures described in detail elsewhere²³ and converted to the absolute scattering intensity for the sample solution (I_sol(q)) and the solvent D₂O (I_D2O(q)). Then, the absolute scattering intensities of solute polymer molecules, I(q) = I_sol(q) − I_D2O(q) − I_in(q), were evaluated as functions of q, where I_in(q) represents a small constant incoherent scattering intensity dependent on the sample solution. We evaluated the I_in(q) for the I(q) data not to show systematic negative values, and the practically determined I_in(q) values were ranged from 7 to 15% of I_D2O(q).

GPC-MALS experiments were kindly carried out in Professor Isogai's laboratory, Graduate School of Agricultural and Life Sciences, the University of Tokyo, using a system consisting of a GPC instrument equipped with a Shodex SB-806M HQ column, Showa Denko K. K. (Tokyo), and a MALS instrument: DAWN HELEOS-II system equipped with a laser source at a wavelength of 658 nm (Wyatt Technology Co., Santa Barbara). Details of the GPC-MALS systems and operating conditions are available elsewhere.²⁴

Results and discussion

S-WANS profiles of MC and HpMC in aqueous solution

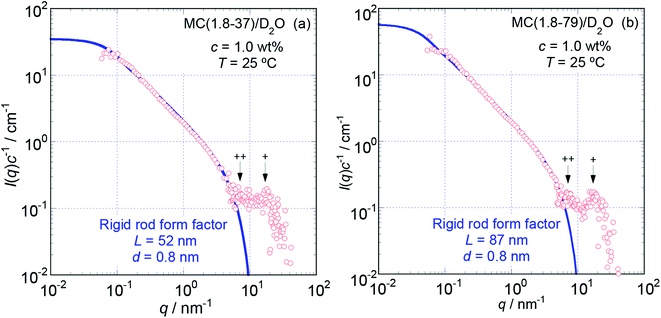
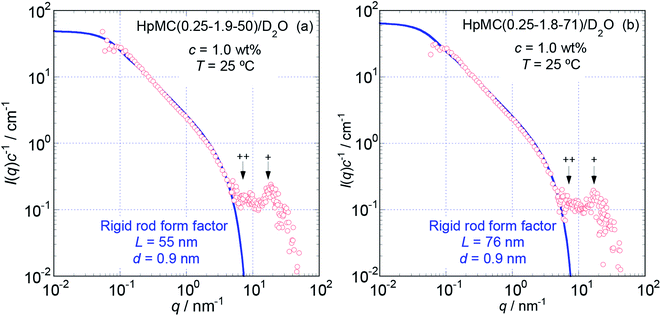
Because the obtained I_sol(q) data after 1 and 3 hours of neutron beam exposure of the same sample solution showed essentially identical q dependence, and an increase in accumulating time simply reduced the degree of uncertainty in the obtained I_sol(q) profiles, we concluded that there was no damage in the tested samples caused by exposure to the neutron beam. Fig. 1 and 2 show the obtained q dependencies of the concentration-reduced absolute scattering intensities, I(q)c⁻¹, for aqueous (D₂O) solutions of MC and HpMC samples, respectively, in a q range lower than 10 nm⁻¹. All I(q)c⁻¹ profiles seen in these figures for the identical sample species coincide well with each other irrespective of the c values. This observation reveals that the obtained I(q) profiles are essentially determined as the form factors of isolated MC and HpMC molecules, and the contribution of the structure factor resulting from intermolecular interactions to the I(q) data was not significant in the examined c range lower than 1.0 wt%. A small difference in chemically modified conditions between the MC and HpMC samples, i.e., the total amount of protons, is responsible for a weak difference in the magnitude of I(q)c⁻¹ values at the same q value.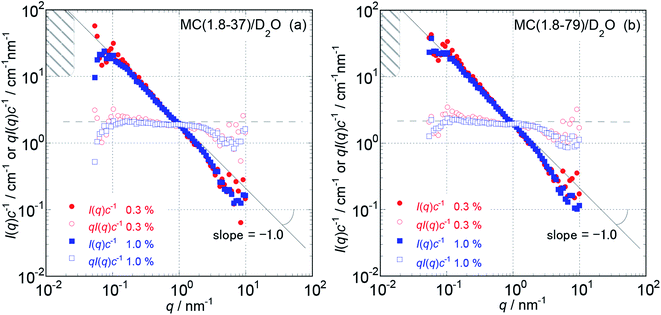

Fig. 1 The dependencies of the concentration reduced scattering intensities, I(q)c⁻¹, on the magnitude of scattering vector, q, and that of the products of qI(q)c⁻¹ for MC (1.8-37) (a) and MC (1.8-79) (b) in aqueous (D₂O) solutions at concentrations of 0.3 to 1.0 wt% and 25 °C in a low q range from 0.05 to 10 nm⁻¹. The hatched regions in the figures indicate a q range where the I(q)c⁻¹ curves almost approached plateau values, I(0)c⁻¹, which were calculated from the L values summarized in Table 1.

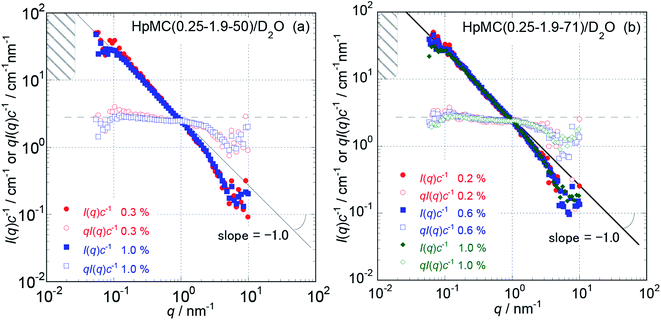Fig. 2 The dependencies of I(q)c⁻¹ and qI(q)c⁻¹ on q for HpMC (0.25-1.9-50) (a) and HpMC (0.25-1.9-71) (b) in aqueous (D₂O) solutions at concentrations ranging from 0.2 to 1.0 wt% and 25 °C in the low q range from 0.05 to 10 nm⁻¹. The hatched regions in the figures indicate a q range where the I(q)c⁻¹ curves approach plateau I(0)c⁻¹ values calculated from the L values summarized in Table 1.

Unfortunately, the plateau values, I(0)c⁻¹, of the I(q)c⁻¹ profiles that are typically observable in a sufficiently low q range, which was expected for usual isolated polymer molecules in a dilute regime in LS experiments, were not observed in this study due to the limitation of the smallest q value reachable with the used S-WANS instrument “TAIKAN”. However, the relationship I(q)c⁻¹ (or I(q)) ∝ q⁻¹ was clearly observed over one decade in a q range from 0.05–1.0 nm⁻¹, as seen in Fig. 1 and 2 for all MC and HpMC samples. This observed inversely proportional relationship strongly revealed that form factors for the MC and HpMC samples were essentially described with that for rigid rod particles.²⁵ Because no plateau region was observed in I(q)c⁻¹ (or I(q)) data as seen in Fig. 1 and 2, the dimensions of MC and HpMC molecules examined are larger than the value of 20 nm, which is the reciprocal of the smallest q value used in this study. Combining the obtained S-WANS profiles and LS data obtained in a q range lower than S-WANS experiments for the same samples demonstrates the Guinier-type q dependence of the form factor given by P(q) ≈ 1 − (1/3)〈R_g²〉q², where 〈R_g²〉 represents the mean square of the rotational radius of examined particles irrespective of the shapes of the particles.²⁵ Because GPC-MALS experiments simultaneously provide M_w and 〈R_g²〉^1/2 data for examined polymer samples, it is quite useful to determine the form factors of MC and HpMC molecules precisely, including the average length (L) and diameter (d) values.

In the case of the form factor of a sufficiently long rigid rod possessing an L much longer than d, the rotational radius, 〈R_g²〉^1/2, is theoretically calculated to be L² = 12〈R_g²〉.^12,25 Thus, we could estimate the average length, L, for the MC and HpMC molecules from their 〈R_g²〉 values determined by GPC-MALS experiments assuming the long rigid rod condition; the results are tabulated in Table 1. According to the Guinier-type relationship described above, P(q) = 0.92 at q = (1/2) × (〈R_g²〉^1/2)⁻¹. This estimation proposes that the form factor corresponding to I(q) (or I(q)c⁻¹) almost reaches a constant region in a range of q < (1/2) × (〈R_g²〉^1/2)⁻¹, irrespective of the shapes of the particles. From the 〈R_g²〉^1/2 data seen in Table 1, we evaluated q ranges in which I(q)c⁻¹ curves would show plateau values and showed the plateau q ranges with hatched parts in Fig. 1 and 2. It was likely that the plateau I(q)c⁻¹ regions were not far from the measured q ranges, and there was no additional q^−β dependence possessing β > 1 in the I(q)c⁻¹ profiles in a narrow q region between (1/2) × (〈R_g²〉^1/2)⁻¹ and 0.05 nm⁻¹, which was the smallest measuring q value in this study. Consequently, here, we might conclude that the MC and HpMC molecules possessed rigid rod shapes with an L dependent on the molar mass in aqueous solutions. It is known that the so-called Holzer plot,^26,27 qI(q)c⁻¹ vs. q, provides π/L as a plateau value, qI(q)(I(0))⁻¹, which was observable in a medium q regime in the case of rigid rods with a length of L. Thus, if one knows the value of L, the I(0)c⁻¹ value can be evaluated from the L value. Fig. 1 and 2 also contain the Holzer plots for the aqueous solution of the MC and HpMC samples, which clearly demonstrate the presence of plateaus in a q range from 0.1 to 1.0 nm⁻¹ in all sample solutions. Consequently, we can determine the I(0)c⁻¹ values by taking the L values obtained by GPC-MALS experiments, which are summarized in Table 1.

To more precisely consider the size and shape, including the L and d values for the examined MC and HpMC molecules dissolved in water at 25 °C, we carried out curve fitting procedures for the I(q)c⁻¹ curves using a theoretically calculated form factor for a rigid rod²⁵ with a finite d value. Fig. 3 and 4 show the q dependence profiles of the c reduced scattering intensities, I(q)c⁻¹, for all the MC and HpMC samples at c = 1.0 wt%, respectively, in the full measured q range from 0.05 to 100 nm⁻¹. In addition to the presence of a regime showing the relationship I(q)c⁻¹ ∝ q⁻¹ already discussed above, the I(q)c⁻¹ curves show slightly decreasing behaviour related to the contribution of the average diameter, d, at q ∼ 4 nm⁻¹, and small but non-negligible interference peaks were newly recognized at q = 7 and 17 nm⁻¹ in all examined samples. The solid thick lines in Fig. 3 and 4 represent the theoretically calculated best fit I(q)c⁻¹ curves for rigid rod particles²⁵ taking the L and I(0)c⁻¹ values summarized in Table 1 for each sample and adjustable d values seen in the figures. The agreement between the experimental and theoretical I(q)c⁻¹ curves is excellent. Thus, we might conclude that the shape of the examined MC and HpMC molecules dissolved in aqueous solutions is well described with rigid rods possessing average diameters of d = 0.8 and 0.9 nm, respectively, and L is dependent on M_w. The fact that the determined d values were slightly different for MC and HpMC samples proposes that the d value was sensitively influenced by a small difference in the chemically modified condition between the MC, DS = 1.8 (and MS = 0), and HpMC samples, DS = 1.9 and MS = 0.25. It is interesting to note that the temperature dependence of the dehydration behaviour and phase separation (cloud point) temperatures for the MC and HpMC samples in aqueous solutions were substantially different from each other depending on the chemically modified condition.¹¹

Fig. 3 The dependencies of I(q)c⁻¹ on q for MC (1.8-37) (a) and MC (1.8-79) (b) in aqueous (D₂O) solutions at c = 1.0 wt% and 25 °C in the full q range examined from 0.05 to 100 nm⁻¹. The solid thick lines represent the best fit theoretical curves calculated for rigid rod particles with the length, L, and diameter, d, shown in the figures. Symbols + and ++ indicate the positions of small interference peaks.

Fig. 4 The dependence of I(q)c⁻¹ on q of HpMC(0.25-1.9-50) (a) and HpMC(0.25-1.9-71) (b) in aqueous (D₂O) solutions at c = 1.0 wt% and 25 °C in the full q range examined from 0.05 to 100 nm⁻¹. The solid thick lines represent the best fit theoretical curves calculated for rigid rod particles with the L and d values shown in the figures. Symbols + and ++ indicate the positions of small interference peaks.

In many cases, the diameter or radius of rod-like particles have been discussed by using a so-called cross-section plot, ln{qI(q)} vs. q², of which the slope provides the mean diameter of the cross-section of rod-like particles in the manner −(1/16)d².²⁸ Although we did not show the cross-section plots for the examined samples here, the evaluated d value via the cross section plots was determined to be ca. 0.72 nm for MC samples and ca. 0.82 nm for HpMC samples. Since these d values evaluated via the cross-section plot were close to those resulting from the curve fitting procedure described above, and differences between them were only ca. 10%, we concluded that the cross-section plot method was likely also able to evaluate the d value rather precisely for the MC and HpMC samples.

On the other hand, to evaluate the persistence length, l_p, of semi-flexible polymer molecules from scattering data obtained by SANS or SAXS experiments, the so-called Kratky plot, q²I(q) vs. q, is sometimes quite useful.²⁹ In the Kratky plot, a certain q value, q*, at which q²I(q) starts to demonstrate a proportional relationship, such as q²I(q) ∝ q, gives the l_p value in the manner l_p ≈ (q*)⁻¹. When we generated Kratky plots for the S-WANS data of the MC and HpMC samples, the q²I(q) data clearly showed proportionality to q over the q range from 0.05 to 1.0 nm⁻¹ and were followed by a decrease in proportionality in a q range higher than 3.0 nm⁻¹. Thus, since the characteristic q* value was never found in a low q range, the l_p value for the MC and HpMC samples should have been much longer than (0.05 nm⁻¹)⁻¹ (=20 nm) in aqueous solutions. Consequently, we concluded, again, that all examined MC and HpMC molecules did not behave as semi-flexible chains but as rigid rod particles in aqueous solutions.

The presence of small interference peaks at q⁺ = 17 nm⁻¹ in the obtained I(q)c⁻¹ curves corresponding to the form factors seen in Fig. 3 and 4 strongly proposed that there was a characteristic d-spacing (δ⁺) in the structure formed by both the MC and HpMC molecules dissolved in water, which was roughly determined to be δ⁺ = 2π(q⁺)⁻¹ = 0.37 nm. It is worth noting that the observed characteristic d-spacing was not far from but slightly smaller than that found for typical major interference signals in the typical crystalline structure of cellulose, such as cellulose-Iβ (0.395 nm for (020) d-spacing)² and II (0.406 nm for (020) d-spacing).³⁰ Moreover, one is able to find other small interference peaks in each I(q)c⁻¹ curve seen in Fig. 3 and 4 at the q value of ca. 7.0 nm⁻¹. From the value of q⁺⁺ = 7.0 nm⁻¹, another characteristic d-spacing could be evaluated to be δ⁺⁺ = 0.9 nm, which was slightly smaller than the size of the conformational repeating unit, cellobiose (the dimer of glucose), ca. 1.0 nm, of cellulose molecules observed as the unit cell size of the c-axis in all reported crystalline structures of cellulose.^2,3,30–32 These inner structures showing δ⁺ = 0.37 nm and δ⁺⁺ = 0.9 nm constructed in the rigid rods formed by MC and HpMC molecules in aqueous solutions were newly discovered in this study.

Structure and conformation of MC and HpMC molecules in aqueous solutions

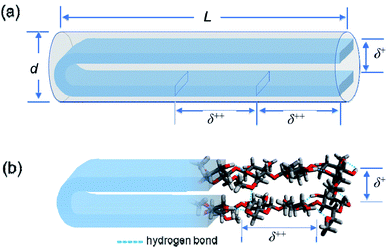
From the values of M_w, DS and MS, the weight average degree of polymerization (DP_w) and the weight average molecular contour length (L_c) could be evaluated for each MC and HpMC sample assuming the average length of a repeating glucose unit to be 0.50 nm (ref. 2, 3 and 30–32) and are summarized in Table 1 together with the values of L_c/L. It is interesting to note that all of the L_c/L values were near 2.0. From the viewpoint of molecular contour length, this observation strongly proposed that the MC and HpMC molecules dissolved in aqueous solutions had a highly extended rigid rod structure or conformation possessing one folded point, similar to “hairpins”, as schematically shown in Fig. 5(a), irrespective of MC and HpMC species and molar mass in the range of M_w < 100 × 10³ g mol⁻¹ examined in this study.

Fig. 5 (a) Schematic representation for a rigid rod particle possessing its length, L, and diameter, d, and a distinctive inner structure demonstrating the two characteristic d-spacings of δ⁺ and δ⁺⁺ in the scattering experiments. (b) Schematic depiction of a speculated hairpin-like rigid rod structure formed by a once-folded MC molecule in a highly extended conformation via many intramolecular hydrogen bonds by the remaining hydroxy groups. The separation between two facing extended cellobiose units determines the characteristic d-spacing of δ⁺ = 0.37 nm, and the size of a repeating cellobiose unit in the formed extended conformation determines the other characteristic d-spacing of δ⁺⁺ = 0.9 nm. Water molecules hydrated to the MC molecule are not shown to reduce the complexity of the schematic picture.

The reason why MC and HpMC molecules behave as perfectly rigid rods and have the inner structure showing the two characteristic d-spacings of δ⁺ = 0.37 nm and δ⁺⁺ = 0.9 nm must be reasonably explained by the use of a rational model. The formation of a number of intramolecular hydrogen bonds between glucose units facing each other in the extended molecular conformation due to the presence of a folded point near the centre of a long molecular chain should be possible by use of remaining hydroxy groups and the help of water molecules hydrated to the MC and HpMC molecules.¹¹

Fig. 5(b) shows a schematic representation of the formation of intramolecular hydrogen bonds in a once-folded extended configuration formed by MC and HpMC molecules in aqueous solutions with the help of hydrated water molecules. The presence of many intramolecular hydrogen bonds should markedly tighten the extended folded structure formed by MC and HpMC molecules and make them behave as rigid rods in aqueous solutions, as observed in this study. A strong tendency to form many intra- and intermolecular hydrogen bonds to make stable crystalline structures, even in chemically reactive aqueous solutions, such as that used in the mercerization process³³ to convert crystalline structures from cellulose-I to cellulose-II under alkaline conditions, is one of the distinctive characteristics of cellulose molecules. Roughly speaking, the speculated hairpin-like structure schematically depicted in Fig. 5(b) was similar to a local structure found in a couple of neighbouring extended cellulose molecules in the crystalline structure of cellulose-II, of which molecular directions are definitely inverted from each other.^30–32 The many formed intramolecular hydrogen bonds would bind up the hairpin-like structure to reduce the separation between facing cellobiose units, i.e., δ⁺, narrower than the d-spacing usually observed in the crystalline structure of cellulose-II. The size of a repeating unit in the formed, extended conformation determines the other characteristic d-spacing of δ⁺⁺ = 0.9 nm along the longer axis of the formed rigid rod structure. The fact that a small interference peak observable at q⁺⁺ = 7.0 nm⁻¹ was well related to the presence of the characteristic d-spacing comparable to the size of a cellobiose repeating unit should be strong evidence for the formation of the highly extended conformation of HpMC and MC molecules even in aqueous solutions, as observed in the crystalline structure. The reason why the δ⁺⁺ value was ca. 10% smaller than the size of a cellobiose unit of 1.0 nm, usually observed as the c-axis unit lattice size in crystalline structures, would be the imperfect alignment of cellobiose (i.e., glucose) units forming the folded extended conformation in aqueous solution. Consequently, making hairpin-like rigid rod particle structures in aqueous solutions via a once-folded highly extended conformation of the MC and HpMC samples was caused by the characteristic ability of cellulose derivatives to form strong hydrogen bonds assisted by the presence of hydrated water molecules.

Conclusions

S-WANS and GPC-MALS experiments for aqueous (D₂O for S-WANS) solutions of the MC and HpMC samples, with a DS = 1.8 of methyl groups and an MS = 0.25 of hydroxypropyl groups and DS = 1.9 of methyl groups, respectively, with M_w < 100 × 10³ g mol⁻¹ clearly revealed that both the MC and HpMC samples dissolved in water possess the structure of rigid rods with average diameters of 0.8 and 0.9 nm, respectively, and a length depending on their molar mass. The formed rigid rods consisted of molecular chains with a once-folded highly extended conformation. Moreover, it was newly discovered that the formed rigid rods possess a characteristic d-spacing of 0.37 nm, corresponding to the average separation between two highly extended molecular chains facing each other due to the presence of a folded point. Another characteristic d-spacing of 0.9 nm was also newly discovered in the formed rigid rod structure, which corresponded to the size of cellobiose repeating units in the extended conformation of MC and HpMC molecules. The ability of forming several strong hydrogen bonds caused by the remaining hydroxy groups in the MC and HpMC molecules, as one of the characteristics of cellulose derivatives, constructed the rigid rod structure via a once-folded highly extended conformation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by JSPS KAKENHI Grant Number JP18K19107. All cellulose ether samples were kindly supplied by Shin-Etsu Chemical Co. Ltd. (Tokyo), and this work was partially supported by the same company. We would like to thank Dr K. Hayakawa, who used to work for Shin-Etsu Chemical Co. Ltd., for his kind collaboration on this study. We are indebted to Dr Y. Ono and Prof. A. Isogai, Graduate School of Agricultural and Life Sciences, the University of Tokyo, for their kind cooperation in GPC-MALS experiments and for a fruitful discussion on the obtained results. The S-WANS experiments at the Materials and Life Science Experimental Facility of the J-PARC were performed under a user programme (Proposal No. 2018B0040).

References

1. D. Klemm, B. Heublein, H.-P. Fink and A. Bohn, Cellulose: Fascinating Biopolymer and Sustainable Raw Material, Angew. Chem., Int. Ed., 2005, 44, 3358–3393.
2. Y. Nishiyama, P. Langan and H. Chanzy, Crystal Structure and Hydrogen-Bonding System in Cellulose Iβ from Synchrotron X-ray and Neutron Fiber Diffraction, J. Am. Chem. Soc., 2002, 124, 9074–9082.
3. Y. Nishiyama, J. Sugiyama, H. Chanzy and P. Langan, Crystal Structure and Hydrogen Bonding System in Cellulose Iα from Synchrotron X-ray and Neutron Fiber Diffraction, J. Am. Chem. Soc., 2003, 125, 14300–143006.
4. Y. Li, X. Liu, Y. Zhang, K. Jiang, J. Wang and S. Zhang, Why Only Ionic Liquids with Unsaturated Heterocyclic Cations Can Dissolve Cellulose: A Simulation Study, ACS Sustainable Chem. Eng., 2017, 5, 3417–3428.
5. K. Kamide, Cellulose and Cellulose Derivatives; Molecular Characterization and its Applications, Elsevier, Amsterdam, 2005, ch. 2 and 3.
6. D. Klemm, B. Philipp, T. Heinze, U. Heinze and W. Wagenknecht, Comprehensive Cellulose Chemistry: Vol. 2 Functionalization of Cellulose, Wiley-VCH Verlag GmbH, Weinheim, 1998, ch. 4.
7. http://polymerdatabase.com/polymerclasses/Cellulosetype.html.
8. http://msdssearch.dow.com/PublishedLiteratureDOWCOM/dh_004f/0901b8038004fb7c.pdf?filepath=eth.
9. https://www.daicel.com/en/business/cellulosic/cellulose-acetate.html.
10. N. Schupper, Y. Rabin and M. Rosenbluh, Multiple Stages in the Aging of a Physical Polymer Gel, Macromolecules, 2008, 41, 3983–3994.
11. K. Arai and T. Shikata, Hydration/Dehydration Behavior of Cellulose Ethers in Aqueous Solution, Macromolecules, 2017, 50, 5920–5928.
12. H. Fujita, Polymer Solutions, Elsevier, Amsterdam, 1990, ch. 2.
13. V. K. Uda and G. Meyerhoff, Hydrodynamische eigenschaften von methylcellulosen in losung, Makromol. Chem., 1961, 47, 168–184.
14. D. S. Poché, A. J. Ribes and D. L. Tipton, Characterization of methocel™: correlation of static light-scattering data to GPC data to GPC molar mass data based on pullulan standards, J. Appl. Polym. Sci., 1998, 70, 2197–2210.
15. C. M. Keary, Characterization of METHOCEL cellulose ethers by aqueous SEC with multiple detectors, Carbohydr. Polym., 2001, 45, 293–303.
16. K. Nishinari, K. Kohyama, P. A. Williams, G. O. Phillips, W. Burchard and K. Ogino, Solution properties of pullulan, Macromolecules, 1991, 24, 5590–5593.
17. Von W. Burchard, Das viskositätsverhalten von amylose in verschiedenen lösungsmitteln, Makromol. Chem., 1963, 64, 110–125.
18. S. Kitamura, K. Kobayashi, H. Tanahashi, T. Ozaki and T. Kuge, Dilute solution properties of starch related polysaccharides. Part 1. On the Mark-Houwink-Sakurada equation for amylose in aqueous solvents, Denpun Kagaku, 1989, 36, 257–264.
19. T. Yanaki, T. Norisuye and H. Fujita, Triple Helix of Schizophyllum commune Polysaccharide in Dilute Solution. 3. Hydrodynamic Properties in Water, Macromolecules, 1980, 13, 1462–1466.
20. R. Bodvik, A. Dedinaite, L. Karlson, M. Bergström, P. Bäverbäck, J. S. Pedersen, K. Edwards, G. Karlsson, I. Varga and P. M. Claessona, Aggregation and network formation of aqueous methylcellulose and hydroxypropylmethylcellulose solutions, Colloids Surf., A, 2010, 354, 162–171.
21. T. Chatterjee, A. I. Nakatani, R. Adden, M. Brackhagen, D. Redwine, H. Shen, Y. Li, T. Wilson and R. L. Sammler, Structure and Properties of Aqueous Methylcellulose Gels by Small-Angle Neutron Scattering, Biomacromolecules, 2012, 13, 3355–3369.
22. T. P. Lodge, A. L. Maxwell, J. R. Lott, P. W. Schmid, J. W. McAllister, S. Morozova, F. S. Bates, Y. Li and R. L. Sammler, Gelation, Phase Separation, and Fibril Formation in Aqueous Hydroxypropylmethylcellulose Solutions, Biomacromolecules, 2018, 19, 816–824.
23. S. Takata, J. Suzuki, T. Shinohara, T. Oku, T. Tominaga, K. Ohishi, H. Iwase, T. Nakatani, Y. Inamura, T. Ito, K. Suzuki, K. Aizawa, M. Arai, T. Otomo and M. Sugiyama, The Design and q Resolution of the Small and Wide Angle Neutron Scattering Instrument (TAIKAN) in J-PARC, JPS Conf. Proc., 2015, 8, 036020.
24. Y. Ono, T. Ishida, H. Soeta, T. Saito and A. Isogai, Reliable dn/dc values of cellulose, chitin, and cellulose triacetate dissolved in LiCl/N,N-dimethylacetamide for molecular mass analysis, Biomacromolecules, 2016, 17, 192–199.
25. A. Guinier and G. Fournet, Small-angle scattering of X-rays. John Wiley & Sons, New York, 1955, ch. 1.
26. A. Holtzer, Interpretation of the angular distribution of the light scattered by a polydisperse system of rods, J. Polym. Sci., 1955, 17, 432–434.
27. K. Terao, M. Murashima, Y. Sano, S. Arakawa, S. Kitamura and T. Norisuye, Conformational, Dimensional, and Hydrodynamic Properties of Amylose Tris(n-butylcarbamate) in Tetrahydrofuran, Methanol, and Their Mixtures, Macromolecules, 2010, 43, 1061–1068.
28. P. Mittelbach, Zur Röntgenkleinwinkelstreuung verdünnter kolloider Systeme. VIII, Acta Phys. Austriaca, 1964, 19, 53–102.
29. Small Angle X-ray Scattering, ed. G. Glatter and O. Kratky, Academic Press, London, 1982, pp. 361–386.
30. M. Wada, M. Ike and K. Tokuyasu, Enzymatic hydrolysis of cellulose I is greatly accelerated via its conversion to the cellulose II hydrate form, Polym. Degrad. Stab., 2010, 95, 543–548.
31. K. Kobayashi, S. Kimura, E. Togawa and M. Wada, Crystal transition from Na–cellulose IV to cellulose II monitored using synchrotron X-ray diffraction, Carbohydr. Polym., 2011, 83, 483–488.
32. P. Langan, Y. Nishiyama and H. Chanzy, X-ray structure of mercerized cellulose II at 1Å resolution, Biomacromolecules, 2001, 2, 410–416.
33. S. V. Heines, John Mercer and mercerization, 1844, J. Chem. Educ., 1944, 21, 430–433.

---