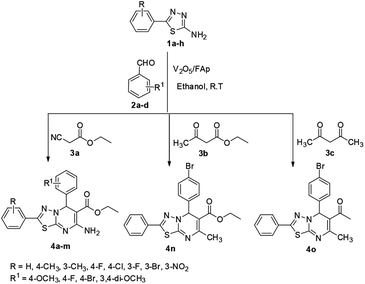
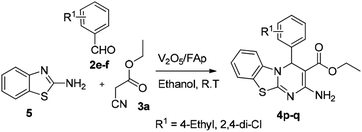
Open Access Article
Open Access ArticleGreen synthesis and characterisation of novel [1,3,4]thiadiazolo/benzo[4,5]thiazolo[3,2-a]pyrimidines via multicomponent reaction using vanadium oxide loaded on fluorapatite as a robust and sustainable catalyst†
Nagaraju Kerru,
Lalitha Gummidi,
Surya Narayana Maddila,
Sandeep V. H. S. Bhaskaruni,
Suresh Maddila and
Sreekantha B. Jonnalagadda *
*
School of Chemistry & Physics, University of KwaZulu-Natal, Westville Campus, Chiltern Hills, Durban-4000, South Africa. E-mail: jonnalagaddas@ukzn.ac.za; Fax: +27 31 2603091; Tel: +27 31 2607325
First published on 27th May 2020
Abstract
We synthesised materials with different loadings of vanadia on fluorapatite (V2O5/FAp), fully characterised their structural properties using various spectral techniques including TEM, BET, XRD, FT-IR, SEM and EDX and assessed their prowess as catalysts. The 2.5% V2O5/FAp exhibited excellent activity for the synthesis of novel [1,3,4]thiadiazolo[3,2-a]pyrimidines and benzo[4,5]thiazolo[3,2-a]pyrimidines. The one-pot three-component fusion reaction between chosen substrates of 1,3,4-thiadiazole-amines or 2-amino-benzothiazole, aldehydes and active methylene compounds in ethanol solvent at room temperature gave an excellent yield of products (90–97%) in a swift reaction (25–30 min). The advantages of this protocol are rapid synthesis, mild reaction conditions, green solvent, easy work-up, eco-friendliness, reusability of catalyst and no need for column chromatography.
Introduction
In organic synthesis, the use of green principles and efficient catalysts to achieve excellent yields is always a cherished goal.1 In recent times, the use of heterogeneous catalysts in organic synthesis has significantly increased, due to their stability and tunable properties.2 Fluorapatite (FAp) (Ca10(PO4)6F2) is an inexpensive material with the capability to accommodate different anionic and cationic ions, making it suitable for several applications.3 FAp crystallises in a hexagonal crystal arrangement, with phosphate and calcium ions arranged over the fluoride ions.4 Due to its remarkable ion exchangeability with a variety of metal ions, it is a component of different frame supported metal composites, with high stability and tunable acid–base properties.4 The tunable properties of FAp and metal amended FAp have imparted flexibility as heterogeneous catalysts. The multiple active sites (Lewis/Brønsted acidic and basic sites), present could facilitate different valuable organic conversions.5 The acidic sites are produced from the PO4 group of phosphorous and Ca2+. The basic sites are generated from the PO4 group of oxygen and F−, which are tightly crammed on its fluorapatite surface.6 Several fluorapatite has been explored as catalysts for the carbon–carbon and carbon–nitrogen bond construction reactions.7–9 FAps also play an essential role in numerous biomedical applications.10 Thus, FAp proves an ideal material for a broad spectrum of applications, including catalysis. Likewise, supported metal oxide catalysts have been utilised over the years in various synthetic organic applications.11 Many transition metal oxides, in particular, vanadium oxide are known as efficient heterogeneous catalysts in several value-added organic transformations.12–14 The empty d-orbitals of vanadium cation serve as electron acceptor sites, and oxyanions serve as electron donors rendering good surface catalytic properties to vanadia.15,16 The acid–base pairs of vanadium oxides also increase their importance in catalytic science. Recently, our research group reported the synthesis and characterization of various metal loaded fluorapatite materials and their scope as heterogeneous catalysts in multicomponent organic synthesis with excellent yields.17–20 Based on that experience, we examined the synergic activity of fluorapatite and vanadium oxide to enhance the efficiency of value-added organic conversions.Multicomponent reaction (MCR) is a valued technique in organic synthesis, drug innovation platforms and the development of a range of biologically relevant molecules. Broadly used MCR, of Biginelli type, involves the cyclo-condensation of an aldehyde, active methylene compounds and various aminoazoles, to give the corresponding dihydropyrimidines.21,22 MCR heterocyclisations involving aminoazoles are key building blocks in synthesis, as they especially contain alternative nucleophilic reaction centres facilitating their cyclo-condensations with carbonyl and active methylene compounds.23–26 The MCR approach in organic synthesis, in combination with green solvents and recyclable catalysts, has created a cost-effective and ecologically positive impact on the chemical and pharmaceutical arenas.
The chemistry of the fused heterocycles, 1,3,4-thiadiazole-pyrimidines and benzo[4,5]thiazolo[3,2-a]pyrimidines is of continued interest. These are well-known structural analogues of various building blocks in several drug candidates.27 The synthesis of novel functionalized [1,3,4]thiadiazolo[3,2-a]pyrimidine and benzo[4,5]thiazolo[3,2-a]pyrimidines received significant attention from the synthetic and medicinal chemists, owing to their wide variety of biological profiles, including the antitubercular and antibacterial,28 antiviral,29,30 anticancer,31 antibiofilm32 and antitumor33 activities. Therefore, the syntheses of 1,3,4-thiadiazole/benzothiazole-pyrimidine derivatives are highly valuable for their immense pharmacological potential.
However, many synthetic protocols are not straightforward and involve multiple steps, often demanding the separation and purification of the reaction intermediates. For example, 2-sulfamoyl-5H-[1,3,4]-thiadiazolo[3,2-a]pyrimidine-6-carboxamides were synthesised from 5-amino-[1,3,4]thiadiazole-2-sulfonamide via a two-step approach.34 Azab et al. have reported a two-step method for 5H-1,3,4-thiadiazolo[3,2-a]pyrimidin-5-ones, which involved the reaction of 2-amino-1,3,4-thiadiazoles to ethyl cyanoacetate and tandem reduction and deamination in the presence of phosphorus pentoxide–formic acid.35 Zhao et al. have described the synthesis of 5H-[1,3,4]thiadiazolo[3,2-a]pyrimidine-6-carboxylate derivatives using aldehydes, 2-amino-thiadiazole and acetoacetate by one-pot MCR strategy under microwave irradiation.36 The synthesis of anticancer compounds, 7-substituted-phenyl-8,8a-dihydro-7H-[1,3,4]thiadiazolo[3,2-α]pyrimidine-6-carbonitriles was achieved by Tiwari and co-workers from the one-pot reaction of 5-(4-chlorophenyl)-1,3,4-thiadiazol-2 amine, aromatic aldehydes and malononitrile under ultrasonic irradiation and NaOH.37 Recently, Kasaboina et al. have also reported the synthesis of benzosuberone-linked to thiadiazolo[3,2-a]pyrimidine-6-carboxylates reacting benzosuberone with 1,3,4-thiadiazol-2 amine, ethyl acetoacetate and substituted benzaldehydes in polyethylene glycol (PEG) under reflux condition.38 Recent literature also shows the increased interest of researchers towards the synthetic protocols for benzothiazole-pyrimidine derivatives. Many types of catalysts have been described to promote the synthesis of benzothiazole-pyrimidine derivatives via a three-component reaction of aldehydes, 2-aminobenzothiazole and β-keto ester. The different heterogeneous catalysts employed include Fe3O4@nano-cellulose/Cu(II), nano-kaolin/Ti4+/Fe3O4, nano-cellulose/BF3/Fe3O4 and nano-Fe3O4@SiO2–TiCl3, to mention a few.26,39–41
Although [1,3,4]thiadiazole-pyrimidine synthetic procedures involving MCRs exist, many suffer from the by-product formation, lesser yields and need for hazardous chemicals or harsh reaction conditions. Thus, from the viewpoint of environmental safety and sustainability, it is rewarding to design efficient green one-pot methodologies to synthesise the 1,3,4-thiadiazole/benzothiazole-pyrimidine analogues, which can provide better yields in shorter reaction times and substrates variability.
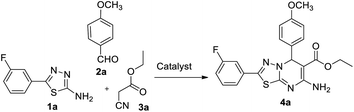
In our endeavour to develop new and green methodologies by exploring MCR strategy, we earlier reported a few value-added organic conversion protocols involving reusable heterogeneous catalysts for libraries of different biological potent heterocycles.18–20 Based on the literature survey, no studies are available using a combination of vanadium oxide loaded fluorapatite as catalyst in synthetic organic applications. This communication describes the preparation of materials with different wt% vanadia loaded on fluorapatite, and a simple one-pot procedure for the synthesis of novel [1,3,4]thiadiazolo[3,2-a]pyrimidine and benzo[4,5]thiazolo-[3,2-a]pyrimidine derivatives. The three-component condensation reactions using 2.5% V2O5/FAp as the catalyst and absolute ethanol as solvent at room temperature offered excellent yields for all derivatives in short reaction times (Schemes 1 and 2). We used spectroscopic techniques, TEM, BET, powder-XRD, FT-IR, SEM and EDX analysis to characterise the catalyst material and to confirm all the target molecules fully by NMR and HRMS analysis.
Experimental
V2O5/FAp catalyst preparation
We prepared the composites with different wt% of vanadium on fluorapatite (1, 2.5 and 5 wt%) by a co-precipitation adopting the literature reported procedure.42 1.5 mmol of trisodium phosphate dodecahydrate (Na3PO4·12H2O) was suspended in deionised water (25 mL) in a 50 mL of the beaker. Next, 0.5 mmol of sodium fluoride (NaF) was gradually added to that solution under constant stirring for 30 min at room temperature. Then, 2.5 mmol of calcium nitrate tetrahydrate was slowly added to this solution under continuous stirring for a further 15 min. Finally, the calculated volume of 0.5 mmol of 99.9% vanadium oxide was added slowly to the mixture solution, and the stirring continued for 6 h. Subsequently, centrifuged the suspension several turns by repetitively rinsing with deionised water. The obtained composite materials were dried in the heating oven at 110 °C for 10 h, followed by calcinated at 350 °C for 4 h under continuous airflow.General procedure for the synthesis of [1,3,4]thiadiazolo[3,2-a]pyrimidine and benzo[4,5]thiazolo[3,2-a]pyrimidine derivatives (4a–q)
A mixture of different substituted 1,3,4-thiadiazole-amine (1a–h, 1 mmol) or 2-aminobenzathiazole (5, 1 mmol), selected benzaldehyde (2a–f, 1 mmol) and active methylene compounds (3a–c, 1 mmol) together with the heterogeneous catalyst (2.5% V2O5/FAp; 30 mg) was added to 5 mL of absolute ethanol solvent in an RB flask. The reaction mixture was kept at R.T for 25 to 30 min under constant stirring. TLC monitored the progress of the reaction. After completion of the reaction, the catalyst was recovered from the reaction mixture by simple filtration, adding excess ethyl acetate. The recovered catalyst material was used for the subsequent cycles. The solvent from the reaction mixture was concentrated by rotatory evaporation under vacuum to harvest the solid product. The product was recrystallised under hot ethanol conditions to achieve the corresponding clean products. Employing different spectroscopic methods (HRMS, FT-IR, 1H and 13C NMR; ESI†), the structures of all synthesised molecules were elucidated.Results and discussion
Characterisation of the catalyst
Fig. 1 illustrates the SEM, EDX and TEM images of the prepared vanadium oxide loaded fluorapatite (2.5% V2O5/FAp) material. The SEM morphology (Fig. 1a) shows the fluorapatite particles arranged in the uniform needle and rod-like shapes and vanadium oxide particles widely in close aggregates on the surface of FAp (Fig. 1c). Fig. 1b exhibits the EDX spectrum, showing the presence of F, P, Ca and V elements in the composite material. The TEM (Fig. 1d) displays the rod-shaped vanadium oxide particles firmly sprouted and masked on the surface of fluorapatite. The average particle size was about 20–30 nm in length and 10–15 nm in diameter.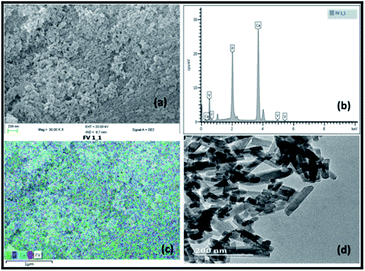 | ||
| Fig. 1 (a) SEM-micrograph, (b) EDX spectrum, (c) SEM-mapping and (d) TEM-micrograph of 2.5% V2O5/FAp catalyst. | ||
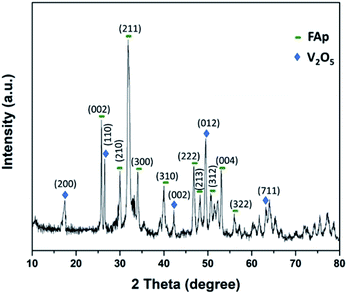
Fig. 2 illustrates the powder-XRD spectrum of 2.5% V2O5/FAp catalyst and the overlying intense peaks with 2θ standards varying between 10° to 80° in the crystalline phases. The intense diffraction signals identified at 2θ values of 25.5°, 29.9°, 32.0°, 34.1°, 40.1°, 46.6°, 48.1°, 50.6°, 53.2° and 55.8° are a good index of the fluorapatite plans (002), (210), (211), (300), (310), (222), (213), (312), (004) and (322), and were appropriately compatible to the standard pattern of fluorapatite (JCPDS-15-0876). Furthermore, the additional diffraction peaks at 17.5°, 26.5°, 42.2°, 49.4° and 63.0°, and were respectively indexed to the (200), (110), (002), (012) and (711) plans of the V2O5 (JCPDS-4-1426).12 The XRD results confirm the high degree of crystallinity of vanadium oxide loaded on fluorapatite (V2O5/FAp).
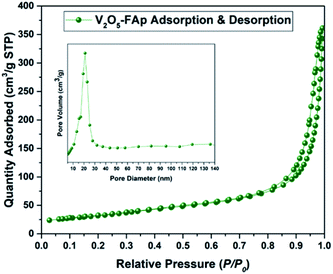
Fig. 3 shows the Brunauer Emmett Teller (BET) analysis of V2O5/FAp composite and nitrogen adsorption–desorption isotherms. The porous properties and BET surface area of the V2O5/FAp material were assessed by nitrogen adsorption at 77 K. As-obtained catalyst material can be classified as type-IV isotherm with stepwise desorption and adsorption hysteresis loop and P/P0 range was 0.76–0.95. The nature of the as-prepared material was a mesoporous material (inset of Fig. 3). The catalyst composite recorded 113.4496 m2 g−1 of BET surface area, 200.394 Å of pore size and 5692 cm3 g−1 of the pore volume. The high specific surface areas of V2O5/FAp composite might be the reason for the excellent catalytic activity, owing to the more active sites over the material surface, facilitating more interactions with substrates.
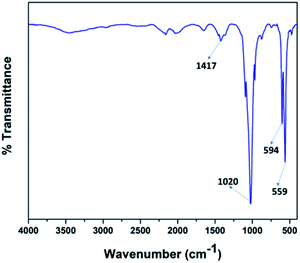
Fig. 4 illustrates the FT-IR spectra of the V2O5/FAp material and the most prominent absorption peaks were at 1417 cm−1, 1020 cm−1, 594 cm−1, and 559 cm−1, from the stretching and bending frequencies of phosphate (PO43−) and carbonate (CO32−) groups.42 The stretching vibrational frequency observed at 1417 cm−1, belongs to the carbonate groups (CO32−). The most characteristic absorption peak displayed at 1020 cm−1 corresponds to the PO43− the group of P–O linkages. The other vibrational bands identified at 594 cm−1 and 559 cm−1 were due to the O–P–O bonds. These results indicate that the calcium phosphate and carbonate ions are on the surface accessible to the reacting substrates.
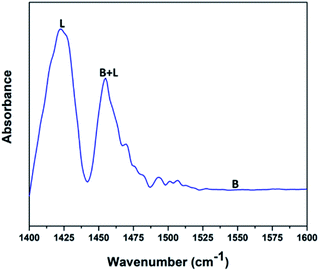
Fig. 5 shows the pyridine-infrared spectra reflecting the nature of vanadium oxide acidic sites on the FAp surface. The major vibrational peak exhibited at 1422 cm−1 represents the Lewis acidic sites on the surface of the V2O5/FAp composite. The minor vibrational band at 1454 cm−1 indicates both the Brønsted and Lewis acidic sites. No absorption band detected between 1550 and 1600 cm−1, suggests that the no apparent Brønsted acidic sites exist.43 Therefore, as-obtained material constituted of strong Lewis acidic sites. The catalysed organic reaction is presumably accelerated by the availability of acidic sites on the V2O5/FAp material surface.
Catalytic activity
Primarily, we chose 1,3,4-thiadiazole-amine (1a), para-methoxy benzaldehyde (2a) and ethyl cyanoacetate (3) as the starting materials for the one-pot reaction (Scheme 1). To identify the appropriate catalyst, we examined the activity of a range of different acidic, basic and metal-oxide catalysts (30 mg per 1 mmol of aldehyde) with ethanol as solvent (Table 1). The reaction in the absence of catalyst gave a trace of the product (4a) under both R.T and reflux conditions for about 24 h (Table 1, entry 1). Further, in the presence of different inorganic and organic catalysts such as NaOH, KOH, K2CO3, Cs2CO3, triethylamine, DABCO and pyridine, gave poor yields of the desired product (4a) at room temperature (Table 1, entries 2–8). The reaction examined with various Brønsted acid catalysts also delivered poor yields of the product (Table 1, entries 9–13). Then, the activity with diverse metal oxide catalysts (Table 1, entries 14–17). Among them, vanadium pentoxide (V2O5) offered a better yield (62%) of the desired product. Furthermore, the fluorapatite (FAp) also gave a decent product yield (Table 1, entry 18). FAp is amphoteric and can provide both Lewis acidic and basic sites, while P–O− and F− are responsible for the Lewis basic sites and Ca2+ is responsible for acidic sites.17 The obtained results reveal that both V2O5 and FAp demonstrated promising results as catalysts. Hence, we further investigated the efficacy of the combination of V2O5 and FAp, by preparing different wt% (1, 2.5 and 5%) of vanadium oxide loaded on fluorapatite composite (V2O5/FAp). Initially, the title reaction was carried out with 1% vanadium oxide on FAp as a catalyst that occurred smoothly offering 88% yield in 30 min (Table 1, entry 19).| Entry | Catalyst | Reaction conditions | Time (h) | Yieldb (%) |
|---|---|---|---|---|
| a Reaction conditions: 1,3,4-thiadiazole-amine (1a; 1 mmol), 4-methoxy benzaldehyde (2a; 1 mmol), ethyl cyanoacetate (3a; 1 mmol) and solvent (5 mL).b Isolated yields.c Time in min. | ||||
| 1 | — | R.T/reflux | 24 | Trace/18 |
| 2 | NaOH | R.T | 12 | 20 |
| 3 | KOH | R.T | 12 | 23 |
| 4 | K2CO3 | R.T | 10.0 | 19 |
| 5 | Cs2CO3 | R.T | 8.0 | 28 |
| 6 | Et3N | R.T | 8.0 | 38 |
| 7 | DABCO | R.T | 7.0 | 24 |
| 8 | Pyridine | R.T | 9.0 | 17 |
| 9 | p-TSA | R.T | 7.0 | 31 |
| 10 | HCl | R.T | 9.0 | 29 |
| 11 | AcOH | R.T | 10.0 | 37 |
| 12 | H2SO4–SiO2 | R.T | 5.0 | 42 |
| 13 | HClO4–SiO2 | R.T | 6.0 | 39 |
| 14 | SiO2 | R.T | 6.5 | 41 |
| 15 | Bi2O3 | R.T | 4.0 | 52 |
| 16 | ZnO | R.T | 3.5 | 51 |
| 17 | V2O5 | R.T | 2.5 | 62 |
| 18 | FAp | R.T | 1.5 | 67 |
| 19 | 1% V2O5/FAp | R.T | 25c | 88 |
| 20 | 2.5% V2O5/FAp | R.T | 25c | 97 |
| 21 | 5% V2O5/FAp | R.T | 25c | 93 |
| 22 | 2.5% Bi2O3/FAp | R.T | 25c | 79 |
| 23 | 2.5% ZnO2/FAp | R.T | 25c | 72 |
By using 2.5% V2O5/FAp, the reaction gave a 97% yield, with the reaction time remained unchanged (Table 1, entry 20). Further, with 5% V2O5/FAp, unanticipatedly, the yield decreased to 93% (Table 1, entry 21). The variation in the activity of 1, 2.5 and 5 wt% V2O5/FAp could be attributed to the available active sites on the catalyst surface, which influence the catalytic efficiency. Generally, the particles are on the surface of the material can act as the Lewis acid centres, and help to activate the organic reactions.44,45 The 2.5% of V2O5/FAp material exhibited superior catalytic activity for the desired product transformation. The efficiency could be due to the even distribution of vanadium oxide nanoparticles on the fluorapatite lattice surface (Fig. 1d). The 1 wt% V2O5/FAp material showed lower performance, possibly due to a lesser number of active sites on the catalyst material surface. Though more vanadium is present in 5% V2O5/FAp, the inferior activity could be due to higher agglomeration of the vanadia particles on the surface of fluorapatite.46 With agglomeration, the vanadium oxide particles form clusters, thus lowering the number of available vanadia, hence decreasing the number of available active sites on the catalyst surface to promote the reaction. The properties of the composite of vanadium and fluorapatite are more tunable (stability and acidity) than fluorapatite or vanadia alone.3,47 The amphoteric nature of fluorapatite and acid sites of V2O5 played a crucial role in enhancing the reaction yield. We also examined the efficacy of 2.5% Bi2O3/FAp and 2.5% ZnO2/FAp as catalysts, which respectively gave 79% and 72% yield, but much lower than with V2O5/FAp. The better performance could be attributed to the stronger acidic nature of vanadia.
The nature of the solvent varies the solubility of the reactants and catalyst efficiency. Efficacy of different polar-aprotic (DMF, CH3CN and THF), non-polar (toluene) and polar-protic (H2O, MeOH and EtOH) solvents were studied (Table 2, entries 2–8). Under solvent-free conditions, the no product formed even after 24 h (Table 2, entry 1). Among all the tested solvents, ethanol proved a superior result. Furthermore, to optimise the amount of 2.5% V2O5/FAp, and the reaction was conducted by using the different amounts of catalyst material (10, 20, 30 and 40 mg) (Table 3, entries 1–4). The 10 mg of 2.5% V2O5/FAp as catalyst yielded 83% in 50 min reaction time, and 20 mg resulted in the 92% yield in 35 min. The reaction with 30 mg of the catalyst gave a 97% yield in 25 min. No further improvement in the harvest (97%) or reaction time noticed with 40 mg. Therefore, 30 mg of 2.5% V2O5/FAp catalyst was taken as the ideal amount and ethanol solvent medium at room temperature as the optimised reaction conditions.
| Entry | Solvent | Time (min) | Yield (%) |
|---|---|---|---|
| a Reaction conditions: 1,3,4-thiadiazole-amine (1a; 1 mmol), 4-methoxy benzaldehyde (2a; 1 mmol), ethyl cyanoacetate (3a; 1 mmol), 2.5% V2O5/FAp (30 mg) and solvent (5 mL) at R.T. — no reaction detected. | |||
| 1 | Solvent-free | 1440 | — |
| 2 | DMF | 360 | 67 |
| 3 | CH3CN | 120 | 49 |
| 4 | Toluene | 360 | 34 |
| 5 | THF | 300 | 47 |
| 6 | MeOH | 35 | 83 |
| 7 | EtOH | 25 | 97 |
| 8 | Water | 90 | 62 |
| Entry | Catalyst (mg) | Time (min) | Yield (%) |
|---|---|---|---|
| a Reaction conditions1,3,4-thiadiazole-amine (1a; 1 mmol), 4-methoxy benzaldehyde (2a; 1 mmol), ethyl cyanoacetate (3a; 1 mmol) and ethanol (5 mL) at R.T. | |||
| 1 | 10 | 50 | 83 |
| 2 | 20 | 35 | 92 |
| 3 | 30 | 25 | 97 |
| 4 | 40 | 25 | 97 |
The optimised protocol was used for the synthesis of a series of seventeen [1,3,4]thiadiazolo[3,2-a]pyrimidine and benzo[4,5]thiazolo[3,2-a]pyrimidine derivatives (4a–q) to establish its broader applicability (Schemes 1 and 2). The reactions conducted using different substituted 1,3,4-thiadiazole-amines (1a–h) or 2-amino-benzothiazole (5) and benzaldehydes (2a–f) with varied active methylene compounds, such as ethyl cyanoacetate, ethyl acetoacetate and acetylacetone (3a–c) (Table 4) afforded excellent yields (90–97%) of respective functionalized [1,3,4]thiadiazolo[3,2-a]pyrimidine and benzo[4,5]thiazolo[3,2-a]pyrimidine scaffolds in 25–30 min. Initially, we investigated the scope of 1,3,4-thiadiazole-amine with various aldehydes and ethyl cyanoacetate. We found that various electron-rich and electron-deficient groups substituted on the phenyl ring of the aldehydes were well-tolerated and provided the corresponding products with excellent yields (Table 4, entries 4a–m). Other active methylene compounds ethyl acetoacetate and acetylacetone, smoothly participated in this reaction and gave impressive yields of 95% and 93%, respectively (Table 4, entries 4n and 4o). The scope of the reaction was also examined with different groups (F, Cl, Br, NO2 and CH3) substituted on the 1,3,4-thiadiazole-amines. In all the cases, the reaction worked well and afforded the desired products in excellent yields (Table 4, entries 4a–d). Additionally, we examined the scope of aminoazole, the 2-amino-benzothiazole also undergone this reaction smoothly to provide the desired products in significant yields (97% and 96%) (Table 4, entries 4p and 4q), at room temperature with ethanol solvent in the presence of 30 mg of the 2.5% V2O5/Fap catalyst. Therefore, the present protocol has general applicability and accommodates a diversity of substitution patterns. All the novel derivatives synthesised were fully characterised by various spectroscopic methods, FT-IR, HRMS, 1H and 13C NMR analysis (ESI†).
| Entry | R | R1 | 3a–c | Time (min) | Yieldb (%) |
|---|---|---|---|---|---|
| a Reaction conditions: 1,3,4-thiadiazole-amines (1a–h) or benzo[d]thiazol-2-amine (5) (1 mmol), benzaldehydes (2a–f) (1 mmol), active methylene compound (3a–c) (1 mmol) and ethanol (5 mL) at R.T.b Isolated yields.c Benzo[d]thiazol-2-amine was used as a substrate. | |||||
| 4a | 3-F | 4-OCH3 | CNCH2CO2Et | 25 | 97 |
| 4b | 3-Br | 4-OCH3 | CNCH2CO2Et | 28 | 96 |
| 4c | 4-CH3 | 4-OCH3 | CNCH2CO2Et | 30 | 93 |
| 4d | 3-NO2 | 4-OCH3 | CNCH2CO2Et | 25 | 90 |
| 4e | 3-F | 4-F | CNCH2CO2Et | 28 | 91 |
| 4f | 3-Br | 4-F | CNCH2CO2Et | 30 | 92 |
| 4g | 3-CH3 | 4-F | CNCH2CO2Et | 25 | 93 |
| 4h | 4-Cl | 3,4-Di-OCH3 | CNCH2CO2Et | 30 | 92 |
| 4i | H | 3,4-Di-OCH3 | CNCH2CO2Et | 28 | 95 |
| 4j | 4-F | 3,4-Di-OCH3 | CNCH2CO2Et | 25 | 91 |
| 4k | 3-F | 3,4-Di-OCH3 | CNCH2CO2Et | 30 | 95 |
| 4l | 3-Br | 3,4-Di-OCH3 | CNCH2CO2Et | 26 | 91 |
| 4m | 4-CH3 | 3,4-Di-OCH3 | CNCH2CO2Et | 27 | 92 |
| 4n | H | 4-Br | CH3COCH2CO2Et | 28 | 95 |
| 4o | H | 4-Br | CH2(COCH3)2 | 30 | 93 |
| 4p | — | 4-Et | CNCH2CO2Et | 30 | 97c |
| 4q | — | 2,4-Di-Cl | CNCH2CO2Et | 28 | 96c |
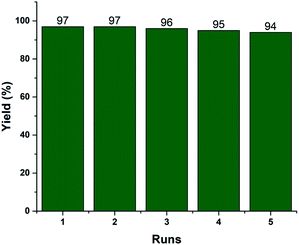
Recyclability is one of the vital efficiency parameters of a heterogeneous catalyst. We investigated the reusability of the recovered 2.5% V2O5/FAp material. The catalyst was recovered by simple filtration after completion of the reaction from the reaction mixture by washed with ethyl acetate and dried in an oven (110 °C) for 2 h. The dried catalyst was reused, and similar activity was observed up to the fifth run under identical reaction conditions (Fig. 6). The FT-IR and EDX spectra and SEM image of the reused catalyst material after the fifth cycle displayed no significant changes in the morphology and elemental composition as compared to the fresh catalyst (Fig. S1, ESI†). The data supports that there is no erosion of the active material from the support, and the catalyst material proved to be highly robust, preserving its crystalline structure even after repeated use.
The advantage of the present protocol can be acknowledged concisely by comparing the results with the other reported methods with different catalyst materials concerning the reaction time, the yield of the product and reaction conditions. Table 5 demonstrates that the reactions in the current study are considerably faster and give superior returns at room temperature.
| S. no. | Catalyst | Reaction conditions | Time (min) | Yield (%) |
|---|---|---|---|---|
| a Synthesised 1,3,4-thiadiazolo[3,2-a]pyrimidines.b Synthesised benzo[4,5]thiazolo[3,2-a]pyrimidines. | ||||
| 1 | Catalyst-freea | Microwave/65 °C/acetic acid | 40 | 85 (ref. 36) |
| 2 | NaOHa | Ultrasonic/80 °C/ethanol | 60 | 89 (ref. 37) |
| 3 | PEG-400a | 80 °C/PEG-400 | 360 | 80 (ref. 38) |
| 4 | P2O5a | 100 °C/HCOOH | 720 | 93 (ref. 25) |
| 5 | p-TSAa | Microwave/100 °C/water | 5 | 96 (ref. 48) |
| 5 | Fe3O4@nano-cellulose/Cu(II)b | 80 °C/solvent-free | 30 | 97 (ref. 26) |
| 6 | Nano-kaolin/Ti4+/Fe3O4b | 100 °C/solvent-free | 90 | 95 (ref. 39) |
| 7 | Nano-cellulose/BF3/Fe3O4b | 100 °C/solvent-free | 45 | 98 (ref. 40) |
| 8 | Nano-Fe3O4@SiO2–TiCl3b | 100 °C/solvent-free | 45 | 90 (ref. 41) |
| 9 | 2.5% V2O5/FAp | RT/ethanol | <30 | 97 (This work) |
The MCRs with V2O5/FAp composite as a catalyst displayed greater efficiency compared with the other catalysts reported because of its synergetic effect of the composite. Optimal distribution of the acidic and basic sites on the surface of V2O5/FAp composite possibly contributed to its enhanced efficiency, which is evident from the high yields, selectivity and speed of the reaction achieved. Therefore, the composite of vanadium oxide on fluorapatite proves to be a superior catalyst with enormous scope and use in MCRs. Furthermore, the literature survey suggests that there were no reports on the use of V2O5/FAp mixed material as a catalyst in any organic synthesis.
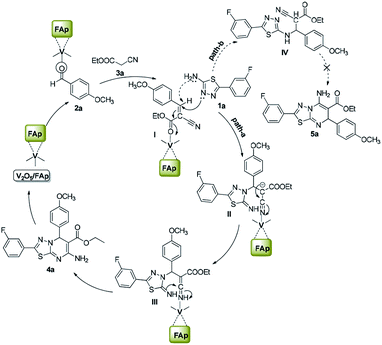
Scheme 3 illustrates the proposed mechanism for the creation of 1,3,4-thiadiazole-pyrimidine via a three-component one-pot condensation reaction. The reaction probably occurs on the surface of V2O5/FAp, as it can provide necessary Lewis acidic and basic sites to catalyse the reaction. The carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) group of aldehydes (2a) adsorbed on the acidic sites of vanadia on the surface of the catalyst, get activated leading to the Knoevenagel condensation with active methylene compound (3a), furnishing a key condensation intermediate (I). There can be two possible mechanistic pathways. Meanwhile, the Brønsted and Lewis basic sites of catalyst (FAp) coordinate with the 1,3,4-thiadiazole-amine (1a) and facilitate the rearrangement of electrons, which promote a Michael type addition with condensed intermediate (I) generating intermediate (II) in the path-A. The transient intermediate (II), finally undergoes an intramolecular cyclisation, followed the ring closer to give the target 1,3,4-thiadiazole-pyrimidine derivative (4a).
O) group of aldehydes (2a) adsorbed on the acidic sites of vanadia on the surface of the catalyst, get activated leading to the Knoevenagel condensation with active methylene compound (3a), furnishing a key condensation intermediate (I). There can be two possible mechanistic pathways. Meanwhile, the Brønsted and Lewis basic sites of catalyst (FAp) coordinate with the 1,3,4-thiadiazole-amine (1a) and facilitate the rearrangement of electrons, which promote a Michael type addition with condensed intermediate (I) generating intermediate (II) in the path-A. The transient intermediate (II), finally undergoes an intramolecular cyclisation, followed the ring closer to give the target 1,3,4-thiadiazole-pyrimidine derivative (4a).
Alternatively, in path-B, 1,3,4-thiadiazole-amine (1a) may also react with the intermediate (I) via 1,3-addition reaction to generate intermediate IV, which constitutes a minor pathway. However, we did not observe product 5a. These reactions preferably go through a nucleophile attack, via a regioselective β-carbon of intermediate (I).48 The role of V2O5/FAp probably would be Lewis acidic characteristic for the activation of the nitrile to transform into an amine. Therefore, amphoteric properties of V2O5/FAp composite with the synergic effect and a high specific surface area containing V2O5/FAp enhance the number of active catalytic sites, which proves it as a highly efficient catalyst in these value-added one-pot reactions.
Conclusions
Using V2O5/FAp as a catalyst, we reported a highly efficient one-pot protocol for the synthesis of seventeen novel [1,3,4]thiadiazolo[3,2-a]pyrimidine and benzo[4,5]thiazolo[3,2-a]pyrimidine analogues. The synergy between the strong acidic properties of vanadia and the amphoteric nature of 2.5% V2O5/FAp composite exhibited superior catalytic activity in ethanol medium at R.T. offering excellent yield (90–97%) of the target products in 25–30 min. TEM, BET, SEM, XRD, EDX and FT-IR analysis were used to characterise the prepared catalyst materials. In comparison with other reported catalysts, the V2O5/FAp promoted reaction offers high yields of products at room temperature in shorter reaction time. Other benefits of the proposed protocol are simple separation and recyclability catalyst, green solvent and no need for column chromatography. Furthermore, this method delivers an excellent atom economy (97%) and carbon efficiency (100%) with remarkable economic and eco-friendly returns.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thanks to the University of KwaZulu-Natal, Durban, South Africa for financial support and research facilities.References
- G. J. Hutchings, J. Mater. Chem., 2009, 19, 1222–1235 RSC.
- A. Fihri, C. Len and R. S. Varma, Coord. Chem. Rev., 2017, 347, 48–76 CrossRef CAS.
- W. Wang, W. Du, Y. Zhang, A. Wang and L. Zhang, React. Kinet., Mech. Catal., 2018, 125, 965–981 CrossRef CAS.
- P. Comodi, Y. Liu, P. F. Zanazzi and M. Montagnoli, Phys. Chem. Miner., 2001, 28, 219–224 CrossRef CAS.
- S. Sebti, R. Tahir, R. Nazih, A. Saber and S. Boulaajaj, Appl. Catal., A, 2002, 228, 155–159 CrossRef CAS.
- H. E. Mason, F. M. McCubbin, A. Smirnov and B. L. Phillips, Am. Mineral., 2009, 94, 507–516 CrossRef CAS.
- M. Zahouily, Y. Abrouki, B. Bahlaouan, A. Rayadh and S. Sebti, Catal. Commun., 2003, 4, 521–524 CrossRef CAS.
- K. Mori, T. Hara, T. Mizugaki, K. Ebitani and K. Kaneda, J. Am. Chem. Soc., 2003, 125, 11460–11461 CrossRef CAS.
- T. Hara, S. Kanai, K. Mori, T. Mizugaki, K. Ebitani, K. Jitsukawa and K. Kaneda, J. Org. Chem., 2006, 71, 7455–7462 CrossRef CAS PubMed.
- K. Pajor, L. Pajchel and J. Kolmas, Materials, 2019, 12, 2683 CrossRef CAS PubMed.
- S. V. H. S. Bhaskaruni, K. K. Gangu, S. Maddila and S. B. Jonnalagadda, Chem. Rec., 2019, 19, 1793–1812 CrossRef CAS.
- S. Maddila, S. N. Maddila, S. B. Jonnalagadda and P. Lavanya, J. Heterocycl. Chem., 2016, 53, 658–664 CrossRef CAS.
- S. V. H. S. Bhaskaruni, S. Maddila, W. E. van Zyl and S. B. Jonnalagadda, Catal. Today, 2018, 309, 276–281 CrossRef CAS.
- V. D. B. C. Dasireddy, S. Singh and H. B. Friedrich, Appl. Catal., A, 2013, 456, 105–117 CrossRef CAS.
- J. Sun, X. Li, Q. Zhao, J. Ke and D. Zhang, J. Phys. Chem. C, 2014, 118, 10113–10121 CrossRef CAS.
- X. Liu, J. Zeng, H. Yang, K. Zhou and D. Pan, RSC Adv., 2018, 8, 4014–4031 RSC.
- K. K. Gangu, S. Maddila, S. N. Maddila and S. B. Jonnalagadda, Molecules, 2016, 21, 1281 CrossRef PubMed.
- S. N. Maddila, S. Maddila, N. Kerru, S. V. H. S. Bhaskaruni and S. B. Jonnalagadda, ChemistrySelect, 2020, 5, 1786–1791 CrossRef CAS.
- N. Kerru, L. Gummidi, S. N. Maddila, S. V. H. S. Bhaskaruni and S. B. Jonnalagadda, Appl. Organomet. Chem., 2020, 34, e5590 CrossRef CAS.
- N. Kerru, L. Gummidi, K. K. Gangu, S. Maddila and S. B. Jonnalagadda, ChemistrySelect, 2020, 5, 4104–4110 CrossRef CAS.
- H. Sheibani and F. Hassani, J. Heterocycl. Chem., 2011, 48, 915–920 CrossRef CAS.
- E. A. El-Rady, J. Heterocycl. Chem., 2014, 51, 869–875 CrossRef CAS.
- N. Seyyedi, F. Shirini, M. Safarpoor, N. Langarudi and S. Jashnani, J. Iran. Chem. Soc., 2017, 14, 1859–1867 CrossRef CAS.
- W. M. Basyouni, S. Y. Abbas, N. M. Abdelazeem, K. A. M. El-Bayouki and M. Y. El-Kady, Synth. Commun., 2019, 49, 3112–3120 CrossRef CAS.
- H. R. Dong, Z. L. Gao, R. S. Li, Y. M. Hu, H. S. Dong and Z. X. Xie, RSC Adv., 2014, 4, 55827–55831 RSC.
- N. Safajoo, B. B. F. Mirjalili and A. Bamoniri, RSC Adv., 2019, 9, 1278–1283 RSC.
- F. A. Ragab, H. I. Heiba, M. G. El-Gazzar, S. M. Abou-Seri, W. A. El-Sabbagh and R. M. El-Hazek, RSC Med. Chem., 2016, 7, 2309–2327 RSC.
- D. Cai, Z. H. Zhang, Y. Chen, X. J. Yan, S. T. Zhang, L. J. Zou, L. H. Meng, F. Li and B. J. Fu, Med. Chem. Res., 2016, 25, 292–302 CrossRef CAS.
- S. F. Mohamed, E. M. Flefel, A. G. Amr and E. Shafy, Eur. J. Med. Chem., 2010, 45, 1494–1501 CrossRef CAS.
- A. D. Borthwick, D. E. Davies, P. F. Ertl, A. M. Exall, T. M. Haley, G. J. Hart, D. L. Jackson, N. R. Parry, A. Patikis, N. Trivedi, G. G. Weingarten and J. M. Woolven, J. Med. Chem., 2003, 46, 4428–4449 CrossRef CAS.
- E. Flefel, M. Salama, M. El-Shahat, M. El-Hashash and A. El-Farargy, Phosphorus, Sulfur Silicon Relat. Elem., 2007, 182, 1739–1756 CrossRef CAS.
- B. Pan, R. Huang, L. Zheng, C. Chen, S. Han, D. Qu, M. Zhu and P. Wei, Eur. J. Med. Chem., 2011, 46, 819–824 CrossRef CAS.
- M. T. Gabr, N. S. El-Gohary, E. R. El-Bendary and M. M. El-Kerdawy, Eur. J. Med. Chem., 2014, 85, 576–592 CrossRef CAS.
- N. S. El-Gohary and M. I. Shaaban, Arch. Pharm. Chem. Life Sci., 2015, 348, 283–297 CrossRef CAS.
- M. E. Azab, S. S. Abdel-Wahab, N. F. Mahmoud and G. A. Elsayed, J. Heterocycl. Chem., 2018, 55, 2349–2359 CrossRef CAS.
- B. Zhao, Y. Xu, Q. G. Deng, Z. Liu, L. Y. Wang and Y. Gao, Tetrahedron Lett., 2014, 55, 4521–4524 CrossRef CAS.
- S. V. Tiwari, J. A. Seijas, M. P. Vazquez-Tato, A. P. Sarkate, D. K. Lokwani and A. P. G. Nikalje, Molecules, 2016, 21, 894 CrossRef PubMed.
- S. Kasaboina, R. Bollu, P. M. Gomedhika, V. Ramineni, L. Nagarapu, N. Dumala, P. Grover and J. B. Nanubolu, Tetrahedron Lett., 2018, 59, 3015–3019 CrossRef CAS.
- B. B. F. Mirjalili and R. Soltani, RSC Adv., 2019, 9, 18720–18727 RSC.
- B. B. F. Mirjalili and F. Aref, Res. Chem. Intermed., 2018, 44, 4519–4531 CrossRef CAS.
- S. A. Fazeli-Attar and B. B. F. Mirjalili, Res. Chem. Intermed., 2018, 44, 6419–6430 CrossRef CAS.
- K. K. Gangu, S. Maddila, S. N. Maddila and S. B. Jonnalagadda, RSC Adv., 2016, 6, 58226–58235 RSC.
- J. Sun, K. Zhu, F. Gao, C. Wang, J. Liu, C. H. F. Peden and Y. Wang, J. Am. Chem. Soc., 2011, 133, 11096–11099 CrossRef CAS PubMed.
- F. M. Moghaddam and H. Saeidian, Mater. Sci. Eng., B, 2007, 139, 265–269 CrossRef CAS.
- S. Farhadi and M. Zaidi, J. Mol. Catal. A: Chem., 2009, 299, 18–25 CrossRef CAS.
- N. Kerru, S. V. H. S. Bhaskaruni, L. Gummidi, S. N. Maddila, S. Rana, P. Singh and S. B. Jonnalagadda, Appl. Organomet. Chem., 2019, 33, e4722 CrossRef.
- S. Sumathi and B. Gopal, React. Kinet., Mech. Catal., 2016, 117, 77–86 CrossRef CAS.
- P. Wadhwa, T. Kaur, N. Singh, U. P. Singh and A. Sharma, Asian J. Org. Chem., 2016, 5, 120–126 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02298e |
| This journal is © The Royal Society of Chemistry 2020 |