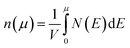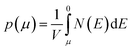Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ternary selenides A2Sb4Se8 (A = K, Rb and Cs) as an n-type thermoelectric material with high power factor and low lattice thermal conductivity: importance of the conformationally flexible Sb–Se–Se–Sb bridges†
Changhoon Lee‡
 a,
Sujee Kim‡b,
Won-Joon Son
a,
Sujee Kim‡b,
Won-Joon Son c,
Ji-Hoon Shim*a and
Myung-Hwan Whangbo*def
c,
Ji-Hoon Shim*a and
Myung-Hwan Whangbo*def
aDepartment of Chemistry, Pohang University of Science and Technology, Pohang, 37673, Korea. E-mail: jhshim@postech.ac.kr
bDivision of Advanced Nuclear Engineering, Pohang University of Science and Technology, Pohang, 37673, Korea
cSamsung Advanced Institute of Technology (SAIT), Samsung Electronics, 130 Samsung-ro, Yeongtong-gu, Suwon 16678, Korea
dDepartment of Chemistry, North Carolina State University, Raleigh, NC 27695-8204, USA. E-mail: whangbo@ncsu.edu
eState Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter (FJIRSM), Chinese Academy of Sciences (CAS), Fuzhou, 350002, China
fState Key Laboratory of Crystal Materials, Shandong University, Jinan, 250100, China
First published on 7th April 2020
Abstract
We investigated the thermoelectric properties of the layered ternary selenides A2Sb4Se8 (A = K, Rb and Cs) and the lattice thermal conductivity of K2Sb4Se8 on the basis of DFT calculations, to find that these selenides are a high-performance n-type thermoelectric material. The Seebeck coefficients and power factors calculated for the electron carriers of A2Sb4Se8 (A = K, Rb and Cs) are greater than those of the well-known thermoelectric materials Bi2Te3 and PbTe. The lattice thermal conductivity κlatt of K2Sb4Se8 is comparable to that of PbTe, well-known for its low lattice thermal conductivity. In terms of both electronic and phonon structures, the structural parts of the A2Sb4Se8 (A = K, Rb and Cs) phases crucial for their thermoelectric properties are the conformationally-flexible Sb–Se–Se–Sb bridges that interlink between their structurally rigid units.
Introduction
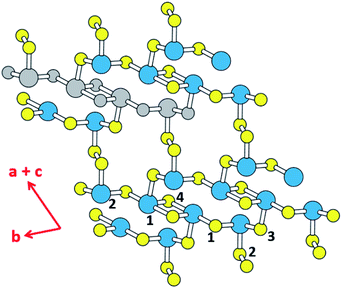
Thermoelectricity enables a direct conversion between thermal and electrical energies, so materials exhibiting thermoelectricity have received much attention for power generation and cooling.1,2 In particular, thermoelectric power generation is potentially important for waste heat collection and efficient energy utilization, although its application is limited due to the low efficiency of thermoelectric devices. The efficiency of a thermoelectric material at a given temperature T depends on the figure of merit, ZT = S2σT/κ, where σ, κ and S are the electrical conductivity, the thermal conductivity and the Seebeck coefficient, respectively.3 The amount of power generated by a thermoelectric material is related to the power factor, S2σ, which is the major element governing the magnitude of ZT.4 Another element raising the ZT is a low thermal conductivity κ, which is composed of the electric thermal conductivity (κel) and the lattice thermal conductivity (κlatt), that is, κ = κel + κlatt. κel is directly proportional to the carrier concentration, n, because κel ∝ σ via the Wiedemann–Franz law, κel = LσT,5 where L is Lorenz number, and because σ ∝ n. In general, a high figure of merit ZT requires a compromise between the carrier concentration and the thermal conductivity.6,7 In terms of the carrier densities affecting the thermoelectric properties of a material, the electronic states lying close to its conduction band minimum (CBM) and valence band maximum (VBM) (i.e., those typically within ∼0.5 eV of the CBM or the VBM) are found to be crucial.8 From the viewpoint of understanding the structure–property relationship governing the thermoelectric properties of a material, it is important to find which structural part of the material is largely responsible for those states close to the CBM and VBM.The binary tellurides Bi2Te3 (ref. 9a) and PbTe9b are well-known efficient thermoelectric materials. It is of interest and importance to search for a potential high-performance thermoelectric material that can be as efficient as Bi2Te3 and PbTe. In the present work we carry out DFT calculations to explore the thermoelectric properties of the layered ternary selenide K2Sb4Se8 (ref. 10) as well as its isostructural phases Rb2Sb4Se8 (ref. 11a) and Cs2Sb4Se8.11b As depicted in Fig. 1, K2Sb4Se8 consists of Sb4Se8 layers separated by K+, and each layer is made up of Sb(1)Se4 seesaw units, Sb(2)Se3 pyramids, and Se2 dimers. There are two types of cross-linked rings in each Sb4Se8 layer; one is the 12-membered ring made up of two Sb(1)2Se6 and two Sb(2)Se3 units, and the other is the 14-membered ring made up of four Sb(2)Se3, two Se(2)2 and two Sb(1)Se4 seesaw units. From the viewpoint of understanding the lattice thermal conductivity of K2Sb4Se8, it is more convenient to consider each Sb4Se8 layer in terms of the “Sb4Se6” chains made up of cross-linked 12-membered rings, which run along the b-direction. For clarity, one Sb4Se6 repeat unit of this chain is colored in grey in Fig. 1. When these Sb4Se6 chains are bridged by the Se(2)2 dimers to form 14-membered rings between the Sb4Se6 chains, we obtain the Sb4Se8 layer.
Since the Sb–Se(2)–Se(2)–Sb bridges have a high conformational flexibility (namely, a soft potential energy curve with respect to a small variation in the dihedral angle ∠Sb–Se(2)–Se(2)–Sb), it is expected that the Sb4Se8 layer is more rigid along the Sb4Se6 chain direction (i.e., along the b-direction for K2Sb4Se8) than along the interchain direction [i.e., along the (a + c)-direction for K2Sb4Se8]. In addition, the K2Sb4Se8 crystal should be least rigid along the interlayer direction because there is no covalent bonding between adjacent Sb4Se8 layers. In this low-dimensional structure of K2Sb4Se8 as determined by X-ray diffraction, the unit cell parameters are large so that the lattice thermal conductivity would be low with short mean path for acoustic phonons.12 Thus, it is worthwhile investigate the possibility that K2Sb4Se8 as well as its two isostructural selenides, Rb2Sb4Se8 and Cs2Sb4Se8, are a high-performance thermoelectric material. In the present work, we examine the Seebeck coefficients and power factors of A2Sb4Se8 (A = K, Rb, Cs) and the lattice thermal conductivity of K2Sb4Se8 on the basis of DFT calculations, to predict that the ternary selenides A2Sb4Se8 (A = K, Rb, Cs) are a high-performance thermoelectric material comparable in efficiency to, or better than, the well-known thermoelectric materials Bi2Te3 and PbTe.
Details of calculations
Our DFT calculations employed the frozen-core projector augmented wave (PAW) method13 encoded in the Vienna ab initio simulation package (VASP),14 with the generalized-gradient approximation (GGA)15 of Perdew, Burke and Ernzerhof (PBE) for the exchange–correlation functional and the plane-wave-cut-off energy of 450 eV. The BoltzTrap code16 was used to calculate the thermoelectric properties of all K2Sb4Se8 systems, which solves the semi-classical Boltzmann equation using the rigid band approach.17,18 This method has been successful in calculating the transport properties and predicting the optimal doping levels for thermoelectric materials.17–20 To ensure the convergence of the calculated thermoelectric properties, the irreducible Brillouin zone was sampled by a set of 2000 k-points. The BoltzTrap code allows one to calculate the electrical conductivity σ, the Seebeck coefficient S, and the power factor S2σ/τ under the assumption that the electron momentum relaxation time τ is independent of energy. We employ the latter assumption, because there is currently no information about the τ of A2Sb4Se8. The power factors calculated under this assumption are greater than the experimental values,21 but this overestimation arises in part from the fact that the band gaps are under estimated by DFT calculations. We note that the thermoelectric properties of numerous systems have been explained by using this assumption.22 We simulate the phonon behavior of K2Sb4Se8 by using the frozen phonon method implemented in Phono3py23 to investigate the lattice thermal conductivity.Electronic structures
The electronic structure calculated for K2Sb4Se8 is presented in terms of the total density of states (DOS) in Fig. 2a, and in terms of band dispersion relations in Fig. 2b along several wave vector directions of the first Brillouin zone (Fig. 2c). K2Sb4Se8 has a band gap of ∼1.0 eV. The projected DOS (PDOS) calculated for the Sb and Se atoms of K2Sb4Se8 are presented in Fig. 3. The PDOS plots for the Se(1), Se(3) and Se(4) are very similar but differ considerably from that for Se(2). In the occupied states of the PDOS, the Se(1), Se(3), and Se(4) each show two band blocks, which represent the bonding states between Sb and Se and the nonbonding states of Se. In contrast, the Se(2) shows roughly three band blocks, which arise from the Se(2)–Se(2) bonding states in addition to the Se–Sb bonding and the Se nonbonding states.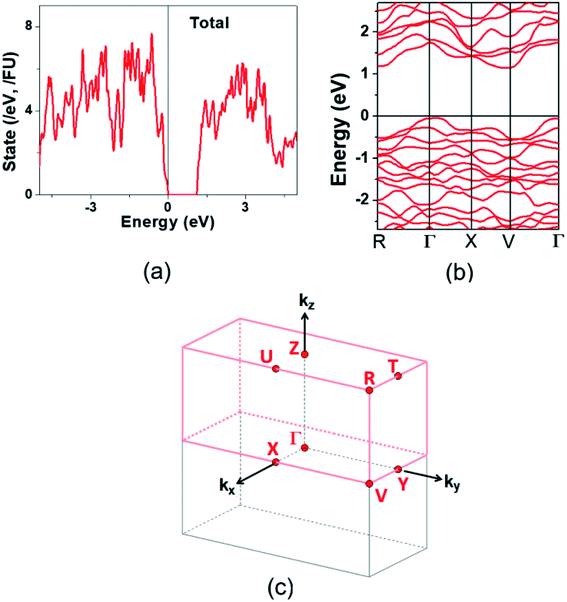 | ||
Fig. 2 Electronic structure calculated for K2Sb4Se8: (a) Total DOS plot. (b) Band dispersion relations. (c) First Brillouin zone associated with a crystal lattice of space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . . | ||
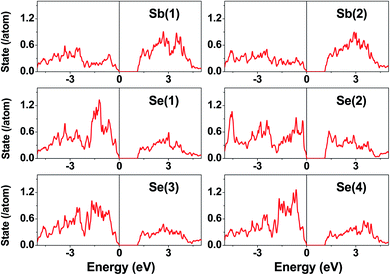 | ||
| Fig. 3 PDOS plots calculated for the Sb(1), Sb(2), Se(1), Se(2), Se(3), and Se(4) atoms of K2Sb4Se8. | ||
This reflects that the formal oxidation state of Se(1), Se(3), and Se(4) atoms is −2 whereas that of the Se(2) is −1. At the CBM and VBM, the Se(2) contributes more strongly than does the Se(1), Se(3) or Se(4) atom, and than does the Sb(1) or Sb(2) atom. Since the thermoelectric properties of a material are mainly influenced by the electronic states lying very close to its CBM and VBM (i.e., typically those within ∼0.5 eV from the VBM and CBM),8 the thermoelectric properties of K2Sb4Se8 should be strongly influenced by the electronic structures associated with the Se(2)2 dimer units. The total DOS plots of Rb2Sb4Se8 and Cs2Sb4Se8, presented in Fig. S1 in the ESI,† are very similar to that of K2Sb4Se8 presented in Fig. 2.
Thermoelectric properties
We calculate the Seebeck coefficients of A2Sb4Se8 (A = K, Rb, Cs) at 300 K as a function of the chemical potential μ. In terms of the rigid band approximation, the electron density can be introduced into A2Sb4Se8 by raising the Fermi level Ef from the CBM, so the chemical potential μ defined as μ = Ef − CBM, with the electron density n(μ) given bywhere V is the unit cell volume, and N(E) the total DOS at energy E. Similarly, the hole density can be introduced into A2Sb4Se8 by lowering the Fermi level Ef from the VBM, so the chemical potential μ is defined as μ = VBM − Ef, with the hole density p(μ) given by
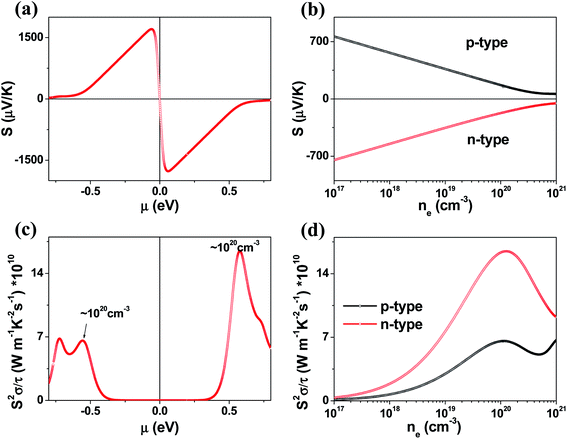
The μ-dependence of the Seebeck coefficients S calculated for K2Sb4Se8 (Fig. 4a) shows two peaks at μ ≈ ±0.061 eV with S ≈ ±1700 μV K−1. These values are considerably greater than those of the well-known thermoelectric materials Bi2Te3 (the calculated S ≈ ±250 μV K−1)16 and PbTe (the calculated S ≈ ±350 μV K−1).20 The dependence of S on the electron density and that on the hole density (Fig. 4b) reveals that the S decreases in magnitude steadily with increasing either the electron or the hole density. Under the assumption that the relaxation times τ is energy-independent, we calculate the power factor S2σ/τ. The calculated S2σ/τ is presented as a function of μ (Fig. 4c) and as a function of the carrier density (Fig. 4d). The power factor for the electron carriers is considerably greater than that for the hole carriers (e.g., the n-type S2σ/τ is larger than the p-type S2σ/τ by a factor of ∼2). This reflects that the electrical conductivity for the electron carriers is much greater than that for the hole carriers. The Seebeck coefficients and the power factors calculated for Rb2Sb4Se8 and Cs2Sb4Se8 are summarized in Fig. S2, S3, and S5 in the ESI,† respectively. They are very similar to those described for K2Sb4Se8 described above.
We also investigated the temperature dependence of the Seebeck coefficients S and the power factor S2σ/τ for A2Sb4Se8 for A = K, Rb and Cs (Fig. S5 in the ESI†). In comparing these values of the three compounds, it is necessary to consider the possible uncertainties in their carrier densities. Thus, we calculate the Seebeck coefficients S and the power factor S2σ/τ for different carrier densities within the range between 1 × 1019 to 5 × 1020 cm−3. Fig. S5† reveals that, for both electron and hole carriers, the Seebeck coefficients S and the power factor S2σ/τ (in the upper and down panels, respectively) gradually increases with temperature. This is due to the increase in thermal energy. The power factor for the electron carriers is considerably greater than that for the hole carriers reflecting that the electrical conductivity for the electron carriers is much greater than that for the hole carriers.
The band dispersion relations calculated for K2Sb4Se8 (Fig. 2b) show that K2Sb4Se8 has an indirect band gap with the CBM at the M point and the VBM at the Γ point. The VBM has a hole valley at Γ, while the CBM has an electron valley and pseudo electron valley at M and R, respectively. The presence of flat band dispersion relations enhances the DOS and hence the carrier density. Since the CBM has more valleys than does the VBM, the carrier concentration should be enhanced near the CBM,24 so that the electrical conductivity is higher for the electrons than for the holes. This explains why the n-type power factor is considerably higher than the p-type power factor despite that the calculated Seebeck coefficients for the hole and electron carriers are similar. The band dispersion relations of Rb2Sb4Se8 and Cs2Sb4Se8, presented in Fig. S4 in the ESI,† are very similar to that of K2Sb4Se8 described above.
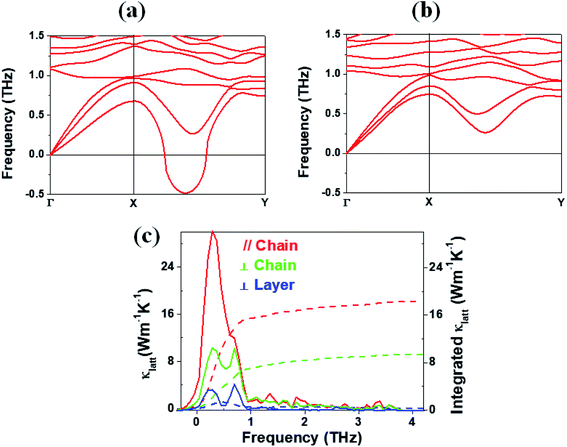
Lattice thermal conductivity
In general, a low lattice thermal conductivity κlatt is found for a low dimensional material with heavy elements and large unit cell parameters. K2Sb4Se8 is such a material. As already discussed (see Fig. 1), each Sb4Se8 layer of K2Sb4Se8 is more rigid along the Sb4Se6 chain direction (i.e., the b-direction for K2Sb4Se8) than along the interchain direction within a Sb4Se8 layer [i.e., the (a + c)-direction for K2Sb4Se8]. Thus, the thermal transport of K2Sb4Se8 should occur largely along the b-direction, and that along the (a + c)-direction should be weak, and so should be that along the (a–c)-direction (i.e., the interlayer direction). We examine the phonon properties and the lattice thermal conductivity of K2Sb4Se8 using the Phono3py23 code combined with DFT calculations. The phonon dispersion relations calculated for K2Sb4Se8 using the experimental structure, shown in Fig. 5a, reveal the presence of an imaginary vibrational frequency. This indicates that the crystal structure as determined by X-ray diffraction measurements has a structural instability, suggesting the possibility that the real crystal structure has structural defects such as the charge density wave, local kinks, and fluctuations that are not detected by X-ray diffraction.25 This imaginary frequency disappears when the phonon dispersion relations are calculated for the structure of K2Sb4Se8 optimized by DFT calculations (Fig. 5b). Nevertheless, there exist low-frequency phonons, indicating the presence of a soft potential, which is associated most likely with the conformationally-flexible Sb–Se–Se–Sb bridges.We calculate the lattice thermal conductivities by solving the linearized phonon Boltzmann equation with the single-mode relaxation time approximation, results of which are presented in Fig. 5c. As expected from the crystal structure of K2Sb4Se8, the thermal conductivities decrease in the order, the Sb4Se6 chain direction > the interchain direction of the Sb4Se8 layer > the interlayer direction. The lattice thermal conductivity κlatt of K2Sb4Se8 is estimated to be 5.32 W mK−1, which is comparable to that of PbTe (with calculated κlatt ≈ 2 W mK−1),26 a well-known material for low lattice conductivity. The low lattice thermal conductivity of K2Sb4Se8 is attributed to a decreased mean free path resulting from the large unit cell parameters, the low dimensional structure, and the structural instability arising from the conformationally flexible Sb–Se(2)–Se(2)–Sb bridges. For each b–Se(2)–Se(2)–Sb bridge, the potential energy curve with respect to a small change in the ∠Sb–Se(2)–Se(2)–Sb dihedral angle should be soft. It is most likely that the soft motions of the crystal lattice involve the slipping of each Sb4Se6 chain against its neighboring Sb4Se6 chains within each Sb4Se8 layer. The Sb–Se(2)–Se(2)–Sb bridges would act as phonon scattering centers rather than phonon transmittance paths due to their conformational flexibility. The lattice thermal conductivities of Rb2Sb4Se8 and Cs2Sb4Se8 should be similar to that of K2Sb4Se8 because Rb2Sb4Se8 and Cs2Sb4Se8 are very similar to K2Sb4Se8 in atomic and electronic structures.
Discussion
Our calculations suggest that the ternary selenides A2Sb4Se8 (A = K, Rb, Cs) have high Seebeck coefficients, high power factors for the electron carriers, and low thermal conductivities. We estimate the ZT value of K2Sb4Se8 at T = 300 K by using the calculated lattice thermal conductivity κlatt of 5.32 W mK−1 and the relaxation time τ ≈ 2 × 10−14 s. In general, the relaxation time τ of conventional semiconductors is of the order of 10−14 s.27 For example, the relaxation times τ ≈ 2 × 10−14 and 3 × 10−14 s reproduce the experimental resistivities of Bi2Te3 and PbTe, respectively.27,28 The ZT values of K2Sb4Se8 estimated by using τ ≈ 2 × 10−14 s are presented in Fig. 6. The μ-dependence of the ZT (Fig. 6a) shows a peak at μ ≈ 0.56 eV with ZT ≈ 0.27, and another peak at μ ≈ −0.54 eV with ZT ≈ 0.14. The dependence of ZT on the carrier densities (Fig. 6b) reveals a peak at the electron carrier density of ∼1020 cm−3, which corresponds to the chemical potential μ ≈ 0.56 eV, and another peak at the hole carrier density of ∼7 × 1019 cm−3, which corresponds to the chemical potential μ ≈ −0.54 eV. The ZT of K2Sb4Se8 is greater for the electron carriers than for the hole carriers by a factor of ∼2. The calculated ZT values of K2Sb4Se8 are comparable to those estimated for Bi2Te3.27c,29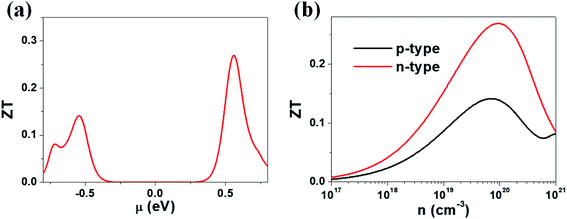 | ||
| Fig. 6 ZT values calculated for K2Sb4Se8 with τ ≈ 2 × 10−14 s: (a) the μ-dependence of the ZT using κlatt = 5.32 W mK−1. (b) The carrier density dependence of the ZT using κlatt = 5.32 W mK−1. | ||
We note that the electronic states crucial for determining the n-type (p-type) Seebeck coefficients are those lying mainly within ∼0.5 eV from the CBM (VBM).8 Such states of A2Sb4Se8 (A = K, Rb, Cs) are represented largely by the Se(2) atoms forming the Sb–Se(2)–Se(2)–Sb bridges between two adjacent Sb4Se6 chains in each Sb4Se8 layer. Furthermore, the lattice thermal conductivity of A2Sb4Se8 (A = K, Rb, Cs) is expected to be lowered by the Sb–Se(2)–Se(2)–Sb bridges because they are conformational flexible as mentioned above. Thus, in terms of both electronic and vibrational factors, the Sb–Se(2)–Se(2)–Sb bridges play a crucial role in enhancing the thermoelectric properties of A2Sb4Se8 (A = K, Rb, Cs).
Concluding remarks
Our work suggests that the layered ternary selenides A2Sb4Se8 (A = K, Rb, Cs) are a promising thermoelectric material comparable in efficiency to, or better than, the well-known thermoelectric materials such as Bi2Te3 and PbTe. The power factor and ZT values estimated for the electron carriers are considerably greater than those for the hole carriers by a factor of ∼2. Thus, the ternary selenides A2Sb4Se8 (A = K, Rb, Cs) are predicted to be a high-performance n-type thermoelectric material. The electronic and phonon structures associated with the Se(2)2 dimer units of the conformationally-flexible Sb–Se(2)–Se(2)–Sb bridges are crucial in determining the thermoelectric properties of A2Sb4Se8 (A = K, Rb, Cs).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2017R1D1A1B03036257), Supercomputing Center/Korea Institute of Science and Technology Information with supercomputing resources including technical support (KSC-2018-CHA-0019).Notes and references
- G. S. Nolas, J. Sharp and H. Goldsmid, Thermoelectrics: Basic Principles and New Materials Developments, Springer, New York, 2001 Search PubMed.
- D. M. Rowe, Thermoelectrics Handbook: Macro to Nano, CRC Press, Boca Raton, 2006 Search PubMed.
- A. J. Minnich, M. S. Dresselhaus, G. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466–479 RSC.
- L. L. Baranowski, G. J. Snyder and E. S. Toberer, J. Appl. Phys., 2013, 115, 126102 CrossRef.
- R. Franz and G. Wiedemann, Ann. Phys., 1853, 165, 497–531 CrossRef.
- J. Q. He, M. G. Kanatzidis and V. P. Dravid, Mater. Today, 2013, 16, 166–176 CrossRef CAS.
- L. D. Zhao, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2014, 7, 251–268 RSC.
- (a) C. Lee, J. H. Shim and M.-H. Whangbo, Inorg. Chem., 2018, 57, 11895–11900 CrossRef CAS PubMed; (b) C. Lee, J. N. Kim, J.-Y. Tak, H. K. Cho, J. H. Shim, Y. S. Lim and M.-H. Whangbo, AIP Adv., 2018, 8, 115213 CrossRef; (c) C. Lee, T.-H. An, E. E. Gordon, H. S. Ji, C. Park, J. H. Shim, Y. S. Lim and M.-H. Whangbo, Chem. Mater., 2017, 29, 2348–2354 CrossRef CAS.
- (a) S. Nakajima, J. Phys. Chem. Solids, 1963, 24, 479–485 CrossRef CAS; (b) N. Bouad, L. Chapon, R.-M. Marin-Ayral, F. Bouree-Vigneron and J. C. Tedenac, J. Solid State Chem., 2003, 173, 189–195 CrossRef CAS.
- W. S. Sheldrick and M. Wachhold, Z. Kristallogr. NCS, 1998, 213, 25 CAS.
- (a) W. S. Sheldrick and M. Wachhold, Z. Kristallogr. NCS, 1998, 213, 24 CAS; (b) W. S. Sheldrick and J. Kaub, Z. Anorg. Allg. Chem., 1986, 536, 114–118 CrossRef CAS.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8639 CrossRef CAS PubMed.
- (a) P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed; (b) G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. K. H. Madsen and D. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146 CrossRef CAS PubMed.
- T. J. Scheidemante, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210 CrossRef.
- (a) L. Chaput, P. Pécheur, J. Tobola and H. Scherrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085126 CrossRef; (b) X. Gao, K. Uehara, D. D. Klug, S. Patchkovskii, J. S. Tse and T. M. Tritt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125202 CrossRef.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195217 CrossRef.
- W. Chen, J.-H. Pöhls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, G. M. Gibbs, H. Zhu, M. Asta, G. J. Snyder, B. Meredig, M. A. White, K. Perssonae and A. Jain, J. Mater. Chem. C, 2016, 4, 4414–4426 RSC.
- (a) C. Lee, J. Hong, M.-H. Whangbo and J. H. Shim, Chem. Mater., 2013, 25, 3745–3752 CrossRef CAS; (b) C. Lee, J. Hong, W. R. Lee, D. Y. Kim and J. H. Shim, J. Solid State Chem., 2014, 211, 113–119 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- (a) J. Hong, C. Lee, J.-S. Park and J. H. Shim, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035445 CrossRef; (b) J. Xin, Y. Tang, Y. Liu, X. Zhao, H. Pan and T. Zhu, npj Quantum Mater., 2018, 3, 9 CrossRef; (c) Y. Tang, Z. M. Gibbs, L. A. Agapito, G. Li, H.-S. Kim, M. B. Nardelli, S. Curtarolo and G. J. Snyder, Nat. Mater., 2015, 14, 1223–1228 CrossRef CAS PubMed; (d) R. Hanus, X. Guo, Y. Tang, G. Li, G. J. Snyder and W. G. Zeier, Chem. Mater., 2017, 29, 1156–1164 CrossRef CAS.
- (a) H. B. Nielsen and M. Ninomiya, Prog. Theor. Phys., 2005, 113, 603–624 CrossRef; (b) H. Kim, C.-J. Kang, K. Kim, J. H. Shim and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165130 CrossRef.
- (a) Z. Tian, J. Garg, K. Esfarjani, T. Shiga, J. Shiomi and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184303 CrossRef; (b) J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205203 CrossRef; (c) T. Shiga, J. Shiomi, J. Ma, O. Delaire, T. Radzynski, A. Lusakowski, K. Esfarjani and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155203 CrossRef.
- (a) H.-W. Jeon, H.-P. Ha, D.-B. Hyun and J.-D. Shim, J. Phys. Chem. Solids, 1991, 52, 579–585 CrossRef CAS; (b) T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210 CrossRef; (c) B.-L. Huang and M. Kaviany, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125209 CrossRef.
- S. Ahmad and S. D. Mahanti, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165203 CrossRef.
- (a) I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904 CrossRef; (b) J. N. Kim, M. Kaviany and J.-H. Shim, Phys. Rev. B, 2016, 93, 075119 CrossRef; (c) M.-Y. Han, Y. Jin, D.-H. Lee and S.-J. Kim, Mater, 2017, 10, 1235 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1 (the PDOS plots calculated for Rb2Sb4Se8 and Cs2Sb4Se8), Fig. S2 (the thermoelectric properties of Rb2Sb4Se8 calculated as a function of the chemical potential and the carrier density), Fig. S3 (the thermoelectric properties of Cs2Sb4Se8 calculated as a function of the chemical potential and the carrier density), Fig. S4 (the band dispersion relations calculated for Rb2Sb4Se8 and Cs2Sb4Se8), and Fig. S5 (the temperature dependence of the Seebeck coefficients S (upper panels) and the power factor S2σ/τ (down panels) plots calculated for K2Sb4Se8, Rb2Sb4Se8, and Cs2Sb4Se8). See DOI: 10.1039/d0ra01751e |
| ‡ First two authors contributed equally to this work and should be considered co-first authors. |
| This journal is © The Royal Society of Chemistry 2020 |