DOI:
10.1039/D0RA01735C
(Paper)
RSC Adv., 2020,
10, 22242-22249
Enhanced capacitive performance by improving the graphitized structure in carbon aerogel microspheres†
Received
23rd February 2020
, Accepted 4th June 2020
First published on 10th June 2020
Abstract
Herein, good electrical conductivity and high specific surface area carbon aerogel (CA) microspheres were synthesized by a facile and economical route using a high temperature carbonization and CO2 activation method. The electroconductive graphitized structure of the CA microspheres could be easily improved by increasing the carbonization temperature. Then the CA microspheres were activated with CO2 to increase the specific surface area of the electrode material for electric double layer capacitors (EDLC). The sample carbonized at 1500 °C for 0.5 h and CO2 activated at 950 °C for 8 h showed an acceptable specific surface area and excellent cycle performance and rate capability for EDLC: 98% of the initial value of the capacitance was retained after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, a specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 at 2 A g−1.
000 cycles, a specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 at 2 A g−1.
1. Introduction
With the ever-increasing demand for high performance energy storage devices, supercapacitors have been widely studied for their extremely high power density, long cycle life, and reasonable energy density.1–3 The electric double layer capacitors (EDLC) are some of the most important supercapacitors that store energy through charge separation at the electrochemical interface between a carbon-based electrode and a liquid electrolyte. Carbon aerogels (CAs) are promising electrode materials for EDLC due to their excellent properties of interconnected three-dimensional networks, large surface area, and high electrical conductivity.4,5 However, the complexity and high cost of preparation of the CA monolith limit their popularization.5 To overcome this limitation, CA microspheres have drawn more attention because of their more economic preparation process6 compared to CA monoliths.
For EDLC application, the specific surface area of the carbon electrode material is an important factor in the electrical double layer (EDL) formation. However, the low cost CA microspheres generally suffer from a low specific surface area. In order to attain high specific surface area CAs, activation methods involving chemical activation and physical activation are applied. The chemical activation process is to impregnate the raw CAs with certain chemicals (typically strong base7,8) prior to carbonization at lower temperatures (450–900 °C). And during the physical activation method, the as-prepared CAs is thermal treatment in the presence of an oxidizing agent such as carbon dioxide.9–13 The main advantage of physical activation over chemical activation is that it avoids the incorporation of impurities cause by the activating agent, which is the most commonly used activation method for CAs.
Apart from specific surface area, good electrical conductivity and effective pore size distribution of carbon electrode also affect the performance of supercapacitors. Specifically, the good electrical conductivity of electrode materials will greatly affect the rate capability and cycle life of supercapacitors.14 In order to improve the electrical conductivity of carbon-based materials, an efficient way of heteroatom doping (such as nitrogen15–17 and phosphorusc18) is commonly applied. However, the heteroatom doping method always complicated the preparation procedure of CAs. Interestingly, a simple way to improve the electrical conductivity of CAs is increasing the graphitized structure in CAs,19 which could easily achieving via increasing the carbonization temperature. After carbonization at high temperature and further CO2 activation, the CAs with high specific surface area and good electrical conductivity can be expected obtained.
In this work, to address both good electrical conductivity and high specific surface area, a facile and economical synthesis route was developed to construct CA microspheres by the combination of two previous breakthroughs. On one hand, the electroconductive graphitized group is introduced by carbonizing CA microspheres at high temperature, and the CA microspheres with various graphitized degree are prepared at different carbonization temperatures. On the other hand, we adopt the CO2 assisted activation method to add more quantities of micropores, and these micropores are able to provide a large surface area to form EDL and expected to exhibit high specific capacitance in EDLC. Using such graphitized CA microspheres as electrode material, supercapacitors are expected to exhibit excellent cycling stability and outstanding rate performance.
2. Experimental section
2.1 Preparation of the materials
CA microspheres were synthesized by inverse emulsion polycondensation of resorcinol (R) and formaldehyde (F), using deionized water and Na2CO3 as solvent and catalyst, respectively. Firstly, the RF solution was prepared by the following approach: R was dissolved in formaldehyde (molar ratios R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F = 1
F = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and stirred for a few minutes to get clear solution; then Na2CO3 solution (0.02 mol L−1) was mixed in the solution by molar ratios of 500
2) and stirred for a few minutes to get clear solution; then Na2CO3 solution (0.02 mol L−1) was mixed in the solution by molar ratios of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (R
1 (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na2CO3), followed adding deionized water to a given volume; this solution was then stirred for about 20 minutes until light yellow RF solution was obtained. Secondly, as shown in Fig. 1, oil phase composed of 600 mL industrial white oil and 6 g surfactant span-80 were added in a three-necked flask which was soaked in a 60 °C oil bath; then the above RF solution was added drop wise to the oil phase and stirred with magnetic stirrer at 1000 rpm. Under the high-speed stirring, RF aqueous solution is dispersed in the oil phase in the shape of microspheres. The solution was stirred at 1000 rpm for 0.5 hours and continued stirred at a decelerated speed of 100 rpm for 12 hours until the dispersive RF microspheres were completely gelled. Thirdly, the gelled RF microspheres were separated from the oil phase by the filtration method and washed several times with dichloromethane, and then dried at ambient condition. Dried RF microspheres were carbonized in a tubular furnace with an argon flow rate of 100 mL min−1 at temperature of 1050 °C for 4 hours to obtain CAs. The graphitization treatment of CA microspheres was carried out in tubular furnace with argon atmosphere at temperature of 1500, 2000, 2500 and 2800 °C for 0.5 hours, respectively, and these graphitized CA microspheres (GCAs) are denoted as G1500, G2000, G2500, G2800, respectively. In the final CO2 activation step, the CAs and GCAs were heated from room temperature to desired temperatures with a heating rate of 10 °C min−1 for a certain time under a steady CO2 flow of 150 mL min−1 (Table 1).
Na2CO3), followed adding deionized water to a given volume; this solution was then stirred for about 20 minutes until light yellow RF solution was obtained. Secondly, as shown in Fig. 1, oil phase composed of 600 mL industrial white oil and 6 g surfactant span-80 were added in a three-necked flask which was soaked in a 60 °C oil bath; then the above RF solution was added drop wise to the oil phase and stirred with magnetic stirrer at 1000 rpm. Under the high-speed stirring, RF aqueous solution is dispersed in the oil phase in the shape of microspheres. The solution was stirred at 1000 rpm for 0.5 hours and continued stirred at a decelerated speed of 100 rpm for 12 hours until the dispersive RF microspheres were completely gelled. Thirdly, the gelled RF microspheres were separated from the oil phase by the filtration method and washed several times with dichloromethane, and then dried at ambient condition. Dried RF microspheres were carbonized in a tubular furnace with an argon flow rate of 100 mL min−1 at temperature of 1050 °C for 4 hours to obtain CAs. The graphitization treatment of CA microspheres was carried out in tubular furnace with argon atmosphere at temperature of 1500, 2000, 2500 and 2800 °C for 0.5 hours, respectively, and these graphitized CA microspheres (GCAs) are denoted as G1500, G2000, G2500, G2800, respectively. In the final CO2 activation step, the CAs and GCAs were heated from room temperature to desired temperatures with a heating rate of 10 °C min−1 for a certain time under a steady CO2 flow of 150 mL min−1 (Table 1).
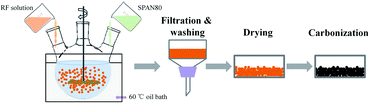 |
| | Fig. 1 Diagram of the preparation process of CA microspheres. | |
Table 1 The temperature and duration of CO2 activation
| Sample |
CAs |
G1500 |
G2000 |
G2500 |
G2800 |
| Temperature (°C) |
950 |
950 |
950 |
950 |
950 |
| Time (hours) |
8 |
8 |
8 |
8 |
8 |
| Designation |
CAs-8 |
G1500-8 |
G2000-8 |
G2500-8 |
G2800-8 |
2.2 Characterization of the samples
The microstructure of the CAs and GCAs were observed using scanning electron microscopy (SEM) and high-resolution transmission electron microscopy (HRTEM). The X-ray powder diffraction (XRD) and Raman spectroscopy (514.5 nm, Spectra Physics) were used to study the crystallographical information and phase state. The chemical composition of the CAs was analysed by X-ray photoelectron spectroscopy (XPS). N2 adsorption and desorption isotherms were conducted with the AUTOSORB-IQ surface area analyzer at 77 K. The specific surface areas were determined on the Brunauer–Emmett–Teller (BET) method.
2.3 Theoretical calculation
Based on the density functional theory implemented in the Vienna Ab initio Simulation Package (VASP), calculations were carried out with employment of the Perdew, Burke, and Ernzerhof exchange-correlation functional within the generalized gradient approximation and the projector augmented-wave pseudopotential.20 A 20.0 × 20.0 × 10.0 Å3 super cell was used in this case. All geometry structures were fully relaxed until the forces on each atom are less than 0.01 eV Å−1. Geometry optimizations and static calculations were performed with 1 × 1 × 1 k-point sampling.
2.4 Electrochemical measurements
Electrochemical experiments were carried out in a symmetrical sandwich-type supercapacitor. The working electrodes were fabricated as follow: the active materials (80 wt%), acetylene black (10 wt%), and polytetrafluoroethylene (10 wt%) was mixed in ethanol and ultrasonicated for 30 min; after dried at 60 °C for 24 h in vacuum, the mixture was pressed onto nickel foam under 20 MPa in round shape with a diameter of 16 mm and mass loading about 8 mg. A symmetrical supercapacitor was assembled in ambient condition after the working electrode was soaked in 6 M (mol L−1) KOH solution and vacuuming for 30 min. A typical cell comprised a pair of electrodes with equal mass of active materials as both positive and negative electrode, a piece of sulfonated polypropylene membrane as separator, and 6 M KOH solution as electrolyte. Cyclic voltammetry (CV, 0–1 V) and electrochemical impedance spectroscopy (EIS, 0.01–100k Hz) measurements were performed by a CHI 760 electrochemical workstation. Rate capability and cycling performance were estimated by galvanostatic charge/discharge (GCD) tests by LAND cell test instrument, and the charge/discharge current were derived from the total mass on both two electrodes.
3. Results and discussion
3.1 Morphologies information
The morphology of the CAs and GCAs were investigated by SEM, as shown in Fig. 2 and S1.† It can be observed that the CAs is spherical in shape with diameters of 1–15 μm (Fig. 2a), possessing a smooth surface without cracks even at high magnification. Additionally, the CAs contains only carbon and oxygen without impurities as demonstrated by the XPS analysis in Fig. S2.† Even after graphitization treatment at different temperature, the morphology of GCAs is observed almost the same as that of CAs. The detailed structures of CAs and GCAs were further disclosed by HRTEM characteristics (Fig. 2 and S1†). Numerous small irregular lattice fringes can be observed for CAs (Fig. 2c), indicating the existence of graphite crystallite or disorder graphite layers in CAs. Furthermore, with the increase of graphitization temperature, the lattice fringes became more clearly and regularly.
 |
| | Fig. 2 SEM images (a and b) and HRTEM images (c and d) of CAs and G2800, respectively. | |
3.2 XRD analysis
XRD analysis is used to further investigate the crystalline structure of the samples. Generally, by using the Bragg and Scherrer equations,21–24 the main characteristic peaks (002 and 100) can determine the carbon crystallite lattice parameters of interlayer spacing (d002), crystallite height (Lc) and crystallite width (La). Where d002 and Lc are measured from the (002) peak with the scattering angle (2θ) at about 26° and the La is measured from the (100) peak with the scattering angle (2θ) at about 44°. However, the main characteristic peaks (002) of CAs and GCAs are asymmetric, as shown in Fig. 3a. It is due to the different carbon crystalline structures of CAs and GCAs. In this study, the carbon crystalline structure of CAs and GCAs are classified into a relatively good crystalline structure (G) and a pool crystalline structure (P) according to the classification by Gao et al.25 The separated Gauss curves for CAs and GCAs are presented in Fig. 3b. The crystallite lattice parameters of separated components also can be calculated from the Bragg and Scherrer equations:| |
d002,G = λ/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,G θ002,G
| (1) |
| |
d002,P = λ/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,P θ002,P
| (2) |
| |
Lc,G = 0.94λ/B002,G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,G θ002,G
| (3) |
| |
Lc,P = 0.94λ/B002,P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,P θ002,P
| (4) |
where λ is the X-ray wavelength (0.15406 nm for Cu radiation), d002,G and d002,C are the interlayer spacing of the separated G component and the separated P component, respectively, the Lc,G and Lc,P, B002,G and B002,P, θ002,G and θ002,P are the corresponding crystallite height, half maximum (FWHM, radians), and scattering angles (radians), respectively. Then the average crystallite lattice parameters are calculated as following equations:| | |
d002,a = XGd002,G + XCd002,G
| (5) |
| | |
Lc,a = XGLc,G + XPLc,P
| (6) |
where d002,a and Lc,a are the average interlayer spacing and the average crystallite height, respectively, XG and XP are the fractions of the G component and the P component, respectively, and the SG and SP are the corresponding areas.
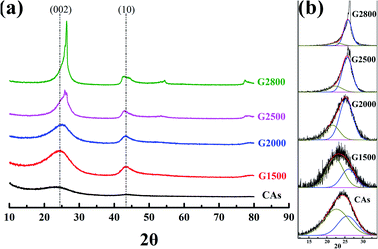 |
| | Fig. 3 XRD patterns (a) and curve-fitting of (002) peaks (b) for CAs and GCAs. | |
The calculated values of all parameters for CAs and GCAs are presented in Table 2. As shown in Fig. 3a, the (002) peak becomes sharper with the increase of graphitized temperature, which indicates that the crystallinity of GCAs is apparently improved. In addition, the position of (002) peak shifts to the high scattering angles while the (10) peak shifts to the low scattering angles along with the rise of graphitized treatment temperature, which implicates the more compact interlayer spacing and the increase of crystallite width of GCAs crystal structure.26 These results are agreement with the calculated crystallite lattice parameters shown in Table 2, while the graphitized treatment temperature increases to 2800 °C, the d002,a decreases to 0.353 nm, the Lc,a increases to 2.950 nm and the La increases to 7.599 nm, respectively. These parameters clearly display the crystal growth process in CAs and GCAs.
Table 2 The XRD structure parameters of CAs and GCAs
| Sample |
d002,G (nm) |
d002,P (nm) |
Lc,G (nm) |
Lc,P (nm) |
XG |
XP |
d002,aa (nm) |
Lc,ab (nm) |
Lac (nm) |
| d002,a: average interlayer spacing. Lc,a: average crystallite height. La: crystallite width. |
| CAs |
0.400 |
0.342 |
1.524 |
1.821 |
0.35 |
0.65 |
0.380 |
1.543 |
4.272 |
| G1500 |
0.352 |
0.417 |
1.597 |
1.450 |
0.38 |
0.62 |
0.376 |
1.627 |
4.389 |
| G2000 |
0.351 |
0.411 |
1.976 |
1.903 |
0.73 |
0.27 |
0.367 |
1.956 |
5.270 |
| G2500 |
0.347 |
0.398 |
2.585 |
1.889 |
0.81 |
0.19 |
0.357 |
2.453 |
6.571 |
| G2800 |
0.345 |
0.407 |
3.062 |
2.200 |
0.87 |
0.13 |
0.353 |
2.950 |
7.599 |
3.3 Raman spectroscope and spectral analysis
To further examine the structure differences of the various graphitized CAs, Raman spectroscopy were measured and shown in Fig. 4. The Raman spectra show two main bands located at about 1350 cm−1 and 1600 cm−1. Each spectrum can be resolved into 4 Lorentzian bands (around 1200, 1350, 1580, and 1620 cm−1) and 1 Gaussian band (around 1530 cm−1).27,28 The G band around 1580 cm−1 corresponds to an ideal graphitic lattice aromatic vibration mode with E2g symmetry. The appearance of band around 1350 cm−1 is commonly called D1 band, which is assigned to a graphitic lattice vibration mode with A1g symmetry.29,30 The D1 band has been suggested to arise from graphene layer carbon atoms in immediate vicinity of a lattice disturbance like the edge of a graphene layer.27,30–32 The band around 1620 cm−1 is called D2 band, corresponding to a graphitic lattice mode with E2g symmetry and involving graphene layers at the surface of a graphitic crystal.27,33 The relative intensities of both the D1 and D2 bands could be used to characterize the degree of disorder in the graphitic structure.34,35 The band at around 1530 cm−1 has been assumed Gaussian line shape and designated D3 band.27,36 This D3 band is originated from the amorphous carbon fraction of carbonaceous materials.28,36 The peak at D1 band exhibits a shoulder at around 1200 cm−1, which has been denominated as D4 band. Dippel et al. tentatively attribute D4 band to sp2–sp3 mixed sites at the periphery of crystallites or to C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations of polyene-like structures.37,38
C stretching vibrations of polyene-like structures.37,38
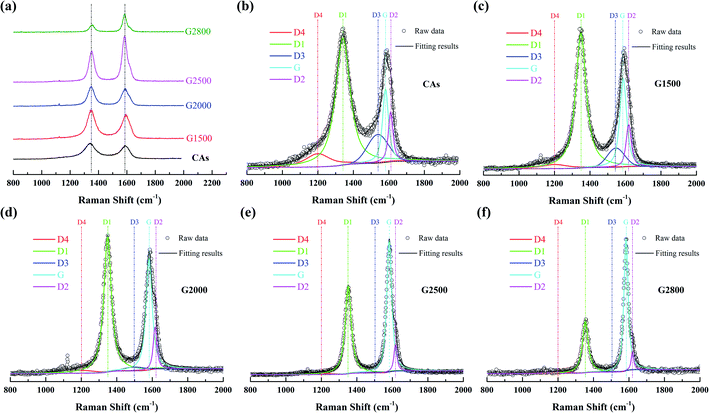 |
| | Fig. 4 First-order Raman spectrum (a) and the relative fitting curve of CAs (b), G1500 (c), G2000 (d), G2500 (e), and G2800 (f). | |
Transformations of Raman spectra as a function of the graphitized-treatment temperature are displayed in Fig. 4. The band area ratios of the defect bands to the G band (appropriately denoted as ID1/IG, ID2/IG, ID3/IG and ID4/IG) and the additional ratio of the G band to the integrated area under the spectrum (IG/IAll) are presented in Table 3 for comparison. During graphitization-treatment, the relative intensities (ratios of band areas) and FWHM of band were significantly changed while their positions almost invariable. Obviously, the intensity (band area) of G band and D1 band varies in the opposite direction, while the two bands become narrower. Such FWHM decreases of D1 band and G band are related to the degree of ordered graphitic structure. Miroslawa Pawlyta et al. found that the Raman-based classification matches well with HRTEM observations: with growing larger of the layers directly imaged by HRTEM image, the G-band becomes sharper.39 Our results are in good agreement with this relationship. In addition, intensities of the D3 band and the D4 band are gradually decrease with the increase of graphitized treatment temperature, and these bands can be neglected for samples heated above 2000 °C. Specifically, the D2 band remains distinct from the G band although its area ratio to the G band is also gradually decreased. As shown in the Table 3, that ID1/IG, ID2/IG, ID3/IG and ID4/IG decrease significantly, while IG/IAll increases significantly with the increase of the graphitic treatment temperature. The decrease of these band ratios means that various crystal defects in CAs are gradually eliminated. In fact, the descend of ID1/IG means that the average plane size of graphitic crystallites increases.40 And the decrease of ID2/IG indicates the decrease of the surface to volume ratio of graphitic crystals, namely the growth of graphitic crystals.33 While the decrease of ID3/IG and ID4/IG means the amorphous carbon transforms into crystalline form. Consequently, more ordered graphitic structure is formed with the increased graphitic treatment temperatures, which lead to the increase of IG/IAll.28
Table 3 The curve-fitted Raman spectra parameters of CAs and GCAs
| Sample |
ID1/IG |
ID2/IG |
ID3/IG |
ID4/IG |
IG/IAll |
| CAs |
4.250 |
0.536 |
0.972 |
0.756 |
0.133 |
| G1500 |
2.539 |
0.356 |
0.403 |
0.198 |
0.222 |
| G2000 |
1.550 |
0.223 |
0.080 |
0.112 |
0.337 |
| G2500 |
0.859 |
0.124 |
— |
— |
0.504 |
| G2800 |
0.558 |
0.080 |
— |
— |
0.611 |
3.4 Porous properties
From the above analysis, the CA microspheres with various graphitized structure have been successfully prepared which are then treated with CO2 activation to improve their surface area. The nitrogen adsorption/desorption isotherms are used to characterize the pore properties of the CAs, GCAs (shown in Fig. 5a) and activated samples (shown in Fig. 5b). And the corresponding pore parameters of BET surface area (SBET) and total pore volume (Vt) are displayed in Table S1.†
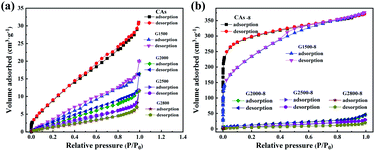 |
| | Fig. 5 Nitrogen adsorption/desorption isotherms of the CAs, GCAs (a) and according activated samples (b). | |
It can be seen from Table S1† that the BET specific surface area of CAs is 42.9 m2 g−1 and decreases with the increase of graphitization temperature. While adopting the CO2 activation, the corresponding BET specific surface area of both CAs and G1500 are greatly increased (Table S1†), but the G2000-8, G2500-8 and G2800-8 are slightly increased. This is attributed to the different reactivity with CO2 of carbon atoms at edge of graphite layer and those interior atoms. Previous studies suggest that the edge structures of carbon basal plane are identified as active sites for the gasification reaction.41–43 With the increased carbonization temperature, the increased graphitized group results in the decrease of carbon atoms at edge of graphite layer act as active sites. Furthermore, our theoretical calculation results also show that the energy required etching a carbon atom from the inside of the graphite layer (Fig. S3†) is about 7.25 eV higher than that required from the edge. In addition, the CAs-8 and G1500-8 exhibit the most increased BET specific surface area (SBET) of 1107 and 715 m2 g−1 (Table S1†), and the corresponding pore parameters and pore size distribution are summarized in Table 4 and Fig. S4,† respectively. As shown in Table 4 and Fig. S4,† CAs-8 exhibit a large micropores surface area (Smic) of 953 m2 g−1 (86% of SBET), implying that the CO2 activation is directly accountable for micropores formation (pore size < 2 nm).44 In contrast, the G1500-8 shows a smaller Smic proportion (64% of SBET) and more mesopores (2 < pore size < 50 nm) distribution than CAs-8. The results suggest that more mesopores are tends to produced by CO2 activation in G1500.
Table 4 Corresponding pore parameters of the CAs-8 and G1500-8
| Sample |
SBETa/(m2 g−1) |
Smicb/(m2 g−1) |
Sextc/(m2 g−1) |
Vtd/(cm3 g−1) |
Vmice/(cm3 g−1) |
Apf (nm) |
| SBET: BET surface area. Smic: micropores surface area. Sext: external surface area including mesopores and macropores. Vt: total pore volume. Vmic: micropore volume. Ap: average pore diameter. |
| CAs |
42.9 |
0 |
42.9 |
0.047 |
0 |
4.5 |
| CAs-8 |
1107 |
953 |
154 |
0.575 |
0.406 |
2.1 |
| G1500 |
22.3 |
0 |
22.3 |
0.039 |
0 |
5.6 |
| G1500-8 |
715 |
464 |
251 |
0.484 |
0.237 |
2.7 |
3.5 Electrochemical performance
The GCD curves of CAs, CAs-8, G1500, and G1500-8 electrodes are shown in Fig. 6a, and the single-electrode specific capacitance Cs is evaluated base on following equation,45| |
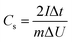 | (9) |
where I is the conducted current, m is the mass of the active materials on one electrode, Δt and ΔU is the discharge-time and the potential difference during the discharge process after the internal resistance (IR) drop. The IR drop is generally associated with the equivalent series resistance (ESR), and the ESR is the sum of resistances including the electronic resistance of electrode, the ions diffusing resistance in the nanopores of electrode materials, and the interfacial resistance between the electrode and the current collector.46,47 The specific capacitances of CAs and G1500 calculated from the discharge curve are 12 and 5.6 F g−1 at current density of 0.2 A g−1, respectively. After CO2 activation, the specific capacitances of CAs-8 and G1500-8 are significantly increased to 115 and 121 F g−1, respectively. Remarkably, the CAs-8 with larger specific surface area (1107 m2 g−1) than G1500-8 (715 m2 g−1) (Table 4) exhibits the lower specific capacitance. This capacitance difference could be attributed to the CAs-8 possess higher micropores content than G1500-8, this high micropores levels cause the harder transportation of electrolyte ions to whole inner surface. In addition, the GCD curves of G2000-8, G2500-8 and G2800-8 at 0.05 A g−1 are shown in Fig. S5.† From the above analysis, it is difficult to improve the specific surface area of G2000, G2500 and G2800 by CO2 activation, resulting in the extremely low specific surface area (Table S1†). And the specific capacitance of G2000-8, G2500-8 and G2800-8 are calculated to be only 12.6, 7.2 and 3 F g−1 even at a low current density of 0.05 A g−1, respectively. Therefore, the electrochemical properties of CAs-8 and G1500-8 are mainly compared in following section.
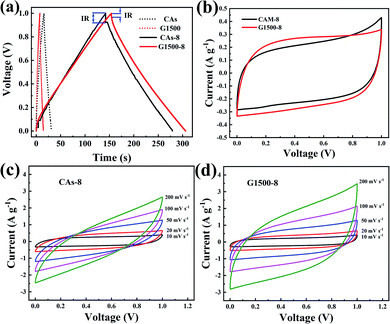 |
| | Fig. 6 The GCD curves of CAs, CAs-8, G1500, and G1500-8 electrodes at 0.2 A g−1 (a) CV curves of the CAs-8 and G1500-8 at scan rate of 10 mV s−1 (b) the CV curves at different scan rates of CAs-8 (c) and G1500-8 (d) electrodes. | |
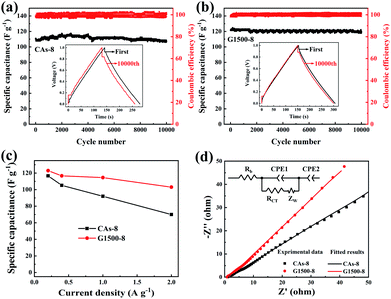
Fig. 6b shows the CV profiles CAs-8 and G1500-8 at a scan rate of 10 mV s−1 in a potential window range of 0–1 V. It is known that a good electrode material for EDLC should be capable of providing very fast electrolyte ion transport pathways, resulting in a rectangular-shaped CV curve.48,49 Hence, the rectangle degree of CV profile can reflect the electrolyte ion diffusion rate within a carbon nanostructure. As show in Fig. 6b, the CV profiles of G1500-8 display a higher rectangle degree than CAs-8, indicating the faster ion diffusion rate of G1500-8 than CAs-8. Furthermore, as show in Fig. 6c and d, the CV curves of CAs-8 display a more severe distortion than G1500-8 at different scan rates. The high rectangle degree and moderately distortion at different scan rates of G1500 electrode is attributed to following factors: (a) the graphitized group can improve its intrinsic conductivity; (b) the mesoporous structure shortens the ion-diffusion route.
Fig. 7a and b shows the performance of the CAs-8 and G1500-8, respectively. After 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, the specific capacitance retention of CAs-8 and G1500-8 is 98% and 92%, respectively. Fig. 7c shows the specific capacitance of CAs-8 and G1500-8 at different current density, and the specific capacitance at 2 A g−1 remains 61% and 84% of the value at 0.2 A g−1 for CAs-8 and G1500-8, respectively. The excellent rate capability and long cycle life of G1500-8 is also suggested by that: (a) the more graphitized group can improve its intrinsic conductivity; and (b) the more mesoporous structure shortens the ion-diffusion route and increases the effective surface area for EDL. Fig. 7d shows the Nyquist plot of the CAs-8 and G1500-8 electrode, and the Nyquist plot can be fitted by the electrical equivalent circuit shown in the figure inset. Generally, the Rb is the combinational resistance of the ionic resistance of the electrolyte, the intrinsic resistance of active materials, and the contact resistance at the active materials/current collector interface; the RCT is the charge-transfer resistance; the CPE1 is double-layer capacitance; ZW is the Warburg impedance; and the CPE2 is the limiting capacitance.11,45,50,51 It is found that the Rb of CAs-8 and G1500-8 is 0.88 and 0.79 Ω, respectively. The lower Rb of G1500-8 is attributed to the higher intrinsic conductivity caused by the more graphite group. Moreover, the RCT of CAs-8 and G1500-8 is 0.26 and 0.15 Ω, respectively, clearly, the more mesoporous structure of G1500-8 shortens the ion-diffusion route resulting in the lower RCT. The sum of Rb and RCT is the main contributor to ESR, which limits the charging/discharging rate of the SCs.45 Furthermore, the higher Warburg angle of G1500-8 than CAs-8 indicates the better ion diffusion performance and capacitive performance of G1500-8. As a results, the G1500-8 with more graphite group and mesoporous structure exhibit the enhanced capacitive performance in EDLC.
000 cycles, the specific capacitance retention of CAs-8 and G1500-8 is 98% and 92%, respectively. Fig. 7c shows the specific capacitance of CAs-8 and G1500-8 at different current density, and the specific capacitance at 2 A g−1 remains 61% and 84% of the value at 0.2 A g−1 for CAs-8 and G1500-8, respectively. The excellent rate capability and long cycle life of G1500-8 is also suggested by that: (a) the more graphitized group can improve its intrinsic conductivity; and (b) the more mesoporous structure shortens the ion-diffusion route and increases the effective surface area for EDL. Fig. 7d shows the Nyquist plot of the CAs-8 and G1500-8 electrode, and the Nyquist plot can be fitted by the electrical equivalent circuit shown in the figure inset. Generally, the Rb is the combinational resistance of the ionic resistance of the electrolyte, the intrinsic resistance of active materials, and the contact resistance at the active materials/current collector interface; the RCT is the charge-transfer resistance; the CPE1 is double-layer capacitance; ZW is the Warburg impedance; and the CPE2 is the limiting capacitance.11,45,50,51 It is found that the Rb of CAs-8 and G1500-8 is 0.88 and 0.79 Ω, respectively. The lower Rb of G1500-8 is attributed to the higher intrinsic conductivity caused by the more graphite group. Moreover, the RCT of CAs-8 and G1500-8 is 0.26 and 0.15 Ω, respectively, clearly, the more mesoporous structure of G1500-8 shortens the ion-diffusion route resulting in the lower RCT. The sum of Rb and RCT is the main contributor to ESR, which limits the charging/discharging rate of the SCs.45 Furthermore, the higher Warburg angle of G1500-8 than CAs-8 indicates the better ion diffusion performance and capacitive performance of G1500-8. As a results, the G1500-8 with more graphite group and mesoporous structure exhibit the enhanced capacitive performance in EDLC.
 |
| | Fig. 7 The cycle performance of the CAs-8 (a) and G1500-8 (b) at the current density of 0.2 A g−1; the rate capability (c), Nyquist plots (d) and equivalent circuit (inset) of CAs-8 and G1500-8, respectively. | |
Finally, we note that the specific surface area of G2000, G2500 and G2800 is hard to improve by CO2 activation for their excessive graphitized group, but the structure of G1500-8 could be significantly improved by CO2 activation. Furthermore, besides the high specific area, the G1500-8 exhibits a high proportion of mesoporous structure. This result is attributed to the moderate content of graphitized group in G1500, which not only improve its intrinsic conductivity but also provide fewer gasification reactive sites during CO2 activation, resulting in the formation of mesopores. These properties are the critical factor of improvements in all electrochemical properties when these CA microspheres are used as electrode of EDLC. However, the extremely low specific surface area of raw CA microspheres limits the further enhancement of G1500-8 performance. As such, the development of modified methods for CA microspheres with high initial surface area and moderate graphitized group formation should be intensified.
4. Conclusions
To summary, our incorporating considerations both increasing graphitized structure and CO2 activation are proved to obtain CAs microsphere with improved electoral conductivity and high surface area. The sample G1500-8 carbonized at 1500 °C for 0.5 h and CO2 activated at 950 °C for 8 h exhibit the acceptable specific surface area of 715 m2 g−1 and the excellent cycle performance and rate capability for EDLC: 98% capacitance retain of initial value after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 even at 2 A g−1. Although, the increasing graphitized structure method cannot be used excessively to create electroconductive group to improve the electrical conductivity of CAs, which is an important and facile route to improve the electrochemical performance of carbon electrode materials for EDLC.
000 cycles, specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 even at 2 A g−1. Although, the increasing graphitized structure method cannot be used excessively to create electroconductive group to improve the electrical conductivity of CAs, which is an important and facile route to improve the electrochemical performance of carbon electrode materials for EDLC.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (grant no: 11604311). We gratefully appreciated our co-workers for their valuable discussions and assistance in measurements. We are grateful to Qingjun, Zhang, Shufan Chen, Qi Yang, Yong Zeng, and Jia Li (Science and Technology on plasma physics Laboratory, Research Centre of Laser Fusion, China Academy of Engineering physics, Mianyang, China) for their assistance in measurements.
Notes and references
- Y. Wang, Y. Song and Y. Xia, Chem. Soc. Rev., 2016, 45, 5925–5950 RSC
 .
. - J. Jia, X. Liu, R. Mi, N. Liu, Z. Xiong, L. Yuan, C. Wang, G. Sheng, L. Cao and X. Zhou, J. Mater. Chem. A, 2018, 6, 15330–15339 RSC
 .
. - X. Liu, G. Sheng, M. Zhong and X. Zhou, Mater Design, 2018, 141, 220–229 CrossRef CAS
 .
. - A. Allahbakhsh and A. R. Bahramian, Nanoscale, 2015, 7, 14139–14158 RSC
 .
. - F. Li, L. Xie, G. Sun, Q. Kong, F. Su, Y. Cao, J. Wei, A. Ahmad, X. Guo and C.-M. Chen, Micropor Mesopor Mat, 2019, 279, 293–315 CrossRef CAS
 .
. - X. Quan, Z. Fu, L. Yuan, M. Zhong, R. Mi, X. Yang, Y. Yi and C. Wang, RSC Adv., 2017, 7, 35875–35882 RSC
 .
. - X. Zeng, D. Wu, R. Fu, H. Lai and J. Fu, Electrochim. Acta, 2008, 53, 5711–5715 CrossRef CAS
 .
. - J. Wang, X. Yang, D. Wu, R. Fu, M. S. Dresselhaus and G. Dresselhaus, J. Power Sources, 2008, 185, 589–594 CrossRef CAS
 .
. - I. Yang, D. Kwon, M.-S. Kim and J. C. Jung, Carbon, 2018, 132, 503–511 CrossRef CAS
 .
. - S. K. Ling, H. Y. Tian, S. Wang, T. Rufford, Z. H. Zhu and C. E. Buckley, J. Colloid Interface Sci., 2011, 357, 157–162 CrossRef CAS PubMed
 .
. - Y.-M. Chang, C.-Y. Wu and P.-W. Wu, J. Power Sources, 2013, 223, 147–154 CrossRef CAS
 .
. - X. Liu, R. Mi, L. Yuan, F. Yang, Z. Fu, C. Wang and Y. Tang, Front Chem, 2018, 6, 475 CrossRef CAS PubMed
 .
. - N. Liu, J. Shen and D. Liu, Micropor Mesopor Mat, 2013, 167, 176–181 CrossRef CAS
 .
. - X. Liu, S. Li, R. Mi, J. Mei, L.-M. Liu, L. Cao, W.-M. Lau and H. Liu, Appl Energ, 2015, 153, 32–40 CrossRef CAS
 .
. - R. Liu, X. Xi, X. Xing and D. Wu, RSC Adv., 2016, 6, 83613–83618 RSC
 .
. - L. Wang, H. Liu, J. Zhao, X. Zhang, C. Zhang, G. Zhang, Q. Liu and H. Duan, Chem. Eng. J., 2020, 382, 122979 CrossRef
 .
. - Y. Tong, D. Ji, P. Wang, H. Zhou, K. Akhtar, X. Shen, J. Zhang and A. Yuan, RSC Adv., 2017, 7, 25182–25190 RSC
 .
. - X. Yan, Y. Liu, X. Fan, X. Jia, Y. Yu and X. Yang, J. Power Sources, 2014, 248, 745–751 CrossRef CAS
 .
. - W. C. Li, C. L. Mak, C. W. Kan and C. Y. Hui, RSC Adv., 2014, 4, 64890–64900 RSC
 .
. - S. Ni, W. He, Z. Li and J. Yang, J. Phys. Chem. C, 2011, 115, 12760–12762 CrossRef CAS
 .
. - G. A. Zickler, B. Smarsly, N. Gierlinger, H. Peterlik and O. Paris, Carbon, 2006, 44, 3239–3246 CrossRef CAS
 .
. - S. Zuo, J. Liu, J. Yang and X. Cai, Carbon, 2009, 47, 3578–3580 CrossRef CAS
 .
. - F. C. Tai, C. Wei, S. H. Chang and W. S. Chen, J. Raman Spectrosc., 2010, 41, 933–937 CrossRef CAS
 .
. - C. Cen, Y. Zhang, X. Chen, H. Yang, Z. Yi, W. Yao, Y. Tang, Y. Yi, J. Wang and P. Wu, Phys. E, 2020, 117, 113840–113852 CrossRef CAS
 .
. - S. Wu, J. Gu, X. Zhang, Y. Wu and J. Gao, Energ Fuel, 2008, 22, 199–206 CrossRef CAS
 .
. - L. Lu, V. Sahajwalla, C. Kong and D. Harris, Carbon, 2001, 39, 1821–1833 CrossRef CAS
 .
. - A. Sadezky, H. Muckenhuber, H. Grothe, R. Niessner and U. Pöschl, Carbon, 2005, 43, 1731–1742 CrossRef CAS
 .
. - C. Sheng, Fuel, 2007, 86, 2316–2324 CrossRef CAS
 .
. - A. C. Ferrari and J. Robertson, Phys. Rev. B, 2000, 61, 14095–14107 CrossRef CAS
 .
. - Y. Wang, D. C. Alsmeyer and R. L. McCreery, Chem. Mater., 1990, 2, 557–563 CrossRef CAS
 .
. - G. Katagiri, H. Ishida and A. Ishitani, Carbon, 1988, 26, 565–571 CrossRef CAS
 .
. - C. Cen, Z. Chen, D. Xu, L. Jiang, X. Chen, Z. Yi, P. Wu, G. Li and Y. Yi, Nanomaterials, 2020, 10, 1–12 CrossRef PubMed
 .
. - S. Sze, Atmos. Environ., 2001, 35, 561–568 CrossRef CAS
 .
. - A. Yoshida, Y. Kaburagi and Y. Hishiyama, Carbon, 2006, 44, 2333–2335 CrossRef CAS
 .
. - O. Beyssac, B. Goffé, J.-P. Petitet, E. Froigneux, M. Moreau and J.-N. Rouzaud, Spectrochim. Acta, Part A, 2003, 59, 2267–2276 CrossRef
 .
. - T. Jawhari, A. Roid and J. Casado, Carbon, 1995, 33, 1561–1565 CrossRef CAS
 .
. - B. Dippel and J. Heintzenberg, J. Aerosol Sci., 1999, 30, S907–S908 CrossRef
 .
. - B. Dippel, H. Jander and J. Heintzenberg, Phys. Chem. Chem. Phys., 1999, 1, 4707–4712 RSC
 .
. - M. Pawlyta, J.-N. Rouzaud and S. Duber, Carbon, 2015, 84, 479–490 CrossRef CAS
 .
. - F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126–1130 CrossRef CAS
 .
. - J. F. Strange and P. L. Walker, Carbon, 1976, 14, 345–350 CrossRef CAS
 .
. - F. Vallejos-Burgos, N. Díaz-Pérez, Á. Silva-Villalobos, R. Jiménez, X. García and L. R. Radovic, Carbon, 2016, 109, 253–263 CrossRef CAS
 .
. - P. Ehrburger, F. Louys and J. Lahaye, Carbon, 1989, 27, 389–393 CrossRef CAS
 .
. - X. Liu, S. Li, J. Mei, W.-M. Lau, R. Mi, Y. Li, H. Liu and L. Liu, J. Mater. Chem. A, 2014, 2, 14429–14438 RSC
 .
. - J. Zhang and X. S. Zhao, ChemSusChem, 2012, 5, 818–841 CrossRef CAS PubMed
 .
. - Z. Lei, N. Christov and X. S. Zhao, Energy Environ. Sci., 2011, 4, 1866–1873 RSC
 .
. - C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC
 .
. - A. Ghosh and Y. H. Lee, ChemSusChem, 2012, 5, 480–499 CrossRef CAS PubMed
 .
. - E. Frackowiak and F. Béguin, Carbon, 2001, 39, 937–950 CrossRef CAS
 .
. - D. Liu, J. Shen, N. Liu, H. Yang and A. Du, Electrochim. Acta, 2013, 89, 571–576 CrossRef CAS
 .
. - D. Liu, G. Cheng, H. Zhao, C. Zeng, D. Qu, L. Xiao, H. Tang, Z. Deng, Y. Li and B.-L. Su, Nano Energy, 2016, 22, 255–268 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01735c |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Lei Yuana,
Minglong Zhonga,
Shuang Nia,
Fan Yanga,
Zhibing Fua,
Xibin Xua,
Chaoyang Wang*a and
Yongjian Tang*ab
ab,
Lei Yuana,
Minglong Zhonga,
Shuang Nia,
Fan Yanga,
Zhibing Fua,
Xibin Xua,
Chaoyang Wang*a and
Yongjian Tang*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, a specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 at 2 A g−1.
000 cycles, a specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 at 2 A g−1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F = 1
F = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and stirred for a few minutes to get clear solution; then Na2CO3 solution (0.02 mol L−1) was mixed in the solution by molar ratios of 500
2) and stirred for a few minutes to get clear solution; then Na2CO3 solution (0.02 mol L−1) was mixed in the solution by molar ratios of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (R
1 (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na2CO3), followed adding deionized water to a given volume; this solution was then stirred for about 20 minutes until light yellow RF solution was obtained. Secondly, as shown in Fig. 1, oil phase composed of 600 mL industrial white oil and 6 g surfactant span-80 were added in a three-necked flask which was soaked in a 60 °C oil bath; then the above RF solution was added drop wise to the oil phase and stirred with magnetic stirrer at 1000 rpm. Under the high-speed stirring, RF aqueous solution is dispersed in the oil phase in the shape of microspheres. The solution was stirred at 1000 rpm for 0.5 hours and continued stirred at a decelerated speed of 100 rpm for 12 hours until the dispersive RF microspheres were completely gelled. Thirdly, the gelled RF microspheres were separated from the oil phase by the filtration method and washed several times with dichloromethane, and then dried at ambient condition. Dried RF microspheres were carbonized in a tubular furnace with an argon flow rate of 100 mL min−1 at temperature of 1050 °C for 4 hours to obtain CAs. The graphitization treatment of CA microspheres was carried out in tubular furnace with argon atmosphere at temperature of 1500, 2000, 2500 and 2800 °C for 0.5 hours, respectively, and these graphitized CA microspheres (GCAs) are denoted as G1500, G2000, G2500, G2800, respectively. In the final CO2 activation step, the CAs and GCAs were heated from room temperature to desired temperatures with a heating rate of 10 °C min−1 for a certain time under a steady CO2 flow of 150 mL min−1 (Table 1).
Na2CO3), followed adding deionized water to a given volume; this solution was then stirred for about 20 minutes until light yellow RF solution was obtained. Secondly, as shown in Fig. 1, oil phase composed of 600 mL industrial white oil and 6 g surfactant span-80 were added in a three-necked flask which was soaked in a 60 °C oil bath; then the above RF solution was added drop wise to the oil phase and stirred with magnetic stirrer at 1000 rpm. Under the high-speed stirring, RF aqueous solution is dispersed in the oil phase in the shape of microspheres. The solution was stirred at 1000 rpm for 0.5 hours and continued stirred at a decelerated speed of 100 rpm for 12 hours until the dispersive RF microspheres were completely gelled. Thirdly, the gelled RF microspheres were separated from the oil phase by the filtration method and washed several times with dichloromethane, and then dried at ambient condition. Dried RF microspheres were carbonized in a tubular furnace with an argon flow rate of 100 mL min−1 at temperature of 1050 °C for 4 hours to obtain CAs. The graphitization treatment of CA microspheres was carried out in tubular furnace with argon atmosphere at temperature of 1500, 2000, 2500 and 2800 °C for 0.5 hours, respectively, and these graphitized CA microspheres (GCAs) are denoted as G1500, G2000, G2500, G2800, respectively. In the final CO2 activation step, the CAs and GCAs were heated from room temperature to desired temperatures with a heating rate of 10 °C min−1 for a certain time under a steady CO2 flow of 150 mL min−1 (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,G
θ002,G
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,P
θ002,P
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,G
θ002,G
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ002,P
θ002,P
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations of polyene-like structures.37,38
C stretching vibrations of polyene-like structures.37,38


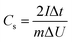
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, the specific capacitance retention of CAs-8 and G1500-8 is 98% and 92%, respectively. Fig. 7c shows the specific capacitance of CAs-8 and G1500-8 at different current density, and the specific capacitance at 2 A g−1 remains 61% and 84% of the value at 0.2 A g−1 for CAs-8 and G1500-8, respectively. The excellent rate capability and long cycle life of G1500-8 is also suggested by that: (a) the more graphitized group can improve its intrinsic conductivity; and (b) the more mesoporous structure shortens the ion-diffusion route and increases the effective surface area for EDL. Fig. 7d shows the Nyquist plot of the CAs-8 and G1500-8 electrode, and the Nyquist plot can be fitted by the electrical equivalent circuit shown in the figure inset. Generally, the Rb is the combinational resistance of the ionic resistance of the electrolyte, the intrinsic resistance of active materials, and the contact resistance at the active materials/current collector interface; the RCT is the charge-transfer resistance; the CPE1 is double-layer capacitance; ZW is the Warburg impedance; and the CPE2 is the limiting capacitance.11,45,50,51 It is found that the Rb of CAs-8 and G1500-8 is 0.88 and 0.79 Ω, respectively. The lower Rb of G1500-8 is attributed to the higher intrinsic conductivity caused by the more graphite group. Moreover, the RCT of CAs-8 and G1500-8 is 0.26 and 0.15 Ω, respectively, clearly, the more mesoporous structure of G1500-8 shortens the ion-diffusion route resulting in the lower RCT. The sum of Rb and RCT is the main contributor to ESR, which limits the charging/discharging rate of the SCs.45 Furthermore, the higher Warburg angle of G1500-8 than CAs-8 indicates the better ion diffusion performance and capacitive performance of G1500-8. As a results, the G1500-8 with more graphite group and mesoporous structure exhibit the enhanced capacitive performance in EDLC.
000 cycles, the specific capacitance retention of CAs-8 and G1500-8 is 98% and 92%, respectively. Fig. 7c shows the specific capacitance of CAs-8 and G1500-8 at different current density, and the specific capacitance at 2 A g−1 remains 61% and 84% of the value at 0.2 A g−1 for CAs-8 and G1500-8, respectively. The excellent rate capability and long cycle life of G1500-8 is also suggested by that: (a) the more graphitized group can improve its intrinsic conductivity; and (b) the more mesoporous structure shortens the ion-diffusion route and increases the effective surface area for EDL. Fig. 7d shows the Nyquist plot of the CAs-8 and G1500-8 electrode, and the Nyquist plot can be fitted by the electrical equivalent circuit shown in the figure inset. Generally, the Rb is the combinational resistance of the ionic resistance of the electrolyte, the intrinsic resistance of active materials, and the contact resistance at the active materials/current collector interface; the RCT is the charge-transfer resistance; the CPE1 is double-layer capacitance; ZW is the Warburg impedance; and the CPE2 is the limiting capacitance.11,45,50,51 It is found that the Rb of CAs-8 and G1500-8 is 0.88 and 0.79 Ω, respectively. The lower Rb of G1500-8 is attributed to the higher intrinsic conductivity caused by the more graphite group. Moreover, the RCT of CAs-8 and G1500-8 is 0.26 and 0.15 Ω, respectively, clearly, the more mesoporous structure of G1500-8 shortens the ion-diffusion route resulting in the lower RCT. The sum of Rb and RCT is the main contributor to ESR, which limits the charging/discharging rate of the SCs.45 Furthermore, the higher Warburg angle of G1500-8 than CAs-8 indicates the better ion diffusion performance and capacitive performance of G1500-8. As a results, the G1500-8 with more graphite group and mesoporous structure exhibit the enhanced capacitive performance in EDLC.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 even at 2 A g−1. Although, the increasing graphitized structure method cannot be used excessively to create electroconductive group to improve the electrical conductivity of CAs, which is an important and facile route to improve the electrochemical performance of carbon electrode materials for EDLC.
000 cycles, specific capacitance of 121 F g−1 at 0.2 A g−1 and 101 F g−1 even at 2 A g−1. Although, the increasing graphitized structure method cannot be used excessively to create electroconductive group to improve the electrical conductivity of CAs, which is an important and facile route to improve the electrochemical performance of carbon electrode materials for EDLC.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





