Atomic dynamics of stress-induced lattice misalignment structures in a KDP subsurface

Abstract

We present an ab initio molecular dynamics study of the thermal stability and dynamics behaviors of lattice misalignment structures (LMSs) in the subsurface layers of KH₂PO₄ (KDP) crystals. The dehydration process at the atomic scale is observed in the LMS system, which is the same as that in a perfect KDP crystal. However, the paths entering the dehydration process are various. The interesting result is that compared with a perfect KDP crystal, many new paths appear in the LMS system, and even in the same paths, the dehydration is more likely to happen in the LMS system. This leads to a dramatic increase in the dehydration numbers in the LMS system, for which the reasons are given in terms of structural deformation and/or uneven distribution of protons. The results elucidate the underlying atomic mechanism of the effect of LMS defects on the thermal stability of KDP material.

---

Introduction

Potassium dihydrogen phosphate (KDP, KH₂PO₄) crystals have attracted intensive interest in the field of optical materials, due to their remarkable nonlinear electro-optical properties¹ and capability of growing to large size,^2–5 leading to many applications in various high-power large-aperture laser systems such as inertial confinement fusion reactors.^6,7 However, the actual laser damage threshold (LDT) of a KDP crystal is usually far below its intrinsic damage threshold, which limits the output power of laser systems.^8–13 It is widely accepted that various defects, including those in the surface/subsurface layers created during KDP lens surfacing, are the main reason for the decline of LDT of KDP.^11–18 These defects may have an impact on the distribution of light and thus affect the LDT of KDP.^19–24 Therefore, besides growing KDP crystals close to perfection, it is also important to obtain smoother surfaces and more damage-free subsurfaces after machining to increase the LDT of KDP.

In recent years, with the improvement of machining technique, a smoother surface of KDP can be produced by different ultra-precision surface machining methods, such as single point diamond turning,^25–27 ultra-precision grinding^28,29 and magnetorheological finishing.³⁰ Even so, after machining, the damage at a more microscopic level still cannot be avoided as expected. Recently, researchers evaluated more precisely the subsurface structure of a KDP crystal after ultra-precision machining by utilizing grazing incidence X-ray diffraction technique. The results show that a shallow subsurface layer of a machined KDP crystal has turned to a lattice misalignment structure (LMS).^31,32 This means that, compared with other machining-induced defects,^11,28 such as pits, cracks, and nicks, such stress-induced subsurface micro “LMS” defect seems impossible to avoid, even with a very advanced surface machining technique. Therefore, clarifying the characteristics of LMS, a kind of “intrinsic” defect or damage, and its effect on the LDT of KDP becomes more important. We have previously published an ab initio study of the lattice misalignment structures in KDP crystals. In this previous work, by utilizing the ab initio static calculations, we found out for the first time various stable lattice misalignment structures by applying stress to KDP crystals, and calculated their electronic band structures and optical absorption properties. The results show that the electronic band structure and the optical absorption of misalignment structure indeed have some differences compared to a perfect KDP crystal.³³

Compared with the static study, the dynamic study on the evolution of the misalignment structure, however, is more important, since it directly determines the material thermal stability under the action of light and heat. This is particularly significant in large-aperture laser systems, where micro-defects may not hinder the device performance, but the growth and even decomposition of defects are catastrophic.^34–37 In the present work, we picked two stable LMSs from our previous static calculations and studied the atomic dynamics behaviors in these misalignment structures by utilizing ab initio molecular dynamics (MD) simulations. We want to see the atomic-level dynamic evolution of LMS, the possible structural damage, the damage pathway and how difficult it is compared with the perfect structure of KDP, and so on. These results are helpful to evaluate the possible adverse effects of such stress-induced “intrinsic” misalignment structure during the working process of KDP components.

Model and method

As shown in Fig. 1(a), we give the unit cell of a perfect KDP crystal, which consists of four KH₂PO₄ molecules and contains two molecule layers. The perfect cell can also be seen in Fig. 1(d), i.e., the colored part, which differs from Fig. 1(a) only in the selection of unit cells; the grey parts are obtained by utilizing the periodic boundary conditions, a perfect bulk is thus formed. In our previous work,³³ we presented a simple and effective method to obtain the atomic configuration of misalignment structure on the (200) plane. Specifically, we moved the grey atoms in the dashed box along the Z direction a small displacement a_z by changing the z-component of vector a, as shown in Fig. 1(d) and (e), the P–O bonds at the (200) boundary of the unit cell were thus slightly deformed [see Fig. 1(e)]. By doing so, we try to model the local strain induced by the stress resulting from the cutting tip. Then, the system was fully relaxed. Through relaxation, the stress in the deformed P–O bonds can be transferred to every layer in the system, during which the (200) LMS appears naturally. More details can be found from ref. 33. Following the similar procedures as the above, we simulated the LMS evolution and obtained lots of local stable LMSs, such as the two representative ones in Fig. 1(b) and (c). Their z-components of vector a change by 8.40 Å and 26.0 Å relative to the perfect KDP structure, as shown in Fig. 1(a)–(c). Different z-components of vector a mean different degrees of misalignment. Compared with the perfect structure (PS) of KDP, both of two LMSs produce obvious deformation [see Fig. 1(a)–(c)]. Specially, the LMS at 8.40 Å (LMS₁) has new radicals of “[HPO₄]²⁻” and “[H₃PO₄]” [see Fig. 1(b)], which is different from that in the PS and the LMS at 26.0 Å (LMS₂).

Fig. 1 The unit cell of a perfect KDP crystal (a). Two stable LMSs with the z-component of vector a of 8.40 Å (b) and 26.0 Å (c). The radicals labeled by the solid and dashed circles in (b) denote radicals of [HPO₄]²⁻ and [H₃PO₄], respectively. The perfect KDP bulk system (d), by adjusting the z-component of vector a, the grey atoms in the dashed box are moved along the Z direction a small displacement a_z (e). The a and c indicate the basis vectors of the unit cell. The white, red, pink and purple balls denote H, O, P and K atoms, respectively, which are all the same in the following figures.

In the present work, aiming at the two LMSs in Fig. 1(b) and (c), we use ab initio MD simulations to study their dynamics behaviors. For comparison, the perfect KDP structure is also studied under the same conditions. We first generate the 2 × 2 × 2 supercells of PS and two LMSs. Then, the three supercells including 256 atoms are fully relaxed. After that, the three optimized systems are heated at a constant temperature of 2000 K. It should be noted that an unreasonable high temperature adopted here for simulation is just to accelerate the chemical reaction, since the simulated time scale (ps) is too short for the chemical processes. The similar practice can be widely found in the literatures.^38–42 A step size of 1.0 fs is used for all MD calculations with each simulation running for approximately 5000 steps.⁴³ In all cases, dynamical equilibrium (based on the total system energy) appears to be reached in about 500 steps. After the systems reach to the dynamical equilibrium, we begin to trace the atomic trajectories. We focus on those steps with obvious atomic position and bond changes to find out the possible structural changes/damages. Then, we further extract the obvious changed structures and fully relax them to judge whether the changed structures can be stable. To compare the difficulty of the possible structural changes/damages in the LMS and PS systems, we performed 30 independent MD simulations for each system.

All calculations including the structural relaxations and MD simulations are performed based on the density function theory (DFT) utilizing the Vienna ab initio simulation program pack (VASP) package.⁴⁴ The exchange–correlation potential is described by the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof functional.⁴⁵ PAW potentials are used for electron–ion interactions. The kinetic energy cutoff for the plane-wave basis is set to be 680 eV, which leads to the converged result for the total system energy better than 1 meV per atom.^21,46 A 2 × 2 × 2 supercell with a 3 × 3 × 3 Monkhorst–Pack k-point mesh is used for all calculations. The conjugate gradient algorithm is used to relax the ions and the residual force on each atom is taken as the convergence criterion which is smaller than 0.01 eV Å⁻¹. With these parameters, the obtained lattice parameters of the relaxed perfect KDP crystal are a = b = 7.44 Å and c = 6.96 Å, which are in excellent agreement with the experimental values of a = b = 7.45 Å and c = 6.97 Å.⁴⁷ Ab initio molecular dynamics (MD) calculations are achieved by the Verlet algorithm and the canonical ensemble (NVT) is adopted using the Nosé thermostat to control temperature.

Results and discussion

Based on the obtained MD trajectories, we first focus on the atomic dynamic evolution in the PS and LMS systems. It is known that in the static perfect KDP structure (paraelectric phase), each oxygen atom connects only one close (O–H) or far (O⋯H) proton through the H-bond (O–H⋯O).^48–53 We will refer to the oxygen atom that connects the proton through the short distance as “O_s” (O–H), and the other case as “O_l” (O⋯H), as shown in Fig. 2(a). In sharp contrast, in the dynamic evolution, as shown in Fig. 2(b)–(d), the oxygen atoms that connect two protons appear in the three systems because of the rotation and movement of PO₄ tetrahedrons, the transfer of protons, and the change in the H-bond length. Here, we use the similar symbols like “O_sl, O_ss and O_sm” to describe these new oxygen states; the subscript “m” (medium) indicates that the proton is approximately located at the midpoint position in the H-bond (O⋯H⋯O/O–H–O), as shown in Fig. 2(d). Another obvious dynamic phenomenon observed in the three systems, especially for the PS and LMS₂ systems, is that the proton may escape from one PO₄ tetrahedron to another, turning two [H₂PO₄]⁻ radicals into one [HPO₄]²⁻ radical and one [H₃PO₄] radical. Lastly but most importantly, when the oxygen state O_sl appears, the special dynamics behavior that probably results in a qualitative change in material usually occurs in the subsequent dynamic evolution. That is dehydration reaction by which some radicals will be decomposed.

Fig. 2 Schematic of atomic configuration of two [H₂PO₄]⁻ radicals in the initial PS system (a). When the systems reach to the dynamical equilibrium, various configurations (b), (c) and (d) appear in any of the three systems. The oxygen atoms marked with black circles and Arabic numerals (1–6) denote five types of oxygen states: O_s and O_l (a), O_sl (b), O_ss (c), and O_sm (d). The subscripts “s” (short), “l” (long) and “m” (medium) describe the distance of proton relative to two oxygen atoms in the O–H⋯O or O⋯H⋯O (O–H–O) bonds, respectively.

We find that the oxygen state O_sl can appear in various possible combinations of PO₄ tetrahedrons and protons, and they all have the potential to dehydrate. In Fig. 3, we give the three instances that correspond to three dehydration paths. Fig. 3(a) displays the PS system. Here, we take the colored atoms (2[H₂PO₄]⁻) as an example, which will be referred to as the “initial combination”. For clarity, we remove the grey atoms in the PS system and only display the initial combination [see Fig. 3(b)]. Through a series of dynamic evolution, as shown in Fig. 3(b) and (c), the initial combination of “2[H₂PO₄]⁻” turns into the combination of “[HPO₄]²⁻ + [H₃PO₄]”, owing to the transfer of protons; besides, the rotation and movement of PO₄ tetrahedrons lead to the formation of the oxygen state “O_sl” [see Fig. 3(c)]. The formation of oxygen state “O_sl” is an important dynamic evolution result, since “O_sl” may evolve into a water molecule in the subsequent evolution, which results in a qualitative change in KDP material [see Fig. 3(d)]. We will refer to the combination in Fig. 3(c) that is going to dehydrate as the “dehydrated combination”. Another two examples for the LMS₁ and LMS₂ systems are given in Fig. 3(e)–(h) and (i)–(l), respectively. Similarly, after a series of dynamic evolution, besides the obvious changes in structure and/or chemical composition, the oxygen state “O_sl” appears in the dehydrated combinations [see Fig. 3(g) and (k)]. Significantly, the oxygen state “O_sl” could also evolve into a water molecule in the subsequent evolution [see Fig. 3(h) and (l)], and the dynamics process from “O_sl” to “H₂O” are fully identical to that in the PS system.

Fig. 3 The supercells of PS (a), LMS₁ (e), and LMS₂ (i), where the colored atoms are referred to as the “initial combination”. For clarity, we only display the initial combinations in (b), (f), and (j). After a series of dynamic evolution, the initial combinations produce obvious changes in structure and/or chemical composition, and generate the oxygen state “O_sl”; we will refer to such changed initial combinations as the “dehydrated combinations” (c), (g), and (k). In the subsequent evolution, the oxygen state “O_sl” evolves into a water molecule (d), (h), and (l). The a and c denote the basis vectors of the unit cell.

Certainly, in the MD simulations, there are more than three types of dehydration paths. In Table 1, we give all the dehydration paths observed in the three systems of PS, LMS₁, and LMS₂, which are numbered by the Arabic numeral “1–14”. The important result, as seen in the second column in Table 1, only three dehydration paths “1, 4, and 10” are in the PS system; the others are all in the LMS systems. In Table 1, we also give the corresponding initial combinations, which are labelled by the symbols of “A₁, A₂, A₃, B₁, …” (see the third column). In the subsequent dynamic evolution, the initial combinations evolve into the dehydrated combinations, in which “O_sl” is formed. As seen in Table 1, some initial combinations evolve into the same dehydrated combination. For example, the initial combinations “A₁, A₂, and A₃” all become into the dehydrated combination “A”. Therefore, there are only six types of dehydrated combinations, which are labeled by the capital letters from “A” to “F” in Table 1. Interestingly, after the formation of “O_sl”, it is through the same dynamics process that the oxygen states “O_sl” in the dehydrated combinations evolve into the water molecules. That is, from the six types of dehydrated combinations to the final dehydrated products, see the fourth to sixth columns in Table 1, the dynamics process from “O_sl” to the “water molecule” are completely the same, indicated by s₁–s₅.

Table 1 The relevant information of the fourteen dehydration paths in the three systems. The initial combinations at s₀ step labeled by the symbols of “A₁, A₂, A₃, B₁, …” are given in the third column. The dehydrated combinations at s₁ step are labeled by the capital letters from A to F in the fourth column. In the subsequent evolution, the oxygen states “O_sl” in the dehydrated combinations all evolve into the water molecules through the same dynamics process, namely “s₁–s₅”. The dehydrated products are given in the last column

Path	System	Initial combination (s0)	Dehydrated combination (s1)	Process	Products (s4, s5)
1	PS, LMS1, LMS2	A1: 2[H2PO4]^−	A: [HPO4]^2− + [H3PO4]	s1–s5	H2O, [PO3]^−, [P2O7]^4−
2	LMS1	A2: [HPO4]^2− + [H2PO4]^−
3	LMS1	A3: [H2PO4]^− + [H3PO4]
4	PS, LMS2	B1: 2[H2PO4]^−	B: 2[H2PO4]^−
5	LMS1	B2: 2[H3PO4]
6	LMS1	C1: [HPO4]^2− + [H3PO4]	C: [H2PO4]^− + [H3PO4]
7	LMS1	C2: [HPO4]^2− + [H2PO4]^−
8	LMS1	C3: [H2PO4]^− + [H3PO4]
9	LMS2	C4: 2[H2PO4]^−
10	PS	D1: 2[H2PO4]^−	D: 2[HPO4]^2−
11	LMS2	E1: 2[H2PO4]^−	E: [HPO4]^2− + [H2PO4]^−
12	LMS1	E2: [H2PO4]^− + [H3PO4]
13	LMS1	E3: [HPO4]^2− + [H2PO4]^−
14	LMS2	F1: 3[H2PO4]^−	F: [HPO4]^2− + [H2P2O7]^2−

---

In Fig. 4, we display the atomic dynamic evolution in the dehydration process, step s₁ to s₅, where only the two protons that form water are given for clarity. In the “s₁” step, the oxygen state O_sl appears in the “dehydrated combination”. Then, in the s₂ step, the H-bond gets shorter/longer, turning the O⋯H–O bond into the O–H–O/O⋯H⋯O bond; this results in the formation of oxygen state O_sm. Next, in the s₃ step, the O–H–O/O⋯H⋯O bond evolves into the O–H⋯O bond, during which the proton successfully escapes from one oxygen atom to the other, the oxygen state O_ss thus formed. Finally, the most remarkable change occurs in the s₄ step, that is, the newly formed oxygen state O_ss is ejected from the PO₄ tetrahedron as a water molecule and leaving behind a [PO₃]⁻ radical. By the way, the newly formed [PO₃]⁻ radical may interact with a nearest [PO₄]³⁻ radical to form a [P₂O₇]⁴⁻ radical in the subsequent dynamic evolution [see Fig. 4(e)]. Indeed, researchers have detected the intermediate product [P₂O₇]⁴⁻ radical in the direct heating of KDP crystals above 500 K.^54,55 Furthermore, we extract the structures in the s₄ and s₅ steps from the MD trajectories and fully relax them, to judge whether the water molecules can exist stably; the results show that the water molecules in both two steps still exist stably after relaxation. In summary, despite the paths (1–14) entering the dehydration process are various, their dehydration processes from “O_sl” to the “water molecule” are the same; that is, after the formation of “O_sl”, it first evolves into “O_sm”, then turns into “O_ss”, eventually the oxygen state “O_ss” liberates from the PO₄ tetrahedron in the form of a water molecule. If only the two protons that form water are considered, the dehydration process can be described as the following equations, which are consistent with the experimental observations.^54,55

Fig. 4 The atomic dynamic evolution from the dehydrated combination (s₁) to the final products (s₄, s₅), where only the two protons that form water are given. In the s₁ step, O_sl appears in the dehydrated combination (a); then in the s₂ (b) and s₃ (c) steps, O_sl evolves into O_sm and then O_ss; the oxygen states are marked by the grey dashed circles; finally, in the s₄ step (d), “O_ss” liberates from the PO₄ tetrahedron in the form of a water molecule and leaving behind a [PO₃]⁻ radical. In the s₅ step, the [PO₃]⁻ radical interacts with an adjacent [PO₄]³⁻ radical to form a [P₂O₇]⁴⁻ radical (e).

To compare the decomposition difficulty of LMS and PS systems, as shown in Fig. 5, we give the statistical results for the dehydrated numbers of each system in the 30 MD simulations. From Fig. 5, we can see that, compared with the PS system, the dehydration paths in the LMS systems increase significantly, especially in the LMS₁ system. Specifically, only three dehydration paths are in the PS system (paths 1, 4, and 10); in sharp contrast, there are nine and five dehydration paths in the LMS₁ and LMS₂ systems, respectively (see Fig. 5). For the LMS₁ system, this result should be mainly attributed to its initial chemical composition. Indeed, in the three initial systems, only the LMS₁ system has different radicals: [HPO₄]²⁻, [H₂PO₄]⁻, and [H₃PO₄]. These different radicals result in the formation of some unique dehydration paths. For example, in the LMS₁ system, there are some dehydration paths that start from the initial combinations which consist of two different radicals, such as “[HPO₄]²⁻ + [H₂PO₄]⁻”, “[H₂PO₄]⁻ + [H₃PO₄]”, etc. (see Table 1); while in the PS and LMS₂ systems, there are no such dehydration paths. For the LMS₂ system, the increased dehydration paths should be caused by the deformed structure. As shown in Fig. 1(a)–(c), the H-bonds in the LMSs are obviously stretched compared with that in the PS. The stretched H-bonds decrease the attraction between the adjacent PO₄ tetrahedrons, making it easier for the PO₄ tetrahedrons to move and rotate. This catalyzes the scission of the H-bond network, making the consequence that the protons in the LMS systems have more transfer degrees of freedom, thus generating more types of dehydration paths in the LMS₂ system.

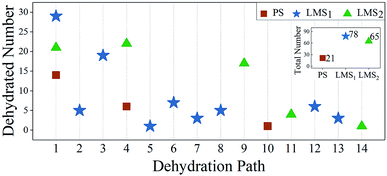Fig. 5 Statistical results for the dehydrated numbers in the PS (red rectangles), LMS₁ (blue stars), and LMS₂ (green triangles) systems. The abscissas (1–14) denote fourteen dehydration paths observed in the three systems (see Table 1). Inset: the total dehydrated numbers for the three systems.

Another interesting result in Fig. 5 is that, in the same dehydration paths, such as path 1 and path 4, the dehydrated numbers for the LMS systems are obviously greater than that of the PS system. There are two possible reasons: on one hand, the PO₄ tetrahedrons in the LMS systems are easier to move and rotate due to the stretched H-bonds, so that the LMS systems are easier to generate the oxygen state “O_sl” compared with the PS system. On the other hand, the protons are unevenly distributed in the initial LMS₁ system. The uneven distribution of protons results in the formation of some radicals in local area with charged states. The radical in the positively state, such as [KH₃PO₄]⁺, is apt to emit a proton outward, while the radical in the negatively state, such as [KHPO₄]⁻, tends to contribute one [OH]⁻. That is, the uneven distribution of protons catalyzes the occurrence of dehydration.

The above facts show that, compared with the PS system, not only do many new dehydration paths appear in the LMS systems, but also the dehydrated numbers of LMS systems increase significantly in the same dehydration paths (see Fig. 5). Therefore, the total dehydrated numbers for both LMS systems are much greater than that of the PS system. As shown in the inset in Fig. 5, for the LMS₁ and LMS₂ systems, there are 78 and 65 dehydrations in the 30 MD simulations with each running for 5000 steps; this is in sharp contrast with the 21 dehydrations in the PS system.

The statistical results in Fig. 5 show that the dehydration paths in the three systems are various; but interestingly, they all contain path “1”, also the numbers of radicals dehydrated through this path account for the largest proportion (see Fig. 5). Thus, we take the path “1” as an example; we calculate the formation energy of the corresponding configurations in dehydration path 1, step s₀ to s₄, in which all the atoms are fully relaxed. The aim is to compare the decomposition difficulty of the same dehydration path in the three systems, and thus to further understand the statistical results. In Fig. 6(a), we display the energy level comparison diagram for the PS (red lines), LMS₁ (blue lines), and LMS₂ (green lines) systems; the abscissas “s₀” and “s₁” correspond to the initial combination “A₁” and the dehydrated combination “A”, respectively (see Table 1); “s₂–s₄” correspond to the corresponding configurations in dehydration path 1; the ordinate denotes the formation energy. The formation energy is calculated by the following equation:^56–58

E_f = E_n − E_n−x (2)

where E_n is the total energy of the supercell; E_n−x is the total energy of the supercell except for the combinations associated with dehydration; n is the number of atoms in the supercell; x is the number of atoms associated with dehydration. From Fig. 6(a), we can see that the energy level diagrams for the three systems are obviously different. Firstly, for the LMS₁ system, the energy difference between the first two steps (s₀–s₁) is lower than that for the other two systems [see Fig. 6(a)]. This means that, compared with the PS and LMS₂ systems, the initial combination “2[H₂PO₄]⁻” in the LMS₁ system is easier to turn into the dehydrated combination “[HPO₄]²⁻ + [H₃PO₄]”. This should be caused by the different radicals in the initial LMS₁ system. That is, the uneven distribution of protons in the background promotes the transformation from the “2[H₂PO₄]⁻” radicals to the “[HPO₄]²⁻ + [H₃PO₄]” radicals. Furthermore, the most remarkable result in Fig. 6(a) is that the maximum energy difference for both LMS systems is lower than that for the PS system. For clarity, we give the energy difference comparison diagram in Fig. 6(b), where ΔE_max = E_max − E_s0, and E_max corresponds to the maximum formation energy at s₂ or s₃ step. From Fig. 6(b), we can clearly see that the energy barrier for the initial combination “2[H₂PO₄]⁻” in the LMS₁ system to dehydrate is lowest, which is consistent with the statistical results in Fig. 5.

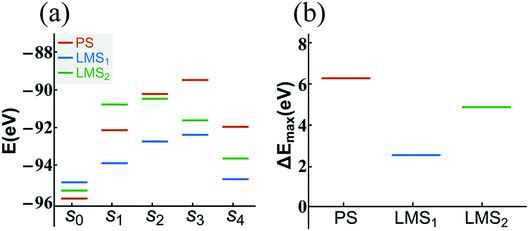Fig. 6 The energy level comparison diagram (a) of dehydration path 1 in the PS (red lines), LMS₁ (blue lines), and LMS₂ (green lines) systems, where the abscissas “s₀” and “s₁” correspond to the initial combination “2[H₂PO₄]⁻” and the dehydrated combination “[HPO₄]²⁻ + [H₃PO₄]”, respectively (see Table 1); “s₂–s₄” correspond to the corresponding configurations in dehydration path 1. For clarity, the energy difference comparison diagram (ΔE_max = E_max − E_s0) is shown in (b).

In summary, compared with the PS system, the LMS systems have more dehydration paths, and even in the same dehydration paths, the LMS systems have lower energy barrier to dehydrate. The results reveal that the LMS defect decomposes more easily than the perfect KDP structure, suggesting that the thermal stability of KDP material would be much affected by such stress-induced subsurface micro LMS defect. Indeed, it has been discovered that the laser-induced or thermal-induced decomposition reactions in general begin with the local reactions in the surface/subsurface layers of KDP.^37,54,55,59 We believe that the LMS defect may play an important role in the decomposition of the surface/subsurface layers of KDP components, and also may be one of the possible reasons for the formation of the laser-induced damages in the use of KDP.

Conclusion

The LMS, which appears in the machining process of KDP, is investigated regarding the dynamics behaviors by utilizing the ab initio MD simulations. The details of atomic dynamic evolution in the three systems of PS, LMS₁ and LMS₂ are obtained. Especially, the dehydration phenomenon is observed, and its process is the same in the three systems. The dehydration process includes the formation of “O_sl”, its transformation, and ejection in the form of a water molecule. However, the paths entering the dehydration process are various. Fourteen dehydration paths are observed in the three systems. The interesting result is that compared with the PS system, a lot of new dehydration paths appear in the LMS systems, and even in the same dehydration paths, the dehydration is more likely to occur in the LMS systems. This leads to the consequence that the total dehydrated numbers in the LMS systems are much greater than that in the PS system, which can be attributed to the deformed structure and/or the uneven distribution of protons. These results suggest that once the LMS defect resulting from processing appears in KDP crystals, the possibility of material decomposition will be greatly increased, which will much affect the damage threshold of KDP components.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Open Research Fund of Key Laboratory of Neutron Physics, CAEP (No. 2014BB07).

References

1. D. Eimerl, Electro-optic, linear, and nonlinear optical properties of KDP and its isomorphs, Ferroelectrics, 1987, 72, 95–139.
2. R. Hawey-Fedder, H. Robey, T. Biesiada, M. Dehaven, R. Floyd and A. Burnham, Rapid Growth of Very Large KDP and KD*P Crystals in Support of the National Ignition Facility, Proc. SPIE, 2000, 4102, 152–161.
3. N. P. Zaitseva, J. J. De Yoreo, M. R. Dehaven, R. L. Vital, K. E. Montgomery, M. Richardson and L. J. Atherton, Rapid growth of large-scale (40–55 cm) KH₂PO₄ crystals, J. Cryst. Growth, 1997, 180, 255–262.
4. C. Maunier, P. Bouchut, S. Bouillet, H. Cabane, R. Courchinoux, P. Defossez, J.-C. Poncetta and N. Ferriou-Daurios, Growth and characterization of large KDP crystals for high power lasers, Opt. Mater., 2007, 30, 88–90.
5. N. Zaitseva and L. Carman, Rapid Growth of KDP-type Crystals, Prog. Cryst. Growth Charact., 2001, 43, 1–118.
6. J. J. De Yoreo, A. K. Burnham and P. K. Whitman, Developing KH₂PO₄ and KD₂PO₄ crystals for the world's most power laser, Int. Mater. Rev., 2002, 47, 113–152.
7. R. Hawley-Fedder, P. Geraghty, S. Locke, M. McBurney, M. Runkel, T. Suratwala, S. Thompson, P. Wegner and P. Whitman, NIF Pockels Cell and Frequency Conversion Crystals, Proc. SPIE, 2004, 5341, 121–126.
8. A. Yokotani, T. Sasaki, K. Yoshida, T. Yamanaka and C. Yamanaka, Improvement of the bulk laser damage threshold of potassium dihydrogen phosphate crystals by ultraviolet irradiation, Appl. Phys. Lett., 1986, 48, 1030–1032.
9. M. F. Singleton, J. F. Cooper, B. D. Andresen and F. P. Milanovich, Laser-induced bulk damage in potassium dihydrogen phosphate crystal, Appl. Phys. Lett., 1988, 52, 857–859.
10. J. Swain, S. Stokowski, D. Milam and F. Rainer, Improving the bulk laser damage resistance of potassium dihydrogen phosphate crystals by pulsed laser irradiation, Appl. Phys. Lett., 1982, 40, 350–352.
11. J. Cheng, M. J. Chen, W. Liao, H. J. Wang, J. H. Wang, Y. Xiao and M. Q. Li, Influence of surface cracks on laser-induced damage resistance of brittle KH₂PO₄ crystal, Opt. Express, 2014, 22, 28740–28755.
12. S. F. Wang, J. Wang, Q. Xu, X. Y. Lei, Z. C. Liu and J. F. Zhang, Influences of surface defects on the laser-induced damage performances of KDP crystal, Appl. Opt., 2018, 57, 2638–2646.
13. S. G. Demos and M. Staggs, Application of fluorescence microscopy for noninvasive detection of surface contamination and precursors to laser-induced damage, Appl. Opt., 2002, 41, 1977–1983.
14. C. W. Carr, H. B. Radousky and S. G. Demos, Wavelength Dependence of Laser-Induced Damage: Determining the Damage Initiation Mechanisms, Phys. Rev. Lett., 2003, 91(1–4), 127402.
15. S. G. Demos, M. Yan, M. Staggs, J. J. De Yoreo and H. B. Radousky, Raman scattering investigation of KH₂PO₄ subsequent to high fluence laser irradiation, Appl. Phys. Lett., 1998, 72, 2367–2369.
16. M. J. Chen, M. Q. Li, C. H. An, L. Zhou, J. Cheng, Y. Xiao and W. Jiang, Influence of Light Intensification by Subsurface Cracks on KH₂PO₄ Crystal's Laser Induced Damage Threshold, Jpn. J. Appl. Phys., 2013, 52(1–8), 032701.
17. M. Q. Li, M. J. Chen, J. Cheng, Y. Xiao and W. Jiang, Two important mechanisms damaging KH₂PO₄ crystal processed by ultraprecision fly cutting and their relationships with cutting parameters, Appl. Opt., 2013, 52, 3451–3460.
18. Y. Zhang, L. C. Zhang, M. Liu, F. H. Zhang, K. Mylvaganam and W. D. Liu, Revealing the mechanical properties of potassium dihydrogen phosphate crystals by nanoindentation, J. Mater. Res., 2016, 31, 1056–1064.
19. T. T. Sui, Y. F. Lian, M. X. Xu, L. S. Zhang, Y. L. Li, X. Zhao, X. G. Xu and X. Sun, Comparison of hydrogen vacancies in KDP and ADP crystals: a combination of density functional theory calculations and experiment, Phys. Chem. Chem. Phys., 2019, 21, 6186–6197.
20. X. Chen, Q. Q. Zhao, X. C. Wang, J. Chen and X. Ju, Linear optical properties of defective KDP with oxygen vacancy: first-principles calculations, Chin. Phys. B, 2015, 24(1–6), 077802.
21. C. S. Liu, N. Kioussis, S. G. Demos and H. B. Radousky, Electron- or Hole-Assisted Reactions of H Defects in Hydrogen-Bonded KDP, Phys. Rev. Lett., 2003, 91(1–4), 015505.
22. C. S. Liu, Q. Zhang, N. Kioussis, S. G. Demos and H. B. Radousky, Electronic structure calculations of intrinsic and extrinsic hydrogen point defects in KH₂PO₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(1–11), 224107.
23. C. S. Liu, C. J. Hou, N. Kioussis, S. G. Demos and H. B. Radousky, Electronic structure calculations of an oxygen vacancy in KH₂PO₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(1–6), 134110.
24. C. D. Marshall, S. A. Payne, M. A. Henesian, J. A. Speth and H. T. Powell, Ultraviolet-induced transient absorption in potassium dihydrogen phosphate and its influence on frequency conversion, J. Opt. Soc. Am. B, 1994, 11, 774–785.
25. Q. Xu and J. Wang, Analysis of the influence of vacuum chucking on the distortion of the KDP crystal, Proc. SPIE, 2000, 4231, 464–468.
26. Q. Xu, J. Wang, W. Li, X. Zeng and S. Y. Jing, Defects of KDP Crystal Fabricated by Single Point Diamond Turning, Proc. SPIE, 1999, 3862, 236–239.
27. P. Lahaye, C. Chomont and P. Dumont, Using a design of experiment method to improve KDP crystals machining process, Proc. SPIE, 1999, 3492, 814–820.
28. D. J. Wu, B. Wang, H. Gao, R. K. Kang and X. S. Cao, Influence of Grinding to the Surface and Subsurface Quality of KDP crystal, Adv. Mater. Res., 2008, 53–54, 203–208.
29. Y. Namba, K. Yoshida, H. Yoshida and S. Nakai, Ultraprecision grinding of optical materials for high power lasers, Proc. SPIE, 1997, 3244, 320–330.
30. J. Menapace, P. Ehrmann and R. Bickel, Magnetorheological finishing (MRF) of potassium dihydrogen phosphate (KDP) crystals: nonaqueous fluids development, optical finish, and laser damage performance at 1064 nm and 532 nm, Proc. SPIE, 2009, 7504(1–12), 750414.
31. N. Hou, Y. Zhang, L. C. Zhang and F. H. Zhang, Assessing microstructure changes in potassium dihydrogen phosphate crystals induced by mechanical stresses, Scr. Mater., 2016, 113, 48–50.
32. N. Hou, Y. Zhang, L. C. Zhang, K. Mylvaganam, J. Q. Wei and F. H. Zhang, An investigation on the surface/subsurface defects in potassium dihydrogen phosphate crystals after fly-cutting, Proc. SPIE, 2016, 9683(1–4), 968309.
33. Y. Hu, Z. Zhu, J. M. Xiao, H. Z. Shao, L. Zhao, M. Xu and J. Zhuang, Atomic scale study of stress-induced misaligned subsurface layers in KDP crystals, Sci. Rep., 2019, 9(1–9), 10399.
34. R. A. Negres, S. O. Kucheyev, P. Demange, C. Bostedt, T. Van Buuren, A. J. Nelson and S. G. Demos, Decomposition of KH₂PO₄ crystals during laser-induced breakdown, Appl. Phys. Lett., 2005, 86(1–3), 171107.
35. A. Surmin, S. Lambert, F. Guillet, B. Minot, D. Damiani and F. Gervais, Thermal mechanism of laser induced damages in KDP crystals, Proc. SPIE, 2007, 6720(1–5), 672007.
36. T. Tsujibayashi, M. Ichimiya, K. Toyoda and N. Ohno, Molecular-Chain Formation Induced by Infrared-Laser Light Observed in L-Cysteine and Potassium Dihydrogenphosphate, Jpn. J. Appl. Phys., 2011, 50(1–4), 101601.
37. S. G. Demos, M. Staggs and M. R. Kozlowski, Investigation of processes leading to damage growth in optical materials for large-aperture lasers, Appl. Opt., 2002, 41, 3628–3633.
38. C. F. Li, Z. Mei, F. Q. Zhao, S. Y. Xu and X. H. Ju, Molecular dynamic simulation for thermal decomposition of RDX with nano-AlH₃ particles, Phys. Chem. Chem. Phys., 2018, 20, 14192–14199.
39. C. Deng, X. G. Xue, Y. Chi, H. Z. Li, X. P. Long and C. Y. Zhang, Nature of the Enhanced Self-Heating Ability of Imperfect Energetic Crystals Relative to Perfect Ones, J. Phys. Chem. C, 2017, 121, 12101–12109.
40. S. I. Stoliarov, R. E. Lyon and M. R. Nyden, A reactive molecular dynamics model of thermal decomposition in polymers. II. Polyisobutylene, Polymer, 2004, 45, 8613–8621.
41. I. V. Schweigert, Quantum mechanical simulations of condensed-phase decomposition dynamics in molten RDX, J. Phys.: Conf. Ser., 2014, 500(1–6), 052039.
42. K. Zhong, J. Liu, L. Y. Wang and C. Y. Zhang, Influence of Atmospheres on the Initial Thermal Decomposition of 1,3,5-Trinitro-1,3,5-triazinane: Reactive Molecular Dynamics Simulation, J. Phys. Chem. C, 2019, 123, 1483–1493.
43. D. J. Carter and A. L. Rohl, Ab initio Molecular Dynamics Simulations of (101) Surfaces of Potassium Dihydrogenphosphate, J. Chem. Theory Comput., 2011, 7, 1604–1609.
44. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
45. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
46. Q. Zhang, F. Chen, N. Kioussis, S. G. Demos and H. B. Radousky, Ab initio study of the electronic and structural properties of the ferroelectric transition, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 65(1–10), 024108.
47. R. J. Nelmes, Structural studies of KDP and the KDP-type transition by neutron and x-ray diffraction: 1970-1985, Ferroelectrics, 1987, 71, 87–123.
48. G. Beutier, S. P. Collins, G. Nisbet, K. A. Akimova, E. N. Ovchinnikova, A. P. Oreshko and V. E. Dmitrienko, Proton configurations in the hydrogen bonds of KH₂PO₄ as seen by resonant x-ray diffraction, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(1–11), 214116.
49. V. H. Schmidt, Review of order-disorder models for KDP-family crystals, Ferroelectrics, 1987, 72, 157–173.
50. A. A. Levin and S. P. Dolin, Molecular Models and Calculations in Microscopic Theory of Order-Disorder Structural Phase Transitions: Application to KH₂PO₄ and Related Compounds, J. Phys. Chem., 1996, 100, 6258–6261.
51. R. J. Nelmes, Z. Tun and W. F. Kuhs, A compilation of accurate structural parameters for KDP and DKDP, and a users guide to their crystal structures, Ferroelectrics, 1987, 71, 125–141.
52. R. J. Nelmes, Recent structural studies of the KDP-type transition: A review, Ferroelectrics, 1984, 53, 207–214.
53. S. Endo, T. Chino, S. Tsuboi and K. Koto, Pressure-induced transition of the hydrogen bond in the ferroelectric compounds KH₂PO₄ and KD₂PO₄, Nature, 1989, 340, 452–455.
54. B. Choi, High temperature phase transitions and thermal decomposition of KH₂PO₄ crytsals, J. Phys. Chem. Solids, 1995, 56, 1023–1030.
55. K. Lee, Hidden nature of the high-temperature phase transitions in crystals of KH₂PO₄-type: is it a physical change?, J. Phys. Chem. Solids, 1996, 57, 333–342.
56. H. Z. Shao, Y. Li, J. H. Zhang, B. Y. Ning, W. X. Zhang, X. J. Ning, L. Zhao and J. Zhuang, Physical mechanisms for the unique optical properties of chalcogen-hyperdoped silicon, Europhys. Lett., 2012, 99, 46005.
57. Z. Zhu, H. Shao, X. Dong, N. Li, B. Y. Ning, X. J. Ning, L. Zhao and J. Zhuang, Electronic Band Structure and Sub-band-gap Absorption of Nitrogen Hyperdoped Silicon, Sci. Rep., 2015, 5(1–9), 10513.
58. H. Sawada and K. Kawakami, First-principles calculation of the interaction between nitrogen atoms and vacancies in silicon, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1851–1858.
59. R. H. Chen, C. C. Yen, C. S. Shern and T. Fukami, Impedance spectroscopy and dielectric analysis in KH₂PO₄ single crystal, Solid State Ionics, 2006, 177, 2857–2864.

---