Dynamics and controllability of droplet fusion under gas–liquid–liquid three-phase flow in a microfluidic reactor

Abstract

Gas–liquid–liquid three-phase flow systems have unique advantages of controlling reagent manipulation and improving reaction performance. However, there remains a lack of insight into the dynamics and controllability of water droplet fusion assisted by gas bubbles, particularly scaling laws for use in the design and operation of complex multiphase flow processes. In the present work, a microfluidic reactor with three T-junctions was employed to sequentially generate gas bubbles and then fuse two dispersed water droplets. The formation of the dispersed phase was divided into multiple stages, and the bubble/droplet size was correlated with operating parameters. The formation of the second dispersed droplet at the third T-junction was accompanied by the fusion of the two dispersed water droplets that were formed. It revealed a two-stage process (i.e. drainage and fusion) for the two droplets to fuse while becoming mature by breaking-up with the secondary water supply stream. In addition, a droplet contact model was employed to understand the influence on the process stability and uniformity of the merged/fused droplets by varying the surfactant concentration (in oil), the viscosity of the water phase, and the flow rates of different fluids. The study provides a deeper understanding of the droplet fusion characteristics on gas–liquid–liquid three-phase flow in microreactors for a wide range of applications.

---

1. Introduction

Microreactors are miniaturized reactors that typically consist of flow channels with characteristic dimensions ranging from a few tens of microns to several hundred microns. Over the last two decades, microreactor technology has been developed and applied as a powerful platform for process intensification owing to its intrinsic advantages, such as fast heat and mass transfer, large surface volume ratio, low reagent hold-up, and controllable laminar flow.^1,2 One of the most extensively studied topics in this field has been focused on two-phase (either liquid–liquid, or gas–liquid) droplets formed along the flow channel network for fluid manipulation, reaction, and/or detection.^3–7 More recently, there has been increasing interest in the more complex three-phase system involving gas–liquid–liquid, such as gas–oil–water, mainly owing to its advantages in, e.g., controlling the segmented flow hydrodynamics,⁸ intensifying the multiphase mass transfer,^9,10 improving the multiphase reaction selectivity and reproducibility,^11,12 and precisely manipulating reaction reagents.¹³

Compared to two-phase droplet systems (gas–liquid or liquid–liquid), the most prominent advantage of the gas–oil–water three-phase system is the effectiveness in regulating the desired droplet merging or coalescence of segmented droplets. Zheng and Ismagilov¹⁴ pioneered the use of segmented aqueous droplets as micro-batch reactors flowing along microchannels by introducing inert gas bubbles for protein crystallization. Önal et al.⁹ developed a gas–liquid–liquid three-phase capillary microreactor with an increased specific surface area for the regioselective catalytic hydrogenation of α,β-unsaturated aldehydes. Su et al.¹⁰ introduced inert gas bubbles as stirrers to enhance the liquid–liquid two-phase mass transfer by a factor of two.

The capability of gas–liquid–liquid microfluidics has also been explored for precisely regulating reagent distribution and mixing.^13,15 Nightingale et al.¹³ investigated two broad strategies, namely, droplet fusion and direct injection, for the quantitative manipulation of two streams of droplet flow. The design of channel network architectures, the precise timing of flow streams, and the necessary external physical fields all play important parts in controlling droplet fusion and/or direct injection.¹⁶ Li et al.¹⁷ designed a multi-junction injection configuration to extend the range of the volumetric ratios, providing a controllable system for evaluating the enzymatic activity of thrombin and determining the coagulation time of human blood plasma. Also, the uniformity of the added/injected reagent volume has been considered to be an important but challenging factor to implement, and only a few reports are available.^18,19 Suhanya et al.¹⁵ advanced the methodology with a direct injection approach in a gas–liquid–liquid droplet reactor for synthesizing monodispersed gold nanostructures. Nightingale et al.¹³ designed a side-channel network for the direct injection of reagents with controlled quantities into the existing droplets.

Along with the device development, efforts have been made to understand the mechanism of the complex multiphase microfluidics.^4,20 Wang et al.²⁰ investigated the mechanisms of bubble and droplet generation and correlated the average droplet volume with the control parameters in a cross-junction microchannel. Yue et al.²¹ identified the conditions for creating gas–liquid–liquid flow patterns of slug flow and parallel-slug flow along a serpentine channel. Liu et al.²² studied the characteristics of bubble splitting under three-phase flow in a double T-junction microchannel, revealing the critical breaking length and the size of the sub-bubble/slug. More recently, Liu et al.²³ further investigated the effects of the three-phase slug sub-regime flow on hydrodynamics and local mass transfer, confirming that the alternate bubble and droplet flow is in favor of mass transfer.

In spite of the great efforts put into studying different aspects of gas–oil–water multiphase microfluidics, there remains a lack of insight into the dynamics and controllability of water droplet fusion, especially the scaling laws for use in the design and operation of such complex flow processes. Therefore, the present study was aimed toward gaining a deeper understanding and further controllability of the droplet fusion process within a microfluidic reactor channel network consisting of three T-junctions for gas bubble and water droplet generation. With oil as the continuous phase, the formation of gas bubbles, the primary water droplets and the secondary water droplets were investigated by varying a range of operational parameters (including flow rates of different phases, aqueous phase viscosity and surfactant concentration), together with force balance analysis, where the two water inlets had different colors to assist visualization. Based on the experimental results, scaling laws were established for correlating the key parameters (including bubble/droplet size, channel geometry and fluidic conditions) governing the bubble/droplet generation. To further understand the dynamics of droplet fusion and ultimately control their fusion, a droplet contact model was employed while identifying two stages across the process, namely, the drainage time and the droplet fusion time. Finally, the uniformity of the fused droplets and the stability of the process under different operating conditions were quantitatively characterized.

2. Experimental section

2.1 Materials

n-Hexadecane (Shanghai Macklin Biochemical Co. Ltd.) with Span80 (Tianjin Zhiyuan Chemical Reagent Co., Ltd.) at selected concentrations were used as the continuous phase. Nitrogen was purchased from Yantai Feiyuan Special Gas Co. Ltd., and was used as the dispersed gas phase. The deionized water (made in-house) dyed with methyl blue (Sinopharm Chemical Reagent Co. Ltd.) and magenta (Tianjin Hengxing Chemical Reagent Manufacturing Co., Ltd.) was introduced into the microreactor as the primary water (pw) and the secondary water (sw) injection, respectively.

2.2 Microreactor design and fabrication

The microreactor was designed to have a microfluidic channel network consisting of a straight main flow channel, an oil inlet to one end of the main channel, three side inlets (linked to three T-junctions, respectively) for gas, first aqueous and second aqueous, and an outlet at the other end of the main channel (Fig. 1a). The straight main channel was 14 cm long with a squared cross-section (600 μm × 600 μm). The side channel linked to TJ-1 as the gas inlet had a cross-section area of 450 μm × 450 μm, while the other two side channels to TJ-2 and TJ-3 had the same squared cross-section of 250 μm × 250 μm for injecting two aqueous phases, respectively. The selection of the different geometries of the three channel cross-sections was aimed toward forming alternating flow patterns of long gas bubbles and small aqueous droplets.

Fig. 1 Schematic of (a, left) the microfluidic channel network design, and (b, right) the experimental set-up.

The microreactor was made according to published procedures with minor adaptations.^24,25 Briefly, the channel network was fabricated by precision milling on a polymethyl methacrylate (PMMA) sheet (thickness 5 mm), which was closed with a cover sheet (thickness 10 mm) by thermal bonding at a temperature of 50 °C after washing both in an ethanol bath at 70 °C for 3 min. Before the experiments, all channels were flushed with n-hexadecane and then deionized water, followed by nitrogen drying.

2.3 Experimental set-up and methods

The experimental set-up is illustrated in Fig. 2b, consisting mainly of the microreactor, fluid feeding/withdrawal, and monitoring systems. During the microreactor operation, the continuous oil phase was supplied through Inlet-1 into the main channel. Dispersed phases were injected through the three side channels via T-junctions into the main channel; gas nitrogen from Inlet-2 through TJ-1, water with methyl blue dye from Inlet-3 through TJ-2, and water with magenta dye from Inlet-4 through TJ-3. PTFE tubes with an internal diameter of 2 mm were used for connecting the feeding syringes to the microreactor inlets, and for linking the outlet to the sample collector. All fluids were driven by syringe pumps (LSP02-1B, Longer Pump, China) into the microreactor at selected flow rates ranging from 120 μL min⁻¹ to 660 μL min⁻¹.

Fig. 2 The development of dispersed gas bubbles in the oil phase around TJ-1.

The microreactor was placed on a microscope (SZX16, OLYMPUS) stage with a high-speed CCD camera (Phantom R311, Vision Research) working at 1000–3200 fps coupled to the microscope (Fig. 2b). This allowed the direct in situ monitoring of the fluidic behaviour within the microchannel, and subsequent processing of the recorded images/videos with an image analysis program (Image J). The experiments were carried out at room temperature. All experiments were repeated three times, and averages were taken over these repeated runs for further analysis.

3. Results and discussion

3.1 Controllable generation of dispersed phase bubbles or droplets at three T-junctions (TJs)

3.1.1 Formation of dispersed gas bubbles around TJ-1. In a typical process for the formation of dispersed gas bubbles, under a steady flow of the oil continuous phase along the main channel, while the dispersed gas phase nitrogen was injected in from Inlet-2, the two immiscible fluids met at the first T-junction (TJ-1) where a gas–oil interface was created which further formed a bubble head (Fig. 2a). With a continuous gas supply, the bubble grew and took more space into and along the main channel (Fig. 2b). On further growth, the bubble flowed along the main channel downstream to a critical point when the neck of the bubble at the junction started to shrink (Fig. 2c), turning the process into another stage of breaking-up of the bubble neck (Fig. 2d). That breaking-up resulted in a mature gas bubble flowing downstream along the main channel (Fig. 2e), while a subsequent bubble head for the dispersed gas phase started to form at junction TJ-1, repeating the cycle of the growing/breaking-up/maturing process.

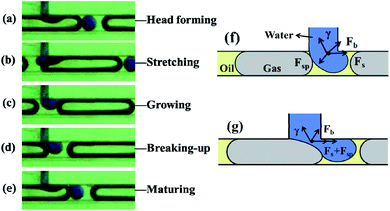
Based on fluid mechanics, this dynamic process is the result of the interplay of multiple significant factors (Fig. 2), including the shear force (F_s) favorable to bubble formation, the gas–oil interfacial tension (γ) hindering the bubble moving downstream, and the static pressure difference across the bubble (F_sp) affecting the geometry of the bubble neck at the junction. When the initial gas–oil interface was created at the junction, F_sp was in the opposite direction to γ, leading to the formation of the bubble head (Fig. 2f). Once the bubble grew and started to “block” the main channel, it caused an increase in F_sp, which together with F_s contributed to the break-up of the bubble neck towards generating a complete mature bubble flowing downstream (Fig. 2g).

In practice, these force-related factors were all determined by the properties of the fluids and the channel wall surface, the channel geometry, and the flow conditions, in particular, the flow rate of each fluid. In a given system, it was the flow rate of each fluid that determined the size (i.e. length) of the bubble formed. Furthermore, an empirical correlation,⁶ regarded as a scaling law for this process (eqn (1)), allowed the length (L_g) of the gas bubbles to be predicted with varying flow rates.

where Q_g and Q_o are the volumetric flow rates of the gas phase and continuous oil phase, respectively, and w is the width of the main channel.

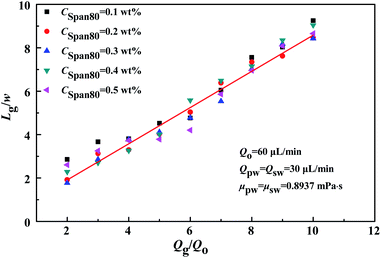
Fig. 3 illustrates the correlation of the bubble length with the flow rate ratio of gas to oil, given a gas inlet channel width of 450 μm and different concentrations of surfactant Span80 (C_Span80). The measurements were taken at fixed flow rates of oil (Q_o = 60 μL min⁻¹) and water injected through both Inlet-3 and Inlet-4 (Q_pw = Q_sw = 30 μL min⁻¹, μ_pw = μ_sw = 0.8937 mPa s). As can be seen from Fig. 3, a good linear relationship was obtained between the dimensionless groups of (L_g/w) and (Q_g/Q_o). Using the experiment data, constants a and b were determined to be 0.09028 and 0.0119 in the system examined. This observation confirmed that the bubble length was independent of the fluid property and also the concentration of surfactant added.²⁶

Fig. 3 The correlation of the gas bubble length with the flow rate ratio (gas/oil).

3.1.2 Formation of dispersed primary water droplets around TJ-2. When the primary water supply (dyed in blue) from Inlet-3 arrived at TJ-2, while the gas bubble dispersed in the continuous phase oil followed from upstream along the main channel, the formation of the water droplets underwent a similar process (i.e. growing/breaking-up/maturing) to the formation of gas bubbles (Fig. 4a–e). However, some unique characteristics were observed with the water droplet being (i) dispersed in oil but not in the gas phase, and (ii) quasi-spherical.

Fig. 4 The formation of the dispersed primary water droplets around TJ-2.

When the head of the blue water droplet started to form at junction TJ-2, it was initially mostly in contact with the long gas bubble. Instead of penetrating the main channel and being broken up by the gas phase, the head was inclined to stretching downstream and slipping along the water–gas interface (Fig. 4a). While the main stream of gas bubbles and oil approximately retained the original velocity, the stretched head of the water droplet switched from its contact with the gas phase to the arriving oil phase (Fig. 4b), where an oil–water interface was formed. As the stretched water droplet completely established an interface with the oil phase, it tended to re-shape and grow in the oil phase (Fig. 4c and d), followed by breaking-up to form a mature water droplet dispersed in the continuous oil phase (Fig. 4e), similar to gas bubble formation (Fig. 2).

This observation was primarily associated with the upstream gas bubbles dispersed in the continuous oil phase, bringing in additional interfaces and more influential forces (Fig. 4f and g). Firstly, the flow rate of the water (injected at 30 μL min⁻¹) was relatively lower than that of the oil and especially the gas (oil 60 μL min⁻¹, gas 120–600 μL min⁻¹). It was unable to take much space in the main channel or “pinch” in the bubble, thus there was no significant pressure difference (F_sp) to break-up the water phase (in contrast to that observed for gas bubble break-up shown in Fig. 2). At the same time, the water–gas interfacial tension (γ) was dominant over the shear force (F_s) of the gas bubble, which also hindered the break-up of the aqueous phase (Fig. 4f and g).

Secondly, the variation in interfacial tension (γ) at different stages played a crucial part in the break-up of the aqueous phase, depending on whether a water–gas or water–oil interface was formed. When the water–oil interface was established, the interfacial tension was smaller than that of the gas–water interface, enabling the breaking-up of the aqueous phase to increase and finally form a droplet (Fig. 4c and d). Also, as the interfacial tension of the gas–oil interface (at the front of the upstream gas bubble) was almost five times larger than that of the oil–water,²⁷ the force (F_b) exerted by the gas–oil interface further contributed to cutting-off the droplet (Fig. 4f and g).

Finally, when the water droplet was formed and dispersed in the continuous oil phase, the droplet tended to become spherical. This can be attributed to the oil–water interfacial tension and also the relatively small amount of water supplied at a lower flow rate. With the matured water droplet dispersed while flowing with the continuous oil phase, a new contact interface was formed between the tip of the inlet water and the upstream gas bubble at TJ-2, repeating another cycle of water droplet formation (Fig. 4e).

As analyzed above, the variation in the interfacial tension had a notable effect on the water droplet formation. This was further investigated by varying the concentration of Span80 in the oil phase ranging from 0.1 wt% to 0.5 wt%, with an attempt to establish a scaling law in the form of eqn (1). The experimental results are depicted in Fig. 5, correlating the droplet size (L_d)/the main channel width (w) with the flow rate ratio (Q_pw/Q_o+g+w) of water/(oil + gas + water), and different concentrations of surfactant Span80 in oil, C_Span80.

Fig. 5 The size of the dispersed primary water droplets as a function of the flow rate ratio of water/(oil + gas + water) around TJ-2.

The effects of surfactant Span80 concentration were noticeable but insignificant. Overall, for both the oil-water and gas–oil interfaces, the decrease in C_Span80 increased both interfacial tensions. The increase in the oil–water interfacial tension was in favor of forming larger droplets, while the increase in the gas–oil interfacial tension had the opposite effect. As a result, the combination of these two forces gave an indistinguishable correlation between the water droplet size and C_Span80. Nevertheless, with the experimental data, it was still possible to correlate the water droplet size with flow rates, as expressed in eqn (2):

where Q_pw and Q_o+g+w are the volumetric flow rates of the primary water injection and the sum of oil, gas and water, respectively.

3.1.3 The formation of dispersed secondary water droplets around TJ-3. At TJ-3, the head of the secondary water supply (dyed in red) injected via Inlet-4 underwent a similar process to that occurring at TJ-2 when it came in contact with the gas bubble to form a head and stretch, before the upstream primary (blue) water droplet dispersed in oil arrived (Fig. 6a). However, it was interesting to observe the merging and fusion processes of the primary and secondary droplets. When the head of the red drop formed an interface with the oil slug, it started to grow while sharing the slug space with the blue droplet (Fig. 6b). With further growth of the red droplet, it started to squash the blue one and caused the deformation of both, where an oil film was believed to exist between them (Fig. 6c). That was followed by the crushing of the separating oil film where both droplets tended to reshape towards spherical, however with direct contact (Fig. 6d). Finally, the two droplets fused and merged, while the neck of the red one at the junction was reduced and eventually cut-off by the upstream gas–oil interface or gas bubble (Fig. 6e).

Fig. 6 The formation of the secondary (red) water droplet and its fusion with the primary (blue) water droplet around TJ-3.

With an additional water droplet formation, the dynamic force balancing around TJ-3 became more complicated as indicated in Fig. 6f and g, compared to that at both TJ-1 and TJ-2. It was again the result of the combination of the interplaying factors including fluid material properties and flow operational parameters. In that regard, a more focused investigation would be carried out for the dynamic process of droplet fusion, as detailed in the following section.

As demonstrated above, by using the microreactor with three T-junctions, the size of dispersed droplets and the fusion between them can be well controlled, which is particularly suitable for synthesizing nanoparticles with high monodispersity through controllable mixing. While the injection of each reactant is independent and predictable, it also provides a useful platform for characterizing chemical reaction kinetics and/or the effect of fluid properties on reactions. Also, the continuous phase as the carrier can prevent the reaction mixture within the droplet from coming into direct contact with the microchannel wall, thus minimizing potential clogging and adhesion to the channel walls by nanoparticles. Moreover, although three T-junctions were designed in this study, additional T-junctions may be incorporated into the microreactor to facilitate complex multi-step reactions.

3.2 Dynamics and controllability during droplet fusion in the vicinity of TJ-3

3.2.1 Typological diagram of the droplet fusion. As the formation of liquid droplets fusion assisted by gas bubbles occurred, it provided a platform for a wide range of applications, e.g. mixing, reaction and analysis, in a controllable manner. To further explore the operational windows for multiple parameters to control the process, typological diagrams (Fig. 7) were obtained under different experimental conditions. By varying the experimental parameters with a range of combinations, three types of (blue and red) water droplet fusion were observed, i.e. fusion, partial fusion and non-fusion, as indicated in different zones (Fig. 7). Some typical images are displayed in Fig. 8, illustrating the processes of different types of fusion at varying stages of flow along the main channel.

Fig. 7 (a) The effects of C_Span80 and Q_g on droplet fusion at TJ-3; (b) the effects of μ_pw and Q_sw on droplet fusion at TJ-3 (C_Span80 = 0.1 wt%).

Fig. 8 Images of three types of droplet fusion around TJ-3 under the experimental conditions specified by the parameters in the order Q_o–Q_g–Q_pw–Q_sw–C_Span80–μ_pw.

As can be seen from Fig. 7a, both the gas flow rate Q_g and the concentration of the surfactant Span80 C_Span80 played a big role in facilitating droplet fusion. This was also associated with the oil film existing between the two droplets before fusion occurred, which acted as a barrier for contact, as shown in the contact model (Fig. 9). In Fig. 9 the contact process of two aqueous droplets is illustrated with two surfactant concentrations. The formation of blue aqueous droplets was via the combined interaction of interfacial tension and oil-phase shearing force as previously discussed. These two forces have the opposite effect on the droplet geometry, therefore resulting in unnoticeable differences in the size of the two blue droplets.

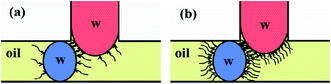Fig. 9 Schematic representation of the droplet contact model with (a) lower and (b) higher surfactant concentrations.

With higher Q_g, smaller water droplets and relatively thicker oil films were formed, where a higher C_Span80 also increased the thickness of the oil film. At the same time, the surfactant molecules were adsorbed on both the primary (blue) water–oil and the secondary (red) water–oil interfaces, where the repulsive forces between the hydrophobic organic groups increased with the increase in C_Span80 (Fig. 9b). As a result, an increase in either Q_g or C_Span80 made it more difficult for direct contact between these two droplets, i.e. preventing them from fusing.

It was interesting to observe the effects of the flow rate for the secondary (red) water supply (Q_sw), and the viscosity of the primary (blue) water phase (μ_pw) on the fusion process (Fig. 7b). At a low Q_sw (≤5 μL min⁻¹), it was likely to form smaller secondary (red) droplets less frequently, where the droplet fusion occurred only with every few blue droplets, termed as partial fusion. By increasing Q_sw to be comparable to Q_pw, it resulted in full fusion. However, when Q_sw was very high, it pushed the process out of the fusion zone, i.e. non-fusion. When the viscosity of the primary (blue) water was increased to a certain level (e.g. 17.96 mPa s), the altered interfacial tension made the fusion more difficult, even ceasing, where the primary droplet became stiffer though slightly deformed (Fig. 8e).

3.2.2 Drainage and fusion during breaking-up. To gain further insight into the fusion mechanism, a closer examination of the process was conducted from the initial contact of droplets, the crushing of the oil film between them, through to full fusion (Fig. 10). For quantification, two parameters were introduced. (i) Drainage time (t_d) refers to the period starting from droplet contact with an oil film switched between them, to the occurrence of the crushing of the oil film for direct droplet contact (Fig. 10a–c). (ii) Fusion time (t_f) represents the period between the occurrence of the oil film crushing and the breaking-up of the secondary water droplet (Fig. 10d–f). The entire time period for both drainage and fusion stages was termed as the breaking-up time (t_b), thus, t_b = t_d + t_f.

Fig. 10 The multi-step process of the fusion of the primary (blue) water droplet and the secondary (red) water droplet around TJ-3.

By varying operational parameters, all three periods were obtained. The results are depicted in Fig. 11. Overall, t_d dominated t_b under all the experimental conditions examined and responded clearly to the varying parameter. Based on the droplet contact model (Fig. 9), this observation was largely associated with the existence of the oil film between the two water droplets before there was direct contact between them, and also with the droplet size together with the fluid property (e.g. viscosity). Thus, an increase in t_d was observed with increasing C_Span80 (Fig. 11a), Q_sw (Fig. 11c) and Q_pw (Fig. 11d), or decreasing Q_g (Fig. 11b), since the thickness of the oil film and the stiffness were increased, creating a harder barrier for direct droplet contact towards fusion.

Fig. 11 The effects of operating conditions on drainage and fusion time.

Once the oil film barrier was broken through, the fusion started and occurred over a much shorter period (t_f < 0.02 s) as compared to the drainage time t_b (up to 0.14 s). It was mainly due to the direct contact and merging of the two water droplets where the fusion was further enhanced by droplet internal mixing, including circulation under flow,^28,29 as shown in Fig. 10e and f. Also, the internal mixing was improved by increasing the overall flow velocity that was dominated by the gas flow rate (an order of magnitude higher than the water flow rate). This resulted in the reduction of t_f with a higher gas flow rate Q_g (Fig. 11b). The effects on the droplet internal process t_f were insignificant when the other operating parameters were varied.

Generally, the flow in the microchannel is limited to laminar, where the Reynolds number is typically of the order of a few tens. Although it is not impossible to achieve turbulence within microchannels, the immense pressure drop would cause difficulties practically. For the purpose of mixing intensification, different mechanisms are commonly applied such as acoustic and magnetic forces or complex channel features. Nevertheless, in the droplet microfluidics under laminar flow, the large specific surface area and the internal circulation in droplets provide sufficient and, more importantly, controllable mixing to enhance mass transfer across the multi-phase interfaces.

3.2.3 Stability and uniformity of fused droplets. To evaluate the process stability and uniformity of the merged and fused droplets, the stability was quantified by measuring the average length of the fused droplets, L_f under different operating conditions, while the uniformity was characterized by obtaining the variation in droplet length under each specific operating condition, V%. The results are illustrated in Fig. 12.

Fig. 12 The effects of the experimental conditions on the stability and uniformity of the fused droplets.

The effect on the length (L_f) of the fused droplets was insignificant with varying surfactant concentration C_Span80 (Fig. 12a) since L_f was approximately the sum of the length of the two individual droplets, both of which had an unnoticeable correlation with C_Span80, (Fig. 3 and 5). At the same time, the addition of surfactant in the oil phase (0.1–0.4 wt%) stabilized the water droplets and thus made the fused ones more reproducible with more uniform sizes.

The influence of Q_g on the fusion droplets is shown in Fig. 12b. The length of the fusion droplets decreased as a result of increasing Q_g as it reduced the sizes of both primary and secondary water droplets (eqn (2)). The variation in the uniformity of the fused droplets was little when Q_g was in the lower range (120–300 μL min⁻¹). In contrast, when Q_g > 300 μL min⁻¹ the variation in the fused droplet sizes increased with increasing Q_g. This was likely associated with the non-uniformity of the gas bubbles produced at a higher gas flow rate, which was about 5 times the oil phase flow rate.

Fig. 12c shows that both the fused droplet size and their uniformity were pronounced by increasing Q_sw in an approximately a linear format, though a relatively small variation in uniformity was observed in the lower range of Q_sw (<30 μL min⁻¹). This was also related to the larger secondary water droplets formed while there was an increase in uncertainty. Also, the viscosity of the primary dispersed water phase had an insignificant effect on both the process stability and uniformity of the fused droplets (Fig. 12d). This may be attributed to the large difference between the inertial forces and viscous forces in the gas–oil–water multiphase flow along a microscale fluidic channel.

4. Conclusions

With a microreactor having three T-junctions and a main flow channel, the dynamics and controllability of droplet fusion were investigated under gas–liquid–liquid multiphase flow. By introducing the gas through the first T-junction, dispersed gas bubbles were formed under a steady flow of the oil continuous phase along the main channel. The injection of the primary water phase via the second T-junction generated water droplets dispersed in the continuous phase. Scaling laws were established by correlating the size of bubbles or droplets with the different flow rates of both fluids. The introduction of the secondary water phase via the third T-junction produced secondary water droplets that were also dispersed in the oil phase. Within the continuous oil phase, the primary and secondary water droplets met, made contact, crushed the oil film barrier between them and finally fused under suitable operating conditions. The conditions were further quantified by identifying the appropriate window for each key parameter and were collectively displayed on typological diagrams for droplet fusion. Closer examinations of the fusion process revealed two stages (i.e. drainage and fusion) for the two droplets to fuse while become mature by breaking-up with the secondary water supply stream. It was found that the drainage time was significantly longer (typically a few times) than the fusion time. A droplet contact model was employed to understand the influence on the process stability and uniformity of the merged/fused droplets by varying the surfactant concentration (in oil), the viscosity of the water phase, and the flow rates of different fluids. It is believed that this systematic investigation can provide useful guidance for understanding and further applying the complex flow process in a range of applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the financial supports from National Natural Science Foundation of China (No. 21978250, 21808194), Natural Science Foundation of Shandong Province (ZR2017BB058) and Key Technology Research and Development Program of Shandong (2019JZZY010410).

References

1. K. Jähnisch, V. Hessel, H. Löwe and M. Baerns, Angew. Chem., Int. Ed., 2004, 43, 406–446.
2. A. J. deMello, Nature, 2006, 442, 394–402.
3. N. Aoki, R. Ando and K. Mae, Ind. Eng. Chem. Res., 2011, 50, 4672–4677.
4. V. M. Rajesh and V. V. Buwa, Chem. Eng. J., 2012, 207–208, 832–844.
5. Q. D. Zhang, C. Y. Zhu, W. Du, C. Liu, T. T. Fu, Y. G. Ma and H. Z. Li, Chem. Eng. Res. Des., 2018, 139, 188–196.
6. P. Garstecki, H. A. Stone and G. M. Whitesides, Phys. Rev. Lett., 2005, 94, 164501.
7. Z. H. Nie, M. S. Seo, S. Q. Xu, P. C. Lewis, M. Mork, E. Kumacheva, G. M. Whitesides, P. Garstecki and H. A. Stone, Microfluid. Nanofluid., 2008, 5, 585–594.
8. C. Q. Yao, Y. Y. Liu, S. N. Zhao, Z. Y. Dong and G. W. Chen, AIChE J., 2017, 63, 1727–1739.
9. Y. Önal, M. Lucas and P. Claus, Chem. Eng. Technol., 2005, 28, 972–978.
10. Y. H. Su, G. W. Chen, Y. C. Zhao and Q. Yuan, AIChE J., 2009, 55, 1948–1958.
11. A. Ufer, D. Sudhoff, A. Mescher and D. W. Agar, Chem. Eng. J., 2011, 167, 468–474.
12. S. K. Yap, Y. Yuan, L. Zheng, W. K. Wong, J. G. Zhang, N. Yan and S. A. Khan, Green Chem., 2014, 16, 4654–4658.
13. A. M. Nightingale, T. W. Phillips, J. H. Bannock and J. C. de Mello, Nat. Commun., 2014, 5, 3777.
14. B. Zheng and R. F. Ismagilov, Angew. Chem., Int. Ed., 2005, 44, 2520–2523.
15. S. Duraiswamy and S. A. Khan, Nano Lett., 2010, 10, 3757–3763.
16. T. Hatakeyama, D. L. Chen and R. F. Ismagilov, J. Am. Chem. Soc., 2006, 128, 2518–2519.
17. L. Li, J. Q. Boedicker and R. F. Ismagilov, Anal. Chem., 2007, 79, 2756–2761.
18. N. Assmann and P. R. von Rohr, Chem. Eng. Process., 2011, 50, 822–827.
19. V. M. Rajesh and V. V. Buwa, Chem. Eng. J., 2018, 345, 688–705.
20. K. Wang, Y. C. Lü, K. Qin, G. S. Luo and T. Wang, Chem. Eng. Technol., 2013, 36, 1047–1060.
21. J. Yue, E. V. Rebrov and J. C. Schouten, Lab Chip, 2014, 14, 1632–1649.
22. Y. Y. Liu, J. Yue, S. N. Zhao, C. Q. Yao and G. W. Chen, AIChE J., 2017, 64, 376–388.
23. Y. Y. Liu, J. Yue, C. Xu, S. N. Zhao, C. Q. Yao and G. W. Chen, AIChE J., 2019 DOI:10.1002/aic.16805.
24. P. Zhang, C. Q. Yao, H. Y. Ma, N. Jin, X. L. Zhang, H. Y. Lü and Y. C. Zhao, Chem. Eng. Sci., 2018, 182, 17–27.
25. H. Y. Ma, N. Jin, P. Zhang, Y. F. Zhou, Y. C. Zhao, X. L. Zhang, H. Y. Lü and J. Liu, Chem. Eng. Res. Des., 2019, 144, 247–257.
26. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446.
27. K. Wang, K. Qin, Y. C. Lü, G. S. Luo and T. Wang, AIChE J., 2015, 61, 1722–1734.
28. A. Ghaini, A. Mescher and D. W. Agar, Chem. Eng. Sci., 2011, 66, 1168–1178.
29. R. S. Abiev, Chem. Eng. J., 2013, 227, 66–79.

---