Open Access Article
Open Access ArticleSynthesis, structure, and electronic properties of the Li11RbGd4Te6O30 single crystal†
Zhi-An Zhua,
Yu-Cong Hea,
Yang-Yang Lvbc,
Jiang-He Feng*d and
Jian Zhou *ace
*ace
aNational Laboratory of Solid State Microstructures, Department of Materials Science and Engineering, Nanjing University, Nanjing, 210093 China. E-mail: zhoujian@nju.edu.cn
bNational Laboratory of Solid State Microstructures, Department of Physics, Nanjing University, Nanjing, 210093 China
cCollaborative Innovation Center of Advanced Microstructure, Nanjing University, Nanjing, 210093 China
dState Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou 350002, China. E-mail: fengjianghe@fjirsm.ac.cn
eJiangsu Key Laboratory of Artificial Functional Materials, Nanjing University, Nanjing, 210093 China
First published on 23rd March 2020
Abstract
Materials with spin dimers have attracted much attention in the last several decades because they could provide a playground to embody simple quantum spin models. For example, the Bose–Einstein condensation of magnons has been observed in TlCuCl3 with anti-ferromagnetic Cu2Cl6 dimers. In this work, we have synthesized a new kind of single-crystal Li11RbGd4Te6O30 with Gd2O15 dimers. This material belongs to the rhombohedral system with the lattice parameters: a = b = c = 16.0948 Å and α = β = γ = 33.74°. First-principles calculations indicate that Li11RbGd4Te6O30 is a wide-bandgap (about 4.5 eV) semiconductor. But unlike many other well studied quantum dimer magnets with an anti-ferromagnetic ground state, the Gd2O14 dimers in Li11RbGd4Te6O30 show ferromagnetic intra-dimer exchange interactions according to our calculations. Our work provides a new material which could possibly extend the studies of the spin dimers.
1. Introduction
Dimerized quantum spin systems are one of the simplest physical models in quantum mechanisms.1 They are closely related to many phenomena associated with condensed matter physics. For example, the widely concerned quantum dimer magnet (QDM) is a quantum magnetism in which a pair of spins are entangled and form an S = 0 singlet state. The singlet ground states act like bosons and their excited triplet states (also called triplons) can undergo Bose–Einstein condensation (BEC), which is one of the most exotic phenomena predicted by quantum mechanics.2,3 Many quantum dimer magnet systems have been reported in the past several decades. A canonical example of a strongly coupled spin-dimer system is TlCuCl3. It is a monoclinic structure composed of planar dimers of Cu2Cl6, which has a strong antiferromagnetic intra-dimer interaction and a much weaker inter-dimer interaction.3–5 BaCuSi2O6 is a quasi-2D square lattice magnetic insulator with a gapped spin dimer ground state and is supposed to be an ideal candidate for studying the BEC of triplons as a function of the external magnetic field.6 Recently, Hester et al.7 reported a new Yb3+ based QDM in the distorted honeycomb-lattice material Yb2Si2O7 with strong spin–orbit coupling (SOC). The intra-dimer bond length of two Yb ions is about 3% shorter than that of the inter-dimer ones, resulting in contrastive exchange interactions Jintra = 0.236 meV and Jinter = 0.06 meV.In addition to BEC, quantum spin dimers are intently associated with other physical phenomena, such as the topologic states research. SrCu2(BO3)2 is the archetypal quantum magnet with a gapped dimer-singlet ground state and triplon excitations to realize the Shastry–Sutherland model.8 The anisotropies arising from the intra-dimer Dzyaloshinskii–Moriya interactions give rise to topological character in the triplon band structure.9,10 Dimers strongly influence the whole magnetic state of crystal. Generally, an isolated dimer is antiferromagnetic coupling and spin dimer materials usually exhibit a quite intricate magnetic property. Jia et al.11 proposed that the breaking bonds in Ge–Ge dimers of SrCo2(Ge1−xPx)2 lead to a paramagnetic–ferromagnetic transition. A weakly coupled spin transition metal Cu dimers and Fe chains compound Cu2Fe2Ge4O13 exhibits that the Cu dimers play the role of media in the indirect magnetic interaction.12 Actually, spin dimers mostly consist of transition metal elements. Compared to 3d electrons in transition metal ion systems, the shielding effect of magnetic 4f electrons with Yb dimers in rare earth metal Cs3Yb2Cl9 and Cs3Yb2Br9 result in smaller exchange interactions, but lead to considerable magnetic dipole–dipole interactions.13 Spin dimer system is under great focus while dimers of rare earth (RE) metal ions have received much less attention.
Here we report a newly synthesized rare earth metal compound Li11RbGd4Te6O30 consisting of Gd2O15 dimers. Our first-principles calculations indicate that Li11RbGd4Te6O30 is a wide-bandgap semiconductor and the Gd3+ ions in the same dimer have a ferromagnetic exchange interaction.
2. Experimental methods
2.1. Synthesis and crystal growth of Li11RbGd4Te6O3
Li11RbGd4Te6O30 was synthesized by the high-temperature solid-state reactions. The reagents of Li2CO3, Rb2CO3, Gd2O3, and TeO2 at the stoichiometric ratio of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 were ground in agate mortar before loaded into a platinum crucible. Then the mixture was heated to 820 °C in 10 h, retained for 2 days, and then cooled to 600 °C at 3–5 °C h−1 rate, thereafter, cooled to room temperature at rate of 20 °C h−1 before the furnace power was switched off. Then colorless and small single crystals can be obtained after the sample being soaked in deionized water for 1 day. Te4+ usually can be oxidized to Te6+ by oxygen during the reaction at high temperature in air.14 Furthermore, the EDS elemental analysis on several single crystals shows an average Rb/Te/Gd molar ratio of 1.0/5.8/3.9 (Fig. S1 in the ESI†), which is consistent with that from single-crystal XRD studies. And ICP measurement confirmed the existence of Li-ion in this compound.
12 were ground in agate mortar before loaded into a platinum crucible. Then the mixture was heated to 820 °C in 10 h, retained for 2 days, and then cooled to 600 °C at 3–5 °C h−1 rate, thereafter, cooled to room temperature at rate of 20 °C h−1 before the furnace power was switched off. Then colorless and small single crystals can be obtained after the sample being soaked in deionized water for 1 day. Te4+ usually can be oxidized to Te6+ by oxygen during the reaction at high temperature in air.14 Furthermore, the EDS elemental analysis on several single crystals shows an average Rb/Te/Gd molar ratio of 1.0/5.8/3.9 (Fig. S1 in the ESI†), which is consistent with that from single-crystal XRD studies. And ICP measurement confirmed the existence of Li-ion in this compound.
2.2. Elemental analyses
Energy-dispersive spectroscopy (EDS) and SEM analyses were accomplished with a JEOL JSM-6700F scanning electron microscope and Hitachi FE-SEM SU8010. Inductively coupled plasma (ICP) measurement was investigated on an Ultima 2 inductively coupled plasma OES spectrometer.2.3. Single crystal structure determination
Platy single crystal was glued onto glass fiber and mounted on a SuperNova (Mo) X-ray Source (λ = 0.71073 Å) at 293(2) K for reflection data collections. The data set was corrected for Lorentz, polarization factors and absorption by the Multi-scan method by the CrysAlisPro software,15 and the R(int) improved from 0.126 (before correction) to be 0.063 (after correction). This structure was solved by direct methods and refined by a full-matrix least-squares fitting on F2 by using SHELX-2018.16 All atoms were refined with anisotropic thermal parameters. The structures were checked for possible twinning and missing symmetry elements by using PLATON, but none was found.172.4. Computational details
Electron properties of Li11RbGd4Te6O30 are calculated by the density functional theory (DFT) implemented in the Vienna ab initio simulation package (VASP).18,19 The projected augmented wave method20,21 and the generalized gradient approximation with the Perdew–Burke–Ernzerhof revised for solids (PBEsol) exchange–correlation functional are used.22 The plane-wave cutoff energy is 520 eV and the Gaussian smearing width is 0.05 eV. Both the internal atomic positions and the lattice constants are allowed to relax until the maximal residual Hellmann–Feynman forces on atoms are smaller than 0.02 eV Å−1. The k-mesh is 2 × 2 × 2 for structural optimization and 4 × 4 × 4 is used for the electron density of states (DOS) calculations. The GGA+U method with the approach described by Dudarev et al.23 is used in our calculations. The effective U of 6.0 eV is used on Gd's f orbitals. Due to the well-known underestimation of bandgap in standard DFT calculations, we also use the modified Becke–Johnson (MBJ) exchange potential,24 which could yield band gaps with an accuracy similar to hybrid functional or GW methods, but in a much less computational cost. The crystal structures are plotted by the VESTA program.253. Results and discussion
3.1. Crystal structure
Our synthesized Li11RbGd4Te6O30 is a colorless and transparent crystal with several hundred-micrometer size (Fig. S2 in the ESI†). It belongs to the rhombohedral system with a space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (No. 167). In experiment, it is more convenient to show the structure in a hexagonal representation, as given in Fig. 1a. The experimental refined structural and crystallographic data are summarized in Table 1. The hexagonal cell parameters are a = b = 9.3415(2) Å and c = 45.4929(15) Å. Equivalently, its primitive cell parameters are a = b = c = 16.0948 Å and α = β = γ = 33.74° in the rhombohedral representation. Li11RbGd4Te6O30 has a very complex crystal structure. Its hexagonal unit cell contains 312 ions and three primitive cells.
c (No. 167). In experiment, it is more convenient to show the structure in a hexagonal representation, as given in Fig. 1a. The experimental refined structural and crystallographic data are summarized in Table 1. The hexagonal cell parameters are a = b = 9.3415(2) Å and c = 45.4929(15) Å. Equivalently, its primitive cell parameters are a = b = c = 16.0948 Å and α = β = γ = 33.74° in the rhombohedral representation. Li11RbGd4Te6O30 has a very complex crystal structure. Its hexagonal unit cell contains 312 ions and three primitive cells.
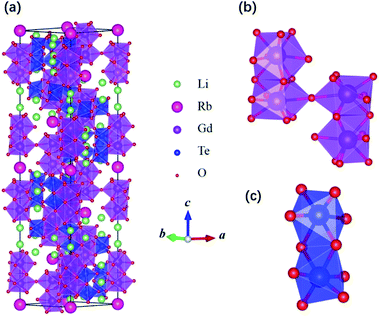 | ||
| Fig. 1 (a) Hexagonal unit cell of Li11RbGd4Te6O30 and the local structure of (b) four GdO9 tetrakaidecahedrons and (c) two TeO6 octahedrons. | ||
| a R1 = ∑||Fo| − |Fc||/∑|Fo|, wR2 = {∑w[(Fo)2 − (Fc)2]2/∑w[(Fo)2]2}1/2. | |
|---|---|
| Formula | Li11RbGd4Te6O30 |
| fw | 2036.41 |
| Temp, K | 293(2) |
| Space group | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
| a/Å | 9.3340(2) |
| c/Å | 45.4665(14) |
| Volume/Å3 | 3430.50(15) |
| Z | 6 |
| Dcalc, g cm−3 | 5.914 |
| F(000) | 5268 |
| Completeness (%) | 99.7 |
| μ, mm−1 | 21.191 |
| GOF on F2 | 1.20 |
| R1, wR2 [I >2σ(I)] | 0.019, 0.0452 |
| R1, wR2 (all data) | 0.020, 0.0456 |
The experimental refined atomic coordinates, Wyckoff positions, equivalent isotropic displacement parameters, and important bond lengths are listed in Tables 2 and 3, respectively. It is found that three types of Li ions occupy the 36f, 12c and 18e sites, while Rb ions occupy the 6b site.
| Atom | Wyckoff | x | y | z | U (eq.) |
|---|---|---|---|---|---|
| Gd(1) | 12c | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
771(1) | 5(1) |
| Gd(2) | 12c | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1538(1) | 5(1) |
| Te(1) | 36f | 6515(1) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058(1) 058(1) |
483(1) | 4(1) |
| Rb(1) | 6b | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0 | 12(1) |
| Li(1) | 12c | 6667 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 333 |
548(4) | 10(3) |
| Li(2) | 36f | 9875(9) | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260(9) 260(9) |
213(2) | 14(2) |
| Li(3) | 18e | 6667 | 6519(12) | 833 | 17(2) |
| O(1) | 36f | 8863(4) | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287(4) 287(4) |
481(1) | 8(1) |
| O(2) | 18e | 6667 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476(4) 476(4) |
833 | 8(1) |
| O(3) | 18e | 6667 | 8755(5) | 833 | 7(1) |
| O(4) | 36f | 6079(4) | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 432(4) 432(4) |
248(1) | 9(1) |
| O(5) | 36f | 4176(4) | 8737(4) | 538(1) | 7(1) |
| O(6) | 36f | 6377(4) | 8623(3) | 182(1) | 8(1) |
| Bond | Distances | BV | BVS | Bond | Distances | BV | BVS |
|---|---|---|---|---|---|---|---|
| Gd(1)–O(5)×3 | 2.340(3) | 0.476 | 3.261 | Rb(1)–O(1)×6 | 2.938(3) | 0.160 | 0.816 |
| Gd(1)–O(1) × 3 | 2.361(3) | 0.449 | Rb(1)–O(6) × 6 | 3.070(3) | 0.112 | ||
| Gd(1)–O(3) × 3 | 2.738(2) | 0.162 | Li(1)–O(4) × 3 | 2.082(10) | 0.189 | 1.021 | |
| Gd(2)–O(4) × 3 | 2.326(3) | 0.476 | 3.291 | Li(1)–O(2) × 3 | 2.165(9) | 0.151 | |
| Gd(2)–O(6) × 3 | 2.505(3) | 0.449 | Li(2)–O(1) | 2.008(9) | 0.231 | 0.855 | |
| Gd(2)–O(5) × 3 | 2.512(3) | 0.162 | Li(2)–O(6) | 2.069(8) | 0.196 | ||
| Te(1)–O(4) | 1.864(3) | 1.1541 | 5.775 | Li(2)–O(6) | 2.093(9) | 0.184 | |
| Te(1)–O(6) | 1.875(3) | 1.120 | Li(2)–O(4) | 2.183(7) | 0.1441 | ||
| Te(1)–O(1) | 1.899(2) | 1.050 | Li(2)–O(5) | 2.318(9) | 0.100 | ||
| Te(1)–O(5) | 1.912(2) | 1.014 | Li(3)–O(3) | 2.087(12) | 0.187 | 0.676 | |
| Te(1)–O(2) | 2.028(2) | 0.741 | Li(3)–O(5) × 2 | 2.193(4) | 0.140 | ||
| Te(1)–O(3) | 2.051(2) | 0.696 | Li(3)–O(1) × 2 | 2.302(3) | 0.105 |
There are two types of Gd ions both occupying 12c sites and every Gd ions have nine neighboring O ions and forms GdO9 tetrakaidecahedrons. For Gd(1), the nine Gd–O bonds have three different lengths: 2.340, 2.361 and 2.738 Å, while the bond lengths of Gd(2)–O are shorter, which are 2.326, 2.505, and 2.512 Å. Two Gd–O tetrakaidecahedrons (Gd(1) and Gd(2)) along the c axis share the same face and forms a Gd2O15 dimer structure. In the a–b plane, two Gd–O tetrakaidecahedrons are also connected by the same O ion. The local structure of four GdO9 tetrakaidecahedrons is separately shown in Fig. 1b. The intra-dimer distance between the two Gd ions in the same dimer is about 3.5 Å, which is much shorter than that of the inter-dimer Gd ions (about 5.4 Å).
The Te ions occupy the 36f site and every Te ion is surrounded by six O ions and forms TeO6 octahedron. The Te–O bond lengths spread from 1.864 to 2.051 Å. The two TeO6 octahedrons along the c axis share the same edge and form a Te2O10 dimer structure, which is shown in Fig. 1c.
Based on the experimental crystal structure, we also implemented a theoretical structural optimization based on the DFT calculation. Both the lattice constants and atomic positions are optimized in a primitive cell. We find the theoretical lattice constants are well consistent with the experimental ones with a maximal error of 0.34% as shown in Table 4. The theoretical atomic positions are also in good agreement with the experimental results, which are not shown here.
| Lattice constant | a (Å) | c (Å) | V (Å3) |
|---|---|---|---|
| Theory | 9.3098 | 45.4157 | 3408.93 |
3.2. Electronic structure
In order to understand the basic physical properties of Li11RbGd4Te6O30, we also calculated its band structure and electronic density of states (DOS) by the first-principles calculations. In general, the normal DFT method cannot deal with the lanthanides correctly due to their strongly correlation of the f electrons. However, in the crystal Li11RbGd4Te6O30, the Gd ions have a valence state of 3+. A Gd3+ ion has 7 electrons, which just fully occupy the majority f orbitals and make the minority f orbitals totally empty (i.e. Gd3+ has a high spin state and a spin magnetic moment of 7 μB). As a result, the f bands of Gd ions should be far away from the Fermi energy and thus Gd3+ ions could be handled reasonably well in the simple GGA+U scheme.On the other hand, since there are 8 Gd ions in the primitive cell (24 ones in a conventional cell) of the Li11RbGd4Te6O30 and it is almost not possible to calculate all the magnetic structures in the first-principles calculations. As we show above, the Gd ions in Li11RbGd4Te6O30 forms dimer structures, it is reasonable to assume that the Gd(1) and Gd(2) in a Gd2O15 dimer has the strongest exchange interaction, while the interactions between different dimmers are weaker. Therefore, we consider eight magnetic configurations in a primitive cell shown in Table 5. The positions of eight Gd ions in the primitive cell are shown in Fig. S3 in the ESI.† The first four configurations in Table 5 have a ferromagnetic intra-dimer coupling while the last four have an anti-ferromagnetic coupling. However, their inter-dimer couplings contain both ferromagnetic and anti-ferromagnetic ones due to the complex connecting relationship between different Gd2O15 dimers. We cannot construct a magnetic configuration with all the inter-dimer coupling being anti-ferromagnetic or ferromagnetic except for the ferromagnetic one (first configuration in Table 5).
| No. | Spin structure | Relative energy (meV) |
|---|---|---|
| 1 | ↑↑↑↑↑↑↑↑ | 0 |
| 2 | ↑↑↑↑↑↑↓↓ | −0.96 |
| 3 | ↑↑↑↑↓↓↓↓ | −1.10 |
| 4 | ↑↑↓↓↑↑↓↓ | −0.83 |
| 5 | ↑↓↑↓↑↓↑↓ | 1.23 |
| 6 | ↑↓↑↓↑↓↓↑ | 1.03 |
| 7 | ↑↓↑↓↓↑↓↑ | 0.03 |
| 8 | ↑↓↓↑↑↓↓↑ | 0.82 |
The total energies of eight spin configurations are also given in Table 5, from which we can find that the first four configurations have lower energies than those of the last four. Therefore, we could expect that the intra-dimer coupling should be ferromagnetic. However, we cannot determine the size of the inter-dimer coupling due to the complex connecting relationship between different dimers. In our calculations, the spin configuration ↑↑↑↑↓↓↓↓ has the lowest energy, which is 1.1 meV per primitive cell (or 0.28 meV per a Gd2O15 dimer) lower than the ferromagnetic one. Such a small energy difference is reasonable since the f orbitals are quite localized. Furthermore, the calculated spin magnetic moment of Gd ions are 7 μB as we expected.
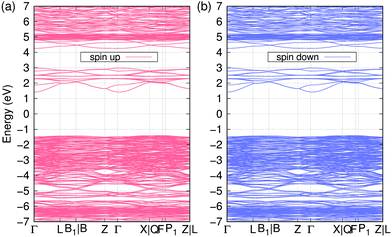
In Fig. 2, we represent the electron band structure of Li11RbGd4Te6O30 with the ↑↑↑↑↓↓↓↓ spin configuration. It is found that the valence bands are quite flat, while the conduction bands are much dispersive. We also can see that there are lots of flat bands around −6.5 and 5 eV, which is supposed to be the occupied and unoccupied f orbitals of Gd ions respectively. We can confirm it later in the DOS calculations. It is obvious that there is a quite large bandgap of 2.8 eV in both spin components. The normal DFT method always underestimate the band gap significantly in semiconductors or insulators. Therefore we also use the MBJ method to obtain a more accurate bandgap. The MBJ calculation results in a much larger bandgap of about 4.5 eV. Since the crystal of Li11RbGd4Te6O30 is quite transparent in the visible light, we think that the experimental band gap should be close to 4.5 eV as we obtained in the MBJ calculation.
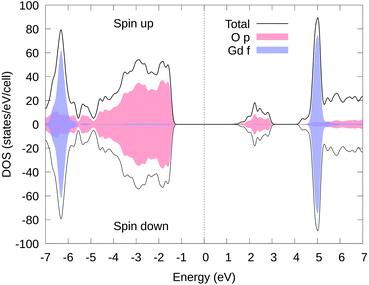
In Fig. 3, we present the total and partial electron DOS of Li11RbGd4Te6O30 in the same magnetic state as used in Fig. 2. It is obvious that the electron states near the Fermi energy are both mainly contributed from O's p orbitals (red). There are two narrow peaks (blue) near −6.5 and 5 eV which are of course the Gd's f orbitals. The DOS of other ions such as Rb, Li, and Te are not shown here since their states are far away from the Fermi energy.
3.3. Discussions
The Gd3+ ions are in high spin states which is confirmed by the first-principles calculations. The exchange interaction between the two Gd ions in the same dimer is shown to be ferromagnetic, however, we still can see that the inter-dimer coupling can not be negligible. From Table 5, it is obvious that the first four spin configurations all have a ferromagnetic coupling in the same dimer but they have different total energies due to the different inter-dimer coupling. This is because the smallest inter-dimer distance (about 5.4 Å) is not that much longer than the intra-dimer one (about 3.5 Å), thus the inter-dimer coupling can not be negligible. However, we can not determine the size of the inter-dimer coupling at present due to the complex crystal structure. From Table 5, we can conclude that the ferromagnetic order is not favored in theory. More experimental works about the magnetic properties of Li11RbGd4Te6O30 should be taken in the future. Nevertheless, the strength of the magnetic coupling is very small due to the much-localized f orbitals of Gd. If Li11RbGd4Te6O30 has a long-range magnetic order, its Néel temperature should be quite low.4. Conclusions
We have synthesized a new rhombohedral crystal Li11RbGd4Te6O30 with Gd2O15 dimer structures. Our experimental refinements and theoretical optimizations give almost the same lattice constants and atomic positions. This indicates that we have obtained a highly reliable crystal structure for the very complex crystal Li11RbGd4Te6O30. Its preliminary electronic and magnetic properties are only studied by the first-principles calculations. It is found that Li11RbGd4Te6O30 is a wide-bandgap (about 4.5 eV) semiconductor. Gd3+ ions are in high spin states with a spin magnetic moment of 7 μB. The exchange interactions between the two Gd3+ ions in the same Gd2O15 dimer are ferromagnetic from our calculations. The inter-dimer couplings can not be negligible but are not determined in the present work. More experimental works about the magnetic properties of Li11RbGd4Te6O30 should be taken in the future. This material could possibly extend the studies of the spin dimers.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the National Key R&D Program of China (Grant No. 2016YFA0201104), National Natural Science Foundation of China (Grant No. 11974163, 11890702, and No. 51721001). Y.-Y. Lv acknowledges the financial support from Innovation Program for the Talents of China Postdoctoral Science Foundation (BX20180137) and support from China Postdoctoral Science Foundation (2019M650105). The numerical calculations in this paper have been done on the computing facilities in the High Performance Computing Center (HPCC) of Nanjing University.References
- D. S. Inosov, Adv. Phys., 2018, 67, 149–252 CrossRef.
- T. Giamarchi, C. Rüegg and O. Tchernyshyov, Nat. Phys., 2008, 4, 198–204 Search PubMed.
- F. Yamada, T. Ono, H. Tanaka, G. Misguich, M. Oshikawa and T. Sakakibara, J. Phys. Soc. Jpn., 2008, 77, 4–7 Search PubMed.
- T. Nikuni, M. Oshikawa, A. Oosawa and H. Tanaka, Phys. Rev. Lett., 2000, 84, 5868 CrossRef CAS PubMed.
- A. Oosawa, T. Kato, H. Tanaka, K. Kakurai, M. Müller and H. J. Mikeska, Phys. Rev. B, 2002, 65, 094426 CrossRef.
- M. Jaime, V. F. Correa, N. Harrison, C. D. Batista, N. Kawashima, Y. Kazuma, G. A. Jorge, R. Stern, I. Heinmaa, S. A. Zvyagin, Y. Sasago and K. Uchinokura, Phys. Rev. Lett., 2004, 93, 087203 CrossRef CAS PubMed.
- G. Hester, H. S. Nair, T. Reeder, D. R. Yahne, T. N. DeLazzer, L. Berges, D. Ziat, J. R. Neilson, A. A. Aczel, G. Sala, J. A. Quilliam and K. A. Ross, Phys. Rev. Lett., 2019, 123, 027201 CrossRef CAS PubMed.
- B. S. Shastry and B. Sutherland, Phys. B+C, 1981, 108, 1069–1070 CrossRef CAS.
- O. Cépas, K. Kakurai, L. P. Regnault, T. Ziman, J. P. Boucher, N. Aso, M. Nishi, H. Kageyama and Y. Ueda, Phys. Rev. Lett., 2001, 87, 167205 CrossRef PubMed.
- J. Romhányi, K. Penc and R. Ganesh, Nat. Commun., 2015, 6, 6805 CrossRef PubMed.
- S. Jia, P. Jiramongkolchai, M. R. Suchomel, B. H. Toby, J. G. Checkelsky, N. P. Ong and R. J. Cava, Nat. Phys., 2011, 7, 207–210 Search PubMed.
- T. Masuda, A. Zheludev, B. Sales, S. Imai, K. Uchinokura and S. Park, Phys. Rev. B, 2005, 72, 094434 CrossRef.
- H. U. Güdel, A. Furrer and H. Blank, Inorg. Chem., 1990, 29, 4081–4084 CrossRef.
- J. H. Feng, C. L. Hu, X. Xu, F. Kong and J. G. Mao, Inorg. Chem., 2015, 54, 2447–2454 CrossRef CAS PubMed.
- CrystalClear, Version 1.3.5, Rigaku Corp., The Woodlands, TX, 1999 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- L. A. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. Dudarev, G. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 221101 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1984029 contains the supplementary crystallographic data of Li11RbGd4Te6O30 for this paper. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra10163b |
| This journal is © The Royal Society of Chemistry 2020 |