Effective estimation of the inhibitor affinity of HIV-1 protease via a modified LIE approach

Abstract

The inhibition of the Human Immunodeficiency Virus Type 1 Protease (HIV-1 PR) can prevent the synthesis of new viruses. Computer-aided drug design (CADD) would enhance the discovery of new therapies, through which the estimation of ligand-binding affinity is critical to predict the most efficient inhibitor. A time-consuming binding free energy method would reduce the usefulness of CADD. The modified linear interaction energy (LIE) approach emerges as an appropriate protocol that performs this task. In particular, the polar interaction free energy, which is obtained via numerically resolving the linear Poisson–Boltzmann equation, plays as an important role in driving the binding mechanism of the HIV-1 PR + inhibitor complex. The electrostatic interaction energy contributes to the attraction between two molecules, but the vdW interaction acts as a repulsive factor between the ligand and the HIV-1 PR. Moreover, the ligands were found to adopt a very strong hydrophobic interaction with the HIV-1 PR. Furthermore, the results obtained corroborate the high accuracy and precision of computational studies with a large correlation coefficient value R = 0.83 and a small RMSE δ_RMSE = 1.25 kcal mol⁻¹. This method is less time-consuming than the other end-point methods, such as the molecular mechanics Poisson–Boltzmann surface area (MM/PBSA) and free energy perturbation (FEP) approaches. Overall, the modified LIE approach would provide ligand-binding affinity with HIV-1 PR accurately, precisely, and rapidly, resulting in a more efficient design of new inhibitors.

---

Introduction

The human immunodeficiency virus (HIV) causes acquired immunodeficiency syndrome (AIDS), which leads to the death of several million people worldwide.¹ Although new patients have been reduced by around ∼40% compared to the peak in 1997, still ∼1.7 million new people have been infected in 2018.¹ Moreover, globally, nearly 40 million people are currently living with HIV/AIDS, but only ∼23 million patients have access to antiviral drugs.¹ The HIV/AIDS epidemic is still one of the most important global health issues. Therefore, the search for a new therapy to prevent HIV continuously attracts a large number of scientists. The scientists have tried to inhibit HIV by preventing viral reproduction through the use of fusion,² reverse transcriptases,³ integrases,⁴ and protease inhibitors.⁵ Recently, the contemporary use of multiple drugs, which target several different HIV targets, are often employed to enhance the treatment efficiency, resulting in the decrease of patient mortality. This method is known as highly active antiretroviral therapy (HAART).⁶ Unfortunately, several resistance issues and unexpected side effects have been recorded over the treatment via HAART.⁷ Designing new inhibitors for HIV targets is still urgent.

The HIV-1 PR enzyme plays an important role in the synthesis of new viruses since it contributes to the cleavage of polyproteins to generate mature components of the HIV virion.⁸ Thus, the inhibition of HIV-1 PR is able to stop virus replication. Severally successful inhibitors have been designed for inhibiting HIV-1 PR and many of them were approved for HIV treatment, such as Amprenavir, Indinavir, Lopinavir, Nelfinavir, Ritonavir, and Saquinavir.⁹ HIV-1 PR inhibitors are currently used alongside reverse transcriptase inhibitors, resulting in an improvement in HIV-1 therapy. However, available HIV-1 PR inhibitors still have many side effects and their efficiency decrease with mutant viral strains.^10,11 Thus, the search of a potential candidate to efficiently inhibit HIV-1 PR still attracts numerous efforts.

Computer-aided drug design (CADD) is a very useful method to shorten the development of new therapy.¹² Several approaches have been established to determine the free energy difference of binding between the ligand and the receptor such as non-equilibrium molecular dynamics (NEMD),^13,14 free energy perturbation (FEP),^15,16 thermodynamic integration (TI),^17,18 molecular mechanic/Poisson–Boltzmann surface area (MM/PBSA),^19–21 linear interaction energy (LIE),^22–25 fast pulling of ligand (FPL),^26,27 biased sampling (US),^28–30 deep learning,³¹ molecular docking,^32,33 and quantitative structure–activity relationship (QSAR) approaches.^34–36 Moreover, it is known that the accuracy of a ligand-binding affinity determination method is normally inversely proportional to the computational cost. In general, a computed method is employed on the number of ligands to analyse. In particular, the screening of million trial ligands is often performed using rapid and low accuracy approaches such as docking and QSAR methods. The testing binding affinity of hundred inhibitors is frequently carried out via an approximate method, which keeps blank between performance and accuracy, as known as MM/PBSA, LIE, FPL, and the US approaches. Time-consuming protocols including NEMD, FEP, and TI usually give results in agreement with experiments. These schemes are usually used to refine the results of an approximate method. Furthermore, the implementation of temperature/Hamiltonian replica exchange molecular dynamics simulations of the free energy perturbation method can present higher accuracy and precision results.^37–39

Approximate methods are often employed to resolve the CADD problem. In particular, the MM/PBSA and LIE end-point approaches are very popular methods. In the MM/PBSA method, binding free energy is evaluated via a combination of molecular mechanics and continuum solvent.^40–42 However, the accuracy of the MM/PBSA method depends on several factors that involve a continuum solvation approach, dielectric constant, and entropic determinations.^43–45 Moreover, when the considered system is larger than 2000 atoms, the entropic estimation via normal mode analysis would cost a large CPU time. Therefore, the entropic calculation is usually carried out in the last snapshot of MD simulations rather than the whole conformation over the equilibrium interval.^43–45 Thus, the statistical significance is unguaranteed. The selection of the dielectric constant also causes issues, resulting in a significant decrease of the obtained accuracy and precision.^43–45 Overall, although the MM/PBSA method is able to estimate reasonable values of ligand-binding affinity, the absolute values do not correlate with the experiments.^46–48

In addition, another end-point free energy estimation approach, LIE, gives successful results to different systems.^49–56 In this approach, the binding free energy difference is computed based on the average of electrostatic and van der Waals (vdW) interaction energy differences of the inhibitor with its neighbouring atoms in various states involving the inhibitor in a solvated complex (bound state – noted as subscript b) and inhibitor in solvation (free state – noted as subscript f). In this context, we have computed the binding free energies of 33 inhibitors interacting with HIV-1 PR by using conventional molecular dynamics (MD) simulations and the LIE approach. In particular, the continuum model was employed to enhance the accuracy of the conventional LIE approach. In the improved LIE method, the contribution of polar free energy was also considered as an important factor controlling the ligand-binding affinity. The scaling factors for electrostatic, vdW and polar terms were fitted considering the binding process of 22 systems and then re-evaluated in 11 systems. The obtained results probably provide an appropriate way to screen a large number of ligands with affinity to HIV-1 PR.

Materials and methods

Initial conformation and parameterization of HIV-1 PR complexes

The three-dimensional structures of 33 HIV-1 PR protease inhibitor complexes (cf. Fig. 1) are deposited in protein data bank with PDB ID: 1AJV,⁵⁷ 1AJX,⁵⁷ 1D4J,⁵⁸ 1EBW,⁵⁸ 1EBZ,⁵⁸ 1EC0,⁵⁹ 1EC2,⁵⁸ 1EC3,⁵⁸ 1G2K,⁶⁰ 1G35,⁶⁰ 1OHR,⁶¹ 1D4H,⁵⁸ 1T3R,⁶² 1W5X,⁵⁹ 1W5Y,⁵⁹ 1XL5,⁶³ 2AQU,⁶⁴ 2BPX,⁶⁵ 2CEJ,⁶⁶ 2CEM,⁶⁶ 2CEN,⁶⁶ 2I0D,⁶⁷ 2Q5K,⁶⁸ 2QI0,⁶⁹ 2UXZ,⁷⁰ 3H5B,⁷¹ 3NU3,⁷² 3O9G,⁷³ 3OXC,⁷⁴ 4DJQ,⁷⁵ 4DJR,⁷⁵ 4U7Q,⁷⁶ and 4U7V.⁷⁶ HIV-1 PR and ions were parameterized using the GROMOS96 43a1 force field⁷⁷ referring the previous works.^26,78 In particular, the protonation states of Asp25A and Asp25B are assigned according to previous works^26,79–83 or predicted via Propka 2.0 (ref. 84) since it has large effects on the ligand-binding affinity estimation. Moreover, the SPC water model was employed to represent water molecules.⁸⁵ The parameters of the ligands were generated via the PRODRG2 webserver,⁸⁶ but the atomic charges were determined by using the restrained electrostatic potential (RESP) approach⁸⁷ calculated by molecular orbital quantum chemical calculations using the Hartree–Fock (HF) functional with the 6-31G(d) basis set.

Fig. 1 Initial structure used for MD simulations of Indinavir bound to HIV-1 PR (PDB ID: 2BPX).

Molecular dynamics (MD) simulations

GROMACS version 5.1.3 (ref. 88) was used to mimic the solvated complexes. In this solvated complex, the HIV-1 PR + inhibitor system was inserted into a periodic boundary dodecahedron box with a volume of ∼367 nm³ and consists of 1 HIV-1 PR molecule, 1 inhibitor, ∼10 880 water molecules, and ∼4–5 Cl⁻ ions to neutralize the system (a total of ∼34 600 atoms). The ligand was put into a periodic boundary dodecahedron box with a volume of ∼74 nm³ and consists of 1 inhibitor molecule and 2400 water molecules (a total ∼7200 atoms). The simulation was carried out with parameters referring to the previous work,^26,89 in which the non-bonded pair cut-off is 1.0 nm. The vdW cut-off is 1.0 nm and the PME method is used for electrostatic interactions. MD simulations were performed in turn according to the following steps: energy minimization, position restraint in NVT ensemble, equilibrate in NPT simulations, and production MD simulations. In particular, the energy minimization was carried out by using the steepest descent approach. NVT and NPT simulations were achieved with an MD length of 100 ps per simulation. During the NVT simulation, the complex was restrained via a small harmonic potential. MD simulations were completed in 20 and 5 ns, which correspond to the solvated complex and isolated ligand in solvation systems, respectively. MD simulations were performed 4 autonomous times to generate 4 independent trajectories with the same initial conformation but different generated velocities.

Data analysis

The root-mean-square-deviations (RMSDs) of all atoms in the starting conformation was determined. Hydrogen bonds (HB) are calculated based on the geometric determination. In particular, the distance between the acceptor (A) and the donor (D) is required to be less than 0.35 nm and the A–H–D angle should be larger than 135° (H is hydrogen). The vdW, electrostatic, and polar interactions were computed to construct estimation models for the LIE method (eqn (3)) via linear regression analysis. The MM/PBSA approach was also carried out to estimate the difference in binding free energy between HIV-1 PR and its inhibitors. The details of the calculations were mentioned in previous studies.⁹⁰

Results and discussion

Structures and energies of complexes during MD simulations

The RMSD of all atoms in the solvated complex was evaluated to determine the equilibrium region (cf. Fig. S1 in ESI†), which was used to evaluate the free energy of interaction between the two molecules, HIV-1 PR and the inhibitor. The RMSD values were quickly enlarged during the first 2 ns of MD simulations and reached equilibrium circumstances after 5 ns of MD simulations, as shown in Fig. 2. RMSD values are smaller than 0.3 nm since the starting conformation is a native structure obtained through experiments. The solvated complex is rigidly stabilized during the last 10 ns of the MD simulations. The free energy estimation was calculated over the 10–20 ns interval of MD simulations. During this time, the protein–ligand interaction can be clarified with a two-dimensional protein–ligand interaction map using the last MD-generated conformations, as shown in Fig. S2 of ESI.† All maps mention that vdW interactions dominate over electrostatic interactions in all complexes. The RMSD of the solvated ligand system is rigidly similar to the complex. The energy calculation was carried out during the 2–5 ns interval of MD simulations.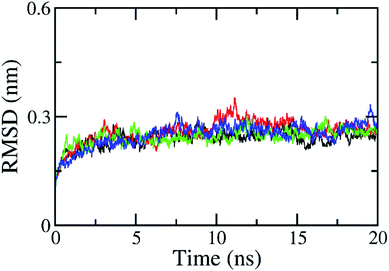

Fig. 2 All-atom RMSD of HIV-1 PR + Indinavir (2BPX) over 4 independent MD trajectories with a length of 20 ns. The complex almost reaches equilibrium region after 5 ns.

In order to estimate the ligand-binding affinity to HIV-1 PR using the LIE approach, the difference of the mean electrostatic (ΔE^cou_b–f) and vdW (ΔE^vdW_b–f) interaction energy between the inhibitor and its neighbouring molecules in a solvated complex of HIV-1 PR (bound state) and in solvation (free state) were calculated over 4 independent MD trajectories. The magnitude of ΔE^vdW_b–f is significantly larger than ΔE^cou_b–f implying the domination of the hydrophobic interaction during the binding process of a ligand to HIV-1 PR, which is consistent with the previous works.^27,78 Moreover, in the modified LIE approach, the influence of conformational entropy⁴⁹ and solvent-accessible surface area (ΔG^sur)^50,91 have also been exercised. The entropic contribution was evaluated by a normal mode approximation. The difference in surface energy (ΔG^sur) was determined by using the Shrake–Rupley method. Furthermore, the difference in the polar interaction energy (ΔG^PB) was calculated as it is probably employed as a term in the LIE function. The ΔG^PB was predicted by numerically resolving the linear Poisson–Boltzmann equation in a continuum solvent approximation. The results obtained are shown in Table 1. In particular, the average of ΔG^sur, ΔG^PB, and −TΔS values are computed as −8.93, 67.4, and 32.68 kcal mol⁻¹, respectively, and are in good agreement with previous studies^92–94 implying the validation of the calculated values.

Table 1 The free energy values obtained from experiments and MD simulations^a

Complexes	ΔE^coub–f	ΔE^vdWb–f	ΔG^sur	ΔG^PB	−TΔS	ΔGEXP
a Experimental values were acquired using the formula ΔGEXP = RT ln Ki, where R is a gas constant, T is the absolute temperature, and Ki is the inhibition constant obtained from previous studies.^58,59,62–76 The computational results were averaged over 4 independent trajectories. The unit of energy is kcal mol^−1.
1D4H	28.20	−43.80	−9.54	80.18	34.73	−13.74
1T3R	21.13	−34.10	−8.01	64.77	32.35	−14.91
1W5X	37.64	−44.50	−9.63	79.57	37.07	−11.54
1W5Y	23.52	−50.69	−9.71	84.82	34.80	−11.65
1XL5	23.72	−37.62	−8.99	58.82	30.73	−10.09
2AQU	12.02	−35.68	−10.00	70.51	36.03	−12.79
2BPX	−6.14	−32.15	−9.17	69.51	32.35	−12.90
2CEJ	23.38	−36.10	−9.19	55.09	31.74	−11.83
2CEM	16.61	−38.03	−9.15	61.60	35.32	−10.87
2CEN	26.06	−44.79	−9.41	68.62	33.93	−11.39
2I0D	24.06	−35.78	−8.92	81.24	33.01	−16.60
2Q5K	6.24	−31.51	−8.97	65.86	30.65	−15.51
2QI0	16.38	−34.69	−8.17	60.51	28.75	−10.13
2UXZ	33.49	−36.04	−9.60	49.54	33.58	−11.64
3H5B	14.43	−32.45	−8.34	69.86	31.91	−13.73
3NU3	14.67	−30.94	−7.62	66.56	28.86	−13.48
3O9G	6.20	−27.26	−8.48	75.99	30.45	−16.88
3OXC	30.11	−36.22	−8.85	53.30	32.85	−11.54
4DJQ	12.60	−28.06	−8.40	71.38	29.72	−14.16
4DJR	24.18	−35.30	−8.31	77.05	29.54	−15.82
4U7Q	29.57	−40.04	−10.18	74.49	41.44	−13.38
4U7V	5.43	−31.10	−7.87	43.50	29.19	−7.54

---

Optimization of LIE equations

As mentioned above, in the original LIE theory, the difference in the binding free energy was estimated based on the difference of ΔE^cou_b–f and ΔE^vdW_b–f (eqn (1)) with the empirical coefficients of α = 0.180 and β ≈ 0.300–0.500, which are validated upon applied receptors such as P450_CAM, potassium channel and aspartic proteases.^95–99 Recent work on amyloid beta-peptide system confirmed that the coefficients are α = 0.288 and β = 0.049.⁸⁹ The use of these coefficients to determine the binding free energy of HIV-1 PR + inhibitor produces a failure since the correlation coefficients are observed as R = 0.20, 0.14, and −0.43 corresponding to the set of empirical parameters of (0.180, 0.500), (0.180, 0.300), and (0.288, 0.049), respectively. Overall, the empirical coefficients are changed depending on the applied receptors. Moreover, although suitable empirical coefficients of the HIV-1 PR system represented with CHARMM force field^100,101 (with α = 0.169 and β = 0.017)¹⁰² were used, an uncorrelated coefficient was observed between the experimental and computed values as R = −0.43.¹⁰² Furthermore, an improved LIE model (eqn (2)) involving surface free energy ΔG^sur (with α = 0.014, β = 0.061, and γ = 0.042)¹⁰³ was also considered to calculate the HIV-1 PR + inhibitor representative by the Amber99 force field.^87,104 Unfortunately, the correlation coefficient between the computational and experimental values is R = 0.22. Therefore, the results obtained implied that the LIE model is also depended on the applied force field to represent the complex.

ΔG_LIE = αΔE^vdW_b–f + βΔE^cou_b–f (1)

where ΔE^vdW_b–f = 〈V^vdW_l–s〉_b − 〈V^vdW_l–s〉_f and ΔE^cou_b–f = 〈V^elec_l–s〉_b − 〈V^elec_l–s〉_f are the difference of the mean electrostatic and vdW interaction energy between the inhibitor and its surrounding molecules in a solvated complex of the receptor (bound state) and in solvation (free state), respectively.

ΔG_LIE = αΔE^vdW_b–f + βΔE^cou_b–f + γΔG^sur (2)

where ΔG^sur is the difference on the surface free energy, which was calculated by using the Shrake–Rupley method.

Because of the failure of the available empirical coefficients, an appropriate set of parameters was generated for HIV-1 PR + inhibitor represented by the GROMOS force field as follow:

ΔG_LIE = αΔE^vdW_b–f + βΔE^cou_b–f + γΔG^PB + δ (3)

where ΔG^PB is the polar interaction free energy, which was estimated via numerically resolving the linear Poisson–Boltzmann equation in continuum solvent approximation. In particular, the empirical coefficients α, β, γ, and δ are found to be of −0.92, −0.11, −0.47, and −23.06 kcal mol⁻¹, respectively (eqn (3)), providing a correlation coefficient of R = 0.84 and a root mean square error (RMSE) of 1.07 kcal mol⁻¹ (Fig. 3) experimentally. In particular, the large negative value of δ implies that the ligand adopts a very strong hydrophobic interaction with HIV-1 PR,^95,105 which is in good agreement with the two-dimensional protein–ligand maps (cf. Fig. S2 in ESI†). The negative value of γ indicates that the polar interaction contributes to the attraction between HIV-1 PR and the inhibitor as well as the contribution of the electrostatic interaction (β < 0). Consequently, the vdW interaction acts as a repulsive factor during the binding process since the parameter α is smaller than zero.

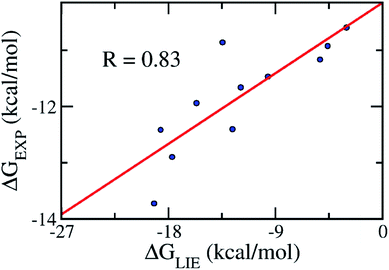
Fig. 3 Correlation between experimental binding free energies and that calculated using the LIE model (eqn (3)) of the training set consisting of 22 complexes (Table 1).

Validation of the model

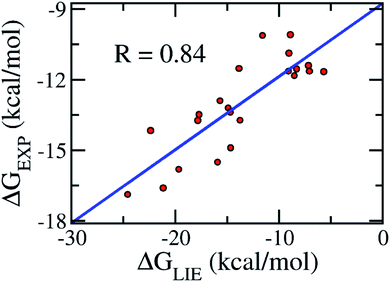
In order to confirm that our proposed coefficients including α, β, γ, and δ still work effectively with other systems, the approach was applied on the testing set consisting of 11 various inhibitors, which were taken randomly (Table 2). The mean values of free energy were calculated and are described in Table 2. The binding free energy between a ligand and HIV-1 PR was then evaluated according to the proposed model (eqn (3)). The results obtained suggested that the proposed LIE approach is rather robust. In particular, the correlation coefficient between the computed and experimental values is R = 0.83 (Fig. 4). The RMSE value was estimated as 1.25 kcal mol⁻¹. Therefore, the accuracy and precision of the proposed model are appropriate to predict the ligand-binding affinity of a trail ligand to the HIV-1 PR system. Furthermore, the small RMSE means that the model can categorize different inhibitors that reveal similar binding free energies.

Table 2 The free energy values obtained from experiments and MD simulations^a

Complexes	ΔE^coub–f	ΔE^vdWb–f	ΔG^sur	ΔG^PB	−TΔS	ΔGEXP
a The experimental values were acquired using the formula ΔGEXP = RT ln Ki, where R is a gas constant, T is the absolute temperature, and Ki is the inhibition constant obtained from previous studies.^57–61 The simulated results were averaged over 4 independent trajectories. The unit of energy is kcal mol^−1.
1AJV	13.49	−38.34	−8.42	50.09	26.77	−10.59
1AJX	5.26	−29.40	−7.76	56.72	25.78	−10.86
1D4J	17.70	−46.77	−9.72	79.69	35.78	−11.47
1EBW	25.56	−33.65	−9.22	71.32	34.24	−12.42
1EBZ	28.40	−42.67	−9.40	86.32	35.12	−12.90
1EC0	21.90	−45.44	−9.62	80.94	34.64	−11.66
1EC2	22.44	−36.36	−10.75	78.56	39.94	−13.73
1EC3	30.66	−42.82	−10.52	75.25	37.29	−12.40
1G2K	14.40	−40.82	−9.14	58.10	30.38	−10.92
1G35	17.31	−42.16	−9.74	61.43	33.75	−11.17
1OHR	11.94	−22.28	−7.93	45.88	27.87	−11.94

---

Fig. 4 Correlation between the experimental binding free energies and that calculated using the LIE model (eqn (3)). The testing set consisted of 11 complexes (Table 2).

CPU time consumption

The estimation of ligand-binding affinity via the LIE scheme was indicated that it is required less computing resources than other end-point approaches such as MM-PBSA or FEP methods.⁸⁹ In fact, in the LIE model, it was not necessary to perform additional computations to calculate the difference in the binding free energy alongside the production MD simulations. All of the free energy terms required to determine the binding free energy can be analyzed via the recorded conformations of the solvated complexes and the isolated ligands in the solution. Moreover, the estimation of the polar interaction energy caused the modified LIE to cost more CPU time than the original. However, since the HIV-1 PR + inhibitor is not very large, the numerical resolution of the Poisson–Boltzmann linear equation in continuum solvent approximation would not cost much CPU time. Furthermore, the applied united-atom GROMOS force field would require significantly less time-consuming CPU than the all-atom force field. In particular, one single calculation to predict the ligand-binding affinity to HIV-1 PR would consume ∼1 day for 4 independent trajectories using a single compute node with dual Xeon E5-2670 V3 with GPGPU acceleration.

Conclusions

Herein, a modified LIE approach has been successfully established to estimate the binding free energy of a ligand to the HIV-1 PR. The results obtained show a good correlation with the experimental data (R = 0.83) with a small RMSE (δ_RMSE = 1.25 kcal mol⁻¹). We have found that the available LIE empirical coefficients are not able to adopt good correlation with the experimental values, especially the united-atom force field model employed to represent the systems.

Polar binding energy emerges as an important factor to control the accuracy in the LIE model. The electrostatic interaction energy contributes to the attraction between two molecules, but the vdW interaction acts as a repulsive factor between the ligand and HIV-1 PR. Furthermore, it was found that the ligands adopted a very strong hydrophobic interaction with the HIV-1 PR.

The CPU time consumption of the modified LIE model is larger than the original, since it spends computing resources to resolve the linear Poisson–Boltzmann equation to estimate the polar interaction free energy. However, the computing resource cost would be significantly lower than that required for the MM-PBSA or FEP methods.⁸⁹

Obtaining an efficient scheme for rapidly and accurately estimating the ligand-binding affinity to the HIV-1 PR system is of great attraction. The proposed LIE model would enhance the development of HIV therapy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research is funded by the Department of Science and Technology of Ho Chi Minh City under grant number 199/2016/HD-SKHCN.

References

1. UNAIDS, Global HIV & AIDS statistics – 2019 fact sheet, 2019, https://www.unaids.org/en/resources/fact-sheet.
2. H. Chong, J. Xue, Y. Zhu, Z. Cong, T. Chen, Y. Guo, Q. Wei, Y. Zhou, C. Qin and Y. He, J. Virol., 2018, 92, e00775-18.
3. L. Tian, M.-S. Kim, H. Li, J. Wang and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 507.
4. S. J. Smith, X. Z. Zhao, T. R. Burke and S. H. Hughes, Antimicrob. Agents Chemother., 2018, 62, e01035-18.
5. A. D. Badley, Cell Death Differ., 2005, 12, 924–931.
6. J. R. Brechtl, W. Breitbart, M. Galietta, S. Krivo and B. Rosenfeld, J. Pain Symptom Manage., 2001, 21, 41–51.
7. R. D. Moore and R. E. Chaisson, AIDS, 1999, 13, 1933–1942.
8. D. E. Clercq, Nat. Rev. Drug Discovery, 2007, 6, 1001–1018.
9. D. E. Clercq, Int. J. Antimicrob. Agents, 2009, 33, 307–320.
10. F. Clavel and A. J. Hance, N. Engl. J. Med., 2004, 350, 1023–1035.
11. D. D. Richman, Nature, 2001, 410, 995–1001.
12. G. R. Marshall, Annu. Rev. Pharmacol. Toxicol., 1987, 27, 193–213.
13. C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690–2693.
14. C. Jarzynski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5018–5035.
15. R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426.
16. D. L. Beveridge and F. M. DiCapua, Annu. Rev. Biophys. Biophys. Chem., 1989, 18, 431–492.
17. J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313.
18. P. Kollman, Chem. Rev., 1993, 93, 2395–2417.
19. P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case and T. E. Cheatham, Acc. Chem. Res., 2000, 33, 889–897.
20. B. Kuhn and P. A. Kollman, J. Med. Chem., 2000, 43, 3786–3791.
21. W. Wang and P. A. Kollman, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 14937–14942.
22. J. Åqvist, C. Medina and J.-E. Samuelsson, Protein Eng., 1994, 7, 385–391.
23. J. Aqvist and J. Marelius, Comb. Chem. High Throughput Screening, 2001, 4, 613–626.
24. J. Åqvist, V. B. Luzhkov and B. O. Brandsdal, Acc. Chem. Res., 2002, 35, 358–365.
25. H. L. N. d. Amorim, R. A. Caceres and P. A. Netz, Curr. Drug Targets, 2008, 9, 1100–1105.
26. S. T. Ngo, H. M. Hung and M. T. Nguyen, J. Comput. Chem., 2016, 37, 2734–2742.
27. S. T. Ngo, M. T. Nguyen and M. T. Nguyen, Chem. Phys. Lett., 2017, 676, 12–17.
28. S. T. Ngo, K. B. Vu, L. M. Bui and V. V. Vu, ACS Omega, 2019, 4, 3887–3893.
29. M. Huang, W. Huang, F. Wen and G. Larson Ronald, J. Comput. Chem., 2017, 38, 2007–2019.
30. N. T. Lan, K. B. Vu, M. K. Dao Ngoc, P.-T. Tran, D. M. Hiep, N. T. Tung and S. T. Ngo, J. Mol. Graphics Modell., 2019, 93, 107441.
31. G. Subramanian, B. Ramsundar, V. Pande and R. A. Denny, J. Chem. Inf. Model., 2016, 56, 1936–1949.
32. P. Ferrara, H. Gohlke, D. J. Price, G. Klebe and C. L. Brooks, J. Med. Chem., 2004, 47, 3032–3047.
33. M. Stahl and M. Rarey, J. Med. Chem., 2001, 44, 1035–1042.
34. H. H. Maw and L. H. Hall, J. Chem. Inf. Comput. Sci., 2002, 42, 290–298.
35. R. Gil-Redondo, J. Klett, F. Gago and A. Morreale, Proteins, 2010, 78, 162–172.
36. C. Coderch, Y. Tang, J. Klett, S.-E. Zhang, Y.-T. Ma, W. Shaorong, R. Matesanz, B. Pera, A. Canales, J. Jimenez-Barbero, A. Morreale, J. F. Diaz, W.-S. Fang and F. Gago, Org. Biomol. Chem., 2013, 11, 3046–3056.
37. W. Jiang and B. Roux, J. Chem. Theory Comput., 2010, 6, 2559–2565.
38. Y. Meng, D. Sabri Dashti and A. E. Roitberg, J. Chem. Theory Comput., 2011, 7, 2721–2727.
39. W. Jiang, J. Thirman, S. Jo and B. Roux, J. Phys. Chem. B, 2018, 122, 9435–9442.
40. J. Wang, P. Morin, W. Wang and P. A. Kollman, J. Am. Chem. Soc., 2001, 123, 5221–5230.
41. B. Kuhn, P. Gerber, T. Schulz-Gasch and M. Stahl, J. Med. Chem., 2005, 48, 4040–4048.
42. R. Giulio, R. A. Del, D. Gianluca and S. Miriam, J. Comput. Chem., 2010, 31, 797–810.
43. T. Hou, J. Wang, Y. Li and W. Wang, J. Chem. Inf. Model., 2011, 51, 69–82.
44. L. Xu, H. Sun, Y. Li, J. Wang and T. Hou, J. Phys. Chem. B, 2013, 117, 8408–8421.
45. S. Genheden and U. Ryde, Expert Opin. Drug Discovery, 2015, 10, 449–461.
46. S. T. Ngo and M. S. Li, J. Phys. Chem. B, 2012, 116, 10165–10175.
47. C. Koukoulitsa, C. Villalonga-Barber, R. Csonka, X. Alexi, G. Leonis, D. Dellis, E. Hamelink, O. Belda, B. R. Steele, M. Micha-Screttas, M. N. Alexis, M. G. Papadopoulos and T. Mavromoustakos, J. Enzyme Inhib. Med. Chem., 2016, 31, 67–77.
48. S. Chakraborty and P. Das, Sci. Rep., 2017, 7, 9941.
49. J. Wang, R. Dixon and P. A. Kollman, Proteins, 1999, 34, 69–81.
50. D. K. Jones-Hertzog and W. L. Jorgensen, J. Med. Chem., 1997, 40, 1539–1549.
51. I. D. Wall, A. R. Leach, D. W. Salt, M. G. Ford and J. W. Essex, J. Med. Chem., 1999, 42, 5142–5152.
52. M. S. Kumar, S. Johan, Å. Johan and K. Jaroslav, J. Comput. Chem., 2012, 33, 2340–2350.
53. U. Uciechowska, J. Schemies, M. Scharfe, M. Lawson, K. Wichapong, M. Jung and W. Sippl, RSC Med. Chem., 2012, 3, 167–173.
54. V. Durmaz, S. Schmidt, P. Sabri, C. Piechotta and M. Weber, J. Chem. Inf. Model., 2013, 53, 2681–2688.
55. V. Poongavanam and J. Kongsted, J. Mol. Graphics Modell., 2016, 70, 236–245.
56. M. van Dijk, A. M. ter Laak, J. D. Wichard, L. Capoferri, N. P. E. Vermeulen and D. P. Geerke, J. Chem. Inf. Model., 2017, 57, 2294–2308.
57. K. Bäckbro, S. Löwgren, K. Österlund, J. Atepo, T. Unge, J. Hultén, N. M. Bonham, W. Schaal, A. Karlén and A. Hallberg, J. Med. Chem., 1997, 40, 898–902.
58. H. O. Andersson, K. Fridborg, S. Löwgren, M. Alterman, A. Mühlman, M. Björsne, N. Garg, I. Kvarnström, W. Schaal, B. Classon, A. Karlén, U. H. Danielsson, G. Ahlsén, U. Nillroth, L. Vrang, B. Öberg, B. Samuelsson, A. Hallberg and T. Unge, Eur. J. Biochem., 2003, 270, 1746–1758.
59. J. Lindberg, D. Pyring, S. Löwgren, Å. Rosenquist, G. Zuccarello, I. Kvarnström, H. Zhang, L. Vrang, B. Classon, A. Hallberg, B. Samuelsson and T. Unge, Eur. J. Biochem., 2004, 271, 4594–4602.
60. W. Schaal, A. Karlsson, G. Ahlsén, J. Lindberg, H. O. Andersson, U. H. Danielson, B. Classon, T. Unge, B. Samuelsson, J. Hultén, A. Hallberg and A. Karlén, J. Med. Chem., 2001, 44, 155–169.
61. S. W. Kaldor, V. J. Kalish, J. F. Davies, B. V. Shetty, J. E. Fritz, K. Appelt, J. A. Burgess, K. M. Campanale, N. Y. Chirgadze, D. K. Clawson, B. A. Dressman, S. D. Hatch, D. A. Khalil, M. B. Kosa, P. P. Lubbehusen, M. A. Muesing, A. K. Patick, S. H. Reich, K. S. Su and J. H. Tatlock, J. Med. Chem., 1997, 40, 3979–3985.
62. D. L. Surleraux, A. Tahri, W. G. Verschueren, G. M. Pille, H. A. de Kock, T. H. Jonckers, A. Peeters, S. De Meyer, H. Azijn, R. Pauwels, M. P. de Bethune, N. M. King, M. Prabu-Jeyabalan, C. A. Schiffer and P. B. Wigerinck, J. Med. Chem., 2005, 48, 1813–1822.
63. E. Specker, J. Böttcher, H. Lilie, A. Heine, A. Schoop, G. Müller, N. Griebenow and G. Klebe, Angew. Chem., Int. Ed., 2005, 44, 3140–3144.
64. J. C. Clemente, R. M. Coman, M. M. Thiaville, L. K. Janka, J. A. Jeung, S. Nukoolkarn, L. Govindasamy, M. Agbandje-McKenna, R. McKenna, W. Leelamanit, M. M. Goodenow and B. M. Dunn, Biochemistry, 2006, 45, 5468–5477.
65. S. Munshi, Z. Chen, Y. Li, D. B. Olsen, M. E. Fraley, R. W. Hungate and L. C. Kuo, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1998, 55, 1053–1060.
66. J. K. Ekegren, N. Ginman, Å. Johansson, H. Wallberg, M. Larhed, B. Samuelsson, T. Unge and A. Hallberg, J. Med. Chem., 2006, 49, 1828–1832.
67. A. Ali, G. S. K. K. Reddy, H. Cao, S. G. Anjum, M. N. L. Nalam, C. A. Schiffer and T. M. Rana, J. Med. Chem., 2006, 49, 7342–7356.
68. G. S. K. K. Reddy, A. Ali, M. N. L. Nalam, S. G. Anjum, H. Cao, R. S. Nathans, C. A. Schiffer and T. M. Rana, J. Med. Chem., 2007, 50, 4316–4328.
69. M. D. Altman, A. Ali, G. S. K. Kumar Reddy, M. N. L. Nalam, S. G. Anjum, H. Cao, S. Chellappan, V. Kairys, M. X. Fernandes, M. K. Gilson, C. A. Schiffer, T. M. Rana and B. Tidor, J. Am. Chem. Soc., 2008, 130, 6099–6113.
70. X. Wu, P. Öhrngren, J. K. Ekegren, J. Unge, T. Unge, H. Wallberg, B. Samuelsson, A. Hallberg and M. Larhed, J. Med. Chem., 2008, 51, 2586.
71. A. K. Ghosh, S. Leshchenko-Yashchuk, D. D. Anderson, A. Baldridge, M. Noetzel, H. B. Miller, Y. Tie, Y.-F. Wang, Y. Koh, I. T. Weber and H. Mitsuya, J. Med. Chem., 2009, 52, 3902–3914.
72. C.-H. Shen, Y.-F. Wang, A. Y. Kovalevsky, R. W. Harrison and I. T. Weber, FEBS J., 2010, 277, 3699–3714.
73. M. N. L. Nalam, A. Ali, G. S. K. K. Reddy, H. Cao, S. G. Anjum, M. D. Altman, N. K. Yilmaz, B. Tidor, T. M. Rana and C. A. Schiffer, Chem. Biol., 2013, 20, 1116–1124.
74. Y. Tie, A. Y. Kovalevsky, P. Boross, Y.-F. Wang, A. K. Ghosh, J. Tozser, R. W. Harrison and I. T. Weber, Proteins, 2007, 67, 232–242.
75. M. K. Parai, D. J. Huggins, H. Cao, M. N. L. Nalam, A. Ali, C. A. Schiffer, B. Tidor and T. M. Rana, J. Med. Chem., 2012, 55, 6328–6341.
76. J. Schimer, M. Pávová, M. Anders, P. Pachl, P. Šácha, P. Cígler, J. Weber, P. Majer, P. Řezáčová, H.-G. Kräusslich, B. Müller and J. Konvalinka, Nat. Commun., 2015, 6, 6461.
77. W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hunenberger, P. Kruger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Biomolecular Simulation: The GROMOS96 Manual and User Guide, Vdf Hochschulverlag AG an der ETH, Zurich, 1996.
78. S. T. Ngo, B. K. Mai, D. M. Hiep and M. S. Li, Chem. Biol. Drug Des., 2015, 86, 546–558.
79. O. Aruksakunwong, P. Wolschann, S. Hannongbua and P. Sompornpisut, J. Chem. Inf. Model., 2006, 46, 2085–2092.
80. T. D. McGee, J. Edwards and A. E. Roitberg, J. Phys. Chem. B, 2014, 118, 12577–12585.
81. L. J. Hyland, T. A. Tomaszek and T. D. Meek, Biochemistry, 1991, 30, 8454–8463.
82. F. Pietrucci, F. Marinelli, P. Carloni and A. Laio, J. Am. Chem. Soc., 2009, 131, 11811–11818.
83. T. Hou, W. A. McLaughlin and W. Wang, Proteins, 2008, 71, 1163–1174.
84. M. Petrek, M. Otyepka, P. Banas, P. Kosinova, J. Koca and J. Damborsky, BMC Bioinf., 2006, 7, 316.
85. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and A. J. Hermans, Intermolecular Forces, Reidel, Dordrecht, Jerusalem, Israel, 1981.
86. A. W. Schuttelkopf and D. M. F. van Aalten, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2004, 60, 1355–1363.
87. C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280.
88. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
89. S. T. Ngo, B. K. Mai, P. Derreumaux and V. V. Vu, RSC Adv., 2019, 9, 12455–12461.
90. S. T. Ngo, H. M. Hung, D. T. Truong and M. T. Nguyen, Phys. Chem. Chem. Phys., 2017, 19, 1909–1919.
91. H. A. Carlson and W. L. Jorgensen, J. Phys. Chem., 1995, 99, 10667–10673.
92. H. Tzoupis, G. Leonis, A. Avramopoulos, T. Mavromoustakos and M. G. Papadopoulos, J. Phys. Chem. B, 2014, 118, 9538–9552.
93. J. Chen, Z. Liang, W. Wang, C. Yi, S. Zhang and Q. Zhang, Sci. Rep., 2014, 4, 6872.
94. K. R. Karnati and Y. Wang, J. Mol. Graphics Modell., 2019, 92, 112–122.
95. M. Almlöf, B. O. Brandsdal and J. Åqvist, J. Comput. Chem., 2004, 25, 1242–1254.
96. F. Österberg and J. Åqvist, FEBS Lett., 2005, 579, 2939–2944.
97. S. Bjelic, M. Nervall, H. Gutiérrez-de-Terán, K. Ersmark, A. Hallberg and J. Åqvist, Cell. Mol. Life Sci., 2007, 64, 2285–2305.
98. T. Hansson, J. Marelius and J. Åqvist, J. Comput.-Aided Mol. Des., 1998, 12, 27–35.
99. M. Almlöf, J. Carlsson and J. Åqvist, J. Chem. Theory Comput., 2007, 3, 2162–2175.
100. A. D. MacKerell, N. Banavali and N. Foloppe, Biopolym, 2000, 56, 257–265.
101. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr, J. Comput. Chem., 2010, 31.
102. D. Huang and A. Caflisch, J. Med. Chem., 2004, 47, 5791–5797.
103. D. Zhang, L. z. Yu, P. L. Huang, S. Lee-Huang and J. Z. H. Zhang, J. Chem. Theory Comput., 2010, 9, 471–485.
104. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
105. Y. Su, E. Gallicchio, K. Das, E. Arnold and R. M. Levy, J. Chem. Theory Comput., 2007, 3, 256–277.

---

Footnote

† Electronic supplementary information (ESI) available: All-atom RMSD during MD simulations. See DOI: 10.1039/c9ra09583g

---