High-pressure formation of antimony nitrides: a first-principles study

Abstract

The structural phase transition, electronic properties, and bonding properties of antimony nitrides have been studied by using the first principles projector augmented wave method. The relationship between the formation enthalpy and the composition of the Sb–N system has been explored. The novel Sb₂N₃ with the Cmcm space group is stable in a narrow pressure range from 100 GPa to 120 GPa. Apart from the Sb₂N₃, two nitrogen-rich phases SbN₂ and SbN₄ were predicted. The SbN₂ with the C2/m space group is stable at 12 GPa and then transforms to the high-pressure phase at 23 GPa. The nitrogen-rich SbN₄ appears at 14 GPa then undergoes C2/m → P1̄ → P1̄ phase transitions, and the calculated pressures of the phase transitions are 31 and 60 GPa, respectively. The nitrogen-rich SbN₂ and SbN₄ have similar structural features. Both SbN₂ and SbN₄ can be seen as a sandwich structure composed of the Sb–N layers and N₂ dimers. The pressure-induced phase transitions of SbN₂ and SbN₄ are accompanied by the electron transfer between the Sb–N layers and N₂ dimers. Moreover, the nitrogen-rich SbN₄ has a higher energy density of 2.42 kJ g⁻¹ and is a potentially high energy density material.

---

Introduction

The single-bonded cubic gauche cg-N is the most famous polymeric nitrogen phase which was first predicted by a theoretical study, then experimentally synthesized by Eremets et al. by using a high-pressure and high-temperature method (P = 100 GPa and T = 2000 K).¹ Previous studies report that the single-bonded cg-N has more than three times higher energy storage capacity than traditional energetic materials. It is well known that the polynitrogens can transform to N₂ molecules under ambient conditions, accompanied by large energy release. There is a large energetic gap between a single bond (∼167 kJ mol⁻¹) and a double/triple bond (∼419 kJ mol⁻¹ and ∼954 kJ mol⁻¹). The polynitrogen materials composed of abundant single and double bonds can be seen as high energy density materials (HEDMs). Although the cg-N is a potential high energy density material, it is predicted to be metastable at 40 GPa and it cannot be quenched under ambient conditions. This is a big problem for practical application. To solve this problem, many polynitrogen materials with lower synthesis pressures and good stabilities have attracted great attention in scientific and industrial research. Firstly, the metal azides have drawn considerable attention due to their unique covalent linear N₃ units in the crystal structures.^2–6 These covalent linear N₃ units have the ability to improve the speed of polymerization and lower the synthesis pressures with respect to the pure nitrogen gas. The metal azides are good starting materials in the high-pressure synthesization of the polynitrogens. Over the years, many metal azides have been studied as HEDMs such as LiN₃, NaN₃, KN₃, AlN₃ and so on.^2,7–13 Furthermore, some nitrogen-rich metal nitrides with higher energy density such as LiN₅, CsN₅, BeN₄, MgN₄, CaN₄, and CaN₅ have also been proposed in experimental and theoretical research.^9,14–21 Recently, in addition to metal nitrides, many non-metal nitrides have also been studied as HEDMs. In the N–H system, a novel N₂H compound with higher energy density (∼4.4 kJ g⁻¹) and higher nitrogen content (96.6%) has been predicted by Yin et al. using the CALYPSO method.²² Batyrev predicted three stable crystalline structures of N–H solids N₉H, N₄H, and N₃H at the pressure range of 10 and 50 GPa.²³ Using the USPEX method, Steele theoretically found two novel compounds ammonium pentazolate (NH₄)(N₅) and pentazole (N₅H) at 30 and 50 GPa, respectively.²⁴ In the B–N system, it is well known that only one stable compound BN is reported in the B–N system. However, an unusual B₃N₅ with high hardness (∼44 GPa) and high energy density (∼3.44 kJ g⁻¹) had been predicted by Li et al.²⁵ Besides, novel high-pressure compounds in the C–N system and S–N system are also considered in the exploration of high-energy materials.^26,27 Up to now, several binary systems have been studied. And some new polynitrogen forms including tetrazadiene (N₄), pentazole (N₅), hexazine (N₆) and extended chains (N_∞) have been reported in these binary systems. However, there are little reports about the pnictogen nitrides, especially in high-pressure studies. Only one report about the P–N system in the high-pressure studies of pnictogen nitrides was published.²⁸ In the P–N system, two novel compounds PN₂ and PN₃ were predicted at high pressures. The metallic PN₃ is a superconductor at 10 GPa with a T_c value of 18 K. The insulating PN₂ is stable at pressures in excess of 200 GPa. The PN₃ has the highest nitrogen content in the P–N compounds. However, only N₂ dimers appear and no polynitrogen forms are observed in the structure of PN₃. Previous reported N₄, N₅, and N₆ units have not been observed in the P–N system. For pnictogen nitrides, the pnictogen elements (As, Sb, and Bi) have the same valence electrons number as that of nitrogen but with a big atomic radius. Therefore, pnictogen elements can enhance the chemical precompression in the pnictogen nitrides while do not change the charge of compounds. Therefore, it can be expected that there are high energy density materials in the pnictogen nitrides. The high-pressure studies of pnictogen nitrides would help to theoretically investigate more promising high-energy materials. These stimulate our interest to prompt in-depth investigations of pnictogen nitrides.

In the present work, we did systemic theoretical study of Sb–N system at high pressure. The formation enthalpy and structural stability of Sb_xN_y have been well investigated. Three novel stable compound Sb₂N₃, SbN₂ and SbN₄ have been found. The Sb₂N₃ with the Cmcm space group is stable in a narrow pressure range from 100 GPa to 120 GPa. The structural phase transition of SbN₂ under high pressure has been uncovered. The monoclinic SbN₂ with C2/m space group is stable at 12 GPa and then transform to high-pressure phase with the same space group at 23 GPa. A nitrogen-rich stoichiometric SbN₄ with the C2/m space group appears at 14 GPa then undergo two phase transitions to low symmetry P1̄ space group phases at 31 GPa and 60 GPa, respectively. The pressure-induced phase transitions of SbN₂ and SbN₄ are accompanied by the electrons transfer between the Sb–N layers and N₂ dimers. Furthermore, we found that the nitrogen-rich SbN₄ phase has a higher energy density of 2.42 kJ g⁻¹.

Computation details

Hear, the theoretical calculations of Sb–N system are performed within the density functional theory (DFT),^29–31 carried out within the Vienna ab initio simulation code VASP, with the projector augmented wave method.^32,33 The Sb 5s²5p³ electrons and N 2s²2p³ electrons are treated as valence electrons, respectively. The Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) exchange and correlation functional are used in our calculations.³⁴ Convergence tests give a kinetic energy cutoff of 800 eV, with a grid of spacing 2π × 0.03 Å⁻¹ for the electronic Brillouin zone integration in all the candidate structures. The geometries of the candidate structures are optimized when the remanent Hellmann–Feynman forces on the ions are less than 0.01 eV Å⁻¹. The phonon frequencies are calculated by using the supercell approach as implemented in the Phonopy code³⁵ and VASP code. The heat of formation (ΔH_f) for various Sb_xN_y compositions are calculated by the equation of ΔH_f = E(Sb_xN_y) − (xE(Sb) + yE(N)), in which the respective solid phase of Sb and N at different pressures are adopted.

Results and discussions

The variable-cell high-pressure structure predictions of the Sb–N system were performed at 0, 20, 40, 60, 80, 100, 120 GPa with the simulation cell containing one to four formula units by using the CALYPSO code.^36,37 The ground-state crystal structures of the antimony nitrides with various stoichiometry were uncovered in the pressure range of 0 to 120 GPa. The convex hull plots of the Sb–N system at the selected pressures were constructed by evaluating the averaged formation enthalpy of the candidate structures relative to the elementary Sb and N solids (Fig. 1). According to the hull data, a compound with a formation enthalpy lying on the convex hull is thermodynamically stable with respect to decomposition into other nitrides or elementary Sb and N solids. We can expect that this compound is experimentally synthesizable at their stable pressures.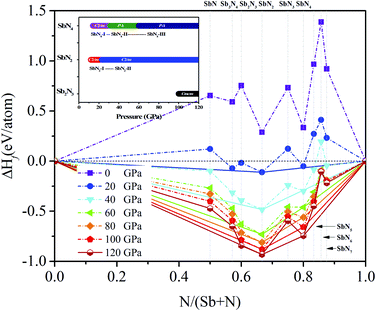

Fig. 1 The convex hull plot of Sb–N system at different pressures. Dotted lines are used to connect the stable phases. The inset is the phase transition sequence of the Sb–N compounds.

It is found that three stable stoichiometry (Sb₂N₃, SbN₂, and SbN₄) appear in our convex hull plots. The SbN₂ is the most stable stoichiometry in the Sb–N system. The Sb₂N₃ with the Cmcm space group is stable in a narrow pressure range of from 100 GPa to 120 GPa. The monoclinic SbN₂ with the C2/m space group (SbN₂-I) is stable at 12 GPa and then transform to high-pressure SbN₂ (SbN₂-II) with the same space group at 23 GPa. A nitrogen-rich stoichiometric SbN₄ with the C2/m space group (SbN₄-I) appears at 14 GPa then undergo two-phase transitions to the low symmetry P1̄ space group at 31 GPa (SbN₄-II) and 60 GPa (SbN₄-III), respectively. From our calculated convex hull data, it is found that the nitrogen-rich SbN_x (x = 5, 6, 7) are also not stable because their formation enthalpy values lie above the convex hull solid lines. Furthermore, there are no stable antimony-rich nitrides in the Sb–N system.

In addition to the thermodynamic stability, we also study the dynamic stabilities of these structures. The phonon spectra are calculated under different pressure conditions. No imaginary frequencies emerge in the whole Brillouin zone of all the predicted phases, indicating the dynamical stability as shown in Fig. 2. At 20 GPa, SbN₂-I and SbN₄-I have some extremely flat phonon bands at higher frequencies of 60–70 THz, indicating the presence of molecular modes of N₂ dimer. In the following part, we mainly study the effect of redundant nitrogen atoms in the Sb–N system. The phase stability, high-pressure phase transition, bonding properties, and potential energy storage applications of antimony nitrides will be discussed.

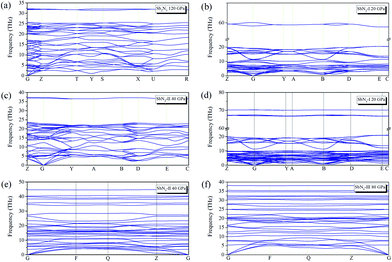Fig. 2 Phonon band structures of (a) Sb₂N₃ at 120 GPa (b) SbN₂-I at 20 GPa (c) SbN₂-II at 40 GPa (d) SbN₄-I at 20 GPa (e) SbN₄-II at 40 GPa (f) SbN₄-III at 80 GPa.

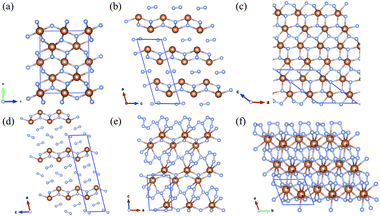
The crystal structures of Sb₂N₃, SbN₂, and SbN₄ are presented in Fig. 3. The crystallographic parameters of the Sb–N compounds are provided in Table S1.† The high-pressure Sb₂N₃ adopts an orthorhombic Cmcm-symmetric structure at 120 GPa as shown in Fig. 3a. The equilibrium lattice parameters of Sb₂N₃ are a = 2.859 Å, b = 8.929 Å, c = 7.002 Å at 120 GPa. The coordination number of Sb atoms is six. While the coordination numbers of N atoms are four and five. There are two type of bonding mode tetrahedron and director plane. SbN₂-I crystallizes with the monoclinic symmetry C2/m space group at 12 GPa. SbN₂-I can be regarded as a sandwich-type structure, composed of Sb–N layer (A layer) and N₂ dimer layer (B layer) with the stacking order of ABABA… along the crystallographic a axis of the monoclinic lattice. The distance between A layers is about 3 Å at 20 GPa. The distances between the Sb and N atoms in A layer are 2.105 Å and 2.183 Å at 20 GPa. The bond length of the N₂ dimer is 1.145 Å. Under compression, the distance between the A layer and B layer decreases greatly. New interaction between A layer and B layer appears with the distance decreasing. The N₂ dimer gets more electron from the Sb atoms of A layer. New ionic bonds between Sb atoms of A layer and N atoms of B layer appears. Then the SbN₂-I phase transforms into the high-pressure SbN₂-II phase at 23 GPa. In SbN₂-II, due to the presence of new ionic bonds between the Sb atoms of A layer and N atoms of B layer, the structure of A layer occurs distortion to make the crystal structure reach a new mechanical balance. The nitrogen-rich phase SbN₄-I adopts the monoclinic C2/m symmetric structure at 14 GPa. SbN₄-I has a similar crystal structure with that of SbN₂-I. The similar sandwich structure feature appears in the SbN₄-I. SbN₄-I is composed of Sb–N layer (A layer) and N₂ dimer layer (B layer) with the stacking order of ABBBABBB… along the crystallographic a axis of monoclinic lattice. Within this structure, the distance between the A layer and A layer is about 8.5 Å. The distances between the Sb and N atoms in the A layer are 2.105 Å and 2.208 Å. The bond lengths of N₂ dimer are 1.113 Å and 1.123 Å. Under compression, the distance between two neighbouring A layers decreases greatly. The N₂ dimer gets close to each other. At 31 GPa, the N₂ dimers transform to the novel quasi-linear nitrogen armchair chains along the crystallographic [110] direction. The bond lengths of the nitrogen–nitrogen bonds are 1.294 Å, 1.311 Å, and 1.336 Å at 40 GPa. The remanent electrons of Sb atom in the A layers transform into the nitrogen armchair chains. However, the only partial nitrogen atom of the armchair chains form ionic bonds with the Sb atoms of A layers. There are lone pair electrons in the nitrogen armchair chains. The SbN₄-I transforms into the P1̄ phase SbN₄-II at 31 GPa. At higher pressures, the SbN₄-II phase transforms into a closed-packed triclinic SbN₄-III phase at 60 GPa. The remanent electrons of nitrogen armchair chains forms ionic bonds with the neighboring Sb atoms of A layers in SbN₄-III phase.

Fig. 3 The crystal structures of antimony nitrides (a) Sb₂N₃ (b) SbN₂-I (c) SbN₂-II (d) SbN₄-I (e) SbN₄-II (f) SbN₄-III. The golden yellow circles represent Sb atoms; the blue circles represent N atoms.

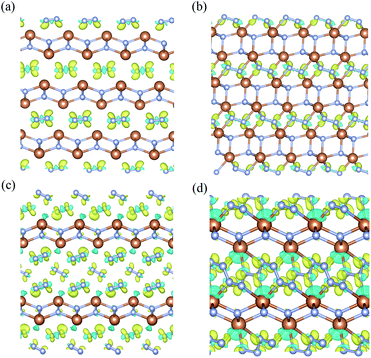
To investigate the nature of the polymerization and formation mechanism of materials, we calculated the electronic structures and Bader charge of the Sb₂N₃, SbN₂, and SbN₄. The projected density of states of these compounds at different pressures is shown in Fig. 4. It is shown that the Sb₂N₃ exhibits a clear metallic feature by the evidence of the finite electronic DOS at the Fermi level. The Sb_s states mainly contribute to the metallic properties of Sb₂N₃. We also calculated the contributions of the Sb–N layer and N₂ dimers or nitrogen armchair chain for the DOS as shown in Fig. S1.† We can find that the N₂ dimer and nitrogen armchair chain have a bigger contribution to the DOS of these compounds. Furthermore, with the pressure increasing more Sb_d states appear in the energy range of −5 and 0 eV in the PDOS of SbN₂-I, SbN₂-II, SbN₄-I, SbN₄-II, and SbN₄-III. This indicates that there is more charge transfer between Sb atoms and N₂ dimers in these nitrogen-rich phases. In addition, in order to better understand the bonding properties between the Sb–N layer and N₂ dimers, we investigated the charge density difference of the nitrogen-rich Sb–N compounds. Fig. 5 shown the charge density difference between the Sb–N layer and N₂ dimers for the SbN₂-I, SbN₂-II, SbN₄-I, and SbN₄-II. For SbN₂, upon the compression, it is found that the electrons localized in the nitrogen–nitrogen bonds of the N₂ dimers transfer to form ionic bonds with the Sb–N layers. For SbN₄, the electrons of the Sb atoms in the Sb–N layers transfer to the N₂ dimers. The Bader charge analysis also confirms this view. Each nitrogen atom of the N₂ dimer gets 0.235 electrons from the Sb–N layer in SbN₂-I. For SbN₂-II, each nitrogen atom of the N₂ dimer gets 0.94 electrons from the Sb–N layer. For SbN₄-I, each nitrogen atom of the N₂ dimer gets 0.04 electrons from the Sb–N layer. For SbN₄-II, each nitrogen atom of the armchair chain gets 0.288 electrons from the Sb–N layer. These suggest that these phases have ionic characteristics. The Sb–N layers behave as electron-donors whose strongly affect the N–N bonding of the polymerization.

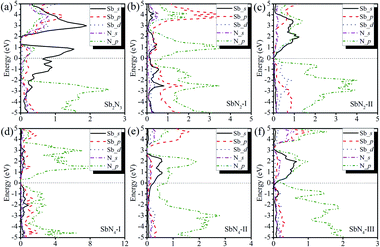Fig. 4 The projected density of state of (a) Sb₂N₃ at 120 GPa (b) SbN₂-I at 20 GPa (c) SbN₂-II at 40 GPa (d) SbN₄-I at 20 GPa (e) SbN₄-II at 40 GPa (f) SbN₄-III at 80 GPa.

Fig. 5 The charge density difference between the Sb–N layer and N₂ dimers for (a) SbN₂-I with the isosurface level of 0.004 e bohr⁻³ (b) SbN₂-II with the isosurface level of 0.023 e bohr⁻³ (c) SbN₄-I with the isosurface level of 0.003 e bohr⁻³ (d) SbN₄-II with the isosurface level of 0.014 e bohr⁻³. The yellow represents the positive value and the green represents the negative value.

Moreover, it is well known that the nitrogen-rich materials are considered to be promising candidates for HEDMs because their decomposition reactions will release large energy. Different from the phosphorus nitrides, SbN₄ has the highest nitrogen contents among the Sb–N compounds and the polymeric nitrogen chains. The calculated energy density of SbN₄, relative to products N₂ and Sb solids, is 2.42 kJ g⁻¹ which is larger than that of typical covalent high energy density material CNO (2.2 kJ g⁻¹)³⁸ and is comparable with other traditional HEDMs (TATB, RDX, and HMX with energy densities of 1 to 3 kJ g⁻¹).³⁹ So SbN₄ can be expected as a possible candidate of HEDMs.

Conclusions

In conclusion, the high-pressure ground-state phases of the stoichiometric binary antimony nitrides are extensively explored. The formation enthalpy and structural stability of the candidate structures have been well investigated. Three novel stable compound Sb₂N₃, SbN₂, and SbN₄ have been predicted. The Sb₂N₃ with the Cmcm space group is stable in a narrow pressure range from 100 GPa to 120 GPa. The nitrogen-rich SbN₂ and SbN₄ have similar structural features. Both SbN₂ and SbN₄ can be seen as a sandwich structure composed of the Sb–N layers and N₂ dimers. Furthermore, the structural phase transition of SbN₂ under high pressure has been uncovered. The SbN₂-I is stable at 12 GPa and then transforms to a high-pressure SbN₂-II phase at 23 GPa. The nitrogen-rich SbN₄-I appears at 14 GPa then undergoes two phase transitions to low symmetry P1̄ space group SbN₄-II and SbN₄-III at 31 GPa and 60 GPa, respectively. The pressure-induced phase transitions of SbN₂ and SbN₄ are accompanied by the electrons transfer between the Sb–N layers and N₂ dimers. Moreover, the nitrogen-rich SbN₄ can be expected to be a potential high energy density material (energy density: 2.42 kJ g⁻¹). The established high-pressure phase diagram of the Sb–N system is of fundamental interest and important for future experiments.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 91745203, 11404134), Jilin Provincial Science and Technology Development Project of China (20160520016JH).

References

1. M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Nat. Mater., 2004, 3, 558–563.
2. X. Wang, J. Li, H. Zhu, L. Chen and H. Lin, J. Chem. Phys., 2014, 141, 044717.
3. J. Jiang, P. Zhu, D. Li, Y. Chen, M. Li, X. Wang, B. Liu, Q. Cui and H. Zhu, J. Phys. Chem. B, 2016, 120, 12015–12022.
4. H. Zhu, F. Zhang, C. Ji, D. Hou, J. Wu, T. Hannon and Y. Ma, J. Appl. Phys., 2013, 113, 033511.
5. H. Zhu, X. Han, P. Zhu, X. Wu, Y. Chen, M. Li, X. Li and Q. Cui, J. Phys. Chem. C, 2016, 120, 12423–12428.
6. D. Li, X. Wu, J. Jiang, X. Wang, J. Zhang, Q. Cui and H. Zhu, Appl. Phys. Lett., 2014, 105, 071903.
7. N. Holtgrewe, S. S. Lobanov, M. F. Mahmood and A. F. Goncharov, J. Phys. Chem. C, 2016, 120, 28176–28185.
8. M. Zhang, H. Yan, Q. Wei and H. Liu, RSC Adv., 2015, 5, 11825–11830.
9. J. Zhang, Z. Zeng, H.-Q. Lin and Y.-L. Li, Sci. Rep., 2014, 4, 4358.
10. F.-C. Liu, Y.-F. Zeng, J.-P. Zhao, B.-W. Hu, E. C. Sañudo, J. Ribas and X.-H. Bu, Inorg. Chem., 2007, 46, 7698–7700.
11. W. Zhu and H. Xiao, J. Phys. Chem. B, 2006, 110, 18196–18203.
12. M. I. Eremets, M. Y. Popov, I. A. Trojan, V. N. Denisov, R. Boehler and R. J. Hemley, J. Chem. Phys., 2004, 120, 10618–10623.
13. Z. Liu, D. Li, S. Wei, W. Wang, F. Tian, K. Bao, D. Duan, H. Yu, B. Liu and T. Cui, Inorg. Chem., 2017, 56, 7494–7500.
14. S. Zhang, Z. Zhao, L. Liu and G. Yang, J. Power Sources, 2017, 365, 155–161.
15. S. Zhu, F. Peng, H. Liu, A. Majumdar, T. Gao and Y. Yao, Inorg. Chem., 2016, 55, 7550–7555.
16. Y. Shen, A. R. Oganov, G. Qian, J. Zhang, H. Dong, Q. Zhu and Z. Zhou, Sci. Rep., 2015, 5, 14204.
17. F. Peng, Y. Yao, H. Liu and Y. Ma, J. Phys. Chem. Lett., 2015, 2363–2366.
18. F. Peng, Y. Han, H. Liu and Y. Yao, Sci. Rep., 2015, 5, 16902.
19. S. Wei, D. Li, Z. Liu, X. Li, F. Tian, D. Duan, B. Liu and T. Cui, Phys. Chem. Chem. Phys., 2017, 19, 9246–9252.
20. S. Yu, B. Huang, Q. Zeng, A. R. Oganov, L. Zhang and G. Frapper, J. Phys. Chem. C, 2017, 121, 11037–11046.
21. S. Wei, D. Li, Z. Liu, W. Wang, F. Tian, K. Bao, D. Duan, B. Liu and T. Cui, J. Phys. Chem. C, 2017, 121, 9766–9772.
22. K. Yin, Y. Wang, H. Liu, F. Peng and L. Zhang, J. Mater. Chem. A, 2015, 3, 4188–4194.
23. I. G. Batyrev, J. Phys. Chem. A, 2017, 121, 638–647.
24. B. A. Steele and I. I. Oleynik, J. Phys. Chem. A, 2017, 121, 1808–1813.
25. Y. Li, J. Hao, H. Liu, S. Lu and J. S. Tse, Phys. Rev. Lett., 2015, 115, 105502.
26. D. Li, F. Tian, Y. Lv, S. Wei, D. Duan, B. Liu and T. Cui, J. Phys. Chem. C, 2017, 121, 1515–1520.
27. K. Xia, J. Sun, C. J. Pickard, D. D. Klug and R. J. Needs, Phys. Rev. B, 2017, 95, 144102.
28. Z. Raza, I. Errea, A. R. Oganov and A. M. Saitta, Sci. Rep., 2014, 4, 05889.
29. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
30. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
31. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
32. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
36. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
37. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
38. Z. Raza, C. J. Pickard, C. Pinilla and A. M. Saitta, Phys. Rev. Lett., 2013, 111, 235501.
39. W. J. Evans, M. J. Lipp, C. S. Yoo, H. Cynn, J. L. Herberg, R. S. Maxwell and M. F. Nicol, Chem. Mater., 2006, 18, 2520–2531.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra09438e

---