Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thickness-dependent fast wetting transitions due to the atomic layer deposition of zinc oxide on a micro-pillared surface†
Libing Duan‡
*,
Xiangyang Ji‡,
Yajie Yang,
Sihang Yang,
Xinjun Lv and
Yanbo Xie *
*
MOE Key Laboratory of Material Physics and Chemistry Under Extraordinary Conditions, School of Science, Northwestern Polytechnical University, Xi'an 710072, China. E-mail: lbduan@nwpu.edu.cn; ybxie@nwpu.edu.cn
First published on 6th January 2020
Abstract
Smart surfaces promote the fundamental understanding of wetting and are widely used in practical applications for energy and water collection. Light-induced switchable wettability facilitated by ZnO coatings, for instance, was developed for liquid manipulation at the surface. However, the transition of wetting states was reported to follow a hydrophobic–hydrophilic cycle in an hour, which is very long and may limit its future applications. We recently discovered that the cycle of the wetting state transitions on inorganic coatings can be shortened to less than 100 seconds by using ALD-coated ZnO on a pillared surface. However, the mechanisms are still unclear. Here, we investigated the effects of coating thickness on the transition speed and found that it significantly depended on the thickness of the coating with the optimal thickness less than 50 nm. We found that the minimum critical time for a wetting state transition cycle was less than 50 seconds with a thickness of 40 nm. Although the transition time of surfaces with coatings over 70 nm thickness remained constant at 10 min for a cycle, it was shorter than those of other deposition techniques for a coarse surface. Here, we propose a “penetration–diffusion” model to explain the fast and thickness-dependent wetting transitions. Our study may provide a new paradigm for fast wetting transition surfaces with cycle time within tens of seconds using a homogeneous thin layer coated on a rough surface.
Introduction
Wetting is a fundamental phenomenon, which has been studied for many decades.1 Inspired by the features of natural materials, many new materials and technologies have been invented to enable a smart-control of wetting states using artificial structures.2–4 The transition of materials between hydrophilic and hydrophobic states has attracted attention for its wide applications, such as self-cleaning,5 anti-fog coating,6 liquid transport7 and microfluidics.8,9 An external stimulus induces a change in the surface energy of materials, resulting in wettability transitions. The stimulus can originate from light, temperature, electrical fields, pH, magnetic field, etc.10 Light is an elegant way to regulate the wettability of materials due to its high precision,11 non-contact controllability and capability to create partially hydrophilic regions.12 Many photo-responsive materials, such as ZnO, TiO2, SnO2 and organic monolayers, have been used for manipulating the surface wettability transitions.13–17Although it has been reported that the wetting transitions on an organic monolayer-coated surface like azobenzene can occur within tens of seconds, it is rarely reported in the case of inorganic coatings. We recently fabricated a surface with fast wetting transitions by depositing an atomic layer of ZnO on a micro-pillared surface.18 The hydrophobic to hydrophilic transition was completed within a minimum of 60 s, and the recovery on the hot plate was reduced to a minimum of 30 s. Our technique could also achieve a wetting transition speed for an inorganic coating, which was significantly higher than the results for those prepared by classic techniques, such as spray drying,15 vapor deposition,19 magnetron sputtering,20 sol–gel method21 and atomic layer deposition.22 However, the mechanisms underlying the fast wetting transitions are still unknown. In this work, we investigated the speed of wetting transitions as a function of the thickness of the ZnO layers deposited by ALD at various heating temperatures. We found the time of wetting transition was thickness-dependent and the optimal thickness for fast wetting transitions was between 10 to 70 nm. The transition speed on surfaces with thickness over 70 nm remained in the order of ten minutes, which is shorter than those obtained with the traditional coating techniques. Finally, we have theoretically illustrated the possible mechanisms of fast wetting transitions using a “penetration–diffusion” model, which relies on the penetration depth of the light and the diffusion length of the ions in the coating layer. Understanding the fast wetting transition mechanism may introduce a class of fast wetting transition surfaces formed from micro-pillared surfaces with nano-thick coating layers, which may be useful for liquid manipulations and the fabrication of smart surfaces.
Fabrication and setup
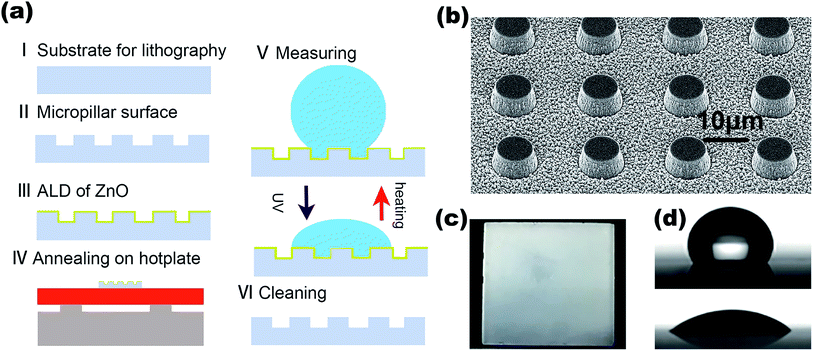
The fabrication process of the micro-pillared chips (Pyrex glass, 2 cm × 2 cm × 0.55 mm) is illustrated in Fig. 1a, showing individual microstructure fabrication and film coating steps. The micro-pillars were first etched by RIE (Plasma Pro 100 Cobra300) by standard photolithography and then coated with a ZnO film using an atomic layer deposition (T-ALD100A) system. The micro-pillars were characterized under a scanning electron microscope (FEI, Verios G4). The free-standing micro-pillar arrays with a center distance of 20 μm and 4 μm depth were fabricated, as shown in Fig. 1b. The substrates were carefully cleaned before each coating process to ensure that it is free of contaminants by following a standard process, which included immersion in dilute hydrochloric acid (20% purity) for 15 minutes, ultrasonic cleaning for 10 minutes, and finally, a cleaning cycle with acetone, alcohol, and deionized water in sequence.The residual water droplets on the surface were dried using an N2 gun and sealed for ALD subsequently. By setting the number of coating cycles (∼0.16 nm per cycle) in the atomic layer deposition system program (diethyl zinc and DI water acted as precursors to provide zinc and oxygen, respectively), the film thickness could be precisely controlled. The coated chip is shown in Fig. 1c. After that, the contact angle reached the maximum with fast annealing in the air on a hot plate at 120 °C for 45 min. The thickness was optically characterized by visible light reflectometry (A3-SR-100, Apris technologies). For contact angle (CA) measurements of ZnO specimens with different thicknesses, we removed the existing ZnO coatings by repeating the cleaning process.
The wettability of the chips was evaluated from the CA values observed with a drop of 5 μL using a contact angle analyzer (POWEREACH, JC2000D2). A typical snapshot from the camera is shown in Fig. 1d to demonstrate the hydrophilic (top) and hydrophobic (bottom) states of the surface of our chips. To investigate the wetting transition speed, we characterized the contact angle after UV exposure or heating at specific time steps. To prevent film damage due to overheating, we performed the experiments in a sequence of temperatures from low to high. UV irradiation was achieved using an uncollimated ultraviolet light source (145 mW cm−2, EPILEDS) placed at 3 cm from the chips in ambient temperature.
Results
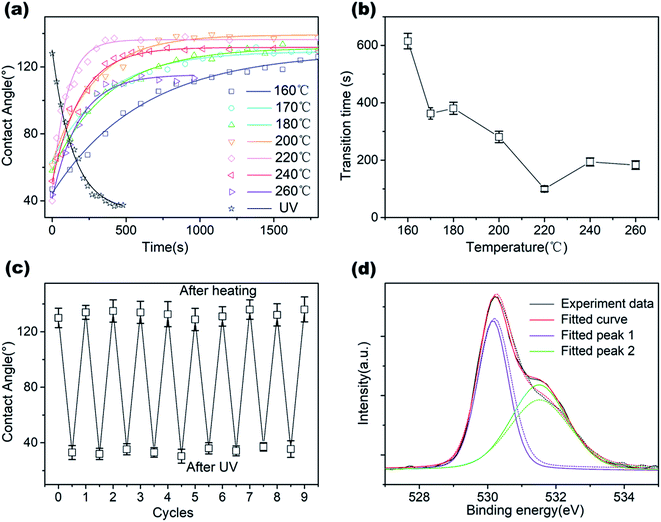
We considered the wettability transitions of the 70 nm-thick ZnO coated micro-pillared chips as an example. The chips were first placed under UV irradiation (145 mW cm−2 with a center wavelength of 365 nm) to investigate the transition from (initial) hydrophobic state to hydrophilic state, shown as black dots in Fig. 2a. CA was measured immediately after UV exposure, and the residual water was blown before subsequent UV irradiation. The time steps indicate the overall duration of exposure under the UV lamp. We found that the exponential decay function fitted well with the CA values measured as a function of time: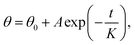 where θ0, A, K are the saturated value at the hydrophilic state, the constant value obtained by fitting, the critical transition time to attain saturation, which represents the speed of transition. A similar tendency of exponential decrease of CA has been reported for TiO2 sol–gel coatings using a comparable statistical analysis to demonstrate the critical transition time (CTT); however, with the cycle of wetting transition extending to an hour.23 As shown in Fig. 2a, we could derive the CTT from a hydrophobic to hydrophilic state as 156 seconds, which is longer than that observed previously for 40 nm thick coatings (60–80 seconds).18 The measured data with 40 nm thickness of the coating was from our previous work for comparison with the critical wetting transition time between different thicknesses. We suspected that it may be relevant to the thickness of the ZnO coating, as discussed below.
where θ0, A, K are the saturated value at the hydrophilic state, the constant value obtained by fitting, the critical transition time to attain saturation, which represents the speed of transition. A similar tendency of exponential decrease of CA has been reported for TiO2 sol–gel coatings using a comparable statistical analysis to demonstrate the critical transition time (CTT); however, with the cycle of wetting transition extending to an hour.23 As shown in Fig. 2a, we could derive the CTT from a hydrophobic to hydrophilic state as 156 seconds, which is longer than that observed previously for 40 nm thick coatings (60–80 seconds).18 The measured data with 40 nm thickness of the coating was from our previous work for comparison with the critical wetting transition time between different thicknesses. We suspected that it may be relevant to the thickness of the ZnO coating, as discussed below.
We further investigated the recovery process from 160 °C to 260 °C by placing the chips on a programmable hotplate for thermal treatment. We divided the total time of the chips on the hot plate into time step (60–120 s) depending on the speed of transitions and investigated the change in CA during the recovery process. CA measurements were done after cooling the chips to room temperature. As we demonstrated previously, the temperature of the chips reached equilibrium within 0.5 seconds after placing on the hotplate, which could be ignored while considering the time of heating.18 We found that the contact angle, after the thermal treatment, increased rapidly at the beginning and then, tended to reach a stable value, matching well with the exponential decrease function: 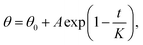 where θ0, A, K are the saturated value at hydrophobic state, the constant value obtained by fitting, and the CTT value for hydrophilic to hydrophobic transition. As the temperature increased, the speed of transition gradually became faster. When the temperature increased to 260 °C, the wetting transitions were irreversible with a lower maximum CA after heating for 960 s, which possibly due to the damage caused by overheating. The ZnO coating on the surface no longer covered the pillars homogeneously, thereby exposing the glass substrate and showing a decrease in the maximum contact angle of the substrates. From the CTT values in Fig. 2a, we could find that the transition speed of wettability is a function of heating temperature in Fig. 2b. With an increase in the temperature, CTT gradually decreased from the initial 600 s to 100–200 s and remained saturated. The surface demonstrated excellent repeatability of the wetting state transitions for over 9 cycles (Fig. 2c), with the contact angles ranging from 30° to 130°, which demonstrated that the surface is promising for future applications. To investigate the mechanisms of the fast transitions, we characterized the morphology changes of the 70 nm-thick ZnO coating on a flat glass slide by atomic force microscopy. The results from the averaged surface roughness did not show a clear change due to UV exposure and the annealing process (ESI S1†).
where θ0, A, K are the saturated value at hydrophobic state, the constant value obtained by fitting, and the CTT value for hydrophilic to hydrophobic transition. As the temperature increased, the speed of transition gradually became faster. When the temperature increased to 260 °C, the wetting transitions were irreversible with a lower maximum CA after heating for 960 s, which possibly due to the damage caused by overheating. The ZnO coating on the surface no longer covered the pillars homogeneously, thereby exposing the glass substrate and showing a decrease in the maximum contact angle of the substrates. From the CTT values in Fig. 2a, we could find that the transition speed of wettability is a function of heating temperature in Fig. 2b. With an increase in the temperature, CTT gradually decreased from the initial 600 s to 100–200 s and remained saturated. The surface demonstrated excellent repeatability of the wetting state transitions for over 9 cycles (Fig. 2c), with the contact angles ranging from 30° to 130°, which demonstrated that the surface is promising for future applications. To investigate the mechanisms of the fast transitions, we characterized the morphology changes of the 70 nm-thick ZnO coating on a flat glass slide by atomic force microscopy. The results from the averaged surface roughness did not show a clear change due to UV exposure and the annealing process (ESI S1†).
Then, XPS was used to investigate the changes in the chemical properties of the surface before and after UV irradiation. A clear change in the shoulder peak at 531.5 eV appeared in the results (Fig. 2d), which indicated that UV irradiation generated oxygen vacancy and absorbed water.24 Although we demonstrated successful wetting transitions on the 70 nm-thick ZnO-coated pillared surface, the response time of the wetting transition was slower than previously reported results, which inspired us to investigate the effect of film thickness on CTT.
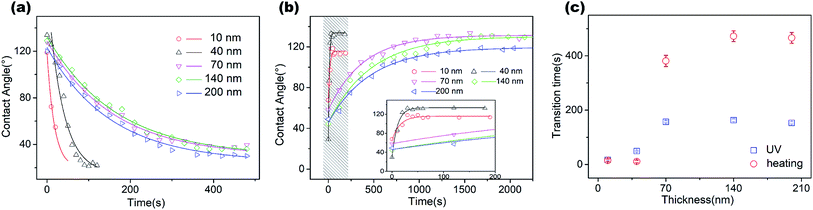
For this, we prepared ZnO coatings on the same substrate with layer thicknesses of 5 nm, 10 nm, 40 nm, 70 nm, 140 nm and 200 nm and found successful reversible transitions in all except the 5 nm-thick coating. To avoid contaminations during measurement, we removed the ZnO coating and carefully cleaned the substrate before coating a ZnO layer of different thickness. We repeatedly UV irradiation to measure the speed of transition from hydrophobic to a hydrophilic state by using time steps (Fig. 3a), while the power density remained at 145 mW cm−2 for all thicknesses of the coating.
The initial contact angle for each sample dramatically decreased from 120° to ∼30° under UV irradiation, exhibiting the law of exponential decay. The fast decrease at the beginning of the UV process was attributed to the high-speed yielding of electron–hole pairs on the initial surface.16 Our measurements presented a clear decrease in transition speed with the thickness increasing from 10 to 70 nm, but reached a plateau for thicknesses over 70 nm. We fitted the exponential decay function for each set of experimental results. The fitted results are presented in Fig. 3c (blue dots). It should be noted that the unstable wetting state at the thickness of 5 nm was possibly due to the inhomogeneity of the film, which didn't cover the surface of the substrate completely. A similar phenomenon was observed by Ahn et al., who reported that the initial growth stage of the film deposited by the ALD method showed island-like spots due to the random adsorption of reactants on the substrate.25 The film became homogeneous when the thickness was over 7.5 nm, showing a uniform layer growth mode and fully-covered coating.
We then performed heat treatment by placing the chips on a 180 °C hot plate to achieve hydrophilic to hydrophobic state transition and derived the effects of film thickness on the transition speed (Fig. 3b). To clearly show the fast transition for the thin layer of the coating, an amplified view of the 10 nm- and 40 nm-thick coating samples are shown in the inset of Fig. 3b. The speed of transition obviously changed with the thickness, with the excellent recovery of CA at the hydrophobic state. It showed that the chips with a thin layer (10–40 nm) of the coating were able to complete a cycle of wetting state transition process within 46 s, which is apparently shorter than the specimens with coating thicknesses over 70 nm (6–7 min). The small difference in the transition speed between the 10 nm and 40 nm coatings is possibly caused because the time of experimental operation is comparable to the wetting transition time (ten seconds).
From the CTT of both UV and thermal transition processes, we could clearly demonstrate the transition speed as a function of thickness, as shown in Fig. 3c. We found the same tendency for both the transition processes with changes in thickness. The CTT dramatically increased with film thickness and then, reached a saturated value. For a complete transition cycle of the hydrophobic and hydrophilic states, it took a minimum of 46 seconds to 10 min as the thickness increased from 10 to 70 nm, and saturation was attained when the thickness was over 70 nm thick (Fig. 3c). There are a few things need to be noted. The CTT of both hydrophilic to hydrophobic and reverse transitions had the same tendency as the function of film thickness. Besides, the longest transition cycle (∼10 min) is still obviously shorter than those observed for coarse surfaces obtained with the other deposition techniques, especially from hydrophilic to hydrophobic state transition by the heating process.26,27 The mechanism of fast transition is critical for further fabrication of fast wetting transition surfaces and relevant applications, which is discussed in the following section with a possible explanation for the thickness-dependent change in wetting transition speed.
Discussion
As described above, the transition of wettability relies on the surface energy changes caused by UV excitation or the annihilation of vacancies on heating. We attributed the fast transition in a wide range of CA to the thin coating of ZnO on the rough surface of micro-pillars machined on a glass substrate. The wetting states in our designed pillars can be categorized to be in the Wenzel state, which was optically observed and matched to the classical wetting theories.18,28 Young's equation illustrates the effects of roughness, showing that the apparent contact angle θ* is relevant to the roughness ratio (r) and Young's contact angle (θ) of an ideal surface, as shown below.29
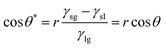 | (1) |
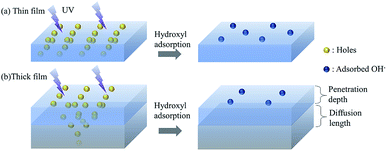
In this section, we discuss the possible mechanisms of the thickness-dependent fast wetting transition and comparison with other film deposition techniques (e.g. sol–gel) by a “penetration–diffusion” model. Two critical physical lengths need to be noted. It has been reported that the UV light can only penetrate δ (typically less than 60 nm)-thick ZnO,31 inducing photon-excited vacancies within this penetrated layer. The vacancies diffuse to an average length Lp over their lifetime,32 which can be estimated by LP = DPτ ∼ 50 nm (μp = 1 cm2 V−1 s−1, τ = 1 ns)33 and is comparable to the penetration distance. Since the surface energy is determined by the concentration of vacancies and the quantity of absorbed water, the generation and diffusion of vacancies, which are thickness-dependent, are directly relevant to wettability.34
Hydrophobic–hydrophilic transition
We first discuss the wetting transitions from hydrophobic to a hydrophilic state under UV exposure. To clearly illustrate the thickness-dependent wetting transitions, we classified the samples into two models – thin film and thick film models. The thin film model was defined to have less thickness than the critical thickness of the penetration depth of the UV light (wavelength of 365 nm), while the thick film was considered to have a film thicker than the sum of penetration depth and diffusion length (>100 nm), where the coated thickness in-between is the transition state from thin film model to thick film model.| E ∝ CPtS | (2) |
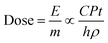 | (3) |
To quantitively discuss this transition in the thick film model, we used the vacancy distribution under one-dimensional stable diffusion, which can be described as:39
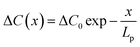 | (4) |
According to the thick film model, the wettability transition is determined by the sum of penetration depth and diffusion length. Thus, the generation of vacancies and the density of hydroxyl adsorption are independent of the film thickness when the thickness increases further. The penetration–diffusion model can possibly also explain the hydrophobic to hydrophilic transition process for classic deposition techniques (like sol–gel), which have a similar transition speed to the thick film model of the ALD-coated ZnO surface on the micro-pillared surface (within a few minutes),41,42 as the saturation time of generated vacancies are determined by the penetration–diffusion length at the surface irrespective of the thickness of the ZnO film.
Hydrophilic–hydrophobic transition
It is well-known that the existence of nanostructures, such as nano-needles or nanoparticles, on a rough surface enhances the range of wettability transitions, according to the wetting theories. However, there are side effects of the wetting transitions on these deposited coarse surfaces with nanostructures. It has been reported that the conduction and migration of vacancies in the nano-confined areas show slower carrier mobility than that in the bulk.47,48 This may limit the speed of diffusion and annihilation of vacancies, inducing a longer time for equilibrium and CA transition on the surface. However, the ALD coating has a homogeneous surface and is in close contact with the substrate, where the micro-pillars perform the role of a rough surface. The film has good contacts with the substrate, avoiding the diffusion of ions in the nano-confined space, resulting in a faster transition for the recovery process. In addition, for the recovery process, the low thermal conduction of the nano-needles seems to be another possible reason,49 slowing down the diffusion and annihilation of vacancies in the nano-needles. For coarse depositions, these nanostructures enhance the range of wettability change. On the contrary, we suspect that due to the joint action of slow migration and poor thermal conduction at the nanostructures, the wetting transition in a rough coating is slower than the homogeneous coating achieved by ALD on a micro-pillared surface. The latter technique possibly can overcome these side effects for the optimization of a fast superhydrophobic–superhydrophilic wetting transition and liquid manipulations in the future.
Conclusion
In this paper, we investigated the wettability transitions of ALD-coated ZnO film on a micro-pillared surface. We found the transition speed was thickness dependent, with a minimum of 35 seconds for hydrophobic to hydrophilic transition under UV irradiation and 11 seconds for recovery from the hydrophilic to hydrophobic state at 40 nm coating thickness. As the film thickness increased, the transition speed remained saturated at 10 min per cycle and was independent of the thickness. The transitions of the ALD-coated micro-pillared surface were much faster than those of other types of deposition techniques. We propose a penetration–diffusion model to explain the fast wetting transition process, which can explain the thickness-dependent wetting transition of the ALD coatings and the difference between ALD coated sample and those coated using other techniques. Our discovery can possibly provide a new paradigm for fast wetting transition surfaces for the manipulation of liquids and the development of smart surfaces due to its fast response, excellent repeatability and ease of fabrication.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the financial support from NSFC (Grant No. U1730133, U1732143), Natural Science Basic Research Plan in Shaanxi province of China (Grant No. 2018JM5039), Fundamental Research Funds for the Central Universities (Grant No. 3102017jc01001, 3102019ghxm020, 3102019PB006), and the ALD coating from Prof. Xuetao Gan and Jianlin Zhao (School of Science, NPU), and the support from Analytical and Testing center of Northwestern Polytechnical University in Xi'an.References
- P. G. Degennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- L. Feng, S. H. Li, Y. S. Li, H. J. Li, L. J. Zhang, J. Zhai, Y. L. Song, B. Q. Liu, L. Jiang and D. B. Zhu, Adv. Mater., 2002, 14, 1857–1860 CrossRef CAS.
- X. F. Gao and L. Jiang, Nature, 2004, 432, 36 CrossRef CAS PubMed.
- C. Hao, Y. Liu, X. Chen, J. Li, M. Zhang, Y. Zhao and Z. Wang, Small, 2016, 12, 1825–1839 CrossRef CAS PubMed.
- Y. Shang, J. Wang, T. Ikeda and L. J. Jiang, J. Mater. Chem. C, 2019, 7, 3413–3428 RSC.
- A. Telecka, N. K. Mandsberg, T. Li, E. Ludvigsen, S. Ndoni, R. Di Mundo, F. Palumbo, J. Fiutowski, S. Chiriaev and R. Taboryski, Nanoscale, 2018, 10, 20652–20663 RSC.
- Y. Guan, Y. Song, H. Li, L. Ye, B. Lu, J. Zang and Y. J. Yu, J. Mater. Chem. C, 2019, 7, 2853–2864 RSC.
- L. Li, Z. Yan, M. Jin, X. You, S. Xie, Z. Liu, A. van den Berg, J. C. T. Eijkel and L. Shui, ACS Appl. Mater. Interfaces, 2019, 11, 16934–16943 CrossRef CAS PubMed.
- H. Gao, Y. Liu, S. Li, G. Wang, Z. Han and L. Ren, Nanoscale, 2018, 10, 15393–15401 RSC.
- N. Verplanck, Y. Coffinier, V. Thomy and R. J. N. S. R. L. Boukherroub, Nanoscale Res. Lett., 2007, 2, 577–596 CrossRef CAS.
- L. Duan, X. Lv, Q. He, X. Ji, M. Sun, Y. Yang, Z. Ji and Y. Xie, Biosens. Bioelectron., 2019, 111886 CrossRef PubMed.
- M. Kamei and T. Mitsuhashi, Surf. Sci., 2000, 463, L609–L612 CrossRef CAS.
- V. Rico, C. Lopez, A. Borras, J. P. Espinos and A. R. Gonzalez-Elipe, Sol. Energy Mater. Sol. Cells, 2006, 90, 2944–2949 CrossRef CAS.
- H. S. Lim, D. Kwak, D. Y. Lee, S. G. Lee and K. Cho, J. Am. Chem. Soc., 2007, 129, 4128–4129 CrossRef CAS PubMed.
- R. D. Sun, A. Nakajima, A. Fujishima, T. Watanabe and K. Hashimoto, J. Phys. Chem. B, 2001, 105, 1984–1990 CrossRef CAS.
- H. Liu, L. Feng, J. Zhai, L. Jiang and D. B. Zhu, Langmuir, 2004, 20, 5659–5661 CrossRef CAS PubMed.
- X. Yue, T. Zhang, D. Yang, F. Qiu and Z. J. C. Li, Cellulose, 2018, 25, 5951–5965 CrossRef CAS.
- Y. Yang, L. Zhang, J. Wang, X. Wang, L. Duan, N. Wang, F. Xiao, Y. Xie and J. Zhao, ACS Appl. Mater. Interfaces, 2018, 10, 19182–19188 CrossRef CAS PubMed.
- D. C. Reynolds, D. C. Look and B. Jogai, Solid State Commun., 1996, 99, 873–875 CrossRef CAS.
- M. Miyauchi, A. Shimai and Y. Tsuru, J. Phys. Chem. B, 2005, 109, 13307–13311 CrossRef CAS PubMed.
- L.-Y. Lin and D.-E. Kim, Thin Solid Films, 2009, 517, 1690–1700 CrossRef CAS.
- X. Meng, X. Wang, D. Geng, C. Ozgit-Akgun, N. Schneider and J. W. Elam, Mater. Horiz., 2017, 4, 133–154 RSC.
- N. Stevens, C. I. Priest, R. Sedev and J. Ralston, Langmuir, 2003, 19, 3272–3275 CrossRef CAS.
- J.-W. Hu, S.-H. Yang and S.-C. Jeng, RSC Adv., 2016, 6, 52095–52100 RSC.
- C. H. Ahn, C. H. Woo, S. Hwang, J. Y. Lee, H. K. Cho, H. J. Cho and G. Y. Yeom, Surf. Interface Anal., 2010, 42, 955–958 CrossRef CAS.
- J. Lue, H. Kai, X. Chen, J. Zhu, F. Meng, X. Song and Z. Sun, Appl. Surf. Sci., 2010, 256, 4720–4723 CrossRef CAS.
- J. Lv, J. Zhu, K. Huang, F. Meng, X. Song and Z. Sun, Appl. Surf. Sci., 2011, 257, 7534–7538 CrossRef CAS.
- P. S. H. Forsberg, C. Priest, M. Brinkmann, R. Sedev and J. Ralston, Langmuir, 2010, 26, 860–865 CrossRef CAS PubMed.
- R. Wenzel, J. Phys. Chem., 1949, 53, 1466–1467 CrossRef CAS.
- R. M. Hewlett and M. A. McLachlan, Adv. Mater., 2016, 28, 3893–3921 CrossRef CAS.
- I. E. Paulauskas, G. Jellison, L. A. Boatner and G. M. Brown, Int. J. Electrochem., 2011, 1–10 Search PubMed.
- A. A. A. Mannanov, M. S. Kazantsev, A. D. Kuimov, V. G. Konstantinov and M. Pshenischnikov, J. Mater. Chem. C, 2018, 7, 60–68 RSC.
- W. Wang, A. Lin and J. D. Phillips, J. Electron. Mater., 2008, 37, 1044–1048 CrossRef CAS.
- H. Hu, H.-F. Ji and Y. Sun, Phys. Chem. Chem. Phys., 2013, 15, 16557–16565 RSC.
- H. Sabbah, J. Coat. Technol. Res., 2017, 14, 1423–1433 CrossRef CAS.
- A. Shiragai, Phys. Med. Biol., 1978, 23, 245–252 CrossRef CAS PubMed.
- Ü. Özgür, Y. I. Alivov, C. Liu, A. Teke, M. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. J. J. o. a. p. Morkoç, J. Appl. Phys., 2005, 98, 11 CrossRef.
- Y. Cong, K. Chen, S. Zhou and L. Wu, J. Mater. Chem. A, 2015, 3, 19093–19099 RSC.
- D. A. Neamen, Semiconductor physics and devices: basic principles, McGraw-Hill, New York, 2012 Search PubMed.
- R. Marin, F. Oussta, S. N. Katea, S. Prabhudev, G. A. Botton, G. Westin and E. Hemmer, J. Mater. Chem. C, 2019, 7, 3909–3919 RSC.
- Z. Zhang, H. Chen, J. Zhong, G. Saraf and Y. Lu, J. Electron. Mater., 2007, 36, 895–899 CrossRef CAS.
- V. Khranovskyy, T. Ekblad, R. Yakimova and L. Hultman, Appl. Surf. Sci., 2012, 258, 8146–8152 CrossRef CAS.
- M. Öztas and M. J. T. S. F. Bedir, Thin Solid Films, 2008, 516, 1703–1709 CrossRef.
- P. Zhang, H. Chen, L. Zhang, Y. Zhang, D. Zhang and L. Jiang, J. Mater. Chem. A, 2016, 4, 12212–12220 RSC.
- C. L. Feng, Y. J. Zhang, J. Jin, Y. L. Song, L. Y. Xie, G. R. Qu, L. Jiang and D. B. Zhu, Langmuir, 2001, 17, 4593–4597 CrossRef CAS.
- E. L. Papadopoulou, V. Zorba, A. Pagkozidis, M. Barberoglou, E. Stratakis and C. Fotakis, Thin Solid Films, 2009, 518, 1267–1270 CrossRef CAS.
- L. K. Jagadamma, M. Abdelsamie, A. El Labban, E. Aresu, G. O. N. Ndjawa, D. H. Anjum, D. Cha, P. M. Beaujuge and A. J. J. o. M. C. A. Amassian, J. Mater. Chem. A, 2014, 2, 13321–13331 RSC.
- J. Yang, H. L. Yip and A. K. Y. J. A. E. M. Jen, Adv. Energy Mater., 2013, 3, 549–565 CrossRef CAS.
- J. Xie, A. Frachioni, D. Williams and W. Jr, Appl. Phys. Lett., 2013, 102, 193101 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra08498c |
| ‡ These authors made equal contributions. |
| This journal is © The Royal Society of Chemistry 2020 |