 Open Access Article
Open Access ArticleGraphene and silicene quantum dots for nanomedical diagnostics
L. B. Drissi*abc,
H. Ouarrada,
F. Z. Ramadana and
W. Fritzsched
aLPHE, Modeling and Simulations, Faculty of Science, Mohammed V University in Rabat, Rabat, Morocco. E-mail: ldrissi@fr.ac.ma
bCPM, Centre of Physics and Mathematics, Mohammed V University in Rabat, Morocco
cHassan II Academy of Science and Technology, Rabat, Morocco
dIPHT, Leibniz Institute of Photonic Technology, Jena, Germany
First published on 3rd January 2020
Abstract
In the present work, the prominent effects of edge functionalization, size variation and base material on the structural, electronic and optical properties of diamond shaped graphene and silicene quantum dots are investigated. Three functional groups, namely (–CH3, –OH and –COOH) are investigated using the first principles calculations based on the density functional, time-dependent density functional and many-body perturbation theories. Both the HOMO–LUMO energy gap, the optical absorption and the photoluminescence are clearly modulated upon functionalization compared to the H-passivated counterparts. Besides the functional group, the geometric distortion induced in some QDs also influences their optical features ranging from near ultra-violet to near infra-red. All these results indicate that edge-functionalizations provide a favorable key factor for adjusting the optoelectronic properties of quantum dots for a wide variety of nanomedical applications, including in vitro and in vivo bioimaging in medical diagnostics and therapy.
Introduction
For several decades, a variety of powerful and long-term fluorescent dyes have acquired tremendous interest, owing to their ability to label and track biological molecules within living cells.1 Small molecules and proteins, such as green fluorescent proteins (GFP), have been proven to be prominent organic fluorophores under incident light in the blue to ultraviolet range.2 However, GFPs present a restrictive drawback in long-term bioimaging because of their low stability against photobleaching due to interactions with surrounding molecules.3Semiconductor quantum dots (SCQDs) constitute an ideal alternative to conventional organic dyes thanks to their excellent photostability and high fluorescence quantum efficiency.4,5 Furthermore, these fluorescent probes can be easily prepared and controlled through chemical methods.6 However, the cytotoxicity of SCQDs, due to the toxic heavy-metal elements they contain, in addition to their poor solubility, preclude their use in biomedical applications.7,8 To overcome this biosafety issue, special interest has been devoted to carbon-based fluorescent nanoparticles.
The discovery of carbon quantum dots, diamond nanocrystals, fluorescent carbon nanotubes and fullerene nanoparticles, is of great interest especially for biomedical research because of their high brightness, significant photobleaching resistance, and low cytotoxicity among other attributes.9 Using hydrothermal cutting of pre-oxidized graphene sheets, graphene quantum dots (CQDs) were fabricated for the first time in 2010.10 They are graphene fragments of nanometric size where charge carriers are confined in three dimensions of space. CQDs combining graphene performance and quantum dot behaviour, offer unusual optoelectronic properties resulting from quantum confinement and edge effects.11
CQDs are environmentally friendly and suitable for biomedical applications like in vivo and in vitro bioimaging, biosensing, drug and gene delivery, DNA cleavage, and cancer therapy.12,13 They are also used in electronic devices such as photodetectors, capacitors, phototransistors and in renewable energy resources.14–16 To adapt and modify CQD properties such as the photoluminescence behaviour, for desired and specific applications, different successful processes have been reported. For example total or partial substitution, adsorption, decoration or chemical functionalization of the edges, size variation and application of the electrical field are all effective methods to control the stability of quantum dots and tune their electronic and optical properties.17–20
Variation of size, shape and zigzag/armchair edge configuration in hexagonal CQDs influences gap energy, excitonic binding energy and singlet-triplet energy splitting which results in the potential photoluminescence required for optoelectronic and photovoltaic devices.21 Si-atoms substituting C-atoms in diamond shaped quantum dots (DSQDs) strongly altered the chemical stability, optoelectronic behavior and excitonic character of pyrene, leading to a wide variety of properties for promising nanoelectronic and nanomedical applications.22 Furthermore, rectangular CQDs were found to be sensitive to the amount and position of substituents as well as to the application of an external electric field dealing with prominent optical absorption ranging from near infra-red (NIR) to UV, making these types of QDs emergent candidates for solar cell applications.23
Theoretical studies have also revealed the significant effect of the type of edge-functionalization and the amount of functional groups in tailoring the optoelectronic properties and photoluminescence behavior of CQDs.24 Upon partial edge-functionalization, the absorption and fluorescence spectra of CQDs are slightly shifted towards lower energies, while a large red-shift occurs for the fully functionalized edges.25 Notably, competition between frontier orbital hybridization and charge transfer clearly affects the energy gap and the exciton-binding energy of coronene structures.26 In NH2 edge-functionalized CQDs, p-orbital hybridization between the C and N atoms at the peripheral sites induces the formation of new energy levels in the form of an interband within the energy gap, yielding tunable PLs for novel optoelectronic devices.27 Additionally, the edge and surface functionalization of the CQDs with oxygen-containing groups leads to a remarkable change in the electronic gap and absorption spectra.28
Experimentally, size-controllable amine-functionalized CQDs show low cytotoxicity and high biocompatibility, in addition to prominent multicolored fluorescence and antimycoplasma properties.29 Likewise, the optical properties have also been tuned by the contour functionalization in green fluorescent CQDs synthesized using a single-step large scale synthesis through acidic treatment of the graphite powder.30 Furthermore, fluorine functionalized CQDs provide a protective shell leading to significant photo- and pH stability, high fluorescence, low cytotoxicity and favorable biocompatibility.31 Therefore, fluorinated GQDs are suitable for long-term and real-time cellular imaging. Interestingly, edge functional groups enhance the solubility of GQDs in water and label cells more efficiently.32
The present paper suggests exploring a class of suitable, multicolored fluorescent DSGQDs and DSSiQDs for biomedical purposes. To do so, first-principle computational methods, namely density function theory (DFT) and many-body perturbation theory (MBPT), were carried out in order to reveal the effect of the molecular edge-functionalization and size on the structural and optoelectronic behavior of the systems. It is shown that the highest occupied molecular orbital (HOMO)– lowest unoccupied molecular orbital (LUMO) energy gap of all functionalized structures undergoes a change with respect to the H-passivated QDs. Among the studied functional groups, –COOH proves to be favourable for the adjustment of the optoelectronic features of the QDs due to the considerable role of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond. Additionally, some substituents induced distortion in the corresponding QDs, leading to absorption and photoluminescence ranging from UV to NIR. The inclusion of many body effects via GW approximation has resulted in a crucial correction of the DFT results, especially for the case of the OH functionalized CQDs owing to the large capacity of this molecular group to remove charge carriers from the C and Si skeleton. Consequently, this reduces the screening and thus improves the electron–electron interaction. Moreover, singlet–triplet energy splitting values are found to be significant seeing the large overlap of electron and hole wave functions, which opens up broad opportunities for their use in optoelectronic and nanomedical applications. Finally, the organic nature and biological properties of these QDs can facilitate their transport across organs and tissues and enhance their uptake by living cells.
O double bond. Additionally, some substituents induced distortion in the corresponding QDs, leading to absorption and photoluminescence ranging from UV to NIR. The inclusion of many body effects via GW approximation has resulted in a crucial correction of the DFT results, especially for the case of the OH functionalized CQDs owing to the large capacity of this molecular group to remove charge carriers from the C and Si skeleton. Consequently, this reduces the screening and thus improves the electron–electron interaction. Moreover, singlet–triplet energy splitting values are found to be significant seeing the large overlap of electron and hole wave functions, which opens up broad opportunities for their use in optoelectronic and nanomedical applications. Finally, the organic nature and biological properties of these QDs can facilitate their transport across organs and tissues and enhance their uptake by living cells.
The document is organized as follows: details on the ab initio calculations are given in the first section. The second section presents the energetic stability, as well as a description of the electronic and optical properties, of edge-functionalized DSQDs. Finally, we summarize and conclude our main findings.
1. Computational methods
First-principles calculations based on DFT have been carried out using the Quantum Espresso simulation package33 employing the generalized gradient approximation GGA-DFT of the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional.34 Norm-conserving pseudopotentials and a plane-wave basis set with a kinetic energy cutoff of 60 Ry were used. Due to the 0-dimensional nature of QDs, all calculations were performed only at Gamma point of the Briouillin zone.The significant quantum confinement effect and the small size of our systems result in decreased screening which enhances the Coulomb interaction between charge carriers, namely electrons and holes. Consequently, excitonic effects become significant so that ground state calculations are no longer reliable to investigate the optoelectronic properties. For that reason, many-body interactions are taken into account in our study. Using the GW approximation, the quasiparticle (QP) corrections to GGA eigenvalues were estimated by solving the following equation:35
| EQPnk = EQPKS + 〈ψnk|Σ(EQPnk) − VKSxc|ψnk〉 |
The excitonic properties were explored by solving the Bethe–Salpeter equation (BSE):36
We also determine the effective mass Meff and the Bohr radius of the exciton given by:
 | (1) |
2. Results and discussion
This section presents the numerical results obtained from ab initio calculations on the effect of size variation and edge-functionalization on the optoelectronic properties of pristine graphene and pure silicene quantum dots. The goal is to tune the various features of these nanostructures in order to increase their suitability for biomedical applications.Structural properties
Two different sizes of diamond shaped graphene and silicene quantum dots are studied. These nanostructures contain a mixture of zigzag edges and armchair corners. The molecular structures of QDs edge-functionalized with the functional groups H, methyl (CH3), hydroxyl (OH) and carboxyl (COOH) are plotted in Fig. 1. With their small size and organic nature, these three molecular substituents provide the QDs with biological and biosafety compatibility. Notice also that in each structure, only the hydrogen passivated to the four seam atoms, namely the atoms connecting the zigzag edges to the armchair corners, are replaced in order to obtain a significant adjustment of the investigated property.22,39 | ||
| Fig. 1 Molecular structures of edge-functionalized CQDs and SiQDs with H, CH3, OH and COOH. Yellow, cyan, purple and red spheres represent carbon, silicon, hydrogen and oxygen atoms, respectively. | ||
Hydrogen passivated C-QDs and Si-QDs, that were successfully fabricated and studied theoretically, are included for comparison.22,39–42 The insight into the molecular geometry of the edge-hydrogenated configurations shows that the hybridization is strongly dependent on the atom type. More precisely, the C–C bond angles range between 118° and 123° for edge-hydrogenated CQDs revealing that carbon atoms are sp2-hybridized. Consequently, CQDs maintain the perfect geometry of pyrene. Likewise, SiQDs decorated with CH3 and COOH substituents maintain the same buckled geometry of a silicene sheet, with Si–Si bond angles ranging between 115° and 120°, which reflects the sp2–sp3 hybridization of Si atoms. However, the situation is different for hydroxylated SiQDs that exhibit a slight distortion at decorated zigzag edges, illustrated by a considerable decrement in the summit bond angle of 105.46° and 103.47° for hydroxylated Si16H10 and Si30H14 with respect to 117.4° and 117.05° found in small and large sized pristine SiQDs.43–45 It is worth noting that, like pyrene, dibenzo-coronene, C30H14, has a point group D2h that is changed to the C2h symmetry in its Si analog Si30H14.
Larger sizes C- and Si-QDs are not considered in this work since they present the least interesting properties compared to the two aforementioned sizes. In addition, for bioimaging applications, small size structures are more desirable for use as fluorescent tags on living cells and tissues because large size QDs affect organ functions.15,46,47
To examine the energy stability of QDs, we determined the harmonic frequencies as depicted in Fig. 2 for the two cases of methylated and carboxylated C30H14–CH3 and C30H14–OH, and as shown in Table 1 for all structures. The absence of imaginary frequencies confirms that the edge-functionalized QDs are all energetically stable. The lowest value of 8.94 cm−1 is observed for Si30H14–COOH. The highest frequency of 3787.84 cm−1 corresponds to Si16H10–OH. The stability of these nanostructures is attributed to the large charge transfer and the ionic bonds between the C/Si skeleton and functional groups.
| Structures | α(1,2,3) | β(4,5,6) | ω | Charge | Ef | Frequency range | EGGAg | EGWg | |
|---|---|---|---|---|---|---|---|---|---|
| H | C16H10 | 120.42 | 120.42 | 4.91 | — | — | 101.07–3204.49 | 2.61 | 6.63 |
| C30H14 | 120.76 | 120.76 | 9.17 | — | — | 47.47–3203.81 | 1.32 | 4.28 | |
| Si16H10 | 117.4 | 117.4 | 14.60 | — | — | 27.21–2230.11 | 1.05 | 3.55 | |
| Si30H14 | 117.05 | 117.05 | 23.85 | — | — | 12.12–2228.90 | 0.506 | 2.38 | |
| CH3 | C16H10 | 123.05 | 123.05 | 4.56 | −0.051 | −5.406 | 64.85–3218.2 | 2.32 | 6.05 |
| C30H14 | 123.09 | 123.09 | 8.68 | −0.054 | −0.781 | 36.75–3201.61 | 1.20 | 4.02 | |
| Si16H10 | 119.72 | 119.72 | 11.29 | −0.106 | −4.475 | 23.59–3137.25 | 1.05 | 3.49 | |
| Si30H14 | 119.96 | 22.78 | −0.102 | −3.218 | 10.65–3138.06 | 0.507 | 2.39 | ||
| OH | C16H10 | 120.66 | 120.66 | 3.38 | −0.237 | −12.038 | 69.61–3762.14 | 2.31 | 6.08 |
| C30H14 | 120.79 | 120.79 | 7.15 | −0.232 | −2.849 | 37.23–3759.88 | 1.19 | 4.05 | |
| Si16H10 | 105.46 | 105.46 | 14.08 | −0.231 | −14.974 | 21.88–3787.84 | 0.84 | 3.26 | |
| Si30H14 | 103.47 | 103.47 | 18.57 | −0.231 | −13.726 | 10.7–3786.27 | 0.55 | 2.46 | |
| COOH | C16H10 | 122.94 | 122.94 | 10.99 | −0.078 | −8.593 | 13.18–3700.35 | 2.01 | 5.46 |
| C30H14 | 123.04 | 123.04 | 17.18 | −0.093 | −0.420 | 24.43–3698.48 | 1.06 | 3.78 | |
| Si16H10 | 116.14 | 116.14 | 17.55 | −0.149 | −6.942 | 17.32–3617.59 | 0.92 | 3.32 | |
| Si30H14 | 116.28 | 116.28 | 28.25 | −0.15 | −5.670 | 8.94–3617.67 | 0.46 | 2.32 |
Electronic properties
The energy gap, that is the difference between the LUMO and the HOMO, is given in Table 1. The ground state calculations performed within the GGA-DFT approach reveal that the H–L (HOMO–LUMO) gap values are sensitive to the edge-functionalization.The functional groups on the diamond-shaped CQD edges, lower the H–L gap in good agreement with their analogs, (i) hexagonal CQDs decorated with –CH3, –NH2, –OH, –F, –CHO, –COOH, –COCH3 and –COOH (ref. 26) and, (ii) C123H38 QDs functionalized with oxygen containing groups.28 Accordingly, upon functionalization, the H–L gap drops by 9.1–23.14% for CQDs since –CH3 functionalized structures possess the highest H–L gap while the lowest gap is that of –COOH. For SiQDs, carboxylation resulted in decreasing the H–L gap due to the existence of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bonds in the –COOH molecules. Besides, in hydroxylated and methylated SiQDs, a small down shift of the H–L gap value is observed only for Si16H10–OH.
O double bonds in the –COOH molecules. Besides, in hydroxylated and methylated SiQDs, a small down shift of the H–L gap value is observed only for Si16H10–OH.
Furthermore, the H–L gap behaviour, that is linked to the type of the functional group, depends strongly on the base material and the size of QDs. Graphene QDs are the most affected systems due to the high electronegativity of carbon atoms compared to silicon. Additionally and regardless of the base material, the smaller the structure the stronger the impact of the studied functional groups. This finding is mainly related to the strong quantum confinement existing in small configurations. It follows that the edge-functionalization is a prominent factor to tailor the H–L gap of the studied systems, especially for hydrogen passivated C-QDs that exhibit a large H–L gap which limits their use in several optical applications. For Si-QD, the control of the H–L energy gap through edge-functionalization opens up the prospect of a novel range of emergent nanomedical applications that require small energy gap values.
To get more insight into this behaviour, we analyse the electron charge density of molecular frontier orbitals plotted in Fig. 3 and 4. In small and large sized CQDs, there is no charge transfer between carbon atoms located along the large diagonal of each structure while a charge transfer occurs especially between hydrogen and carbon atoms in zigzag edges. It follows that both HOMO and LUMO isosurfaces spread in zigzag edges and armchair corners including molecular functional groups and excluding the backbone atoms of QD skeletons. The large hybridization of HOMO and LUMO levels results in the reduction of the H–L gap in accordance with C123 QDs functionalized using oxygen containing groups.28 Additionally, it is clear that the HOMO and LUMO levels of both –CH3 and –OH edge-functionalized structures shift toward higher energies with respect to pyrene, while they shift toward lower energies in COOH–CQDs. This finding can be assigned to the presence of the double bond in the COOH functional group.26
Likewise, smaller SiQDs exhibit a significant hybridization of HOMO and LUMO energies explaining the reduction in energy gap values. Interestingly, in Si16H10–OH, the contribution of –OH to the LUMO is almost absent compared to carbon and the two hydrogen atoms of the large diagonal. It follows a small shift increase in LUMO energy level with respect to Si16H10. For HOMO, a remarkable increase of its energy level arises from the prominent contribution of H-passivated edges and –OH molecules. Therefore, this structure exhibits the largest drop in the electronic gap followed by Si16H10–CH3 and Si16H10–COOH. This difference can be attributed to the slight distortion caused by functionalization48 since the presence of the –OH group deals with a little distortion in Si16H10–OH armchair corners with respect to Si16H10 as reported previously. Larger sized Si30H14 have also shown a large hybridization of frontier molecular orbitals as depicted in Fig. 4. The spacial distribution of HOMO and LUMO is fully localized in the edges including functional groups which led to the enhancement of H–L gap in –CH3 and –OH SiQDs. Additionally, the contribution originating from C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is pronounced which confirms a decrease in the corresponding gap value.
O is pronounced which confirms a decrease in the corresponding gap value.
It is worth noting that the obtained results using DFT-GGA formalism sound very useful and offer a favorable description of the investigated QDs electronic behaviour. However, optoelectronic and nanomedical applications require going beyond the ground state properties by carrying out further calculations employing GW approximations. The inclusion of many-body effects results in significant enhancement of the DFT-GGA gap values as shown in Table 1. Applying QP corrections, the gaps range from 2.718 eV to 4.022 eV for graphene structures and between 1.868 and 2.503 eV for silicene ones. The DFT-GGA energy gaps of pristine as well as edge-functionalized CQDs were enhanced by 36.73–39.36% for small structures and 28.04–30.84% for larger ones. Much smaller percentages are found for SiQDs since the GGA–H–L energy gap values were increased by 25.84–30.0% for small configurations and by 19.61–22.37% for larger systems. These prominent corrections ensure the significant enhancement of energy gap brought by e–e correlation.
Furthermore, unlike SiQDs that keep the same order, the variation order of DFT-GGA gaps is changed for CQDs upon employing the GW approach as shown in Table 2. This can be explained by the fact that some functional groups, like the –OH one, act like electron acceptors and withdraw electrons from carbon atoms. This impacts the charge transfer and reduces the QDs surface electrons. It results in decreasing the screening and enhancing electron–electron interactions. Consequently, the QP corrections as well as the GW energy gap increases.
| GW | GGA | |
|---|---|---|
| C16H10 | Eg(OH) > Eg(CH3) > Eg(COOH) | Eg(CH3) > Eg(OH) > Eg(COOH) |
| C30H14 | Eg(OH) > Eg(CH3) > Eg(COOH) | Eg(CH3) > Eg(OH) > Eg(COOH) |
| Si16H10 | Eg(CH3) > Eg(COOH) > Eg(OH) | Eg(CH3) > Eg(COOH) > Eg(OH) |
| Si30H14 | Eg(OH) > Eg(CH3) > Eg(COOH) | Eg(OH) > Eg(CH3) > Eg(COOH) |
To examine the stability and chemical reactivity of QDs, we compute electrophilicity index ω given in terms of ELUMO and EHOMO as follows:50
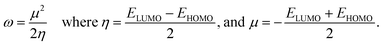 | (2) |
As listed in Table 1, the edge-functionalization decreases the electrophilicity index in all diamond shaped QDs, except for the graphene ones decorated with COOH molecules. This infers that –COOH enhances the reactivity of the corresponding QDs while OH and CH3 make the systems more stable and less reactive.
Finally, different parameters like size, base material, distortion of the structures, substituents and also charge transfer collaborate together to modulate the structural and electronic behaviour of the QDs resulting in a broad class of CQDs and SiQDs, where each structure is distinguished by intrinsic features and different characteristics.
Optical properties
To explore the effects of many-body interactions and excitonic effects on the optical properties of edge-functionalized QDs, Fig. 5 displays the absorption spectra in the absence and the presence of e–h interactions, within GW + RPA and GW + BSE levels, respectively. It results in the inclusion of excitonic effects which induces crucial modification on the peak position and the intensity of the first bright exciton. All curves undergo a red-shift toward lower energies.As listed in Table 3 and displayed in Fig. 6, TDDFT calculations show similar absorption behaviour as the BSE results. More precisely, the optical gap values of both methods sound close and the absorption spectra also exhibits the same features.
 | ||
| Fig. 6 Absorption and photoluminescence spectra of pristine and edge-functionalized QDs obtained via TDDFT method. | ||
| Structures | IbX | Ef | Eabsopt | λabs | Eemopt | λem | Stokes shift | |
|---|---|---|---|---|---|---|---|---|
| H | C16H10 | 1 | 3.746 | 331.00 | 3.412 | 363.4 | 0.334 | |
| C30H14 | 3 | 2.334 | 531.20 | 2.179 | 568.9 | 0.155 | ||
| Si16H10 | 3 | 1.606 | 771.80 | 1.532 | 809.2 | 0.074 | ||
| Si30H14 | 9 | 1.003 | 1235.8 | 0.970 | 1278.0 | 0.033 | ||
| CH3 | C16H10 | 2 | −5.406 | 3.382 | 366.60 | 3.088 | 401.5 | 0.294 |
| C30H14 | 3 | 3.781 | 2.190 | 566.10 | 2.038 | 608.2 | 0.152 | |
| Si16H10 | 3 | −4.475 | 1.594 | 777.90 | 1.511 | 820.4 | 0.083 | |
| Si30H14 | 3 | −3.218 | 0.953 | 1300.9 | 0.719 | 1724.0 | 0.234 | |
| OH | C16H10 | 3 | −12.038 | 3.310 | 374.60 | 3.059 | 405.3 | 0.251 |
| C30H14 | 3 | −2.849 | 2.223 | 557.70 | 2.081 | 595.8 | 0.142 | |
| Si16H10 | 4 | −14.974 | 1.277 | 970.60 | 0.844 | 1469.5 | 0.433 | |
| Si30H14 | 2 | −13.726 | 0.892 | 1389.5 | 0.716 | 1730.8 | 0.176 | |
| COOH | C16H10 | 9 | −8.593 | 3.059 | 405.30 | 2.845 | 435.8 | 0.214 |
| C30H14 | 5 | 0.420 | 1.996 | 621.30 | 1.657 | 748.1 | 0.339 | |
| Si16H10 | 3 | −6.942 | 1.510 | 820.90 | 1.449 | 855.4 | 0.061 | |
| Si30H14 | 3 | −5.670 | 0.961 | 1290.5 | 0.745 | 1663.4 | 0.216 |
In parallel, the photoluminescence spectra depicted in Fig. 6 show a slight shift compared to the absorption curves. This is confirmed through the Stokes shift reported in Table 3 that measures the difference in energy between the absorption and emission peak maxima corresponding to the same electronic transition. Obviously, graphene configurations exhibit significant photoluminescence compared to silicene structures. The wavelengths vary from the near ultra-violet (NUV) to NIR regions of the solar spectrum, reflecting the diversity in their light colors and optical properties. The results obtained for pyrene are in good agreement with experimental measurements.51,52
It is worth noting that the anisotropic behaviour of the optical properties of QDs observed in ref. 39 and 49 disappear under the edges functionalization with OH, CH3 and COOH. Therefore, the optical results, listed in Table 4, including absorption curves, exciton binding energy, Bohr radius and effective mass, do not depend on the light polarization direction. Thus, we only report the results corresponding to the X-direction.
| Structures | EXb | MXe–h | RX | EXopt | λabs | ΔXS–T | IH/L | ε | Transitions | |
|---|---|---|---|---|---|---|---|---|---|---|
| H | C16H10 | 3.21 | 0.268 | 2.104 | 3.42 | 362.53 | 1.27 | 0.90 | 1.067 | H → L (0.67), H−1 → L+1 (−0.21) |
| C30H14 | 1.81 | 0.203 | 3.218 | 2.47 | 501.96 | 1.62 | 0.908 | 1.237 | H → L (0.69), H−1 → L+1 (−0.15), H−2 → L+2 (−0.11) | |
| Si16H10 | 1.99 | 0.229 | 2.892 | 1.56 | 794.77 | 0.66 | 0.871 | 1.253 | H → L (0.66), H−1 → L+1 (−0.22) | |
| Si30H14 | 1.15 | 0.219 | 3.894 | 1.22 | 1016.26 | 0.63 | 0.887 | 1.610 | H → L (0.69), H−1 → L+1 (−0.17), H−2 → L+2 (−0.12) | |
| CH3 | C16H10 | 2.33 | 0.198 | 2.875 | 3.72 | 333.29 | 1.76 | 0.894 | 1.076 | H → L (0.69), H−1 → L+1 (−0.17) |
| C30H14 | 1.65 | 0.121 | 4.370 | 2.37 | 523.14 | 1.62 | 0.909 | 1.000 | H → L (0.70), H−1 → L+1 (−0.13), H−3 → L+2 (−0.10) | |
| Si16H10 | 2.07 | 0.219 | 2.687 | 1.41 | 879.32 | 0.85 | 0.867 | 1.296 | H−1 → L (0.35), H → L+1 (0.60) | |
| Si30H14 | 1.59 | 0.500 | 2.191 | 0.80 | 1549.80 | 0.76 | 0.892 | 2.069 | H → L (0.18), H → L+1 (0.67) | |
| OH | C16H10 | 2.31 | 0.196 | 2.903 | 3.77 | 328.87 | 1.78 | 0.886 | 1.075 | H−1 → L (0.21), H → L+1 (0.67) |
| C30H14 | 1.71 | 0.202 | 3.322 | 2.34 | 529.84 | 1.60 | 0.901 | 1.269 | H→L (0.70), H−1→L+1 (−0.13), H−2 → L+2 (−0.10) | |
| Si16H10 | 1.91 | 0.233 | 2.928 | 1.35 | 918.40 | 0.78 | 0.748 | 1.289 | H → L (−0.71) | |
| Si30H14 | 1.80 | 0.254 | 2.886 | 0.66 | 1878.54 | 0.45 | 0.876 | 1.387 | H → L+2 (0.70) | |
| COOH | C16H10 | 1.65 | 0.142 | 4.032 | 3.81 | 325.42 | 2.03 | 0.866 | 1.083 | H → L (0.69), H−1 → L+1 (−0.13) |
| C30H14 | 1.57 | 0.203 | 3.456 | 2.21 | 561.01 | 1.56 | 0.882 | 1.328 | H−1 → L (0.70) | |
| Si16H10 | 1.95 | 0.254 | 2.772 | 1.37 | 904.99 | 0.88 | 0.865 | 1.333 | H → L (0.68), H−1 → L+1 (−0.19) | |
| Si30H14 | 1.52 | 0.249 | 2.109 | 0.81 | 1530.67 | 0.80 | 0.802 | 2.249 | H→L (0.70), H−1→L+1 (−0.16), H−2 → L+2 (0.11) |
On the other hand, the functionalizations remarkably tune the optical gap and consequently effect the exciton binding energy (EXb) leading to the production of changeable absorption colors ranging from the NUV to the NIR. A first examination reveals that CQDs exhibit considerable EXb compared to SiQDs and that small size structures possess the largest EXb values. In the case of CQDs, a considerable drop in EXb value is obtained through COOH functionalization. This finding is attributed to the large exciton indices that are 9 and 5 for C16H10–COOH and C30H14–COOH, respectively, compared with the 1 and 3 indices found for their H-passivated analogs listed in Table 3. In the case of small SiQDs, the EXb value undergoes a slight decrease upon OH and COOH functionalization. This is due to the increase of exciton index from 3 for Si16H10 to 4 for Si16H10–OH. On the other hand, functionalization of large SiQDs results in shifting-up EXb, especially for Si30H14–OH since the exciton index varies from 9 for Si30H14 to 3. It follows that the optical gap values lead to the absorption of NUV light by the three small edge-functionalized C16H10 configurations while larger functionalized C30H14 can absorb green light. Similarly, the optical gap values of SiQDs are shifted-down upon edge-functionalization revealing NIR behaviour with different wavelength values. Therefore, we obtain QD structures with a wide range of photoluminescence emission colors from visible to NIR, which are recommended for a variety of biomedical applications. In particular, the short-wavelength excitation and emission of QDs, makes it very difficult to detect the luminescent signal in deep human organs and living cells for early disease diagnosis.53 Consequently, the NIR SiQDs seem to be good candidates for injection in vivo to label internal organs like the heart and the liver, while CQDs can be used as in vitro bioimaging agents or in vivo superficial cells and tissues like the skin.
Further insight into the excitonic character of the studied QDs is given by the analysis of the electron probability distribution plotted in Fig. 7 and data reported in Table 4. Clearly, methylated and hydroxylated C16H10 as well as C30H14 maintain the same behaviour as their counterparts pyrene and dibenzo-coronene. Indeed, the electron distribution associated with the first bright exciton is localized along the whole structures with a slight distribution observed on oxygen atoms in hydroxylated C30H14. In the carboxylated configurations, the exciton distribution is mainly localized on –COOH molecules for C16H10 and along the carbon–skeleton with a small amount localized on COOH functionals for C30H14. In the case of SiQDs, the electron distribution is localized along the whole structure excluding CH3 molecule for Si30H14 that shows the smaller Bohr radius RX, given in Å, compared to its pristine counterpart.
 | ||
| Fig. 7 Spatial distribution of the exciton along the X-direction. The hole is represented by the black dot. | ||
Due to the spin–orbit coupling, the mixture of the triplet states with the singlets strongly effects the photoluminescent character of QDs. To highlight the photophysical process that might occur in our edge-functionalized nanostructures, singlet–triplet energy splitting ΔS–T was determined and is listed in Table 4. The ΔS–T values sound significant due to the large overlap between electron and hole wave functions IH/L. They range from 0.76 to 1.76 for methylated configurations and from 0.02 to 1.78 eV in hydroxylated structures. Furthermore, the carboxylated QDs show the highest splitting values ranging from 0.80 to 2.03 eV. More precisely, thermally activated delayed fluorescence (TADF) characterizes C30H14–OH which exhibits very small splitting (ΔS–T < 0.37 eV).54 Conventional fluorescence occurs in all edge-functionalized SiQDs where splitting values range between 0.5 and 1 eV. For large splitting values, the triplet–triplet annihilation (TTA) process takes place in methylated and hydroxylated C16H10 with ET1/ES1 > 0.5 eV. Whereas singlet fission takes place in methylated C30H14 as well as carboxylated C16H10 and C30H14 where ET1/ES1 < 0.5 eV. Where ET1 and ES1 are the energies of the first triplet and singlet excited states, respectively.54 Similar to structures characterized by TADF, such as metal–organic complexes, donor–acceptor molecules or TTA photophysical processes, the studied CQDs can be used as organic light emitting diodes55 or as in vivo biosensors and bioimaging devices.56 Whereas, systems with SF processes are broadly employed to fabricate solar cells.57
Finally, the functionalization represents a helpful means to control and modulate the exchange splitting of excitons paving the way for the construction of novel QDs with desired optoelectronic and photoluminescence properties for nanomedical use.
3. Conclusion
In the present work, we have studied the optoelectronic properties of egde-functionalized CQDs and SiQDs using –CH3, –OH and –COOH molecular substituents. It is found that the functional group type, the size variation and the base material present crucial key factors for tailoring the QDs properties. In particular, the competition between the edge functionalization and the geometry distortion result in some QDs showing considerable influence on their H–L gap, their charge transfer, their optical behavior and their excitonic binding energy with respect to their H-passivated counterparts. Moreover, the large overlap observed in the investigated QDs originates from the significant exciton exchange splitting values. Consequently, it reduces the potential non-radiative transition between singlet and triplet excited states and increases the chances of photophysical processes. Finally, the photoluminescence obtained via TDDFT calculations, that ranges from NUV to visible for CQDs and that occupies a broad range in the NIR for SiQDs, reveals the potential use of edge-functionalized QDs as emergent candidates for nanomedical applications such as in vitro and in vivo bioimaging.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. B. Drissi would like to acknowledge “Académie Hassan II des Sciences et Techniques-Morocco” for financial support. She also acknowledges Alexander von Humboldt Foundation for financial support via the Georg Forster Research Fellowship for experienced scientists (ref. 3 and 4 – MAR 1202992).References
- M. S. T. Gonalves, Fluorescent Labeling of Biomolecules with Organic Probes, Chem. Rev., 2009, 109, 190–212 CrossRef PubMed.
- R. Y. Tsien, The green fluorescent protein, Annu. Rev. Biochem., 1998, 67, 509–544 CrossRef CAS PubMed.
- X. T. Zheng, A. Ananthanarayanan, K. Q. Luo and P. Chen, Glowing graphene quantum dots and carbon dots: Properties, syntheses, and biological applications, Small, 2015, 11, 1620–1636 CrossRef CAS PubMed.
- E. Yaghini, A. M. Seifalian and A. J. MacRobert, Quantum dots and their potential biomedical applications in photosensitization for photodynamic therapy, Nanomedicine, 2009, 4, 353–363 CrossRef CAS PubMed.
- M. Baker, Nanotechnology imaging probes: smaller and more stable, Nat. Methods, 2010, 7, 957–962 CrossRef CAS.
- A. Valizadeh, H. Mikaeili, M. Samiei, S. Farkhani, N. Zarghami, M. Kouhi, A. Akbarzadeh and S. Davaran, Quantum dots: synthesis, bioapplications, and toxicity, Nanoscale Res. Lett., 2012, 7, 480 CrossRef PubMed.
- X. Michalet, F. F. Pinaud, L. A. Bentolila, J. M. Tsay, S. Doose, J. J. Li, G. Sundaresan, A. M. Wu, S. S. Gambhir and S. Weiss, Quantum dots for live cells, in vivo imaging, and diagnostics, Science, 2005, 307, 538–544 CrossRef CAS PubMed.
- Y. Volkov, Quantum dots in nanomedicine: Recent trends, advances and unresolved issues, Biochem. Biophys. Res. Commun., 2015, 468, 419–427 CrossRef CAS PubMed.
- J. Shen, Y. Zhu, X. Yang and C. Li, Graphene quantum dots: emergent nanolights for bioimaging, sensors, catalysis and photovoltaic devices, Chem. Commun., 2012, 48, 3686–3699 RSC.
- D. Pan, J. Zhang, Z. Li and M. Wu, Hydrothermal Route for Cutting Graphene Sheets into Blue-Luminescent Graphene Quantum Dots, Adv. Mater., 2010, 22, 734–738 CrossRef CAS PubMed.
- M. Bacon, S. J. Bradley and T. Nann, Graphene Quantum Dots, Part. Part. Syst. Charact., 2014, 31, 415–428 CrossRef CAS.
- S. Zhu, J. Zhang, C. Qiao, S. Tang, Y. Li, W. Yuan, B. Li, L. Tian, F. Liu, R. Hu, H. Gao, H. Wei, H. Zhang, H. Sun and B. Yang, Strongly green-photoluminescent graphene quantum dots for bioimaging applications, Chem. Commun., 2011, 47, 6858–6860 RSC.
- Y. Wang and A. Hu, Carbon quantum dots: synthesis, properties and applications, J. Mater. Chem. C, 2014, 2, 6921–6939 RSC.
- Z. Jin, P. Owour, S. Lei and L. Ge, Graphene, graphene quantum dots and their applications in optoelectronics, Curr. Opin. Colloid Interface Sci., 2015, 20, 439–453 CrossRef CAS.
- X. Wang, G. Sun, N. Li and P. Chen, Quantum dots derived from two-dimensional materials and their applications for catalysis and energy, Chem. Soc. Rev., 2016, 45, 2239–2262 RSC.
- P. Tian, L. Tang, K. Teng and S. Lau, Graphene quantum dots from chemistry to applications, Mater. Today Chem., 2018, 10, 221–258 CrossRef CAS.
- L. A. Agapito, N. Kioussis and E. Kaxiras, Electric-field control of magnetism in graphene quantum dots: Ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 201411 CrossRef PubMed.
- J. Li and V. B. Shenoy, Graphene quantum dots embedded in hexagonal boron nitride sheets, Appl. Phys. Lett., 2011, 98, 013105 CrossRef.
- X. Li, S. P. Lau, L. Tang, R. Ji and P. Yang, Multicolour light emission from chlorine-doped graphene quantum dots, J. Mater. Chem. C, 2013, 1, 7308–7313 RSC.
- Y. Niko, Y. Hiroshige, S. Kawauchi and G. I. Konishi, Fundamental photoluminescence properties of pyrene carbonyl compounds through absolute fluorescence quantum yield measurement and density functional theory, Tetrahedron, 2012, 68, 6177–6185 CrossRef CAS.
- S. S. Yamijala, A. Bandyopadhyay and S. K. Pati, Structural Stability, Electronic, Magnetic, and Optical Properties of Rectangular Graphene and Boron Nitride Quantum Dots: Effects of Size, Substitution, and Electric Field, J. Phys. Chem. C, 2013, 117, 23295–23304 CrossRef CAS.
- F.-Z. Ramadan, H. Ouarrad and L. B. Drissi, Tuning Optoelectronic Properties of the Graphene-Based Quantum Dots C16−x Six H10 Family, J. Phys. Chem. A, 2018, 122, 5016–5025 CrossRef CAS PubMed.
- Y. Li, H. Shu, S. Wang and J. Wang, Electronic and optical properties of graphene quantum dots: The role of many-body effects, J. Phys. Chem. C, 2015, 119, 4983–4989 CrossRef CAS.
- T. Tabish and S. Zhang, Graphene Quantum Dots: Syntheses, Properties and Biological Applications, in Reference Module in Materials Science and Materials Engineering, Elsevier, 2016 Search PubMed.
- M. Zhao, F. Yang, Y. Xue, D. Xiao and Y. Guo, A Time-Dependent DFT Study of the Absorption and Fluorescence Properties of Graphene Quantum Dots, ChemPhysChem, 2014, 15, 950–957 CrossRef CAS PubMed.
- Y. Li, H. Shu, X. Niu and J. Wang, Electronic and Optical Properties of Edge-Functionalized Graphene Quantum Dots and the Underlying Mechanism, J. Phys. Chem. C, 2015, 119, 24950–24957 CrossRef CAS.
- G. S. Kumar, R. Roy, D. Sen, U. K. Ghorai, R. Thapa, N. Mazumder, S. Saha and K. K. Chattopadhyay, Amino-functionalized graphene quantum dots: origin of tunable heterogeneous photoluminescence, Nanoscale, 2014, 6, 3384–3391 RSC.
- J. Feng, H. Dong, L. Yu and L. Dong, The optical and electronic properties of graphene quantum dots with oxygen-containing groups: a density functional theory study, J. Mater. Chem. C, 2017, 5, 5984–5993 RSC.
- F. Jiang, D. Chen, R. Li, Y. Wang, G. Zhang, S. Li, J. Zheng, N. Huang, Y. Gu, C. Wang and C. Shu, Eco-friendly synthesis of size-controllable amine-functionalized graphene quantum dots with antimycoplasma properties, Nanoscale, 2013, 5, 1137 RSC.
- V. Kumar, V. Singh, S. Umrao, V. Parashar, S. Abraham, A. K. Singh, G. Nath, P. S. Saxena and A. Srivastava, Facile, rapid and upscaled synthesis of green luminescent functional graphene quantum dots for bioimaging, RSC Adv., 2014, 4, 21101–21107 RSC.
- H. Sun, H. Ji, E. Ju, Y. Guan, J. Ren and X. Qu, Synthesis of Fluorinated and Nonfluorinated Graphene Quantum Dots through a New Top-Down Strategy for Long-Time Cellular Imaging, Chem.–Eur. J., 2015, 21, 3791–3797 CrossRef CAS PubMed.
- Z. Qian, J. Ma, X. Shan, L. Shao, J. Zhou, J. Chen and H. Feng, Surface functionalization of graphene quantum dots with small organic molecules from photoluminescence modulation to bioimaging applications: an experimental and theoretical investigation, RSC Adv., 2013, 3, 14571 RSC.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- L. Hedin and B. I. Lundqvistfs, Explicit local exchange-correlation potentials, J. Phys. C: Solid State Phys., 1971, 2064 CrossRef.
- G. Onida, L. Reining and A. Rubio, Electronic excitations: density-functional versus many-body Green’s-function approaches, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37, 785 CrossRef CAS PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Basak, H. Chakraborty and A. Shukla, Theory of linear optical absorption in diamond-shaped graphene quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205404 CrossRef.
- J. M. Robertson, Bond-length variations in aromatic systems, Acta Crystallogr., 1948, 1, 101–109 CrossRef CAS.
- R. W. Havenith, J. H. van Lenthe, F. Dijkstra and L. W. Jenneskens, Aromaticity of Pyrene and Its Cyclopentafused Congeners Resonance and NICS Criteria. An Ab Initio Valence Bond Analysis in Terms of Kekulé Resonance Structures, J. Phys. Chem. A, 2001, 105, 3838–3845 CrossRef CAS.
- J. R. Dias, Isomer enumeration of nonradical strictly peri-condensed polycyclic aromatic hydrocarbons, Can. J. Chem., 1984, 62, 2914–2922 CrossRef CAS.
- S. Biswas, C. Champion, P. F. Weck and L. C. Tribedi, Differential electron emission from polycyclic aromatic hydrocarbon molecules under fast ion impact, Sci. Rep., 2017, 7, 5560 CrossRef PubMed.
- B. Sun, Z. A. Dreger and Y. M. Gupta, High-pressure effects in pyrene crystals: vibrational spectroscopy, J. Phys. Chem. A, 2008, 112, 10546–10551 CrossRef CAS PubMed.
- L. T. Scott, Chemistry at the interior atoms of polycyclic aromatic hydrocarbons, Chem. Soc. Rev., 2015, 44, 6464–6471 RSC.
- R. Zhang and Z. Ding, Recent Advances in Graphene Quantum Dots as Bioimaging Probes, Journal of Analysis and Testing, 2018, 2, 45–60 CrossRef.
- F. Chen, W. Gao, X. Qiu, H. Zhang, L. Liu, P. Liao, W. Fu and Y. Luo, Graphene quantum dots in biomedical applications: Recent advances and future challenges, Frontiers in Laboratory Medicine, 2017, 1, 192–199 CrossRef.
- C. Cocchi, D. Prezzi, A. Ruini, M. J. Caldas and E. Molinari, Electronics and Optics of Graphene Nanoflakes: Edge Functionalization and Structural Distortions, J. Phys. Chem. C, 2012, 116, 17328–17335 CrossRef CAS.
- H. Ouarrad, F.-Z. Ramadan and L. B. Drissi, Size engineering of optoelectronic features of C, Si and CSi hybrid diamond-shaped quantum dots, RSC Adv., 2019, 9, 28609 RSC.
- R. G. Parr, L. V. Szentpály and S. Liu, Electrophilicity index, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- H. D. Smith, C. P. McKay, A. G. Duncan, R. C. Sims, A. J. Anderson and P. R. Grossl, An instrument design for non-contact detection of biomolecules and minerals on Mars using fluorescence, J. Biol. Eng., 2014, 8, 16 CrossRef PubMed.
- L. Piñeiro, M. Novo and W. Al-Soufi, Fluorescence emission of pyrene in surfactant solutions, Adv. Colloid Interface Sci., 2015, 215, 1–12 CrossRef PubMed.
- M. Nurunnabi, Z. Khatun, K. M. Huh, S. Y. Park, D. Y. Lee, K. J. Cho and Y.-k. Lee, In Vivo Biodistribution and Toxicology of Carboxylated Graphene Quantum Dots, ACS Nano, 2013, 7, 6858–6867 CrossRef CAS PubMed.
- T. Chen, L. Zheng, J. Yuan, Z. An, R. Chen, Y. Tao, H. Li, X. Xie and W. Huang, Understanding the Control of Singlet-Triplet Splitting for Organic Exciton Manipulating: A Combined Theoretical and Experimental Approach, Sci. Rep., 2015, 5, 10923 CrossRef PubMed.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Thermally activated delayed fluorescence materials towards the breakthrough of organoelectronics, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS PubMed.
- S. M. Borisov, C. Larndorfer and I. Klimant, Triplet–Triplet Annihilation-Based Anti-Stokes Oxygen Sensing Materials with a Very Broad Dynamic Range, Adv. Funct. Mater., 2012, 22, 4360–4368 CrossRef CAS.
- M. B. Smith and J. Michl, Singlet fission, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |





