Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic hysteresis and strong ferromagnetic coupling of sulfur-bridged Dy ions in clusterfullerene Dy2S@C82†
Denis
Krylov
ab,
Georgios
Velkos
a,
Chia-Hsiang
Chen
ac,
Bernd
Büchner
 a,
Aram
Kostanyan
d,
Thomas
Greber
a,
Aram
Kostanyan
d,
Thomas
Greber
 d,
Stanislav M.
Avdoshenko
d,
Stanislav M.
Avdoshenko
 a and
Alexey A.
Popov
a and
Alexey A.
Popov
 *a
*a
aLeibniz Institute for Solid State and Materials Research, Helmholtzstraße 20, 01069 Dresden, Germany. E-mail: a.popov@ifw-dresden.de
bCenter for Quantum Nanoscience, Institute for Basic Science (IBS), Seoul, Republic of Korea
cDepartment of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 807, Taiwan
dPhysik-Institut der Universität Zürich, Winterthurerstr. 190, CH-8057 Zürich, Switzerland
First published on 29th July 2020
Abstract
Two isomers of metallofullerene Dy2S@C82 with sulfur-bridged Dy ions exhibit broad magnetic hysteresis with sharp steps at sub-Kelvin temperature. Analysis of the level crossing events for different orientations of a magnetic field showed that even in powder samples, the hysteresis steps caused by quantum tunneling of magnetization can provide precise information on the strength of intramolecular Dy⋯Dy interactions. A comparison of different methods to determine the energy difference between ferromagnetic and antiferromagnetic states showed that sub-Kelvin hysteresis gives the most robust and reliable values. The ground state in Dy2S@C82 has ferromagnetic coupling of Dy magnetic moments, whereas the state with antiferromagnetic coupling in Cs and C3v cage isomers is 10.7 and 5.1 cm−1 higher, respectively. The value for the Cs isomer is among the highest found in metallofullerenes and is considerably larger than that reported in non-fullerene dinuclear molecular magnets. Magnetization relaxation times measured in zero magnetic field at sub-Kelvin temperatures tend to level off near 900 and 3200 s in Cs and C3v isomers. These times correspond to the quantum tunneling relaxation mechanism, in which the whole magnetic moment of the Dy2S@C82 molecule flips at once as a single entity.
Introduction
Tremendous progress in lanthanide single-molecule magnets (SMMs) during the last decade had been largely fuelled by the design of new molecules with ever-increasing magnetic anisotropy.1 For single-ion SMMs, ligand-field (LF) splitting has been the main parameter on which experimental and computational studies have focused until recently,2 although the gradual understanding of the paramount role of molecular vibrations now shifts the focus to spin–phonon interactions.2j,3 In polynuclear SMMs, exchange and dipolar interactions between lanthanide ions create a more complex structure of magnetic states than in single-ion magnets, and the presence of such coupled states introduces a strong variation in static and dynamic magnetic properties in comparison with their single-ion counterparts. The most obvious difference is the quenching of zero-field quantum tunneling of magnetization in dinuclear SMMs, which is caused by exchange biasing.4 On the other hand, new relaxation pathways involving low-energy exchange-excited states can appear in dinuclear SMMs and limit their SMM performance.Aside from compounds with lanthanide-radical coupling, which can be very strong,5 magnetic Ln⋯Ln interactions are usually rather weak. The energy difference between the lowest states with ferromagnetically and antiferromagnetically coupled moments, ΔEAFM–FM, is a very important parameter for dinuclear SMMs, but its precise determination is not very straightforward and often relies on the fitting of magnetic data with effective spin Hamiltonians involving some parameterized forms of Ln⋯Ln interactions. EPR studies can in principle provide more precise information on the Ln⋯Ln interactions,6 but for lanthanide ions with strong magnetic anisotropy, such studies encounter serious difficulties and are still rare. At the same time, the orbital mechanisms behind the exchange interactions between lanthanide ions featuring strong spin–orbit coupling are rather complicated.7 This limits the applicability of computational modelling at the same extent and reliability as it is used now for prediction of single-ion magnetic anisotropy in lanthanide molecular magnets.
Endohedral metallofullerenes (EMFs) encaging di-lanthanide clusters bridged via non-metal ions Xq−, such as N3−, S2−, C22−, or O2−, known as clusterfullerenes,8 offer simple models for the studies of Ln⋯Ln interactions. Short Ln–X bonds lead to the strong magnetic anisotropy of Ln ions and the robust SMM behaviour in many Dy-clusterfullerenes.2k,4d,9 The ligand-field (LF) splitting is usually so large that there is no mixing of LF and exchange states, thus simplifying the analysis and allowing to focus only on the exchange excitation in the ground state LF manifold. Note that quite a different situation is found in dimetallofullerenes featuring single-electron lanthanide–lanthanide bonds and hence giant exchange interactions,5c,10 as well as in SMMs with radical bridges,5a,b but we will not consider such molecules in this work.
The first dinuclear EMF-SMM Dy2ScN@C80-Ih revealed the strong influence of Dy⋯Dy interactions on the magnetic hysteresis shape in comparison with mononuclear DySc2N@C80, and indicated a considerable ΔEAFM–FM energy of ca. 6 cm−1.4d Since then, we studied a number of di-nuclear EMFs and found a strong variation of the strength of Dy⋯Dy interactions in them. ΔEAFM–FM in some of those studies was determined by fitting magnetization data.4d,9h,k In many cases it was also established that the relaxation of magnetization occurred via the exchange-excited state, showing Arrhenius behaviour with the barrier equal to ΔEAFM–FM.2k,4d,9b,c,h,i Both approaches have certain limitations. The shape of magnetic susceptibility and isothermal magnetization curves is very sensitive to Ln⋯Ln interactions at low temperatures, but below the blocking temperature of magnetization, SMMs do not exhibit magnetic field and temperature dependence expected in the thermodynamic regime and thus cannot be used for a fitting, whereas higher-temperature curves are less sensitive to the Ln⋯Ln interaction parameters. Arrhenius barriers may be affected by the presence of concurrent relaxation mechanisms and also depend on the accuracy of the measured relaxation times. Note that determination of magnetization relaxation time τM is not straightforward when τM is longer than 104 s or falls into the gap between 0.1–1 s (the upper limit for AC magnetometry) and ∼50 s (the lower accuracy limit for DC magnetometry).
Sub-Kelvin magnetization studies can be very useful for the determination of Ln⋯Ln interaction strength even when hysteresis sets in. Freezing thermal relaxation processes leaves QTM as the main relaxation mechanism. QTM takes places only at the level crossing and thus can give direct information on the interactions and avoids the need for fitting procedures. Such measurements were performed usually with ordered single crystals,4a,11 but their utility for powder samples is not obvious since the distribution of orientations also leads to a distribution of level crossing positions. However, the recent sub-Kelvin magnetometry study of Tb2ScN@C80 (ref. 12) showed that the QTM-related features in magnetic hysteresis of a powder sample can be fairly sharp and may help in the careful description of the low-energy magnetic states in such dinuclear SMMs. Besides, such studies give access to magnetization relaxation dynamics, which would not be accessible otherwise. As mentioned, dinuclear EMF-SMMs often have thermally activated relaxation via the exchange-excited state down to 2 K. But how will the system behave if the temperature is low enough to freeze this process out? What is the time scale of the QTM process in which the coupled moment of two lanthanide ions flips as a single entity? In this work we apply sub-Kelvin magnetometry measurements to two isomers of sulfide clusterfullerene Dy2S@C82 to get a deeper insight into Dy⋯Dy interactions and its influence on the magnetic hysteresis and the relaxation of magnetization in these prototype dinuclear SMMs.
Results and discussion
Molecular structure and alignment of magnetic moments
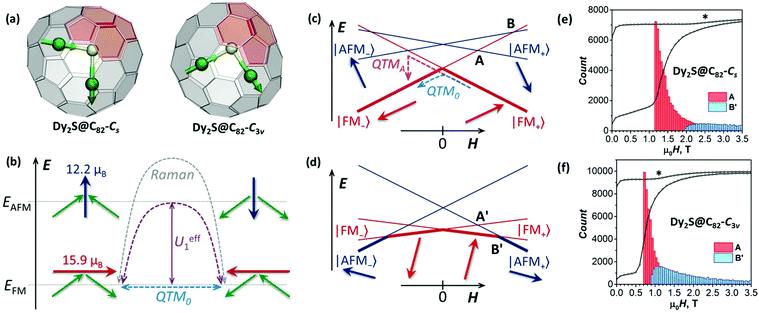
Synthesis and structural characterization of two Dy2S@C82 isomers by single-crystal X-ray diffraction were described previously.9c Crystallographic studies revealed Cs(6) and C3v(8) isomeric structures of the fullerene cage in two EMFs. These isomers share similar cage topology and are different only in the orientation of two pyracelene units highlighted in Fig. 1a. Pseudo-rotation of one CC bond in each pyracelene unit by 90° (known as Stone–Wales transformation) interconverts the fullerene cages.Crystallographic studies gave the Dy–S bond lengths and Dy–S–Dy angles of 2.465(5), 2.518(5) Å and 98.3(2)° in the Cs isomer and 2.437(11), 2.511(9) Å and 94.4(2)° in the C3v isomer. But significant disorder of the metal positions may affect these values. In the molecular structures optimized at the PBE-D level with PAW 4f-in-core potentials (VASP 5.0 code13) the Dy–S bond lengths and Dy–S–Dy angles are 2.484, 2.509 Å and 99.1° in the Cs isomer and 2.489, 2.506 Å and 97.4° in the C3v isomer.
Strong uniaxial ligand field imposed by sulfide ion S2− leads to the orientation of Dy magnetic moments along Dy–S bonds. Different mutual orientations of Dy moments in the dinuclear cluster Dy2S give four states grouped into two quasi-doublets with a perpendicular orientation of the magnetic moment (Fig. 1b). The total magnetic moment of the molecule in each quasi-doublet depends on the Dy–S–Dy angle: μFM = 2 μDy cos(α/2), μAFM = 2 μDy·sin(α/2), where μDy is the magnetic moment of Dy3+ in the ground state, equal to 10μB, and α is the angle between quantization axes of Dy ions and is approximately equal to α ≈ 180° − ∠(Dy–S–Dy). The equality is not rigorous here because quantization axes of Dy ions may deviate slightly from the Dy–S bond directions. Thus, for the Dy–S–Dy angle of 105°, the μFM and μAFM moments are 12.2 and 15.9μB, respectively. In the following, the states with smaller and larger magnetic moments will be defined as antiferromagnetically (AFM) and ferromagnetically (FM) coupled. Note that this notation is rather arbitrary and for a Dy–S–Dy angle of 90° both moments would be equal. The preliminary study showed that the FM state in Dy2S@C82 is lower in energy than AFM.9c
The sharp features in low-T hysteresis curves can be associated with quantum tunnelling of magnetization (QTM). At low T, thermally activated relaxation processes become very slow, which makes relaxation of magnetization via QTM much more pronounced. As the QTM occurs at the avoided level crossing, it is necessary to understand the structure of the Zeeman diagram and possible types of level crossing events. Furthermore, the angular dependence of the Zeeman diagram needs to be understood because experimental studies are performed for powder samples with random orientation of molecules versus the external magnetic field. But first, it is necessary to determine the energy difference between the FM and AFM states.
| Ĥspin = ĤLF1+ ĤLF2− 2j12Ĵ1·Ĵ2 + ĤZEE | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α), where α is the angle between quantization axes of two Dy3+ ions as introduced above.
cos(α), where α is the angle between quantization axes of two Dy3+ ions as introduced above.
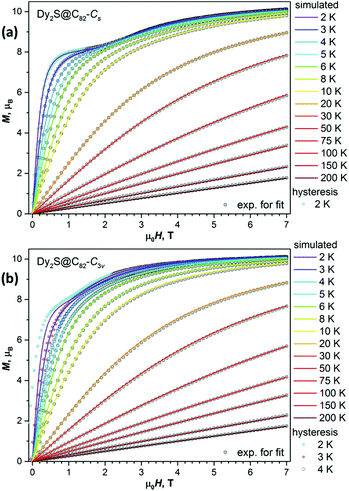
The coupling constant j12 and angle α are determined by fitting the experimental magnetization curves to eqn (1) taking powder-averaging into account using the PHI code14 (Fig. 3). In both molecules, the FM coupling is found in the ground state. For Dy2S@C82-Cs, the best fit is obtained for j12 = 0.160 ± 0.001 cm−1 and α = 72.3 ± 0.1°, which gives ΔEAFM–FM = 11.0 cm−1. For Dy2S@C82-C3v, the optimal j12 is 0.117 ± 0.002 cm−1 and α = 75.7 ± 0.3°, amounting to ΔEAFM–FM = 6.4 cm−1. Assuming that Dy3+ moments are aligned exactly along the Dy–S bonds, these fits give ∠(Dy–S–Dy) angles of 107.7° in Cs and 104.3° in C3v isomers, which is somewhat higher than single-crystal values and DFT predictions for the lowest energy cluster positions. However, in real structures with disordered positions of Dy2S clusters inside fullerenes, the ∠(Dy–S–Dy) angles are not single-valued, and the fits give only an average.
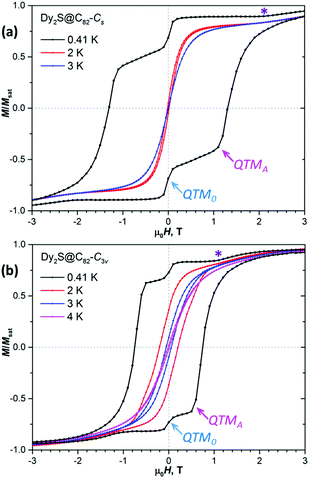
If magnetic field is aligned parallel to the magnetic moment of the FM (or AFM) state, only this state is split by the field, whereas the AFM (or FM) is not affected. The situation for an arbitrary orientation of the field is shown in Fig. 1c and d. In Fig. 1c, orientation of the total magnetic moment of the FM state is close to but not exactly parallel to the field direction. One of the FM doublet components is the ground state of the molecule in the whole field range (|FM+〉 for H > 0 and |FM−〉 for H < 0). The crossing at zero field causes the QTM within the FM doublet, |FM+〉 ↔ |FM−〉 (denoted as QTM0 in Fig. 1b, c and 2). In this process, magnetic moments of both Dy ions flip at once. This is a low-probability process and can be observed only at very low temperature, when faster thermal processes are frozen out. Indeed, a sharp but not strong drop of magnetization can be seen upon zero field crossing in 0.41 K hysteresis curves of both Dy2S@C82 isomers, but this feature is not seen at 2 K and above (Fig. 2).
Another level crossing event of high importance for the understanding of the hysteresis shape is denoted as type A in Fig. 1c. It corresponds to the crossing of the higher-energy FM state with a lower-energy AFM state (e.g., the crossing of |FM+〉 with |AFM−〉 in the negative field, or |FM−〉 with |AFM+〉 in the positive field). Consider evolution of the system in Fig. 1c when the magnetic field is swept from large positive to large negative values. At H > 0, |FM+〉 is the ground state and magnetization is slowly decreasing because of the partial population of other states. At low temperatures, when the thermal relaxation is very slow, magnetization remains almost constant until zero field. During zero-field crossing, the |FM+〉 state can relax to the |FM−〉 state by the QTM0 mechanism. Fig. 2 shows that only ∼15–20% of Dy2S@C82 molecules undergoes the QTM0 and adopts the |FM−〉 state after crossing zero field, whereas the large part remains in the |FM+〉 state, resulting in the positive magnetization in the negative field. For this large part of Dy2S@C82 molecules, the fast relaxation of magnetization is triggered at the next level crossing of type A between |FM+〉 and |AFM−〉 states (also denoted as QTMA in Fig. 1c and 2). The |FM+〉 → |AFM−〉 transition appears to be much more efficient than |FM+〉 → |FM−〉 as evidenced by the abrupt drop of magnetization to negative values beyond the level crossing. It is not clear yet if the QTMA event results in a concerted relaxation to the |FM−〉 state,4b,12 or that the |AFM−〉 state is accessed first and then gradually relaxes to the |FM−〉 state. But the second option would require a thermally activated mechanism, and hence the concerted mechanism is more probable. If after crossing of type A, a part of the molecules still stays in the |FM+〉 state, the next crossing would be of type B with the |AFM+〉 state. It may also trigger the change of the magnetization via |FM+〉 → |AFM+〉 transition, but we do not see corresponding features in hysteresis curves (Fig. 2). Presumably, relaxation of magnetization at the level crossing of type A is very efficient, and the fraction of Dy2S@C82 molecules surviving in the |FM+〉 state beyond this level crossing is very small.
Another possibility not considered yet in our analysis is that the magnetic field is oriented nearly perpendicular to the magnetic moment of the FM state. In this case, |AFM+〉 and |AFM−〉 may become ground states at some large positive and negative fields, respectively (Fig. 1d). Upon reducing the field, |FM+,−〉 states become lower in energy than |AFM+,−〉 giving the level crossing of type B′ (Fig. 1d). Again, a stepwise drop of magnetization is possible at this crossing following the |AFM+〉 ↔ |FM+〉 and |FM−〉 ↔ |AFM−〉 transitions, but it cannot be as pronounced as for type A because the fraction of molecules undergoing this type of crossing in the available field range of [−7, 7] T is relatively small as discussed below. The change of magnetization at the level crossing of type B′ should also occur in the thermodynamic regime, when the relaxation of magnetization is fast. Corresponding features can be identified in magnetization curves recorded below 3–4 K (Fig. 3).
Powder samples such as studied in this work have molecules in different orientations. Therefore, the level crossing event of each type will not occur in one particular field but will be distributed over a certain field range. Depending on the shape of this distribution, QTM features in hysteresis curves may appear as sharp or smeared. To analyse the distributions, we used j12 and α parameters determined from the fits to experimental magnetization curves and calculated level crossing positions for Dy2S@C82 molecules with 105 different orientations of the magnetic field vector around them uniformly distributed on the Fibonacci sphere.§Fig. 1e and f show histograms of level crossing events of types A and B′ for Cs and C3v isomers of Dy2S@C82 in the field range of 0–3.5 T.
For Dy2S@C82-Cs, 58.3% molecules have the crossing of type A between 0 and 7 T, and 42% of these crossings happen between 1.16 and 1.36 T. Likewise, 57.5% of Dy2S@C82-C3v molecules undergo this type of crossing between 0 and 7 T, and 54% of those events fall into the narrow field range between 0.72 and 0.92 T. Thus, crossing events of type A have a very sharp distribution with the asymmetric peak near the smallest field, at which this event can take place. This threshold field (HA) is simply proportional to the energy difference between AFM and FM states:
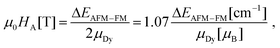 | (2) |
The crossing of type B′, on the other hand, has a less distinct position (Fig. 1e and f). For Dy2S@C82-Cs, 25% of all molecules have this kind of crossing in the field range below 7 T. The smallest field, in which the crossing can take place, is 1.95 T, and the next 0.5 T (1 T) range includes only 16% (33%) of events among the molecules with the B′ point below 7 T. For Dy2S@C82-C3v, the distribution is slightly denser. The fraction of all molecules with B′ crossing below 7 T is 32%, of that 22% (43%) have this crossing in the range of 0.5 T (1 T) above the threshold field of 1.14 T. Thus, in contrast to type A, the crossing of type B′ occurs with a smaller fraction of molecules (hence smaller change of magnetization), and the distribution of the events in the field scale is much broader. Although the corresponding deflection can be seen in the experimental curves (marked with an asterisk in Fig. 1e, f and 2), we cannot determine if this feature occurs because of the QTM-induced relaxation at the level crossing, or because the system simply follows a thermodynamic regime. The lowest field, at which B′ crossing can take place, is defined in eqn (3):
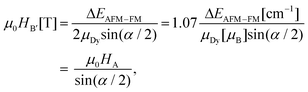 | (3) |
Eqn (3) also allows determination of ΔEAFM–FM if α is known or can be estimated from the known ∠(Dy–S–Dy) angle. But because of the broad distribution of crossing events in powder samples, and because the maximum in the distribution is shifted from the threshold field HB′ (Fig. 1e and f), the corresponding features in magnetization curves are very smeared, and precision of the ΔEAFM–FM value estimated this way for powder samples would be not very high. Anyway, analogs of formulae (3) were used earlier for estimation of exchange interaction in powder samples, mainly for dinuclear complexes with the AFM ground state.4e,15 For oriented single crystals though, the value can be quite accurate.4a,11
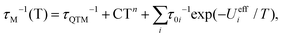 | (4) |
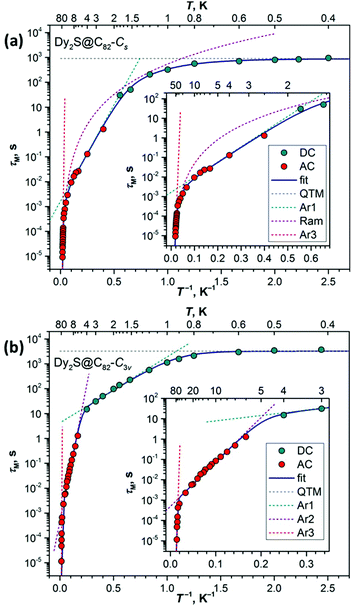 | ||
| Fig. 4 Magnetization relaxation times of (a) Dy2S@C82-Cs and (b) Dy2S@C82-C3v. Dark cyan and red dots are DC and AC measurements, solid lines are fits by a combined equation eqn (1), and dashed lines are contributions of QTM, Raman, and Arrhenius processes. The insets show magnification of higher-temperature parts. | ||
At the lowest temperatures, relaxation time tends to level off, which indicates a transition to the QTM relaxation regime. Characteristic QTM times obtained from the fits are 906 ± 80 s for the Cs isomer and 3224 ± 418 s for the C3v isomer. These rather long times explain why the QTM0 regime can be observed in hysteresis curves only at sub-Kelvin temperature. Consider the FM ground-state of a dinuclear Dy system such as shown in Fig. 1b. If a magnetic moment of one of the metal ions is flipped, the system arrives at the AFM state, which has higher energy. Thus, the ΔEAFM–FM difference prevents zero-field QTM with the flipping of one Dy3+ moment. At the same time, it allows the thermally activated relaxation process with the barrier Ueff1 equal to ΔEAFM–FM (Fig. 1b). We observed this kind of mechanism in many di-nuclear EMFs studied before,2k,4d,9b,c,h,i,k,12 and it can be also recognized in Dy2S@C82. For the Cs isomer, this mechanism dominates between 2 and 10 K, the Ueff1 barrier is 17.9 ± 0.5 K, whereas attempt time τ01 is 1.6 ± 0.2 ms. In the C3v isomer, the barrier is lower, Ueff1 = 6.1 ± 0.4 K, but attempt time is much longer, τ01 = 4 ± 1 s, and the mechanism is operative between 1 and 4 K. Thus, only the use of sub-K temperatures in this work allowed freezing out the Orbach relaxation via the AFM state and we observed the |FM+〉 ↔ |FM−〉 QTM regime, in which the whole magnetic moment of the Dy2S@C82 molecule flips at once (Fig. 1b).
At higher temperature, the mechanism of relaxation changes to Raman in the Cs isomer with C = (1.8 ± 3) 10−3 s−1 K−n, n = 4.0 ± 0.1. For C3v we observe instead another Arrhenius process, with Ueff2 of 50 ± 2 K and τ02 of (4.9 ± 0.7) 10−4 s. The Raman mechanism with a strong coupling to certain low frequency vibration modes, such as endohedral cluster vibrations, is likely to be the reason for this linear regime.16 These Raman mechanisms govern relaxation of magnetization of Dy2S@C82 up to 40–50 K. Above this temperature, another change of the relaxation mechanism takes place for the C3v isomer. This time the Orbach mechanism with the relaxation via ligand-field excited states of Dy3+ ions is likely to play the main role, and we obtain the barrier as high as 1569 ± 180 K. For the Cs isomer the fitting at high temperature is more ambiguous (see Fig. S6†). Similar to the C3v isomer, we can also invoke one more Arrhenius process, which would have a barrier of 683 ± 83 K. At the same time, the Raman process alone also gives a reasonable description of the data. But since the χ′′ signal by these temperatures dropped dramatically and the values were obtained at the limit of the magnetometer sensitivity, the reliability of the determined relaxation times is unfortunately low, which also affects stability and reliability of the fit. We thus prefer to restrain from the further discussion of these barriers.
| EMF | ΔEhyst | U eff1 | ΔEfit | α fit |
|---|---|---|---|---|
| a ΔEhyst, Ueff1, and ΔEfit are estimations of ΔEAFM–FM (in cm−1), respectively, from the QTMA feature in sub-Kelvin hysteresis (Fig. 2), from the Arrhenius regime in relaxation times (Fig. 4), and from the fit of magnetization curves (Fig. 3). The latter also gives αfit as the angle between magnetic moments of Dy3+ ions | ||||
| Dy2S@C82-Cs | 10.7 ± 0.5 | 12.4 ± 0.4 | 11.0 | 72.3 ± 0.1 |
| Dy2S@C82-C3v | 5.1 ± 0.5 | 4.2 ± 0.3 | 6.4 | 75.7 ± 0.3 |
The Dy⋯Dy coupling energy can be further divided into exchange and dipolar contributions, ΔEexchAFM–FM and ΔEdipAFM–FM. The dipolar term can be computed exactly when the Dy⋯Dy distance and orientation of magnetic moments are known. Using the angle from the fit of magnetization curves and Dy–S bond lengths from DFT calculations, ΔEdipAFM–FM values are estimated as 2.2 cm−1 in Cs and 2.3 cm−1 in C3v isomers. ΔEexchAFM–FM, calculated as the difference between total and dipolar interaction energies, therefore is 8.5 cm−1 in Cs and 2.8 cm−1 in C3v isomers (the total energy estimated from hysteresis is used hereafter).
Table 2 compares the values of ΔEAFM–FM, ΔEdipAFM–FM, and ΔEexchAFM–FM from this work to those of other dinuclear Dy metallofullerenes studied earlier,9c,h,i,k including Dy2O, Dy2C2 and Dy2MN (M = Sc, Lu) clusterfullerenes with bridging O2−, C22−, and N3− units. Nitride and carbide clusterfullerenes also exhibited FM interactions between Dy ions, Dy2C2@C82 showing the largest ΔEAFM–FM value of 12.1 cm−1 (determined from Ueff1 in ref. 9c). The ΔEAFM–FM energy in Dy2S@C82-Cs is comparable to this value. Oxide clusterfullerenes with Dy2O clusters tend to show AFM or weak to negligible FM interactions, Dy2O@C82-C2v featuring the largest ΔEAFM–FM gap of −12.9 cm−1. Importantly, all EMF-SMMs have very similar ΔEdipAFM–FM energies, and large variations in total Dy⋯Dy interaction energies across different EMF types are caused by the strong variation of the exchange term.
| EMFb | ΔEtot | ΔEdip | ΔEexch | J tot | J dip | J exch |
|---|---|---|---|---|---|---|
| a ΔEtot is ΔEAFM–FM (in cm−1), whereas ΔEdip and ΔEexch are dipolar and exchange contributions, respectively, and ΔEexch is computed as ΔEtot − ΔEdip; Jtot, Jdip and Jexch are pseudospin coupling constants (in cm−1) from eqn (5). b ΔEtot for Dy2S@C82 is determined from hysteresis in this work, or as Ueff1 for Dy2O@C2n (ref. 9i and k), Dy2C2@C82 (ref. 9c), and Dy2MN@C80 (ref. 9h). In {Cp′2Dy(μ-SR)}2 from ref. 17, R = SiPh3; {Dy2O2}-A is [Dy2(dbm)2(LH2)2]·H2O from ref. 18 (LH3 = (1E,3E)-2-hydroxy-5-methylisophthalaldehyde dioxime, Hdbm = dibenzoylmethane); {Dy2O2}-B is [Dy(L)Cl(CH3OH)]n from ref. 19 (H2L = N′-(5-bromo-2-hydroxybenzylidene)pyrazine-N-oxide-carbohydrazide); {Dy2O2}-C is [Dy2(a'povh)2(OAc)2(DMF)2] from ref. 20 (H2a'povh = N′-[amino(pyrimidin-2-yl)methylene]-o-vanilloyl hydrazine). | ||||||
| Dy2S@C82-Cs | 10.7 | 2.2 | 8.5 | 70.4 | 14.4 | 56.0 |
| Dy2S@C82-C3v | 5.1 | 2.3 | 2.8 | 41.3 | 18.5 | 22.8 |
| Dy2O@C72-Cs | 1.5 | 3.0 | −1.5 | 4.0 | 8.0 | −4.0 |
| Dy2O@C74-C2 | ∼0.1 | 2.6 | −2.5 | 0.2 | 5.1 | −4.9 |
| Dy2O@C82-Cs | −7.5 | 3.0 | −10.5 | −23.3 | 9.3 | −32.6 |
| Dy2O@C82-C3v | −5.4 | 2.5 | −7.8 | −21.6 | 10.2 | −31.8 |
| Dy2O@C82-C2v | −12.9 | 2.6 | −15.6 | −41.9 | 8.6 | −50.5 |
| Dy2C2@C82-Cs | 12.1 | 2.6 | 9.5 | 64.4 | 13.6 | 50.8 |
| Dy2ScN@C80-Ih | 5.6 | 3.3 | 2.3 | 24.9 | 14.5 | 10.4 |
| Dy2LuN@C80-Ih | 3.0 | 3.3 | −0.3 | 12.6 | 14.0 | −1.4 |
| {Cp′2Dy(μ-SR)}2 | −2.0 | −4.4 | −2.2 | −2.2 | ||
| {Dy2O2}-A | 7.0 | 15.0 | 5.5 | 9.5 | ||
| {Dy2O2}-B | 6.0 | 11.4 | 4.6 | 6.8 | ||
| {Dy2O2}-C | −5.3 | −11.0 | −2.7 | −8.4 | ||
To put these values into a broader context of di-lanthanide molecular magnets, we took into account that the most frequently used approach to describe Dy⋯Dy interactions nowadays employs the pseudospin model popularized by Ungur and Chibotaru in their POLY_ANISO code.21 The ground magnetic state of Dy3+ ions is described as a pseudospin ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) = 1/2 with a highly anisotropic g-tensor (close to (0, 0, 20) for the Kramers doublet with dominant mJ = ±15/2 term), and the pseudospin exchange Hamiltonian within the Lines model22 takes the form of eqn (3):
= 1/2 with a highly anisotropic g-tensor (close to (0, 0, 20) for the Kramers doublet with dominant mJ = ±15/2 term), and the pseudospin exchange Hamiltonian within the Lines model22 takes the form of eqn (3):
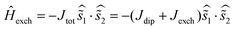 | (5) |
With this Hamiltonian, ΔEAFM–FM = 0.5Jtot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α), and hence Jtot = 450j12 (where j12 is the coupling constant from eqn (1)). The calculated Jtot, Jdip, and Jexch constants for dinuclear EMF-SMMs are listed in Table 2. The Jtot and Jexch values of Dy2S@C82-Cs, 70.4 and 56.0 cm−1, are the largest among all EMF-SMMs.
cos(α), and hence Jtot = 450j12 (where j12 is the coupling constant from eqn (1)). The calculated Jtot, Jdip, and Jexch constants for dinuclear EMF-SMMs are listed in Table 2. The Jtot and Jexch values of Dy2S@C82-Cs, 70.4 and 56.0 cm−1, are the largest among all EMF-SMMs.
We are aware of only two molecular magnets with sulfur-bridged Dy ions other than the Dy2S@C82: Dy4 complex with thiolate ligand bridges,23 and the dinuclear complex with Dy(Cp′)2 units bridged via two (μ-SSiPh3) groups.17 In both systems, Dy⋯Dy coupling is weakly AFM as can be assumed based on the shape of χT curves. The ΔEAFM–FM and Jtot values in {Cp′2Dy(μ-SSiPh3)}2 are −2 and −4.4 cm−1, respectively.
The μ2-O bridges are much more common than μ2-S in dinuclear Dy molecular magnets, especially in the form of {Dy2O2} fragments. For those, we found only three compounds with |Jtot| exceeding 10 cm−1 (Table 2; see ref. 9i for a recent survey of Dy⋯Dy interaction parameters in {Dy2O2} compounds). Two of them have phenoxide bridges with FM coupling and Jtot values of 15.0 and 11.4 cm−1.18,19 In the complex with vanilloyl bridges, the coupling is AFM and Jtot is −11 cm−1.20Table 2 shows that in EMF-SMMs the range of coupling constants can be several times larger. This large difference in Jtot constants may appear somewhat misleading because the ΔEAFM–FM values also depend on the angle between Dy axes. In EMF-SMMs, magnetic moments of Dy ions are usually non-collinear, so the range of the energies is not as high as for the coupling constants. But still, ΔEAFM–FM energies in EMF-SMMs can be considerably larger than those in other {Dy2} molecular magnets.
One reason for this lies in the comparably strong dipolar interactions between Dy moments in EMFs caused by the relatively short Dy⋯Dy distance and suitable Dy–X–Dy angles maximizing dipolar interactions. Yet in many {Dy2O2} compounds, the distances are even shorter than those in EMFs. Thus, we conclude that the exchange interactions between Dy moments in EMFs are mainly responsible for these unprecedentedly strong Dy⋯Dy interactions in EMFs. The reasons for this strong exchange are not clear yet. Short Dy–X bonds leading to enhanced superexchange via the bridging atoms may be one of the reasons. But this factor cannot explain why variation of exchange coupling can be so strong in different cage isomers, such as that found in this work for Cs and C3v isomers of Dy2S@C82 or observed earlier for isomers of Dy2O@C82.9i
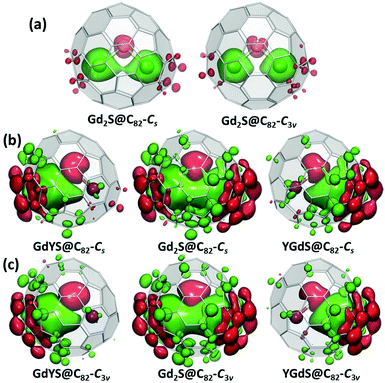
Evidently, the fullerene cage in EMF-SMMs should not be considered as just a container for magnetic species. We suggest that the interaction between Dy ions is also affected through the spin polarization of the fullerene π-system in the spirit of the Ruderman–Kittel–Kasuya–Yosida (RKKY) mechanism of interaction between magnetic atoms via conduction electrons in metals.24 For instance, the RKKY mechanism explains oscillatory distance dependence of interactions between magnetic adatoms in graphene, an infinite limit of the fullerene π-system.25Fig. 5 plots spin density distribution in Gd2S@C82 (S = 15) and GdYS@C82 (S = 8) molecules computed at the PBE0 level with full-electron basis sets.¶ The use of Gd instead of Dy in these calculations allows the application of a single-determinant DFT approach and limits the focus to spin-only contribution to the Ln⋯Ln exchange interactions; spin–orbit coupling effects cannot be captured by this simple approach. Calculations for Gd2S@C82 also allow using broken-symmetry DFT to estimate the exchange coupling between Gd magnetic moments (see ref. 9c and ESI†), but such results cannot be directly transferred to Dy analogs.
When the isovalues of ±0.0012 a. u. are used in plotting the spin density (ρspin) isosurfaces, the surface with positive ρspin (coloured green in Fig. 5a) encompasses two Gd atoms as can be expected for the state with spin multiplicity of S = 15. At the same time, a pronounced negative spin polarization of the bridging sulfur is also well seen. Obviously, superexchange via the μ2-S atom should be considerable in these systems. Besides, the negative spin polarization of fullerene carbon atoms closest to Gd is also visible. The plots with lower spin density isovalues of ±0.00012 a. u. show that spin polarization of carbon atoms with alternating sign extends over the whole fullerene cage. The negative spin polarization of carbons near Gd is changed to the positive one for more distant carbons. Interestingly, although the cage spin polarization patterns calculated for GdYS@C82 molecules resemble closely halves of spin-density plots in Gd2S@C82, they are not completely identical (Fig. 5b and c). Besides, Gd-induced spin polarization of the cage carbons in GdYS@C82 extends to the half of the cage not coordinated to Gd. Thus, there should be non-negligible through-cage interaction between endohedral lanthanide ions. It is reasonable to suggest that through-cage spin–spin interaction pathways should depend on the topology of the fullerene π-systems, and thus be different from cage to cage even when structural parameters of the endohedral cluster are very similar. Further exploration of this effect is worth a detailed study but goes beyond the scope of this work.
Conclusions
In this work, we performed a study of Dy⋯Dy magnetic interactions and low-temperature relaxation dynamics in Dy2S@C82 as a prototype dinuclear SMM with a ferromagnetically coupled ground state. Although the study is performed on powder samples, the broad sub-Kelvin magnetic hysteresis with clear QTM steps observed for both cage isomers of Dy2S@C82 appeared instrumental for the determination of the energy difference between the FM and AFM states. Comparison with the values determined by other approaches, such as fitting of magnetization data or the energy barrier of the Arrhenius relaxation process, showed reasonable agreement. Comparison to other dinuclear SMMs revealed that the Cs(6) isomer of Dy2S@C82 features one of the highest Dy⋯Dy coupling strength values ever reported. Furthermore, the two-fold variation of the Dy⋯Dy coupling strength between two cage isomers is found. This variation cannot be explained by the difference in the structural parameters of the Dy2S cluster in two structures and points to a possibility of the indirect exchange interactions between lanthanide ions via the fullerene π-system.Measurements of the magnetization relaxation time at sub-Kelvin temperatures also allowed achieving a relaxation regime not observed in dinuclear EMF-SMMs before. Typically, the main low-temperature relaxation mechanism in these compounds is the Orbach process with the barrier corresponding to the energy difference between FM and AFM states. In Dy2S@C82 this mechanism is observed down to 1–2 K. But below 1 K, this thermally activated process becomes inefficient, giving way to quantum tunnelling with the simultaneous flip of two Dy moments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the European Union's Horizon 2020 research and innovation programme, European Research Council (grant agreement no. 648295 to A. A. P.), Marie Skłodowska-Curie action (grant agreement no. 748635 to S. M. A.), the Deutsche Forschungsgemeinschaft (grants PO 1602/4-1 and 1602/5-1 to A. A. P.) and the Swiss National Science Foundation (Projects No. 200021L_147201 and No. 206021_- 150784 to T. G.). We appreciate the help from Dr Anja U. B. Wolter and Sebastian Gaß in magnetic measurements and Ulrike Nitzsche for the help with computational resources in IFW Dresden.Notes and references
-
(a) K. L. M. Harriman, D. Errulat and M. Murugesu, Magnetic Axiality: Design Principles from Molecules to Materials, Trends Chem., 2019, 1, 425 CrossRef
; (b) A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Low-coordinate mononuclear lanthanide complexes as molecular nanomagnets, Coord. Chem. Rev., 2018, 367, 163 CrossRef CAS
; (c) J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431 RSC
; (d) E. Bartolomé, A. Arauzo, J. Luzón, J. Bartolomé and F. Bartolomé, in Handbook of Magnetic Materials, ed. E. Brück, Elsevier, 2017, p. 1 Search PubMed
; (e) Z. Zhu, M. Guo, X.-L. Li and J. Tang, Molecular magnetism of lanthanide: Advances and perspectives, Coord. Chem. Rev., 2019, 378, 350 CrossRef CAS
; (f) S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655 RSC
; (g) P. Zhang, L. Zhang and J. Tang, Lanthanide single molecule magnets: Progress and perspective, Dalton Trans., 2015, 44, 3923 RSC
.
-
(a) L. Ungur and L. F. Chibotaru, Ab Initio Crystal Field for Lanthanides, Chem. – Eur. J., 2017, 23, 3708 CrossRef CAS
; (b) L. Ungur and L. F. Chibotaru, Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets, Inorg. Chem., 2016, 55, 10043 CrossRef CAS PubMed
; (c) T. Pugh, N. F. Chilton and R. A. Layfield, A Low-Symmetry Dysprosium Metallocene Single-Molecule Magnet with a High Anisotropy Barrier, Angew. Chem., Int. Ed., 2016, 55, 11082 CrossRef CAS PubMed
; (d) Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2016, 55, 16071 CrossRef CAS PubMed
; (e) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400 CrossRef CAS PubMed
; (f) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef CAS PubMed
; (g) Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829 CrossRef CAS PubMed
; (h) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441 CrossRef CAS PubMed
; (i) C. Wang, R. Sun, Y. Chen, B.-W. Wang, Z.-M. Wang and S. Gao, Assembling High-Temperature Single-Molecule Magnets with Low-Coordinate Bis(amido) Dysprosium Unit [DyN2]+ via Cl-K-Cl Linkage, CCS Chem., 2020, 2, 362 CrossRef
; (j) K.-X. Yu, J. G. C. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. F. Chilton and Y.-Z. Zheng, Enhancing Magnetic Hysteresis in Single-Molecule Magnets by Ligand Functionalization, Chem, 2020, 6, 1777 CrossRef
; (k) D. S. Krylov, F. Liu, S. M. Avdoshenko, L. Spree, B. Weise, A. Waske, A. U. B. Wolter, B. Büchner and A. A. Popov, Record-high thermal barrier of the relaxation of magnetization in the nitride clusterfullerene Dy2ScN@C80-Ih, Chem. Commun., 2017, 53, 7901 RSC
; (l) S. Bala, G.-Z. Huang, Z.-Y. Ruan, S.-G. Wu, Y. Liu, L.-F. Wang, J.-L. Liu and M.-L. Tong, A square antiprism dysprosium single-ion magnet with an energy barrier over 900 K, Chem. Commun., 2019, 55, 9939 RSC
; (m) M. Murrie, A. Canaj, S. Dey, E. Regincós Martí, C. Wilson and G. Rajaraman, Insight into D6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets, Angew. Chem., Int. Ed., 2019, 58, 14146 CrossRef PubMed
; (n) K. R. McClain, C. A. Gould, K. Chakarawet, S. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, High-temperature magnetic blocking and magneto-structural correlations in a series of dysprosium(III) metallocenium single-molecule magnets, Chem. Sci., 2018, 9, 8492 RSC
.
-
(a) A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun., 2017, 8, 14620 CrossRef PubMed
; (b) L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Spin states, vibrations and spin relaxation in molecular nanomagnets and spin qubits: a critical perspective, Chem. Sci., 2018, 9, 3265 RSC
; (c) R. E. P. Winpenny, N. F. Chilton, M. Giansiracusa, D. Collison and A. Kostopoulos, Correlating Blocking Temperatures with Relaxation Mechanisms in Monometallic Single-Molecule Magnets with High Energy Barriers (Ueff > 600 K), Chem. Commun., 2019, 55, 7025 RSC
; (d) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439 CrossRef CAS PubMed
; (e) A. Chiesa, F. Cugini, R. Hussain, E. Macaluso, G. Allodi, E. Garlatti, M. Giansiracusa, C. A. P. Goodwin, F. Ortu, D. Reta, J. M. Skelton and T. Guidi, et al., Understanding magnetic relaxation in single-ion magnets with high blocking temperature, Phys. Rev. B, 2020, 101, 174402 CrossRef CAS
.
-
(a) C. Y. Chow, H. Bolvin, V. E. Campbell, R. Guillot, J. W. Kampf, W. Wernsdorfer, F. Gendron, J. Autschbach, V. L. Pecoraro and T. Mallah, Assessing the exchange coupling in binuclear lanthanide(iii) complexes and the slow relaxation of the magnetization in the antiferromagnetically coupled Dy2 derivative, Chem. Sci., 2015, 6, 4148 RSC
; (b) Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, Strong Axiality and Ising Exchange Interaction Suppress Zero-Field Tunneling of Magnetization of an Asymmetric Dy2 Single-Molecule Magnet, J. Am. Chem. Soc., 2011, 133, 11948 CrossRef CAS PubMed
; (c) F. Habib and M. Murugesu, Lessons learned from dinuclear lanthanide nano-magnets, Chem. Soc. Rev., 2013, 42, 3278 RSC
; (d) R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, K. Krämer, S.-X. Liu, S. Decurtins, A. Popov, S. Yang, L. Dunsch and T. Greber, Tunneling, remanence, and frustration in dysprosium-based endohedral single-molecule magnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060406 CrossRef
; (e) T. Han, M. J. Giansiracusa, Z.-H. Li, Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Exchange-Biasing in a Dinuclear Dysprosium(III) Single-Molecule Magnet with a Large Energy Barrier for Magnetisation Reversal, Chem. – Eur. J., 2020, 26, 6773 CrossRef CAS
.
-
(a) S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Radical ligand-containing single-molecule magnets, Coord. Chem. Rev., 2015, 289–290, 149 CrossRef CAS
; (b) S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant coercivity and high magnetic blocking temperatures for N23− radical-bridged dilanthanide complexes upon ligand dissociation, Nat. Commun., 2017, 8, 2144 CrossRef
; (c) F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz, S. Schiemenz, F. Ziegs and K. Nenkov, et al., Air-stable redox-active nanomagnets with lanthanide spins radical-bridged by a metal-metal bond, Nat. Commun., 2019, 10, 571 CrossRef CAS PubMed
.
-
(a) E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Direct measurement of dysprosium(III)˙˙˙dysprosium(III) interactions in a single-molecule magnet, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed
; (b) M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren, S. Carretta and T. Guidi, et al., Measurement of Magnetic Exchange in Asymmetric Lanthanide Dimetallics: Toward a Transferable Theoretical Framework, J. Am. Chem. Soc., 2018, 140, 2504 CrossRef CAS PubMed
; (c) M. Gysler, F. El Hallak, L. Ungur, R. Marx, M. Hakl, P. Neugebauer, Y. Rechkemmer, Y. Lan, I. Sheikin, M. Orlita, C. E. Anson and A. K. Powell, et al., Multitechnique investigation of Dy3 – implications for coupled lanthanide clusters, Chem. Sci., 2016, 7, 4347 RSC
; (d) R. T. Galeev, L. V. Mingalieva, A. A. Sukhanov, V. K. Voronkova, Y. Peng and A. K. Powell, Exchange Interactions in Heteronuclear Clusters Containing Dysprosium Ions: EPR Spectroscopy Possibility, Appl. Magn. Reson., 2019, 50, 1429 CrossRef CAS
.
-
(a) L. F. Chibotaru and N. Iwahara, Ising exchange interaction in lanthanides and actinides, New J. Phys., 2015, 17, 103028 CrossRef
; (b) N. Iwahara and L. F. Chibotaru, New mechanism of kinetic exchange interaction induced by strong magnetic anisotropy, Sci. Rep., 2016, 6, 24743 CrossRef CAS PubMed
; (c) A. Palii, B. Tsukerblat, J. M. Clemente-Juan and E. Coronado, Magnetic exchange between metal ions with unquenched orbital angular momenta: basic concepts and relevance to molecular magnetism, Int. Rev. Phys. Chem., 2010, 29, 135 Search PubMed
; (d) A. Palii, B. Tsukerblat, S. Klokishner, K. R. Dunbar, J. M. Clemente-Juan and E. Coronado, Beyond the spin model: exchange coupling in molecular magnets with unquenched orbital angular momenta, Chem. Soc. Rev., 2011, 40, 3130 RSC
; (e) N. Iwahara and L. F. Chibotaru, Exchange interaction between J multiplets, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174438 CrossRef
.
-
(a) S. Yang, T. Wei and F. Jin, When metal clusters meet carbon cages: endohedral clusterfullerenes, Chem. Soc. Rev., 2017, 46, 5005 RSC
; (b) A. A. Popov, S. Yang and L. Dunsch, Endohedral Fullerenes, Chem. Rev., 2013, 113, 5989 CrossRef CAS PubMed
.
-
(a) L. Spree and A. A. Popov, Recent advances in single molecule magnetism of dysprosium-metallofullerenes, Dalton Trans., 2019, 48, 2861 RSC
; (b) C. Schlesier, L. Spree, A. Kostanyan, R. Westerström, A. Brandenburg, A. U. B. Wolter, S. Yang, T. Greber and A. A. Popov, Strong carbon cage influence on the single molecule magnetism in Dy–Sc nitride clusterfullerenes, Chem. Commun., 2018, 54, 9730 RSC
; (c) C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov, A. Kostanyan, T. Greber and A. U. B. Wolter, et al., Selective arc-discharge synthesis of Dy2S-clusterfullerenes and their isomer-dependent single molecule magnetism, Chem. Sci., 2017, 8, 6451 RSC
; (d) K. Junghans, C. Schlesier, A. Kostanyan, N. A. Samoylova, Q. Deng, M. Rosenkranz, S. Schiemenz, R. Westerström, T. Greber, B. Büchner and A. A. Popov, Methane as a Selectivity Booster in the Arc-Discharge Synthesis of Endohedral Fullerenes: Selective Synthesis of the Single-Molecule Magnet Dy2TiC@C80 and Its Congener Dy2TiC2@C80, Angew. Chem., Int. Ed., 2015, 54, 13411 CrossRef CAS PubMed
; (e) R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, H. Brune, S. Rusponi, F. Nolting, A. Popov, S. Yang, L. Dunsch and T. Greber, An Endohedral Single-Molecule Magnet with Long Relaxation Times: DySc2N@C80, J. Am. Chem. Soc., 2012, 134, 9840 CrossRef PubMed
; (f) D. Krylov, F. Liu, A. Brandenburg, L. Spree, V. Bon, S. Kaskel, A. Wolter, B. Buchner, S. Avdoshenko and A. A. Popov, Magnetization relaxation in the single-ion magnet DySc2N@C80: quantum tunneling, magnetic dilution, and unconventional temperature dependence, Phys. Chem. Chem. Phys., 2018, 20, 11656 RSC
; (g) A. Brandenburg, D. S. Krylov, A. Beger, A. U. B. Wolter, B. Büchner and A. A. Popov, Carbide clusterfullerene DyYTiC@C80 featuring three different metals in the endohedral cluster and its single-ion magnetism, Chem. Commun., 2018, 54, 10683 RSC
; (h) L. Spree, C. Schlesier, A. Kostanyan, R. Westerström, T. Greber, B. Büchner, S. Avdoshenko and A. A. Popov, Single molecule magnets DyM2N@C80 and Dy2MN@C80 (M = Sc, Lu): The impact of diamagnetic metals on the Dy3+ magnetic anisotropy, Dy⋯Dy coupling, and mixing of molecular and lattice vibrations, Chem. – Eur. J., 2020, 26, 2436 CrossRef CAS PubMed
; (i) W. Yang, G. Velkos, F. Liu, S. M. Sudarkova, Y. Wang, J. Zhuang, H. Zhang, X. Li, X. Zhang, B. Büchner, S. M. Avdoshenko and A. A. Popov, et al., Single Molecule Magnetism with Strong Magnetic Anisotropy and Enhanced Dy⋯Dy Coupling in Three Isomers of Dy-Oxide Clusterfullerene Dy2O@C82, Adv. Sci., 2019, 6, 1901352 CrossRef CAS PubMed
; (j) Y. Li, T. Wang, H. Meng, C. Zhao, M. Nie, L. Jiang and C. Wang, Controlling the magnetic properties of dysprosium metallofullerene within metal-organic framework, Dalton Trans., 2016, 45, 19226 RSC
; (k) G. Velkos, W. Yang, Y.-R. Yao, S. M. Sudarkova, X. Liu, B. Büchner, S. M. Avdoshenko, N. Chen and A. A. Popov, Shape-adaptive single-molecule magnetism and hysteresis up to 14 K in oxide clusterfullerenes Dy2O@C72 and Dy2O@C74 with fused pentagon pairs and flexible Dy–(μ2-O)–Dy angle, Chem. Sci., 2020, 11, 4766 RSC
.
-
(a) G. Velkos, D. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp and H. Dorn,
et al., High blocking temperature of magnetization and giant coercivity in the azafullerene Tb2@C79N with a single-electron Tb–Tb bond, Angew. Chem., Int. Ed., 2019, 58, 5891 CrossRef CAS PubMed
; (b) F. Liu, L. Spree, D. S. Krylov, G. Velkos, S. M. Avdoshenko and A. A. Popov, Single-Electron Lanthanide-Lanthanide Bonds Inside Fullerenes toward Robust Redox-Active Molecular Magnets, Acc. Chem. Res., 2019, 52, 2981 CrossRef CAS PubMed
; (c) F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Single molecule magnet with an unpaired electron trapped between two lanthanide ions inside a fullerene, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed
; (d) Y. Wang, J. Xiong, J. Su, Z.-Q. Hu, F. Ma, R. Sun, X.-Y. Tan, H.-L. Sun, B. Wang, Z. Shi and S. Gao, Dy2@C79N: A New Member of Dimetalloazafullerenes with Strong Single Molecular Magnetism, Nanoscale, 2020, 12, 11130 RSC
.
-
(a) S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Coupling Dy3 Triangles to Maximize the Toroidal Moment, Angew. Chem., Int. Ed., 2012, 51, 12767 CrossRef CAS PubMed
; (b) Y.-X. Wang, W. Shi, H. Li, Y. Song, L. Fang, Y. Lan, A. K. Powell, W. Wernsdorfer, L. Ungur, L. F. Chibotaru, M. Shen and P. Cheng, A single-molecule magnet assembly exhibiting a dielectric transition at 470 K, Chem. Sci., 2012, 3, 3366 RSC
.
- A. Kostanyan, R. Westerström, D. Kunhardt, B. Büchner, A. A. Popov and T. Greber, Sub-Kelvin hysteresis of the dilanthanide single-molecule magnet Tb2ScN@C80, Phys. Rev. B, 2020, 101, 134429 CrossRef CAS
.
-
(a) J. Hafner,
Ab initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29, 2044 CrossRef CAS PubMed
; (b) G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
; (c) G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
; (d) J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
; (e) S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211 CAS
.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed
.
-
(a) X. Yi, K. Bernot, F. Pointillart, G. Poneti, G. Calvez, C. Daiguebonne, O. Guillou and R. Sessoli, A Luminescent and Sublimable DyIII-Based Single-Molecule Magnet, Chem. – Eur. J., 2012, 18, 11379 CrossRef CAS PubMed
; (b) J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Hydroxide-bridged five-coordinate DyIII single-molecule magnet exhibiting the record thermal relaxation barrier of magnetization among lanthanide-only dimers, Chem. Sci., 2017, 8, 1288 RSC
; (c) G. Huang, X. Yi, J. Jung, O. Guillou, O. Cador, F. Pointillart, B. Le Guennic and K. Bernot, Optimization of Magnetic Relaxation and Isotopic Enrichment in Dimeric DyIII Single-Molecule Magnets, Eur. J. Inorg. Chem., 2018, 2018, 326 CrossRef CAS
.
- K. N. Shrivastava, Theory of Spin–Lattice Relaxation, Phys. Status Solidi B, 1983, 117, 437 CrossRef CAS
.
- F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, A High Anisotropy Barrier in a Sulfur-Bridged Organodysprosium Single-Molecule Magnet, Angew. Chem., Int. Ed., 2012, 51, 6976 CrossRef CAS PubMed
.
- W. Zhang, S.-M. Xu, Z.-X. Zhu, J. Ru, Y.-Q. Zhang and M.-X. Yao, Strong intramolecular DyIII–DyIII magnetic couplings up to 15.00 cm−1 in phenoxyl-bridged dinuclear 4f complexes, New J. Chem., 2020, 44, 2083 RSC
.
- X.-Q. Ji, F. Ma, J. Xiong, J. Yang, H.-L. Sun, Y.-Q. Zhang and S. Gao, A rare chloride-bridged dysprosium chain with slow magnetic relaxation: a thermally activated mechanism via a second-excited state promoted by magnetic interactions, Inorg. Chem. Front., 2019, 6, 786 RSC
.
- S. Xue, Y.-N. Guo, L. Ungur, J. Tang and L. F. Chibotaru, Tuning the Magnetic Interactions and Relaxation Dynamics of Dy2 Single-Molecule Magnets, Chem. – Eur. J., 2015, 21, 14099 CrossRef CAS PubMed
.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Interplay of Strongly Anisotropic Metal Ions in Magnetic Blocking of Complexes, Inorg. Chem., 2013, 52, 6328 CrossRef CAS PubMed
.
- M. E. Lines, Orbital Angular Momentum in the Theory of Paramagnetic Clusters, J. Chem. Phys., 1971, 55, 2977 CrossRef CAS
.
- D. N. Woodruff, F. Tuna, M. Bodensteiner, R. E. P. Winpenny and R. A. Layfield, Single-Molecule Magnetism in Tetrametallic Terbium and Dysprosium Thiolate Cages, Organometallics, 2013, 32, 1224 CrossRef CAS
.
-
(a) M. A. Ruderman and C. Kittel, Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons, Phys. Rev., 1954, 96, 99 CrossRef CAS
; (b) T. Kasuya, A Theory of Metallic Ferro- and Antiferromagnetism on Zener's Model, Prog. Theor. Phys., 1956, 16, 45 CrossRef
; (c) K. Yosida, Magnetic Properties of Cu-Mn Alloys, Phys. Rev., 1957, 106, 893 CrossRef
.
-
(a) S. R. Power and M. S. Ferreira, Indirect Exchange and Ruderman–Kittel–Kasuya–Yosida (RKKY) Interactions in Magnetically-Doped Graphene, Crystals, 2013, 3, 49 CrossRef CAS
; (b) K. Szałowski, RKKY coupling between impurity spins in graphene nanoflakes, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205409 CrossRef
; (c) J. Klinovaja and D. Loss, RKKY interaction in carbon nanotubes and graphene nanoribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 045422 CrossRef
.
-
(a) F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed
; (b) F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CAS
; (c) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree-Fock exchange, Chem. Phys., 2009, 356, 98 CrossRef CAS
.
-
(a) D. A. Pantazis and F. Neese, All-Electron Scalar Relativistic Basis Sets for the Lanthanides, J. Chem. Theory Comput., 2009, 5, 2229 CrossRef CAS PubMed
; (b) D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms, J. Chem. Theory Comput., 2008, 4, 908 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, VMD - Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0qi00771d |
| ‡ The magnetization was measured in a Quantum Design MPMS3 vibrating sample magnetometer (VSM) with a 3He cryostat. |
| § The ensemble of Zeeman diagrams was computed for 105 different orientations of the magnetic field vectors evenly spaced along with the Fibonacci sphere grid points, assuming Hamiltonian eqn (1). The massive data were generated and analyzed using in-house Python scripts while the Hamiltonian eigenproblems were solved using the PHI code.14 |
| ¶ DFT calculations for Gd2S@C82 and GdYS@C82 molecules were performed with the Orca 4.2.1 suite26 using the PBE0 functional, DKH scalar-relativistic correction, and SARC-TZVP basis sets.27 Spin-densities are visualized with VMD.28 |
| This journal is © the Partner Organisations 2020 |