Weak exchange coupling effects leading to fast magnetic relaxations in a trinuclear dysprosium single-molecule magnet†
Abstract
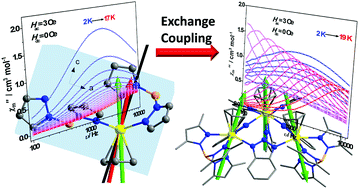
Investigating the magnetic anisotropy and magnetic interactions of lanthanide complexes is of vital importance for an in-depth understanding of their magnetic properties. Herein, we reported the synthetic, structural and magnetic studies of a triangular type dysprosium complex (1Dy3, [{(Cp)(Tp*)Ln(μ-bta)}3·2(thf)], Cp = C5H5, Tp* = hydrotris(3,5-dimethyl-1-pyrazolyl)borate anion, btaH = 1H-1,2,3-benzotriazole). 2Dy ([(Cp)Dy(Tp)2·C7H8], Tp = hydrotris(1-pyrazolyl)borate) was investigated by single-crystal angular-resolved susceptibility measurements and computational studies to help understand the magnetic anisotropy of 1Dy3. The easy axis of three DyIII ions in 1Dy3 was orientated out of the triangular dysprosium plane. The exchange interactions were small (−0.85 cm−1) but caused remarkable effects on magnetic relaxations at low temperature. In the temperature range from 2 K to 4 K, magnetic relaxation occurred via the exchange-coupled low-lying excited states, inhibiting magnetic hysteresis. Our study showed that weak intramolecular magnetic interactions can significantly affect the dynamic properties in the low temperature regime.


 Please wait while we load your content...
Please wait while we load your content...