Open Access Article
Open Access ArticleSynthesis of cyclic polymers and flaws of the Jacobson–Stockmayer theory†
Hans R.
Kricheldorf
*a,
Steffen M.
Weidner
 b and
Felix
Scheliga
a
b and
Felix
Scheliga
a
aInstitut für technische und Makromolekulare Chemie, Bundesstr. 45, D-20146 Hamburg, Germany. E-mail: hrkricheldorf@aol.de
bFederal Institute of Materials Research and Testing – BAM, Richard Willstätter Str. 11, D-12489 Berlin, Germany
First published on 13th March 2020
Abstract
Cyclic poly(L-lactide)s were prepared by ring-opening polymerization combined with simultaneous polycondensation (ROPPOC) in bulk at 160 °C with dibutyltin bis(4-cyanophenoxide) as catalyst. It is demonstrated by MALDI TOF mass spectrometry and 1H NMR end group analyses that cycles are formed by end-to-end cyclization in addition to “back-biting” transesterification. Formation of high molar mass cyclic poly(L-lactide)s by means of several more reactive ROPPOC catalysts presented previously and in new experiments is discussed. These experimental results, together with theoretical arguments, prove that part of the Jacobson–Stockmayer theory is wrong. The critical monomer concentration, above which end-to-end cyclization is seemingly impossible, does not exist and reversible like irreversible polycondensations can theoretically proceed up to 100% conversion, so that finally all reaction products will necessarily adopt a cyclic architecture.
Introduction
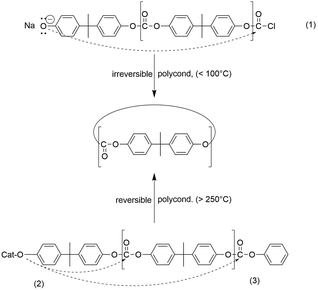
In 1950 Jacobson and Stockmayer published two papers (the second paper co-authored by C. O. Beckmann) which belong to the most frequently cited papers in polymer science.1,2 At that time these publications revolutionized the understanding of polymerization processes and polymer properties. The four most important aspects of their work, (the so-called Jacobson–Stockmayer theory) may be summarized as follows:(I) Polyester and polyamide syntheses may be based on reversible chain growth reactions, so that the resulting polymers are thermodynamically stable materials in contrast to the polymers resulting from chain growth polymerizations of α-olefins or vinyl monomers.
(II) Low molar mass cycles are formed by the attack of the most reactive chain end onto ester (amide) groups of the backbone (so-called “back-biting”, see Scheme 1). The existence of “back-biting” has the consequence that ring-chain equilibration occurs in combination with ring–ring and chain–chain equilibration.2
(III) The number distribution of the cycles decreases with the degree of polymerization (DP) according to DP−5/2.
(IV) When compared at a fixed conversion the fraction of cyclics increases with decreasing initial monomer concentration (IMC) and below a critical concentration (CC) 100% cycles are formed at 100% conversion, whereas at higher IMCs quantitative cyclization is impossible.
The statement of point I was quite new and surprising, because the polymerizations known at that time were either irreversible (e.g. all polymerizations of vinyl monomers and olefins) and yielded thermodynamically unstable polymers, or the reversible character was still unknown (e.g. syntheses of Nylons). The statement of point II was a further revolution, because Carothers and Flory had declared in their theory of step-growth polymerizations that formation of cycles does not play any role.3–5 Since they exclusively discussed irreversible polycondensations (although, ironically, their experimental work concerned reversible ones), their dogma explicitly meant that end-to-end (ete) cyclization cannot take place. The existence of “back-biting” was not taken into account. Stockmayer and co-workers admitted that inefficient ete-cyclization of low oligomers may occur,2 but they followed the dogma of Carothers and Flory for higher oligomers and polymers. J + S wrote (p. 1607, ref. 2): “Formation of rings occurs here primarily by ester interchange, very few of the chains present being small enough to give rings directly by intramolecular esterification”.
The statement of point III was later confirmed by various authors, primarily by Semlyen and co-workers, but mainly for oligomers with DPs < 10 prepared in solution.6–12 However, it has not been proved that the DP−5/2 law correctly describes the molecular weight distribution of a completely cyclized polycondensate prepared in bulk.
Concerning point IV, Jacobson and Stockmayer summarized the results of their calculations in the diagram of Fig. 1. Curve A represents the CC case, while curves B and C describe the course of polycondensations at IMCs above CC. Curve C is representative for polycondensations conducted in bulk. Jacobson and Stockmayer1 and later Flory5 calculated that the maximum weight fraction (ρw) of rings formed in a polycondensation at 100% conversion (p = 1) will amount to approximately 4% for “a2 + b2” monomers and around 8% for “a−b” monomers (the probability of cyclization is twice as high “for a−b” monomers, because all chains have one “a” and one “b” end group). It is important for the proper understanding for point IV and its discussion below, that it represents nothing but the consequence of a mathematical approach. Neither Stockmayer nor Flory have ever published any experimental data confirming this calculation.
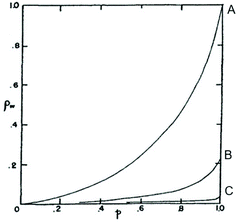 | ||
| Fig. 1 Weight fraction of cyclics (ρw) versus conversion (p) for a2 + b2 polycondensations calculated for reversible a2 + b2 polycondensations (case IIIa) with three different initial monomer concentrations. Curve A represents the critical concentration and curve C polycondensation in bulk. Reproduction of Fig. 2 in ref. 1 with permission American Institute of Physics. | ||
In the years 1972–1975 Stepto and coworkers13,14 and Gordon and Temple15,16 used (and compared) three different mathematical methods to calculate the course of irreversible polycondensations. All three mathematical models yielded the same trend.
(A) Ete-cyclization competes with chain-growth (intermolecular condensation) at any stage and any monomer concentration (see Scheme 1).
(B) The fraction of cyclics increases with conversion.
(C) At 100% conversion all reaction products are cycles.
Fig. 2 illustrates the results of two mathematical approaches published by Gordon and Temple. Their calculations were later confirmed by Horbach et al. via end group analyses of poly(bisphenol-A carbonate)s17 and mainly by Kricheldorf and co-workers via MALDI-TOF mass spectrometry of numerous polycondensates for masses up to 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da.18–21 On the basis of these calculations and experimental results the first author has criticized point IV of the JS theory with the following argument.22 When end-to-end cyclization can occur in irreversible step-growth polymerizations, why should it be impossible in reversible polycondensations under similar conditions? The existence of “back-biting” does not reduce the reactivity of end groups. When the end groups are reactive enough to undergo ete-cyclization in irreversible polycondensations they should also be reactive enough for ete-cyclization in reversible polycondensations under identical conditions.
000 Da.18–21 On the basis of these calculations and experimental results the first author has criticized point IV of the JS theory with the following argument.22 When end-to-end cyclization can occur in irreversible step-growth polymerizations, why should it be impossible in reversible polycondensations under similar conditions? The existence of “back-biting” does not reduce the reactivity of end groups. When the end groups are reactive enough to undergo ete-cyclization in irreversible polycondensations they should also be reactive enough for ete-cyclization in reversible polycondensations under identical conditions.
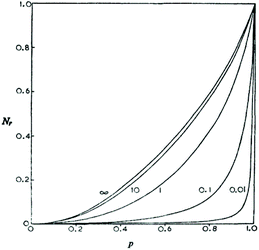 | ||
| Fig. 2 Number fraction of cyclics versus conversion calculated for irreversible polycondensations with different initial monomer concentrations. Curve 0.01 represents polycondensation in bulk. Reproduction of Fig. 2 in ref. 13 with permission of the Royal Society of Chemistry. | ||
The experimental results contributed by the first author and co-workers about ten years ago concerned syntheses of Nylons.23,24 Because of their importance they will be discussed again with a modified interpretation in the light of the ROPPOC concept (first section of Results and discussion). At that time Kricheldorf and co-workers were not able to characterize the architecture of the high molar mass fraction of their nylons. In this context it was the purpose of this work to demonstrate that certain reversible polycondensations can yield cyclic polymers containing approximately 95 weight and number% (and more) of cycles including rings with molar masses around 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da and higher. In combination with further theoretical arguments it should be demonstrated, that the Jacobson–Stockmayer-theory is incorrect with regard to point IV.
000 Da and higher. In combination with further theoretical arguments it should be demonstrated, that the Jacobson–Stockmayer-theory is incorrect with regard to point IV.
Experimental
Materials
L-Lactide was purchased from TCI Chemicals (Eschborn, Germany) and twice recrystallized from toluene. “Toluene 99.89% extra dry” from ACROS Chemicals (Geel Belgium) was used for this purpose. The recrystallized L-lactide had a Tm of 98.7–99.0 °C as determined by differential-scanning-calorimetry at a heating rate of 5 K min−1. The linear poly(L-lactide)s Purapol L105 and NW 3152D were purchased from Carbion Purac and Nature Works respectively for comparison with the cyclic polylactides listed in Tables 1 and 3. Both commercial poly(L-lactide)s showed identical viscosity-molecular weight correlations.| Catalyst | Lac/Cat | Temp. | M n | M w | Ref. |
|---|---|---|---|---|---|
| Bu2SnOPF | 100/1 | 160 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
25 |
| Bu2SnOPF | 400/1 | 160 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
25 |
| Bu2SnSPF | 100/1 | 160 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
26 |
| Bu2SnMBT | 100/1 | 160 | 9500 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
26 |
| SnOct2 + HSPF | 1000/1 | 160 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
27 |
| Bu3SnCl | 100/1 | 160 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
28 |
| Bu3SnCl | 200/1 | 160 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
28 |
| Bu3SnCl | 400/1 | 160 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
28 |
| Ph2SnCl2 | 100/1 | 160 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
28 |
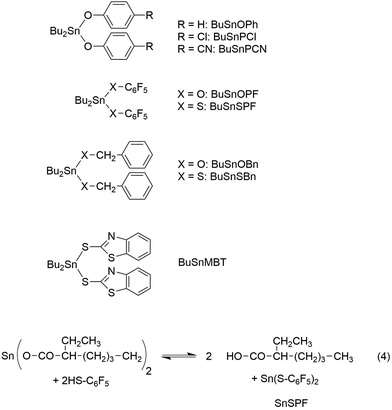
Benzyl alcohol, benzyl mercaptane, 4-cyanophenol, 2-mercaptobenzothiazole, pentafluorophenol, pentafluorothiophenol and dibutyltin oxide were purchased from Alfa Aesar (Karlsruhe, Germany) and used as received. The syntheses and properties of dibutyltin bisbenzyloxide, dibutyltin bis benzyl mercaptide, dibutyltin bisphenoxide, dibutyltin bis(4-cyanophenoxide), dibutyltin bispentafluoro-phenoxide and dibutyltin bis(pentafluoro-thiphenolate) have previously been reported (for formulas see Scheme 2).25,26
ROPPOC of L-lactide with dibutyltin bis(4-cyanophenoxide), (BuSnCN)
L-Lactide 14.4 g (100 mmol) was weighed into a 50 mL flame-dried Erlenmeyer flask in an atmosphere of argon and the catalyst (0.25 mmol) was added in the form of a crystalline powder. The reaction vessel was immersed in an oil bath preheated to 160 °C and after several hours (see Table 1) part of the reaction product was removed with a spatula.ROPPOC of L-lactide with dibutyltin bis(pentafluorothiophenolate), (BuSnSPF)
Bu2SnSPF (0.4 mmol) was weighed into a 50 mL flame-dried Erlenmeyer flask, a stirring bar and freshly recrystallized L-lactide (40 mmol) was added under a blanket of argon. The reaction vessel was immersed into an oil bath preheated to 140, 160 or 180 °C. After 2 h (140 °C) or 1 h, part of the reaction product was removed with a spatula.Measurements
The 400 MHz 1H NMR spectra were recorded on a Bruker Avance 400 FT NMR spectrometer in 5 mm sample tubes. CDCl3 containing TMS served as solvent and shift reference.Matrix-assisted laser desorption/ionization time-of-flight (MALDI TOF) mass spectrometry was performed using an Autoflex III (Bruker Daltonik GmbH, Bremen) equipped with a Nd-YAG laser (355 nm). trans-2-[3-(4-tert-Butylphenyl)-2-methyl-2-propenylidene]malononitrile (DCTB) dissolved in tetrahydrofuran (10 mg mL−1) was doped with potassium trifluoroacetate and used as matrix. Matrix solution was premixed with the analyte solution (chloroform, 4 mg mL−1) in a ratio of 5/1(v/v). 1 μL of the resulting solution was deposited on the sample target. At least 2000 single spectra recorded at different positions (linear positive mode) within the spots were accumulated. The instrument was previously calibrated with PEO standards.
For the GPC experiments a modular system kept at 40 °C (isocratic pump, 1 mL min−1, refractive index detector, RI-501-Shodex) was applied. Samples were manually injected (100 μL, 2–4 mg mL−1). For instrument control and molecular weight calculation the Clarity software (GPC extension, DataApex) was used. The calibration was performed using polystyrene standard sets (Polymer Standards Service – PSS, Mainz, Germany). For the determination of the Mark–Houwink–Sakurada (MHS) relationship of intrinsic viscosities a viscometer (Viscostar, Wyatt, Germany) and a multiangle laser light scattering (MALS) detector (Dawn EOS, Wyatt, Germany) were used. Instrument software (Astra 6.1, Wyatt) was used for calculation.
Results and discussion
Syntheses of nylons
In two papers, syntheses of nylon-6 and of a nylon-7 copolyamide derived from smaller amounts of 1,6-diaminoheane and suberic acid were described.23,24 This copolymer structure improved the solubility but looked like a homopolymer in the mass spectra. Since the results obtained from both monomer combinations were almost identical, the discussion is focused on the nylon-6 case. Two different monomers may be used for the synthesis of nylon-6, namely ε-caprolactam and ε-aminohexanoic acid (Scheme 3).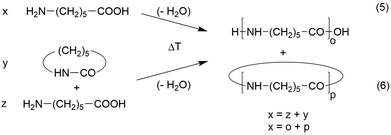 | ||
| Scheme 3 Syntheses of nylon-6 by reversible polycondensation of ε-amino caproic acid or by ROPPOC of ε-caprolactam. | ||
When ε-aminocaproic acid is used at temperatures above 230 °C, a normal reversible polycondensation takes place which includes formation of caprolactam and higher cyclic oligomers by back-biting. When the less expensive ε-caprolactam serves as monomer initiated by ε-aminocaproic acid or water (typical for the technical production) a so-called ROPPOC synthesis will proceed. ROPPOC means ring-opening polymerization in combination with simultaneous polycondensation. The ROPPOC approach is advantageous for preparative purposes, because the lactam represents a conversion of functional groups just at the beginning of the polymerization. For example, a 1/1 mixture of lactam and ε-aminohexanoic acid corresponds to a polycondensation of ε-aminocaproic acid with 50% conversion. Hence, under equilibrium conditions both monomer systems will yield identical reaction products when the conversion of functional groups is identical. The conversion of monomers is correlated with their equilibrium concentration. It is evident that from the preparative point of view, that the POPPOC method with a large amount of lactam is advantageous for high molecular weights, because it is not easy to remove the liberated water from the reaction mixture based on neat ε-aminohexanoic acid.
Kricheldorf et al. have studied various monomer ratios and optimized the reaction conditions for the highest possible conversion as indicated by the highest accessible molecular weight. An optimized sample was then fractionated by precipitation and extracted with suitable non-solvents and in this way 27 weight% of the reaction product was removed (the cyclic topology was proven by mass spectrometry). Interestingly the MALDI TOF mass spectrum of the insoluble remainder still displayed peaks of cyclics and no peaks of linear chains. This finding indicates that at least 40 weight% of the original nylon sample consisted of cyclics a value five times higher than calculated by JS and thus in contradiction to the JS theory. Further confirmation of this critique came from the MALDI TOF mass spectra. The best mass spectrum displays peaks of cycles up to a mass of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da corresponding to a degree of polymerization around 90. Such large cycles are certainly formed to a large extent (perhaps even exclusively) by ete-cyclization, because the amino end group is far more nucleophilic than the amide nitrogen, and the CO2H end group is more electrophilic than the amide CO. This conclusion is in contradiction to the statement of JS cited in the Introduction. Furthermore, the mass spectra disagree with another aspect of the JS theory. JS calculated (p. 1605, ref. 1): “The rings formed are small species, their number average degree of polymerization (aDPc) never rising above 4 (for case III; meaning a2 + b2 systems).This calculation was later confirmed by Flory (p. 330 in ref. 5). Such a low aDPc is incompatible with the mass spectra, in as much as the MALDI TOF mass spectra considerably underestimate high molar mass species. This conclusion is confirmed by the mass spectra of the cyclic polylactides discussed below. Unfortunately, Kricheldorf et al. were not able at that time to characterize the topology of the high molar mass species with masses above 50
000 Da corresponding to a degree of polymerization around 90. Such large cycles are certainly formed to a large extent (perhaps even exclusively) by ete-cyclization, because the amino end group is far more nucleophilic than the amide nitrogen, and the CO2H end group is more electrophilic than the amide CO. This conclusion is in contradiction to the statement of JS cited in the Introduction. Furthermore, the mass spectra disagree with another aspect of the JS theory. JS calculated (p. 1605, ref. 1): “The rings formed are small species, their number average degree of polymerization (aDPc) never rising above 4 (for case III; meaning a2 + b2 systems).This calculation was later confirmed by Flory (p. 330 in ref. 5). Such a low aDPc is incompatible with the mass spectra, in as much as the MALDI TOF mass spectra considerably underestimate high molar mass species. This conclusion is confirmed by the mass spectra of the cyclic polylactides discussed below. Unfortunately, Kricheldorf et al. were not able at that time to characterize the topology of the high molar mass species with masses above 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. However, this problem was solved, when (more recently) ROPPOC syntheses of cyclic polylactides were studied.
000 Da. However, this problem was solved, when (more recently) ROPPOC syntheses of cyclic polylactides were studied.
ROPPOC syntheses of cyclic poly(L-lactide)s
For three reasons L-lactide was preferentially used for an exploration of the usefulness of the ROPPOC method in the field of aliphatic polyesters. First, polylactides are biosourced and biodegradable polymers which have meanwhile found numerous in applications in various fields, so that an increasing number of chemical companies have launches its technical production. The properties of cyclic polylactides are different from those of their linear counterparts and may be of technical interest, provided that a simple method for the synthesis of high molar products is available. Second, L-lactide is easier to obtain in a dry and pure form than δ-valerolactone or ε-caprolactone. Third, due to its dimeric structure it has an important analytical advantage. A clean ROP or REP free of transesterification will exclusively yield even-numbered polylactides (linear or cyclic depending on the polymerization mechanism). Formation of odd-numbered cyclics which can easily be detected by mass spectrometry, indicates the existence of ring-chain equilibration via backbiting. This information cannot be retrieved from monomeric species such as lactones or cyclic carbonates. This aspect is important for the purpose of this study, because the existence of ring chain equilibration is characteristic for reversible polycondensations and a prerequisite of the JS-theory.The polymerization of lactide or other cyclic esters with various tin catalysts is advantageous for preparative purposes and for mechanistic studies, because it allows for a systematic variation of the ester end group and its reactivity. This goal is difficult to achieve with linear monomers, because the preparation of activated esters of ω-hydroxy acids is difficult and acid chlorides of hydroxyacids are unstable anyway. Furthermore, when a cyclic monomer is used instead of a linear one, it may be possible to prepare linear polymers by normal ROP under conditions allowing for the suppression of back-biting and end-to-end cyclization. These linear polyesters are needed as reference for comparisons of hydrodynamic volumes with samples prepared via ROPPOC. In contrast, it is almost impossible to prepare perfectly linear polyesters by polycondensation of linear monomers up to high conversions. The catalysts successfully used for ROPPOC syntheses of cyclic poly(L-lactide)s are summarized in Table 1 together with the pertinent references.
A schematic illustration of such a ROPPOC concerning the experiments listed in Table 1, is presented in Schemes 4 and 5. Characteristic for this mechanism is the initial formation of even-numbered polylactide chains due to rapid propagation, because the tin alkoxide end group is the most nucleophilic species in the reaction mixture. When an initiator generates a activated CO end group which is considerably more electrophilic than the ester groups of the main chain, it can undergo efficient intermolecular and intramolecular condensation steps in analogy to the situation in a normal polycondensation. Hence, formation of large rings will occur by ete-cyclization in addition to the formation of smaller cycles by back-biting. A characteristic difference between both types of cyclization is the exclusive formation of even cycles, when transesterification reactions are absent (Scheme 4) whereas back-biting automatically produces equimolar amounts of even and odd cycles (Scheme 5). As soon as odd linear chains are formed, ete-cycliaztion will also generate odd rings.
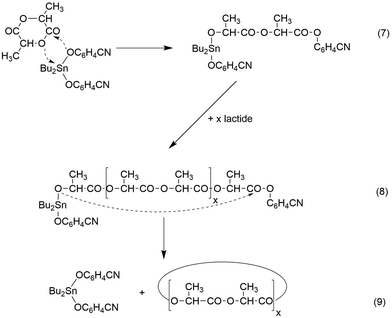 | ||
| Scheme 4 ROPPOC synthesis of cyclic polylactides with BuSnPCN in bulk (see Table 2). | ||
Experimental evidence for this course of the ROPPOC approach was obtained when the in situ generated SnSPF catalyst (Scheme 2) was used for polymerizations in bulk at 160 °C.27 At a Lac/Cat ratio of 2000/1 and a reaction time of 1 h even-numbered linear chains having thioester (SC6F5) end groups were the largely predominant species (Fig. 3A). After doubling of the catalyst concentration and a time of 4 h no linear chains were detectable in the mass spectra anymore (Fig. 3B).
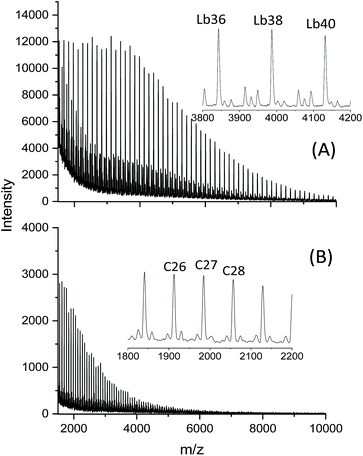 | ||
| Fig. 3 MALDI-TOF mass spectra of poly(L-lactide)s polymerized with pentafluoroprthiophenol+SnOct2 in bulk: (A) 160 °C/1 h with In/Cat = 2000/1, (B) 160 °C/4 h with In/Cat = 1000/1 (reprinted from ref. 27 with permission of Wiley). | ||
In a previous study dealing with the usefulness of dibutyltin bisphenoxides as ROPPOC catalysts for lactides26 two important trends were elaborated. The four catalysts used in that work, BuSnOPh, BuSnPCl, BuSnPCN and BuSnOPF (Scheme 2) are based on a series of phenols with increasing acidity. In the absence of steric hindrance, higher acidity of the phenol entails higher electrophilicity of the ester group derived from it. When BuSnOPh and BuSnOPF were compared under identical reaction conditions, the mass spectrum of the polylactide produced with BuSnOPh displayed a large fraction of linear chains having phenylester end groups (Fig. 4A). With BuSnOPF no linear chains were detectable anymore (Fig. 4B).
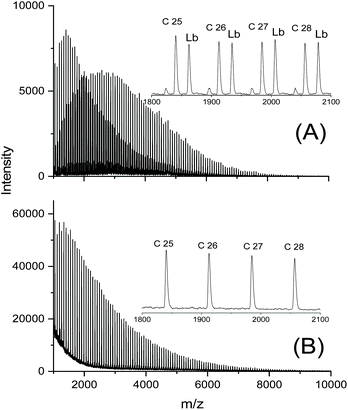 | ||
| Fig. 4 MALDI TOF mass spectra of polylactides prepared in bulk at 160 °C/1 h: (A) with BuSnOP, (B) with BuSnOPF. Lb denotes linear chains having a phenyl ester end group. | ||
The MHS measurements, shown in Fig. 5, confirmed that the high molecular weight fraction of the BuSnOPF-initated sample was cyclic. These measurements compare the intrinsic viscosity of a potentially cyclic polymer with the viscosity of the linear counterpart. It is a theoretically and experimentally well-established fact that the hydrodynamic volume (and thus, the intrinsic viscosity) of cyclic polymers amounts to only 2/3 of that of the linear chains. Such MHS measurements are performed with a SEC apparatus equipped with triple detection. Since the RI-detector of the SEC apparatus responds to the mass and not to the number of polymer chains, these MHS measurements reflect the weight fraction of polymer chains or rings. The accuracy of these measurements is low and does allow one to distinguish between 95 and 92 or 98% of cyclization. But this shortcoming is not relevant for the purpose of this work, because a weight fraction of cycles >90% and rings having DPs > 1000 are so far from the values calculated by J + S and Flory, that they disprove the JS theory.
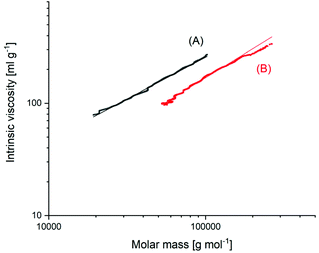 | ||
| Fig. 5 MHS measurements of (A) linear polylactide Purapol L105, (B) polylactide prepared with BuSnOPF in bulk at 160 °C/1 h (see Fig. 4B). | ||
The experiments with BuSnOPh, BuSnPCN (see next par.) and BuSnOPF demonstrate the tremendous influence of the ester end group on the extent of cyclization, an effect which can only be explained by ete-cyclization, because these catalysts generate the same nucleophilic (Sn–O–CH) end group, which is responsible for the back-biting.
As expected, the dibutyltin derivative of 4-cyanophenol (BuSnPCN in Scheme 2) had a medium reactivity which allowed for monitoring the progress of cyclization via mass spectrometry over a period of several hours.25 In this work this ROPPOC was studied over a longer period of time and the conversion of monomer and CH-OH end groups (signal at 4.35 ppm) was determined by 1H NMR spectroscopy. As demonstrated by the results summarized in Table 2, the monomer conversion was complete within 1 h, but the conversion of end groups resulting from ete-cyclization continued over the following 8 h (longer times caused thermal degradation). The assignment of end group consumption to cyclization was confirmed by MALDI TOF mass spectrometry as illustrated by Fig. 6 and Fig. S1 (ESI†). These mass spectra also proved that 1 h sufficed for full even–odd equilibration of the reaction mixture. Therefore, these experiments demonstrate that the ete-cyclization of longer chains is a relative slow process when compared with propagation and with the reversible formation of cyclic oligomers by back-biting.
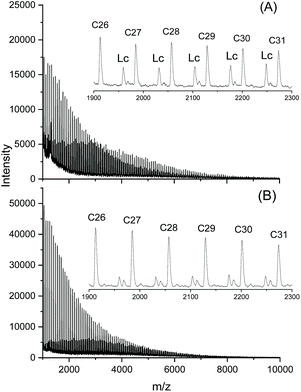 | ||
| Fig. 6 MALDI-TOF mass spectra of poly(L-lactide) catalyzed with BuSnPCN at 160 °C: (A) after 0.3 h; (B) after 2 h. Lc denotes linear chains having 4-cyanophenyl ester end groups. | ||
| Exp. no. | Time (h) | Conv.a (%) | HOCHb | M n | M w | Đ |
|---|---|---|---|---|---|---|
| a Conversion of L-lactide. b Relative to all methine (O-CH-CO) protons. | ||||||
| 1 | 0.3 | 97–98 | 1/100 | 8000 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4.6 |
| 2 | 1.0 | 97–98 | 1/115 | 9000 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4.0 |
| 3 | 2.0 | 97–98 | 1/130 | 9400 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3.7 |
| 4 | 4.0 | 97–98 | 1/180 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
3.5 |
| 5 | 8.0 | 97–98 | 1/210 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3.6 |
| 6 | 24.0 | >99 | — | 5700 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
4.0 |
In another paper experiments with BuSnOBn, BuSnSBn and BuSnSPF were reported.27 The BuSnOBn-initiated polymerization is an example of a normal ROP where the end group is less reactive than the ester groups in the backbone, so that ete-cyclization is absent or negligible. Correspondingly, the mass spectrum (Fig. 7A) displays the peaks of linear chains having benzyl ester end groups. Due to the higher reactivity of the thioester end group generated by BuSnSBn the mass spectrum of the resulting polylactide displayed a mixture of linear and cyclic species (Fig. 7B) quite analogous to Fig. 6B. The higher reactivity of thioesters is well known from the activation of acetyl groups as thioesters of coenzyme-A in the human metabolism. Finally, a polymerization was performed with BuSnSPF under the same conditions (no. 1, Table 3) and then the mass spectrum exclusively displayed peaks of cycles (Fig. 8A). The MHS diagram of Fig. 8B confirmed that even the high molar mass fraction almost completely consisted of cycles.
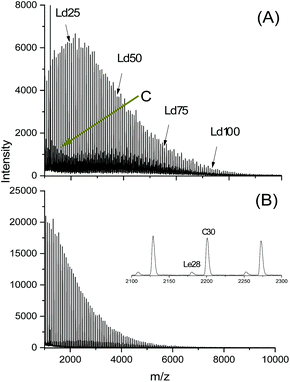 | ||
| Fig. 7 MALDI-TOF mass spectra of polylactides prepared in bulk at 160 °C/4 h, Lac/Cat = 200/1: (A) with BiSnOBn, Ld denotes linear chains having benzyl ester end groups, (B) with BuSnSBn, Le denotes linear chains having thiobenzyl ester end groups (reproduced from ref. 27 with permission of Wiley). | ||
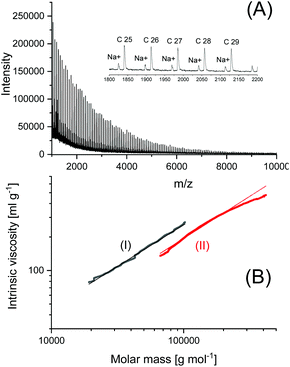 | ||
| Fig. 8 Polylactide prepared with BuSnSPF in bulk at 160 °C/4 h (no. 1, Table 3): (A) MALDI-TOF mass spectrum, (B) MHS measurement with Purapol as linear standard (I). | ||
| Exp. no. | Lac/Cat | Temp. (°C) | Time (h) | M n | M w | Đ |
|---|---|---|---|---|---|---|
| 1 | 200/1 | 160 | 4 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
198![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.2 |
| 2 | 100/1 | 180 | 1 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3.0 |
| 3 | 100/1 | 160 | 2 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.8 |
| 4 | 100/1 | 140 | 4 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.7 |
At that time when the first experiments with BuSnSBn and BuSnSPF were performed, the authors were unable to perform MHS measurements.27 Therefore, three more experiments with BuSnSPF were now conducted for his work and their results summarized in Table 3 (no. 2–4). A Lac/Cat ratio of 100/1 was used, because the highest molecular weights were obtained with this low ratio. The MALDI-TOF spectra exclusively displayed peaks of cycles (in agreement with Fig. 8A), and the MHS measurements confirmed again, that also in those cases the high molar fraction almost completely consisted of cyclic polylactides (Fig. S2 and S3, ESI†). These results confirm the message of Fig. 4 and 5. The reactivity of the ester end group is decisive for existence and extent of the ete-cyclization. This aspect is not included in the JS theory which has an extremely narrow experimental basis. J + S exclusively studied the proton-catalyzed polycondensation of 1,10-decanediol with adipic acid.
Therefore, they could not learn and imagine, how important a variation of end groups is. A second flaw of the JS theory is discussed in connection with eqn (3).
Finally, it should be mentioned that after optimization of the reaction conditions cyclic polylactides were also obtained, when commercial tributyltin chloride or diphenyltin dichloride were used as catalysts due to the intermediate formation of acid chloride end groups.28 Examples of MALDI mass spectra and MHS measurements were reproduced as Fig. S4 and S5 in the ESI.† In summary, all these ROPPOC syntheses of cyclic polylactides gave a consistent picture and this picture is in total contradiction to the JS concept of critical concentration.
Theoretical considerations
It may be objected that the ROPPOC syntheses discussed above are not included in the Jacobson–Stockmayer definition of reversible polycondensations, because the majority of the monomers is cyclic and consumed by ring-opening polymerization and not by condensation steps. For the following reasons this argumentation is incorrect. Firstly, since “back-biting” is a reversible reaction, every reversible polycondensation includes as many growing steps via ring-opening as degradation steps by “back-biting”, otherwise high molar mass polycondensates would never be formed. In this regard there is no fundamental difference between a normal reversible polycondensation and a ROPPOC process involving equilibration reactions. Secondly, it is a fundamental law of chemistry that any equilibrium is independent on the reaction pathway (and its kinetic course) leading to it, and the MALDI TOF spectra of the polylactides clearly demonstrates that the ROPPOC syntheses conducted at temperatures of 160–180 °C involve total equilibration of even and odd-numbered chains or cycles. The validity of this law in polymer chemistry has recently been demonstrated by the authors.29 Ethyl ε-hydroxycaproate was polycondensed and an ethanol-initiated ROP of ε-caprolactone was conducted under identical conditions with the same efficient transesterification catalyst Bu2SnO (Scheme 6). After 3 days both polymerizations gave almost identical results with regard to molecular weights, dispersities and mass spectra (for those syntheses of pol(ε-caprolactone) a high degree of cyclization was neither expected nor intended due to the low reactivity of the ethyl ester end group).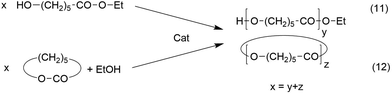 | ||
| Scheme 6 ROPPOC synthesis of cyclic polylactides with BuSnCN in bulk (see Table 2). | ||
At this point the meaning of three fundamental equations of step-growth polymerizations merit discussion. The first example is eqn (1), Carothers definition of the conversion for step-growth polymerization. This equation was elaborated on the basis of Carothers experiments with reversible polycondensations yielding polyesters or polyamides. This equation does not discriminate between reversible and irreversible polycondensations and neither Carothers, nor Flory nor Stockmayer have presented arguments showing that this equation is limited to irreversible polycondensations. According to this equation 100% conversion (i.e. p = 1) means Nat = Nbt = 0 for equal amounts of “a” and “b” functional groups. When all functional groups are consumed, the reaction product cannot contain linear chains anymore. Since the reaction product cannot have vanished to the nowhere, all reaction products must have a cyclic architecture.
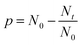 | (1) |
The second example is eqn (2), Flory's formulation for the most probable distribution of the number of linear species in a step-growth polymerization.
| nx = px−1 × (1 − p) | (2) |
Here “nx” is the number of linear species having an identical degree of polymerization. Originally, this equation was elaborated by Flory for irreversible polycondensations, and in this case eqn (2) describes the number (frequency) distribution of the entire polycondensate. After having accepted the JS theory, Flory calculated that his equation is still valid, but confined to the fraction of linear chains in an reversible polycondensation.5 This calculation was later experimentally confirmed by Niehaus and Jackson.30 Hence, this equation also concerns reversible polycondensation. Regardless, if reversible or irreversible, this equation also tells that at 100% conversion all linear species must have disappeared.
The third example is eqn (3), the so-called “law of self-dilution”.31 In this equation [La] is the molar concentration of all active linear species including monomers and polymers. This equation says that the molar concentration of all linear species steadily decreases with higher conversions, and due to the Ruggli–Ziegler-Dilution-Principle this systematic dilution favours cyclization until at 100% conversion all linear species have disappeared.
| [La]t = [La]0 × (1 − p) | (3) |
The consequences of this equation for the probability of ete-cyclization was first discussed by the first author.30 In principle, Flory knew this equation, but since he denied the existence of ete-cyclization, neither he nor J + S did interpret it in the way the author did. In connection with the JS theory eqn (3) is of particular interest, because it offers an explanation, why the JS theory is, in principle, correct (and an immensely important contribution to the theory of polycondensation), although its mathematical equations do not match the experimental reality with regard to the concept of CC. The steady dilution of the linear species has the consequence, that somewhere above 99% conversion the molar concentration of all linear species approaches CC. Yet, in that regime J + S predicted themselves that 100% conversion will yield 100% cycles (see next par.). Therefore, all polycondensations must end up with 100% cycles regardless of the IMC.
To escape from the afore-mentioned consequences of eqn. (1)–(3), one reviewer has proposed the following hypothesis. “However, I think that the correct interpretation of p = 1 in this case is as a limit – i.e. p arbitrarily close to, but still <1. One could imagine that the situation when only one single pair of chain ends remains. The polymer consists of a single linear chain and an unknown number of cyclic species. JS (for IMC > CC) predicts that the single linear chain will be of very high molecular weight, while the cyclic species will be of low molecular weight. In this situation the number fraction of cyclic species is arbitrarily close to 1, but its weight fraction may be significantly <1”. For the following reasons, the authors cannot accept this hypothesis. First, in the diagrams of JS and Flory the abscissa representing the conversion ends up with 1.0 and not with values <1. Second, none of them has discussed that their theory is correct up to a p shortly before 1, but wrong at 1.0. Third, J + S definitely discussed the consequences of 100% conversion: p. 1605 in ref. 1: “For p = 1 the ring fraction by weight increases linearly with B′/c, i.e. with dilution, until B′/c reaches 0.19, above which the equilibrium is 100% rings”, and “The result off dilution beyond critical is chiefly to decrease average size of the rings formed at 100% reaction”. Therefore, it is neither a tic nor a trick of the authors to discuss the consequences of 100% conversion, but just an extension of the discussion raised by J + S. Fourth, the hypothesis that immediately before p = 1 the reaction mixture consists of one giant chain and a large number of small cycles is in perfect agreement with the JS theory and the assumption that ete-cyclization does not occur. But this assumption is in total contradiction to the MALDI TOF mass spectra and to the MHS measurements presented in this work. Furthermore, it ignores the consequences of eqn (3). Finally, it should be taken into account that Flory's dogma of non-existing ete-cyclization has proven wrong, and J + S have never demonstrated that ete-cyclization is impossible.
In summary, all three equations convey the same message, regardless of reversible or irreversible step-growth polymerization, 100% conversion means that all reaction products have a cyclic topology. The message of eqn (1)–(3) is in perfect agreement with the mathematical treatment of irreversible polycondensations as presented by Stepto et al. or Gordon and Temple (Fig. 2),13–16 and with experimental results of this work and previous publications,25–27 but it is in total contradiction to the Jacobson–Stockmayer calculation of a critical IMC above which total cyclization should be impossible.
Conclusions
The previously published experimental results23–27 and the new results presented in this study demonstrate that the ROPPOC approach may yield cyclic polycondensates containing at least 40 weight% and in favourable cases up to 95 weight and number% or more of cyclic polymers even when performed in bulk under conditions including equilibration reactions. These results are in agreement with a stringent and consistent interpretation of the fundamental equations ((1)–(3)), which do not differentiate between reversible and irreversible polycondensations. Hence, both reversible and irreversible polycondensations have in common that 100% cycles may, in principle, be obtained when an ideal polycondensation reaches 100% conversion. In contrast, J + S concluded: “Thus, a critical phenomenon arises which is formally analogous to the well-known Bose–Einstein condensation; there is a critical concentration, below which the condensing system can be converted entirely into rings, but above which this not possible”.1 This mathematical conclusion was combined with a strong believe in the absence of ete-cyclization based on Flory's dogma. However, this believe is in total contradiction to the mass spectra and MHS measurements presented above. The reasons, why the JS theory fails to describe the experimental reality for polycondensations conducted at high IMC's, are twofold. First, their experimental basis was extremely small exclusively consisting of polycondensations of 1,10-decane diol with adipic acid. Therefore, J + S did not have the opportunity to learn that a broad variation of the reactivity of end groups has a strong influence on the course of reversible polycondensations, above all on the extent of ete-cyclization. Second, ignoring the existence of ete-cyclization also had the consequence that the “Law of self-dilution” (eqn (3)) was not taken into account.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We wish to thank Prof. G. Luinstra, H. U. Moritz (Institute TMC Hamburg) and Dr S. Rost (Elantas AG, Hamburg) for financial support, Dr S. Stahl (Inst. TMC Hamburg) for helpful discussions and Mrs R. Laging (BAM, Berlin) for the SEC measurements.Notes and references
- H. Jacobson, C. O. Beckmann and W. H. Stockmayer, J. Chem. Phys., 1950, 18, 1607–1612 CrossRef CAS.
- H. Jacobson and W. H. Stockmayer, J. Chem. Phys., 1950, 18, 1600–1606 CrossRef CAS.
- W. H. Carothers, Chem. Rev., 1931, 8, 353–426 CrossRef CAS.
- P. J. Flory, Chem. Rev., 1946, 39, 137–197 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- J. F. Brown and S. Gm, J. Am. Chem. Soc., 1965, 87, 931–932 CrossRef.
- J. B. Carmichael, D. J. Gordon and F. J. Isackson, J. Phys. Chem., 1967, 71, 2011–2015 CrossRef CAS.
- J. B. Carmichael and J. B. Kinsinger, Can. J. Chem., 1964, 42, 1996–2007 CrossRef CAS.
- S. J. Clarson, in Cyclic Polymers, ed. J. A. Semlyen, Kluver Academic Publ., Dordrecht, 2nd edn, 2000, ch. 5 Search PubMed.
- J. Roovers, Macromolecules, 1988, 21, 1517–1521 CrossRef CAS.
- J. A. Semlyen, Large ring molecules, John Wiley & Son Ltd, 1996 Search PubMed.
- J. A. Semlyen, Cyclic polymers, Springer, 2000 Search PubMed.
- J. L. Stanford, R. F. T. Stepto and D. R. Waywell, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 1308–1326 RSC.
- R. F. T. Stepto and D. R. Waywell, Makromol. Chem., 1972, 152, 263–275 CrossRef CAS.
- M. Gordon and W. B. Temple, Makromol. Chem., 1972, 152, 277–289 CrossRef CAS.
- M. Gordon and W. B. Temple, Makromol. Chem., 1972, 160, 263–276 CrossRef CAS.
- A. Horbach, H. Vernaleken and K. Weirauch, Makromol. Chem., 1980, 181, 111–124 CrossRef CAS.
- H. R. Kricheldorf, Acc. Chem. Res., 2009, 42, 981–992 CrossRef CAS PubMed.
- H. R. Kricheldorf, D. Fritsch, L. Vakhtangishvili, N. Lomadze and G. Schwarz, Macromolecules, 2006, 39, 4990–4998 CrossRef CAS.
- H. R. Kricheldorf and G. Schwarz, Macromol. Rapid Commun., 2003, 24, 359–381 CrossRef CAS.
- H. R. Kricheldorf, G. Schwarz and S. C. Fan, High Perform. Polym., 2004, 16, 543–555 CrossRef CAS.
- H. R. Kricheldorf, Polycondensations - History and New Results, Springer, 2014 Search PubMed.
- H. R. Kricheldorf, M. Al Masri and G. Schwarz, Macromolecules, 2003, 36, 8648–8651 CrossRef CAS.
- H. R. Kricheldorf and N. Lomadze, Polym. Sci., Ser. C, 2009, 51, 133–147 CrossRef.
- H. R. Kricheldorf and S. M. Weidner, Eur. Polym. J., 2018, 109, 360–366 CrossRef CAS.
- H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 3767–3775 CrossRef CAS.
- H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 1915–1925 CrossRef CAS.
- H. R. Kricheldorf, S. M. Weidner and F. Scheliga, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 952–960 CrossRef CAS.
- H. R. Kricheldorf, S. Weidner and F. Scheliga, Polym. Chem., 2017, 8, 1589–1596 RSC.
- D. E. Niehaus and C. Jackson, Polymer, 2000, 41, 259–268 CrossRef CAS.
- H. R. Kricheldorf, Macromol. Rapid Commun., 2009, 30, 1371–1381 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0py00226g |
| This journal is © The Royal Society of Chemistry 2020 |