Tacticity dependence of single chain polymer folding

Abstract

Precision polymerization techniques offer the exciting opportunity to manufacture single-chain nanoparticles (SCNPs) with intramolecular crosslinks placed in specific positions along the polymer chain. Earlier studies showed that synthetic polymer chains can fold into defined SCNP conformations through a reversible two-state process, similar to that observed for small peptides and proteins – yet far behind in its structural sophistication. While the natural structures of proteins arise from polypeptides of perfectly defined stereochemistry, the role of main-chain stereochemistry on SCNP folding remains largely unexplored. To investigate the effect of tacticity on SCNP architectures, the development of specific simulation strategies is critical to provide reliable data. Herein, we investigate the structural transitions of SCNPs of different stereochemistries, i.e. atactic, syndiotactic and isotactic of various lengths (L = 10 to L = 30) using all-atom Monte-Carlo simulations. The results indicate that structural transitions occur in syndiotactic polymers at lower temperature compared to atactic and isotactic polymer chains. The effect of main chain stereochemistry on the transition temperature was found to be especially pronounced for shorter polymer chains of length L = 10 to L = 20.

---

Introduction

Mimicking complex macromolecular architectures of natural biomacromolecules, such as proteins, yet on the basis of entirely synthetic polymeric systems, provides a promising pathway to design functional single-chain polymers.¹ Polymeric single-chain nanoparticles (SCNP) and dendrimers have been widely investigated to mimic the assembly principles of natural polymers, comprising well-defined macromolecular structures that can be modified for different purposes.² In SCNPs, the main chain of a precursor polymer is decorated with crosslinking points, which can form either covalent or non-covalent bonds.^3–5 Upon a specific stimulus, the formation of bonds between these crosslinking entities over extended distances along the backbone transforms the macromolecules into compact conformations.^6–8 In analogy to biological systems, we refer to these structures in the following as ‘folded’ conformations. In these distinct conformations, the SCNP may perform specific functions, such as sensing or catalysis, and even enable applications in nanomedicine.⁹ Architectures of SCNPs can be readily adjusted by varying the polymer backbone, the chemical nature of the crosslinking points, and functional side chains to generate stable polymeric nanoparticles with the desired function.^9–12 Synthetic access to well-defined precursor polymers is enabled by reversible deactivation radical polymerization processes, such as reversible addition–fragmentation chain-transfer (RAFT),^13,14 nitroxide-mediated polymerization (NMP)^15,16 or combinations of atom transfer radical polymerization (ATRP)^12,17–19 with modular ligation protocols.^20–22

In the context of single-chain folding technology, two distinct synthetic strategies are generally applied: ‘selective point folding’ and ‘repeat unit folding’.^11,22 In selective point folding, well defined 3D structures are generated by placing complementary recognition units at defined positions along the lateral polymer chain. While this approach provides control over the folded structure, inserting the recognition motifs along the polymer chain is synthetically challenging.^23–29 On the other hand, the repeat unit folding approach is synthetically more accessible, however, it leads to folded polymers of less defined structures.^30–33 By combining orthogonal crosslinking chemistries in a single polymer chain, it is possible to fine-tune the assembly properties. In comparison to biological macromolecules with well-defined secondary structures, the precise conformation of current SCNPs remains largely uncontrolled. The critical lack of perfectly defined SCNP conformations raises the question whether it is possible to place crosslinking groups along the polymer chain in a distance that essentially constrains the conformation of the backbone to a unique three-dimensional structure. Comparison with naturally occurring macromolecules – such as enzymes – suggests that a spatial control with an accuracy of a few Å is still sufficient to ensure potential functions, such as binding to other molecules or enzymatic reactions.^34,35 As a model system, we herein investigate SCNP folding driven by specially designed hydrogen donor/acceptor moieties positioned along the lateral polymer chain, which have the additional benefit that the rigidity of the hydrogen bond donor acceptor pair helps to constrain the backbone.^19,22,23 Further development of the underlying selective point folding approach may enable the design of structurally well-defined polymer units, which assemble into biomimetic systems that surpass the stability of their biological counterparts.^31–33 However, one of the synthetic limitations is the lack of control over the stereochemistry of the macromolecule during synthesis. It has been shown that the properties of polymers, such as thermal and mechanical behavior, are strongly influenced by the stereochemistry of the polymer chain.³⁶ While the stereochemistry of polypeptides in nature is highly defined comprising L-amino acids, the effect of stereochemistry on the folding synthetic polymer chains remains largely unexplored. Therefore, it is important to investigate the influence of polymer chain tacticity on the folding of SCNPs. The required thorough investigation is only possible through extensive atomistically resolved molecular simulations for a range of temperatures and polymer chain lengths, resulting in a full thermodynamic characterization of the structural transitions and a detailed view of the conformational distribution of these polymers, which are presently difficult to obtain experimentally. Using all atom Monte-Carlo (MC) simulations, we investigate here the single-chain folding of α,ω-functionalized polystyrenes of specific tacticities carrying complementary binding sites at both chain termini as depicted in Scheme 1, which can link reversibly by the formation of hydrogen bonds.

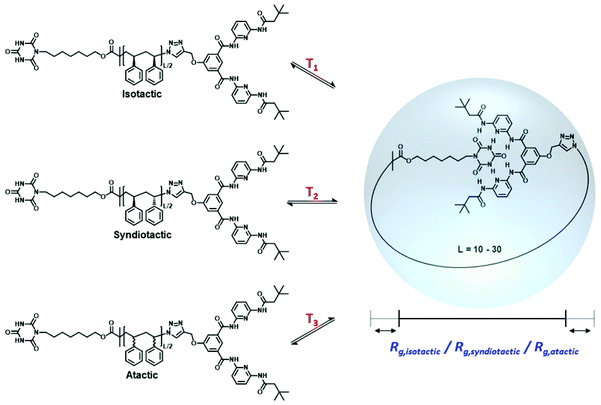Scheme 1 Single chain folding of isotactic, syndiotactic and atactic α,ω-functionalized polystyrene chains occurring at different temperatures and yielding different radii of gyration (R_g).

Methods

Herein, α,ω-functionalized polystyrene chains with different stereochemistries, i.e. atactic, syndiotactic and isotactic are investigated with different chain lengths of L = 10, 12, 14, 16, 18, 20 and 30. While for the syndiotactic and isotactic polymers there is only one stereochemistry, respectively, there are many possible sequences for the atactic polymers for each chain length. The different random stereochemistries of atactic polymer chains studied in this work (shown in Fig. S1 and S2†) are labelled as A-1, A-2, A-3, A-4 and A-5. For clarity, we investigate in one simulation always configurations for a fixed stereochemistry of the polymer backbone, which does not change during a simulation. Each polymer has two hydrogen bonding recognition units based on six-point cyanuric acid (CA) Hamilton wedge (HW) interaction (Fig. 1). The CA–HW pair configurations were optimized using a semiempirical quantum chemistry PM7 method. We applied the same workflow as described in ref. 19 for all simulations. For each chain length, L, a very long all-atom Metropolis Monte Carlo simulation at constant temperatures in the range from 280 K to 330 K was performed using SIMONA.³⁷ Each simulation comprises of O(10⁹) steps resulting in hundreds of opening–closing transitions to characterize fully the thermodynamic equilibrium as a function of chain-length and stereochemistry. To model the conformation of the polymers, the General Amber Force field (GAFF) was used and partial charges were computed according to the AM1-BCC method.³⁸ Experimental measurements of vdW dispersion forces between alkyl chains and different solvents have shown that the vdW interaction energies in solutions are an order of magnitude smaller than the energies between alkyl chains and vacuum.³⁹ Therefore, we scaled the vdW contribution in the force field by a factor 0.1 to implicitly take into account the effect of van der Waals interaction with solvent. The binding energy of the CA–HW recognition pair lies at 57.7 kJ mol⁻¹ according to QM calculations.¹⁹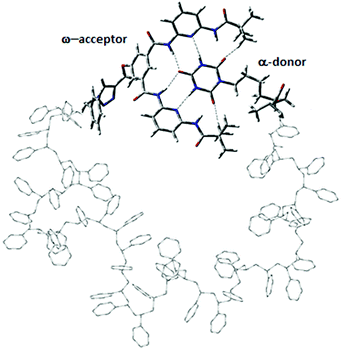

Fig. 1 Model system of a polystyrene precision designed polymer with α,ω-donor–acceptor for single chain self-assembly. Hydrogen bonds are shown with dashed lines.

Using the force field parameters with ε = 1, the energy difference of ΔE = 130.5 kJ mol⁻¹ were obtained which is much larger than the value predicted by QM calculations. Therefore, the ε = 2.6 was used in all simulations to match the QM and force field calculations. The radius of gyration R_g was calculated from Monte Carlo trajectories using VMD considering only the backbone atoms of each polymer system (α and ω end groups are excluded).⁴⁰

Results and discussion

Thermodynamic parameters and transition temperature

At each temperature, a probability density function p(E) can be calculated as a function of the potential energy from the Monte Carlo trajectories, allowing to calculate the free energy F as a function of the potential energy p(E):

F(E) = −RT ln p(E) (1)

where R is the gas constant. The potential energy E of the system can be used as a reaction coordinate because opening or closing the CA–HW pair results in the most significant energy change in the system. The occupation probability density at two temperatures for syndiotactic and isotactic and a sample sequence of an atactic polymer, each of L = 14 is depicted in Fig. 2. The maxima of the probability density represent the closed and open configurations of the polymer are shown in the insets. The maxima in the occupation profiles can be used to define two states (closed (A) and open (B)) for which representative configurations are shown in Fig. 2(a). We compute the difference in the free energy ΔF, using the probability density using eqn (1). The value of folding temperature (T_m) was defined by the condition ΔF(T_m) = 0. In analogy to protein folding, the folding temperature (or transition temperature) is the temperature at which the equal occupancy of the open and closed conformations exist. We choose this expression inspired by protein-folding because we are interested in folded conformations that are structurally unique, mimicking their natural inspiration.

Fig. 2 Probability density for (a) syndiotactic (b) isotactic (c) atactic polymers of L = 14 at two temperatures. The simulation temperatures are indicated in the legend boxes. In all simulations two maxima are found, corresponding to the open and closed conformations of the CA–HW pair. The relative occupancy depends on the temperature. The insets illustrate representative conformations associated with the open (red) and closed (blue) conformations, respectively.

Conformational transitions

As illustrated in Fig. 3(b) for one particular atactic polymer sequence, we can observe hundreds of opening–closing transitions to fully characterize the thermodynamic equilibrium as a function of chain-length and stereochemistry. Fig. 3(a) is a sample trajectory for one of the five atactic chains investigated from which two recurring values of radius of gyrations and energy could be observed. In Fig. 3(b), configurations with a large R_g correspond to fully open CA–HW pairs, while conformations with low-R_g correspond to fully closed CA–HW pair. Intermediate conformations, in which not all hydrogen bonds of the CA–HW pair are closed exist, yet are so transient that they are not visible in the Fig. 3(b). Comparison of the closed conformation of the Hamilton Bridge in the molecular mechanics conformation shows excellent agreement with Density-functional theory (DFT) calculations regarding the angle of the two groups and the relative angle between them, independent of the configuration of the polymer.¹⁹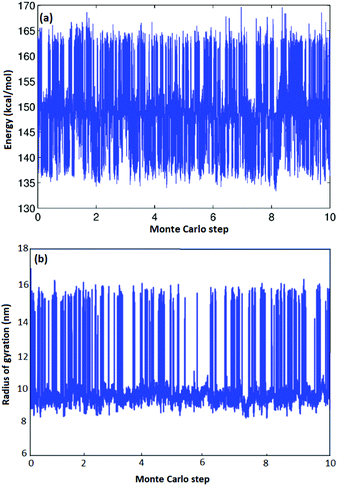

Fig. 3 Energy and radius of gyration vs. Monte Carlo steps (×108) for A-1 atactic polymers of L = 14.

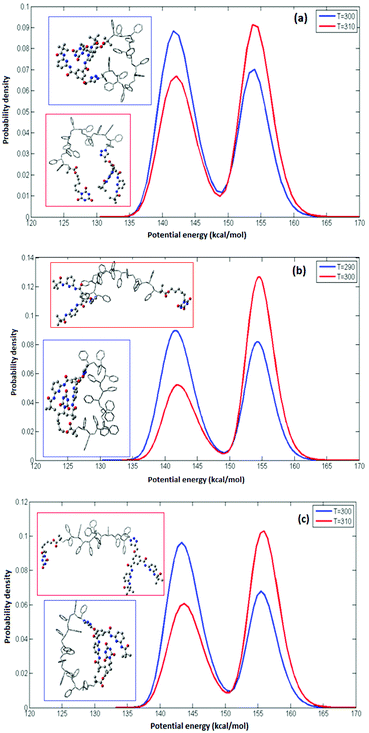
The simulations were performed for polymers of various lengths as a function of temperature. Based on these data, we computed free-energy diagrams for the radius of gyration vs. temperature in a potential-of-mean force approach using the occupation probabilities for each radius of gyration. Representative probability plots for five configurations of atactic polymers with random stereochemistries are shown in Fig. 4(a)–(e) and for isotactic and syndiotactic polymers are depicted in Fig. 4(f) and (g) for the chain length of L = 14. The corresponding probability plots for polymer chains of length L = 18, 20 and 30 are also illustrated in Fig. S3–S5.† In each plot, we observe a high relative population of the enthalpically favoured closed conformation at lower temperatures and a high relative population of the entropically favoured open configuration at higher temperatures. The data illustrates a clear two-state behaviour, allowing us to define a “folding” or “closing” temperature as the temperature of equal occupancy of the folded and the open conformation, which is shown as a dashed line in each plot.

Fig. 4 Free energy diagrams for (a) A1, (b) A2, (c) A3, (d) A4 and (e) A5 conformations of atactic polymers of length L = 14 derived from the trajectories. The “folding” temperature corresponding to equal occupancy of the open and closed conformation is shown as a dashed line in each plot. (f) Free energy diagram of a syndioactic polymer of the same length. (g) Free energy diagram of isotactic polymer of the same length.

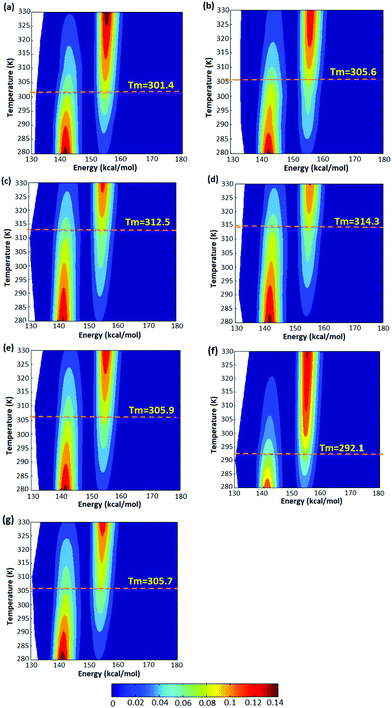
As illustrated in Fig. 4, thermodynamic properties of the five atactic configurations investigated do not differ significantly. We observe folding temperatures of 301.4, 305.6, 312.5, 314.3 and 305.9 K for A-1, A-2, A-3, A-4 and A-5 atactic polymers of L = 14 which is comparable to the T_m = 305.7 for the isotactic polymer configuration of the same length. For the syndiotactic polymers we found a somewhat lower folding temperature of 292.1 K, which is related to the stereochemistry of the backbone in syndiotactic polymers. The stereochemistry may therefore influence interatomic energetics mediated by vdW and hydrogen bonding which has been also shown in earlier studies.⁴¹

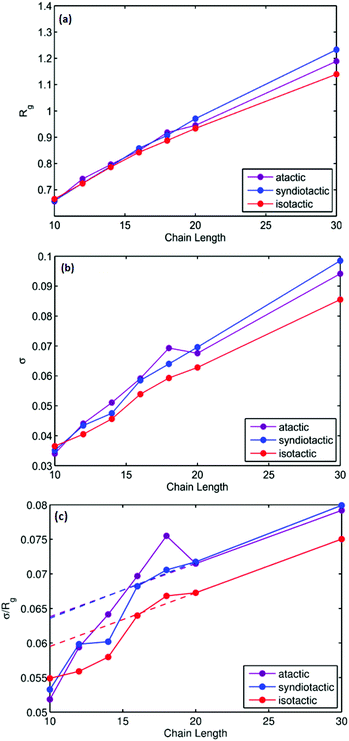
Thermodynamic parameters including ΔH, ΔS and folding temperatures (T_m) for all studied systems are reported in Table S1.† As is shown in Table S1,† the folding temperature for atactic polymers has fluctuations up to 10 degrees for the same chain length. The atactic polymers investigated form a representative sample of the large possible set of conformations that can be constructed for a given chain length. Fig. 5(a) illustrates folding temperatures for isotactic, syndiotactic and atactic polymers as a function of chain length. It shows that the folding temperature for chain lengths smaller than L = 20 depends on the tacticity of the polymer chains, e.g. syndiotactic polymers display lower folding temperatures than isotactic and atactic polymers. This is in a good agreement with the corresponding trend of ΔS values illustrated in Fig. 5(b), where syndiotactic polymers of chain lengths smaller than L = 20 have higher ΔS values than those of atactic and isotactic polymers. These results indicate a tacticity dependence on the SCNPs’ behaviour at chain length smaller that L = 20, which is driven by entropy effects. However, for polymer chains of L = 30 very close folding temperatures for atactic, isotactic and syndiotactic polymer chains were observed, suggesting that the folding temperature is less affected by the stereochemistry of longer polymer chains. Next, we subdivide the trajectories into open and closed conformations according to the thresholds derived from the free-en ergy diagrams, enabling us to independently characterize the closed conformations, a task that would be difficult to achieve experimentally. All data presented in the following refers to the subset of closed conformations. Fig. 6(a) shows the radius of gyration for atactic, isotactic and syndiotatctic polymer chains as a function of chain length. Isotactic polymers have slightly smaller radius of gyration than atactic and syndiotactic polymers. As R_g values reported in Fig. 6(a) are the mean values, Fig. 6(b) illustrates the width of distribution of radius of gyration (σ) as a function of the chain length. For isotactic polymer chains, σ is smaller compared to atactic and syndiotactic chains. Reduced fluctuation of radius of gyration for isotactic, atactic and syndiotactic polymers as a function of L are shown in Fig. 6(c).

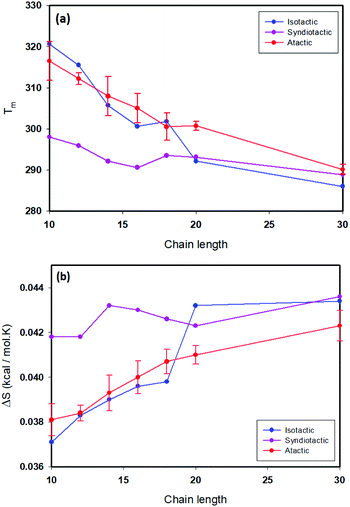Fig. 5 (a) Folding temperature as a function of chain length for isotactic, syndiotactic and atactic polymers, (b) Δs as a function of chain length for isotactic, syndiotactic and atactic polymers.

Fig. 6 (a) Radius of gyration (R_g) as a function of chain length (L), (b) width of the distribution of radius of gyration (σ) as a function of chain length (L) and (c) Reduced width of the R_g distributions as a function of the chain length for atactic, syndiotactic and isotactic polymers.

For isotactic polymer chains, reduced fluctuation of radius of gyrations are smaller than those of atactic and syndiotactic polymers for all chain lengths, indicating that collapsing into a unique structure is more probable for isotactic polymers. Highly ordered adjacent neighbouring units cause more pronounced steric effects and therefore lower the flexibility in isotactic polymers, which induce immersion of unique folded structures. However, for small chain length polymers of L = 10, all polymers have very similar reduced fluctuations of radius of gyration, suggesting that for small chain lengths polymers SCNPs of all stereochemistries collapse into unique folded structures.

Conclusions

Herein, we explore the effect of tacticity on the folding behaviour of different single polymer chain lengths using Monte-Carlo simulation, which allowed sampling of a very large conformational space. Thermodynamic properties of reversible single chain polymer folding were calculated using probability density histograms obtained from simulations containing hundreds of opening-closing transitions. We find that syndiotactic polymers have lower folding temperatures compared to isotactic and atactic chains, which is driven by entropic effects. Our results demonstrate that the tacticity dependence of folding temperatures is especially pronounced for polymers of shorter chains (shorter than L = 20) compared to longer polymer chains of lengths (L = 30). From the calculated reduced fluctuation of the radius of gyration, it is concluded that isotactic polymers collapse more probably into a unique structure, due to the steric effects and low flexibility of the polymer chain. Moreover, short chain polymers of L = 10, can collapse into unique folded structures which is independent of tacticity. To enable a direct comparison of our theoretical results with experimental investigations in the future, scattering techniques such as small-angle neutron and X-ray scattering (SANS and SAXS) are ideal tools to reveal radii of gyration and chain conformations of SCNPs in solution. Our results underline the importance of the main chain stereochemistry in designing short chain SCNPs. From an experimental point of view it is critical to understand the polymer architecture that lead to SCNPs capable of folding into a unique structure, which is a prerequisite for the synthesis of functional SCNPs with structures as defined as their natural paragons – i.e. proteins.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

W. W and C. B.-K. acknowledge funding for the current study in the contact of the SFB 1176 funded by the Deutsche Forschungsgemeinschaft. E. S. and W. W. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy via the Excellence Cluster 3D Matter Made to Order (EXC-2082/1-390761711), by the Carl Zeiss Foundation through the “Carl-Zeiss-Focus@HEiKA”. C.B.-K. acknowledges funding via a Laureate Fellowship by the Australian Research Council (ARC). C. B.-K and H. F. acknowledge continued key support from the Queensland University of Technology (QUT) through the Centre for Materials Science.

Notes and references

1. C. K. Lyon, A. Prasher, A. M. Hanlon, B. T. Tuten, C. A. Tooley, P. G. Frank and E. B. Berda, Polym. Chem., 2015, 6, 181–197.
2. J. W. Lockman, N. M. Paul and J. R. Parquette, Prog. Polym. Sci., 2005, 30, 423–452.
3. T. Mes, R. van der Weegen, A. R. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2011, 50, 5085–5089.
4. B. S. Murray and D. A. Fulton, Macromolecules, 2011, 44, 7242–7252.
5. S. Mavila, O. Eivgi, I. Berkovich and N. G. Lemcoff, Chem. Rev., 2015, 13, 878–961.
6. E. A. Appel, J. Dyson, J. del Barrio, Z. Walsh and O. A. Scherman, Angew. Chem., Int. Ed., 2012, 51, 4185–4189.
7. J. Zhang, G. Gody, M. Hartlieb, S. Catrouillet, J. Moffat and S. Perrier, Macromolecules, 2016, 49, 8933–8942.
8. J. Zhang, J. Tanaka, P. Gurnani, P. Wilson, M. Hartlieb and S. Perrier, Polym. Chem., 2017, 8, 4079–4087.
9. N. D. Knöfel, H. Rothfuss, J. Willenbacher, C. Barner-Kowollik and P. W. Roesky, Angew. Chem., Int. Ed., 2017, 56, 4950–4954.
10. J. Willenbacher, K. N. Wuest, J. O. Mueller, M. Kaupp, H. A. Wagenknecht and C. Barner-Kowollik, ACS Macro Lett., 2014, 3, 574–579.
11. O. Altintas and C. Barner-Kowollik, Macromol. Rapid Commun., 2016, 37, 29–46.
12. D. E. Whitaker, C. S. Mahon and D. A. Fulton, Angew. Chem., 2013, 125, 990–993.
13. J. Chiefari, Y. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562.
14. G. Moad, Polym. Chem., 2017, 8, 177–219.
15. C. J. Hawker, A. W. Bosman and E. Harth, Chem. Rev., 2001, 101, 3661–3688.
16. A. C. Schmidt, H. Turgut, D. Le, A. Beloqui and G. Delaittre, Polym. Chem., 2020, 11, 593–604.
17. K. Matyjaszewski and J. Xia, Chem. Rev., 2011, 101, 2921–2990.
18. M. Ouchi, T. Terashima and M. Sawamoto, Chem. Rev., 2009, 109, 4963–5050.
19. D. Danilov, C. Barner-Kowollik and W. Wenzel, Chem. Commun., 2015, 51, 6002–6005.
20. A. Sanchez-Sanchez, I. Asenjo-Sanz, L. Buruaga and J. A. Pomposo, Macromol. Rapid Commun., 2012, 33, 1262–1267.
21. C. Barner-Kowollik and A. J. Inglis, Macromol. Chem. Phys., 2009, 210, 987–992.
22. O. Altintas and C. Barner-Kowollik, Macromol. Rapid Commun., 2012, 33, 958–971.
23. C. J. Hawker and K. L. Wooley, Science, 2005, 309, 1200–1205.
24. T. Terashima, T. Mes, T. F. De Greef, M. A. Gillissen, P. Besenius, A. R. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2011, 133, 4742–4745.
25. B. V. Schmidt, N. Fechler, J. Falkenhagen and J. F. Lutz, Nat. Chem., 2011, 3, 234–238.
26. N. Hosono, M. A. Gillissen, Y. Li, S. S. Sheiko, A. R. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2013, 135, 501–510.
27. R. K. Roy and J. F. Lutz, J. Am. Chem. Soc., 2014, 136, 12888–12891.
28. O. Shishkan, M. Zamfir, M. A. Gauthier, H. G. Börner and J. F. Lutz, Chem. Commun., 2014, 50, 1570–1572.
29. A. Sanchez-Sanchez, A. Arbe, J. Colmenero and J. A. Pomposo, ACS Macro Lett., 2014, 3, 439–443.
30. O. Altintas, E. Lejeune, P. Gerstel and C. Barner-Kowollik, Polym. Chem., 2012, 3, 640–651.
31. O. Altintas, T. Rudolph and C. Barner-Kowollik, J. Polym. Sci. A: Polym. Chem., 2011, 49, 2566–2576.
32. O. Altintas, P. Gerstel, N. Dingenouts and C. Barner-Kowollik, Chem. Commun., 2010, 46, 6291–6293.
33. O. Altintas, P. Krolla-Sidenstein, H. Gliemann and C. Barner-Kowollik, Macromolecules, 2014, 47, 5877–5888.
34. Y. W. Dong, M. L. Liao, X. L. Meng and G. N. Somero, Proc. Nat. Acad. Sci. U. S. A., 2018, 115, 1274–1279.
35. H. J. Dyson and P. E. Wright, Chem. Rev., 2004, 104, 3607–3622.
36. A. Ismael, A. Van Reenen and T. Mokrani, J. Mater. Sci., 2016, 22, 381–389.
37. T. Strunk, M. Wolf, M. Brieg, K. Klenin, A. Biewer, F. Tristram, M. Ernst, P. J. Kleine, N. Heilmann, I. Kondov and W. Wenzel, J. Comput. Chem., 2012, 33, 2602–2613.
38. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
39. L. Yang, C. Adam, G. S. Nichol and S. L. Cockroft, Nat. Chem., 2013, 5, 1006–1010.
40. W. Humphrey, A. Dalke and K. Schulten, VMD - Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38.
41. A. l. Mamun and M. A. Khan, Can. Chem. Trans., 2014, 2, 46–56.

---

Footnote

† Electronic supplementary information (ESI) available: Stereochemistries of atactic polymers, free energy diagrams, folding temperatures and thermodynamic properties for isotactic, syndiotactic and atactic polymers of different chain lengths. See DOI: 10.1039/d0py00133c

---