Open Access Article
Open Access ArticleFractography of poly(N-isopropylacrylamide) hydrogel networks crosslinked with mechanofluorophores using confocal laser scanning microscopy†
Maria
Stratigaki
 a,
Christoph
Baumann
a,
Christoph
Baumann
 a,
Lambert C. A.
van Breemen
a,
Lambert C. A.
van Breemen
 b,
Johan P. A.
Heuts
b,
Johan P. A.
Heuts
 c,
Rint P.
Sijbesma
c,
Rint P.
Sijbesma
 *c and
Robert
Göstl
*c and
Robert
Göstl
 *a
*a
aDWI – Leibniz Institute for Interactive Materials, Forckenbeckstr. 50, 52056 Aachen, Germany. E-mail: goestl@dwi.rwth-aachen.de
bDepartment of Mechanical Engineering, Polymer Technology, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
cLaboratory of Supramolecular Polymer Chemistry, Institute for Complex Molecular Systems, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: r.p.sijbesma@tue.nl
First published on 26th July 2019
Abstract
Due to their soft and brittle nature, the mechanical characterization of polymer hydrogels is a difficult task employing traditional testing equipment. Here, we endowed poly(N-isopropyl acrylamide) (PNIPAAm) hydrogel networks with Diels–Alder adducts of π-extended anthracenes as mechanofluorophore crosslinkers. After swelling the networks with varying amounts of water and subjecting them to force, we visualized the subsequent fluorescence caused by covalent bond scission with confocal laser scanning microscopy (CLSM) and related the intensities to the macroscopic fracture mechanics and the elastic moduli recorded with traditional uniaxial compression. The sensitivity of the mechanofluorophores allowed the analysis of low levels of mechanical stress produced via a hand-induced needle-puncturing process and, thus, is an alternative to conventional force application methods. The detection and precise localization of covalent bond scission via CLSM helps elucidating the interrelationship between molecular structure and the macroscopic properties of chemically crosslinked polymeric hydrogels. We believe that this micro-scale mechanophore-assisted fractography can establish a new paradigm for the mechanical analysis of soft matter in fields covering traditional polymer and life sciences.
1 Introduction
Hydrogels are crosslinked polymeric networks that can absorb and retain large amounts of water. Their drastic volume changes in response to specific external stimuli, such as temperature and pH, render them promising biocompatible materials in applications for sensors, tissue engineering, or drug delivery.1 However, their success as structural materials is largely impeded by their intrinsic fragility along with their extreme softness, both stemming from the low density of polymer chains in the water-swollen state. Hence, the study of their mechanical properties is of particular interest, yet very much complicated by the severe limitations regarding the utilization of conventional measurement methods and techniques.2,3To overcome these challenges, it is important to develop more sophisticated experimental methodologies and characterization techniques. Conventional measurement methods can be adapted for the mechanical characterization of soft polymer materials to determine their elastic behavior and response, based on the principles of indentation4,5 or cavitation rheology.6 Concomitantly, the traditional fractography methods, such as atomic force or electron microscopy probe the fracture surface of materials, but are time-consuming and only work post-mortem. However, since the accumulation of non-reversible ruptured bonds is the dominant mechanism leading to failure in polymeric structures, it is important that imminent fracture is reported prior to the formation of any visible macroscopic cracks that will ultimately evolve into the decomposition of the polymer.7 In recent years, the force-induced selective scission of covalent and non-covalent bonds was exploited to generate molecules that change their photophysical properties upon the application of mechanical stress and strain, thus allowing the optical detection of material damage.8,9 While the seminal development of such molecules changing their absorption spectra (mechanochromophores) can be regarded as elegant, their investigation on small scales was hampered intrinsically by the Lambert–Beer law.10 Hence, more sensitive and scalable approaches were required leading to the genesis of mechanoluminescence and mechanofluorochromism techniques.11–15 Mechanofluorophores were successfully employed to locally visualize stress concentrations in a wide range of materials, including hydrogels.16,17 Yet, up to today and to the best of our knowledge, the analysis techniques employed for the study of mechanical failure in materials are limited to the macro-scale. However, a holistic description of fracture mechanisms requires to precisely resolve smaller feature-sizes on the micro-scale, as this information is valuable for tailor-making polymeric structures with distinct mechanical properties, such as biomimetic gels,18 smart skin,19 or muscle-like materials.20
Here we report the integration of the Diels–Alder adduct of a π-extended anthracene and maleimide, previously synthesized in our group,21 as covalent crosslinker into PNIPAAm hydrogel networks, endowing these soft materials with stress-sensing capability (Scheme 1). This mechanofluorophore is excellently photostable, exhibits a high fluorescence quantum yield (72%), and can be observed with outstanding signal-to-noise ratio due to its “turn-on” nature. We rely on PNIPAAm as a typical and well-investigated thermoresponsive hydrogel with mechanical behavior that can be fine-tuned depending on its water-absorption capability.2,22,23 By unprecedented analysis relying on CLSM, we explore the fracture behavior of the PNIPAAm hydrogels on the micro-scale after employing a convenient and easy-to-implement needle-puncturing method for mechanical disruption. We make a productive correlation of material properties and mechanophore fluorescence after fracture by the precise localization of stress accumulation around a defined region of interest.
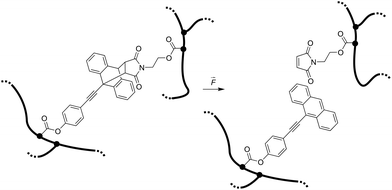 | ||
| Scheme 1 Force-induced cycloelimination of Diels–Alder adduct from 9-π-extended anthracene and maleimide in a crosslinked polymeric hydrogel network. | ||
2 Experimental section
2.1 Materials
The PNIPAAm hydrogel networks were synthesized by free radical polymerization. Commercially available materials were supplied by Sigma-Aldrich and used as described in Table 1, while the synthesis of the mechanophore crosslinker was based on our own previous work. The overall crosslink density was 2 mol% with a mechanophore crosslinker content of only 0.02 mol%. The prepolymer solution (NIPAAm, tetraethylene glycol dimethacrylate (TEGDMA), azobisisobutyronitrile (AIBN), and mechanophorecrosslinker dissolved in dioxane and degassed with Ar flow for 30 s) was heated for 5 min to completely dissolve solid residues, and was then poured into Teflon molds to anneal for 24 h at 65 °C under N2 atmosphere. The formed networks were washed in ethanol for a minimum of 24 h, and were then dried in vacuo for another 24 h. The controlled swelling of the networks to different degrees (ds) was accomplished by weighing the dry samples (md) with a precision balance and then subsequently adding the required amount of water (mw) with a gastight microliter syringe to reach the desired swollen mass (ms) which was determined after 24 h: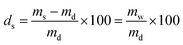 | (1) |
| Material | Role | Amount | Comments |
|---|---|---|---|
| NIPAAm | Monomer | 1000 mg, 8.84 mmol | Purified by recrystallization from hexane at 65 °C |
| TEGDMA | Crosslinker | 53 μL, 0.175 mmol | Purified by passing through a short column of basic Al2O3 |
| AIBN | Initiator | 3.63 mg, 0.022 mmol | Recrystallized from MeOH at 45 °C |
| Diels–Alder adduct | Mechanophore crosslinker | 1.010 mg, 1.767 μmol | Synthesized according to our previous work21 (Scheme 1) |
| Dioxane | Solvent | 1 mL | Distilled before use |
Equilibrium swelling was achieved by immersing the networks into excess of deionized H2O for 24 h. In every case, the exact ds for each individual sample was verified prior to imaging, compression, or other measurements.
2.2 Methods
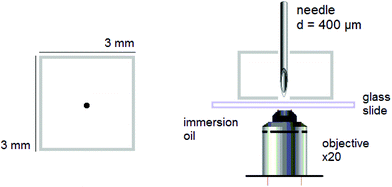
Puncture. Dry rectangular specimens of ca. 3 × 3 × 3 mm3 were individually and prior any further experiments swollen to different ds varying from 0 to equilibrium. Then, they were punctured with a stainless steel needle. The diameter of the needle was purposefully chosen to a minimum, i.e. 400 μm, to form a fluorescent circular trace, due to mechanofluorophore activation, that is smaller than the field of view of the used microscope, and therefore could be clearly visualized and analyzed. The beveled-tip of the needle accommodated an easier penetration into the (dry or slightly swollen) glassy materials.24 The needle was inserted vertically into the center-region of the PNIPAAm networks, and penetrated the bulk of each sample until it exited the opposite surface (Fig. 1).
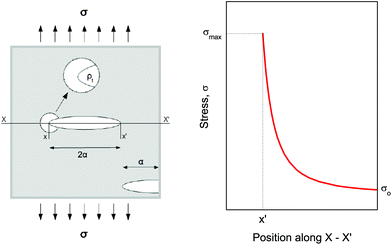
Compression. In a second step, the punctured rectangular samples were compressed by hand with the use of laboratory tweezers, and were then subsequently visualized by CLSM. The small size of the hydrogel samples facilitated an approximately parallel placement between the tweezers (Fig. S1†). The applied force was gradually increased in order to deform the samples macroscopically, but without producing any visible failure (fracture) of the specimen. A needle-punctured hydrogel is essentially a square plate with an internal void that acts as a stress raiser upon force application.25 The stress is amplified from a nominal σo to a σmax due to stress concentration around the tip of the flaw:
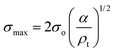 | (2) |
Fluorescence. A confocal laser scanning microscope (Leica LASX TCS SP8) was used to perform the analysis and record the respective images. Wet mounting of the samples onto microscope cover glasses was realized with the use of an immersion oil (n = 1.5180). The scanning range was determined based on previous measurements21 performed via UV-vis and fluorescence spectroscopy to determine the absorption and emission characteristics of the mechanofluorophore in solution. It can be seen in Fig. 3 that the mechanofluorophore absorbs at around 400 nm, and emits by exhibiting two characteristic peaks at 450 nm. The lower bound of the scanning range was assigned a value to maintain the minimum from the excitation laser's wavelength (Table 2).
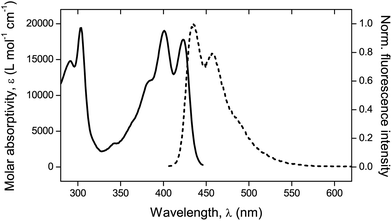 | ||
| Fig. 3 UV-vis absorption spectrum (solid line) and normalized fluorescence emission spectrum (dashed line). λexc = 372 nm. | ||
| Parameters | |
|---|---|
| Excitation laser | UV 405 nm |
| Scan format (x × y) | 1024 × 1024 pixels |
| Scan speed | 400 Hz |
| Magnification | 20× |
| Scanning wavelength regime | 420–550 nm |
| Pinhole | Airy 1 |
| Line average | 8 |
3 Results and discussion
3.1 Confocal laser scanning microscopy
The mechanophore activation was initially recorded by performing a λ-scan from 420 to 550 nm, under a laser excitation wavelength of 405 nm (Fig. S2†). The emission spectrum with the two characteristic vibronic transitions of the anthracene at around 450 nm was in agreement with previous measurements. The recorded images were of sub-micrometer resolution with a pixel size of 758 nm. The scale bar in all images is 100 μm.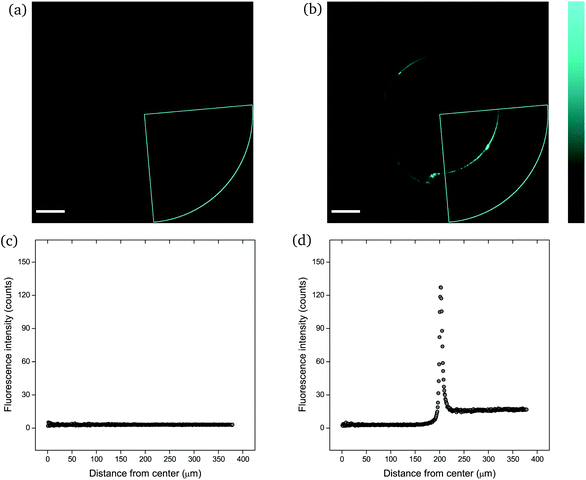 | ||
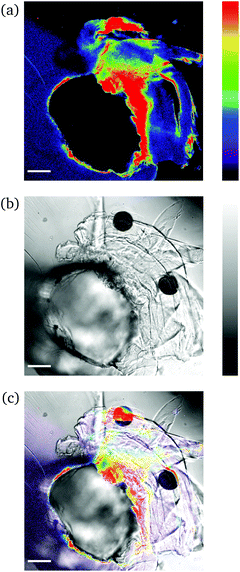
| Fig. 4 CLSM images (a and b) and fluorescence intensity analysis with ImageJ (c and d) for rectangular PNIPAAm hydrogel samples crosslinked with mechanofluorophore for a scanning regime of 420–550 nm under a 405 nm excitation laser: (a and c) before and (b and d) after needle-puncturing. The scale bar is 100 μm. The intensity values span the 0–255 scale; 0 for black and 255 for cyan. Note here that the slightly deformed fluorescence circular shape is due to cutting of the needle tip after exiting the sample. Respective CLSM images for rectangular PNIPAAm hydrogel samples with various swelling degrees are provided in Fig. S4.† | ||
It should be noted that the cone chosen for the pristine sample (Fig. 4a) was identical to the one for the punctured sample (Fig. 4b) only for comparison reasons, in terms of fluorescence intensity. For every image captured with the confocal laser scanning microscope, the whole circular trace was scanned sequentially by maintaining a constant integration angle at 90°. The cone with the highest intensity value was finally used for the analysis each time.
The calculated maximum fluorescence intensity values for all punctured samples are shown as a function of ds in Fig. 5. The error bars in both the x-axis and the y-axis stem from the calculation of a mean value with a standard deviation from two to five measurements. It is evident that the intensity after fracture decreases with swelling degree, i.e. with the further hydration of the networks. A relatively high fluorescence activation might be discerned in this graph for samples with low water contents, an intermediate activation at swelling degrees around 25%, and low to near-zero activation for higher ds.
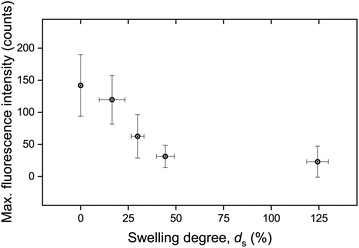 | ||
| Fig. 5 Maximum fluorescence intensity as a function of swelling degree. The data have been derived by calculating the mean value and standard deviation stemming from two to five measurements. | ||
It is important to note that the possible effect of mechanophore dilution upon volume expansion by water-swelling was ruled out. For this, the fluorescence intensity of swollen samples after puncturing was recorded and quantitatively compared with identical microscopy measurements after the same samples were completely dried in vacuo (Fig. S3†). The deviation was negligible and could therefore only explain a minor fraction of the observed decrease moreover demonstrating that the activated mechanofluorophores were not susceptible to fluorescence quenching by water.
This simple needle-puncturing of the hydrogel networks with integrated mechanofluorophores could be further utilized for the local mapping of stress concentrations with the aid of CLSM, as shown in Fig. 6. The color spectrum allowed a distinct visualization of stress accumulation due to the asymmetrical beveled needle and its slightly diagonal insertion into the sample that maximized just at its tip (red-colored region). These fluorescence intensity maps are comparable to the fracture mechanics models employed for stress analysis in typical material-failure scenarios27 and hence could be exploited in conjunction for the study of materials fracture mechanics.
Low degree of swelling. For ds in the order of 10 to 22%, deformation of the hydrogels was hard to achieve as these were in a glassy state and exhibited a rigid behavior. The samples were deformed upon excess application of force and did not return to their original shape instantly, as the polymeric chains were fixed in a frozen state and were not able to rotate and translocate freely. A typical deformation structure of glassy polymers can be discerned in Fig. 7. Crazes formed due to the application of external force and appeared as a surface phenomenon with long and fine lines emanating from the circular disturbance. The lack of any visible fluorescent crazes suggests that mechanical integrity of the network remained unaffected, as these did not evolve into macroscopic cracks. We hypothesize that the lack of fluorescent crazes might be attributed to the correlation of crazing to molecular separation with disentanglement and sliding of polymer chains, rather than the scission of covalent bonds.28
Intermediate degree of swelling. For ds = 28% the samples were easily deformed and returned to their original shape without any delay after removal of force application. It appears that in this regime, the polymeric chains exhibited a rubber-like elasticity. The propagation of a crack initiating from the circular hole can be seen in Fig. 8. The main crack propagated at some distance from the tip and then forked into secondary branches by distributing the stress intensity locally through bifurcation.
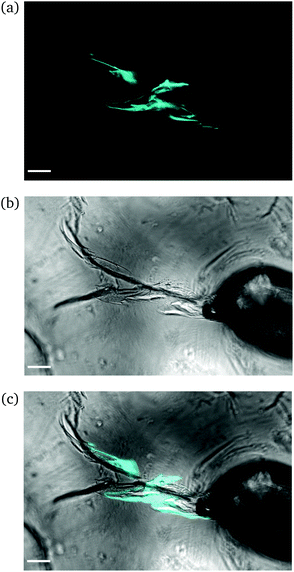 | ||
| Fig. 8 CLSM images of a rectangular PNIPAAm hydrogel sample swollen to ds = 28% after puncturing with a needle and subsequent compression with tweezers. Annotations as in Fig. 6. The scale bar is 100 μm. Note how the fluorescence follows the propagation of the crack. | ||
High degree of swelling. Fragmentation of the samples was effortlessly (and unintentionally) induced upon compression with laboratory tweezers for ds from 36% up to 123%, as the highly swollen samples were very fragile. Fig. 9 portrays the formation of channels originating locally from the region where the needle was inserted into the samples. The channels (discerned by their distinct fluorescence lines) were formed upon application of force to redistribute the water throughout the hydrogel network and/or expel any excess amount. The rearrangement of H2O related to complex fluid–solid interaction during compression and subsequent deformation of the hydrogel samples. Given the unconfined compression that was realized here, and the anticipated variation in strain response throughout the hydrogel network, the effect of poroviscoelastic parameters needs to be considered.29 However, this is beyond the scope of this study.
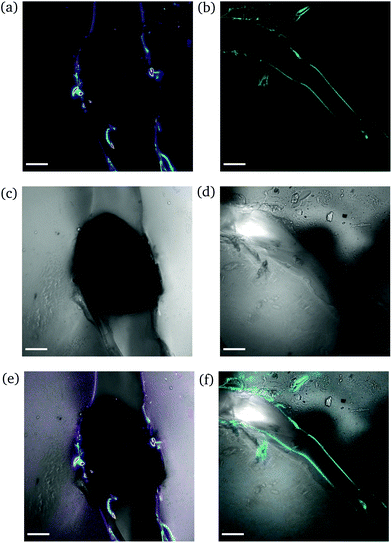 | ||
| Fig. 9 CLSM images of a rectangular PNIPAAm hydrogel sample swollen to ds = 36% after puncturing with a needle and subsequent compression with tweezers. The images on the left (a, c and e) and the images on the right (b, d and f) illustrate different regions of the same sample. Annotations as in Fig. 7. The scale bar is 100 μm. | ||
3.2 Elastic modulus
Given the biological and biomedical applications of hydrogels, it is crucial to maintain control not only over their physicochemical response, but also their mechanical behavior over a range of swelling degrees. In this study, the elastic (Young's) modulus of the hydrogel networks was determined, as it is a fundamental and well-defined mechanical property that can reflect their integrity and can be fine-tuned upon their water absorption capability.30Fig. 10b depicts the measured elastic moduli E as a function of ds, calculated from the respective stress–strain curves (Fig. 10a). The non-swollen samples were relatively stiff with E exceeding the value of 100 MPa. A decreasing E with increasing ds can be discerned, with values lying around a few MPa for ds ∼ 20–30%, while dropping as low as <1 MPa for ds up to 180%. Given that native biological materials cover multiple orders of magnitude regarding their elastic modulus,31 this swelling-induced softening of the PNIPAAm networks can serve as a good model to investigate the mechanical properties of bio-analogous hydrogels.
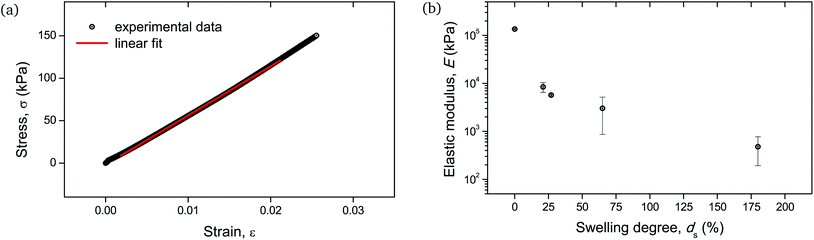 | ||
| Fig. 10 Mechanical behavior of cylindrical PNIPAAm hydrogel samples determined by uniaxial compression: (a) stress–strain curve of a hydrogel sample swollen to ds = 27%. The linear fit of the curve for the determination of the elastic modulus is also shown with a solid line. Respective curves and linear fits for all measured samples are provided in Fig. S5.† (b) E as a function of ds. The error bars are the result of two uniaxial compression measurements performed on individual hydrogel specimens. | ||
As the mechanical testing for the determination of the elastic modulus was based on an unconfined configuration, the cylindrical hydrogel samples were allowed to have a non-restricted expansion in the radial direction during compression. Therefore, the enhanced variation in moduli values for samples with relatively high water content, i.e. ds > 30%, (Fig. 10b) could be attributed to the cumulative effect of viscoelastic response of the polymeric chains along with the poroelastic behavior due to the H2O molecules in the networks, as it is apparent that for these swelling degrees the presence of water becomes significant.32,33
3.3 Correlation between macroscopic observations and fluorescence intensity
We exerted low levels of mechanical disruption to the networks with the use of a needle, which was employed before in the study of puncture-resistant hydrogels34 and the fracture behavior of soft gels and solids.24,35 Alongside, the compression of the samples with the use of common laboratory tweezers provided valuable information over the macroscopic behavior and deformation response of the hydrogels. The optical transparency of the samples allowed us to correlate the subsequent micro-scale analysis and visualization of bond scission by fluorescence intensity to the macroscopic structure and properties.Based on the macroscopic observations of the fracture behavior of the hydrogels, we anticipated that upon hydration of the gels with excess of water, the fluorescence intensity would maximize as a result of extensive bond scission within the brittle and fragile materials. However, we found that for high ds the fluorescence intensity leveled off to near-zero.
These macroscopic observations on the deformation response of the hydrogels corroborated the presence of a glass-to-rubber transition upon hydration. It can be argued that beyond a critical ds, the interaction between the solid and the liquid phase of the hydrogel was altered, also affecting the fracture mechanism. Indeed, it became apparent that beyond ds ∼ 25% the fluorescence signal leveled off and reached a plateau (Fig. 5). An analogous trend was recorded for E as a function of ds (Fig. 10b). Although the low level force applied to puncture a dry sample (in its glassy state) and a swollen sample (in a rubbery state) possibly varied, this did not affect the fracture process, since the insertion of the needle through the sample translated into the cutting of a finite number of polymer chains.
We ascribed this supposed glass-to-rubber transition to the reduction of physical crosslinks between the polymer chains from a certain ds on, due to their saturation with water. We hypothesized that the hydrophilic NIPAAm moieties were initially hydrated upon exposure of a dry sample to H2O, as the completely hydrated state of PNIPAAm relies on the formation of three hydrogen bonds per repeating unit.36 These water molecules were directly attached to the polar groups and constituted the “bound” water that was strongly associated with the polymer. Additionally absorbed water existed in a “free” state that could be easily removed, as it filled the free volume in the polymer mesh, and in a “semi-bound” state relating to the physically trapped water. These reduced intersegmental attractions between the polymer chains due to their preferential hydrogen bonding to water were proposed to lead to a significant reduction in tensile strength in UV-cured crosslinked polymers upon water absorption when exposed to high humidity conditions.37 Indeed, the secondary hydrogen bonds that were formed between the chains might contribute to the rigidity and toughness of the polymer,38 and lead to a reduction in elastic modulus with increasing water content as they become fewer.39 The increased presence of physical crosslinks in the form of intermolecular H-bonds between the polymeric chains was also found to play a dominant role in the behavior of PNIPAAm gels, as their elastic moduli in the collapsed state were significantly higher than those in the swollen state.40 Generally, H-bonds are mechanochemically weak and can be readily disrupted. However, our results corroborate a synergistic effect between physical and chemical crosslinks, as a mechanism for stress distribution among the chains and effective transfer of load to the mechanophores, which is known to be influenced by parameters such as chain entanglements and interactions among them.41
Besides the existence of different states of water in the hydrogel, the effect of local inhomogeneities should also not be ruled out.42 In heterogeneous polymeric systems, such as the one under investigation, multiple length scales are present with both short and long chain segments throughout the formed network. Upon force application, stress concentrates on the shortest chain which must already be in its fully stretched state for failure to occur. Therefore, a “pre-stretched” state of several small segments can also be considered to cause a type of random-scission along the network leading to near-zero mechanophore scission.
4 Conclusions
We showed that the integration of mechanofluorophores into PNIPAAm hydrogel networks in the form of chemical crosslinks facilitated the investigation of their molecular structure – macroscopic property interrelationships via the mapping of mechanical stresses and the local imaging of forces with the use of confocal laser scanning microscopy with μm-resolution. With this unprecedented analysis method, we elucidated the mechanical behavior of these PNIPAAm hydrogels with different water contents. We found that the dissolution of H-bonds upon swelling of the materials resulted in gradually reduced mechanical performance and completely altered their respective fracture mechanisms. Contrarily to our expectations, the easy fracture of highly swollen samples led to the scission of fewer mechanofluorophores compared to the lowly swollen states, though covalent bond scission along the network backbone was abundant. These results suggest that H-bonds significantly contribute to stress-distribution in PNIPAAm hydrogels and assist to scatter covalent bond scission throughout the material. The latter may function as a sacrificial element warranting the mechanical integrity of PNIPAAm hydrogels with low to moderate water content. This might also be the case for other hydrogels, other acrylamides for instance, with analogous H-bonding behavior. Concludingly, we believe that this unique methodology will be useful for the investigation of a wide range of mechanical phenomena in soft matter, even in a directly quantitative context, that proved to be difficult to analyze with traditional mechanical characterization techniques.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Erasmus+ framework is acknowledged for supporting the mobility of M. S. as a recent PhD graduate to DWI. R. G. and C. B. are grateful for support by a Freigeist-Fellowship of the Volkswagen Foundation. Parts of the analytical investigations were performed at the Center for Chemical Polymer Technology CPT, which was supported by the European Commission and the federal state of North Rhine-Westphalia (Grant No. 300088302). Financial support is acknowledged from the European Commission (EUSMI, 731019).References
- E. Caló and V. V. Khutoryanskiy, Eur. Polym. J., 2015, 65, 252–267 CrossRef.
- M. A. Haq, Y. Su and D. Wang, Mater. Sci. Eng., C, 2017, 70, 842–855 CrossRef PubMed.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed.
- D. Lee, M. M. Rahman, Y. Zhou and S. Ryu, Langmuir, 2015, 31, 9684–9693 CrossRef CAS PubMed.
- J. T. Pham, F. Schellenberger, M. Kappl and H.-J. Butt, Phys. Rev. Mater., 2017, 1, 015602 CrossRef.
- S. Kundu and A. J. Crosby, Soft Matter, 2009, 5, 3963–3968 RSC.
- A.-D. N. Celestine, N. R. Sottos and S. R. White, Strain, 2019, 55, e12310 CrossRef.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martinez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS.
- R. Göstl, J. M. Clough and R. P. Sijbesma, Mechanochemistry in Materials, Royal Society of Chemistry, 2017, pp. 53–75 Search PubMed.
- J. Li, C. Nagamani and J. S. Moore, Acc. Chem. Res., 2015, 48, 2181–2190 CrossRef CAS.
- Z. Chi, X. Zhang, B. Xu, X. Zhou, C. Ma, Y. Zhang, S. Liu and J. Xu, Chem. Soc. Rev., 2012, 41, 3878–3896 RSC.
- B. R. Crenshaw and C. Weder, Macromolecules, 2006, 39, 9581–9589 CrossRef CAS.
- Y. Chen and R. P. Sijbesma, Macromolecules, 2014, 47, 3797–3805 CrossRef CAS.
- J. W. Kim, Y. Jung, G. W. Coates and M. N. Silberstein, Macromolecules, 2015, 48, 1335–1342 CrossRef CAS.
- C. Calvino, L. Neumann, C. Weder and S. Schrettl, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 640–652 CrossRef CAS.
- K. R. Fitch and A. P. Goodwin, Chem. Mater., 2014, 26, 6771–6776 CrossRef CAS.
- F. Cellini, L. Block, J. Li, S. Khapli, S. D. Peterson and M. Porfiri, Sens. Actuators, B, 2016, 234, 510–520 CrossRef CAS.
- M. Fernández-Castano Romera, R. Göstl, H. Shaikh, G. Ter Huurne, J. Schill, I. Voets, C. Storm and R. Sijbesma, J. Am. Chem. Soc., 2019, 141, 1989–1997 CrossRef.
- X.-Q. Wang, C.-F. Wang, Z.-F. Zhou and S. Chen, Adv. Opt. Mater., 2014, 2, 652–662 CrossRef CAS.
- T. Matsuda, R. Kawakami, R. Namba, T. Nakajima and J. P. Gong, Science, 2019, 363, 504–508 CrossRef CAS.
- R. Göstl and R. P. Sijbesma, Chem. Sci., 2016, 7, 370–375 RSC.
- A. Halperin, M. Kröger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS.
- F. Afroze, E. Nies and H. Berghmans, J. Mol. Struct., 2000, 554, 55–68 CrossRef CAS.
- S. Das and A. Ghatak, J. Mater. Sci., 2011, 46, 2895–2904 CrossRef CAS.
- W. Callister and D. Rethwisch, Materials Science and Engineering: An Introduction, Wiley, 8th edn, 2009 Search PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- A. Mohammadipour and K. Willam, J. Appl. Mech., 2016, 83, 071003 CrossRef.
- R. N. Haward, H. E. Daniels and L. R. G. Treloar, J. Polym. Sci., Part B: Polym. Phys., 1978, 16, 1169–1179 CAS.
- D. Caccavo, S. Cascone, G. Lamberti and A. A. Barba, Chem. Soc. Rev., 2018, 47, 2357–2373 RSC.
- K.-i. Hoshino, T. Nakajima, T. Matsuda, T. Sakai and J. P. Gong, Soft Matter, 2018, 14, 9693–9701 RSC.
- R. Lanza, R. Langer and J. Vacanti, Principles of Tissue Engineering, Elsevier Science, 2011 Search PubMed.
- J. Delavoipière, Y. Tran, E. Verneuil and A. Chateauminois, Soft Matter, 2016, 12, 8049–8058 RSC.
- M. L. Oyen, Int. Mater. Rev., 2014, 59, 44–59 CrossRef CAS.
- Y. Liu, W. Zhou, Q. Zhou, K. Peng, A. Yasin and H. Yang, RSC Adv., 2017, 7, 29489–29495 RSC.
- S. Fakhouri, S. B. Hutchens and A. J. Crosby, Soft Matter, 2015, 11, 4723–4730 RSC.
- L. Tavagnacco, E. Zaccarelli and E. Chiessi, Phys. Chem. Chem. Phys., 2018, 20, 9997–10010 RSC.
- D. A. Bolon, G. M. Lucas, D. R. Olson and K. K. Webb, J. Appl. Polym. Sci., 1980, 25, 543–553 CrossRef CAS.
- N. Lakhera, K. E. Smith and C. P. Frick, J. Appl. Polym. Sci., 2013, 128, 1913–1921 CAS.
- A. Hamouda, J. Mater. Process. Technol., 2002, 124, 238–243 CrossRef CAS.
- T. Takigawa, T. Yamawaki, K. Takahashi and T. Masuda, Polym. Gels Networks, 1998, 5, 585–589 CrossRef.
- C. Lee, B. Beiermann, M. Silberstein, J. Wang, J. Moore, N. Sottos and P. Braun, Macromolecules, 2013, 46, 3746–3752 CrossRef CAS.
- M. N. Silberstein, L. D. Cremar, B. A. Beiermann, S. B. Kramer, T. J. Martinez, S. R. White and N. R. Sottos, J. Mech. Phys. Solids, 2014, 63, 141–153 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9PY00819E |
| This journal is © The Royal Society of Chemistry 2020 |