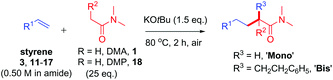Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Base-catalyzed C-alkylation of potassium enolates with styrenes via a metal–ene reaction: a mechanistic study†
Joshua P.
Barham
 *ab,
Thierry N. J.
Fouquet
*ab,
Thierry N. J.
Fouquet
 a and
Yasuo
Norikane
a and
Yasuo
Norikane
 a
a
aNational Institute of Advanced Industrial Science and Technology, Tsukuba Central 5, 1-1-1 Higashi, Tsukuba, Ibaraki 305-8565, Japan. E-mail: j.barham@saidagroup.jp
bSAIDA FDS INC., 143-10, Isshiki, Yaizu, Shizuoka, 425-0054, Japan
First published on 25th February 2020
Abstract
Base-catalyzed, C-alkylation of potassium (K) enolates with styrenes (CAKES) has recently emerged as a highly practical and convenient method for elaboration or synthesis of pharmaceutically-relevant cores. K enolate-type precursors such as alkyl-substituted heterocycles (pyridines, pyrazines and thiophenes), ketones, imines, nitriles and amides undergo C-alkylation reactions with styrene in the presence of KOtBu or KHMDS. Surprisingly, no studies have probed the reaction mechanism beyond the likely initial formation of a K enolate. Herein, a synergistic approach of computational (DFT), kinetic and deuterium labelling studies rationalizes various experimental observations and supports a metal–ene-type reaction for amide CAKES. Moreover, our approach explains experimental observations in other reported C-alkylation reactions of other enolate-type precursors, thus implicating a general mechanism for CAKES.
Introduction
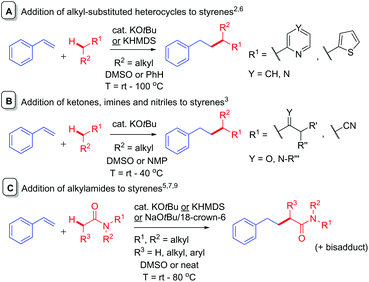
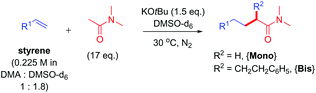
The addition of simple pre-made alkyllithium compounds to styrenes is a known reaction1 and is used in anionic polymerization chemistry.2 While the addition of alkylpotassiums to styrenes is rare, in recent years, C-Alkylation of K Enolates with Styrenes (CAKES) is emerging as a practical, convenient, high-yielding method for elaboration or synthesis of pharmaceutically-relevant cores.3–5 KOtBu-catalyzed CAKES of alkyl-substituted heterocycles (pyridines, pyrazines, thiophenes) were reported around five decades ago (Fig. 1A)6 and the scope of alkylpyridine CAKES was recently extended by Guan et al., using KHMDS and elevated temperatures (ca. 100 °C).4 KOtBu-catalyzed ketone, imine and nitrile CAKES was reported two decades ago by Knochel et al. (Fig. 1B), but no mechanistic rationale was available at that time.3 Pines first reported KOtBu-catalyzed amide CAKES;7 using N-methyl-2-pyrrolidinone (NMP) and N-methyl-2-piperidone (NMPI) as substrates. Historically, C-alkylation of most aforementioned substrates is accomplished via initial deprotonation employing a strong base (NaH, LDA, sec-BuLi).8Such reactions require an inert atmosphere, moisture-free conditions and cryogenic temperatures. In contrast, KOtBu-mediated amide CAKES are performed successfully at elevated temperatures (>80 °C), under air and ambient moisture if stoichiometric base is used (Fig. 1C),5 and are applicable to a variety of amides beyond NMP and NMPI (including acyclic alkylamides). Kobayashi et al. recently reported successful amide CAKES at rt with catalytic quantities (5–6 mol%) of base (KHMDS) and 18-crown-6 as a promotor under inert (Ar) atmosphere.9 The term ‘CAKES’ is coined due to the general requirement for potassium bases; sodium bases succeed under certain conditions but reactions are sluggish, requiring higher temperatures or complexing additives.4,5
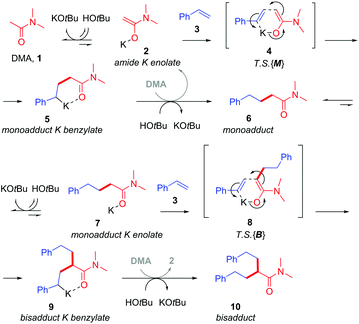
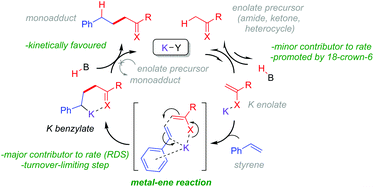
Base-catalyzed CAKES reactions have been proposed to proceed via initial formation of a K enolate,4–7,9 yet little evidence has actually been presented for this species.10 This is especially curious given that the pKa values of K enolate precursors like 4-methylpyridine,11 acetonitrile12 and N,N-dimethylacetamide13 are considerably higher (pKa = 31–35 in DMSO) than those of the conjugate acids of bases employed like HOtBu14 and HMDS (pKa = 26–29 in DMSO).14 Previous studies have then proposed the formal nucleophilic addition of the K enolate to styrene,7,9 the direct outcome of which is a strongly basic benzylic alkylpotassium which appears to be considerably higher in energy than its K enolate and styrene precursors (the pKa of PhMe is ca. 43 in DMSO).15 Despite this, no evidence for a transition state (T.S.) or even rationale, to explain how such an endergonic process might occur, has been presented. The free energy barrier to such a T.S. would have to be low enough to be accessible at rt or the somewhat elevated temperatures often employed. Oligomers are not observed, suggesting the benzylic alkylpotassium is stabilized and cannot undergo addition to a second styrene. This implicates the heteroatom of the K enolate precursor (for example, the O atoms of alkylamides or N atoms of alkylpyridines) in coordinating a closed-type T.S. and in stabilizing the benzylic alkylpotassium as recently proposed by us (Fig. 2).
To our knowledge, computation has not yet been undertaken to probe the T.S. and energetics of CAKES reactions. Herein, we disclose a detailed mechanistic model constructed by a synergy of computational (DFT), kinetic and deuterium labelling studies, revealing a metal–ene T.S. in N-alkylamide CAKES. Various experimental observations are rationalized; such as the bisadduct/monoadduct (B/M) selectivity, the effect of styrene electronics, the roles of additives (18-crown-6) and bases (NaOtBu vs. KOtBu) in the reaction and the reactivity differences between acyclic vs. cyclic amide substrates. Moreover and importantly, our mechanistic picture accords with observations in other (ketone and alkylpyridine) CAKES, thus implicating our model as a general mechanism for each class of compound.
Results and discussion
Investigation of bisadduct/monoadduct selectivity
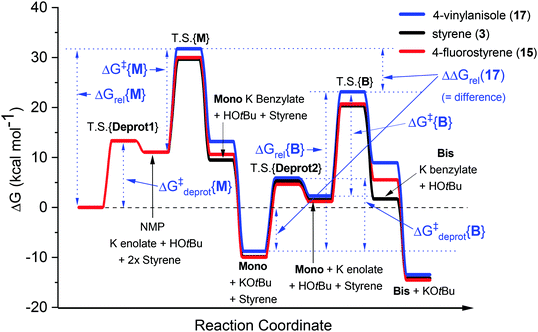
In our recent study,5 we found that the B/M selectivities of less-reactive acyclic amides such as N,N-dimethylacetamide (DMA, 1) were heavily influenced by the styrene electronics (3, 11–17). Monoadduct 6 is the expected main product because (i) a larger concentration of DMA (as solvent) than 6 occurs throughout the reaction and (ii) the rate of bisadduct 10 formation is limited by the concentration of 6 which is zero at T = 0 and increases during the reaction. Notwithstanding this, we reasoned the influence of styrene electronics on B/M selectivity could be rationalized by the free energy difference (ΔΔGrel) between the respective T.S. free energies leading to bisadduct (ΔGrel{B}) and monoadduct products (ΔGrel{M}) relative to their initial starting materials.16 This was deemed a more robust method than comparing the difference in formal T.S. energy barriers relative to their respective K enolate precursors (ΔΔG‡ = ΔG‡{B} − ΔG‡{M}), because the second (monoadduct) deprotonation step is affected by the nature of the styrene and contributes to the overall bisadduct formation rate.DFT calculations used the M06-2X functional17 with a 6-31++G(d,p) basis set18 on all atoms (except Br atoms, to which a pseudo-potential was applied).19 The C-PCM implicit solvent model,20 as implemented in Gaussian09,21 assumed DMA, DMSO or PhH, depending on the reactions investigated. This was more appropriate than modelling explicit solvation in order to build a general model which could be applied to several different reaction classes. Results were compared to those from the B3LYP (unrestricted) functional22 with a 6-31+G(d,p) basis set (see ESI†).23Fig. 3 shows the computed free energy profile of the proposed reaction mechanism (Fig. 2) for four styrenes in DMA (1) solvent. Fig. 4 shows the T.S. for deprotonation of 1 by KOtBu (T.S.{Deprot1}) and the metal–ene T.S. 4 (T.S.{M}).
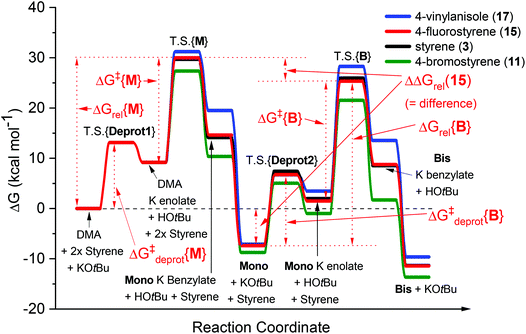 | ||
| Fig. 3 Computed free energy profiles for reactions of DMA (1) with various styrenes in DMA solvent. The transition states for reactions of monoadduct K benzylate or bisadduct K benzylate with proton sources are not shown. DFT calculations were performed17–22 with details as in ESI.† | ||
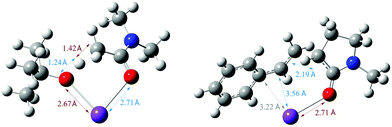 | ||
| Fig. 4 Optimized structures for T.S.{Deprot1} and T.S.{M} for reaction of DMA, showing the lengths of forming and breaking bonds. | ||
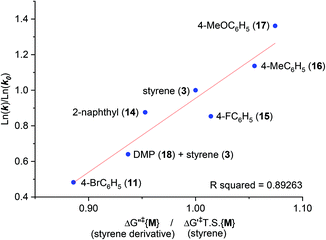
It was assumed that KOtBu deprotonates 1 and is regenerated by deprotonation of HOtBu by monoadduct K benzylate 5 to afford 6 (likewise for the pathway to 10). Since benzylic alkylpotassium 5 (and 9) are more potent bases than KOtBu, it was proposed their deprotonation of 1 (or 6) propagates a catalytic cycle.5,9 Yet the stark pKa difference between 1/6 and HOtBu is likely more important than their available concentration difference and favors the reaction pathway regenerating KOtBu. In support of this, computation found the T.S. for deprotonation of 1 by 5 (ΔG‡deprot = 15.9 kcal mol−1) was less accessible than that of deprotonation of 1 by KOtBu (ΔG‡deprot = 13.1 kcal mol−1); deprotonation of HOtBu was a much more kinetically accessible pathway for 5 (ΔG‡deprot = 0.3 kcal mol−1). Reactions of 1 with various styrenes were all exergonic with accessible free energy barriers (ΔG‡1 = 16.2–22.0 kcal mol−1) at the previously applied5 reaction temperatures (Table 1).24 A larger ΔΔGrel (= ΔGrel{B} − ΔGrel{M}) means slower relative kinetics of the reaction of monoadduct (6) to give bisadduct (10) would direct styrene consumption towards the reaction of 1 to form 6, hence decreasing the B/M ratio. Conversely, a smaller ΔΔGrel would encourage bisadduct (10) formation and would increase the B/M ratio. Gratifyingly, a strong negative correlation was found between (i) the free energy difference between the transition states for formation of bisadducts and monoadducts (ΔΔGrel) and (ii) the B/M selectivity determined experimentally (Fig. 5). The outlier to this trend (not plotted) was 13, which gave a relatively large ΔΔGrel for its high B/M selectivity.
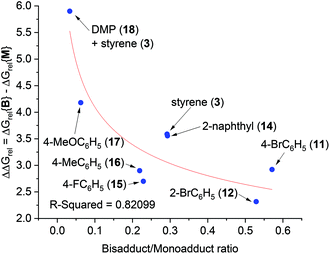 | ||
| Fig. 5 Free energy difference (ΔΔGrel) between T.S.{B} and T.S.{M} vs. bisadduct/monoadduct ratio for reactions of DMA with various styrenes. | ||
| Entry | R1/R2 | ΔG‡1 {M} | ΔGrel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a {A} a {A} |
ΔGrel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a {B} a {B} |
ΔΔG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rel rel |
ΔΔG‡deprot | B/Mb |
|---|---|---|---|---|---|---|---|
| DFT calculations were performed17–22 with details as in ESI.† For the computational profile of the DMP + styrene reaction, see ESI.†a Free energies (kcal mol−1) relative to the initial starting materials (amide + 2x styrene + KOtBu), see ESI† for further details.b Bis/mono selectivities were determined by the 1H NMR yields of the crude reaction products in a previous report as previously described.5 | |||||||
| 1 | 4-BrC6H5(11)/H | 18.2 | 27.4 | 30.3 | 2.9 | 0.6 | 0.57 |
| 2 | 2-BrC6H5(12)/H | 16.2 | 25.4 | 27.7 | 2.3 | 0.3 | 0.53 |
| 3 | 2-Py(13)/H | 16.8 | 26.0 | 30.1 | 4.1 | 0.1 | 0.42 |
| 4 | 2-Naphthyl(14)/H | 19.5 | 28.7 | 32.2 | 3.6 | 1.5 | 0.29 |
| 5 | Ph(3)/H | 20.5 | 29.7 | 33.3 | 3.6 | 1.6 | 0.29 |
| 6 | 4-FC6H5(15)/H | 20.8 | 30.0 | 32.7 | 2.7 | 1.0 | 0.23 |
| 7 | 4-MeC6H5(16)/H | 21.6 | 30.8 | 33.7 | 2.9 | 1.0 | 0.22 |
| 8 | 4-MeOC6H5(17)/H | 22.0 | 31.2 | 35.4 | 4.2 | 0.7 | 0.06 |
| 9 | Ph(3)/Me(18) | 19.2 | 29.5 | 35.4 | 5.9 | 5.1 | N/A |
To probe further, we computed the free energy difference in the barriers for deprotonation (formation of amide K enolate vs. monoadduct K enolate), ΔΔG‡deprot, which affects the overall rate by controlling the available concentrations of reacting K enolate. For the reaction of 13, ΔΔG‡deprot was notably lower than other reactions, offsetting effect of ΔΔGrel. For 17, a very high ΔΔG‡deprot reinforced the large ΔΔGrel in explaining a very low B/M selectivity. For N,N-dimethylpropionamide (DMP, 18) + styrene, which gave exclusive monoadduct formation, ΔΔG‡deprot was very high and was likely influential on the B/M selectivity. In fact, ΔG‡deprot{B}, was approaching (85% the value of) the value of ΔG‡{B}. In all other cases, values of ΔG‡deprot{B} varied between 56–74% of their respective ΔG‡{B}.
Investigation of styrene electronics and kinetics
We then proceeded to measure the kinetic profiles of reactions of DMA with the same selection of styrenes by in situ NMR spectroscopy using a variable temperature probe fixed at 80 °C (Table 2). As opposed to our previous study where reactions were prepared under ambient air/moisture,5 herein kinetic study reactions were prepared within an N2 glovebox in NMR tubes using commercial KOtBu (sublimed grade 99.99%), DMSO-d6 solvent (D, 99.9%) and degassed (3× freeze/pump/thaw) reagents (NMP/DMA/DMP) that had been dried overnight over activated 4 Å molecular sieves. Otherwise, KOtBu/amide equivalents (relative to styrene) and order of addition accorded with the previous study.5 Reactions were first order with respect to styrene, with Fig. 6 showing a non-linear positive relationship between the ratio of experimental (initial)25 rate constants, (Ln(k)/Ln(k0); k and k0 refer to the reactions of styrene derivative and styrene, respectively) and the ratio of computed free energy barriers for the first metal–ene T.S. (ΔG′′‡{M}/ΔG′‡{M}; superscripts ′′ and ′ refer to the reactions of styrene derivative and styrene, respectively).| Entry | R1 | k (× 10−3)a | Ln(k) /Ln(k0) | ΔG′′‡{M}b/ΔG′‡{M}c |
|---|---|---|---|---|
| DFT calculations were performed17–22 with details as in ESI.†a Experimentally-determined rate constant (s−1) for conversion of styrene.b Free energy barrier relative to the amide K enolate precursor for the reaction of styrene derivative.c Free energy barrier relative to the amide K enolate precursor for the reaction of styrene.d Rate constant obtained from extrapolation of an Arrhenius plot due to impracticality of measuring the rate at 30 °C, see ESI† for details.e 25 mol% of KOtBu was employed.f N,N-Dimethylpropionamide (DMP, 18) was used instead of DMA.g Here, k refers to the reaction of DMP (18) with styrene measured in DMP solvent.h Here, ΔG′′‡ refers to the reaction of DMP (18) with styrene (DMA solvent was assumed) and ΔG′‡ refers to the reaction of DMA (1) with styrene. | ||||
| 1 | 4-BrC6H5(11)d | 22.730 | 0.482 | 0.886 |
| 2 | 4-FC6H5(15) | 1.240 | 0.853 | 1.014 |
| 3 | 2-Naphthyl(14) | 1.040 | 0.876 | 0.953 |
| 4 | Ph(3) | 0.392 (= k0) | 1.000 | 1.000 (= ΔG′‡) |
| 5 | 4-MeC6H5(16)d | 0.135 | 1.136 | 1.055 |
| 6 | 4-MeOC6H5 (17)d | 0.023 | 1.362 | 1.074 |
| 7e | Ph(3) | 0.414 | 1.000 | — |
| 8f | Ph(3) | 6.600 | 0.640g | 0.937h |
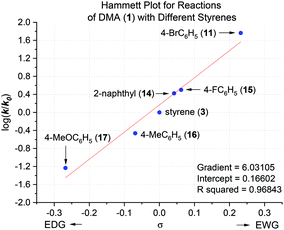
Here, the free energy barriers (ΔG‡, not ΔGrel) are examined on the logical assumption that the initial rates correspond to the formation of the monoadduct and are unaffected by formation of the bisadduct. Fig. 6 identifies the initial metal–ene reaction (T.S.{M}) as a rate-determining step (RDS) for styrene conversion, strengthening the computational mechanistic model. Although a catalytic loading of KOtBu (20 mol%) failed to deliver products under previously-reported ambient air/moisture conditions,5 we confirm catalytic activity under air- and moisture-free conditions herein,26 consistent with previous reports.6,9 In fact, the reaction rate is unchanged (Table 2, entry 7 vs. entry 4). DMP (18) gave a notably faster reaction rate than DMA (1), despite a similar T.S. free energy barrier difference (entry 9 vs. entry 4). The effect of styrene electronics on the rate of reaction was clearly depicted by a linear Hammett plot (Fig. 7),27 demonstrating that all substrates proceed through the same T.S. and follow the same RDS. Notably, the configuration/bond distances of T.S.{M} (Fig. 4) for the reaction of DMA with styrene resemble those previously reported for an analogous intramolecular reaction of an anionic oxime with a pendant styrene.23e
Investigation of cyclic amides
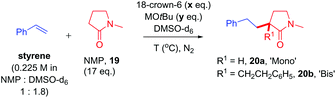
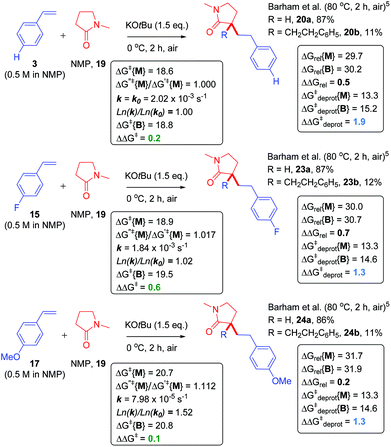
Next, we proceeded to examine the reactions of cyclic amides, such as NMP (19), with styrene as the ‘electrophile’ in DMSO solvent (Fig. 8). Compared to acyclic amides, cyclic amides like 19 give greater conversions over time and lower B/M selectivities (B/M = 20b/20a = 0.13 for 19).5,28 Under similar29 conditions, sarcosine anhydride (21) gave perfect monoadduct (22a) selectivity as previously reported.5 Although the second reaction with styrene could take place at the alternative α-carbon to that of the first reaction, formation of 22a and 22b was assumed for fair computational comparison with 19. The ΔΔGrel (and ΔΔGdeprot) value was more positive for reaction of 21 than reaction of 19. Unfortunately, the reaction of sarcosine anhydride was not amenable to kinetic analysis by 1H NMR under the standard conditions employed herein due to solubility issues. Next, we examined the previously-reported reactions of NMP with styrenes 3, 15 and 17 (Fig. 9).5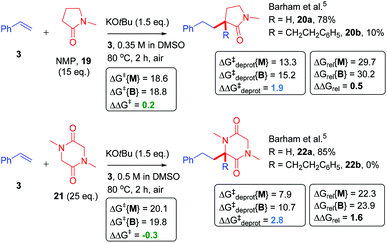 | ||
| Fig. 8 Application of model to cyclic amide CAKES. Deprotonation and metal–ene-type T.S. barriers for monoadduct (ΔG‡deprot{M} and ΔG‡{M}) and bisadduct formation (ΔG‡deprot{B} and ΔG‡{B}) for the reaction of cyclic amides with styrene in DMSO solvent and their previously-reported experimental selectivity.5 DFT calculations were performed17–22 with details as in ESI.† Free energies are given in kcal mol−1. | ||
 | ||
| Fig. 9 Application of model to NMP CAKES with different styrenes. Deprotonation and metal–ene-type T.S. barriers and relative free energies (kcal mol−1) for monoadduct (ΔG‡deprot{M}, ΔG‡{M}, ΔGrel{M}) and bisadduct formation (ΔG‡deprot{B}, ΔG‡{B}, ΔGrel{B}) for the reaction of NMP with various styrenes in DMSO solvent compared with their previously-reported experimental selectivity.5 DFT calculations were performed17–22 with details as in ESI.† Rate constant data was obtained in DMSO-d6 solvent and under N2 atmosphere, see ESI.† ΔG′′‡ and ΔG′‡ refer to reactions of NMP (19) with styrene and styrene derivative, respectively. | ||
As opposed to DMA, the B/M selectivity of NMP's reactions with various styrenes was not influenced by styrene electronics. Computation (assuming DMSO solvent) resulted in a smaller difference in the range of ΔΔGrel values (= 0.2 to 0.7) for all three styrene partners (Fig. 9), compared to that observed for DMA (ΔΔGrel values = 2.3 to 4.2). Interestingly, ΔΔG‡deprot values were very similar, allowing reassurance to directly compare the differences in free energy barriers for mono- vs. bisadduct formation (ΔΔG‡), which were also similar. Kinetic profiles found the reaction of NMP faster than DMA, entirely consistent with a lower ΔG‡{M} for NMP (together with a slightly lower ΔG‡deprot{M} and lower ΔGrel{M}) as found by computation. The free energy barriers for monoadduct formation (ΔG‡{M}) were in the order 3 ≤ 15 ≪ 17 (Fig. 10), entirely consistent with the order of rate constants. The aforementioned relationship between Ln(k)/Ln(k0) and ΔG′′‡{M}/ΔG′‡{M} holds, confirming the overall rate of acyclic amides CAKES is determined by ΔG‡{M}. Counterintuitively, for 3, 15 and 17, the values of ΔΔGrel are smaller for NMP than for DMA, yet NMP gives lower B/M selectivity. Here, ΔΔG‡deprot (which determines the relative concentrations of available reacting amide K enolate and monoadduct K enolate) clearly becomes more influential than ΔΔGrel as substitution increases at the K-enolate. For DMA + styrene (B/M = 0.292), ΔΔG‡deprot = 1.6. For NMP + styrene (B/M = 0.128), ΔΔG‡deprot = 1.9. For DMP + styrene (exclusive monoadduct), ΔΔG‡deprot = 5.1.
 | ||
| Fig. 10 Computed free energy profiles for reactions of NMP (19) with various styrenes. The transition states for reactions of monoadduct K benzylate or bisadduct K benzylate with proton sources are not shown. DFT calculations were performed17–22 with details as in ESI.† | ||
Deuterium labelling investigation
Hartwig et al. highlighted the importance of conducting separate reactions in parallel to draw valid conclusions about KIEs.30 Intramolecular31 or intermolecular32 competition experiments can present ‘false positive’ results that cannot conclusively identify the RDS (or turnover-limiting step).33 Therefore, to further investigate the role of deprotonation in amide CAKES, NMP and NMP-d9 were compared in parallel under conditions demonstrated affording incomplete conversion (10 min at 0 °C gave a 40% yield of 20a) and were quenched after an identical time (Fig. 11A). Quantitative deuteration at the benzylic position confirmed the presence of a benzylic alkylpotassium. The decreased yield of 20a-d9 highlighted the importance of deprotonation at the α-amido position, consistent with the observation of 20a-d8 which likely formed via deprotonation of 20a-d9.34 We then compared reactions of NMP and NMP-d9 in parallel under slightly modified conditions using DMSO-d6 solvent,35 which allowed the reaction progress to be monitored over time by 1H NMR spectroscopy. The initial rates of styrene conversion (kH and kD) were used to determine the KIE (KIE = 2.2).25 This moderate primary KIE identifies one of two possibilities: (1) deprotonation is irreversible and is the RDS or (2) deprotonation is reversible and occurs before the RDS, such that an observed KIE results from an equilibrium isotope effect on that deprotonation step. The latter situation is likely considering the aforementioned (i) pKa difference between HOtBu and amides and (ii) influence of styrene electronics on the reaction rate.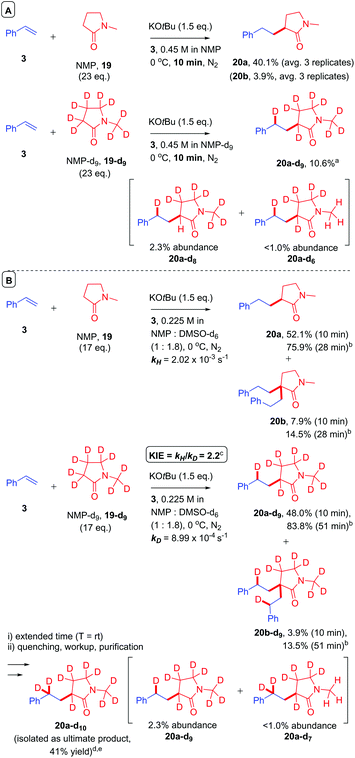 | ||
Fig. 11 Deuterium labelling experiments. Unless otherwise stated, yields were determined by 1H NMR by comparison to 1,3,5-trimethoxybenzene (1.0 eq.) as an internal standard. Structures of deuterated products were established by MALDI and ESI-MS (see ESI†). a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Abundances of partially-deuterated compounds 20a-d8 and 20a-d6 were determined relative to the ionization of 20a-d9 at 100%.36b Abundances of partially-deuterated compounds 20a-d8 and 20a-d6 were determined relative to the ionization of 20a-d9 at 100%.36b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Reaction was deemed complete (<5% styrene) at this time. c Reaction was deemed complete (<5% styrene) at this time. c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KIE was determined based on the conversion of styrene over time and by comparison to 1,3,5-trimethoxybenzene (1.0 eq.) as an internal standard (see ESI†). d KIE was determined based on the conversion of styrene over time and by comparison to 1,3,5-trimethoxybenzene (1.0 eq.) as an internal standard (see ESI†). d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Following 1 h of reaction time at 0 °C the reaction was allowed to warm to rt and product 20a-d10 isolated after extended time (see ESI†). e Following 1 h of reaction time at 0 °C the reaction was allowed to warm to rt and product 20a-d10 isolated after extended time (see ESI†). e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Abundances of partially-deuterated compounds 20a-d9 and 20a-d7 were determined relative to the ionization of 20a-d10 at 100%.36 Abundances of partially-deuterated compounds 20a-d9 and 20a-d7 were determined relative to the ionization of 20a-d10 at 100%.36 | ||
After completion of the reactions by 1H NMR (28 min for NMP + styrene vs. 51 min for NMP-d9 + styrene), the yields and B/M selectivities for each reaction were similar. Although the reaction of NMP-d9 + styrene in DMSO-d6 was essentially complete after 51 min at 0 °C (see ESI†), it was left for extended time at rt prior to quenching. After quenching, workup and purification, the product ultimately isolated from the reaction was 20a-d10 (which contained low abundances of 20a-d9 and 20a-d7 by mass spectrometry, see ESI†). The deuteration of benzylic positions in the presence of KOtBu and deuterium sources (NMP-d9 or DOtBu) is feasible.37
Investigation of base, 18-crown-6, ambient air/moisture conditions and DMSO co-solvent
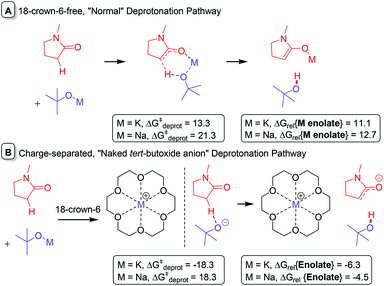
The moderate primary KIE observed is entirely consistent with the fact that C-alkylation reactions of amides with styrenes are dependent on the strength of base employed, with strong sodium/potassium bases such as KHMDS, NaHMDS, KOtBu, KOtAm and KOH all giving successful reactions, while weak potassium bases KF, K2CO3 and weak organic bases DABCO and DBU gave no reaction under the same conditions.5 Under the previously reported conditions (ambient air/moisture), NaOtBu alone led to successful reaction of NMP but 18-crown-6 was required for successful reaction of DMA at 80 °C.5 In addition, 18-crown-6 appeared to increase reactivity of DMA and NMP in the presence of KOtBu (and NaOtBu).5 These observations are consistent with other reports of C-alkylation of weakly-acidic compounds with styrene4,9 showing the rate-enhancing effects of 18-crown-6.We elected to measure the kinetic profiles of reactions of NMP + styrene under different conditions (nature and equivalents of base, 18-crown-6 as an additive, use of ambient air/moisture) by in situ NMR spectroscopy (Table 3). Under the standard (air-and moisture-free) conditions herein, the reaction of NMP proceeded rapidly at 0 °C (entry 1). Use of catalytic (25 mol%) KOtBu ca. halved the reaction rate (entry 3) and gave 20a,38 in stark contrast to reactions of DMA where the same reaction rate was observed for either 25 mol% of 1.5 eq. KOtBu. The reaction was significantly retarded by preparing under ambient air/moisture with non-degassed and non-dried solvents (as supplied), such that 25 °C was required to observe a similar rate constant to the reaction under standard conditions at 0 °C (entry 4 vs. entry 1). In line with the observed KIE, these observations confirm the deprotonation steps in the reaction mechanism (e.g.Fig. 12, pathway A) do influence the overall kinetics of amide CAKES. While styrenes are known as common radical acceptors at the terminal position,39 amide CAKES proceeded successfully in air and in the presence of TEMPO (1 eq.) as reported previously,5 and no radical species were detected by EPR spectroscopy studies herein (see ESI†).
 | ||
| Fig. 12 Pathways for deprotonation of NMP by KOtBu/NaOtBu in absence and presence of 18-crown-6. Free energies are given in kcal mol−1. DFT calculations were performed17–22 with details as in ESI.† | ||
| Entry | Conditions | k (× 10−3)a | ΔG‡deprot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
ΔGrel {Enolate}b |
|---|---|---|---|---|
| DFT calculations were performed17–22 with details as in ESI.†a Experimentally-determined rate constant (s−1) for conversion of styrene.b Free energy ΔGrel or free energy barrier ΔG‡deprot relative to the initial starting materials for the deprotonation of styrene (e.g. amide + 2x styrene + KOtBu for entry 1), see ESI† for further details.c Rate constant determined by extrapolating an Arrhenius plot (see ESI† for details).d The reaction was prepared under ambient air/moisture with non-degassed and non-dried fresh reagents.e For purposes of computation, the 18-crown-6/M+ complex as an innocent bystander and formation of the “naked” amide enolate from tert-butoxide anion and NMP were assumed (see ESI†).f Styrene was fully converted at 0 °C before the first NMR scan (2 min); lower temperatures could not be employed due to reaction mixture freezing. Free energies given in kcal mol−1. | ||||
| 1 | M = K, T = 0, x = 0, y = 1.5 | 2.020 | 13.3 | 11.1 |
| 2 | M = K, T = 30, x = 0, y = 1.5 | 104.976c | — | — |
| 3 | M = K, T = 0, x = 0, y = 0.25 | 1.190 | — | — |
| 4d | M = K, T = 25, x = 0, y = 1.5 | 2.303 | — | — |
| 5e | M = K, T = 0, x = 1.5, y = 1.5 | N/Af | −18.3 | −6.3 |
| 6 | M = Na, T = 80, x = 0, y = 1.5 | 2.750 | 21.3 | 12.7 |
| 7e | M = Na, T = 80, x = 1.5, y = 1.5 | — | 18.3 | −4.5 |
The reaction rate was too fast to measure in the presence of 18-crown-6 (entry 5 vs. entry 1), confirming that 18-crown-6 promotes the reaction. Presumably, sequestering of potassium cation enhances the basicity of the tert-butoxide anion as is previously reported,40 giving rise to a lower barrier for the transition state of deprotonation (Fig. 12, pathway Bvs.A). Computationally, this was found to be the case (entry 5 vs. entry 1); ΔG‡deprot was negative (barrierless) and the combined relative energy of products (ΔGrel{Enolate}) was markedly lower for pathway B, even exothermic. Substitution of KOtBu with NaOtBu significantly retarded the reaction; the use of NaOtBu required 80 °C to observe a comparable rate constant (Table 3, entry 6 vs. entry 1) consistent with a higher ΔG‡deprot. Promotion of the NaOtBu-mediated reaction by 18-crown-6 as disclosed previously5 is rationalized by the reaction of the “naked” tert-butoxide anion with NMP and an 18-crown-6/Na+ complex having a lower ΔG‡deprot (entry 7 vs. entry 6). That an exotherm was observed when KOtBu and 18-crown-6 were mixed in NMP (before styrene addition), but not in the case of NaOtBu, is consistent with ΔGrel values in pathway B. Alternative scenarios, like deprotonation of an 18-crown-6/M cation/NMP complex by “naked” tert-butoxide anion, or deprotonation of NMP by an 18-crown-6/MOtBu complex, were investigated computationally (see ESI†). Although such scenarios cannot be ruled out, the former could not account for the experimentally observed exotherm while the latter gave a T.S. too hindered to be computed.
Rate enhancement in a mechanistic step following the initial deprotonation cannot be ruled out at this stage. While computation of a metal–ene-type T.S. involving co-ordination of 18-crown-6 was too sterically encumbered and led to dissociation, the reversibility of K+/Na+ complexation by 18-crown-6 increases markedly in DMSO/amide-based solvents41 such that solvated K+/Na+ may still be available to construct the metal–ene-type T.S. A non-cyclic, open T.S. in which potassium cation is absent cannot be ruled out (see ESI† and later discussion on 4-alkylpyridine). Nonetheless, a strong argument can be made for rate acceleration via pathway B due to the observed KIE. It is possible that other rate-enhancing additives (LiCl/PMDTA)31,42 used in these types of reactions function via a similar mechanism.
DMSO has been employed as a co-solvent in previous reports of C-alkylations with styrene, allowing the K-enolate precursor substrate loading to be lowered.3,5,7 For the purposes of kinetic NMR studies herein, DMSO-d6 was employed as a co-solvent. Therefore, we desired to probe the role of DMSO-d6. When reactions in DMSO-d6 co-solvent were compared to reactions using the amide substrate (DMA or NMP) as solvent (quenched after a given time), we found higher product yields in the former case.26,38 Elsewhere, it is known that solvation of KOtBu in DMSO increases the basicity of the tert-butoxide anion.43 Deuterated products were not observed in any reactions of non-deuterated DMA or NMP using DMSO-d6 as solvent. Given the similar B/M selectivity with vs. without DMSO solvent (Fig. 11) and previous literature results that have used DMSO/NMP interchangeably,3,5,7 there is no reason to suspect a role for DMSO/dimsyl anion44 in the reaction mechanism beyond promoting base reactivity or stabilizing intermediates/T.S.es.
A general mechanism for C-alkylation with styrenes
Based on the fact that monoadduct and bisadduct products have been observed in other previously reported C-alkylation reactions,3,4 we postulated that the previously-mentioned metal–ene-type mechanism may be a general pathway for this recently trending class of reaction and applied our computational model accordingly. The C-alkylation of cyclohexanone (25) with styrene reported by Knochel gave good selectivity for the monoadduct 26a (60% yield) and some bisadduct 26b (B/M = 0.15),45 whereas the reaction of α-tetralone (27) gave monoadduct 28a (68% yield) and no bisadduct (28b) was reported. In order to confirm whether the bisadduct 28b was formed or not, the reaction of 27 was repeated. In our hands, the reaction gave 28a (85% yield) and 28b (11% yield) as determined by NMR analysis of the crude reaction products by comparison to an internal standard. Thus, a marginally higher selectivity for monoadduct 28a was observed in the reaction of α-tetralone (B/M = 0.13).46 The reactions were then computed according to our model which successfully found metal–ene T.S.es for each reaction. In line with the B/M selectivity difference, α-tetralone gave both a more positive ΔΔGrel than 25 and a more positive ΔΔG‡deprot (Fig. 13). The free energy barriers for the first metal–ene T.S. (ΔG‡{M}) were almost identical for 25 and 27. That ΔG‡deprot{M} was more positive for 27 contrasted with the faster kinetics of 27, revealing a limitation in the current model which could not account for the known acidifying effect of the arene on the α-carbon of the ketone.47 Overall, ketone CAKES seem to follow a similar mechanism to amide CAKES.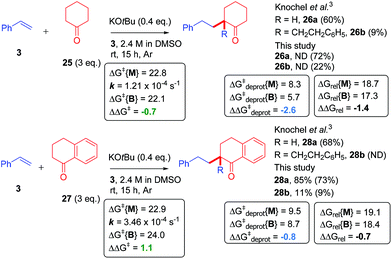 | ||
| Fig. 13 Application of model to ketone CAKES. ND, not determined. Transition state relative free energies (kcal mol−1) for monoadduct (ΔGrel{M}) and bisadduct formation (ΔGrel{B}) for the reaction of cyclic ketones with styrene in DMSO are compared with their previously-reported experimental selectivity.3 DFT calculations were performed17–22 with details as in ESI.† Rate constant data was obtained using DMSO-d6 as solvent, see ESI.† Yields were determined by 1H NMR by comparison to 1,3,5-trimethoxybenzene (1.0 eq.) as an internal standard. Isolated yields are shown in parenthesis. | ||
Finally, the reactions of alkylpyridines with styrene in benzene, as reported by Guan,4 were investigated. Here, the previously-reported4 B/M selectivity shifted drastically when comparing 2-methylpyridine (29) (B/M = 0.28) to 4-methylpyridine (31) (B/M = 1.38). This led Guan to propose an interaction between the pyridyl N atom and the catalyst (KHMDS) facilitated the catalytic C–H alkylation reaction. Herein, computation showed that the potassium cation interacted strongly with the pyridyl N atom as well as the π-system of styrene in the T.S. of the 2-methylpyridine (29) reaction. The consequence of this interaction was a more hindered T.S. in the case of the bisadduct formation. As expected, the ΔΔGrel for 2-methylpyridine reaction was more positive than that of the 4-methylpyridine reaction and accorded with the change in B/M selectivity (Fig. 14). This was reinforced by a more positive ΔΔG‡deprot in the 2-methylpyridine reaction.
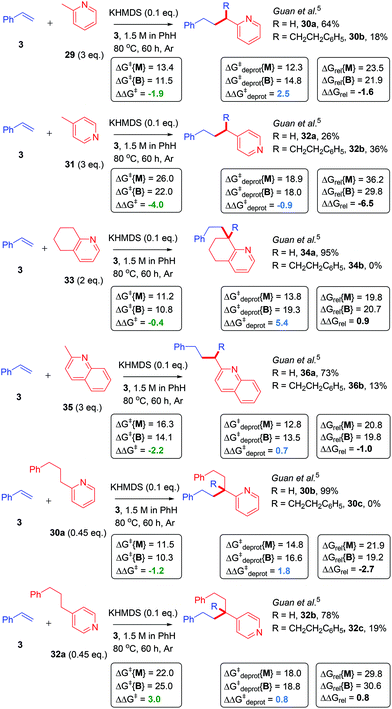 | ||
| Fig. 14 Application of model to alkylpyridine CAKES. Transition state relative free energies for monoadduct (ΔGrel{Mono}) and bisadduct formation (ΔGrel{Bis}) for the reaction of alkylpyridines with styrene in PhH are compared with their previously-reported experimental selectivity.4 DFT calculations were performed17–22 with details as in ESI.† For reactions of 30a and 32a, yields previously reported are based on the alkylpyridine starting material.4 ND, not determined. | ||
A substituted, cyclic 2-alkylpyridine (33) gave perfect monoadduct selectivity,4 in accordance with decreased B/M selectivity observed for cyclic/substituted vs. acyclic/unsubstituted amides (such as DMA vs. NMP observed earlier) and in accordance with both its more positive ΔΔGrel and more positive ΔΔG‡deprot than 29. The reaction of 2-methylquinoline (35), which gave slightly lower B/M selectivity vs.29,4 had a marginally more positive ΔΔGrel value (despite a less positive ΔΔG‡deprot value). The reaction of monoadduct 30a gave exclusively 30b when compared to the reaction of 29, while the B/M selectivity in the reaction of monoadduct 32a decreased (but was not exclusive for 32b) compared to the reaction of 31.4 The latter case could be explained by its more positive ΔΔGrel and ΔΔG‡deprot values compared to 31, while the former case showed a discrepancy between the computation and B/M selectivity, revealing a limitation in the model. Overall, results are consistent with previous observations for amide CAKES (DMA vs. DMP vs. NMP), suggesting that ΔΔGrel tends to govern B/M selectivity for alkylpyridine CAKES where the K-enolate motif is unsubstituted, while ΔΔG‡deprot tends to govern B/M selectivity where the K-enolate motif is substituted/cyclic.
It is noted that the metal–ene-type T.S. proposed herein is geometrically inaccessible for the reaction of 4-alkylpyridine. This reaction must proceed via an open T.S. where the potassium cation is absent (is bound to the pyridine lone pair instead), hence the T.S. suffers a significantly higher free energy barrier ΔG‡. This can be seen when comparing ΔG‡ or ΔGrel values in the reactions of 29vs.31, or 30avs.32a. While the heteroatom-stabilized metal–ene-type T.S. is favored, the open T.S. is accessible at high enough temperatures/with strong enough base.48 A moderate primary KIE (2.7–3.3) was observed by Guan for this KHMDS-catalyzed reaction of alkylpyridines with styrene and it was concluded that the C–H cleavage step was the RDS.4 However, since the reactivity therein similarly was influenced by the electronics of the styrene (this was also reported by Knochel3) and since the moderate primary KIE is similar to that observed herein, it is postulated that the mechanistic picture for alkylpyridine CAKES reflects the scenario of NMP (19) herein: a reversible C–H cleavage step which influences the concentration of reacting alkylpotassium species and is subject to a KIE, followed by a higher energy, rate-determining metal–ene-type transition state.
Based on the results of this study, we propose a general working mechanism for CAKES (Fig. 15). Deprotonation of the enolate precursor by the potassium base proceeds via an equilibrium to generate a low concentration of K enolate. Although K enolates could not be observed previously4 or herein by 1H NMR, we tentatively propose their detection by UV-vis spectroscopy analysis of the colored reaction mixture (see ESI†). This deprotonation step is a minor contributor to the overall rate by controlling the available equilibrium concentration of K enolate and it can be influenced by the choice and loading of base as well as co-ordinating additives. The K enolate then undergoes addition to the styrene via a metal–ene reaction, which is the RDS (major contributor to the overall rate) and the turnover-limiting step. Deprotonation of the in situ-formed conjugate acid by the K benzylate is kinetically favoured, completing the CAKES catalytic cycle. The metal–ene-type reaction involving K enolates is in accordance with expectations from intramolecular magnesium–ene reactions of Grignard reagents (or those of alkyllithium or alkylzinc reagents)49 first reported by Lehmkuhl50 and popularized by Oppolzer51 in the 1980s. To our knowledge, this study confirms the first example of a metal–ene-type reaction involving K enolates.
Conclusions
Base-catalyzed amide CAKES have been studied using a synergistic approach of computation and experimental kinetic studies. A mechanism proceeding through metal–ene-type transition states sufficiently explains experimental selectivity and reactivity (rate) differences when different styrene partners or different amide partners are used. The role of additives 18-crown-6 is rationalized. Computational barriers are accessible at the reaction temperatures employed and agree with rate constants obtained by kinetic data, thus corroborating a pathway proceeding through a benzylic alkylpotassium species. Notably, our mechanistic picture explains the experimental observations in other (ketone and alkylpyridine) CAKES, hence gathering all these reaction classes under the umbrella of a general reaction mechanism. We hope that this study might shed light on related reactivity31,52 in this field. Further investigations are ongoing in our laboratory.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Kazuhiko Yamasaki (AIST, Tsukuba) for assistance and advice on NMR. We thank Mrs Sayaka Nakamura and Prof. Hiroaki Sato (AIST, Tsukuba) for assistance with MALDI-HRMS, ESI MS and MS MS analysis. We thank Dr Yoong-Kee Choe (AIST, Tsukuba) for advice on DFT calculation methods. We thank Mr Masato Yamazoe and Prof. Kazuhiro Morimoto (University of Tsukuba) and Prof. John C. Walton (University of St. Andrews) for assistance with EPR measurements and interpretation of spectra, respectively. We thank Dr Daniel T. Payne (NIMS, Tsukuba) for helpful discussions. J. P. B. is a former JSPS International Research Fellow and is grateful for financial support from JSPS. This work was supported by JSPS KAKENHI Grant Number JP18F19030.Notes and references
- For examples, see: (a) T. Fujita, S. Watanabe, K. Suga and H. Nakayama, Synthesis, 1979, 310–311 CrossRef CAS; (b) H. Pines and N. E. Sartoris, J. Org. Chem., 1969, 34, 2113–2118 CrossRef CAS; (c) X. Wei and R. J. K. Taylor, Chem. Commun., 1996, 187–188 RSC.
- For examples, see: (a) M. Merton, Anionic Polymerisation: Principles and Practice, Academic Press, New York, 1983, pp. 13–85 Search PubMed; (b) R. Waack and M. A. Doran, J. Org. Chem., 1967, 32, 3395–3399 CrossRef CAS.
- (a) A. L. Rodriguez, T. Bunlaksunanusom and P. Knochel, Org. Lett., 2000, 2, 3285–3287 CrossRef CAS PubMed; (b) T. Bunlaksunanusom, A. L. Rodriguez and P. Knochel, Chem. Commun., 2001, 745–746 RSC.
- D. Zhai, X. Zhang, Y. Liu, L. Zheng and B.-T. Guan, Angew. Chem., Int. Ed., 2018, 57, 1650–1653 CrossRef CAS PubMed.
- J. P. Barham, S. Tamaoki, H. Egami, N. Ohneda, T. Okamoto, H. Odajima and Y. Hamashima, Org. Biomol. Chem., 2018, 16, 7568–7573 RSC.
- H. Pines and W. M. Stalick, Tetrahedron Lett., 1968, 34, 3723–3726 CrossRef CAS . For an addition to styrene in the presence of dispersed potassium or sodium, see: H. Pines and N. E. Sartoris, J. Org. Chem., 1969, 34, 2113–2118 CrossRef.
- Styrenes as well as trimethylvinylsilane, butadiene and isoprene can be employed in the case of cyclic alkylamides, see: H. Pines, S. V. Kannan and J. Simonik, J. Org. Chem., 1971, 36, 2311–2315 CrossRef CAS.
- For selected examples, see: (a) W. S. Fones, J. Org. Chem., 1949, 14, 1099–1102 CrossRef CAS; (b) R. P. Woodbury and M. W. Rathke, J. Org. Chem., 1978, 43, 881–884 CrossRef CAS; (c) P. Beak and W. J. Zajdel, J. Am. Chem. Soc., 1984, 106, 1010–1018 CrossRef CAS; (d) P. Beak and W. K. Lee, J. Org. Chem., 1990, 55, 2578–2580 CrossRef CAS; (e) R. K. Dieter, G. Oba, K. R. Chandupatla, C. M. Topping, K. Lu and R. T. Watson, J. Org. Chem., 2004, 69, 3076–3086 CrossRef CAS PubMed; (f) R. B. Lettan II, C. V. Galliford, C. C. Woodward and K. A. Scheidt, J. Am. Chem. Soc., 2009, 131, 8805–8814 CrossRef PubMed.
- Styrenes as well as heteroatom(P, Si and S)-substituted alkenes can be employed in the case of acyclic alkylamides, see: Y. Yamashita, R. Igarashi, H. Suzuki and S. Kobayashi, Org. Biomol. Chem., 2018, 16, 5969–5972 RSC.
- In ref. 4, kinetic isotope effect (KIE) studies were used to infer that the rate determining step of the reaction of 2-methylpyridine with styrene was the initial benzylic C–H deprotonation. The proposed potassium enolate intermediate (potassium picoline) could not be observed when treating 2-methylpyridine with KHMDS only.
- F. G. Bordwell, Acc. Chem. Res., 1988, 21, 456–463 CrossRef CAS.
- F. G. Bordwell, M. Van der Puy and N. R. Vanier, J. Org. Chem., 1976, 41, 1883–1885 CrossRef CAS.
- V. S. Bryantsev, J. Uddin, V. Giordani, W. Walker, D. Addison and G. V. Chase, J. Electrochem. Soc., 2013, 160, A160–A171 CrossRef CAS.
- S. Tabassum, O. Sereda, P. V. G. Reddy and R. Wilhelm, Org. Biomol. Chem., 2009, 7, 4009–4016 RSC.
- F. G. Bordwell, D. Algrim and N. R. Varnier, J. Org. Chem., 1977, 42, 1817–1819 CrossRef CAS.
- For a recent example of similar computational rationalization of the experimental selectivity, see: J. P. Barham, M. P. John and J. A. Murphy, J. Am. Chem. Soc., 2016, 138, 15482–15487 CrossRef CAS PubMed.
- (a) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed; (b) Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef.
- (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS; (b) M. J. Frisch, J. A. People and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS; (c) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS; (d) J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016–5021 CrossRef CAS; (e) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- (a) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS; (b) M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- (a) P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef; (b) W. Kohn and L. Sham, J. Phys. Rev., 1965, 140, A1133–A1138 CrossRef; (c) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukada, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- For recent applications of these DFT theory levels to mechanistic studies, see: (a) G. Hirata and H. Maeda, Org. Lett., 2018, 20, 2853–2856 CrossRef CAS PubMed; (b) J. P. Barham, S. E. Dalton, M. Allison, G. Nocera, A. Young, M. P. John, T. McGuire, S. Campos, T. Tuttle and J. A. Murphy, J. Am. Chem. Soc., 2018, 140, 11510–11518 CrossRef CAS PubMed; (c) A. S.-K. Tsang, A. Kapat and F. Schoenebeck, J. Am. Chem. Soc., 2016, 138, 518–526 CrossRef CAS PubMed; (d) M. Salamone, G. A. DiLabio and M. Bietti, J. Org. Chem., 2011, 76, 6264–6270 CrossRef CAS PubMed; (e) X. Peng, B. M. K. Tong, H. Hirao and S. Chiba, Angew. Chem., Int. Ed., 2014, 53, 1959–1962 CrossRef CAS PubMed.
- Reactions with a 20 kcal mol−1 barrier proceed spontaneously at rt. At 25 °C, a fraction of 2.21 × 10–15 molecules have energies exceeding the activation energy according to the Boltzmann distribution. This translates to reactions with 33.4 kcal mol−1 barriers proceeding spontaneously at 80 °C.
- Data points between at least the first 200–700 s of the reaction were used, depending on the reaction speed. At least 6 data points were used for fitting the initial rates. See ESI for details.†.
- See ref. 5 and ESI therein. Under ambient air/moisture a 20 mol% loading of KOtBu gave almost no reaction of DMA (1) + styrene (1% 6) yet a 60 mol% loading gave near-full conversion to products (71% 6, 16% 10), see ref. 5 (Table S2.1). To confirm that catalytic activity was enabled by absence of ambient air/moisture and not by DMSO-d6 cosolvent (Table 2, entry 7 herein), the reaction of styrene and DMA (1) using 25 mol% KOtBu was repeated in absence of DMSO-d6 and gave 6 (36%) and 10 (12%) upon quenching after 2 h. In presence of DMSO-d6 cosolvent (Table 2, entry 7), the combined products 6 + 10 = ca. 83% after ca. 2 h based on the kinetic plot, see ESI.†.
- Hammett substituent coefficients were assumed based on the corresponding benzoic or naphthoic acids, see: D. H. McDaniel and H. C. Brown, J. Org. Chem., 1958, 23, 420–427 CrossRef CAS.
- This pattern was also observed for the C-alkylation of 2-alkylpyridines in ref. 4, where products ‘3sa’ and ‘3ta’ in that paper resulted from acyclic and cyclic substrates, respectively. Product ‘3ta’ was obtained in higher yield at lower temperature than ‘3sa’.
- Although these previously-reported5 conditions in DMSO solvent (Fig. 8) differ slightly in styrene concentration and equivalents of amide, inviting the thought that greater equivalents of 21 could have given rise to higher B/M selectivity, in fact the reaction of styrene (0.45 M) in NMP solvent gave an identical B/M selectivity (Fig. 9). The similar B/M ratios for reactions with vs. without DMSO (Fig. 11) supports the conclusion that DMSO does not participate in the reaction mechanism.
- E. M. Simmons and J. F. Hartwig, Angew. Chem., Int. Ed., 2012, 51, 3066–3072 CrossRef CAS PubMed.
- I. Sato, Y. Yamashita and S. Kobayashi, Synthesis, 2019, 51, 240–250 CrossRef CAS.
- For an example study showing that an intermolecular competition cannot identify C-H cleavage as the turnover-limiting step, see: L. M. Geary and P. G. Hultin, Eur. J. Org. Chem., 2010, 5563–5573 CrossRef CAS.
- For example studies appropriately selected to identify C–H cleavage as the turnover-limiting step, see: (a) H. Y. Sun, S. I. Gorelsky, D. R. Stuart, L.-C. Campeau and K. Fagnou, J. Org. Chem., 2010, 75, 8180–8189 CrossRef CAS PubMed; (b) Ref. 4 .
- The NMP-d9 supplier's specification of D-incorporation at 99% can account for the 0.8% relative abundance of 20a-d6 but cannot account for the entire 2.3% relative abundance of 20a-d8, which must therefore form under the reaction conditions and may be rationalized by adventitious water present in reagents/solvents/KOtBu. Total water content in NMP-d9 was determined at 3400 ppm (Karl Fischer) by the supplier.
- While D-incorporation at the benzylic position from DMSO-d6 solvent cannot be completely ruled out in Fig. 11B reactions, the NMR spectrum over time showed signals consistent with 20a-h18 only (see ESI†). Benzylic D-incorporation observed in Fig. 11A reactions strongly implicates the NMP-d9 as the source of D.
- The ionization behavior of all deuterated analogues of 20a was assumed to be identical, given their structural similarity.
- J. P. Barham, G. Coulthard, R. G. Kane, N. Delgado, M. P. John and J. A. Murphy, Angew. Chem., Int. Ed., 2016, 55, 4492–4496 CrossRef CAS PubMed.
- To confirm catalytic activity was enabled by absence of ambient air/moisture and not by DMSO-d6 cosolvent (Table 3, entry 3), the reaction of styrene and NMP (19) using 25 mol% KOtBu was repeated in absence of DMSO-d6 and gave 20a (50%) and 10 (3%) upon quenching after 1 h. In presence of DMSO-d6 cosolvent (Table 3, entry 3), the combined products 20a + 20b = ca. 100% after ca. 1 h based on the kinetic plot, see ESI.†.
- (a) G. Moad, E. Rizzardo and D. H. Solomon, Macromolecules, 1982, 15, 909–914 CrossRef CAS; (b) M. Nakajima, Q. Lefebvre and M. Rueping, Chem. Commun., 2014, 50, 3619–3622 RSC.
- For previous reports regarding 18-crown-6 increasing reactivity by complexing potassium cations to generate a more reactive “naked” anion, or insights into the 18-crown-6/KOtBu complex, see: (a) C. L. Liotta and H. P. Harris, J. Am. Chem. Soc., 1974, 96, 2250–2252 CrossRef CAS; (b) F. L. Cook, C. W. Bowers and C. L. Liotta, J. Org. Chem., 1974, 39, 3416–3418 CrossRef CAS; (c) S. Alunni, E. Baciocchi and P. Perucci, J. Org. Chem., 1976, 41, 2636–2638 CrossRef CAS; (d) C. Kleeberg, Z. Anorg. Allg. Chem., 2011, 637, 1790–1794 CrossRef CAS.
- (a) V. P. Solov'ev, N. N. Strakhova, O. A. Raevsky, V. Rudiger and H.-J. Schneider, J. Org. Chem., 1996, 61, 5221–5226 CrossRef; (b) G. Wipff, P. Weiner and P. Kollman, J. Am. Chem. Soc., 1982, 104, 3249–3258 CrossRef CAS.
- Y. Yamashita, K. Minami and S. Kobayashi, Chem. Lett., 2018, 47, 690–692 CrossRef CAS.
- (a) B. G. Chatterjee, R. F. Abdulla and N. L. Nyss, Z. Naturforsch., B: J. Chem. Sci., 2014, 8, 771–773 Search PubMed; (b) P. Venturello and M. Barbero, Sci. Synth., 2006, 8, 1361–1364 Search PubMed.
- For examples of dimsyl anion generation when DMSO is treated with NaOtBu/KOtBu, see: (a) O. Bortolini, G. Fantin, V. Ferretti, M. Fogagnolo, P. P. Giovannini, A. Massi, S. Pacifico and D. Ragno, Adv. Synth. Catal., 2013, 355, 3244–3252 CrossRef CAS; (b) J. P. Barham, G. Coulthard, K. E. Emery, E. Doni, F. Cumine, G. Nocera, M. P. John, L. E. A. Berlouis, T. McGuire, T. Tuttle and J. A. Murphy, J. Am. Chem. Soc., 2016, 138, 7402–7410 CrossRef CAS PubMed; (c) M. E. Budén, J. I. Bardagí, M. Puiatti and R. A. Rossi, J. Org. Chem., 2017, 82, 8325–8333 CrossRef PubMed.
- In ref. 3, cyclohexanone gave a ‘6–11%’ yield of bisadduct; the mean average yield (9%) was assumed for this study.
- Isolated yields of 26a/26b and 28a/28b suffered somewhat due to failure of column chromatography to separate monoadducts from bisadducts and the requirement for multiple GPC purifications. The NMR yields of 26a and 26b could not be determined due to overlapping peaks in the NMR spectrum of crude products; but analysis of the mass spectra of crude reaction products supported the conclusion of a lower B/M ratio in the reaction of 27, see ESI.†.
- F. G. Bordwell and J. A. Harrelson Jr., Can. J. Chem., 1990, 68, 1714–1718 CrossRef CAS.
- A recent report, ref. 31, showed successful addition of potassium benzylate species (generated from alkylarenes by KCH2TMS) to stilbenes and vinylsilanes, but unsuccessful addition to styrenes. Based on the mechanism identified herein for analogous reactions, the co-ordinating heteroatom setting up the metal–ene transition state is unnecessary for reactivity (due to the likely small pKa difference between the initial and final potassium benzylates) but its absence presumably decreases stability of the formed potassium benzylate and promotes oligomerization.
- W. Oppolzer, Angew. Chem., Int. Ed. Engl., 1989, 28, 38–52 CrossRef.
- H. Lehmkuhl and D. Reinehr, J. Organomet. Chem., 1970, 25, C47–C50 CrossRef CAS.
- Selected examples: (a) W. Oppolzer and K. Bättig, Tetrahedron Lett., 1982, 23, 4669–4672 CrossRef CAS; (b) W. Oppolzer and A. F. Cunningham, Tetrahedron Lett., 1986, 27, 5467–5470 CrossRef CAS.
- Y.-F. Liu, L. Zheng, D.-D. Zhai, X.-Y. Zhang and B.-T. Guan, Org. Lett., 2019, 21, 5351–5356 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, key NMR spectra, UV-visible absorption studies, EPR studies, kinetic plots, computational studies and coordinates. See DOI: 10.1039/C9OB02495F |
| This journal is © The Royal Society of Chemistry 2020 |