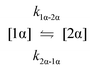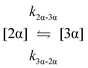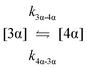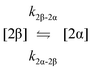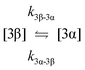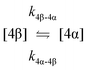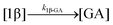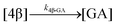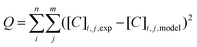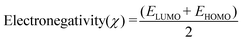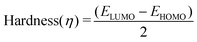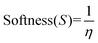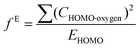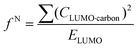Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic modelling of acyl glucuronide and glucoside reactivity and development of structure–property relationships†
Peter R.
Bradshaw
 a,
Selena E.
Richards
a,
Selena E.
Richards
 b,
Ian D.
Wilson
a,
Andrew V.
Stachulski
c,
John C.
Lindon
b,
Ian D.
Wilson
a,
Andrew V.
Stachulski
c,
John C.
Lindon
 a and
Toby J.
Athersuch
a and
Toby J.
Athersuch
 *a
*a
aDepartment of Metabolism, Digestion and Reproduction, Faculty of Medicine, Imperial College London, Sir Alexander Fleming Building, South Kensington, London, SW7 2AZ, UK. E-mail: toby.athersuch@imperial.ac.uk; Tel: +44 (0)20 7594 3806
bDepartment of Chemistry, Khalifa University of Science and Technology, Abu Dhabi, United Arab Emirates
cDepartment of Chemistry, The Robert Robinson Laboratories, University of Liverpool, Liverpool L69 7ZD, UK
First published on 31st January 2020
Abstract
Acyl glucuronide metabolites have been implicated in the toxicity of several carboxylic acid-containing drugs, and the rate of their degradation via intramolecular transacylation and hydrolysis has been associated with the degree of protein adduct formation. Although not yet proven, the formation of protein adducts in vivo – and subsequent downstream effects – has been proposed as a mechanism of toxicity for carboxylic acid-containing xenobiotics capable of forming acyl glucuronides. A structurally-related series of metabolites, the acyl glucosides, have also been shown to undergo similar degradation reactions and consequently the potential to display a similar mode of toxicity. Here we report detailed kinetic models of each transacylation and hydrolysis reaction for a series of phenylacetic acid acyl glucuronides and their analogous acyl glucosides. Differences in reactivity were observed for the individual transacylation steps between the compound series; our findings suggest that the charged carboxylate ion and neutral hydroxyl group in the glucuronide and glucoside conjugates, respectively, are responsible for these differences. The transacylation reaction was modelled using density functional theory and the calculated activation energy for this reaction showed a close correlation with the degradation rate of the 1-β anomer. Comparison of optimised geometries between the two series of conjugates revealed differences in hydrogen bonding which may further explain the differences in reactivity observed. Together, these models may find application in drug discovery for prediction of acyl glucuronide and glucoside metabolite behaviour.
Introduction
The reactivity of the acyl glucuronide conjugates of drugs and other xenobiotics has been studied extensively on account of their potential hepatotoxicity1–4 (as have the corresponding S-acyl-CoA thioesters which are also chemically reactive).5–8 Acyl glucuronides are formed through the conjugation of α-D-glucuronic acid with the carboxylic acid group of a xenobiotic in the presence of membrane-bound UDP-glucuronosyltransferase (UGT) enzymes. The 1-β-O-acyl glucuronides that form can undergo a cascade of spontaneous chemical reactions including acyl migration, anomerisation, and hydrolysis to produce seven further positional anomers: 1-α, 2-α, 2-β, 3-α, 3-β, 4-α, 4-β, the aglycone, and both α- and β-glucuronic acid.9–11 The rates at which these reactions proceed have been shown to be dependent on the aglycone structure,12,13 the pH,14 the composition of the reaction medium,15 and temperature.16 The overall rate of disappearance of the 1-β-O-acyl glucuronide, termed the degradation rate (kd) is a combination of (i) the initial rate of acyl migration from the 1-β to the 2-β anomer and (ii) hydrolysis of the 1-β-O-acyl glucuronide.Glucuronidation is typically considered to be a detoxification process that aids the elimination of xenobiotics from the body, but it is possible for the positional anomers of acyl glucuronides to irreversibly bind to endogenous proteins, a process that is thought to potentiate toxicity.3,15,17,18 It has been proposed that the kd of the 1-β-O-acyl glucuronide is related to the incidence of protein binding, and hence potential toxicity.19 As a consequence, previous studies have attempted to relate glucuronide acyl migration reaction rates to observed in vivo toxicity.20 Despite an apparent correspondence, a direct causal link has yet to be established.
Whilst glucuronides are common metabolites of xenobiotics, there are relatively few well-documented examples of glucose conjugates (glucosides) of xenobiotics in the literature (e.g. see Meech et al. (2012)21). The majority of these are ether glucosides, with the most commonly-reported/observed being ethanol glucoside (a constituent of rice wine and saki) that appears to be excreted unchanged in the urine following dietary exposure.22 Ether glucosides of phenolic drugs (and their metabolites) have also been detected e.g. mycophenolic acid in humans23 and the hydroxylated metabolites of diclofenac in the mouse.24 The formation of acyl glucosides in vitro using microsomal preparations has been reported for several xenobiotics, including (R)- and (S)-ibuprofen,25 pranoprofen26 and the experimental endothelin antagonist Compound A.27 Acyl glucoside metabolites of pranoprofen have also been observed in the mouse.28,29 As we have previously reported,30 acyl glucosides, can also undergo acyl migration, anomerisation, and hydrolysis in a similar way to their acyl glucuronide analogues (Scheme 1).
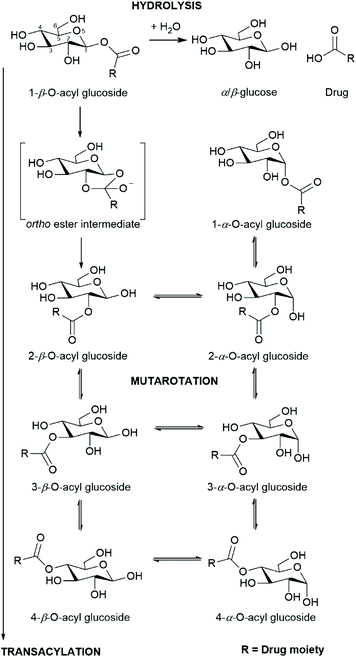 | ||
| Scheme 1 Selected reactions of acyl glucosides: hydrolysis, anomerisation/mutarotation, and transacylation. | ||
On account of their similarity in structure and propensity to undergo transacylation, anomerisation, and hydrolysis, it is reasonable to hypothesise that the acyl glucoside and acyl glucuronide metabolites of a given xenobiotic will display a similar pattern of adduct formation. The rate of transacylation of acyl glucuronides has been linked to the extent of protein adduct formation in vitro and in vivo, with faster kd rates associated with increased adduct formation.31,32 Accordingly, accurate predictive models for the rate of degradation of acyl glucuronides/glucosides may be useful for highlighting drug candidates likely to form protein adducts that may potentiate toxicity.
There are few examples of detailed kinetic models for acyl glucuronide/glucoside degradation in the literature, reflecting the difficulty of obtaining the necessary authentic standards/materials, and the need to monitor multiple interconverting chemical species efficiently and accurately. While the synthetic routes for these two classes of acyl-conjugates are now well established,33–36 detailed kinetic analyses (e.g. derivation of individual reaction rate constants using computer modelling) has been performed for the positional anomers of only a few acyl glucuronides. Several approaches for solving the set of partial differential equations for kinetic modelling have been used to date. Akira et al. (1998)37 and Hasegawa et al. (2001)38 explored the degradation kinetics of ketoprofen and 2-phenylpropionic acid acyl glucuronides using a Runge–Kutta–Gill method and a least-squares estimation using the steepest descent method for analysis. By contrast, Mortensen et al. (2001, 2002)39,40 generated kinetic rate constants from concentration data and a kinetic model solved by the Gepasi program to acquire reaction kinetics for the acyl glucuronide metabolites of both enantiomers of naproxen. Sidelmann et al. (1996)41 used a program called Kinetic to simulate the reaction product profiles using a series of differential equations by a semi-implicit Euler method for 2-fluorobenzoyl acyl glucuronide.
Structure–property relationships have been derived to quantify electronic and steric structural differences of aglycones and their effect on the rate of degradation of the resulting acyl glucuronide conjugates.13,42–44 Empirical and theoretical descriptors such as pKa, partial atomic charges, Hammett constants, Taft steric constants, 1H and 13C NMR chemical shifts have been utilised in models for the prediction of the degradation rate. Similar quantitative models have been developed for the prediction of methyl ester hydrolysis as a proxy for acyl glucuronide degradation.45 In an alternative approach, Berry et al. (2009)9 modelled the transition structure of the transacylation reaction from the 1-β-O-acyl glucuronide to the 2-β-O-acyl glucuronide to predict the rate of degradation of four substituted phenylacetic acid 1-β-O-acyl glucuronides. They observed that the calculated activation energy of the transacylation reaction was highly correlated with the observed in vitro degradation rate. Furthermore, partial atomic charges and the energy of the lowest unoccupied molecular orbital, calculated for the transition structure, showed high correlation with the in vitro kd.9 Whilst progress has been made in the use of structural features/descriptors to predict the rate of degradation of acyl glucuronides, less attention has been paid to their acyl glucoside counterparts.
In this paper, we report the full kinetic modelling of a series of phenylacetic acid acyl glucuronides; these are compared to the previously published glucoside series.30 Using density functional theory (DFT) we have characterised the ground state and transition structures related to the initial transacylation reaction (1-β-O-acyl glucoside to 2-β-O-acyl glucoside) for four phenylacetic acid acyl glucosides; this facilitated direct comparison to the previously-reported glucuronide series.
Experimental
Chemical synthesis and kinetic rate measurement by 1D 1H NMR spectroscopy of 1-β-O-acyl glucuronides and glucosides
Four phenylacetic acid compounds were selected for this study: (i) phenylacetic acid PAA; (ii) (R)-α-methyl phenylacetic acid, (R)-MPA; (iii) (S)-α-methyl phenylacetic acid, (S)-MPA, (iv) α,α′-dimethyl phenylacetic acid DMPA (see ESI† for chemical structures). For each, the 1-β-O-acyl glucuronide and 1-β-O-acyl glucoside conjugates were synthesised using a selective acylation method.9,30 Degradation rates were obtained from Berry et al. (2009) and Iddon et al. (2011). For each series of conjugates the authors used 1D 1H NMR spectroscopy to monitor the intensities of the β-anomeric proton doublet; the logarithms of these intensities were plotted against time, with the slope of the graph providing the kd value. First-order kinetics had been assumed in all cases.Kinetic modelling
The 1D 1H NMR spectra were filtered, smoothed and baseline corrected as previously described.30 Selected assignments of anomeric protons and protons adjacent to the O-acyl group are given in Table 1, and also shown on Fig. 1. In order to derive accurate peak integral areas, each of the peaks in Table 1 was curve-fitted in MATLAB using Peakfit.46 The input parameters for Peakfit were: (i) the 1H NMR spectral profiles and ppm axis; (ii) the chemical shifts of each peak centre (δ, ppm); (iii) the peak width; peak multiplicity, i.e. for a doublet, number of peaks set to 2. The peak shape used for fitting was a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Gaussian and Lorentzian. The number of fitting trials was set to 50. The peak area was calculated using the cumulative trapezoidal rule and was applied to the linear combination of the fitted peaks. The peak areas of selected resonances were measured relative to that of the internal standard (2,2,3,3-trimethylsilylpropanoic acid-d4) TSP-d4 peak (set to unity), providing a relative measure of concentration.
1 mixture of Gaussian and Lorentzian. The number of fitting trials was set to 50. The peak area was calculated using the cumulative trapezoidal rule and was applied to the linear combination of the fitted peaks. The peak areas of selected resonances were measured relative to that of the internal standard (2,2,3,3-trimethylsilylpropanoic acid-d4) TSP-d4 peak (set to unity), providing a relative measure of concentration.
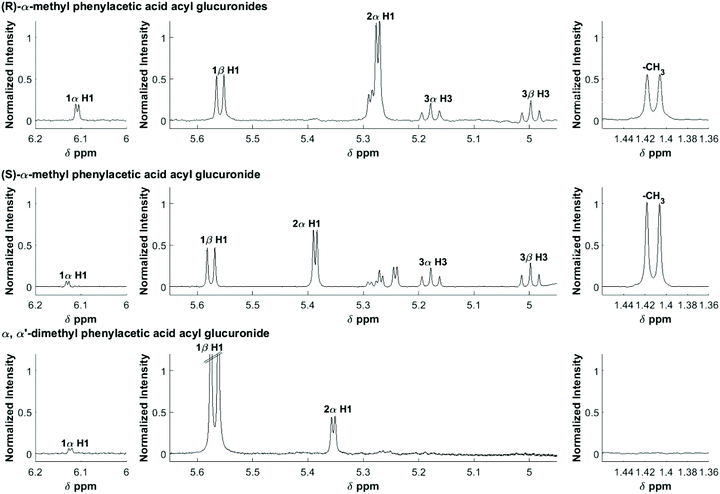 | ||
| Fig. 1 600 MHz 1H NMR spectra of an equilibrium mixture following the degradation of the acyl glucuronides of R-MPA, S-MPA, and DMPA. The assignments are shown for selected protons. | ||
| Positional anomera | Proton | (R)-MPAb | (S)-MPAb | DMPAb |
|---|---|---|---|---|
| a 1-β denotes the 1-β-O-acyl glucuronides, and the other anomers are labelled by analogy. b d (doublet); t (triplet). c Methyl peaks come from both the aglycone and transacylated anomers. d Methyl peaks from DMPA are outside the spectral window. | ||||
| 1-β | H1 | 5.56 (d) | 5.58 (d) | 5.57 (d) |
| 1-α | H1 | 6.11 (d) | 6.13 (d) | 6.12 (d) |
| 2-α | H1 | 5.27 (d) | 5.39 (d) | 5.35 (d) |
| 3-β | H3 | 5.00 (t) | 5.00 (t) | — |
| 3-α | H3 | 5.18 (t) | 5.18 (t) | — |
| Methyl aglyconec | –CH3 | 1.41 (d) | 1.41 (d) | —d |
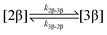
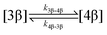
The kinetic models used to describe the acyl migration, anomerisation and hydrolysis reactions of acyl glucuronides of (R)-MPA, (S)-MPA and DMPA are given in Table 2. First order irreversible models were used to describe the first acyl migration and hydrolysis reactions (reactions (1), (10)–(17)) and first order reversible models were used to describe the subsequent acyl migrations and anomerisation reactions (reactions (2)–(9)). The scheme is similar to that shown previously for the acyl glucosides but lacks the 6-O-acyl anomers.
The model predictions were obtained by solving the differential equations:
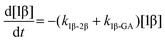 | (1) |
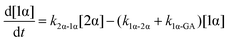 | (2) |
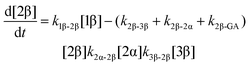 | (3) |
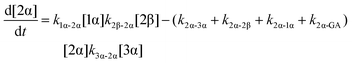 | (4) |
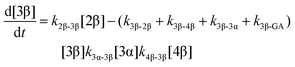 | (5) |
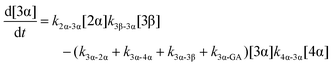 | (6) |
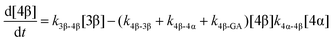 | (7) |
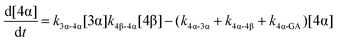 | (8) |
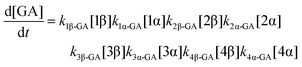 | (9) |
For the parameter estimation the following objective function was minimised:
Modelling of the intramolecular transacylation reaction of acyl glucosides and calculation of molecular descriptors using DFT
The chemical structures of PAA, (R)-MPA, (S)-MPA and DMPA anionic acyl glucosides were generated in GaussView.48 GMMX conformational searches were performed using the Merck Molecular Force Field 94 (MMFF94) with an energy window of 3.5 kcal mol−1 yielding ground state conformers that were subsequently optimised to local minima with the Becke 3-parameter, Lee–Yang–Parr hybrid functional (B3LYP)49–52 with the 6-31G(d,p)53–62 basis set using Gaussian09-D01.63For each optimised conformer, unidimensional relaxed scans were performed with decreasing distance between the alkoxide oxygen and the carbonyl carbon to aid in the discovery of transition structures for the transacylation reaction. Putative transition structures from the results of the scans were optimised using the B3LYP/6-31G(d,p) model chemistry. Harmonic vibrational frequency calculations were performed at the same level of theory to confirm structures were minima (ground states) and transition states. Single point energy calculations for the ground and transition structures were performed using the B3LYP/6-31++G(d,p) model chemistry using the polarisable continuum model (PCM) of solvation to produce comparable energies to Berry et al. (2009).9
Molecular descriptors for the optimised structures were calculated: partial atomic charges were assigned using natural population analysis (NPA) using the Natural Bond Orbital (NBO; version 3.1) program.64 Energies of the highest occupied molecular orbital (EHOMO) and lowest unoccupied molecular orbital (ELUMO) were used to calculate values for electronegativity (χ), hardness (η), electrophilicity (ω) and softness (S)65–68 as follows:
Indices of frontier electron density (Fukui indices) were calculated for the carbonyl carbon and alkoxide oxygen of each glucoside as defined by:
where values for CHOMO·oxygen are the coefficients of the atomic orbital of the alkoxide oxygen in the HOMO and values for CLUMO·carbon are the coefficients of the atomic orbital of the carbonyl carbon in the LUMO. Electron affinity was determined as the electronic energy difference between the acyl glucoside (EN) and the acyl glucoside with an additional electron (EN+1) at the geometry of the EN system:
| A = EN − EN+1 |
Values for the polar surface area and Connolly molecular surface area were calculated using Chem3D v16.0.1.4.
Results and discussion
Kinetic modelling of the transacylation, anomerisation and hydrolysis of acyl glucuronides and glucosides
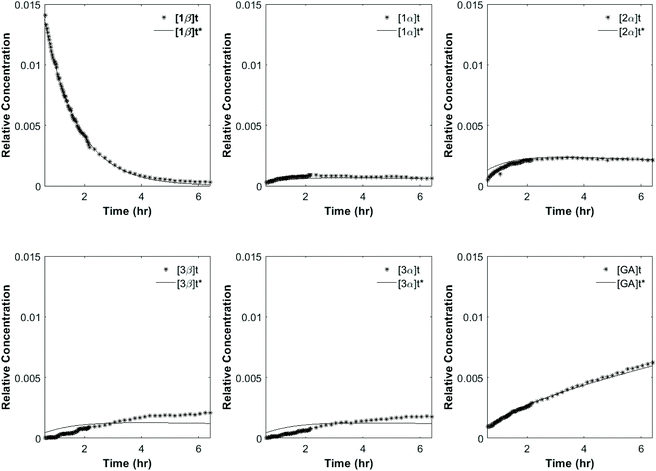
As previously reported,9,30 the glucosides and glucuronides of PAA, (R)-MPA, (S)-MPA, and DMPA acyl were each incubated (37 °C, pH 7.4), and rates of disappearance of the 1-β anomers of the glucoside/glucuronides determined using 1H NMR spectroscopy (Fig. 2). The values for kd and t1/2 for each of the acyl glucosides and glucuronides obtain by Berry et al. (2009) and Iddon et al. (2011) are summarised in Table 3; the unsubstituted PAA acyl glucoside had the fastest t1/2 value of 0.49 h, with (R)-MPA and (S)-MPA (one methyl group at the α-carbon) reacting more slowly, with t1/2 values of 0.89 h and 1.46 h each respectively. DMPA, substituted with two methyl groups at the α-carbon position, had the slowest overall reaction rate, with a t1/2 value of 16 h.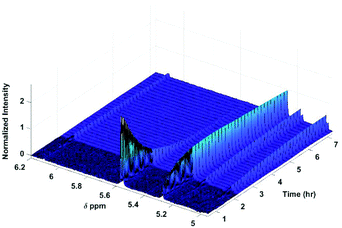 | ||
| Fig. 2 600 MHz 1H NMR spectra of selected protons following the degradation of the acyl glucuronides. Assignments of anomeric protons and protons adjacent to the O-acyl group are given in Table 1. | ||
| Compound | k d (h−1) | t 1/2 (h) | H% | AM% | ΔE | |
|---|---|---|---|---|---|---|
| Acyl glucuronide | PAA | 2.353 | 0.29 | — | — | 5.52 |
| (R)-MPA | 0.903 | 0.78 | 5.6 | 94.4 | 6.16 | |
| (S)-MPA | 0.405 | 1.71 | 11.1 | 88.9 | 6.84 | |
| DMPA | 0.029 | 23.30 | — | — | 9.54 | |
| Acyl glucoside | PAA | 1.419 | 0.49 | 15.0 | 85.0 | 8.53 |
| (R)-MPA | 0.782 | 0.89 | 3.6 | 96.4 | 8.70 | |
| (S)-MPA | 0.476 | 1.46 | 11.8 | 88.2 | 9.82 | |
| DMPA | 0.043 | 16.00 | 5.0 | 95.0 | 11.41 |
The measured kd values for each of these acyl glucosides were largely similar to those previously reported for their corresponding acyl glucuronide analogues; the unsubstituted and mono-methyl substituted compounds having nearly the same t1/2 values, but with a large difference between the t1/2 values of the di-methylated compounds (16 h and 23.3 h for the acyl glucoside and acyl glucuronide, respectively). Some patterns also remained true when comparing the PAA series of acyl glucosides and glucuronides with the ibuprofen acyl glucuronides.69 Thus, as is known for this class of compounds, the unsubstituted and mono-methyl substituted compounds were characterised by relatively fast reaction rates, with the unsubstituted being the fastest, and the (R)- and (S)-compounds having a reaction rate ratio of approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The di-methylated compounds had considerably slower reaction rate half-lives of up to 13 times that of the (S)-α-methyl compounds.
1. The di-methylated compounds had considerably slower reaction rate half-lives of up to 13 times that of the (S)-α-methyl compounds.
The contribution of hydrolysis to the overall reaction was determined by integration of the aglycone or α-glucose peaks and is reported in Table 3 alongside the relative contributions from acyl migration. It can be seen that, in buffer, the acyl migration dominates the overall reaction for both acyl glucosides and acyl glucuronides; hydrolysis accounts for only a small percentage of the overall degradation, unlike observations in plasma where hydrolysis is shown to predominate.70,71
To investigate the reactivity of the acyl glucosides and glucuronides of PAA, (R)-MPA, (S)-MPA, and DMPA in detail, the individual reaction rates of acyl migration and hydrolysis in buffer were calculated based on the kinetic model shown in Scheme 1 and Table 2 using the kinetic simulation program GEPASI. The model assumes that the acyl migration reactions are reversible except for the initial acyl migration and occur between the neighboring glucose/glucuronic acid hydroxyl groups. Fig. 3 shows the curve-fitting of the experimentally-derived data, using the acyl glucuronides of (R)-MPA as an exemplar. The average rate constants for acyl migration and hydrolysis reaction for each acyl glucoside and glucuronide of PAA, (R)-MPA, (S)-MPA, and DMPA are presented in Table 4.
| Acyl glucuronides kd (×102) | Acyl glucosides kd (×102) | |||||||
|---|---|---|---|---|---|---|---|---|
| Reaction | k/h−1 | (R)-MPA | (S)-MPA | DMPA | PAA | (R)-MPA | (S)-MPA | DMPA |
| Acyl migration | k 1β-2β | 81.82 ± 0.07 | 34.78 ± 0.04 | 3.252 ± 0.008 | 141.5 ± 0.0 | 75.1 ± 4.6 | 47.3 ± 1.0 | * |
| Acyl migration | k 2β-3β | 84.1 ± 0.1 | 48.6 ± 0.1 | * | 120.2 ± 0.4 | 80.0 ± 4.3 | 40.3 ± 1.7 | 4.2 ± 0.1 |
| Acyl migration | k 3β-2β | 110.6 ± 0.2 | * | * | 65.8 ± 18.9 | 114.6 ± 18.5 | 46.4 ± 9.7 | * |
| Acyl migration | k 3β-4β | 99.9 ± 0.1 | * | * | 94.5 ± 20.0 | 62.1 ± 13.9 | 99.4 ± 3.4 | 155.0 ± 88.7 |
| Acyl migration | k 4β-3β | 62.4 ± 0.2 | * | * | 17.4 ± 16.4 | 57.3 ± 28.9 | 853.8 ± 136.9 | * |
| Acyl migration | k 1α-2α | 489 ± 3 | 235 ± 1 | 84.2 ± 0.4 | 974.4 ± 88.4 | 667.9 ± 107.6 | 935.0 ± 167.2 | * |
| Acyl migration | k 2α-1α | 149.8 ± 0.6 | 22.01 ± 0.07 | 9.47 ± 0.04 | 153.4 ± 15.4 | 173.7 ± 17.0 | 134.3 ± 11.5 | * |
| Acyl migration | k 2α-3α | * | 8.06 ± 0.04 | 35.1± 0.2 | 64.7 ± 3.8 | 36.2 ± 6.2 | 12.4 ± 4.9 | * |
| Acyl migration | k 3α-2α | 545 ± 2 | 17.6 ± 0.1 | 85.6 ± 0.5 | 48.8 ± 17.9 | 51.8 ± 12.1 | * | * |
| Acyl migration | k 3α-4α | * | * | * | 70.1 ± 20.3 | 65.3 ± 16.9 | 22.3 ± 1.5 | * |
| Acyl migration | k 4α-3α | * | 49.6 ± 0.1 | * | 58.3 ± 52.4 | * | * | * |
| Hydrolysis | k 1β-GA | 7.86 ± 0.04 | 9.25 ± 0.04 | * | 4.6 ± 3.1 | 3.9 ± 0.4 | 6.0 ± 0.1 | |
| Hydrolysis | k 2β-GA | * | 52.8± 0.3 | * | ||||
| Hydrolysis | k 3β-GA | * | * | * | ||||
| Hydrolysis | k 4β-GA | * | * | * | ||||
| Hydrolysis | k 1α-GA | * | * | * | * | 53.2 ± 10.8 | 88.9 ± 6.8 | |
| Hydrolysis | k 2α-GA | * | * | * | ||||
| Hydrolysis | k 3α-GA | * | * | * | ||||
| Hydrolysis | k 4α-GA | 32.8 ± 0.2 | * | * | ||||
Comparing the average rate constants of the acyl glucuronides with the analogues acyl glucoside compounds, shows the same trend in the reactivity of the compounds. The unsubstituted compound has the fastest reaction rates, followed by the mono-methyl substituted compounds, which have a reaction ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The di-methylated compounds have the slowest reaction rates. Furthermore, the full kinetic analysis of the acyl glucuronides series (as with the acyl glucoside series30) shows excellent agreement with the simple degradation rates where both transacylation and hydrolysis are modelled. For example, the combined (R)-MPA 1-β → 2-β transacylation and the hydrolysis of 1-β anomer; the rate constant is 0.90 h−1 from the simple degradation measurements and 0.90 h−1 by combining the rate constants from the detailed kinetic modelling. In the (S)-MPA series the rate constant for the aforementioned reactions are 0.41 h−1 and 0.44 h−1 respectively (see Tables 3 and 4).
1. The di-methylated compounds have the slowest reaction rates. Furthermore, the full kinetic analysis of the acyl glucuronides series (as with the acyl glucoside series30) shows excellent agreement with the simple degradation rates where both transacylation and hydrolysis are modelled. For example, the combined (R)-MPA 1-β → 2-β transacylation and the hydrolysis of 1-β anomer; the rate constant is 0.90 h−1 from the simple degradation measurements and 0.90 h−1 by combining the rate constants from the detailed kinetic modelling. In the (S)-MPA series the rate constant for the aforementioned reactions are 0.41 h−1 and 0.44 h−1 respectively (see Tables 3 and 4).
Comparison of the degradation rate constant of 1-β for the fastest-reacting compounds using both simple measured values and the full kinetic model (1-β → 2-β and 1-β → GA) shows (R)-MPA acyl glucuronide reacts faster than (R)-MPA acyl glucoside. It has been implied that the presence of the carboxylate function in the glucuronides increases the reactivity.30 The reverse was observed for the degradation rate constant of 1-β from both simple measured values and the full kinetic model (1-β → 2-β and 1β → GA) of (S)-MPA and DMPA. In these cases, the glucuronides have the slower degradation kinetics. It has been suggested that the carbohydrate structural effect is subtle and is less than that caused by relatively small changes in the aglycone.30
For each transacylation step (reactions (1)–(6), Table 2), the average rate constants calculated from the full kinetic analysis for (R)-MPA acyl glucuronides were generally higher than the (R)-MPA acyl glucosides. The reverse was true for (S)-MPA, where for each transacylation step, the average rate constants calculated from the full kinetic analysis for the acyl glucuronide were generally slower than the acyl glucoside. No comparison could be made for DMPA as most kd values had large uncertainties in their determination. The 1-α anomers of both acyl glucuronides and acyl glucosides all showed rapid reactions rates, faster than their corresponding 1-β anomers. This has been attributed to the exo-anomeric effect and the favorable cis-ring fusion in the transition state and the expulsion of a better leaving group.30 However, 1-α acyl glucuronides showed slower average rates than their equivalent 1-α glucosides. The calculation of the rate constants for hydrolysis is based on the changes in intensities of the methyl peaks which were attributed to the aglycone as a first approximation. It is known that the final equilibrium reaction mixture also contained some transacylated anomers so the hydrolysis rate constants will be subject to some error and that is reflected in the large uncertainty of the derived values. The interpretation of the hydrolysis rates is outside the scope of this study which is concerned with glucoside/glucuronide transacylation kinetics.
From the measured degradation kinetics, the acyl glucosides and glucuronides of the same model compounds had the same degradation rate half-lives for unsubstituted and mono-methyl substituted α-carbons. It was demonstrated from both the full kinetic model and the measured degradation rates, that the reaction for the acyl glucoside with 2 methyl groups at the α-carbon was much faster than that of the equivalent glucuronide. The diastereoisomers for the acyl glucosides and glucuronides both have a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction rate ratio as seen for all (R)- and (S)-arylpropionic acid acyl glucuronides;40,69,72–74 therefore the reaction rate must be dependent on the stereochemistry as they are both electronically equivalent.
1 reaction rate ratio as seen for all (R)- and (S)-arylpropionic acid acyl glucuronides;40,69,72–74 therefore the reaction rate must be dependent on the stereochemistry as they are both electronically equivalent.
Modelling of the intramolecular transacylation reaction of acyl glucosides
Transition structures for the intramolecular transacylation reaction of the series of phenylacetic acid acyl glucuronides derivatives has been studied previously using DFT.9 In the present work, a similar DFT approach has been utilised, modelling the initial transacylation reaction from 1-β-O-acyl glucoside through the ortho ester intermediate (transition structure) to the 2-β-O-acyl glucoside for the four phenylacetic acid acyl glucosides (Scheme 1). This allowed the molecular properties of these acyl glucosides to be investigated in relation to their differential rates of degradation, permitting a comparison to similar analyses previously performed for acyl glucuronide degradation under the same conditions.The series of 1-β-O-acyl glucosides were generated in silico and conformational searches were performed using the GMMX software; six ground states (GS) were identified from the GMMX search for PAA. Unidimensional scans were performed on each optimised ground state in Gaussian with decreasing distance between the alkoxide oxygen and carbonyl carbon; optimisation of the putative transition structures from the scans resulted in three transition structures (TS) for PAA. Similar conformational searches and unidimensional scans were performed for (R)-MPA, (S)-MPA and DMPA. Five GS and three TS were found for both (R)- and (S)-MPA and ten GS and six TS for DMPA. Cartesian coordinates of the lowest energy GS and TS for each acyl glucoside are included in the ESI.†
As described by Berry et al. (2009),9 as the transacylation reaction of the acyl glucuronides proceeds, the distance between the alkoxide oxygen and carbonyl carbon decreases (distance a) and the bond between the carbonyl carbon and oxygen elongates (distance b). For PAA acyl glucuronide, distance a decreased from 3.69–4.78 Å to 1.82–2.27 Å and distance b increased from 1.32–1.34 Å to 1.38–1.46 Å.9 In the present study, similar changes were observed when moving from the acyl glucoside ground states to the transition structures. Thus, for the PAA acyl glucoside distance a, decreased from 3.35–4.18 Å to 1.76–1.87 Å. However, a much smaller elongation of distance b was observed for the acyl glucoside of PAA compared to the equivalent acyl glucuronide, from 1.21 Å to 1.22 Å. Similar changes in distance a and b were observed for (R)-MPA, (S)-MPA and DMPA (see ESI† for details). The improper torsion angle between the oxygen on carbon 1 of the pyranose ring, the carbonyl carbon, carbonyl oxygen and α carbon was measured for the ground and transition structures for each acyl glucoside. Moving from the ground state to the transition structure, the carbonyl carbon is bent out of the trigonal planar conformation, as observed by the decrease in the angle when moving from the ground states (PAA 177.47°, (R)-MPA 178.00°, (S)-MPA 178.91°, DMPA 179.40°) to the transition structures (PAA 128.84°, (R)-MPA 134.92°, (S)-MPA 135.91°, DMPA 127.82°) for each acyl glucoside.
Activation energies (ΔE) for the transacylation reaction were calculated for each transition structure at the B3LYP/6-31++G(d,p) level of theory, and the lowest energy TS for each acyl glucoside was identified as PAA 8.53 kcal mol−1, (R)-MPA 8.70 kcal mol−1, (S)-MPA 9.82 kcal mol−1 and DMPA 11.41 kcal mol−1. Linear regression of the ΔE (kcal mol−1) of the lowest energy TS for each acyl glucoside against the logarithm of the degradation rate (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd) showed a close negative correlation with the log
kd) showed a close negative correlation with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd (r2 = 0.95). In Table 3 a comparison of the ΔE calculated in the present study for acyl glucosides at the B3LYP/6-31++G(d,p) level of theory and the ΔE for the acyl glucuronide calculated previously9 at the same level of theory is provided. The closer orientation of the alkoxide oxygen to the carbonyl carbon (distance a) of the acyl glucosides compared to the equivalent acyl glucuronides resulted in a higher ΔE of transacylation for these compounds. As noted by Iddon et al. (2011)30 and discussed above, the degradation constants of the two series are not linearly related, as the degradation of the PAA and (R)-MPA acyl glucosides proceeded more slowly than the degradation of the equivalent acyl glucuronides. Whereas, the degradation of the acyl glucosides of (S)-MPA and DMPA occurred more rapidly than seen for the respective acyl glucuronides (Table 3). Although the calculated ΔE can account for the differences in degradation rates across the acyl glucoside and acyl glucuronide series separately, it does not explain this non-linear relationship between the degradation of the equivalent acyl glucuronides and glucosides.
kd (r2 = 0.95). In Table 3 a comparison of the ΔE calculated in the present study for acyl glucosides at the B3LYP/6-31++G(d,p) level of theory and the ΔE for the acyl glucuronide calculated previously9 at the same level of theory is provided. The closer orientation of the alkoxide oxygen to the carbonyl carbon (distance a) of the acyl glucosides compared to the equivalent acyl glucuronides resulted in a higher ΔE of transacylation for these compounds. As noted by Iddon et al. (2011)30 and discussed above, the degradation constants of the two series are not linearly related, as the degradation of the PAA and (R)-MPA acyl glucosides proceeded more slowly than the degradation of the equivalent acyl glucuronides. Whereas, the degradation of the acyl glucosides of (S)-MPA and DMPA occurred more rapidly than seen for the respective acyl glucuronides (Table 3). Although the calculated ΔE can account for the differences in degradation rates across the acyl glucoside and acyl glucuronide series separately, it does not explain this non-linear relationship between the degradation of the equivalent acyl glucuronides and glucosides.
Berry et al., (2009)9 described the conformations of the major TS for each acyl glucuronide, the most favourable conformers for both of the PAA and (R)-MPA acyl glucuronides were found to have the carbonyl oxygen pointing “up” whereas for (S)-MPA and DMPA the oxygen faced “down”. The differences in structure were rationalised as the equivalent structures for (S)-MPA and DMPA, with the oxygen atom facing “up”, would result in an unfavourable orientation, with the bulky methyl group close to the axial hydrogen on carbon 1 of the pyranose ring9 (refer to Scheme 1 1-β-O-acyl anomer for atom numbering). Here, we have described similar observations for the acyl glucosides, with the carbonyl oxygen atom pointing “down” for (S)-MPA and DMPA (Fig. 4). The oxygen atom in the (R)-MPA acyl glucoside also faced “up” as was observed for the acyl glucuronide of (R)-MPA, however the carbonyl oxygen faced “down” for PAA acyl glucoside in contrast for the most favourable TS of the acyl glucuronide of PAA (Fig. 4). PAA TS 1 and TS 2 have similar structures with the aromatic ring in the plane with the pyranose ring (Fig. 5), changing the oxygen atom from facing “down” to “up” results in a small increase in the activation energy of 0.88 kcal mol−1. In the absence of an α-methyl substitution the structural configuration with the oxygen atom facing “down” does not lead to a large increase in activation energy as observed with (S)-MPA and DMPA.
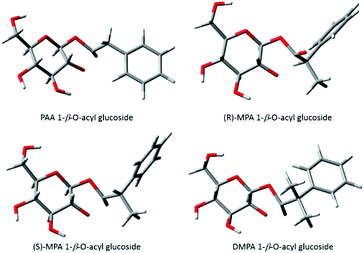 | ||
| Fig. 4 Lowest energy conformations of transition structures of the transacylation reaction for phenylacetic acid acyl glucosides. | ||
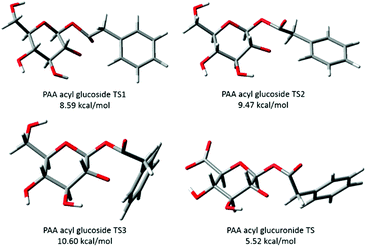 | ||
| Fig. 5 Transition structures of phenylacetic acid (PAA) 1-β-O-acyl glucoside and 1-β-O-acyl glucuronide. Activation energies calculated at the B3LYP/6-31++G(d,p) level of theory. Acyl glucuronide output obtained from the ESI† of Berry et al. (2009)9 and generated in GaussView. | ||
For the acyl glucuronides the axial hydrogen at carbon 1 of the pyranose ring was found to be in close proximity to the hydrogen of the α carbon of the aglycone for PAA (2.12 Å) and (R)-MPA (2.14 Å).9 This distance was larger for the acyl glucosides, at 2.50 Å for (R)-MPA and 2.96 Å for the second TS of PAA (with the carbonyl oxygen pointing “up”). For (S)-MPA and DMPA, the distance between the carbonyl oxygen and axial hydrogen carbon 1 was also larger for the acyl glucoside compared to the glucuronides. This distance increased from 2.66 Å and 2.74 Å for the acyl glucuronides of (S)-MPA and DMPA, respectively, to 2.86 Å and 2.82 Å for the equivalent acyl glucoside.
Fig. 5 also shows the lowest energy TS of the PAA acyl glucuronide generated in GaussView using the optimised Cartesian coordinates output provided by Berry et al. (2009).9 As indicated, a hydrogen bond between the hydroxyl hydrogen on carbon 4 and the carboxylate side chain is observed for the acyl glucuronide. Whereas, the neutral alcohol side chain and hydroxyl hydrogen on carbon 4 face away from each other in the acyl glucosides. This intramolecular hydrogen bonding was observed for the four lowest energy TS of the acyl glucuronide and was absent in the equivalent acyl glucosides. Generation of the lowest energy TS structures of the series of acyl glucuronides from the outputs provided previously9 in GaussView allowed the measurement of this hydrogen bond. The hydrogen bond was found to be 1.65 Å for the acyl glucuronides of PAA, (R)-MPA, and DMPA, and 1.66 Å for (S)-MPA. The alcohol side chain of the acyl glucosides participated in hydrogen bonding with oxygen 5 of the pyranose ring, with bond lengths of 2.13 Å for PAA and 2.14 Å for the (R)-MPA, (S)-MPA and DMPA acyl glucosides. The stronger intramolecular hydrogen bonding observed in the acyl glucuronide metabolites may stabilise the TS leading to a lower activation energy than for the equivalent acyl glucosides.
Johnson et al. (2007)69 investigated the rate of degradation of analogues of ibuprofen acyl glucuronides. Esterification of the carboxylate side chain of the glucuronic acid decreased the rate of degradation by a factor 2 and 3, for the ethyl and allyl ester derivatives, respectively, compared to the rate of ibuprofen acyl glucuronide degradation. The authors hypothesised that the increased stability of the ester derivatives of ibuprofen may be due to long range electronic effects or intermolecular general base catalysis,69 further suggesting that the intermolecular general base catalysis was inhibited following esterification of the carboxylate ion. Notwithstanding the possible role of the intermolecular catalysis mechanism, the results presented here suggest the change in rate of degradation may potentially be due to esterification weakening the hydrogen bond between the carboxylate side chain and hydroxyl hydrogen on carbon 4. Such an effect could lead to a higher activation energy for the formation of the transition structure, and a slower rate of degradation. Further in silico investigations of the side chain in these ester derivatives compared with acyl glucuronides and glucosides could further illuminate the role that the side chain of the pyranose ring has on degradation.
Examination of molecular descriptors of acyl glucosides
A range of descriptors were calculated for the ground state and transition structures for the series of acyl glucosides to help rationalise the difference in degradation rates across the series. Linear regression of each descriptor with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd was performed and the coefficients and error terms for each descriptor are shown in Tables 5 and 6. For the GS, the electron affinity was shown to have good correlation (R2 = 0.92) with the rate of degradation and the equation for this descriptor is shown in Table 5. Electron affinity decreased across the series with increasing stability of the acyl glucoside conjugate.
kd was performed and the coefficients and error terms for each descriptor are shown in Tables 5 and 6. For the GS, the electron affinity was shown to have good correlation (R2 = 0.92) with the rate of degradation and the equation for this descriptor is shown in Table 5. Electron affinity decreased across the series with increasing stability of the acyl glucoside conjugate.
| Ground states | ||||
|---|---|---|---|---|
| Property | Coefficient | Standard error | p-Value | R 2 |
| PAC – partial atomic charge determined using natural population analysis.a Calculated EHOMO values were constant across the series of acyl glucosides. | ||||
| Acyl oxygenPAC | 65.731 | 41.144 | 0.25 | 0.56 |
| Carbonyl carbonPAC | −219.158 | 104.965 | 0.17 | 0.69 |
| Carbonyl oxygenPAC | −44.363 | 43.884 | 0.42 | 0.34 |
| Alkoxide oxygenPAC | 26.526 | 373.870 | 0.95 | 0.00 |
| E HOMO | N/Aa | N/A | N/A | N/A |
| E LUMO | 177.778 | 241.154 | 0.54 | 0.21 |
| ΔEHOMO–ELUMO | 177.778 | 241.154 | 0.54 | 0.21 |
| Electron affinity (A) | 0.057 | 0.012 | 0.04 | 0.92 |
| χ | 355.556 | 482.309 | 0.54 | 0.21 |
| η | 355.556 | 482.309 | 0.54 | 0.21 |
| ω | −170.748 | 227.565 | 0.53 | 0.22 |
| S | −2.807 | 3.833 | 0.54 | 0.21 |
| f N | 0.060 | 0.048 | 0.34 | 0.44 |
| f E | 90.542 | 94.957 | 0.44 | 0.31 |
| PSA/CMSA | 37.011 | 19.061 | 0.19 | 0.65 |
| Electron affinity | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd = 0.057A–5.197 kd = 0.057A–5.197 |
|||
| Transition structures | ||||
|---|---|---|---|---|
| Property | Coefficient | Standard error | p-Value | R 2 |
| PAC – partial atomic charge determined using natural population analysis. | ||||
| Acyl oxygenPAC | 19.132 | 14.180 | 0.31 | 0.48 |
| Carbonyl carbonPAC | −147.293 | 73.397 | 0.18 | 0.67 |
| Carbonyl oxygenPAC | 49.565 | 24.423 | 0.18 | 0.67 |
| Alkoxide oxygenPAC | −26.887 | 11.237 | 0.14 | 0.74 |
| E HOMO | −94.303 | 149.824 | 0.59 | 0.17 |
| E LUMO | −357.371 | 110.516 | 0.08 | 0.84 |
| ΔEHOMO–ELUMO | −27.345 | 150.216 | 0.87 | 0.02 |
| Activation energy | −0.490 | 0.078 | 0.02 | 0.95 |
| Electron affinity (A) | 0.020 | 0.027 | 0.53 | 0.22 |
| χ | −287.421 | 169.588 | 0.23 | 0.59 |
| η | −54.690 | 300.523 | 0.87 | 0.02 |
| ω | 364.716 | 88.785 | 0.05 | 0.89 |
| S | 0.597 | 3.290 | 0.87 | 0.02 |
| f N | 0.011 | 0.006 | 0.18 | 0.67 |
| f E | −1.372 | 2.368 | 0.62 | 0.14 |
| PSA/CMSA | 45.164 | 16.224 | 0.11 | 0.79 |
| Activation energy | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd = −0.490ΔE + 4.301 kd = −0.490ΔE + 4.301 |
|||
| E LUMO | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd = −357.371ELUMO − 5.146 kd = −357.371ELUMO − 5.146 |
|||
| Electrophilicity | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd = 364.716ω − 24.747 kd = 364.716ω − 24.747 |
|||
A larger number of descriptors for the TS (Table 6) showed good correlation with the rate of degradation compared to the GS; including the ELUMO (R2 = 0.84), electrophilicity index (R2 = 0.89), and activation energy (R2 = 0.95). The equations for these three descriptors are shown in Table 6. As ELUMO increased the rate of degradation slowed (increased stability), whereas the electrophilicity index of the acyl glucoside increased with faster rates of degradation as observed for electron affinity with the ground states. Parr et al. (1999)68 defined electrophilicity (ω) as a function of both the chemical potential (μ) of a species and its hardness (η), ω = μ2/2η. Using the Kohn–Sham analogue of Koopmans theorem for DFT, the chemical potential, hardness, and electrophilicity of a species can be defined from the energies of the frontier molecular orbitals (ELUMO and EHOMO).65,66,68,75 The electron affinity, ELUMO and electrophilicity are related terms that define the capacity of a species to accept electrons (a single electron in the case of affinity).68 As the transacylation and hydrolysis reactions of the acyl glucosides (degradation rate) both occur through nucleophilic attack on the carbonyl carbon (carbon accepting electrons), it is therefore expected that these descriptors would rationalise the observed differences. The electrophilicity index is a measure of the “electrophilic power” of a ligand and therefore the increasing value seen for the index with faster rates of degradation is to be expected. The unsubstituted PAA is a better electrophile than the methyl-substituted analogues, and therefore more readily undergoes nucleophilic reactions.
Previously, good correlation of the ELUMO (r2 = 0.90) was observed with the rate of acyl glucuronide degradation, whereas electrophilicity index showed poor correlation.9 Whilst these results are indicative, further computational investigations using data derived from a larger series of acyl glucuronides and acyl glucosides, would confirm the utility of these electronic descriptors to predict the rate of degradation.
This study highlights a potential role that acyl glucosides may play in the toxicology of carboxylic acid containing compounds and merits further investigation. Whilst acyl glucoside conjugates are minor metabolites (based on the current literature) the transacylation/hydrolysis kinetics observed compare well to those of the corresponding acyl glucuronides. It is currently unknown whether such acyl glucosides form protein adducts in vitro or in vivo, but it seems highly probable that they will, and therefore future investigations will be needed to examine their alkylating capacity. The in vitro data on which the kinetic and DFT modelling was performed were measured in aqueous buffer. This allows rapid, and facile, measurement of kd values and direct calculation of the amount of non-enzymatic hydrolysis and transacylation, making it well suited to screening in discovery/early development. Clearly, assuming that the model is accurate, much of this screening could now be done in silico prior to any synthesis and this, combined with our existing understanding of the QSAR of the transacylation/hydrolysis of glucuronides/glucosides, could be used to guide the selection of compounds for future medicinal chemistry. As is the case for all in vitro/in silico models, the in vivo kinetics of the acyl glucuronides and glucosides are much more complex and would still need to be determined. However, the advantages of being able to remove obviously poor candidates from consideration, based on their calculated reactivity are clear.
Conclusions
In this paper we have completed full kinetic analysis on a series of acyl glucuronide compounds; including (R)- and (S)-α methyl phenylacetic acid and α,α′-dimethyl phenylacetic acid acyl glucuronides and compared the average rate constants for each transacylation and hydrolysis step to the equivalent acyl glucoside compounds reported previously.30 The full kinetic analysis showed excellent agreement with the simple degradation rates of 1-β anomer where both transacylation (1-β → 2-β) and hydrolysis (1-β → GA) were modelled. Comparison of the average rate constants for each transacylation step revealed fastest-reacting compounds from the acyl glucuronide series had higher rates compared to the analogous acyl glucoside compounds. This trend was reversed for slower reacting compounds. The 1-α anomers of both the acyl glucuronide and glucoside series all showed rapid reaction rates, faster than their 1-β anomers. This was attributed to exo-anomeric effects and the favourable cis-ring fusion in the transition state and the expulsion of a better leaving group.30 Differences in the reactivity of the acyl glucuronide and glucoside series has been attributed to the presence of the carboxylate function in the acyl glucuronide compounds which causes the overall reactivity to increase for the fast reacting compounds, but to slow down for the slower reacting compounds. This would cause an increase in transacylation but have no effect on hydrolysis, implying a steric effect – as opposed to electronic effect in the reaction rate.30The intramolecular transacylation reaction of the series of phenylacetic acid acyl glucosides were modelled using DFT, as previously performed for the equivalent acyl glucuronides. Along with the identification of the transition structures of this reaction, a range of molecular descriptors for the ground and transition structures were calculated to rationalise the difference in reactivity across the series of acyl glucosides. The conformations of the acyl glucosides were found to be largely similar to the acyl glucuronides but differed due to their intramolecular hydrogen bonding. The charged carboxylate ion of the glucuronic acid formed a strong hydrogen bond with the hydroxyl hydrogen on carbon 4. In contrast, the acyl glucoside formed weaker hydrogen bonds between the alcohol side chain of the glucose molecule and oxygen 5 of the glucose ring. The stronger hydrogen bonding observed in the acyl glucuronides likely accounts for the lower activation energy of the acyl glucuronides calculated previously compared to the activation energy of the acyl glucosides calculated in the present study. The electron affinity of the ground states and the calculated activation energy, ELUMO and electrophilicity index of the lowest energy transition structures of the acyl glucoside series showed great correlation with the rate of degradation and maybe useful for predicting the rate of degradation of future drug candidate metabolites.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Medical Research Council (MRC) is acknowledged for funding P.R.B via a MRC-Integrative Toxicology Training Partnership (ITTP) PhD studentship.References
- S. L. Regan, J. L. Maggs, T. G. Hammond, C. Lambert, D. P. Williams and B. K. Park, Biopharm. Drug Dispos., 2010, 31, 367–395 CrossRef CAS PubMed.
- T. R. Van Vleet, H. Liu, A. Lee and E. A. G. Blomme, Toxicol. Lett., 2017, 272, 1–7 CrossRef CAS PubMed.
- E. M. Faed, Drug Metab. Rev., 1984, 15, 1213–1249 CrossRef CAS PubMed.
- D. A. Smith, T. Hammond and T. A. Baillie, Drug Metab. Dispos., 2018, 46, 908–912 CrossRef CAS PubMed.
- M. Darnell and L. Weidolf, Chem. Res. Toxicol., 2013, 26, 1139–1155 Search PubMed.
- T. Lassila, J. Hokkanen, S.-M. Aatsinki, S. Mattila, M. Turpeinen and A. Tolonen, Chem. Res. Toxicol., 2015, 28, 2292–2303 Search PubMed.
- J. Shang, R. Tschirret-Guth, M. Cancilla, K. Samuel, Q. Chen, H. R. Chobanian, A. Thomas, W. Tong, H. Josien, A. V. Buevich and K. Mitra, Chem. Res. Toxicol., 2019 DOI:10.1021/acs.chemrestox.9b00226.
- M. Darnell, K. Breitholtz, E. M. Isin, U. Jurva and L. Weidolf, Chem. Res. Toxicol., 2015, 28, 886–896 Search PubMed.
- N. G. Berry, L. Iddon, M. Iqbal, X. Meng, P. Jayapal, C. H. Johnson, J. K. Nicholson, J. C. Lindon, J. R. Harding, I. D. Wilson and A. V. Stachulski, Org. Biomol. Chem., 2009, 7, 2525–2533 RSC.
- W. Bonner, J. Org. Chem., 1959, 24, 1388–1390 CrossRef CAS.
- O. Corcoran, R. W. Mortensen, S. H. Hansen, J. Troke and J. K. Nicholson, Chem. Res. Toxicol., 2001, 14, 1363–1370 Search PubMed.
- A. W. Nicholls, K. Akira, J. C. Lindon, R. D. Farrant, I. D. Wilson, J. Harding, D. A. Killick and J. K. Nicholson, Chem. Res. Toxicol., 1996, 9, 1414–1424 Search PubMed.
- S. J. Vanderhoeven, J. Troke, G. E. Tranter, I. D. Wilson, J. K. Nicholson and J. C. Lindon, Xenobiotica, 2004, 34, 889–900 CrossRef CAS PubMed.
- J. Hasegawa, P. C. Smith and L. Z. Benet, Drug Metab. Dispos., 1982, 10, 469–473 CAS.
- H. Spahn-Langguth and L. Z. Benet, Drug Metab. Rev., 1992, 24, 5–47 CrossRef CAS PubMed.
- P. C. Smith, J. Hasegawa, P. N. Langendijk and L. Z. Benet, Drug Metab. Dispos., 1985, 13, 110–112 CAS.
- T. G. Hammond, X. Meng, R. E. Jenkins, J. L. Maggs, A. S. Castelazo, S. L. Regan, S. N. L. Bennett, C. J. Earnshaw, G. P. Aithal, I. Pande, J. G. Kenna, A. V. Stachulski, B. K. Park and D. P. Williams, J. Pharmacol. Exp. Ther., 2014, 350, 387–402 CrossRef PubMed.
- R. N. Monrad, J. C. Errey, C. S. Barry, M. Iqbal, X. Meng, L. Iddon, J. A. Perrie, J. R. Harding, I. D. Wilson, A. V. Stachulski and B. G. Davis, Chem. Sci., 2014, 5, 3789–3794 RSC.
- L. Z. Benet, H. Spahn-Langguth, S. Iwakawa, C. Volland, T. Mizuma, S. Mayer, E. Mutschler and E. T. Lin, Life Sci., 1993, 53, PL141–PL146 CrossRef CAS PubMed.
- R. Sawamura, N. Okudaira, K. Watanabe, T. Murai, Y. Kobayashi, M. Tachibana, T. Ohnuki, K. Masuda, H. Honma, A. Kurihara and O. Okazaki, Drug Metab. Dispos., 2010, 38, 1857–1864 CrossRef CAS PubMed.
- R. Meech, J. O. Miners, B. C. Lewis and P. I. Mackenzie, Pharmacol. Ther., 2012, 134, 200–218 CrossRef CAS PubMed.
- C. Teague, E. Holmes, E. Maibaum, J. Nicholson, H. Tang, Q. Chan, P. Elliott and I. Wilson, Analyst, 2004, 129, 259–264 RSC.
- M. Shipkova, V. W. Armstrong, E. Wieland, P. D. Niedmann, E. Schütz, G. Brenner-Weiß, M. Voihsel, F. Braun and M. Oellerich, Br. J. Pharmacol., 1999, 126, 1075–1082 CrossRef CAS PubMed.
- S. Sarda, C. Page, K. Pickup, T. Schulz-Utermoehl and I. Wilson, Xenobiotica, 2012, 42, 179–194 CrossRef CAS PubMed.
- D. Buchheit, C.-A. Dragan, E. I. Schmitt and M. Bureik, Drug Metab. Dispos., 2011, 39, 2174–2181 CrossRef CAS PubMed.
- N. ARIMA, J. Pharmacobiodyn., 1990, 13, 724–732 CrossRef CAS PubMed.
- C. Tang, J. H. Hochman, B. Ma, R. Subramanian and K. P. Vyas, Drug Metab. Dispos., 2003, 31, 37–45 CrossRef CAS PubMed.
- N. ARIMA, J. Pharmacobiodyn., 1990, 13, 733–738 CrossRef CAS PubMed.
- N. ARIMA and Y. KATO, J. Pharmacobiodyn., 1990, 13, 719–723 CrossRef CAS PubMed.
- L. Iddon, S. E. Richards, C. H. Johnson, J. R. Harding, I. D. Wilson, J. K. Nicholson, J. C. Lindon and A. V. Stachulski, Org. Biomol. Chem., 2011, 9, 926–934 RSC.
- M. Castillo and P. C. Smith, Drug Metab. Dispos., 1995, 23, 566–572 CAS.
- L. T. Wade, J. G. Kenna and J. Caldwell, Chem. Res. Toxicol., 1997, 10, 546–555 Search PubMed.
- M. Nagao, M. Suzuki and Y. Takano, Tetrahedron Lett., 2016, 57, 3339–3343 CrossRef CAS.
- A. V. Stachulski, J. R. Harding, J. C. Lindon, J. L. Maggs, B. K. Park and I. D. Wilson, J. Med. Chem., 2006, 49, 6931–6945 CrossRef CAS PubMed.
- J. A. Perrie, J. R. Harding, D. W. Holt, A. Johnston, P. Meath and A. V. Stachulski, Org. Lett., 2005, 7, 2591–2594 CrossRef CAS PubMed.
- E. R. Bowkett, J. R. Harding, J. L. Maggs, B. K. Park, J. A. Perrie and A. V. Stachulski, Tetrahedron, 2007, 63, 7596–7605 CrossRef CAS.
- K. Akira, T. Taira, H. Hasegawa, C. Sakuma and Y. Shinohara, Drug Metab. Dispos., 1998, 26, 457–464 CAS.
- H. Hasegawa, K. Akira, Y. Shinohara, Y. Kasuya and T. Hashimoto, Biol. Pharm. Bull., 2001, 24, 852–855 CrossRef CAS PubMed.
- R. W. Mortensen, O. Corcoran, C. Cornett, U. G. Sidelmann, J. C. Lindon, J. K. Nicholson and S. H. Hansen, Drug Metab. Dispos., 2001, 29, 375–380 CAS.
- R. W. Mortensen, U. G. Sidelmann, J. Tjørnelund and S. H. Hansen, Chirality, 2002, 14, 305–312 CrossRef CAS PubMed.
- U. G. Sidelmann, S. H. Hansen, C. Gavaghan, H. A. J. Carless, J. C. Lindon, R. D. Farrant, I. D. Wilson and J. K. Nicholson, Anal. Chem., 1996, 68, 2564–2572 CrossRef CAS PubMed.
- A. Baba and T. Yoshioka, Chem. Res. Toxicol., 2009, 22, 158–172 Search PubMed.
- T. Yoshioka and A. Baba, Chem. Res. Toxicol., 2009, 22, 1559–1569 Search PubMed.
- A. Baba and T. Yoshioka, Chem. Res. Toxicol., 2009, 22, 1998–2008 Search PubMed.
- T. Potter, R. Lewis, T. Luker, R. Bonnert, M. A. Bernstein, T. N. Birkinshaw, S. Thom, M. Wenlock and S. Paine, J. Comput.-Aided Mol. Des., 2011, 25, 997–1005 CrossRef CAS PubMed.
- T. O′haver and P. Emeritus, Pragmatic Introduction to Signal Processing Applications in scientific measurement, 2019 Search PubMed.
- P. Mendes, Bioinformatics, 1993, 9, 563–571 CrossRef CAS PubMed.
- R. Dennington, A. T. Keith and M. J. Millam, GaussView Version 6.0.16, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209–214 CrossRef CAS.
- M. S. Gordon, Chem. Phys. Lett., 1980, 76, 163–168 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, D. J. DeFrees, J. A. Pople and M. S. Gordon, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- R. C. Binning and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216 CrossRef CAS.
- J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016–5021 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2016.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, Natural Bond Orbital Version 3.1, 2001 Search PubMed.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- M. Karelson, V. S. Lobanov and A. R. Katritzky, Chem. Rev., 1996, 96, 1027–1044 CrossRef CAS.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- C. H. Johnson, I. D. Wilson, J. R. Harding, A. V. Stachulski, L. Iddon, J. K. Nicholson and J. C. Lindon, Anal. Chem., 2007, 79, 8720–8727 CrossRef CAS.
- C. H. Johnson, E. Karlsson, S. Sarda, L. Iddon, M. Iqbal, X. Meng, J. R. Harding, A. V. Stachulski, J. K. Nicholson, I. D. Wilson and J. C. Lindon, Xenobiotica, 2010, 40, 9–23 CrossRef CAS PubMed.
- E. S. Karlsson, C. H. Johnson, S. Sarda, L. Iddon, M. Iqbal, X. Meng, J. R. Harding, A. V. Stachulski, J. K. Nicholson, I. D. Wilson and J. C. Lindon, Rapid Commun. Mass Spectrom., 2010, 24, 3043–3051 CrossRef CAS PubMed.
- E. Skordi, I. D. Wilson, J. C. Lindon and J. K. Nicholson, Xenobiotica, 2005, 35, 715–725 CrossRef CAS PubMed.
- C. Volland, H. Sun, J. Dammeyer and L. Z. Benet, Drug Metab. Dispos., 1991, 19, 1080–1086 CAS.
- H. Spahn, S. Iwakawa, E. T. Lin and L. Z. Benet, Pharm. Res., 1989, 6, 125–132 CrossRef CAS PubMed.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ob02008j |
| This journal is © The Royal Society of Chemistry 2020 |