Selective shortening of gold nanorods: when surface functionalization dictates the reactivity of nanostructures

Abstract

The selective shortening of gold nanorods (NRs) is a directional etching process that has been intensively studied by UV-Vis spectroscopy because of its direct impact on the optical response of these plasmonic nanostructures. Here, liquid-cell transmission electron microscopy is exploited to visualize this peculiar corrosion process at the nanoscale and study the impacts of reaction kinetics on the etching mechanisms. In situ imaging reveals that anisotropic etching requires a chemical environment with a low etching power to make the tips of NRs the only reaction site for the oxidation process. Then, aberration-corrected TEM and atomistic simulations were combined to demonstrate that the disparity between the reactivity of the body and the ends of NRs does not derive from their crystal structure but results from an inhomogeneous surface functionalization. In a general manner, this work highlights the necessity to consider the organic/inorganic natures of nanostructures to understand their chemical reactivity.

---

1. Introduction

Oxidative etching plays a key role in the dynamics of metallic nanostructures in their formation or application media. On the one hand, the use of oxidizing agents and coordination ligands for the metal ions is a well-known strategy to shape metal nanoparticles during liquid-phase synthesis.¹ On the other hand, oxidative degradation is an integral part of the life cycle of nanomaterials, especially when used in fuel cells^2,3 and biological media.^4–8 Therefore, understanding the atomic-scale mechanisms of nanomaterial dissolution in liquid electrolyte is of primary importance to design more efficient nanotechnologies. In that regards, liquid cell transmission electron microscopy (LCTEM) has become a method of choice to observe the oxidative etching of individual nanostructures such as metallic nanoparticles^9–17 and nanoalloys^18–21 and it has provided a unique observation window on the intermediate nanostructures formed during these dynamic processes. Like the nucleation and growth of nanoparticles,^22,23 the dissolution mechanisms are simultaneously driven by kinetic and thermodynamic effects that depend on the reaction speed and the structural stability of nanomaterials, respectively. Therefore, LCTEM allowed highlighting the effects of oxidation potential, nanoparticle faceting and crystal defects on selective-etching processes.^11–13,20 However, the influence of surface functionalization on the corrosion dynamics has always been disregarded, although the nature and spatial distribution of organic shells are known to affect the stability and reactivity of nanostructures.^4,6,24,25

From theoretical point of view, different approaches have been actively developed to understand the role of surfactants on the structure of metal nanoparticles.^26,27 Generally, methods of quantum chemical calculations enable a detailed study of a system at the atomic level, but the computational cost for such methods is high. To overcome these difficulties, classical molecular dynamic (MD) approaches involving force fields with different level of accuracy were developed to investigate the evolution of large molecular assemblies for long periods. Moreover, many MD works focused on the interaction between surfactants and metal surfaces have been performed to explain the growth of anisotropic nanostructures coated with ligands such as citrate, piptide, CTAB ….^28–31 However, to our knowledge such theoretical approaches have never been used to reveal the effect of surface functionalization on the dissolution processes of nanoparticles.

In the present study, we combine experimental and theoretical investigations to demonstrate at the atomic scale the key roles of degradation kinetics and capping agents in the selective shortening of gold nanorods (NRs) in oxidative media.

2. Experimental section and methods

2.1. Nanorods and chemicals

Citrate-coated gold NRs were purchased from Nanocomposix Inc. According to the supplier, the gold NRs were first fabricated by a conventional wet-chemical method assisted by cetyl trimethylammonium bromide (CTAB). This very common surfactant is then replaced by sodium citrate molecules. The NRs are highly purified to remove all residual reactants following synthesis and dispersed in Milli-Q water. Other chemicals used for liquid-cell TEM were purchased from Sigma Aldrich Inc., with ACS Reagent grade.

2.2. TEM experiments and data processing

All TEM experiments were performed on a JEOL ARM 200F microscope equipped with a CEOS aberration corrector for the objective lens and a cold field emission electron source.³² We used a 200 kV acceleration voltage.

Liquid STEM imaging was performed using a liquid-cell TEM holder commercialized by Protochips Inc. A colloidal suspension of citrate-coated gold NRs dispersed in an acidic saline solution containing 1 M of NaCl and 10⁻² M of HCl was encapsulated in the liquid-cell by using the conventional loading process.^22,23 The Au spacers of the liquid cell were 150 nm thick and the experiments were performed in the corners of the observation window, where the liquid thickness is minimum. The acidic saline solution was continuously flowing into the liquid-cell during the experiment with a flow rate of 5 μL min⁻¹. STEM HAADF imaging was performed with a pixel dwell time of 5 μs and a probe current of 1.1 10⁸ electron per s. The electron dose rate was then tuned with the STEM magnification. The dose rate given in electron per s per Ų, can be calculated by dividing the probe current by the irradiated area (i.e. the image area in STEM mode). Videos of NRs etching were acquired with a frame rate of one image per second using Digital Micrograph software. The length and width evolution of NRs during the etching processes was extracted with an automated video processing using Fiji and a homemade Python code.

Aberration-corrected HRTEM imaging was exploited to study the spatial distribution of citrate coating on NRs deposited on a thin carbon film. Using the CEOS aberration corrector, the first order aberrations (A1 and C1 (i.e. the focus)), the second-order aberrations (A2, B2) and the third order aberrations (C3, A3 and S3) were tuned below 2 nm, 20 nm and 1 μm, respectively. These optical conditions optimize the contrast of organic molecules adsorbed on gold nanocrystals because they minimize the noise arising from the carbon substrate and they avoid the contrast delocalization of the gold surfaces. We note that the citrate layer is more easily detected on NRs flatly deposited on the carbon film than on NRs laying at the edge of carbon film which highlights the influence of the local environment of NRs on the conformation the citrate layer.

The following digital processing was applied to HRTEM images to better visualize the citrate layers. We used a low-pass filter with cutoff frequency at 3 nm⁻¹ to suppress the atomic contrast of the NR and to make the citrate layer the area of the images with the highest local intensities. Then, the color thresholding method implemented in Digital micrograph software allows us coloring in hot colors the high signal of the citrate layer.

To take into account the high variability in thickness of the citrate coating, the average thickness of citrate layer on the body, the tips and the corners of the NRs was calculated by measuring the average thickness on 5 nm long surface sections. These measurements were performed over 15 NRs (corresponding to 1000 nm of analyzed projected surface).

2.3. Grand canonical monte carlo (GCMC) simulations

At first, the atomic position of a 13 nm long and 5.8 nm wide NR was calculated with the Nanofabric software.³³ Then, the Au–Au interaction is modeled by a tight-binding semi-empirical potential within the second moment approximation. Such model is particularly well suited to model transition and noble metals where the cohesion is governed by the d-electron band.^34,35 The parameters for gold, fitted on the bulk cohesive energy, lattice parameter and elastic constants, can be found in Chmielewski et al.³⁶ This model, both fast to compute and accurate, is then implemented in a MC code using GC algorithm with fixed temperature and Au chemical potential (μ_Au). The GC algorithm used consists in a series of MC steps. Each step randomly alternates displacement moves but also attempts to incorporate and remove Au atoms in a previously defined active zone. In order to mimic the etching process from the surface, the active zone for extracting/inserting Au atoms is defined as a region ± 5 Å from the surface of the NR. It is important to specify that in order to respect the detailed balance and thus ensure that the Markov chain is satisfied, both events (extraction and incorporation of Au atoms) are to be tried.³⁷ Although studying etching, one cannot simply extract only the Au atoms which would bias the simulation. In the present work, we typically performed up to 2000–8000 MC steps to get a complete degradation of the NP depending on μ_Au. Within each MC step, we systematically performed 2000 attempted displacement trials per atom. To extract or incorporate Au atoms, 500 attempts were made and ended as soon as one successful event has occurred. We then performed GCMC simulations at T = 500 K and different μ_Au ranging from −3.75 to −3.95 eV. The Au chemical potential is referred to a fictitious ideal monoatomic gas, explaining its values that are of the order of the cohesive energies of Au in FCC bulk (e.g. −3.81 eV per at. in our TB model). Depending on the value of μ_Au (at a given T), one would tend to favor the adsorption or extraction of Au atoms. In our case, we worked in a chemical potential range below −3.70 eV to observe the dissolution of the NRs.

In order to analyze the etching mechanisms in detail, we calculated a desorption rate through the tip and body of the NR defined as follows: desorption rate = n_Au^removed/A where A is the surface of the tip or body of the NR and n_Au^removed is the number atoms removed during the MC simulation on each surfaces. Consequently, the calculation of the desorption rate implies determining the surface of the tip and the body of the NR during the simulation. However, the surface of the NP is always evolving. At the atomic scale, it is therefore difficult to represent it as a multifaceted NR as can be seen in its initial state. A simple way to approximate the surface of the object is to assimilate it to a cylinder closed by two half-spheres. By doing so, the cylinder corresponds to the body of the NR and the two half-spheres to the tip (Fig. S1†).

2.4. DFT calculations

Theoretical calculations were performed within plane-wave pseudopotential method based on density functional theory as implemented in the Vienna Ab initio Simulation Package (VASP).^38,39 Ions are described by employing PAW pseudopotential for atomic core region.^40,41 The exchange–correlation energy was calculated within the Perdew, Burke, and Ernzerhof formulation of the generalized-gradient approximation (GGA-PBE).^42,43 After the extensive test calculations for the total energy convergence, the kinetic energy cut-off for plane wave expansion was set to 400 eV. Six Au surface orientations (111), (100), (110) (for low index surfaces) and (221), (311), (331) (for high index surfaces) were considered. The Au surfaces were simulated by the (4 × 4) slab models containing 6 atom layers, in which the 2 bottom layers are fixed to mimic the bulk state. The calculated equilibrium lattice constant of the bulk was found to be of 4.17 Å, which is in good agreement with the experimental value of 4.08 Å.⁴⁴ The slab models are separated with a 15 Å vacuum space along the Z-axis and the K points is set as (2 × 2 × 1). The geometry of the acetate and citrate molecules in a gas phase is optimized in a 15 Å × 15 Å × 15 Å cubic box; the k-point sampling is set as (1 × 1 × 1). The convergence criterion for the electronic self-consistent cycle was fixed to 10⁻⁶ eV per supercell. Atomic positions and lattice parameters were both relaxed using the conjugate gradient algorithm until all the forces are below 0.02 eV Å⁻¹. The surface energies of Au(111), Au(100) and Au(110) are calculated to be 0.64 J m⁻², 0.80 J m⁻² and 0.91 J m⁻², respectively. Even underestimated compared with the experimental value of 1.5 J m⁻², these DFT predicted surface energies are in good agreement with the literature.⁴⁵ More theoretical details and comparisons with other DFT functional could be found in our previous works.^46,47 The electronic structure of the adsorption systems was analyzed through Bader charge density analysis⁴⁸ with the implementation of Henkelman and co-workers⁴⁹ which allows analyzing the density issued from VASP code. From a theoretical point of view, classic DFT cannot accurately capture weak interactions such as van der Waals forces and it is always difficult to ascertain the existence of a physisorbed molecular state on the gold surfaces. In order to evaluate the effect of the dispersion correction term in the DFT calculated adsorption energies of citrate molecules, we employed the dispersion term DFT-D3 proposed by Grimme⁵⁰ and implemented in the VASP code. However, although we have adopted the dispersion correction in the above calculations, the DFT-GGA method tends to underestimate the energies (surface energies and adsorption energies), which is a well-known artifact.⁵¹

3. Results and discussion

3.1. In situ imaging of selective-etching processes

The dissolution of 50 nm long and 13 nm wide gold NRs coated with citrate molecules was followed at the nanoscale by LCTEM in an acidic saline solution containing 1 M of NaCl and 10⁻² M of HCl (Fig. 1). As the corrosion of NRs only occurs under electron beam irradiation (see ex situ control experiment in ESI, Fig. S2†), the reactive oxygen species (ROS) produced by water radiolysis, particularly hydroxyl radicals (OH˙) and hydrogen peroxide (H₂O₂), are obviously implied in the oxidizing reactions. By studying the colloidal stability of gold nanoparticles under electron-beam irradiation in various saline solutions, Hermannsdörfer and coworkers demonstrated that the etching of gold nanoparticles requires, as in our experiment, high NaCl concentration and low pH.¹⁰ They concluded that the strong oxidizing power of OH˙ and H₂O₂ drives this corrosion processes but the presence of chlorine ions (Cl−) is necessary to lower the redox potential of the reaction and stabilize tetrachloro gold complexes ([AuCl₄]⁻)_. The reactivity of ROS increases at low pH, because a high concentration of oxonium ions favors the formation of H₂O. The ROS-induced degradation of gold nanostructures that also occurs in a slower way in cellular media,⁸ can be summarized as followed:

Au⁰ + 4Cl⁻ → [AuCl₄]⁻ + 3e⁻

3e⁻ + 3OH˙ → 3OH⁻

3OH⁻ + 3H⁺ → 3H₂O

H₂O₂ + 2H⁺ + 2e⁻ → 2H₂O

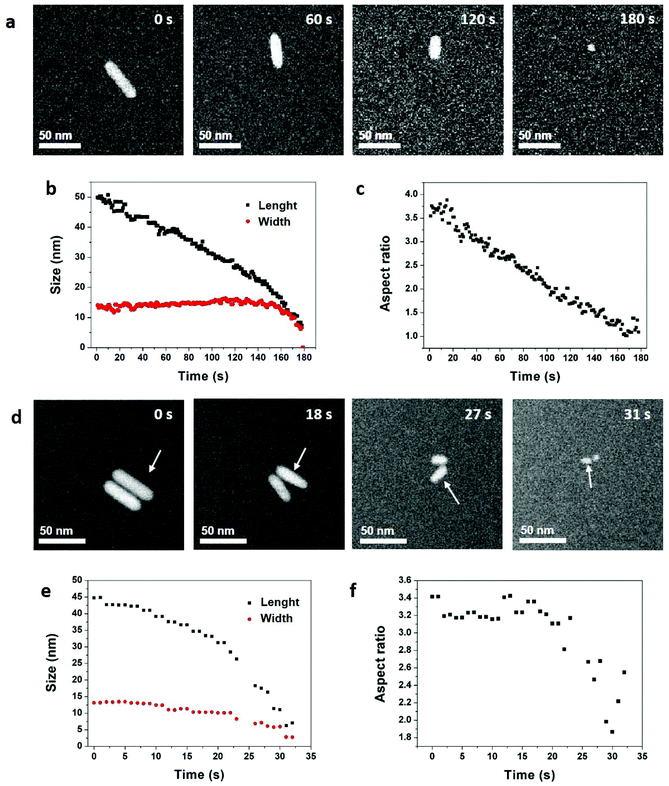Fig. 1 Reaction-kinetics effects on the etching processes of gold NRs in an acidic saline solution. (a) STEM HAADF image series acquired with an electron dose rate of 3.3 electron per s per Ų. The acquisition time is indicated in the top right corner of each image. See Video 1 in ESI.† Time evolution of the NR (b) length, width, and (c) aspect ratio. (d) STEM HAADF image series acquired with an electron dose rate of 20.5 electron per s per Ų. The acquisition time is indicated in the top right corner of each image. See Video 2 in ESI.† Time evolution of the NR (e) length, width, and (f) aspect ratio. The analyzed NR is indicated by arrows in (d). The shape evolution of the other NR is quantified in Fig. S4.†

In these conditions, with an electron dose rate of 3.3 electrons per s per Ų, the dissolution time of NRs varies from 100 seconds (Fig. S3†) to 180 seconds (Fig. 1a) but the etching process is always selective. Indeed, the length of the NRs decreases linearly with time while their width remains constant until spherical nanostructures remain (Fig. 1b). Then, the etching rate accelerates leading to a quick disappearance of the nanocrystals. Consequently, the aspect ratio of the nanostructures (i.e. length/width) decreases linearly with time from 3.8 to 1 (Fig. 1c and S3†). As the concentration of ROS increases with the electron dose rate,⁵² LCTEM also offers the possibility to modulate the etching kinetics and visualize its impacts on the degradation mechanisms. As illustrated in Fig. 1d and e, with a dose rate of 20.5 electrons per s per Ų the dissolution of NRs takes only about 30 seconds and both the length and width decrease over time. Throughout this fast dissolution process, the width and length loss percentages have the same time dependence (Fig. S4b†) resulting in a constant aspect ratio of the nanostructures, except for the very last seconds in which their shape anisotropy decreases (Fig. 1f and S4†). These speed-controlled experiments reveal a transition between a low driving force regime leading to the slow selective shortening of NRs and a high-driving force regime in which fast and more isotropic dissolution are observed. These real-time in situ observations confirm in a straightforward manner many studies carried out by UV-Vis spectroscopy on the colloidal stability of NRs in oxidative media with various concentration of etching agent.^13,53–56 To summarize, in the high driving force regime, the dissolution kinetics is dominated by the high etching power of the solution which depends on the concentrations of ROS and Cl⁻, whereas the low driving force regime allows visualizing the difference in reactivity between the body and the two tips of NRs and the observed selective etching is then driven by the intrinsic thermodynamic properties of nanostructures.

3.2. Why the ends of nanorods are more reactive?

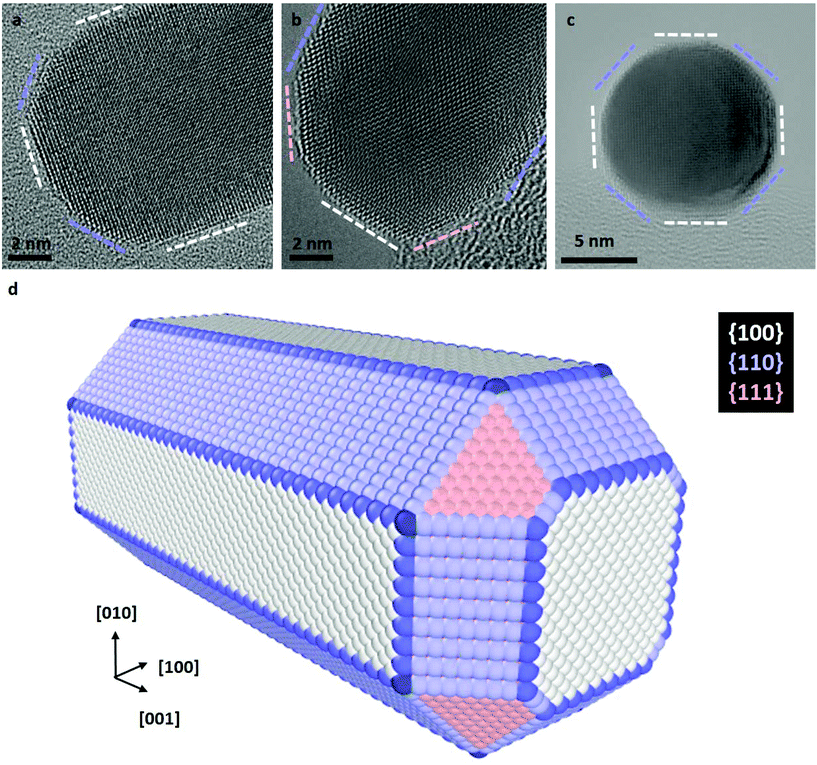
The preferential etching of NR's ends can either be explained by the surface structure of nanocrystals (i.e. defects and faceting) that modifies the local reactivity or by an inhomogeneous passivation layer that dictates surface accessibility for etching agents.^{12,17,25,54,55} In the following, we combined aberration-corrected HRTEM imaging and atomistic simulations to evaluate the respective impacts of the crystal surface and the citrate coating on the anisotropic etching of NRs. At first, we performed atomic-scale TEM investigations under vacuum to determine the faceting of nanocrystals. The HRTEM images of nanostructures along the [100], [110] and [001] zone axes (Fig. 2a–c) clearly reveal that the body of the rods exhibits four {100} and four {110} faces, whereas the tips consist of four {110} and four {111} faces (herein referred to as the corners of the NRs) together with a {100} face at the apex. If small terraces and steps are occasionally observed at the interface between faces, NRs are monocrystalline and do not present classical defects of FCC metals, such as stacking faults or twin planes. These results is consistent with the 3D shape of NRs obtained by seed-mediated growth in aqueous solution, assisted by the surfactant cetyltrimethylammonium bromide (CTAB),⁵⁷ and it confirms that the surface exchange protocol used to replace the CTAB with citrate capping agents does not affect the faceting of nanostructures (see section 2.1).

Fig. 2 Atomic-scale faceting of nanorods. Aberration-corrected TEM images of NRs along the (a) [100], (b) [110] and (c) [001] zone-axis orientations. The white, blue and pink dashed lines indicate the {100}, {110} and {111} edge-on facets, respectively. In image (c) the NR is seen along its anisotropy axis. (d) Scheme of the atomic scale faceting of NRs deduced from HRTEM images. This 3D nanostructure is used as a starting point of Monte Carlo simulations.

To determine if the selective shortening of NRs origins from their atomic-scale faceting, Grand Canonical Monte Carlo (GCMC) simulations were performed using a specific N-body potential derived from the second moment approximation of the tight-binding scheme.^34,35 The chemical reactions involve in the gold etching, is translated in the GCMC algorithm into a change of chemical potential of Au atoms (μ_Au).⁵⁸ As required in GCMC simulations that take the system to thermodynamic equilibrium, long atomic relaxations are performed after each accepted Au removal, as well as attempts to incorporate Au atoms in the structure.³⁷ Simulation details are provided in section 2.3. Starting from a 13 nm by 5.8 nm NR containing about 19 000 atoms with the same crystal faceting than the NRs studied experimentally (Fig. 2d), we simulated atomic-desorption processes with various chemical potentials at 500 K until the NR completely dissolved (Fig. 3a). As expected, the stronger (i.e. the more negative) the chemical potential, the faster the dissolution of the NR (Fig. S5a†), but regardless of the chemical potential, the number of extracted atoms per MC step is constant until 6000 atoms remain within the nanostructures, then the dissolution process speeds up. This size effect on the desorption processes is explained by the decrease in the cohesive energy of nanocrystals when their dimensions are reduced to a few nanometers (Fig. S5b†).^36,59 It is worth noting that this effect occurs in a size range (width < 3.5 nm) which prevents its experimental observation because of the resolution limit of our LCTEM experiments and the very short life time of degraded NRs with a size below 5 nm. The coordination-number distribution of extracted atoms shows that strong chemical potential favors the extraction of atoms with higher coordination numbers (Fig. S5c†), which reflects the possibility to extract atoms with higher desorption energies (Fig. S5d†). More importantly, GCMC simulations never show a selective shortening of NRs but rather isotropic dissolution processes. As illustrated in Fig. 3 and S6† for the weaker and stronger chemical potentials, respectively, the reduction in length and width of the NRs follow very similar trends (Fig. 3b and S6b†) and we measure similar desorption rates on the body and at the tips of NRs (Fig. 3c and S6c†) throughout the simulations. Consequently, the aspect ratio of NRs increases when the dissolution process speeds up because the loss percentage is more important along the width than along the length (Fig. 3d and S6d†). Fig. 3a and S6a† also show that the initial crystal facets of NRs rapidly transform into rough surfaces which likely favors the isotropic degradation of the NRs. It also indicates that atomic desorption goes faster than surface diffusion that should maintain the facetted morphology of nanocrystals. Ultimately, the disagreements between the LCTEM observations and the GCMC simulations reveal that crystal-faceting alone does not explain the directional etching of gold NRs observed experimentally in the low driving force regime. The isotropic etching observed in the GCMC simulations that does not take into account the effects of the ligands on the thermodynamic properties of nanostructures, simply results from the very similar surface structure of the body and ends of NRs. Indeed, they both exhibit {100} and {110} faces and the {111} faces that are only observed on the tips are known to be the most stable gold surface.⁶⁰

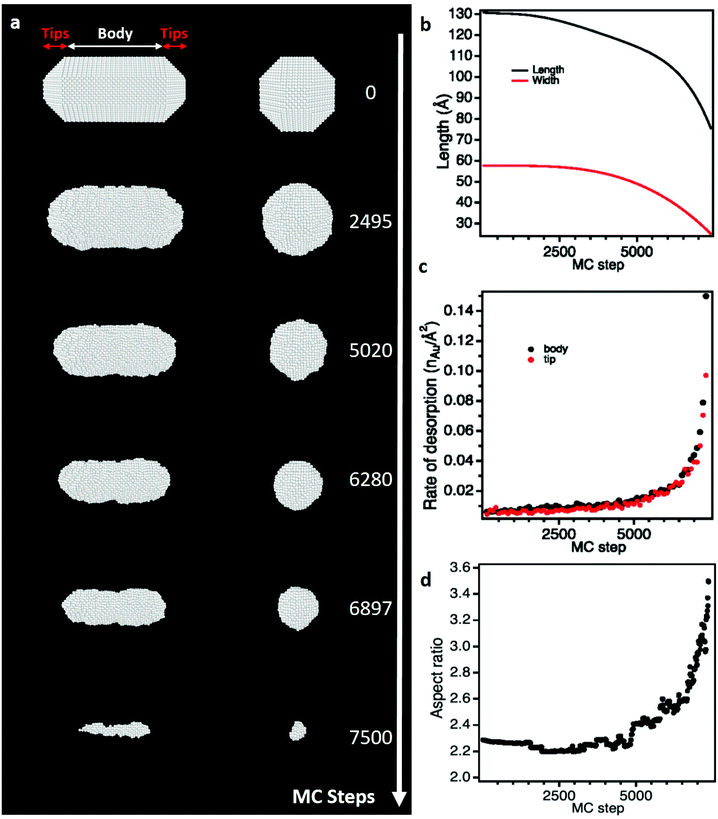Fig. 3 Monte Carlo (MC) simulations of the dissolution of a citrate-free NR using a weak chemical potential (μ_Au = −3.75 eV). (a) Snapshot images of the simulated NR seen along its transversal (left) and longitudinal (right) axes at different MC steps. (b) Length and width of the NR as function of MC step. (c) Rate of desorption of gold atoms on the tips and the body of the NR as function of MC step. (d) Aspect ratio of the NR as function of MC step. see Video 4 in ESI† and calculation details section 2.3.†

Since surface functionalization reduces access to gold nanocrystals for the chelating agent and stabilizes crystal surface, we evaluate the role of citrate coating in the chemical etching of NRs by studying both experimentally and theoretically the citrate/Au interfaces. The absence of delocalization contrast at the edges of nanocrystals and the low noise level arising from the amorphous substrate are two characteristic features of aberration-corrected HRTEM images acquired close to zero focus⁶¹ that allow revealing the inhomogeneous distribution of the citrate layer over the NRs (Fig. 4a and S7†).⁴ Obviously, these HRTEM images provide only a partial view of these soft/hard material interfaces since the citrate layer can be detected only if it is not superimposed with the gold crystal. Moreover, the conformation of the organic layer around the NRs is very likely influenced by the local environment of the NRs during the deposition and drying processes. Nevertheless, in general, we observe much more citrate on the body of the NRs than at the extremities. Local-thickness measurements of the citrate layer illustrated in Fig. 4a have resulted in an average thickness (T̄_cit) of 4.5 ± 3.0 nm and 1.9 ± 0.7 nm on the body and the tips of the NRs, respectively (see details in section 2.2). More precisely, the corners of the NRs are the less covered surfaces with a T̄_cit of only 1.1 ± 0.5 nm with a minimum for the {111} corners (T̄^{111}_cit = 0.8 ± 0.2). These atomic scale observations of dried nanostructures highlight the lower density of citrate layers on the (111) facets, and more generally on the tips of NRs. Note that, it would be very interesting, but still challenging, to confirm these results by LCTEM to minimize experimental artefacts.

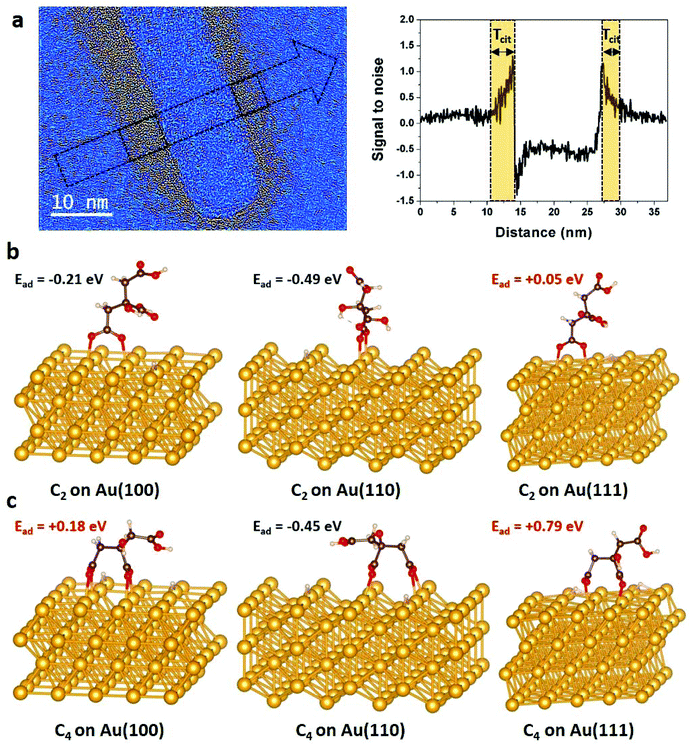Fig. 4 Spatial distribution of citrate functionalization over gold NRs. (a) Low-pass filtered HRTEM image of a NR acquired close to zero focus. A color thresholding process was applied to display the citrate layer around the NR in hot colors (see details in section 2.2). On the right, signal to noise ratio profile measured along the arrow seen on the image, on which we can measure the local thickness of citrate (T_cit) on each side of the NR's body. Optimized C2 (b) and C4 (c) configurations of citrate on {100}, {110} and {111} gold surfaces and their corresponding adsorption energies obtained by DFT calculations (see details in section 2.3 and in ESI†). Au, C, O and H atoms are represented in yellow, black, red and white, respectively.

At first attempt to explain theoretically this inhomogeneous citrate coating, DFT calculations were performed to determine the binding modes and adsorption energies of citrate molecules, which contain three carboxylate groups (Fig. S8†), on {100}, {110} and {111} gold surfaces. We considered the dissociative adsorption via carboxylate O–H terminal where H atom was assumed to be dissociated in the solution and to diffuse onto the Au surface (Fig. S9†). In agreement with the recent results of Al-Johani et al.,⁶² we found that carboxylate groups tend to bridge two Au surface atoms, with each carboxylate oxygen interacting with one Au atom. On {100}, {110} and {111} gold surfaces, carboxylate-group adsorption is always stronger when bridging two first neighbor Au atoms (see details in ESI, Fig. S10 and Table S1†). We found that citrate anions have two stable geometries on gold surfaces: the C₂ conformation, where one terminal carboxylate group links to the gold surface (Fig. 4b) and the C₄ configuration, where one terminal and the central carboxylate groups interact with the substrate (Fig. 4c). Interestingly, the calculated adsorption energies (E_ad) show endothermic adsorption over {111} surfaces for both C₂ (E_ad = 0.05 eV) and C₄ (E_ad = 0.79 eV) configurations, whereas exothermic adsorptions are found for the C₂ configuration over the {100} surface (E_ad = −0.21 eV) and for both the C₂ (E_ad = −0.49 eV) and C₄ (E_ad = −0.45 eV) over the {110} surface. The strong adsorption of citrates on {110} surfaces is due to stronger charge transfers from the under-coordinated gold surface to the molecules (Fig. S11†).

In order to go further in the comprehension of the reactivity of the different facets of gold NRs toward citrate molecules, we performed additional calculations on high index surfaces such as {221}, {311} and {331}. These latter could be representative of step atoms at the edge of small terraces that are sometimes observed at the interfaces between faces on the tips of NRs (Fig. S12†). DFT results show that these sites are also exothermic adsorption points for citrate molecules with competitive adsorption energies (E_ad < −0.30 eV) (see details in ESI, Fig. S13 and Table S2†). All these theoretical calculations emphasis that the {111} surfaces are the least prone to citrate adsorption. In line with HRTEM observations, this indicates that the {111} corners of NRs are less protected by the citrate layer which favors their degradation. Therefore, in the low driving force regime, these easily accessible surfaces are very likely the most, if not the only, reactive site for oxidative etching which drives the selective shortening of NRs. The more isotropic etching observed in the high driving force regime is due to the higher etching power of the solution that either becomes too strong for the citrate-covered surfaces or results in the degradation of the citrate shield itself.

Interestingly, the identified distribution of citrates over gold NR facets and their role in the anisotropic dissolution is very similar to the identified distribution of surfactants and their role in the anisotropic growth phenomena. Indeed, using molecular dynamic simulations, Sulpizi et al.²⁸ have identified the role of surfactant layer that preferentially covers the (100) and (110) facets, leaving the (111) facets unprotected. This inhomogenous surfactant layer promotes anisotropic growth with the less protected tips growing faster, which explains the shape of NRs. Facet-specific coverage has been also reported by Heinz and coworkers for peptides on Pt nanoparticles.³¹ Moreover, these authors have introduced the concept of soft epitaxial binding mechanism, which control the facet recognition and binding strength in solution.⁶³

It is worth noting that our DFT calculations of single adsorbed citrate molecule interacting with gold surfaces are an initial proof of the effect of ligands on the protection of NRs from degradation and that further analyses should be undertaken. Indeed, it is actually well known that for charged molecules, such as citrate, the contribution of the polarization effect to the adsorption energy should be taken into account.^64,65 The development of an accurate force field including polarization effects and the possible influence of the solvent and the charged species generated by its radiolysis to implement in molecular dynamic simulations is an essential future step to reproduce the observed dissolution process.

4. Conclusion

Real-time monitoring of reaction processes is crucial for understanding the reaction mechanisms. So far, UV-Vis spectroscopy has been the standard method to characterize in real time the corrosion of gold NRs and reveal selective-shortening processes because the resulting blue shift of the longitudinal surface plasmon resonance of NRs allows tracking the decrease of their aspect-ratio.^13,53–55 In that regards, this impact visible to the naked eye on the optical response of the solution opens up new perspectives for sensing applications.⁵⁶ In this letter, we exploited LCTEM to directly image and control the oxidative etching gold NRs. For the first time, we found experimental conditions that allows visualizing the selective shortening of gold NRs at the nanoscale. These in situ investigations confirmed that this directional etching process requires reducing the etching power of the solution to make the tips of the NRs the only reaction site. Then, we combined HRTEM and atomistic simulations to establish the link between the anisotropic dissolution of NRs and their structural properties. We demonstrated that the higher reactivity of NR tips is not due to their intrinsic crystal structure but results from a less abundant citrate coating. These results highlight the key role of surface accessibility in corrosion processes and the necessity to consider the structure of organic/inorganic interfaces to understand the degradation of nanostructures.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We gratefully acknowledge the help of Yann Le Bouar for the use of the Nanofabric Software Developed for the geometrical construction of free or supported crystalline nanoclusters. We also acknowledge the financial support of the Region Ile-de-France (convention SESAME E1845 for the JEOL ARM 200F electron microscope installed at the University of Paris), the Labex SEAM, the CNRS and the ANR (CYCLYS project).

References

1. Y. Zheng, J. Zeng, A. Ruditskiy, M. Liu and Y. Xia, Chem. Mater., 2014, 26, 22–33.
2. R. Borup, J. Meyers, B. Pivovar, Y. S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson, F. Garzon, D. Wood, P. Zelenay, K. More, K. Stroh, T. Zawodzinski, J. Boncella, J. E. McGrath, M. Inaba, K. Miyatake, M. Hori, K. Ota, Z. Ogumi, S. Miyata, A. Nishikata, Z. Siroma, Y. Uchimoto, K. Yasuda, K.-I. Kimijima and N. Iwashita, Chem. Rev., 2007, 107, 3904–3951.
3. D. Friebel, D. J. Miller, D. Nordlund, H. Ogasawara and A. Nilsson, Angew. Chem., Int. Ed., 2011, 50, 10190–10192.
4. L. Lartigue, D. Alloyeau, J. Kolosnjaj-Tabi, Y. Javed, P. Guardia, A. Riedinger, C. Pechoux, T. Pellegrino, C. Wilhelm and F. Gazeau, ACS Nano, 2013, 7, 3939–3952.
5. Y. Javed, L. Lartigue, P. Hugounenq, Q. L. Vuong, Y. Gossuin, R. Bazzi, C. Wilhelm, C. Ricolleau, F. Gazeau and D. Alloyeau, Small, 2014, 10, 3325–3337.
6. J. Kolosnjaj-Tabi, Y. Javed, L. Lartigue, J. Volatron, D. Elgrabli, I. Marangon, G. Pugliese, B. Caron, A. Figuerola, N. Luciani, T. Pellegrino, D. Alloyeau and F. Gazeau, ACS Nano, 2015, 9, 7925–7939.
7. N. Feliu, D. Docter, M. Heine, P. del Pino, S. Ashraf, J. Kolosnjaj-Tabi, P. Macchiarini, P. Nielsen, D. Alloyeau, F. Gazeau, R. Stauber and W. Parak, Chem. Soc. Rev., 2016, 45, 2440–2457.
8. A. Balfourier, N. Luciani, G. Wang, G. Lelong, O. Ersen, A. Khelfa, D. Alloyeau, F. Gazeau and F. Carn, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 103–113.
9. Y. Jiang, G. Zhu, F. Lin, H. Zhang, C. Jin, J. Yuan, D. Yang and Z. Zhang, Nano Lett., 2014, 14, 3761–3765.
10. J. Hermannsdörfer, N. de Jonge and A. Verch, Chem. Commun., 2015, 51, 16393–16396.
11. J. B. Wu, W. P. Gao, H. Yang and J. M. Zuo, ACS Nano, 2017, 11, 1696–1703.
12. M. R. Hauwiller, L. B. Frechette, M. R. Jones, J. C. Ondry, G. M. Rotskoff, P. Geissler and A. P. Alivisatos, Nano Lett., 2018, 18, 5731–5737.
13. M. R. Hauwiller, J. C. Ondry, C. M. Chan, P. Khandekar, J. Yu and A. P. Alivisatos, J. Am. Chem. Soc., 2019, 141, 4428–4437.
14. A. Hutzler, B. Fritsch, M. P. M. Jank, R. Branscheid, R. C. Martens, E. Spiecker and M. Marz, Adv. Mater. Interfaces, 2019, 6, 1901027.
15. T. Su, Z. L. Wang and Z. W. Wang, Small, 2019, 15, 1900050.
16. J. Sung, B. K. Choi, B. Kim, B. H. Kim, J. Kim, D. Lee, S. Kim, K. Kang, T. Hyeon and J. Park, J. Am. Chem. Soc., 2019, 141, 18395–18399.
17. X. Ye, M. R. Jones, L. B. Frechette, Q. Chen, A. S. Powers, P. Ercius, G. Dunn, G. M. Rotskoff, S. C. Nguyen, V. P. Adiga, A. Zettl, E. Rabani, P. L. Geissler and A. P. Alivisatos, Science, 2016, 354, 874–877.
18. S. F. Tan, G. H. Lin, M. Bosman, U. Mirsaidov and C. A. Nijhuis, ACS Nano, 2016, 10, 7689–7695.
19. N. Ahmad, G. Wang, J. Nelayah, C. Ricolleau and D. Alloyeau, J. Microsc., 2018, 269, 117–133.
20. H. Shan, W. P. Gao, Y. L. Xiong, F. L. Shi, Y. C. Yan, Y. L. Ma, W. Shang, P. Tao, C. Y. Song, T. Deng, H. Zhang, D. R. Yang, X. Q. Pan and J. B. Wu, Nat. Commun., 2018, 9, 1011.
21. E. Sutter, K. Jungjohann, S. Bliznakov, A. Courty, E. Maisonhaute, S. Tenney and P. Sutter, Nat. Commun., 2014, 5, 4946.
22. N. Ahmad, G. Wang, J. Nelayah, C. Ricolleau and D. Alloyeau, Nano Lett., 2017, 17, 4194–4201.
23. D. Alloyeau, W. Dachraoui, Y. Javed, H. Belkahla, G. Wang, H. Lecoq, S. Ammar, O. Ersen, A. Wisnet, F. Gazeau and C. Ricolleau, Nano Lett., 2015, 15, 2574–2581.
24. Y. N. Xia, Y. J. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103.
25. H. Yuan, K. P. F. Janssen, T. Franklin, G. Lu, L. Su, X. Gu, H. Uji-i, M. B. J. Roeffaers and J. Hofkens, RSC Adv., 2015, 5, 6829–6833.
26. N. Almora-Barrios, G. Novell-Leruth, P. Whiting, L. M. Liz-Marzán and N. López, Nano Lett., 2014, 14, 871–875.
27. J. Feng, J. M. Slocik, M. Sarikaya, R. R. Naik, B. L. Farmer and H. Heinz, Small, 2012, 8, 1049–1059.
28. S. K. Meena and M. Sulpizi, Angew. Chem., 2016, 128, 12139–12143.
29. J. A. da Silva, P. A. Netz and M. R. Meneghetti, Langmuir, 2019, 36, 257–263.
30. S. K. Meena and M. Sulpizi, Langmuir, 2013, 29, 14954–14961.
31. H. Ramezani-Dakhel, L. Ruan, Y. Huang and H. Heinz, Adv. Funct. Mater., 2015, 25, 1374–1384.
32. C. Ricolleau, J. Nelayah, T. Oikawa, Y. Kohno, N. Braidy, G. Wang, F. Hue, L. Florea, V. P. Bohnes and D. Alloyeau, Microscopy, 2013, 62, 283–293.
33. Y. L. Bouar, http://zig.onera.fr/~lebouar/?page_id=35.
34. F. Ducastelle, J. Phys., 1970, 31, 1055–1062.
35. V. Rosato, M. Guillope and B. Legrand, Philos. Mag. A, 1989, 59, 321–336.
36. A. Chmielewski, J. Nelayah, H. Amara, J. Creuze, D. Alloyeau, G. Wang and C. Ricolleau, Phys. Rev. Lett., 2018, 120, 025901.
37. D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2002.
38. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
41. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1396.
44. C. Kittel, Introduction to Solid State Physics, Wiley, New York, 1996.
45. N. E. Singh-Miller and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235407.
46. A. Chmielewski, J. Meng, B. Zhu, Y. Gao, H. Guesmi, H. L. N. Prunier, D. Alloyeau, G. Wang, C. Louis and L. Delannoy, ACS Nano, 2019, 13, 2024–2033.
47. B. Zhu, H. Guesmi, J. Creuze, B. Legrand and C. Mottet, Phys. Chem. Chem. Phys., 2015, 17, 28129–28136.
48. F. W. Bader, Atoms in molecules: a quantum theory, Oxford Science, Oxford, UK, 1990.
49. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
50. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
51. S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930.
52. N. M. Schneider, M. M. Norton, B. J. Mendel, J. M. Grogan, F. M. Ross and H. H. Bau, J. Phys. Chem. C, 2014, 118, 22373–22382.
53. T. S. Sreeprasad, A. K. Samal and T. Pradeep, Langmuir, 2007, 23, 9463–9471.
54. C.-K. Tsung, X. Kou, Q. Shi, J. Zhang, M. H. Yeung, J. Wang and G. D. Stucky, J. Am. Chem. Soc., 2006, 128, 5352–5353.
55. R. Zou, X. Guo, J. Yang, D. Li, F. Peng, L. Zhang, H. Wang and H. Yu, CrystEngComm, 2009, 11, 2797–2803.
56. L. Saa, M. Coronado-Puchau, V. Pavlov and L. M. Liz-Marzán, Nanoscale, 2014, 6, 7405–7409.
57. B. Goris, S. Bals, W. Van den Broek, E. Carbó-Argibay, S. Gómez-Graña, L. M. Liz-Marzán and G. Van Tendeloo, Nat. Mater., 2012, 11, 930–935.
58. J.-W. Snoeck, G. Froment and M. Fowles, J. Catal., 1997, 169, 240–249.
59. W. H. Qi, M. P. Wang and G. Y. Xu, Chem. Phys. Lett., 2003, 372, 632–634.
60. L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202.
61. D. Alloyeau, T. Oikawa, J. Nelayah, G. Wang and C. Ricolleau, Appl. Phys. Lett., 2012, 101, 121920.
62. H. Al-Johani, E. Abou-Hamad, A. Jedidi, C. M. Widdifield, J. Viger-Gravel, S. S. Sangaru, D. Gajan, D. H. Anjum, S. Ould-Chikh, M. N. Hedhili, A. Gurinov, M. J. Kelly, M. El Eter, L. Cavallo, L. Emsley and J.-M. Basset, Nat. Chem., 2017, 9, 890–895.
63. J. Feng, R. B. Pandey, R. J. Berry, B. L. Farmer, R. R. Naik and H. Heinz, Soft Matter, 2011, 7, 2113–2120.
64. I. L. Geada, H. Ramezani-Dakhel, T. Jamil, M. Sulpizi and H. Heinz, Nat. Commun., 2018, 9, 1–14.
65. H. Heinz, R. Vaia, B. Farmer and R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr06326f

---