Amphiphilic gold nanoparticles perturb phase separation in multidomain lipid membranes

Abstract

Amphiphilic gold nanoparticles with diameters in the 2–4 nm range are promising as theranostic agents thanks to their spontaneous translocation through cell membranes. This study addresses the effects that these nanoparticles may have on a distinct feature of plasma membranes: lipid lateral phase separation. Atomic force microscopy, quartz crystal microbalance, and molecular dynamics are combined to study the interaction between model neuronal membranes, which spontaneously form ordered and disordered lipid domains, and amphiphilic gold nanoparticles having negatively charged surface functionalization. Nanoparticles are found to interact with the bilayer and form bilayer-embedded ordered aggregates. Nanoparticles also suppress lipid phase separation, in a concentration-dependent fashion. A general, yet simple thermodynamic model is developed to show that the change of lipid–lipid enthalpy is the dominant driving force towards the nanoparticle-induced destabilization of phase separation.

---

Introduction

The study of the molecular mechanisms of nanoparticle (NP)–lipid bilayer interactions is the first step towards the understanding of the biological effects of NPs on cell membranes. A better understanding of the NP–lipid interface at the fundamental level can assist the design and engineering of NPs with a controlled interaction with the membrane biological environment. Here we focus on monolayer-protected gold nanoparticles (Au NPs) that are designed to enter living cells for diagnostic or therapeutic purposes.^1,2 The NP size determines to a large extent the internalization mechanism: large NPs, with a diameter >10 nm, are usually internalized via active, endocytic pathways, while smaller NPs can access both the endocytic and the passive translocation pathway.³ In particular, small Au NPs functionalized by a mixture of hydrophobic and hydrophilic ligands have been shown to stably interact with model membranes⁴ and even translocate through cell membranes via energy independent mechanisms.^5,6 Experimental and computational approaches have joined their efforts in the last decade to elucidate the molecular mechanisms^7–10 of passive interaction between small metal NPs and model lipid bilayers, showing how all the physico-chemical characteristics of the NP–lipid interface, including NP surface chemistry,¹¹ patterning,^4,5,12–14 charge,¹⁵ and lipid composition,^16,17 concur with comparable influence to determine the fate of the NP at the bilayer surface.

On the lipid side of the NP–lipid interface, lipid heterogeneity is a key ingredient of any model system aiming to approach the complexity of biological membranes. In biological membranes, lipids can separate laterally into dynamic nanocompartments with distinct composition and physical properties.¹⁸ These nanocompartments, or rafts, are self-assembled and specialized nanodomains, enriched in cholesterol and glycosphingolipids (such as gangliosides).¹⁸ The lateral phase separation originating the liquid ordered phase of rafts provides different lipid and protein diffusion rates and the possibility of spatial compartmentalization and segregation; rafts are directly involved in receptor and protein trafficking processes, signal transduction, as well as endocytic and exocytic membrane translocation pathways.¹⁹ Multicomponent synthetic lipid membranes that exhibit spontaneous lipid phase separation into liquid ordered (Lo) and liquid disordered (Ld) lipid phases, on the micron scale, have long been used as synthetic models of raft-forming biological membranes. Recently, the direct imaging of both micro and nano domains in giant plasma membrane vesicles has reinforced the belief that the physical driving forces underlying phase separation in synthetic membranes are the same regulating the appearance of nanodomains in biological membranes.^20–22

Despite the important role played by rafts at biological level, the study of the effects of monolayer-protected metal NPs on the phase separation of model lipid bilayers is still in its infancy. For the smallest NPs (<4 nm in diameter), the fluidity of the liquid disordered phase seems to favor spontaneous NP-membrane interactions²³ and NP embedding;²⁴ another driving force for the localization of NPs in the Ld – Lo bilayer is the minimization of the hydrophobic mismatch between the NP and the lipid phase: a behavior that may be modulated by tuning the NP size, the degree of hydrophobicity and length of its ligand shell.^25,26 Larger metal NPs, which are expected to adsorb at the membrane surface without being embedded, have been also reported to affect lipid packing and membrane rigidity.^27,28 On the membrane surface, the curvature has been called into play as a driving force favoring the adsorption of cationic Au NPs at the boundary between liquid ordered and disordered domains.^23,29 Overall, the picture emerging from these works shows a subtle dependence of the interaction between NPs and phase separated bilayers on the NP size and surface, and on the lipid composition, structure and mechanical properties, but a comprehensive view is still lacking. And most importantly, with the available knowledge no prediction on the effect that a specific NP may have on the stability of phase separation can be attempted.

Here we consider amphiphilic Au NPs, with a diameter of 2–4 nm, functionalized by a mixture of hydrophilic (anionic) and hydrophobic ligands and study their interaction with a model multidomain bilayer whose lipid composition mimics that of the neuronal plasma membrane. Indeed, in neuronal membranes, rafts have been shown to regulate fundamental membrane functions, such as signal transduction and membrane elasticity, thus impacting the exocytosis of synaptic vesicles and the release of neurotransmitters.^19,30,31

We find, by atomic force microscopy (AFM) images and quartz crystal microbalance with dissipation monitoring (QCM-D) measurements, that Au NPs stably interact with the model neuronal membranes, leading to the formation of bilayer-embedded, two-dimensional, ordered NP supra-aggregates. We show that Au NPs can suppress lipid phase separation, in a concentration-dependent fashion. We interpret this result using a simple thermodynamic model and computational simulations. We show that upon addition of a small concentration of NPs in the bilayer, the change of lipid–lipid enthalpy is the dominant driving force towards the NP-induced destabilization of phase separation. Our model can be applied to any small, bare or monolayer-protected NP with a size comparable to the membrane thickness and, based on the knowledge of the NP surface functionalization and of the membrane lipid composition, it allows to predict whether the NP will have the tendency to stabilize or destabilize the lipid lateral phase separation.

Results and discussion

Experimental amphiphilic NPs and multidomain lipid membranes

Amphiphilic Au NPs having negative surface charge (NP−) were synthesized following a one-phase protocol (see the Experimental methods and Fig. S1†). The NP− core size was estimated by transmission electron microscopy (TEM) as 2.7 ± 0.8 (σ) nm. The Au core was functionalized by a thiol mixture composed of the hydrophobic 1-octanethiol (OT) and the negatively charged 11-mercapto-1-undecanesulfonate (MUS). Nuclear magnetic resonance (NMR) measurements, after decomposition, indicate a final MUS : OT ratio of 80 : 20. The NP− ζ-potential was −51 ± 5 mV, a value that assures colloidal stability. The vesicles representative of the neuronal plasma membrane (M1) are composed by 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), sphingomyelin (SM), cholesterol (chol) and ganglioside GM1 in the molar ratio DOPC : SM : chol : GM1 63 : 31 : 1 : 5.^32,33 M1 vesicles showed a ζ-potential of −64 ± 3 mV, due to the negatively charged GM1. This composition spontaneously leads to ordered – disordered lateral phase separation in the bilayer, with ordered domains enriched in SM, cholesterol and GM1.^18,29,34 Control experiments were performed on other two phase-separating membrane compositions showing ordered – disordered phase immiscibility:^32,35 M2 vesicles composed of DOPC : SM : chol 66 : 33 : 1 (molar ratio) and M3 vesicles composed of DOPC : DPPC : chol 40 : 40 : 20 (molar ratio), where DPPC is the saturated phospholipid 1,2-dipalmitoyl-sn-glycero-3-phosphocholine. Multidomain vesicles were then deposited on a solid substrate, where their rupture leads to the formation of a supported lipid bilayer (SLB). Fig. 1 shows the typical morphology of our multidomain SLB for the GM1-containing neuronal membrane with composition M1. The ordered phase is well visible, with domains having regular height profiles (Fig. 1a and b). The height difference between the two phases is Δz = 2.4 ± 0.3 (σ) nm, in agreement with previous AFM measurements on GM1-containing ordered domains.^32,36,37 Both the amount of large and small ordered domains and their lateral sizes display an intrinsic degree of variability within the sample, which is typical of the morphology of multidomain lipid bilayers (see also Fig. S2†). GM1-free M2 and M3 multidomain SLBs are reported in Fig. S3;† their Δz characterization is shown in Table S1 and Fig. S4.†

Fig. 1 Formation of ordered and disordered domains by segregation of lipid species in M1 SLBs. a AFM image showing the typical morphology of ordered – disordered phase separation; roundish ordered domains of different size are surrounded by the continuous disordered phase. b Height profile (bottom) of two ordered domains taken along the white dashed lines in the AFM image (top). c Top and side view of a disordered – ordered phase separation, at equilibrium, in the simulated model bilayer (DLiPC in red, SM in light pink, GM1 in yellow, chol in grey).

Computational models of the amphiphilic NPs and of the multidomain lipid bilayers

Our computational model of the ligand-protected NP− has a coarse grained resolution and is compatible with the Martini coarse grained force field³⁸ for biomolecular simulations. The model is described in detail in our previous publications.^9,39 Here, we consider NP− with an Au core diameter of 2 or 4 nm, functionalized by a mixture of MUS and OT ligands, in the 70 : 30 ratio (Fig. 2a). The in silico multidomain membranes are modeled by the Martini force field³⁸ as well. The model neuronal plasma membrane is composed by a mixture of 1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DLiPC), SM, cholesterol and GM1, in the proportion DLiPC : SM : chol : GM1 56 : 18 : 17 : 9 (Fig. 2b). The simulated M1 membrane contains a lipid with a double unsaturation and significantly more cholesterol than the M1 composition used in the experiments. This modification is necessary to obtain a stable Lo – Ld phase separation in the simulations, with Lo – Ld domains characterized by neat boundaries and stable over a long simulation time scale (about 50 μs, Fig. S5†). A snapshot of the membrane, with converged Lo – Ld phase separation, is shown in Fig. 1c. Control simulations have been performed also with the alternative composition M3, in which DOPC has been replaced by DLiPC, in the same proportion used in the experiments (DLiPC : DPPC : chol 40 : 40 : 20). The reliability of the Martini coarse grained model to look at the interaction between model anionic Au NPs and phosphatidylcholine bilayers has been thoroughly discussed in our previous works.^9,11,39 We showed⁹ that the absence of long-range electrostatic interactions of the standard Martini model accelerates the kinetics of NP-membrane interactions, but does not alter the nature of the molecular mechanisms involved.^39,40

Fig. 2 Coarse grained models of the NP− and the lipids used to assemble the in silico multidomain M1 membrane. a Ligand-protected NP− with diameter of 4 nm. Anionic hydrophilic ligands (MUS) in cyan, hydrophobic ligands (OT) in blue, Au atoms in yellow. b Structural formula and coarse grained representation of the lipids.

We first aimed at verifying by QCM-D and AFM in which experimental conditions the NP− interact with the multidomain supported bilayers. We tested two alternative methods to incorporate NP− into the lipid bilayer, as described in the following sections.

Amphiphilic NPs weakly adsorb on the SLB disordered phase

We injected the NP− in the QCM chamber after the formation of the M1 SLB. The frequency signal, shown in Fig. 3d, indicates that the NP− interact with the preformed SLB on a time scale of hours. The data confirm that the interaction is weak, leading to transient adsorption of NP− that can spontaneously desorb from the bilayer and can be completely removed by the sample upon rinsing. The maximum adsorbed mass, as calculated from the normalized frequency decrease in the first two hours, corresponds to 54 ng cm⁻² of NP−. After complete NP− removal by rinsing, the bilayer is intact, as indicated by the recovery of the starting frequency. Dissipation is almost not affected by NP−, and after rinsing the bilayer is as rigid as before NP− addition, confirming that NP− are not incorporated by the bilayer but are only weakly adsorbed on top of it. In AFM experiments, we deposited different amounts of NP− on preformed multidomain M1 SLBs and waited different incubation times before imaging, as detailed in the Experimental methods and in Fig. S6.† We could not observe any NP− in images taken 40 minutes after deposition, suggesting a weak interaction of monomeric NP− with the bilayer surface. Only after several hours, it was possible to observe large NP− clusters adsorbed on the bilayers (Fig. 3a–c), presumably formed as a consequence of nanoparticle diffusion on top of the bilayer. Even according to AFM the interaction between the NP− and the M1 SLB is weak, as the NP− clusters were often dragged by the AFM tip and most NP− clusters could be removed from the bilayer by rinsing.

Fig. 3 Incubation of NP− on preformed multidomain M1 SLBs: NP− slowly and weakly adsorb on the disordered phase. a AFM image acquired ∼40 min after the addition of NP− (20 μL, 0.12 mg mL⁻¹). b AFM image acquired ∼15 h after the addition of NP− (10 μL, 0.12 mg mL⁻¹). c AFM image acquired ∼40 h after the addition of NP− (40 μL, 0.12 mg mL⁻¹). NP− clusters are higher (i.e., lighter in color) than the ordered domains. d QCM-D curves showing the frequency variation, Δf, and dissipation variation, ΔD, recorded after NP− injection onto a preformed M1 SLB (7^th overtone). e Simulation snapshot of a NP− adsorbed onto Ld phase, at 5.2 nm from the membrane midplane. f Potential of mean force (PMF) profiles for the adsorption of a single NP− onto Lo and Ld phase of the GM1-containing membrane. See the Materials and methods section for PMF and error estimation details.

This weak adsorption of NP− on top of the supported bilayer is coherent with the state of the art knowledge about the mechanism of interaction between MUS : OT NP− and neutral phosphatidylcholine bilayers. The partial or total embedding of anionic NPs in the bilayer is characterized by large free energy barriers,^8,9 which can be lowered by the presence of defects.⁴⁰ The molecular mechanism allowing for the stabilization of the NP-membrane interaction requires the transient exposure of one or more hydrophobic lipid tails to the NP interface.^10,41 These lipid tail protrusions are more likely to take place at bilayer edges, such as those forming at the perimeter of hole defects in SLBs.⁴⁰ Our M1 SLB samples, though, are defect free on a scale of tens of μm (Fig. 3a–c and Fig. S7†). Furthermore, the physical constraints imposed by the solid support on the defect-free SLB is likely to suppress lipid dynamics in both in-plane⁴² and out-of-plane directions, slowing down the kinetics of NP-bilayer interactions.

As we observed in our AFM images that the vast majority of NP− clusters are located in the disordered phase of M1 SLBs (Fig. 3a–c), we used molecular dynamics (MD) simulations to understand what is the molecular mechanisms of adsorption of the NP− on the Ld phase and to quantify the thermodynamic advantage of the Ld–NP interaction over the Lo–NP interaction. In our MD simulations, when the NP− (of 2 and 4 nm in diameter) were initially placed in the water phase, not in contact with the membrane surface, either they spontaneously adsorbed onto the Ld phase (Fig. 3e), or they transiently adsorbed onto the Lo phase and then quickly (after ∼100 ns) diffused towards the Ld phase, where they remained for the rest of the simulated time (20 μs). On the Ld phase, the NP− adsorbed more stably and closer to the membrane midplane than on the Lo phase, as disorder allows for the necessary conformational adjustments of the lipid headgroups in contact with the NP−.

We calculated the free energy of adsorption of a single NP− on the surface of the Ld and Lo phase of M1 bilayers. The potential of mean force profiles shown in Fig. 3f indicate that the Ld phase, with a binding free energy of ∼18 kJ mol⁻¹ (∼9k_BT), is favored over the Lo phase (∼11 kJ mol⁻¹, ∼5k_BT). This substantial difference between the two phases agrees with the experimental results.

Membrane fluctuations influence NP uptake

The slow and relatively weak adsorption of NP− onto the preformed M1 bilayer is consistent with the previous experimental observation of little to no absorption of anionic Au NPs injected on GM1-containing multidomain SLBs of slightly different composition.²⁹ On the other hand, the same anionic MUS : OT Au NPs are known to interact stably with neutral phosphatidylcholine vesicles^4,43 and with multicomponent vesicles containing significant percentages of DOPC and SM.²⁴ Our previous computational results also indicate that the spontaneous incorporation of anionic MUS : OT Au NPs in free standing, liquid disordered phosphatidylcholine bilayers^9,11,39 is possible, though characterized by slow kinetics. Membrane fluctuations and unrestrained lipid diffusion in the vesicle bilayer allow for the transient defects that stabilize the contact with the anionic NP and, if the NP size permits it, also allow for the incorporation of the anionic NP into the bilayer core.

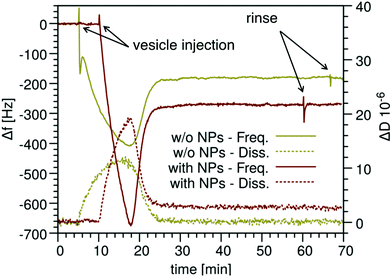
To overcome the motional constraints imposed on the membrane by the solid support and yet exploit AFM imaging and QCM-D investigation for the characterization of a stable NP-bilayer complex, we devised a second experimental set-up in which NP− are pre-incubated with multidomain lipid vesicles for a variable lag of time. After pre-incubation, the vesicles are deposited on the substrate (mica or the QCM-D sensor), where they rupture and form a SLB with embedded NP− (see the Experimental methods and Fig. S6†). Utilizing the QCM-D technique, we verified the uptake of NP− by the bilayer of pre-incubated M1 vesicles, as shown in Fig. 4. The QCM traces indicate the adhesion of a larger mass in the case of pre-incubated vesicles than without NP− during the entire process of SLB formation. The frequency shift when SLBs are formed corresponds to Δm = 267 ± 18 ng cm⁻². Interpreting this difference as the mass of the embedded NP−, we calculated that the number of embedded NP− is ≈0.017 NP− nm⁻². Since for the lipids we obtained a value of 1.34 molecule nm⁻², the calculated ratio between the number of lipid molecules and the number of NP− is ∼80 lipids/NP− (see the ESI† for details). Such a large NP− uptake is confirmed by AFM imaging, which we will discuss in detail in the next sections. To further confirm the role of membrane fluctuations in favoring the full embedding of NP− into the M1 bilayer, we monitored by QCM-D and AFM imaging the NP− uptake in a control membrane with a larger mechanical rigidity. M2 bilayers, which differ from M1 membranes only in the removal of the GM1 component, are expected to have a stiffer disordered phase than M1 bilayers.^37,44 After the same pre-incubation time of M2 vesicles with NP−, both QCM-D and AFM data, reported in Fig. S8,† confirm that the M2 composition shows a lower NP− uptake than the M1 composition.

Fig. 4 M1 SLB formation in the QCM-D chamber after deposition of lipid vesicles with and without NP−. Frequency variation (continuous lines), Δf, and dissipation variation (dotted lines), ΔD, recorded after injection in the QCM-D chamber of M1 lipid vesicles alone and M1 lipid vesicles pre-incubated with NP− for 4 h (7^th overtone). The vesicles alone were injected at t = 5 min, the vesicles pre-incubated with NP− at t = 10 min. The traces are typical of SLB formation via vesicle fusion. The adsorbed mass is higher in the case of the vesicles pre-incubated with NP−. When the vesicles attached to the substrate, a positive ΔD was recorded, indicating the presence of a viscoelastic film (i.e., the vesicles layer). During vesicle fusion ΔD decreased gradually to zero.

Now that we have devised an experimental protocol assuring a spontaneous, consistent and stable uptake of NP− into the M1 membranes, we can proceed with the investigation of the effects of NP− absorption on the properties of the multidomain bilayer.

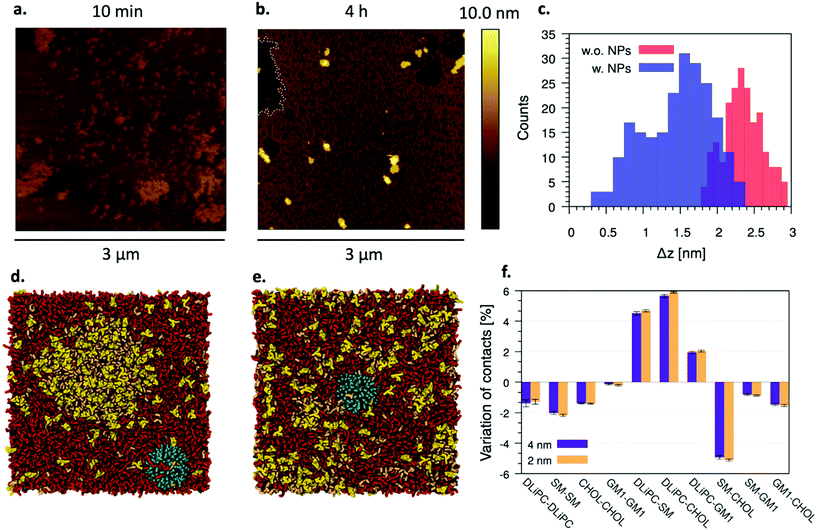
Amphiphilic NPs alter the membrane phase separation

Fig. 5a and b show the AFM images of M1 SLBs formed after vesicle pre-incubation with NP− for 10 min and 4 h, respectively. Contrary to what happens when preformed SLBs are incubated with NP− (Fig. 3a–c), only 10 minutes of vesicle pre-incubation with NP− are sufficient to alter the shape and compactness of ordered domains, which here have irregular shapes and ragged boundaries, with an overall morphology dramatically different from that observed in the absence of NP− (Fig. 1a and b). The distribution of the height difference (Δz) between ordered and disordered domains is way broader than without NP− and shifts from Δz = 2.4 ± 0.3 (σ) nm (without NP−) to Δz = 1.5 ± 0.5 (σ) nm after 10 min of pre-incubation, as shown by the histograms in Fig. 5c. When the NP− are pre-incubated for longer times (4 h in Fig. 5b), the ordered – disordered phase separation vanishes. Here, it is possible to identify sparse disordered patches and few NP− clusters, but most of the sample is characterized by a new rough phase containing both lipids and NP−. The structural features of this mixed NP-lipid phase will be discussed in more detail in the next sections.

Fig. 5 Alteration of ordered – disordered phase separation upon interaction between the M1 vesicle bilayer and NP−. a AFM image showing the ordered domain fragmentation induced by NP– (20 μL, 0.12 mg mL⁻¹) after 10 min of pre-incubation. b AFM image showing the disappearance of ordered – disordered phase separation induced by NP− (20 μL, 0.12 mg mL⁻¹) after 4 h of pre-incubation. The dashed white contour shows one of the sparse disordered patches within the new rough phase. c. Comparison of the distributions of height difference (Δz) between ordered and disordered domains in M1 SLBs without NP− (red bars) and in M1 SLBs deposited after 10 min of pre-incubation with NP− (blue bars). d Top view of a starting configuration from a simulation in which a single NP− (4 nm in diameter) is embedded in the Ld phase of a M1 membrane with a stable Lo – Ld phase separation. e End configuration (20 μs later), in which the lateral phase separation is no more appreciable. f Percentual variation of lipid-lipid contacts in the bilayer containing the NP−, with respect to the case in which the bilayer does not contain NP− and shows stable Lo – Ld domains. See the Materials and methods section for further details on the contact analysis and error estimation.

Our MD simulations also show that after the spontaneous adsorption of the NP− on the Ld phase (Fig. 5d), the Lo – Ld phase separation is altered and no clear Lo domain can be detected anymore (Fig. 5e, ∼20 μs later). We observe the disappearance of the Lo – Ld phase separation independently of the NP− size (2 or 4 nm in core diameter), and on the degree of NP− penetration into the membrane core. The mixing of the lipid species in the M1 bilayer can be quantified by means of lipid–lipid contacts; Fig. 5f shows the variation of lipid–lipid contacts in the simulated bilayer upon the incorporation of a single NP−. At equilibrium, the contacts between the unsaturated lipid, DLiPC, and the lipids that enrich the Lo phase (SM, cholesterol, and GM1) increase at the expense of all intra-domain contacts. The adsorption of the NP− on a bilayer with the same composition, but no lateral phase separation, is thermodynamically favored with respect to the adsorption on both the Ld and Lo phases, as shown by the free energy profile of adsorption reported in Fig. S9.†

Here, both AFM imaging and MD simulations indicate that the NP− can alter the membrane phase separation of the model neuronal membrane with composition M1.

In the next section, we propose a simple thermodynamic model to explain this behavior.

NPs disrupt phase separation by altering lipid–lipid interactions

In lipid bilayers, Lo – Ld spontaneous phase separation results from the minimization of Gibbs free energy. A lipid mixture that, at equilibrium, is found in the Lo – Ld coexistence state is such that:

ΔG_S→M = ΔH_S→M − TΔS_S→M > 0 (1)

The transformation from a phase separated bilayer (state S) to a mixed bilayer (state M) implies an enthalpic penalty (usually referred to as “enthalpy of mixing”) and an entropic gain.⁴⁵ The entropic term comprises both lipid configurational entropy and mixing entropy, the latter being the most significant. In the following, we will omit the S → M subscript for the sake of notation simplicity, but all energy differences will refer to an S → M transformation. We want to analyze the situation in which a phase separated membrane hosts a certain concentration of NP inclusions. We assume that the partitioning of the inclusions into the membrane hydrophobic core is favorable from a thermodynamic point of view, that is to say, we assume that the NPs penetrate the membrane core spontaneously. Once inside the membrane, the sign of ΔG^NP will determine whether the NPs cause lipid mixing or not:

ΔG^NP = ΔH^NP − TΔS^NP (2)

where the NP superscript indicates the presence of NPs in the bilayer. We further assume that the molar concentration of NPs remains way lower than lipid concentration, c_NP ≪ c_lip. If this condition is satisfied, ΔS^NP ∼ ΔS. The enthalpy difference is then what determines whether the membrane hosting the NPs will or will not have a different tendency to mix with respect to the membrane without NPs. There are two possible scenarios:

1. ΔH > ΔH^NP. In this case, the presence of NPs embedded in the Ld domain of the phase separated bilayer reduces the stability of the phase separated state. We expect the term ΔH^NP to depend on c_NP. There may be a threshold in the NP concentration, c_tr, at which the mixed state becomes equally favorable than the phase separated state (ΔH^NP = TΔS^NP). For concentrations higher than c_tr, the mixed state is favored over the phase separated state. This seems to be the case for the NP− in the M1 bilayer, in which phase separation is no more observed when a large number of NP− are embedded in the bilayer during pre-incubation (Fig. 4 and Fig. 5a and b);

2. ΔH^NP > ΔH. This means that the presence of NPs stabilizes phase separation. This stabilization may be due to different NP-lipid interactions. NPs may for example accumulate at phase boundaries driven by hydrophobic mismatch, reducing line tension at the Lo – Ld interface.²³ Or, NPs may have extremely favorable dispersion interactions with lipids in the Ld phase, such as fullerenes and other small hydrophobic molecules.^46,47

Relatively short equilibrium MD simulations allow for the explicit calculation of the enthalpic terms in eqn (1) and (2), as detailed in the ESI.† In this way, MD can be effectively used as a predictive tool to assess the propensity of NPs of different composition to alter or stabilize phase separation in multicomponent lipid bilayers. We thus calculated ΔH and ΔH^NP for NP− in M1 bilayers. We found that indeed ΔH > ΔH^NP, and conclude that the NP− inclusion in the bilayer core disfavors phase separation by altering the enthalpic gain associated with lipid–lipid interactions within Ld domains (Table 1). We also tested this approach on two control cases, in which both the NP surface chemistry and the bilayer composition were varied. We used hydrophobic nanoparticles and M3 membranes, as detailed in the ESI (Tables S2 and S4†). The model correctly predicts the effect of NPs on lipid lateral phase separation for both controls, as confirmed by experimental data taken from this work and from the literature.

Table 1 Enthalpies of the M1 bilayer with and without an embedded NP−. This table is expanded with the control cases in Table S2†

Membrane composition	ΔH S→M [kJ mol^−1]	NP type (NP/lipid molar ratio in simulation)	ΔH ^NP S→M [kJ mol^−1]	Model prediction	Exp. validation
M1 DLiPC : SM : chol : GM1 56 : 18 : 17 : 9 2850 lipids	+9.96 10^3	NP−(0.35 10^−3)	−1.2 10^3	destabilize phase separation already at low concentration	This work

---

Amphiphilic NPs form ordered supramolecular aggregates within the membrane

A more in-depth investigation of the new rough phase observed after pre-incubation of M1 bilayers with NP− for 4 h (Fig. 5b) revealed membrane patches displaying ordered NP− lattices. This behavior is completely absent after NP− incubation on preformed SLB (Fig. 3a–c and Fig. S7†). Fig. S12a† shows a representative image of these peculiar patches already after pre-incubation for 10 min. With a pre-incubation of only a few minutes, these lattices are isolated and not widespread. They become much more evident and uniformly distributed throughout the bilayer when the pre-incubation time is increased to a few hours. Fig. 6a shows the periodic NP− lattice observed after pre-incubation for 4 h. The supramolecular aggregate is quite regular, as shown by the digital zoom in Fig. 6a in which an ordered lattice is recognizable. The periodicity of the NP− lattice is highlighted also by the height profile of a NP− row and the Fourier transform shown in Fig. S12c and d,† respectively. The NP–NP distance is equal to 7.5 ± 0.1 nm, as shown by the histogram in Fig. 6b. The standard deviation, 1.6 nm, of NP–NP distances is consistent with the NP− size distribution. In addition, we measured the height difference Δz between these supramolecular aggregates and the disordered phase, by sampling the height step along the contour of disordered patches located within the widespread lattice (e.g., the one outlined by the dashed white contour in Fig. 5b). The histogram of Δz is shown in Fig. 6c and it reveals that the NP− are at least partially embedded into the bilayer, since Δz = 1.2 ± 0.3 (σ) nm, way below the mean NP− diameter (Fig. S13†).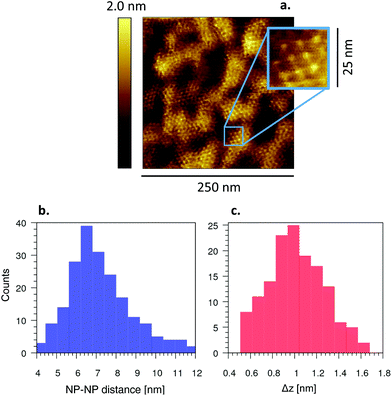

Fig. 6 Supramolecular lattice formed by M1 bilayer-embedded NP−. a Widespread NP− lattice, imaged by AFM, after 4 h of pre-incubation with NP− (20 μL, 0.12 mg mL⁻¹). Digital zoom of the area with blue contour showing the lattice order at higher magnification. b Distribution of NP–NP distances. c Distribution of the height of the supramolecular lattice, Δz, measured with respect to the disordered phase. Δz data have been collected along the contour of the sparse disordered patches located within the widespread NP− lattice (e.g., the one outlined by the white dashed line in Fig. 5b).

In order to assess the thermodynamic stability of NP− aggregates within the M1 bilayer, and characterize NP− aggregation with molecular resolution, we performed simulations in which two or more NP− were embedded in the bilayer. In unbiased simulations NP− with a diameter of 2 nm form transient dimers within the simulation time scale (10 μs). On the contrary, two NP− with a diameter of 4 nm spontaneously form a stable dimer, as shown in Fig. 7a and b. From a thermodynamic point of view, dimerization appears to be highly favored for 4 nm NP− (Fig. 7c). The fine size dependence of NP-bilayer interactions is expected in this specific system.⁴³ As a rule of thumb one may expect that, if NP aggregation is membrane-driven, it may be observed only for NPs whose size is comparable to or larger than the membrane thickness. Indeed, the characterization of membrane deformation when small, 2 nm NP− are embedded in the bilayer indicate little to no perturbation of the bilayer structure; on the contrary, NP− with a diameter of 4 nm can protrude significantly out of the bilayer. The NP− we consider (2 and 4 nm in diameter) are representative of the range of sizes of the experimental sample (Fig. S13†), and we speculate that the transition from the non-aggregation to the aggregation regime happens in between 2 and 4 nm in diameter. An in-depth exploration of this effect will deserve our attention in future work. Here we investigate in detail the structural features of the dimer formed by the 4 nm NP−. In between the NP− forming the dimer, the charged MUS ligands lead to the formation of a small nanopore,¹⁶ containing both counterions and water molecules (see Fig. 7b). Once formed, the pore is stable for several microseconds and does not grow in size, so that no further membrane damage has been observed. The formation of nanopores at the interface between adjacent NP− allows the ligands to re-orient all around the NP−. The different configurations adopted by the ligands when the NP− is embedded in the membrane in the monomeric and dimer state are shown in Fig. S14.†

Fig. 7 Simulations show the spontaneous aggregation of bilayer-embedded NP− into ordered aggregates. a Top view of the spontaneous dimerization of two NP− (4 nm diameter) embedded in the bilayer. b Side view of the NP− dimer, in which the formation of a nanopore is shown. Lipid headgroups are shown as semi-transparent surface, lipid tails are not shown for clarity, Na⁺ ions are shown in red and water in blue. c Potential of mean force (PMF) for the dimerization of 2 NP− (4 nm) embedded in the bilayer. In the inset, the NP–NP radial distribution function, g(r), obtained during the unbiased run with 7 NP− embedded in the bilayer. See the Materials and methods section for PMF and error estimation details. d Top view of the initial configuration of an MD simulation in which 7 NP− (4 nm), embedded in the bilayer, are let to freely diffuse in the bilayer. e Hexagonal aggregate spontaneously formed by the 7 NP− after 23 μs of simulations, and stable until the end of the run (30 μs). f Height profile of a single NP− and of a dimer of NP− (4 nm), averaged along the simulation time.

After having proved the spontaneous tendency to dimerization, we continued the investigation of NP− aggregation using bigger systems containing several NP− embedded in the bilayer. As a first test, we started with a preformed hexagonal lattice containing 7 NP− (see Fig. S15†) and we verified by unbiased MD simulations that the aggregate is stable for 10 μs. During this MD run small pores spontaneously formed between the NP−, as already observed for dimers. We also used a starting configuration (Fig. 7d) in which 7 NP− do not interact with each other, with the aim to assess if an ordered lattice can spontaneously form. After ∼23 μs of unbiased run, the NP− form a stable hexagonal aggregate (see the Movie S1†), in which the NP–NP distance nicely match the experimental data (first neighbor peak at 7.5 nm, shown in the inset of Fig. 7c). Once again, in between the NP− forming the hexagonal aggregate we can observe the spontaneous formation of small pores. On the microsecond time scale, nanopores can open and close several times, occupying in turn the interstitial space between different pairs of NP−.

Fig. 7f shows the protrusion of a single NP− and of a NP− dimer on top of the bilayer obtained from unbiased MD simulations. In both experiments and simulations, the NP− average height over the bilayer is way below the NP− diameter. This is coherent with a picture in which the NPs are partially embedded into the bilayer. More quantitatively, the slight difference of the height difference Δz between NP− and the disordered phase in simulations and in experiments (average protrusion of 1.5 nm in the simulations vs. 1.2 nm in the experiments, see Fig. 6c) can be attributed to the size dispersion of NP− in the experimental sample.

Materials and methods

The experimental uncertainties reported in the paper refer to standard errors. When the standard deviation (σ) is used, it is explicitly indicated.

Experimental methods

Materials for anionic NP synthesis. Gold(III) chloride trihydrate (HAuCl₄·3H₂O, ≥99.999% trace metal basis), 1-octanethiol (OT, ≥98.5%), sodium borohydride (NaBH₄, fine granular, ≥96%), ethanol absolute (>99.8%), anhydrous methanol (99.8%), methanol (≥99.9%), acetone (≥99.9%) were purchased from Sigma Aldrich and used without further purification. Sodium 11-mercapto-1-undecanesulfonate (MUS, 93%) was prepared in house applying few minor modifications to the procedure published by Guven et al.⁴⁸ Information on the MUS synthesis and purification is reported in the ESI (Fig. S16 and Tables S6 and S7†). All aqueous solutions were prepared using water purified with a Milli-Q ultrapure water system (MilliPore).

Anionic NP synthesis. To obtain amphiphilic and negatively charged NPs (NP−) we followed, with few minor modifications as reported in the ESI,† the one-phase approach described by Guven et al.⁴⁸ (Fig. S1†). Prior to all characterizations and experimental investigations, final NP− were suspended in water. The NP size distribution was measured by transmission electron microscopy (TEM) and dynamic light scattering (DLS). To check whether the final product was free from unbounded ligands and to characterize the MUS : OT ligand ratio, ¹H NMR analysis was performed before and after decomposition of the gold core, respectively. The colloidal stability of NP− dispersions was assessed by ζ-potential measurements.

Materials for multidomain lipid vesicle preparation. 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC, 18 : 1), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC, 16 : 0), sphingomyelin (SM) (brain, porcine), and ganglioside GM1 (brain, ovine – sodium salt) were purchased from Avanti Polar Lipids. Cholesterol (chol), chloroform (≥99.5%), and methanol (≥99.9%) were purchased from Sigma Aldrich. All chemicals were used without further purification; all aqueous solutions were prepared using water purified with a Milli-Q ultrapure water system (MilliPore).

Multidomain lipid vesicle preparation. Multidomain vesicles were prepared from the following lipid mixtures: DOPC : SM : chol : GM1 63 : 31 : 1 : 5, DOPC : SM : chol 66 : 33 : 1, and DOPC : DPPC : chol 40 : 40 : 20. These molar compositions are referred to as M1,³² M2³² and M3,³⁵ respectively. Only the M1 GM1-containing composition is representative of the neuronal plasma membrane. M2 and M3 compositions were used for control experiments. We used multidomain vesicles to prepare multidomain SLBs for both AFM and QCM-D investigations. Briefly, stoichiometric quantities of the four components dissolved in chloroform : methanol (2 : 1, v/v) were mixed and then dried under gentle nitrogen flux. The solvent evaporation was performed at 60 °C, above the transition temperature of all the lipids in the mixture. The dried lipid film was stored one day under mild vacuum and resuspended in water at a lipid concentration of 0.5 mg mL⁻¹. For QCM-D measurements, the film was hydrated to a lipid concentration of 1 mg mL⁻¹ in phosphate buffered saline (PBS; 1×) to help the merge of the vesicles on the sensor of the QCM-D chamber.⁴⁹ The lipid suspension was first sonicated for 15 min at 60 °C and then extruded 11 times at the same temperature to form unilamellar vesicles. Extrusion was performed using the Avanti Mini-Extruder (Avanti Polar Lipids) with a 100 nm pore size polycarbonate membrane. All vesicle suspensions were stored in a fridge at 4 °C and used within few days. Vesicle size distribution and colloidal stability were measured by DLS and ζ-potential measurements, respectively.

Electron microscopy analysis. Bright-field transmission electron microscopy (BF-TEM) images of NP− were collected using a Tecnai G2 F20 TWIN TMP TEM, operated at 200 kV. BF-TEM characterization allowed the investigation of both NP− core morphology and size. Sample preparation and results are reported in the ESI (Fig. S13 and Table S5†).

Dynamic light scattering and ζ-potential analyses. NP− and vesicle hydrodynamic size distributions in water were measured by dynamic light scattering (DLS) analysis. In addition, ζ-potentials were evaluated from electrophoretic mobility measurements to assess the colloidal stability of final suspensions. Both DLS and ζ-potential measurements were performed using a Malvern Zetasizer Nano ZS instrument (Malvern Instruments, UK). Sample preparation and results are reported in the ESI (Tables S5 and S8,† respectively for NP− and vesicles).

¹H NMR analysis. NMR spectra of NP− were recorded with a Varian Mercury Plus 300 (300 MHz for ¹H) spectrometer equipped with ATB (USA) broad band probe at 27 °C using as internal standard tetramethylsilane (TMS, 0.00 ppm). ¹H NMR analysis was used to assess the presence of unbound ligands and to assess the ligand shell composition, after decomposition of the gold core.⁴⁸ Sample preparation and results are reported in the ESI (Fig. S17†).

AFM analysis. We used atomic force microscopy (AFM) imaging to study both the morphology of M1, M2 and M3 multidomain SLBs and the effect of NP− on the phase separation. Tapping mode AFM images were acquired in liquid (Milli-Q water) using a Multimode SPM equipped with “E” scanning head (maximum scan size 15 μm) and driven by a Nanoscope V controller (Digital Instruments-Bruker). V-shaped silicon nitride cantilevers with an elastic constant of 0.24 N m⁻¹ (DNP-10, Bruker) were used. The drive frequency was in the range 12–14 kHz, the scan rate was in the range 0.5–1.5 Hz. All mean height differences (Δz) reported in the paper were calculated counting at least 200 values on 5 different AFM images. The same counting was considered for the NP – NP horizontal distance shown in Fig. 6b.

AFM samples without anionic NPs. For each bilayer, a diluted vesicle suspension (40 μL, 0.1 mg mL⁻¹) and a fresh CaCl₂ solution (10 μL, 10 mM) were deposited onto an approximately 1.0 × 1.0 cm² freshly cleaved mica foil glued on a metal support. Samples were stored for 10 min at room temperature and then incubated for 15 min at 60 °C in a close chamber at 100% relative humidity. The samples were let to cool down at room temperature and finally gently rinsed with Milli-Q water. This step is necessary to remove non-deposited vesicles from the liquid prior to AFM investigation. AFM imaging usually started at least two hours after rinsing.

AFM samples with anionic NPs. Aqueous NP− dispersions were filtered using a 20 nm pore size filter (Anotop 10, Whatman) before the interaction with multidomain membranes. The concentration of filtered dispersions was determined by absorption measurements after calibration, using a Jasco V-530 UV/VIS spectrophotometer. For all the experiments, a 0.12 mg mL⁻¹ (1.2 μm) filtered NP− stock solution was used. NP− were added to the multidomain bilayer following two different procedures: (a) in the incubation method, NP− were added on a preformed multidomain bilayer; (b) in the pre-incubation method, NP− were pre-incubated with multidomain vesicles before their deposition on mica and planar bilayer formation. A schematic drawing illustrating the two addition methods is shown in Fig. S6.† With the incubation method, a drop of NP− dispersion was cast onto a preformed multidomain SLB obtained as described above. The bilayer was rinsed with Milli-Q water immediately before NP− addition and no second rinse was carried out before AFM investigation. Different NP− volumes were tested (10–20–40 μL). Each bilayer was observed either shortly after the addition of NP− or after several hours (Fig. 3a–c and Fig. S7†). With the pre-incubation method, multidomain vesicles (40 μL, 0.1 mg mL⁻¹) and NP− (20 μL) were pre-incubated for different times (10 min and 4 h) before their deposition on mica and the addition of CaCl₂ to induce vesicle fusion. Each SLB sample prepared with this protocol was rinsed a few hours before AFM investigation. In both methods, NP− were let to interact with the multidomain membrane before AFM imaging. In the first method, NP− interact directly with a supported planar membrane, whereas in the second case the interaction takes place in the presence of the curved and free-standing membrane of the vesicle, without any constraints from the substrate.

QCM-D analysis. QCM-D measurements were performed with a QCM-Z500 (KSV, Finland) microbalance equipped with a thermostated flow chamber. SiO₂ coated gold sensors (resonance frequency 5 MHz) were used. Before usage, the sensors were subjected to UV/Ozone for 10 min. The higher harmonics 3^rd–11^th (overtones) were recorded every 1 s during all experiments. Before starting the measurement, the chamber and the access tubing to the chamber (pre-chamber) were filled with PBS and let to equilibrate at 40 °C until the frequencies of all overtones were stable.

QCM-D samples without anionic NPs. For bilayer formation, the concentrated vesicle suspension (1 mg mL⁻¹) was diluted in PBS to a final concentration of 0.25 mg mL⁻¹. The vesicle suspension (2 mL) was injected into the thermostated pre-chamber and let to equilibrate at 40 °C for 30 min. When all overtones were stable, the recording was started and the frequencies of all overtones set as baselines (i.e., frequency, f, and dissipation, D, zero values); after 300 s or 600 s the vesicle suspension was injected in the chamber, carefully avoiding microbubble formation. After the SLB formation the buffer was exchanged to PBS (thermostated at T = 40 °C) to remove the vesicle excess and subsequently exchanged to ultrapure water (thermostated at T = 40 °C). Finally, the temperature was set to T = 22 °C.

QCM-D samples with anionic NPs. Also in QCM-D measurements, NP− were added to the bilayer using the two procedures described for the AFM measurements (see Fig. S6†). As for AFM investigation, the same 0.12 mg mL⁻¹ filtered NP− stock solution was used for all experiments. In the case of the incubation method, after SLB formation and rinsing, a diluted NP− water dispersion (2 mL, 0.03 mg mL⁻¹) was injected in the pre-chamber, let to equilibrate at 22 °C for 20 min and then injected in the chamber. The monitoring of all overtones was carried out for 18 h, at a sampling rate of 10 s. The solution containing excess NP− was finally exchanged to ultrapure water. In the case of the pre-incubation method, vesicles (500 μL, 1 mg mL⁻¹) and NP− (500 μL) were added to PBS (1 mL), to obtain final concentrations of 0.25 mg mL⁻¹ and 0.03 mg mL⁻¹, respectively. Vesicles were incubated with NP− for 4 h; then, the vesicles suspension was injected in the QCM pre-chamber at 40 °C and let to equilibrate for 30 min before starting the measurement. The recording of f and D of all overtones was started immediately after vesicle injection in the chamber; the buffer was exchanged to PBS after vesicle fusion and SLB formation.

The data were interpreted in the assumption of rigid film formation; in this case, the Sauerbrey equation describes the relationship between Δf and mass variation (Δm): Δm = −CΔf, with C = 17.8 ng cm⁻² Hz⁻¹ (for a quartz crystal oscillating at 5 MHz).

Computational methods

Computational model of multidomain lipid membrane. The multidomain membrane is a quaternary mixture of DLiPC : SM : chol : GM1 56 : 18 : 17 : 9 modeled by the Martini coarse grained force field.^50,51 For GM1 we used the topology proposed by Dasgupta et al.:⁵² this parametrization combines the bonded parameters by López et al.⁵³ with the non-bonded parameters by Gu et al.⁵⁴ In this description, the tendency of GM1 to self-aggregation shows a good agreement with the experimental data and it does not suffer from strong clustering behavior as observed with alternative topologies. For the other lipids the standard Martini topology is used.^50,55 The membrane reference system consists of 2850 lipids solvated by approximately 35 coarse grained water beads per lipid and salt at a physiological concentration (150 mM); the final system size is 30 × 30 × 18 nm³. We started from a preformed multidomain membrane generated using the insane.py script⁵⁶ (see the ESI† for details). Then, the lipids diffuse from the Lo phase to the Ld phase and vice versa until the convergence of the number of contacts between the different types of lipids is reached (about 20 μs). The system is then simulated at equilibrium for 30 μs. The NP− are inserted in the aqueous phase of the equilibrated system resulting in the different configurations presented in the Table S9† together with all relevant simulation parameters. All the MD simulations were performed with Gromacs v. 2018.⁵⁷

Computational model of anionic NP. The core of the 2 nm NP− is made of 144 Au atoms and 60 S atoms, in an atomistic representation, as described in our previous works.^9,11,39 The core of the 4 nm NP−, instead, is a hollow sphere made of 346 Au atoms and 240 S atoms placed at the same distance from the center of the sphere, as shown in the ESI.† An elastic network with constant 1500 kJ mol⁻¹ and a cut-off of 0.8 nm, is used between Au–Au, S–S and Au–S atoms in order to maintain the spherical shape of the 4 nm NP−. The S atoms are randomly chosen on the NP surface in order to have the same ligand density of the 2 nm NP− (ρ_L = 4.78 ligands nm⁻²). The ligands are MUS and OT in 70 : 30 ratio, and their coarse grained Martini model is described in our previous publications.^9,39

Unbiased MD simulations. The full list of the unbiased simulations used in this work is reported in Table S9.† All the MD simulations were performed in the NPT ensemble: velocity rescale thermostat⁵⁸ was used to keep constant temperature (T = 310 K, τ_T = 1 ps) while the Berendsen⁵⁹ (τ_P = 4 ps) and the Parrinello–Rahman⁶⁰ (τ_P = 12 ps) barostats were used in the equilibration and production runs, respectively, to keep constant pressure (P = 1 bar), with semi-isotropic coupling. The time step used was 20 fs for all simulations, except for the reference membrane system (30 fs). van der Waals and electrostatic interactions were treated with the cut-off method (r_c = 1.1 nm, ε_r = 15).

Free energy calculations. The potential of mean force (PMF) profiles were derived by means of the umbrella sampling technique. The PMF profiles of the adsorption of the 4 nm MUS : OT 70 : 30 NP− on the Lo (DLiPC : SM : chol : GM1 1 : 45 : 16 : 38), Ld (DLiPC : SM : chol : GM1 72 : 10 : 12 : 6) and homogeneous (DLiPC : SM : chol : GM1 56 : 18 : 17 : 9, with no Lo – Ld domains) phase were calculated using, as a reaction coordinate, the vertical distance between the center of mass (COM) of the membrane and the COM of the NP−. The umbrella harmonic potential had a spring constant of 1000 kJ mol⁻¹ nm⁻². For each phase, windows of 0.15 nm width were used to sample the distance in the range 5–8 nm, for a total simulated time of about 12 μs and 24 μs for the equilibration and production runs, respectively. The starting configuration consisted of a NP− placed above the membrane, in the water phase. The membrane had either the composition of the Lo, Ld or homogeneous phase, and contained 574, 574 and 1346 lipids, respectively. Each lipid phase was equilibrated for 1 μs in order to ensure the membrane equilibrium. The lipid composition in the Lo and Ld phase were obtained with an in-house script relying on python MDAnalysis libraries.^61,62 The script is freely available upon request. The NP-membrane complex was solvated with coarse grained water, counter ions and physiological salt solution.

For what concerns the PMF profile of the NP− dimerization in the membrane, only the homogeneous phase was considered. The reaction coordinate was the distance between the NP− COM along the membrane plane and an umbrella potential with a spring constant of 400 kJ mol⁻¹ nm⁻² was used. To generate the PMF, 11 windows were used in the range 7–9 nm and 19 windows in the range 9–14.8 nm, for a total simulated time of 1.5 μs and 40 μs for the equilibration and production runs, respectively. In the starting configurations two NP− were placed inside the membrane at a given distance between them, performing a pre-equilibration of 50 ns, before starting the umbrella sampling window simulation. In that case, a box of about 31 × 31 × 13.5 nm³ with a membrane made of 2978 lipids, solvated with coarse grained water, Na⁺ counter ions, and physiological salt solution (150 mM), was previously generated and pre-equilibrated. All the PMF profiles and the associated error estimation via bootstrapping of trajectories were computed with the Gromacs tool wham.⁶³

Contacts analysis. The percentual variation of lipid–lipid contacts of Fig. 5f is computed as follows. First the lipid–lipid contacts as a function of the time are obtained with the Gromacs mindist tool with a cut-off distance of 0.8 nm. Then, they are averaged over time and normalized respect to the sum of all lipid–lipid contacts. The variation between the case with NP− and the case of pure bilayer is computed and plotted in Fig. 5f. The standard deviation is propagated accordingly.

Conclusions

We have shown, by means of AFM and QCM-D, that small, amphiphilic, and negatively charged Au NPs (NP−) can significantly perturb the lipid lateral organization of a model neuronal plasma membrane. These NP−, which have the peculiar capability to enter the cell via passive plasma membrane translocation,¹⁴ can alter the stability of ordered domains, leading to their suppression, and form stable, widespread supramolecular aggregates in which NP− are organized in ordered, two-dimensional lattices comprising NP− and lipids.

The NP− studied in this work disfavor phase separation in a concentration-dependent fashion: when the uptake is very large, as in our model neuronal membranes M1, the ordered – disordered phase separation vanishes. We have provided a simple thermodynamic model to interpret the effect of NP− on lipid phase separation. The model shows that the lipid–lipid enthalpy difference between the phase-separated and the mixed bilayer, with and without NPs, is the main physical indicator of the effect that the NP will have on lipid phase separation. The model is quite general: we tested it on three different NP-bilayer compositions and it can be applied to any NP embedded in the bilayer core and with a size comparable to the thickness of the bilayer. MD simulations can be used as effective tools to predict whether a specific NP will have the tendency to disrupt or stabilize the ordered – disordered phase separation.

We envisage that the same approach could be used to investigate the effects of other membrane inclusions, such as transmembrane peptides and proteins, on the lateral heterogeneity of lipid membranes.^64,65 Among transmembrane proteins one can find examples of both raft-stabilizing^66,67 and raft-destabilizing proteins.⁶⁸ These two opposite behaviors may also belong to the same protein in slightly different lipid environments. Gramicidin-A, for example, is a hydrophobic helical peptide that has been shown to partition in the disordered domain of DOPC/DSPC/cholesterol mixtures and then, depending on the relative lipid composition, stabilizes or destabilizes lipid lateral phase separation.⁶⁸

We also investigated in detail the formation of ordered NP− aggregates within the bilayer. The interaction of the single NP− with lipids is favored by hydrophobic contacts, and this explains the spontaneous incorporation of the monomeric NP− in the bilayer.^8,14 When a single NP− is embedded in the bilayer, though, its charged ligands are strongly confined to the polar interface of the membrane. Ligand flexibility is a peculiar feature of these monolayer-protected NPs. Thanks to the large flexibility of thiol ligands, the NP is able to adapt to different environments by exposing more or less hydrophobic surface to the surrounding. When embedded (or snorkeled) in the bilayer, the NP adopts a roughly cylindrical shape exposing its lateral surface, which is made of hydrophobic carbon chains, to the lipid tails, and its hydrophilic basis, covered by the sulfonate ligand terminals, to the water phase. Such a configuration closely resembles that of many transmembrane proteins. Taking the comparison further, the physical factors determining protein–protein aggregation in membranes are present also in the case of amphiphilic Au NPs. The presence of a hydrophobic mismatch between the protein (or NP) and the hosting lipid domain can cause protein (or NP) aggregation.^67,69 Protein- (or NP-) induced membrane curvature can also cause aggregation as a result of the minimization of membrane deformation. In the case of NPs, ligand flexibility, which is large compared to protein conformational flexibility, concur to stabilize NP aggregates: after NP–NP aggregation has taken place, the ligands re-orient all around the NP− and ion-stabilized transient water nanopores form in the interstices between adjacent NP− surfaces. An in-depth analysis of the different driving forces causing the aggregation of NP− in phosphocholine bilayers will be the object of future work.

We speculate that the combination of the NP targeting potential and the high degree of order of these NP aggregates within the membrane may be exploited also for sensing purposes, in vitro. The self-assembly of NPs in the bilayer environment may be exploited for the creation of new hybrid materials containing ordered two-dimensional NP lattices with selective response to electromagnetic radiation. As for NP applications in biomedicine, our data provide yet another evidence that the specific physical and chemical features of the nano-bio interface, involving both the NP surface functionalization and the bilayer composition, are crucial issues in shaping the nano-bio interaction. More efforts need to be devoted to the understanding of the molecular details of such interaction, also by means of combined experimental and computational approaches, towards the rational design of NPs as drug vectors, transducers, or imaging probes.

Author contributions

EC and SS contributed equally to the work. GR and AR conceived the idea. EC performed the nanoparticle synthesis, membrane preparation, DLS characterization and most of the AFM imaging and contributed to the MUS synthesis. SS performed most of the simulations. ALdM and DB performed the remaining of the computational work. DO and CC contributed to AFM imaging. SD performed the QCM-D measurements. CL performed all NMR characterizations and supervised the MUS synthesis. RB performed the TEM imaging. GR, AR, FC, CC, FS and DB supervised the different stages of the computational and experimental work. All authors discussed the results. GR, SS, EC and AR wrote the manuscript with contributions by all other authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

GR acknowledges funding from the ERC Starting Grant BioMNP 677513. EC thanks Manuela De Franco for her precious contributions to nanoparticle and MUS syntheses.

Notes and references

1. P. Pengo, M. Şologan, L. Pasquato, F. Guida, S. Pacor, A. Tossi, F. Stellacci, D. Marson, S. Boccardo, S. Pricl and P. Posocco, Eur. Biophys. J., 2017, 1–23.
2. S. Rana, A. Bajaj, R. Mout and V. M. Rotello, Adv. Drug Delivery Rev., 2012, 64, 200–216.
3. Y. Jiang, S. Huo, T. Mizuhara, R. Das, Y. Lee, S. Hou, D. F. Moyano, B. Duncan, X. Liang and V. M. Rotello, ACS Nano, 2015, 9, 9986–9993.
4. R. C. Van Lehn, P. U. Atukorale, R. P. Carney, Y.-S. Yang, F. Stellacci, D. J. Irvine and A. Alexander-Katz, Nano Lett., 2013, 13, 4060–4067.
5. A. Verma, O. Uzun, Y. Hu, Y. Hu, H.-S. Han, N. Watson, S. Chen, D. J. Irvine and F. Stellacci, Nat. Mater., 2008, 7, 588–595.
6. A. Verma and F. Stellacci, Small, 2010, 6, 12–21.
7. R. C. Van Lehn and A. Alexander-Katz, J. Phys. Chem. A, 2014, 118, 5848–5856.
8. R. C. Van Lehn and A. Alexander-katz, PLoS One, 2019, 14, e0209492.
9. S. Salassi, F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. C, 2017, 121, 10927–10935.
10. R. C. Van Lehn and A. Alexander-Katz, Soft Matter, 2015, 11, 3165–3175.
11. S. Salassi, E. Canepa, R. Ferrando and G. Rossi, RSC Adv., 2019, 9, 13992–13997.
12. P. Gkeka, L. Sarkisov and P. Angelikopoulos, J. Phys. Chem. Lett., 2013, 4, 1907–1912.
13. R. C. Van Lehn and A. Alexander-Katz, Soft Matter, 2014, 10, 648–658.
14. S. Sabella, R. P. Carney, V. Brunetti, M. A. Malvindi, N. Al-Juffali, G. Vecchio, S. M. Janes, O. M. Bakr, R. Cingolani, F. Stellacci and P. P. Pompa, Nanoscale, 2014, 6, 7052–7061.
15. A. Chompoosor, G. Han and V. M. Rotello, Bioconjugate Chem., 2008, 19, 1342–1345.
16. P. Angelikopoulos, L. Sarkisov, Z. Cournia and P. Gkeka, Nanoscale, 2017, 9, 1040–1048.
17. F. Lolicato, L. Joly, H. Martinez-Seara, G. Fragneto, E. Scoppola, F. Baldelli Bombelli, I. Vattulainen, J. Akola and M. Maccarini, Small DOI:10.1002/smll.201805046.
18. E. Sezgin, I. Levental, S. Mayor and C. Eggeling, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374.
19. Z. Korade and A. K. Kenworthy, Neuropharmacology, 2008, 55, 1265–1273.
20. I. Levental and H. Wang, J. Lipid Res., 2020, 61(5), 592–594.
21. F. A. Heberle, M. Doktorova, H. L. Scott, A. Skinkle, M. N. Waxham and I. Levental, PNAS, 2020, 117, 19943–19952.
22. G. Li, Q. Wang, S. Kakuda and E. London, J. Lipid Res., 2020, 61, 758–766.
23. J. K. Sheavly, J. A. Pedersen and R. C. Van Lehn, Nanoscale, 2019, 11, 2767–2778.
24. P. U. Atukorale, Y.-S. Yang, A. Bekdemir, R. P. Carney, P. J. Silva, N. Watson, F. Stellacci and D. J. Irvine, Nanoscale, 2015, 11420–11432.
25. X. Chen, P. Tieleman and Q. Liang, Nanoscale, 2018, 2481–2491.
26. X. Lin, X. Lin and N. Gu, Nanoscale, 2020, 12, 4101–4109.
27. A. Bhat, L. W. Edwards, X. Fu, D. L. Badman, S. Huo, A. J. Jin and Q. Lu, Appl. Phys. Lett., 2016, 109(26), 263106.
28. A. Tiwari, A. Prince, M. Arakha, S. Jha and M. Saleem, Nanoscale, 2018, 10, 3369–3384.
29. E. S. Melby, A. C. Mensch, S. E. Lohse, D. Hu, G. Orr, C. J. Murphy, R. J. Hamers and J. A. Pedersen, Environ. Sci. Nano, 2016, 3, 45–55.
30. J. Egawa, M. L. Pearn, B. P. Lemkuil, P. M. Patel and B. P. Head, J. Physiol., 2016, 594, 4565–4579.
31. A. Linetti, A. Fratangeli, E. Taverna, P. Valnegri, M. Francolini, V. Cappello, M. Matteoli, M. Passafaro and P. Rosa, J. Cell Sci., 2010, 123, 595–605.
32. R. Oropesa-Nuñez, S. Seghezza, S. Dante, A. Diaspro, R. Cascella, C. Cecchi, M. Stefani, F. Chiti and C. Canale, Oncotarget, 2016, 7, 44991–45004.
33. G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124.
34. N. Puff, C. Watanabe, M. Seigneuret, M. I. Angelova and G. Staneva, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2105–2114.
35. S. L. Veatch and S. L. Keller, Biophys. J., 2003, 85, 3074–3083.
36. M. Leri, R. Oropesa-Nuñez, C. Canale, S. Raimondi, S. Giorgetti, E. Bruzzone, V. Bellotti, M. Stefani and M. Bucciantini, Biochim. Biophys. Acta, Gen. Subj., 2018, 1862, 1432–1442.
37. M. Leri, F. Bemporad, R. Oropesa-Nuñez, C. Canale, M. Calamai, D. Nosi, M. Ramazzotti, S. Giorgetti, F. S. Pavone, V. Bellotti, M. Stefani and M. Bucciantini, J. Cell. Mol. Med., 2016, 20, 1443–1456.
38. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
39. F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. Lett., 2015, 6, 3175–3179.
40. R. C. Van Lehn, M. Ricci, P. H. J. Silva, P. Andreozzi, J. Reguera, K. Voïtchovsky, F. Stellacci and A. Alexander-Katz, Nat. Commun., 2014, 5, 4482.
41. M. A. Tahir, R. C. Van Lehn, S. H. Choi and A. Alexander-Katz, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1207–1215.
42. R. S. Gunderson and A. R. Honerkamp-Smith, Biochim. Biophys. Acta, Biomembr., 2018, 1860, 1965–1971.
43. P. U. Atukorale, Z. P. Guven, A. Bekdemir, R. P. Carney, R. C. Van Lehn, D. S. Yun, P. H. Jacob Silva, D. Demurtas, Y. S. Yang, A. Alexander-Katz, F. Stellacci and D. J. Irvine, Bioconjugate Chem., 2018, 29, 1131–1140.
44. N. Fricke and R. Dimova, Biophys. J., 2016, 111, 1935–1945.
45. P. F. F. Almeida, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 72–85.
46. J. Barnoud, G. Rossi and L. Monticelli, Phys. Rev. Lett., 2014, 112, 068102.
47. J. Barnoud, G. Rossi, S. J. Marrink and L. Monticelli, PLoS Comput. Biol., 2014, 10(10), e1003873.
48. Z. P. Guven, P. H. J. Silva, Z. Luo, U. B. Cendrowska, M. Gasbarri, S. T. Jones and F. Stellacci, J. Visualized Exp., 2019, e58872.
49. E. Reimhult, M. Zäch, F. Höök and B. Kasemo, Langmuir, 2006, 22, 3313–3319.
50. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
51. D. H. De Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Comput. Phys. Commun., 2015, 199, 1–7.
52. R. Dasgupta, M. S. Miettinen, N. Fricke, R. Lipowsky and R. Dimova, PNAS, 2018, 115(22), 5756–5761.
53. C. A. López, Z. Sovova, F. J. Van Eerden, A. H. De Vries and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 1694–1708.
54. R. X. Gu, H. I. Ingólfsson, A. H. De Vries, S. J. Marrink and D. P. Tieleman, J. Phys. Chem. B, 2017, 121, 3262–3275.
55. M. N. Melo, H. I. Ingólfsson and S. J. Marrink, J. Chem. Phys., 2015, 143, 243152.
56. T. A. Wassenaar, H. I. Ingólfsson, R. A. Bockmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155.
57. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25.
58. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
59. H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
60. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182.
61. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
62. R. Gowers, M. Linke, J. Barnoud, T. Reddy, M. Melo, S. Seyler, J. Domański, D. Dotson, S. Buchoux, I. Kenney and O. Beckstein, in Proceedings of the 15th Python in Science Conference, ed. S. Benthall and S. Rostrup, 2016, pp. 98–105.
63. J. S. Hub, B. L. de Groot and D. Van Der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720.
64. W. F. Zeno, A. Rystov, D. Y. Sasaki, S. H. Risbud and M. L. Longo, Langmuir, 2016, 32, 4688–4697.
65. C. S. Scheve, P. A. Gonzales, N. Momin and J. C. Stachowiak, J. Am. Chem. Soc., 2013, 135, 1185–1188.
66. C. S. Ho, N. K. Khadka, F. She, J. Cai and J. Pan, Langmuir, 2016, 32, 6730–6738.
67. L. V. Schäfer, D. H. de Jong, A. Holt, A. J. Rzepiela, A. H. de Vries, B. Poolman, J. A. Killian and S. J. Marrink, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1343–1348.
68. E. Hassan-Zadeh, F. Hussain and J. Huang, Langmuir, 2017, 33, 3324–3332.
69. S. Katira, K. K. Mandadapu, S. Vaikuntanathan, B. Smit and D. Chandler, eLife, 2016, 5, e13150.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr05366j

---