Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis of the atomic structure of CdS magic-size clusters by X-ray absorption spectroscopy†
Ying
Liu
 *a,
Lei
Tan
*a,
Lei
Tan
 a,
Giannantonio
Cibin
b,
Diego
Gianolio
b,
Shuo
Han
c,
Kui
Yu
c,
Martin T.
Dove
ade and
Andrei V.
Sapelkin
a,
Giannantonio
Cibin
b,
Diego
Gianolio
b,
Shuo
Han
c,
Kui
Yu
c,
Martin T.
Dove
ade and
Andrei V.
Sapelkin
 *a
*a
aCentre of Condensed Matter and Materials Physics, Queen Mary University of London, Mile End Road, E1 4NS, London, UK. E-mail: a.sapelkin@qmul.ac.uk
bDiamond Light Source Ltd, Harwell Science and Innovation Campus, Didcot, OX11 0DE, UK
cInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu, People's Republic of China
dDepartment of Physics, School of Sciences, Wuhan University of Technology, 205 Luoshi Road, Hongshan District, Wuhan, Hubei 430070, People's Republic of China
eCollege of Computer Science, Sichuan University, Chengdu 610065, People's Republic of China
First published on 16th September 2020
Abstract
Magic-size clusters are ultra-small colloidal semiconductor systems that are intensively studied due to their monodisperse nature and sharp UV-vis absorption peak compared with regular quantum dots. However, the small size of such clusters (<2 nm), and the large surface-to-bulk ratio significantly limit characterisation techniques that can be utilised. Here we demonstrate how a combination of EXAFS and XANES analyses can be used to obtain information about sample stoichiometry and cluster symmetry. Investigating two types of clusters that show sharp UV-vis absorption peaks at 311 nm and 322 nm, we found that both samples possess approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Cd
1 Cd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio and have similar nearest-neighbour structural arrangements. However, both samples demonstrate a significant departure from the tetrahedral structural arrangement, with an average bond angle determined to be around 106.1° showing a bi-fold bond angle distribution. Our results suggest that both samples are quasi-isomers – their core structures have identical chemical compositions, but different atomic arrangements with distinct bond angle distributions.
S ratio and have similar nearest-neighbour structural arrangements. However, both samples demonstrate a significant departure from the tetrahedral structural arrangement, with an average bond angle determined to be around 106.1° showing a bi-fold bond angle distribution. Our results suggest that both samples are quasi-isomers – their core structures have identical chemical compositions, but different atomic arrangements with distinct bond angle distributions.
Introduction
Inorganic quantum dots (QDs) are nanoparticles with dimensions of around 1–100 nm and exhibit significant size-dependent changes in their electronic and optical properties due to the quantum confinement effect.1–8 Thus, precise control of particle size is one of the critical elements in the synthesis of functional inorganic QDs. Over the past decades, several synthesis methods have been developed for this purpose, including molecular beam epitaxy, metal–organic chemical vapour deposition and colloidal techniques. The colloidal process, in particular, has been studied extensively due to a combination of simplicity and reproducibility.9 As a consequence, the unique properties of QDs and advances in their synthesis have resulted in them having a wide range of applications10 in multiple areas including bioimaging,11 quantum LEDs,12 lasers and electroluminescent devices.13 Virtually all the above applications rely on the ability to tune emission spectra with, preferably, narrow emission lines. While the emission peak position depends on the particle size and can now be precisely controlled, the emission linewidth is determined, among other things, by the particle size distribution, which is typically finite (i.e. when a system is not monodisperse). The latter is a consequence of the classical nucleation and growth process.14However, it has recently been found that during the nucleation process, persistent optical absorption peaks appear and remain sharp.15–27 Their peak position and width suggest that they originate from ultra-small particles of identical size (i.e. monodisperse). Mass spectrometry and optical absorption suggest that these QDs do not follow the continuous nucleation and growth model typical of colloidal synthesis. Recently, a two-pathway model was proposed for the development of colloidal QDs,28–30 the model of which contains the evolution of these particles, named magic-size clusters (MSCs) to distinguish them from the conventional ultra-small regular quantum dots (RQDs).
These MSCs show great promise in the atomic-scale control of QDs with electronic and optical properties engineered precisely for applications. Understanding the atomic structure of MSCs is essential for gaining insights into their electronic and optical properties, as well as for the understanding of their synthesis. Besides, it has recently been found31 that some CdS MSCs of size around 2 nm undergo a reversible isomerisation transition upon changing temperature in which one optical absorption peak will gradually disappear, and another peak grows with the two peaks located at 311 and 322 nm. However, the exact nature and the pathway of this transformation are still under debate. Recent work suggests that these two CdS MSCs possess different atomic structures,32 although the nature of the differences is unclear. This is a consequence of the significant challenges encountered using standard structural analysis techniques (e.g. X-ray and electron diffraction, Raman scattering, etc.) in the characterisation of ultra-small non-periodic systems. Recent analysis29 of MSCs’ structure using the X-ray pair-distribution function suggests that their atomic arrangements are different from those found in the bulk CdS (zinc blende or wurtzite structure) and the regular QDs (cubic, zinc blende structure). This prompted a random structure search approach33 that indicated a gradual transformation from a cage-like to a bulk-like structure as the number of atoms in a cluster increases. Despite these recent advances in structural characterisation, the atomic structure of the CdS MSCs is still under debate.
The combination of X-ray absorption near edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) analyses, in particular, has proved to be a robust methodology for the characterisation of complex systems.34–38 This approach can provide both local symmetry information (through XANES) as well as structural and stoichiometry information (through EXAFS) that can be used as an input for subsequent analysis of scattering data and computer modelling. Here we utilised X-ray absorption spectroscopy (XAS) to establish a rational basis for understanding the local atomic arrangement and Cd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio in MSC samples that undergo isomerisation transition.31
S ratio in MSC samples that undergo isomerisation transition.31
Results and discussion
It is previously established32 that the CdS MSCs with 311 nm and 322 nm (labelled as MSC-311 and MSC-322, respectively) optical absorption wavelength have a particle size of about 1–2 nm. Here, we used both EXAFS and XANES parts of the X-ray absorption spectra for the analysis of their atomic structures.Extended X-ray absorption fine structure and model-free data analyses
The recorded Cd K-edge EXAFS signals (k2χ(k)) following background removal and the corresponding magnitudes of Fourier transforms (FT) of CdS samples (MSC-311, MSC-322, RQD-355 and the crystalline reference) are shown in Fig. 1a and b. The RQD-355 sample is the RQD with an absorption wavelength of 355 nm. Here, k2χ(k) is the oscillation observed in the absorption coefficient as a result of photoelectron interference. From the k2χ(k) data in Fig. 1a, we can see the difference between the QD signals and the crystalline CdS signal as the latter contains a pronounced oscillation with a high-frequency wave (shown as grey circles) and a slower decaying amplitude at a high k range, indicating a more ordered structure. The discrepancies between the three QDs are relatively small. Some shifts in the oscillation between MSC-311 and MSC-322 can be spotted at 3, 6 and 8 Å−1, as shown in Fig. 1a (see dashed circles). This observation is consistent with the X-ray PDF result published previously32 as MSC-311 and MSC-322 showed different radial distance distribution functions in the long R range (5–15 Å) in the PDF.The corresponding FT magnitudes shown in Fig. 1b reveal the information about the atomic structure around the absorbing atom. Here, we observe differences in the radial distance peak position for the first peak (about 2.1 Å) and the second peak (about 3.8 Å). There is also a small reduction in the interatomic distance in the first FT peak position in the bulk–RQD–MSC sequence. The first peak in the bulk CdS at around 2.2 Å corresponds to the Cd–S shell at around 2.2 Å. The first shell in the CdS QDs is broader and shifted to a shorter distance. The signal from the second peak (Cd–Cd shell features prominently in the bulk CdS just below 4 Å) is very weak in RQDs and MSCs indicating a significant degree of disorder. The different locations of the second peak (3.5 Å vs. 3.9 Å, see the inset in Fig. 1b) in MSCs compared to the RQDs indicate significant bond angle distortions in these systems compared to the bulk crystalline sample. Furthermore, the MSC-311 sample shows no clear second shell (Cd–Cd) signal suggesting that the disorder is the largest for this sample. However, while apparent differences (at about 3, 8 and 10 Å−1) can be observed between the RQDs and MSCs in the k2χ(k) data, these are not as obvious in the corresponding FTs that look somewhat similar, especially the first peak. Hence, we used the Cauchy wavelet transform39 (see Fig. 1c), which is capable of visualising the EXAFS spectra in three dimensions: the wavevector k, the radial distance R and the wavelet transform modulus. The wavelet transformation could discriminate the overlapping radial distance peaks whose signals are derived from a different region in the k range. As a result, we determined multiple contributions to the first radial distance peak. Indeed, a split (indicated by arrows) was observed in the first peak originating from a low k range. It shows a substantial contribution to the overall shape from two sources. One is at a slightly shorter R (around 1.8 Å in Fig. 1b), and another one is at a longer R (about 2.2 Å in Fig. 1b), suggesting the presence of Cd–O bonding in the sample. Furthermore, on close inspection, the second peaks (at about 4.0 Å) in RQD-355 and MSC-322 shown in the wavelet transformation have similar patterns with a k-space contribution between 3 Å−1 and 12 Å−1. In contrast, in MSC-311, most of the input comes from the 2–8 Å−1 range. This is a clear indication of structural differences not only between the bulk CdS and nanoparticles, but also between the two MSCs.
Having identified detectable differences in the EXAFS signal between MSCs, we carried out a numerical analysis to further explore their nature. Our approach for EXAFS analysis is based on the modern X-ray absorption spectroscopy theory that a combination of experiments together with the data analysis can yield an agreement between the data and a model down to the noise level.40 The EXAFS signal χ(k) can be described by the following expression.41
 | (1) |
In the widely used EXAFS analysis package DEMETER,43 the oscillatory EXAFS signal is fit by a least-squares routine, but the analysis procedure requires a structural model as an initial guess in the fitting process. Such an approach works well for systems where a reasonable assumption can be made about the structure based on complementary information obtained from other sources. However, the problem with MSCs is that their structure is generally unknown. The bulk CdS structure may be a misleading initial guess since for small clusters a variety of structures can be stable (or metastable) depending on particle size.33
Hence, we carried out further refinement using a model-free approach44 (custom-written Python code) minimising the sum of squared residual45 between the fit results and experiment, while making no assumptions about the structure of the sample. Such an approach ignores MS calculations, but the MS provides a negligible contribution to the overall signal in low-coordinated systems with large disorder.40 In this model-free analysis, we treated the EXAFS signal of a single path as amplitude and as a frequency-modulated function of the form:
χj(k) = Aj(k)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2kRj + δj(k)) sin(2kRj + δj(k)) | (2) |
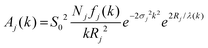 | (3) |
We considered three scattering paths to fit the EXAFS equation: Cd–O, Cd–S and Cd–Cd (second shell). Each path can be represented individually using eqn (1). The sum of three paths is χ(k), which corresponds to the experimental EXAFS signal. The amplitude term fj(k) and phase δj(k) have been extracted from eqn (2) and (3) using bulk CdS and CdO data with the procedure similar to that described previously.46 The corresponding structural parameters in the bulk references are listed in Table S1.† We compared extracted and calculated (using FEFF) scattering amplitudes and phases for the three scattering paths (see Fig. S1†). While the amplitude and phase are similar in the Cd–O path, the amplitudes in the other two paths are larger at a low k range and smaller at a high k range in the experimental data than the calculated ones. In the following analysis, we used parameters extracted from the experimental bulk reference to fit the model (eqn (1)) to the experimental data. The fitted parameters are NjS02 and σj2 in the three scattering paths: Cd–O, Cd–S and Cd–Cd, while Rj was defined based on the results of PDF analysis.29 The fitting process was carried out using a differential evolution algorithm47 to find an optimum of the minimum of the sum of squared residuals (SSR) between the experiment and the model. The SSR value was used to compare with the fitting in the widely used Artemis43 EXAFS analysis code. Note that for the given data range, the values of SSR are very sensitive to the signal-to-noise ratio, which depends on the number of averaged scans and the amount of sample in the beam. Hence, it is instructive to compare the SSR between the methods of analysis for a given sample and not between the samples for a given method. The fitted spectra for the three QDs and the bulk reference are shown in Fig. 2a where the positions and amplitudes of the fitted curves in both model-free approach and Artemis are in good agreement with the experimental data. We chose the model-free fit result rather than Artemis here since it utilised the backscattering amplitudes extracted from the experimental reference. The probability density histograms for the fitted coordination numbers are shown in Fig. 2b. The fitted variables for the model-free approach are listed in Table 1. The value of the amplitude factor, S02, is typically found to be close to 1.48 Thus, NjS02 can serve as a reference for the relative changes in Nj. The numerical analysis shows both MSCs have a similar coordination number, while RQD-355 shows a smaller Cd–O and larger Cd–S coordination number. The results suggest a reduction in the first shell Cd–S coordination numbers in the CdS bulk–RQD–MSC sequence, indicating a smaller particle size for MSCs. This is consistent with the PDF data reported previously.29 At the same time, the Cd–O coordination numbers show a slight increase, which is again consistent with the smaller particle size for MSCs and, therefore, a larger surface-to-volume ratio of Cd atoms. Furthermore, observation of the second coordination shell (Cd–Cd) in the FT magnitude MSC-322 (see the inset in Fig. 1b) provides an opportunity to calculate the average value of the Cd–S–Cd bond angle with the fitted Cd–S distance of 2.4881(98) Å and Cd–Cd distance of 3.9769(96) Å. This was found to be 106.1(1.1)°, which is lower than 109.47° expected for a perfect tetrahedral structure. The data also suggest that angle disorder is larger in the MSC-311 sample since no clear second shell signal can be seen.
| Scattering path | N j S 0 2 (mean) | Standard deviation | SSR | ||
|---|---|---|---|---|---|
| Model-free | Artemis | ||||
| RQD-355 | Cd–O | 2.67 | 0.37 | 0.85 | 0.64 |
| Cd–S | 3.05 | 0.30 | |||
| Cd–Cd | 5.76 | 3.31 | |||
| MSC-311 | Cd–O | 3.38 | 0.37 | 0.22 | 0.47 |
| Cd–S | 2.62 | 0.26 | |||
| Cd–Cd | 5.57 | 3.25 | |||
| MSC-322 | Cd–O | 3.24 | 0.38 | 1.08 | 1.24 |
| Cd–S | 2.57 | 0.27 | |||
| Cd–Cd | 5.40 | 3.28 | |||
The data in Table 1 clearly show that the Cd–S coordination number is lower than the value (4) found for the bulk CdS. This, together with the increase in Cd–O coordination, points to the large proportion of Cd atoms located at the surface of the QDs. Based on these observations, with the mass spectroscopy results31 of MSC-311 and MSC-322 (MSC mass ∼5160 Da), we can calculate the stoichiometry of CdxSy. The calculation is based on the following assumptions: (i) the MSCs remain four-coordinated; (ii) the S atoms are fully capped with Cd; and (iii) the clusters have a spherical shape. Considering the atomic masses of Cd (112.41 Da) and S (32.06 Da), we can write 112.41x + 32.06y ≈ 5160. Since MSCs are monodisperse particles, both x and y must be integers. Based on these assumptions and considering that the Cd–S coordination number in MSC-311 and MSC-322 is around 2.6 (see Table 1), we can write 4y/x ≈ 2.6. Solving for x and y gives x ≈ 39 and y ≈ 25, while constructing a spherical cluster, we arrive at the following three options that are close to the experimental data: Cd38S28, Cd39S24 and Cd40S21. Analysis of coordination in clusters gives the Cd–S coordination numbers of 2.95, 2.46 and 2.10, and atomic masses of 5169, 5154 and 5170 Da, respectively, with Cd39S24 showing a coordination number which sits closest to the MSC Cd–S coordination data shown in Table 1.
X-ray absorption near-edge structure
Having analysed the EXAFS data, we moved our attention to the near-edge part of the spectra that is sensitive to the oxidation states and the local symmetry. The XANES data (K and L3 absorption edges) for the bulk CdS, MSCs and their derivatives are shown in Fig. 3a and b. In Fig. 3a, all QD spectra show sharp absorption (“white line”) just above the absorption K-edge, while retaining some of the features of the bulk CdS spectrum. The sharp white lines at the Cd K-edge XANES of these QDs suggest the presence of oxygen around the Cd atoms. The data also indicate that there is a gradual evolution of the XANES as the cluster size is reduced (from bulk to RQDs to MSCs, see Fig. S2 in the ESI†), which is particularly evident for peak B. Still, evolution can also be seen for the peak A. These data suggest significant changes in the local atomic environment and/or local coordination. To shed light onto the origin of these changes, we investigated the L3-edge absorption spectra where the energy resolution is better49 (2.5 eV vs. 7.3 eV) than at the K-edge due to the decreased core-hole lifetime at the K-edge. Indeed, the experimental data (and XANES calculations for a number of CdS crystalline structures) for the crystalline CdS reference at the Cd K-edge show rather featureless spectra (see Fig. S3a†), while the Cd L3-edge data are rich in features between the 3530 eV and 3590 eV range (Fig. S3b†). The most obvious result here is the disappearance of the feature designated as peak C (see Fig. 3b) and the development of a prominent feature D at around 3560 eV. The gradual evolution of the spectra below 3560 eV suggest the increase of a local disorder without significant structural changes.To further explore the nature of the observed differences, we carried out XANES calculations utilising the FDMNES code,50–52 which uses a finite difference method to solve the Schrödinger equation in the model, and stoichiometric information we obtained from the EXAFS data. For this purpose, several structures were prepared, including crystalline systems and clusters. It is well known that the reduction of system size down to the nanoscale results in an increase of the surface-to-bulk ratio of atoms, inevitably leading to a more significant influence of surface oxides53,54 and contraction of the average bond length55,56 at the surface. The reduced bond length results in higher local electron density. Increased electron density is also found in materials under pressure.57,58 Therefore, it is logical to assume that these systems may adopt structures favoured under compression. Hence, we investigated the effects of (i) oxidation, (ii) structure (i.e. polymorphism) and (iii) size (e.g. bulk vs nanoscale) on XANES spectra. Within this context, the model systems with tetrahedral (F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, zinc blende) and octahedral (Fm
3m, zinc blende) and octahedral (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structures were investigated. Furthermore, it is known that the transformation path under compression in ultra-small semiconductor nanoparticles with the tetrahedral structure results in the octahedral-like distortion towards the β-Sn (I41/amd) structure.59 Hence, this structure has also been included in our simulations.
m) structures were investigated. Furthermore, it is known that the transformation path under compression in ultra-small semiconductor nanoparticles with the tetrahedral structure results in the octahedral-like distortion towards the β-Sn (I41/amd) structure.59 Hence, this structure has also been included in our simulations.
We first examined the effect of oxidation. From the calculated results of CdO as a function of the coordination shell number around the absorbing atom (see Fig. S4†), we quickly established that CdO is responsible for the feature D in the MSC XANES at around 3564 eV. We also established that the contribution of CdO in MSCs does not extend beyond the first coordination shell (see the evolution of the CdO XANES in Fig. S4†). Based on the simulated CdO spectra, the slight difference in the intensity of the feature D and the small energy shift (about 1.2 eV) between the MSC-311 and MSC-322 samples (indicated by an arrow in Fig. 3b) may be due to the different oxygen content in the MSC samples. The derivatives of the experimental spectra and the CdO single-shell model indicate that the latter reproduces some, but not all the features in the data. This is not surprising as we already know from the EXAFS analysis that Cd–S bonding is also present in all the samples.
We then investigated the possibility for several polymorphs of CdS to be responsible for the observed XANES signal. To this end, we attempted to reproduce the experimental data as a weighted sum of CdS and CdO with signals calculated within 3 Å around the absorbing atoms (Cd) from their corresponding crystal structures. We found that neither tetrahedral (F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, zinc blende), nor octahedral (Fm
3m, zinc blende), nor octahedral (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structures could adequately reproduce the experimental data (see Fig. S5 and S6†) with the β-Sn-like (I41/amd) arrangement providing the closest fit (Fig. S7†). These results suggest that there is some sort of systematic distortion of the tetrahedral structure (of which β-Sn-like arrangement can be considered as a limiting case59) in these systems.
m) structures could adequately reproduce the experimental data (see Fig. S5 and S6†) with the β-Sn-like (I41/amd) arrangement providing the closest fit (Fig. S7†). These results suggest that there is some sort of systematic distortion of the tetrahedral structure (of which β-Sn-like arrangement can be considered as a limiting case59) in these systems.
Having identified the β-Sn-like structure as a potential candidate, we prepared an oxygen-terminated cluster of a suitable size (based on the mass spectroscopy results31 and our EXAFS results above). We also introduced another candidate: the InP-like32,60 cluster structure that has been suggested previously to be a good atomistic model both for MSC-322 and MSC-311 clusters,34 while its stoichiometry (In37P20) fits well with our EXAFS data. Again, an oxygen-terminated cluster of a suitable size has been prepared for XANES calculations. The spectra (the sum of XANES calculations over all Cd atoms in the clusters) are shown in Fig. 3c and d, which demonstrate excellent agreement of the Cd37S20O94 InP-like signal with the experimental data (Fig. 3d). This is consistent with the X-ray scattering results reported previously.32 However, there is still a small discrepancy at around 3585 eV (see the arrow in Fig. 3d). This discrepancy can be accounted for the feature at about 3580 eV in the β-Sn-like cluster (Fig. 3c), thus suggesting that a related distortion may be present.
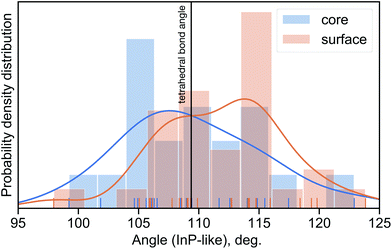
Considering the above-mentioned results, we analysed the bond angle distribution in the InP-like CdS cluster used for XANES calculations. The results are shown in Fig. 4, together with the corresponding angles of the perfect tetrahedral structure. The angle distribution analysis suggests that there is a tendency for bi-fold angle distribution with the maximum of the angle distribution in the core at around 107°, while the corresponding maximum at the surface is around 115°. The average bond angle for the core is in good agreement with the EXAFS data reported above where the value of 106.1(1.1)° was found. Therefore, we conclude that the introduction of bi-fold distortion into a perfect tetrahedral system results in a better agreement between calculations and experimental data and it is among such systems that one should be looking for potential candidates for a model structure.
Conclusion
The XAS data were analysed for two CdS MSC samples prepared by the colloidal synthesis method. The EXAFS analysis showed a reduced first coordination shell distance and a broader distance distribution around the Cd atoms in the MSCs than in the bulk reference. The split in the peak corresponding to the first coordination shell observed in the wavelet transformation indicated that the Cd atoms are also bonded with another element besides the S atoms. Both XANES and EXAFS show that the surface of the CdS clusters is capped with O bonded to Cd. We used a model-free structural analysis method to establish that the stoichiometric Cd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio of the MSCs is about 2
S ratio of the MSCs is about 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The XANES analysis revealed that out of several potential candidates examined, the InP-like structure reported previously32 results in the best fit to the data. We also show that the average bond angle in the core of CdS clusters is 106.1(1.1)° and is well below the value 109.47° expected for a perfect tetrahedral structure. Further analysis of the bond angle distribution in the InP-like cluster used for the best fit to the XANES signal shows evidence of bi-fold bond-angle distribution between the core and the surface of the CdS MSCs. Finally, combined EXAFS and XANES analysis suggests that it is the change in the bond angle distribution that is responsible for the recently observed31 thermally induced reversible structural isomerisation in these systems.
1. The XANES analysis revealed that out of several potential candidates examined, the InP-like structure reported previously32 results in the best fit to the data. We also show that the average bond angle in the core of CdS clusters is 106.1(1.1)° and is well below the value 109.47° expected for a perfect tetrahedral structure. Further analysis of the bond angle distribution in the InP-like cluster used for the best fit to the XANES signal shows evidence of bi-fold bond-angle distribution between the core and the surface of the CdS MSCs. Finally, combined EXAFS and XANES analysis suggests that it is the change in the bond angle distribution that is responsible for the recently observed31 thermally induced reversible structural isomerisation in these systems.
Overall, we conclude that the combination of EXAFS and XANES analyses can be used as an effective tool to investigate the structure of MSCs as it allows the establishment of sample stoichiometry and testing of potential structural models against the experimental data. These data can then provide effective guidance to construct atomistic models of MSCs.
Experimental and data analysis
Two CdS MSC samples and one RQD sample with UV-vis absorption peaks at 311 nm (MSC), 322 nm (MSC) and 355 nm (RQD) were analysed together with the CdS bulk reference. They were labelled after the type of QDs and their corresponding absorption peak positions as MSC-311, MSC-322 and RQD-355, respectively. Their absorption spectra are shown in Fig. S8.† MSC-311 could transform to MSC-322 after heating at 50 °C, while MSC-322 could transform back at a temperature lower than 25 °C. All the QD samples are synthesized in oleic acid, resulting in oleic acid capped products. XAS measurement (performed at beamline B18, step size: 0.4 eV and energy resolution: ΔE/E = 1.4 × 10−4) was carried out at the Diamond synchrotron light source. The EXAFS was recorded in liquid N2 at a temperature of 90 K for the Cd K-edge and at room temperature for the Cd L3-edge. The CdS bulk sample with the zinc blende structure (space group: F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) was used here as the reference to our experimental data.
3m) was used here as the reference to our experimental data.
The XAS data reduction and analysis were carried out using the DEMETER package43 and Pyspline61 in the standard way.46 The parameters used in the data reduction included the background removal threshold Rbkg (0.8), the k-window for FT (2–16.5 Å−1) and the k-weight (k2). The wavelet transformation was calculated with k2χ(k) data from the previous data reduction process. It used the code from the study by Munoz et al.39 Then we carried out the data analysis process in two routes: calculation and experiment. In the calculation route, parameters such as backscattering amplitude f(k), mean free path λ(k) and phase shift δ(k) were calculated with the bulk structure using FEFF.42,62 These parameters were then applied in DEMETER package43 to fit the QD samples. The QD samples were also fit using the in-house code in the experiment route. We filtered the EXAFS signal for their first Cd–S, Cd–Cd (in bulk CdS) and Cd–O (in bulk CdO) radial distance peaks. Then the f(k) related term and δ(k) corresponding to each distance peak were computed. In the fitting process, we used the differential evolution method to achieve the global minimum of the SSR between the experiment and the model for multiple variables. The fitting process was looped 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times to create probability density distribution for each variable.
000 times to create probability density distribution for each variable.
The XANES simulated spectra were measured using FDMNES.50 The finite difference method (FDM) was used for XANES calculations, which goes beyond the muffin-tin approximation typically used for multiple-scattering calculation for solving the excited state. The CdS zinc blende crystal structure was determined to verify the accuracy of FDMNES (see Fig. S9 in the ESI†). All clusters were relaxed using CrystalMaker63 prior to the XANES calculations.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
Y. L. and L. T. received financial support from the Chinese Scholarship Council and the Queen Mary University of London. This research utilised Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT.64 This work has been supported in part by the BBSRC (grant number BB/J001473/1).Notes and references
- A. Ekimov and A. Onushchenko, Sov. J. Exp. Theor. Phys. Lett., 1981, 34, 345 Search PubMed.
- L. E. Brus, J. Chem. Phys., 1984, 80, 4403–4409 CAS.
- A. I. Ekimov, A. L. Efros and A. A. Onushchenko, Solid State Commun., 1985, 56, 921–924 CAS.
- L. Brus, J. Phys. Chem., 1986, 90, 2555–2560 CAS.
- L. Brus, Curr. Opin. Colloid Interface Sci., 1996, 1, 197–201 CAS.
- A. P. Alivisatos, Science, 1996, 271, 933–937 CrossRef CAS.
- P. Alivisatos, in Pure and Applied Chemistry, 2000, vol. 72, pp. 3–9 Search PubMed.
- M. Cahay, Quantum Confinement VI: Nanostructured Materials and Devices: Proceedings of the International Symposium, Electrochemical Society, 2001 Search PubMed.
- Y. Masumoto and T. Takagahara, Semiconductor Quantum Dots: Physics, Spectroscopy and Applications, 2002 Search PubMed.
- J. Owen and L. Brus, J. Am. Chem. Soc., 2017, 139, 10939–10943 CrossRef CAS.
- W. J. Parak, D. Gerion, T. Pellegrino, D. Zanchet, C. Micheel, S. C. Williams, R. Boudreau, M. A. Le Gros, C. A. Larabell and A. P. Alivisatos, Nanotechnology, 2003, 14, R15 CrossRef CAS.
- S. Coe, W. K. Woo, M. Bawendi and V. Bulović, Nature, 2002, 420, 800–803 CrossRef CAS.
- V. I. Klimov, Science, 2000, 290, 314–317 CrossRef CAS.
- M. J. Enright, A. Ritchhart and B. M. Cossairt, Encycl. Inorg. Bioinorg. Chem., 2020, 1–11 Search PubMed.
- Z. A. Peng and X. Peng, J. Am. Chem. Soc., 2002, 124, 3343 CrossRef CAS.
- H. Wang, A. Tashiro, H. Nakamura, M. Uehara, M. Miyazaki, T. Watari and H. Maeda, J. Mater. Res., 2004, 19, 3157–3161 CrossRef CAS.
- A. D. Dukes, J. R. McBride and S. J. Rosenthal, Chem. Mater., 2010, 22, 6402–6408 CrossRef CAS.
- A. Kasuya, R. Sivamohan, Y. A. Barnakov, I. M. Dmitruk, T. Nirasawa, V. R. Romanyuk, V. Kumar, S. V. Mamykin, K. Tohji, B. Jeyadevan, K. Shinoda, T. Kudo, O. Terasaki, Z. Liu, R. V. Belosludov, V. Sundararajan and Y. Kawazoe, Nat. Mater., 2004, 3, 99–102 CrossRef CAS.
- Y. Wang, Y. Zhou, Y. Zhang and W. E. Buhro, Inorg. Chem., 2015, 54, 1165–1177 CrossRef CAS.
- M. J. Bowers, J. R. McBride and S. J. Rosenthal, J. Am. Chem. Soc., 2005, 127, 15378–15379 CrossRef CAS.
- B. S. Kudera, M. Zanella, C. Giannini, A. Rizzo, Y. Li, G. Gigli, R. Cingolani, G. Ciccarella, W. Spahl, W. J. Parak, L. Manna, S. Kudera, M. Zanella, C. Giannini, A. Rizzo, Y. Li, G. Gigli, R. Cingolani, G. Ciccarella, W. Spahl, W. J. Parak and L. Manna, Adv. Mater., 2007, 19, 548–552 CrossRef.
- Y. T. Nien, B. Zaman, J. Ouyang, I. G. Chen, C. S. Hwang and K. Yu, Mater. Lett., 2008, 62, 4522–4524 CAS.
- M. Li, J. Ouyang, C. I. Ratcliffe, L. Pietri, X. Wu, D. M. Leek, I. Moudrakovski, Q. Lin, B. Yang and K. Yu, ACS Nano, 2009, 3, 3832–3838 CrossRef CAS.
- J. Ouyang, M. B. Zaman, F. J. Yan, D. Johnston, G. Li, X. Wu, D. Leek, C. I. Ratcliffe, J. A. Ripmeester and K. Yu, J. Phys. Chem. C, 2008, 112, 13805–13811 CrossRef CAS.
- Q. Yu and C. Y. Liu, J. Phys. Chem. C, 2009, 113, 12766–12771 CrossRef CAS.
- M. Sun and X. Yang, J. Phys. Chem. C, 2009, 113, 8701–8709 CrossRef CAS.
- F. S. Riehle, R. Bienert, R. Thomann, G. A. Urban and M. Krüger, Nano Lett., 2009, 9, 514–518 CrossRef CAS.
- J. Zhang, L. Li, N. Rowell, T. Kreouzis, M. Willis, H. Fan, C. Zhang, W. Huang, M. Zhang and K. Yu, J. Phys. Chem. Lett., 10(11), 2725–2732 CrossRef CAS.
- J. Zhang, X. Hao, N. Rowell, T. Kreouzis, S. Han, H. Fan, C. Zhang, C. Hu, M. Zhang and K. Yu, J. Phys. Chem. Lett., 2018, 9, 3660–3666 CrossRef CAS.
- C. Palencia, K. Yu and K. Boldt, ACS Nano, 14(2), 1227–1235 CrossRef CAS.
- B. Zhang, T. Zhu, M. Ou, N. Rowell, H. Fan, J. Han, L. Tan, M. T. Dove, Y. Ren, X. Zuo, S. Han, J. Zeng and K. Yu, Nat. Commun., 2018, 9, 1–10 CrossRef.
- L. Tan, A. J. Misquitta, A. Sapelkin, L. Fang, R. M. Wilson, D. S. Keeble, B. Zhang, T. Zhu, F. S. Riehle, S. Han, K. Yu and M. T. Dove, Nanoscale, 2019, 11, 21900–21908 RSC.
- L. Tan, C. J. Pickard, K. Yu, A. Sapelkin, A. J. Misquitta and M. T. Dove, J. Phys. Chem. C, 2019, 123, 29370–29378 CrossRef CAS.
- B. Ammundsen, D. J. Jones and J. Rozière, J. Solid State Chem., 1998, 141, 294–297 CrossRef CAS.
- S. Kobayashi, I. R. M. Kottegoda, Y. Uchimoto and M. Wakihara, J. Mater. Chem., 2004, 14, 1843 RSC.
- B. Ammundsen, D. J. Jones, J. Rozière and G. R. Burns, Chem. Mater., 1996, 8, 2799–2808 CrossRef CAS.
- W.-S. Yoon, M. Balasubramanian, K. Y. Chung, X.-Q. Yang, J. McBreen, C. P. Grey and D. A. Fischer, J. Am. Chem. Soc., 2005, 127, 17479–17487 CrossRef CAS.
- D. Hara, J. Shirakawa, H. Ikuta, Y. Uchimoto, M. Wakihara, T. Miyanaga and I. Watanabe, J. Mater. Chem., 2002, 12, 3717–3722 RSC.
- M. Munoz, P. Argoul and F. Farges, Am. Mineral., 2003, 88, 694–700 CrossRef CAS.
- A. V. Sapelkin and S. C. Bayliss, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1–4 CrossRef.
- G. Bunker, Nucl. Instrum. Methods Phys. Res., 1983, 207, 437–444 CrossRef CAS.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513 RSC.
- B. Ravel and M. Newville, in Journal of Synchrotron Radiation, International Union of Crystallography, 2005, vol. 12, pp. 537–541 Search PubMed.
- G. Dalba, P. Fornasini, R. Grisenti, D. Pasqualini, D. Diop and F. Monti, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 4793–4802 CrossRef CAS.
- T. J. Archdeacon, Correlation and Regression Analysis: A Historian's Guide, University of Wisconsin Press, 1994 Search PubMed.
- D. C. Koningsberger, B. L. Mojet, G. E. Van Dorssen, D. E. Ramaker, G. E. Van Dorssen and D. E. Ramaker, Top. Catal., 2000, 10, 143–155 CrossRef CAS.
- R. Storn and K. Price, J. Global Optim., 1997, 11, 341–359 CrossRef.
- M. Roy and S. J. Gurman, J. Synchrotron Radiat., 1999, 6, 228–230 CrossRef CAS.
- M. O. Krause and J. H. Oliver, J. Phys. Chem. Ref. Data, 1979, 8, 329–338 CrossRef CAS.
- Y. Joly, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–10 CrossRef.
- O. Bunǎu and Y. Joly, J. Phys.: Condens. Matter, 2009, 21(34), 345501 CrossRef.
- S. A. Guda, A. A. Guda, M. A. Soldatov, K. A. Lomachenko, A. L. Bugaev, C. Lamberti, W. Gawelda, C. Bressler, G. Smolentsev, A. V. Soldatov and Y. Joly, J. Chem. Theory Comput., 2015, 11, 4512–4521 CrossRef CAS.
- S. Pokrant and K. B. Whaley, Eur. Phys. J. D, 1999, 6, 255–267 CrossRef CAS.
- H. Yoshida, S. Nonoyama and Y. Y. T. Hattori, Phys. Scr., 2005, T115, 813 CrossRef CAS.
- L. Pizzagalli, J. E. Klepeis and F. Gygi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1–5 CrossRef.
- W. Little, A. Karatutlu, D. Bolmatov, K. Trachenko, A. V. Sapelkin, G. Cibin, R. Taylor, F. Mosselmans, A. J. Dent and G. Mountjoy, Sci. Rep., 2014, 4, 1–6 Search PubMed.
- Z. Li and X. Peng, J. Am. Chem. Soc., 2011, 133, 6578–6586 CrossRef CAS.
- A. P. Alivisatos, S. H. Tolbert and A. P. Alivisatos, Science, 1994, 265, 373–376 CrossRef.
- N. R. C. Corsini, Y. Zhang, W. R. Little, A. Karatutlu, O. Ersoy, P. D. Haynes, C. Molteni, N. D. M. Hine, I. Hernandez, J. Gonzalez, F. Rodriguez, V. V. Brazhkin and A. Sapelkin, Nano Lett., 2015, 15, 7334–7340 CrossRef CAS.
- D. C. Gary, S. E. Flowers, W. Kaminsky, A. Petrone, X. Li and B. M. Cossairt, J. Am. Chem. Soc., 2016, 138, 1510–1513 CrossRef CAS.
- A. Tenderholt, B. Hedman and K. O. Hodgson, in AIP Conference Proceedings, 2007, vol. 882, pp. 105–107 Search PubMed.
- J. J. Rehr, J. J. Kas, M. P. Prange, A. P. Sorini, Y. Takimoto and F. Vila, C. R. Phys., 2009, 10, 548–559 CrossRef CAS.
- D. C. Palmer, Z. Kristallogr. – Cryst. Mater., 2015, 230, 559–572 CAS.
- T. King, S. Butcher and L. Zalewski, Apocrita – High Performance Computing Cluster for Queen Mary University of London, 2017 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Stoichiometry calculation procedures. See DOI: 10.1039/d0nr05186a |
| This journal is © The Royal Society of Chemistry 2020 |