Taming the thermodiffusion of alkali halide solutions in silica nanopores

Abstract

Thermal fields give rise to thermal coupling phenomena, such as mass and charge fluxes, which are useful in energy recovery applications and nanofluidic devices for pumping, mixing or desalination. Here we use state of the art non-equilibrium molecular simulations to quantify the thermodiffusion of alkali halide solutions, LiCl and NaCl, confined in silica nanopores, targeting diameters of the order of those found in mesoporous silica nanostructures. We show that nanoconfinement modifies the thermodiffusion behaviour of the solution. Under confinement conditions, the solutions become more thermophilic, with a preference to accumulate at hot sources, or thermoneutral, with the thermodiffusion being inhibited. Our work highlights the importance of nanoconfinement in thermodiffusion and outlines strategies to tune mass transport at the nanoscale, using thermal fields.

---

1 Introduction

Nanoscale devices are used in single molecule analysis,¹ mixing, pumping² separation of fluids,^3–5 or water desalination.^6–8 Many of these applications rely on nanometric insulating membranes, decorated with nanopores that span the membrane thickness (see e.g.ref. 1, 9 and 10). Nanopores can be used to regulate the transport of ions and macromolecules between two fluid reservoirs, while the fluid flow is driven by electrostatic,^8,11,12 pressure^13,14 or chemical potential gradients.¹⁵

Nanopores can be manufactured using a wide variety of materials: silica,^6,12,14–16 graphene,⁷ carbon nanotubes^2,3,11 or zeolites.^8,13 Some of these nanostructures were inspired by protein ion channels,¹⁷ hence providing a route to mimic the transport conditions in biological systems.¹⁸ Electrostatic fields are widely used to induce mass transport, while thermal fields have received less attention so far. However, recent studies demonstrated the use of thermal gradients in desalination processes, e.g. via reverse electrodialysis.¹⁹ Thermal gradients have the potential to open a whole new range of nanofluidic applications.²⁰

Here we investigate the thermodiffusion of alkali halide solutions confined in silica nanopores under the influence of thermal fields. Silicon based nanomaterials are suitable for device applications, since they feature excellent bio-compatibility and bio-degradability.²¹ These properties make silica a key material in wet technologies concerned with water desalination,⁶ biosensing,²¹ detection of macromolecules^22–24 or the separation of chemicals.⁵

Experimental and molecular simulations studies have shown that silica nanopores influence the structure and dynamics of confined water. As a matter of fact, the freezing temperature of water or the vapour pressure required for condensation are influenced by the confinement conditions.²⁵ These changes in the phase behaviour of water are accompanied by a general slowing down of the dynamics of the molecules with decreasing nanopore radius.²⁶ The diffusion coefficient decreases due to the adsorption of water at the nanopore surface.^27,28 The modification of dynamics of water and ions under confinement is of particular interest to us, since it might influence the thermodiffusive response of the solutions with respect to bulk, specifically the sign and strength of the Soret coefficient.

In this work we investigate the thermodiffusion of alkali halide solutions under nanoconfinement conditions. We study concentrated LiCl and NaCl solutions confined in nanopores made of amorphous silica. Using non-equilibrium molecular dynamics simulations we show that the interplay of the solution–silica interactions and the nanoconfinement influences the thermodiffusive response of the solutions. We show that changes in the temperature and salt composition result in enhanced thermophilicity of the solution or inhibition of thermodiffusion.

2 Methods

We show in Fig. 1 the model used in this work. The system consists of aqueous solutions of LiCl or NaCl confined in a silica nanopore. To simulate periodic systems in the direction of the thermal gradient we considered two nanopores, surrounded by a bulk solution. We applied a thermal gradient across the nanopore by heating or cooling one layer of atoms (the silanols groups) at the edges of the nanopore (see highlighted regions at T_C and T_H). The temperature gradient was applied across the nanopore by restraining the position of the silanol groups at the edge of the amorphous silica (ASiO₂) channel and thermostatting them at high (T_H = 400 K) and low (T_C = 200 K) temperatures. The thermal gradients were generated by rescaling the velocities of the atoms in the thermostatting regions indicated in Fig. 1, in magenta (hot layer) and cyan (cold layer). No thermostat was applied to the aqueous solution or the rest of the atoms inthe silica nanopore. The temperature rescaling was performed every time-step using the v-rescale thermostat,²⁹ with the temperature set at specific (H)ot and (C)old values, and the linear momentum reset every time-step (see ref. 30). At the stationary state, the nanopore separates two reservoirs at constant temperature, hot and cold, as shown in Fig. 1. Although the temperature gradient generated in the simulations is large, ∼30 K nm⁻¹, the response of the solutions is in the linear regime.⁴ We found that the temperature profile reaches the stationary result in ∼0.1–1 ns, while the concentration gradient requires significant equilibration times (τ_∇x), which can be estimated from the diffusion coefficient of the solution (D) and the distance between the hot and cold regions (L): τ_∇x ∼ L²/D. For typical values of D ∼ 10⁻⁹ m² s⁻¹ and L ∼ 6 nm, the relaxation time is τ_∇x ∼ 30–40 ns. We ensured the equilibration period was longer than this time. Our simulations involve equilibration times of 50 ns. The simulations were performed using the Leap Frog algorithm with a time-step of 2 fs. All the trajectories generated in this work were obtained using GROMACS v.4.63.³¹

Fig. 1 Snapshot of a LiCl aqueous solution confined in an amorphous silica nanopore under a thermal gradient ∼30 K nm⁻¹ and pore radius 1.5 nm. The ions are represented in green – Cl⁻ and violet – Li⁺ spheres, and the water molecules are shown in white – hydrogen and red – oxygen. The thermostatting layers are highlighted in cyan (cold layer) and magenta (hot layer) while the ASiO₂ channel is represented as a grey surface. This surface was generated by using a spherical probe of radius 0.2 nm. Pan Panels (a) and (b) show a section of the pore along the pore axis, and a top view perpendicular to the pore axis, respectively.

The silica nanopore was built from a pre-equilibrated configuration of bulk silica by carving a cylindrical pore. Further information on the procedure to build the amorphous silica nanopore is reported in the ESI.† To model silica interactions we used the CLAYFF force field,¹⁶ which predicts structural properties in close agreement with those measured using neutron diffraction data (see Table S2 in ESI†). The silica surface in contact with water was hydroxilated using the approach discussed in ref. 16 (see ESI†). This procedure results in a silanol density of 5.7 sites per nm² (calculated by considering the ratio between the number of silanol groups in the nanopore and the cylindrical area of the pore, namely 2πRL, where R is the radius of the pore, L is the pore length). This value is close to the surface density reported in previous simulations (6.6–7.6 sites per nm²),^6,16 and experiments (4.6–4.9 sites per nm²).³² We consider pH values consistent with no excess charge on the silica surface, similar to the simulations set-up studied in ref. 6, or more recently in ref. 33.

LiCl and NaCl aqueous solutions were modelled using the SPC/E model of water³⁴ and the force field by Dang et al.^35–38 for the ions interactions. We showed in our previous works that these force fields reproduce the experimental thermodiffusive behaviour of LiCl solutions, including the temperature and concentrations dependence, in particular the change in sign and minimum of the Soret coefficient.^39,40 The average concentration of salt in all our computations is 1.0 mol kg⁻¹, not far from the typical concentration of sea water. This concentration allows direct comparison of our results for confined solutions with previous data for bulk solutions. We performed simulations with 5 independent silica nanopores. The results were obtained by averaging the data for these different trajectories. The cumulative production time spanned typically 2–4 μs.

The thermodiffusion behaviour was investigated using two nanopores with radii 1.5 nm (R₁) and 2.0 nm (R₂), and temperature profiles covering the range 240–340 K. Experimental studies indicate that alkali halides feature a transition from thermophobic (enrichment of salt in the cold region) at high temperatures, to thermophilic behaviour (enrichment of salt in the hot region) at low temperatures.⁴¹ The temperature range chosen in our work targets the temperature range where the transition is observed, to assess the importance of confinement effects on the thermophilic character of the solutions.

The Soret coefficient was calculated from the analysis of the number fraction of salt, ∇x₁, and temperature, ∇T, gradients using the equation:⁴²

where x₁ and x₂ represent the number fraction of salt and solvent, respectively, and J₁ = 0 indicates that the calculation is performed in absence of a mass flux. The temperature dependence of the simulated Soret coefficients was fitted to the Iacopini et al.⁴³ empirical equation for further analysis, s_T(T) = s^∞_T[1 − exp((T₀ − T)/τ)], where s^∞_T and T₀ represent the asymptotic limit of the Soret coefficient and the inversion temperature, respectively, and the constant τ quantifies the temperature dependence of s_T.

We performed our simulations at 600 bar and ∇T ∼ 30 K nm⁻¹ in order to compare the thermodiffusive response of the confined solutions with the one reported in ref. 44 for bulk solutions. We reported previously that the Soret coefficient shows a small dependence with pressure in the range 100–600 bar.^40,44

3 Results and discussion

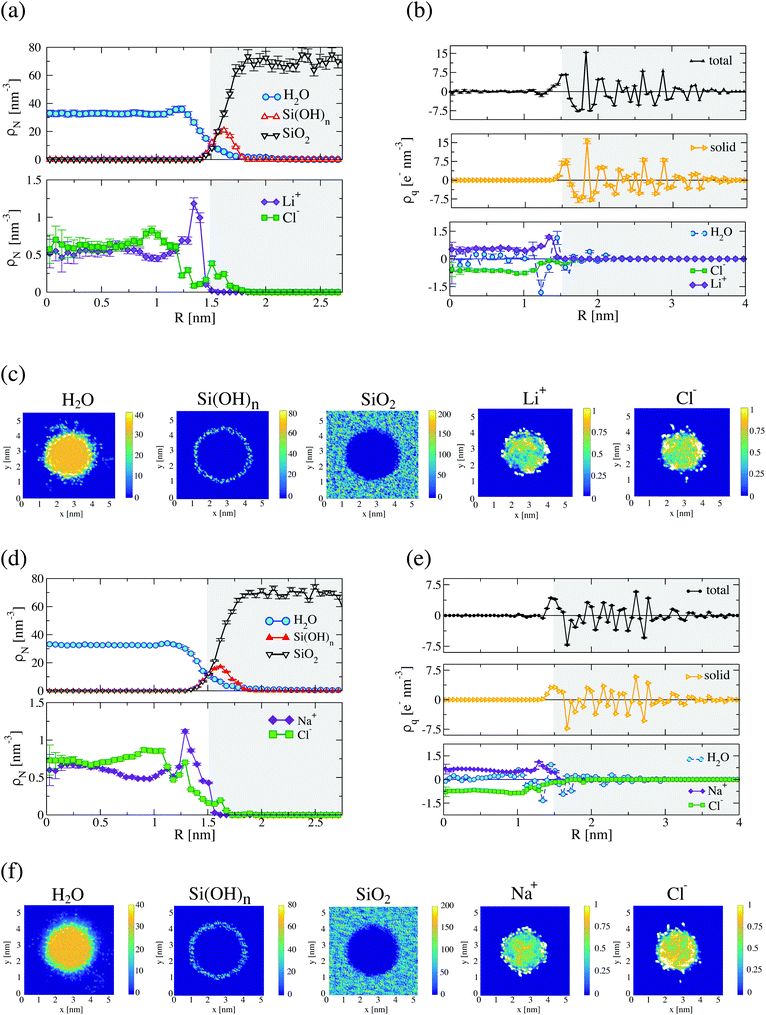
The structural properties of confined LiCl and NaCl aqueous solutions, were obtained from the analysis of the last 5 ns of the trajectory, using nanopores with radii R = 1.5 nm and R = 2 nm at temperature T = 300 K (see Fig. 2 and 3). Water interacts with the silica surface establishing hydrogen bonds. We observe a significant degree of overlap between water and the surface, and a slight enhancement of the water structure next to the surface (see Fig. 2(a) for LiCl and Fig. 2(d) for NaCl aqueous solutions). The analysis of the radial charge density (see Fig. 2(b) for LiCl and Fig. 2(e) for NaCl aqueous solutions) indicates that the water molecules reorient when they come in contact with silica, with the hydrogen atoms approaching the surface closer than the oxygen.^16,26,27,33 The roughness of the silica surface facilitates the percolation of water through the solid. This is reflected in the slow decay of the water density profile as it meets the silica surface (see Fig. 2(a and d) and Fig. S4 in the ESI†). Moving towards the interior of the pore the water density converges to the bulk value at 300 K (33 molecules per nm³) in about 1 nm from the surface. The adsorption of water in the pore is also evident in the contour density profiles (see Fig. 2(c) for LiCl and Fig. 2(f) for NaCl aqueous solutions), confirming the penetration of a small amount of water inside silica.

Fig. 2 Number and charge densities as a function of the radial distance from the pore axis for LiCl (a and b) and NaCl (d and e), respectively. The grey region represents the location of silica. (c and f) Contour densities on the x–y plane showing the number density of water, Li⁺, Na⁺, Cl⁻, silanol groups (Si(OH)_n, with n = 1, 2, 3) and silicon dioxide SiO₂. All the data correspond to a nanopore of radius R = 1.5 nm, temperature T = 300 K, and LiCl (a–c) or NaCl (d–e) aqueous solutions. The density was computed using cylindrical shells of width δr = 0.0549 nm.

Fig. 3 Normalised radial distribution functions g(r) and coordination numbers N_C for LiCl (a–f) and NaCl (g–l) solutions under bulk conditions (R_∞) and under confinement in nanopores of radii 1.5 nm (R₁) and 2.0 nm (R₂). OW and HW represent the oxygen and hydrogen atoms of water molecules and O and H the oxygen and hydrogen atoms at the silica surface. (c and i) Snapshots of the water solvation shells of Li⁺/Na⁺ (purple) and Cl⁻ (green) in bulk (left panels) and at the silica surface (right panels), respectively. All the results correspond to 300 K and the g(r) are normalised using their corresponding value at g(r = 1.5 nm). The oxygen and hydrogen atoms in the water molecules and the silanols groups in silica are represented with red and white spheres. Silicon atoms are represented as yellow spheres.

The densities of the LiCl and NaCl solutions in the nanopore of 1.5 nm radius are 1023.2 ± 8.8 kg m⁻³ and 1056.2 ± 5.9 kg m⁻³, respectively, very similar to the bulk densities of LiCl (1031.9 kg m⁻³) and NaCl (1055.7 kg m⁻³) at concentration 1.0 mol kg⁻¹ and 300 K. The number fraction of LiCl ions x_ions = x_Li + x_Cl = x_ions/(x_ions + x_water) = (4.5 ± 0.2) × 10⁻² at the surface is higher than that in the interior of the pore, x_ions = (3.50 ± 0.2) × 10⁻², highlighting the strength of the silica–ion interactions, which induces the formation of a double layer structure where a small amount of Cl⁻ ions adsorb around the silanol groups, and the Li⁺ adsorbs immediately above, with a concomitant depletion of Cl⁻ ions (see Fig. 2(a)). The number density profiles for NaCl solution are very similar (cf.Fig. 2(a and d)). Na⁺ adsorbs at the silica surface resulting in a density peak with number fraction x_ions = x_Na + x_Cl = x_ions/(x_ions + x_water) = (4.4 ± 0.2) × 10⁻². As for the LiCl case, the number density decreases reaching a lower value in the interior of the pore, x_ions = (3.93 ± 0.2) × 10⁻². Overall, the results show the stronger affinity of cations towards the silica surface.

The build up of double layers at the silica surface can be quantified using the radial charge density (see Fig. 2(b and e)). We observe charge separation at the surface, with the system reaching electroneutrality in ∼1 nm from the silica surface, i.e. a correlation length similar to that observed above for water. As a comparison, the Debye length that quantifies the screening of electrostatic interactions in bulk at 1 mol kg⁻¹ is ∼0.3 nm. The oscillatory behaviour of the charge densities (see Fig. 2(a and d)) highlights the importance of confinement and excluded volume effects in defining the interfacial structure of the ions in the nanopore.

The confinement disrupts the first solvation shell of the water molecules and of the ions. These changes are reflected in the radial distribution functions, g(r) (see Fig. 3) and the coordination numbers, N_C. The total coordination number is fairly constant, while part of the hydrogen bonds between water molecules are replaced by water–silica ones (see Fig. 3(a and b) for the LiCl solution and Fig. 3(g and h) for the NaCl solution). We find a stronger modification of the water structure in the NaCl solutions, with the total coordination number N_C,total = N_C,OW–HW + N_C,O–HW + N_C,OW–H changing from 3.7 in the bulk to 3.4 for nanopore with radius R₁ = 1.5 nm, showing a dehydration of the water molecules under confinement conditions. The amount of salt in the nanopore does also change with the nanopore radius: at temperature 300 K, the average mole fraction of NaCl inside the R₁ pore is x_ions/(x_ions + x_water) = (1.89 ± 0.1) × 10⁻² and (1.65 ± 0.1) × 10⁻² for LiCl, while it increases to (2.27 ± 0.1) × 10⁻² and to (2.20 ± 0.1) × 10⁻² for NaCl and LiCl, respectively, in the pore of radius R₂ = 2 nm.

The hydration shell of the ions is also influenced by the interactions with silica. Li⁺ features a strong solvation shell in bulk, and it is coordinated to four water molecules in a tetrahedral arrangement (see snapshot in Fig. 3(c and i)). In contact with the surface, Li⁺ looses part of its solvation shell, and it coordinates with the negatively charged groups in silica, namely the dangling oxygen ≡SiO⁻ and the siloxane bridges ≡Si–O–Si≡ (see Fig. 3(c, d and f)). The Cl⁻–water coordination number also decreases upon adsorption, with Cl⁻ ions loosing about one water molecule, which is replaced by coordinating to the silanol groups, OH (see snapshots in Fig. 3(c) and radial distribution function and coordination number in Fig. 3(e and f)). The hydration shells of Na⁺ and Cl⁻ change in a similar fashion with the nanopore radius (see Fig. 3(i) for snapshots of the solvation shell, Fig. 3(j and k) for radial distribution functions and Fig. 3(l) for variation of the coordination number with the pore size). In bulk, Na⁺ binds to the solvation water less strongly than Li⁺. We find that under confinement conditions Na⁺ looses 2 molecules of water, resulting in a higher dehydration, and under-coordination with respect to the bulk system.

We have demonstrated above that confinement influences the structure of the solutions. This should be reflected in the thermodiffusive response of the confined solutions. To address this point we applied a temperature gradient across the nanopores using the nanopore radii, R₁ = 1.5 nm and R₂ = 2 nm. The solutions reach the stationary state in ∼36 ns, and developing well defined temperature and concentration profiles. We have represented in Fig. 4(a) and (b) the temperature profiles along the z axis, and on the y–z plane, respectively.

Fig. 4 Temperature and density profiles along the nanopore axial direction. (a) Total temperature along the y–z axis obtained as a projection of the 3-D temperature profile of the total system for nanochannel of radius R₁ = 1.5 nm. (b) Individual contribution to the temperature profile along the z axis for R₁. Concentration profile of 1.0 mol kg⁻¹ LiCl (c) and NaCl (d) aqueous solutions along the confined systems for ASiO₂ of radius 1.5 nm (R₁ – top panel) and 2.0 nm (R₂ – bottom panel). The concentration profile of Li⁺ or Na⁺ ions are represented as violet diamonds, and Cl⁻ as green squares. A snapshot of the pore is shown in each panel to indicate the location of SiO₂ (grey) and the thermostats (hot – red, cold – cyan).

The regions containing the bulk solutions, at both sides of the nanopore, are at constant temperature (see Fig. 4), determined by thermostats, T_H (higher temperature) and T_C (lower temperature). As expected, these bulk solutions do not feature a concentration gradient. We obtain a well defined thermal gradient along the nanopore, with a temperature drop between the hot and cold regions equivalent to a thermal gradient of ∇T ∼ 30 K nm⁻¹. The magnitude of this gradient is within the normal range employed in non-equilibrium molecular dynamics simulation studies, e.g. of bulk water and LiCl aqueous solutions.^30,39 It was demonstrated in those works that the solutions feature a linear response for gradients of this magnitude. The temperature of the confined solution is very similar to the temperature of the silica nanopore, with some thermal slip connected to the different thermal transport properties of silica and the aqueous solution. Similar behaviour has been reported before in simulations of simple models of nanopores.⁴ The temperature decreases along the axial direction of the nanopore without noticeable changes in the radial direction (see Fig. 4(a)).

At the stationary state the density of LiCl solutions in the cold and the hot reservoirs are slightly different ρ = 1054.3 ± 3.4 kg m⁻³ and 986.5 ± 0.8 kg m⁻³, respectively. The concentration of salt is also different (see Table 1 for data corresponding to all the systems investigated in this work). These changes in density can be understood in terms of thermal expansion. The average concentration of salt in the small and large nanopore are slightly different: 1.38 ± 0.18 mol kg⁻¹ for the larger pore and 0.98 ± 0.18 mol kg⁻¹ for the narrower. These small changes in the average concentration do not influence significantly the thermodiffusive response in that concentration and temperature range analysed,⁴⁴ and, therefore, a comparison of the results obtained with both nanopores is possible.

Table 1 Concentration of salt in mol kg⁻¹ in the hot and cold reservoir and inside the pore for nanopores of radius 1.5 nm (R₁) and 2.0 nm (R₂)

	R 1			R 2
	Hot reservoir	Cold reservoir	Nanopore	Hot reservoir	Cold reservoir	Nanopore
LiCl	0.950 ± 0.017	0.907 ± 0.020	1.048 ± 0.055	1.181 ± 0.016	1.080 ± 0.013	1.446 ± 0.044
NaCl	0.950 ± 0.022	0.822 ± 0.029	1.106 ± 0.045	1.273 ± 0.028	1.180 ± 0.020	1.436 ± 0.047

---

We calculated the Soret coefficient by analysing the local temperatures and concentrations along the pore (see Fig. 5(a and b) for LiCl and Fig. 5(c and d) for NaCl aqueous solutions). We compare our results with the data obtained in ref. 39 and 45 for bulk solutions in the same temperature range and for the same models investigated in this work. Bulk solutions feature clear maxima, indicating a change in sign of the Soret coefficient, at T₀ ∼ 300 K (LiCl) and T₀ ∼ 260 K (NaCl). Under confinement conditions, the maxima shift to higher temperature, or disappear (cf. data for R₁, R₂ and R_∞ is Fig. 5). At low temperature, <T₀, both LiCl and NaCl solutions are thermophilic, and the salt accumulates in the hot region. Confinement effects have little impact on the sign of the Soret coefficient at low temperatures. However, confinement effects become important at T > T₀. At 340 K the Soret coefficient of LiCl changes significantly, becoming negative (thermophilic solution) for the smallest nanopore, R₁. Similar behaviour is observed in NaCl solutions. In this case, confinement effects inhibit the Soret effect (see data in Fig. 5(d) at 360 K and s_T ∼ 0 for NaCl). These changes in the Soret coefficient can lead to a significant modification of the concentration gradient, since the concentration varies exponentially with the value of the Soret coefficient and the temperature difference between Hot and Cold regions, namely, b_H/b_C = exp(−s_T(T_H − T_C)), where b_α is the concentration in region α.

Fig. 5 Temperature dependence of the salt concentration and the Soret coefficient of LiCl (a and b) and NaCl (c and d) solutions. Results for nanopores of radius 1.5 nm (R₁), 2.0 nm (R₂) and bulk solutions (R_∞) (taken from ref. 39 and 45) are shown. The symbols represent the data obtained from the NEMD simulations and the lines the fitting curves of the simulated data to the equation by Iacopini et al.⁴³

Previous investigations of simple fluids modelled with Lennard-Jones potentials in nanopores, did not find a measurable dependence of the thermal diffusion coefficient with confinement.⁴⁶ Therefore, our results highlight important differences in the thermodiffusive behaviour of simple fluids and aqueous solutions, under confinement conditions.

The thermodiffusive response of the solutions under confinement must be connected to structural and dynamic changes induced by the substrate on the solvation layer of the ions, as well as to ion adsorption on the silica surface. Indeed, previous studies demonstrated that nanopores induce significant changes in the properties of water, e.g. inhibiting the freezing transition at 273 K.²⁵ The depression of the freezing temperature with pore size was shown to be consistent with the Gibbs–Thompson equation, underlying the importance of curvature effects in the properties of liquid water under confinement conditions. Experimentally, it has been proposed that first order freezing transitions disappear in pore sizes of the order of 1.5 nm and below, with the freezing temperature dropping to 225–230 K for wider pores (2.0 nm radius). The curvature effect along with the reduction in the melting temperature associated to the addition of salt, indicates that the Soret coefficients investigated here could be measured at the lower of temperatures reported here (see Fig. 5(b) and (d)).

The impact of confinement on the melting temperature has been interpreted before using a two state model, consisting of free water molecules and water molecules adsorbed at the surface, with the adsorption involving typically one or two layers of molecules.²⁵ The existence of layers with properties that differ from those of bulk water is supported by molecular dynamics simulations,²⁶ which showed that the overall number of hydrogen bonds per water molecule increases slightly at the silica surfaces due to additional water–silica contributions. The formation of a hydrogen bond network between water and silica leads to a reduction of the number of hydrogen bonds between water molecules. These changes are also visible in our simulations (see Table 2). With reference to the bulk system, the total number of hydrogen bonds per water molecule decreases for all the temperature considered (see Table 2).

Table 2 Average number of hydrogen bonds per water molecule for NaCl and LiCl solutions in nanopores and in bulk. We assumed that a hydrogen bond is formed when the oxygen–oxygen distance is <0.35 nm and the angle between the vector connecting the oxygen atoms and the oxygen–hydrogen covalent bond vector is smaller than 30°. This criterion was applied to both water molecules or atoms on the silica surface

T/K	Radius/nm	LiCl			NaCl
		N HBW–W	N HBW–wall	N HB	N HBW–W	N HBW–wall	N HB
240	1.5	2.76 ± 0.04	0.45 ± 0.02	3.22 ± 0.12	2.76 ± 0.03	0.44 ± 0.01	3.20 ± 0.08
	2.0	2.91 ± 0.07	0.30 ± 0.01	3.22 ± 0.19	2.90 ± 0.09	0.31 ± 0.01	3.21 ± 0.25
	Bulk	3.60 ± 0.05	—	3.60 ± 0.05	3.58 ± 0.05	—	3.58 ± 0.05
300	1.5	2.61 ± 0.03	0.42 ± 0.01	3.03 ± 0.09	2.61 ± 0.04	0.42 ± 0.02	3.03 ± 0.10
	2.0	2.73 ± 0.05	0.29 ± 0.02	3.02 ± 0.15	2.73 ± 0.07	0.29 ± 0.01	3.01 ± 0.20
	Bulk	3.38 ± 0.05	—	3.38 ± 0.05	3.37 ± 0.05	—	3.37 ± 0.05
360	1.5	2.47 ± 0.07	0.39 ± 0.01	2.84 ± 0.01	2.46 ± 0.06	0.40 ± 0.01	2.86 ± 0.16
	2.0	2.57 ± 0.04	0.28 ± 0.01	2.84 ± 0.11	2.56 ± 0.05	0.28 ± 0.01	2.84 ± 0.12
	Bulk	3.14 ± 0.04	—	3.14 ± 0.04	3.13 ± 0.01	—	3.13 ± 0.01

---

The importance of hydrogen bonding on thermodiffusion has been discussed before by Wiegand et al.⁴⁷ At low temperature hydrogen bonds between water molecules are more favourable, and the solution is thermophilic; while at high temperature the hydrogen bonds are disrupted and the solution is thermophobic. This idea seems consistent with our results. At high temperature the number of hydrogen bonds in the bulk systems is lower and the solution is thermophobic (s_T > 0). For systems under nano-confinement, the total number of hydrogen bonds is lower than in bulk, and it decreases with temperature (see Table 2 and Fig. S7 in ESI†), which correlates well with our observation that under nanoconfiment the solution features a stronger thermophilic response, with the ions accumulating preferentially in hot regions.

We established in our previous work that the solvation structure of the ions, particularly Li⁺, has a significant impact on the magnitude of the Soret coefficient.⁴⁴ Increasing the number of water molecules around Li⁺ makes the solution more thermophobic. We find that this observations is also followed by the system investigated in this work. We tested this notion by calculating the radial distribution functions of Li⁺/Na⁺–OW, Cl⁻–HW and Li⁺/Na⁺–O, Cl⁻–H, namely between the ions and the oxygen and hydrogen in water (OW, HW) or the silica surface (O, H) (see Fig. 3(d and e) for LiCl and Fig. 3(j and k) for NaCl). The confinement induces structural changes in the radial distribution functions, which are reflected in the different heights of the main peaks, while the position of the peaks is independent on confinement. In the bulk solution, water forms a tetrahedral shell around Li⁺, and the coordination number is 4 (see Fig. 3(c and f)). The water solvation number around Li⁺ decreases with the radius of the nanopore (3.7 and 3.3 for R₂ = 2 nm R₁ = 1.5 nm, respectively). We find that confined solutions are more thermophilic, hence consisting with our observation⁴⁴ that higher water solvation favours thermophobicity. The tetrahedral structure of water around the anions is gradually disrupted under confinement too. The coordination number Cl⁻–HW decreases from 6.7 to 6.15 for R₂ = 2 nm, and 6.2 for R₁ = 1.5 nm for LiCl solutions. Similarly, the water solvation shell around anions and cations for NaCl solutions is disrupted under confinement (see Fig. 3(i–l)). The number of water molecules around Na⁺ decreases from 5.8 in bulk to 4.1 for R₂ = 2 nm and 4.0 for R₁ = 1.5 nm. The coordination number around the anion Cl⁻ decreases from 7.0, in bulk, to 5.4 and 5.1 for R₂ and R₁, respectively, for NaCl solutions. Very similar trends were reported by Haria et al.^12,14 in 0.5 M NaCl aqueous solutions under confinement. We observe an increase of the ion pairing when the solution is under confinement condition (see Fig. S9 of ESI†). However, the percentage of ion clustering is small, ≤3.5% for NaCl and ≤0.8% for LiCl, suggesting that the increase of ion pairing will have a minor impact on the observed thermodiffusive response.

4 Conclusions

We have investigated the thermodiffusive response of aqueous solutions confined in silica nanopores with radii (1.5–2.0 nm) of the order of those found in mesoporous silica nanostructures, such as MCM-41, or chip-based pores.^9,23,24 Using non-equilibrium molecular dynamics simulations we have shown that the confinement effects and solution–silica interactions reduce significantly the thermophobic behaviour of 1 mol kg⁻¹ LiCl and NaCl aqueous solutions at temperatures >320 K. For very small pores, 1.5 nm radius, the Soret coefficient, s_T, of the LiCl changes sign, with the solution becoming thermophilic (s_T < 0) and the salt accumulating in hot regions. At high temperatures, the confinement of NaCl solution in these small nanopores inhibits the Soret effect entirely (s_T ∼ 0).

Our results provide insight on possible synergies between nanopore size and temperature to induce salt separation or enrichment by applying thermal fields. This information might be relevant to design separation devices that exploit the application of thermal fields. However, the Soret coefficients under confinement conditions are of similar magnitude as those obtained in bulk, s_T ∼ 10⁻³ K⁻¹, hence significant thermal gradients would be required to induce large changes in salt concentration inside the nanopores. Large gradients, 10^6–8 K m⁻¹, are achievable using nanopores, e.g. by using plasmonic devices,⁴⁸ or relatively modest temperature drops between bulk reservoirs, 1–10 K, across nanopores with nanometer lengths, 10–100 nm.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the Leverhulme Trust (Grant No. RPG-2018-384) and the EPSRC (EP/J003859/1) for financial support, and the Imperial College High-Performance Computing Service for providing computational resources.

References

1. T. Albrecht, Annu. Rev. Anal. Chem., 2019, 12, 371–387.
2. J. W. Feng, H. M. Ding, C. L. Ren and Y. G. Ma, Nanoscale, 2014, 6, 13606–13612.
3. D. Takaiwa, E. Yamamoto and K. Yasuoka, Nanoscale, 2015, 7, 12659–12665.
4. A. Lervik and F. Bresme, Phys. Chem. Chem. Phys., 2014, 16, 13279–13286.
5. T. R. Gaborski, J. L. Snyder, C. C. Striemer, D. Z. Fang, M. Hoffman, P. M. Fauchet and J. L. McGrath, ACS Nano, 2010, 4, 6973–6981.
6. K. Leung, S. B. Rempe and C. D. Lorenz, Phys. Rev. Lett., 2006, 96, 095504.
7. S. Sahu and M. Zwolak, Nanoscale, 2017, 9, 11424–11428.
8. S. Murad and J. Lin, Ind. Eng. Chem. Res., 2002, 41, 1076–1083.
9. J. B. Edel and T. Albrecht, Engineered Nanopores for Bioanalytical Applications, William Andrew, 2013.
10. T. Albrecht, Curr. Opin. Electrochem., 2017, 4, 159–165.
11. K. Ritos, M. K. Borg, N. J. Mottram and J. M. Reese, Philos. Trans. R. Soc., A, 2016, 374, 20150025.
12. N. R. Haria and C. D. Lorenz, Phys. Chem. Chem. Phys., 2012, 14, 5935–5944.
13. S. Turgman-Cohen, J. C. Araque, E. M. Hoek and F. Escobedo, Langmuir, 2013, 29, 12389–12399.
14. N. R. Haria and C. D. Lorenz, J. Phys. Chem. C, 2015, 119, 12298–12311.
15. F. Rizzi, R. E. Jones, B. J. Debusschere and O. M. Knio, J. Chem. Phys., 2013, 138, 194104.
16. I. C. Bourg and C. I. Steefel, J. Phys. Chem. C, 2012, 116, 11556–11564.
17. L. Mereuta, I. Schiopu, A. Asandei, Y. Park, K.-S. Hahm and T. Luchian, Langmuir, 2012, 28, 17079–17091.
18. J. Hong, J. B. Edel and A. J. de Mello, Drug Discovery Today, 2009, 14, 134–146.
19. A. M. Benneker, T. Rijnaarts, R. G. Lammertink and J. A. Wood, J. Membr. Sci., 2018, 548, 421–428.
20. S. Tseng, Y.-M. Li, C.-Y. Lin and J.-P. Hsu, Nanoscale, 2016, 8, 2350–2357.
21. F. Peng, Y. Su, Y. Zhong, C. Fan, S.-T. Lee and Y. He, Acc. Chem. Res., 2014, 47, 612–623.
22. R. L. Fraccari, P. Ciccarella, A. Bahrami, M. Carminati, G. Ferrari and T. Albrecht, Nanoscale, 2016, 8, 7604–7611.
23. C.-C. Chien, S. Shekar, D. J. Niedzwiecki, K. L. Shepard and M. Drndić, ACS Nano, 2019, 13, 10545–10554.
24. P. Karau and V. Tabard-Cossa, ACS Sens., 2018, 3, 1308–1315.
25. A. Schreiber, I. Ketelsen and G. Findenegg, Phys. Chem. Chem. Phys., 2001, 3, 1185.
26. A. A. Milischuk and B. M. Ladanyi, J. Chem. Phys., 2011, 135, 174709.
27. Q. Zhang, K.-Y. Chan and N. Quirke, Mol. Simul., 2009, 35, 1215–1223.
28. M. Collin, S. Gin, B. Dazas, T. Mahadevan, J. Du and I. C. Bourg, J. Phys. Chem. C, 2018, 122, 17764–17776.
29. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
30. F. Römer, A. Lervik and F. Bresme, J. Chem. Phys., 2012, 137, 074503.
31. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
32. L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38.
33. C. D. Daub, N. M. Cann, D. Bratko and A. Luzar, Phys. Chem. Chem. Phys., 2018, 20, 27838–27848.
34. H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269.
35. L. X. Dang, J. Chem. Phys., 1992, 96, 6970–6977.
36. L. X. Dang and B. C. Garrett, J. Chem. Phys., 1993, 99, 2972–2977.
37. D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766.
38. L. X. Dang, J. Am. Chem. Soc., 1995, 117, 6954–6960.
39. S. Di Lecce, T. Albrecht and F. Bresme, Sci. Rep., 2017, 7, 44833.
40. S. Di Lecce and F. Bresme, Mol. Simul., 2019, 45, 351–357.
41. F. Römer, Z. Wang, S. Wiegand and F. Bresme, J. Phys. Chem. B, 2013, 117, 8209–8222.
42. S. de Groot and P. Mazur, Non-equilibrium Thermodynamics, Dover Publications, 1984.
43. S. Iacopini, R. Rusconi and R. Piazza, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 19, 59–67.
44. S. Di Lecce, T. Albrecht and F. Bresme, Phys. Chem. Chem. Phys., 2017, 19, 9575–9583.
45. S. Di Lecce and F. Bresme, J. Phys. Chem. B, 2018, 122, 1662–1668.
46. R. Hannaoui, G. Galliero, H. Hoang and C. Boned, J. Chem. Phys., 2013, 139, 114704.
47. D. Niether and S. Wiegand, J. Phys.: Condens. Matter, 2019, 31, 503003.
48. C. R. Crick, P. Albella, B. Ng, A. P. Ivanov, T. Roschuk, M. P. Cecchini, F. Bresme, S. A. Maier and J. B. Edel, Nano Lett., 2015, 15, 553–559.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/D0NR04912C

‡ Current address: School of Chemistry, University of Birmingham, Edgbaston, B15 2TT, Birmingham, UK.

---