Hyperbranched DNA clusters†
Abstract
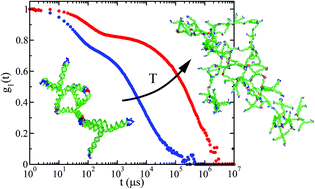
Taking advantage of the base-pairing specificity and tunability of DNA interactions, we investigate the spontaneous formation of hyperbranched clusters starting from purposely designed DNA tetravalent nanostar monomers, encoding in their four sticky ends the desired binding rules. Specifically, we combine molecular dynamics simulations and Dynamic Light Scattering experiments to follow the aggregation process of DNA nanostars at different concentrations and temperatures. At odds with the Flory–Stockmayer predictions, we find that, even when all possible bonds are formed, the system does not reach percolation due to the presence of intracluster bonds. We present an extension of the Flory–Stockmayer theory that properly describes the numerical and experimental results.
- This article is part of the themed collections: Editor’s Choice: Recent breakthroughs in nanobiotechnology and 2020 Nanoscale HOT Article Collection


 Please wait while we load your content...
Please wait while we load your content...