Two-dimensional ferromagnetism in CrTe flakes down to atomically thin layers†
Abstract
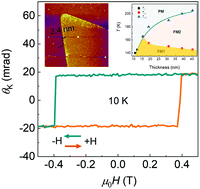
Two-dimensional (2D) ferromagnetism has attracted intense attention as it provides a platform for the investigation of fundamental physics and the emerged devices. Recently, the discovery of intrinsic 2D ferromagnet has enabled researchers to fabricate ultrathin devices, which can be controlled by external fields. Nevertheless, 2D ferromagnetic materials are mostly obtained by mechanical exfoliation methods with uncontrollable size and thickness, which make the device fabrication processes time-consuming and difficult to expand in industries. Therefore, the development of a controllable fabrication process for the synthesis of 2D intrinsic magnetic materials is necessary. In this study, a new 2D ferromagnet, chromium tellurium (CrTe), was successfully synthesized by the chemical vapor deposition (CVD) method, and the magnetism was studied by the magneto-optical Kerr effect (MOKE) technique. The results demonstrated that CrTe flakes exhibit hard magnetism with strong perpendicular anisotropy. As the thickness varies from 45 nm to 11 nm, the hard magnetism sustains quite well, with the Curie temperature TC decreasing from 205 K to 140 K. Our study presents a new ultrathin hard magnetic material, which has the potential to be fabricated and applied in spintronic devices massively.
- This article is part of the themed collection: Editor’s Choice: Controlling anisotropy in nanomaterials


 Please wait while we load your content...
Please wait while we load your content...