Quantitative determination of mechanical stability in the novel coronavirus spike protein
Abstract
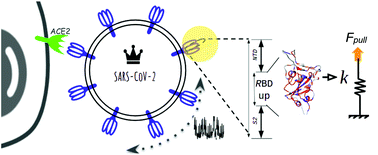
We report on the novel observation about the gain in nanomechanical stability of the SARS-CoV-2 (CoV2) spike (S) protein in comparison with SARS-CoV from 2002 (CoV1). Our findings have several biological implications in the subfamily of coronaviruses, as they suggest that the receptor binding domain (RBD) (∼200 amino acids) plays a fundamental role as a damping element of the massive viral particle's motion prior to cell-recognition, while also facilitating viral attachment, fusion and entry. The mechanical stability via pulling of the RBD is 250 pN and 200 pN for CoV2 and CoV1 respectively, and the additional stability observed for CoV2 (∼50 pN) might play a role in the increasing spread of COVID-19.
- This article is part of the themed collections: Coronavirus articles - free to access collection, Editor’s Choice: Recent breakthroughs in nanobiotechnology, 2020 Nanoscale HOT Article Collection and Nanoscale Most Popular 2020 Articles


 Please wait while we load your content...
Please wait while we load your content...