The optical nanosizer – quantitative size and shape analysis of individual nanoparticles by high-throughput widefield extinction microscopy

Abstract

Nanoparticles are widely utilised for a range of applications, from catalysis to medicine, requiring accurate knowledge of their size and shape. Current techniques for particle characterisation are either not very accurate or time consuming and expensive. Here we demonstrate a rapid and quantitative method for particle analysis based on measuring the polarisation-resolved optical extinction cross-section of hundreds of individual nanoparticles using wide-field microscopy, and determining the particle size and shape from the optical properties. We show measurements on three samples consisting of nominally spherical gold nanoparticles of 20 nm and 30 nm diameter, and gold nanorods of 30 nm length and 10 nm diameter. Nanoparticle sizes and shapes in three dimensions are deduced from the measured optical cross-sections at different wavelengths and light polarisation, by solving the inverse problem, using an ellipsoid model of the particle polarisability in the dipole limit. The sensitivity of the method depends on the experimental noise and the choice of wavelengths. We show an uncertainty down to about 1 nm in mean diameter, and 10% in aspect ratio when using two or three color channels, for a noise of about 50 nm² in the measured cross-section. The results are in good agreement with transmission electron microscopy, both 2D projection and tomography, of the same sample batches. Owing to its combination of experimental simplicity, ease of access to statistics over many particles, accuracy, and geometrical particle characterisation in 3D, this “optical nanosizer” method has the potential to become the technique of choice for quality control in next-generation particle manufacturing.

---

1. Introduction

Nanoparticles (NPs) of various chemical compositions, sizes, shapes, and surface-functionalizations are ubiquitous in modern research and industry, with uses ranging from drug-delivery,¹ biomedical imaging² and sensing,^3,4 to catalysis⁵ and photovoltaics.⁶ For all these applications, knowledge of the NP size and shape is a key requirement. Notably, many NPs used in the aforementioned fields have dimensions well below the diffraction limit (of about 250 nm) for visible light. This presents a significant challenge for the quantification of the size and shape of individual NPs using optical microscopy.

The industry standard for accurate determination of NP sizes and geometry is electron microscopy, particularly transmission electron microscopy (TEM). TEM provides very high resolution, down to atomic detail, owing to the small wavelength of an electron beam, but is complex, expensive, and “low-throughput” in terms of the number of NPs examined in one field of view and corresponding statistics.⁷ An alternative, non-optical technique to characterize particle size distributions is tunable resistive pulse sensing^8–10 (TRPS), which detects the change of the ionic current when a particle passes through a membrane pore. The change in electric resistance is related to the volume, and thus a sizing can be achieved on this premise. The method is high-throughput, accurate, can cover a wide range of particle sizes, and offers the additional benefit of charge and concentration measurement, but is typically limited to NPs larger than about 60 nm, does not provide shape information, and requires calibration before each measurement session.

Centrifugation^10,11 techniques measure particle size distributions via sedimentation rates, allowing good determination even with polydisperse samples, and in some cases are capable of resolution down to 1 nm. However, these are inherently ensemble techniques, do not offer shape information, and require or assume a homogeneous particle material density. A related group of methods is field-flow fractionation, which use flow-based elution and separation of particulates. Asymmetric flow field-flow fractionation (AF₄),^10,12 uses two flow sources to separate and elute particles, and is often combined with dynamic light scattering (DLS) and multi-angle light scattering (MALS). AF₄-DLS-MALS^10,12,13 has been shown to be a robust particle characterization method even capable of providing some indirect shape information by comparing the geometric (MALS) and hydrodynamic (DLS) radii. The setups can however be costly, requiring of significant expertise and sample species-specific setup to make sure samples properly elute.

Recently, a variant of DLS has been developed, called particle tracking analysis¹⁴ (PTA), which observes Brownian motion of single particles over time to determine their hydrodynamic radius. As with DLS, PTA typically has issues for NP sizes below 20 nm due to their weak scattering. Neither DLS nor PTA can provide information on NP shapes.

Notably, it is possible to relate the magnitude of light absorbed and/or scattered by a NP, with its size and shape. In other words, the optical absorption and/or scattering cross-sections, σ_abs and σ_sca respectively, or their sum, known as the extinction cross-section, σ_ext, carry information on the NP geometry. σ_abs can be measured via a technique called photothermal imaging^15–17 (PTI), achieving detection of gold nanoparticles (GNP) down to about 1.4 nm.¹⁸σ_ext has been measured by spatial modulation microscopy^16,19,20 (SMS), with demonstrated detection down to about 2 nm, and GNPs in this size range exhibit σ_ext around 1 nm². However, both techniques require expensive apparatus, careful calibration, and are slow, being laser-scanning based, implying a limitation on throughput. A more direct absorption measurement technique^21,22 employing laser scanning without modulation has demonstrated detection of absorption of single molecules with σ_ext ≈ σ_abs ≈ 0.1 nm². However, this method is also slow and not amenable to high-throughput characterization. Darkfield microscopy is used to measure σ_sca, and can typically detect particles down to about 20 nm size for gold and silver nanospheres or dielectric particles such as polystyrene beads down to about 70 nm size^23–25 or nanodiamonds.²⁶ In this case, the limit is most significantly a practical one, as scattering by the target NPs is overwhelmed by scattering of their surroundings (typically dielectric debris). Furthermore, σ_sca scales as the 6th power of the radius for NPs of dimensions within the dipole approximation, suggesting significant requirements on acquisition time and camera noise properties for particle sizes well below 20 nm.

Ref. 27 presents an on-chip sensing device based on whispering gallery modes (WGM), exhibiting detection and sizing of (non-absorbing) potassium chloride and polystyrene particles from 60 nm to about 200 nm when probing with light close to infrared (wavelength λ = 670 nm). This technique is notably not limited to the spherical assumption, since the signal is related to the polarizability of the NPs, and thus various shape models could be implemented. However, careful fabrication of the WGM resonator is critical. Ref. 28 uses widefield reflection microscopy, exploiting the interference between the scattered light of NPs and the substrate reflection, measured as a function of defocus. GNPs and polystyrene beads of 50–70 nm size were separated and their size determined by a machine learning approach. Differential interference contrast wide-field imaging has been used to determine the orientation of gold nanostars,²⁹ but not their cross-sections.

We have recently shown that a simple transmission based technique using only widefield illumination is capable of simultaneously detecting hundreds of NPs with σ_ext down to 1 nm², corresponding to a 2 nm GNP.^30–32 This procedure is rapid, quantitative and can be augmented using excitation light of varying polarisation direction, to gain information on the NP shape, and of varying wavelength, to gather material and shape-specific spectral properties. It is however not a trivial task to solve the inverse problem, i.e. to derive size and shape parameters from the measurement of σ_ext, especially when treating hundreds of NPs measured simultaneously.

In this paper, we introduce a method solving this inverse problem. We measure σ_ext with a simple wide-field technique on hundreds of individual GNPs, both nominally spherical and rod-shaped, and simulate σ_ext using a semi-analytical model in the dipole limit. We demonstrate that a retrieval of the NP size, shape, and orientation in three dimensions is possible, by fitting the measurements with the model. The accuracy of this “optical nanosizer” is discussed in relation to the measurement parameters, and bench-marked against state-of-the-art TEM and STEM 2D projection and STEM tomography.

2. Method and model

An object in an incident electromagnetic (EM) field will remove and redistribute power from that field resulting in a “shadow” being cast. In the limit of an object much larger than the wavelength λ, the shadow can be approximated by a simple projection of the object's cross-section orthogonal to the propagation direction, hence geometrical optics provides a suitable platform by which to determine the projected physical size and shape of the object. However, diffraction effects dominate for objects whose diameter D is comparable to, or smaller than the wavelength (D < λ), which in the visible wavelength range is the case for a NP. In this diffraction-limited regime, the “shadow” cast by the NP would be imaged as a shape close to the point spread function (PSF) of the imaging system. The exact form depends on the optics involved, the wavelength and polarisation of the incident light, the NP material, size, shape, and the refractive index of the environment. We also note that the PSF is in principle extended, and one needs to consider the area integral of the intensity of the PSF over the plane of projection, to determine the power removed by the particle from the incident field. In practice, one needs to limit integration to a range close to the diffraction limited size in order to control noise and surrounding structure, as we have discussed previously.³³ From these measurements, using the incident intensity I_inc, the absorbed power P_abs, and the scattered power P_sca, the optical absorption and scattering cross-sections, σ_abs = P_abs/I_inc and σ_sca = P_sca/I_inc, respectively, can be determined, whose sum is called the extinction cross-section, σ_ext = σ_abs + σ_sca = P_ext/I_inc. Now, measuring these quantities as a function of wavelength and light polarization, and modelling them, the NP properties such as orientation, size, shape, and material can be inferred.

We describe here the model we use to determine the cross-sections σ_abs, σ_sca, and σ_ext from the NP properties. We assume the incident field to be a plane wave and a linear optical response of the NP. For NPs much smaller than the wavelength, D/λ ≪ 1, one can disregard the phase difference of the field across the NP, a situation called the Rayleigh regime (or dipole limit). For larger particles, an analytical treatment for spherical particles is given by Mie theory. However, the resulting expressions contain infinite sums, and elliptical particles cannot be treated analytically. Therefore, the present work uses a description in the Rayleigh regime, for which simple analytical expressions exist even for elliptical shapes, given by the Rayleigh–Gans theory.³⁴ This choice is not mandatory, but reduces the numerical effort in the present work, particularly when comparing the model to the measurements of hundreds of NPs. The accuracy of the dipole approximation is evaluated for spherical gold NPs in the ESI section II.D.†

For an ellipsoidal NP, it is useful to choose a Cartesian reference system of unit vectors , with κ = x′, y′, and z′, in the directions of the NP semi-axes of lengths a, b, and c, which are ordered so that a ≥ b ≥ c. The polarisability of the NP in its reference frame is then given by

where α_j, with indices j = a, b, c, are the NP polarisabilities for electric fields orientated along the NP's semi-axes. They are given bywith the NP volume V, the complex relative permittivity of the NP ε_NP = ε₁ + iε₂, the positive relative permittivity ε_m of the surrounding dielectric medium, the permittivity of free space ε₀, and the depolarisation factors L_j. Note that the permittivities are frequency-dependent. Further, we note that in non-magnetic materials the relative permittivity is related to the refractive index by . 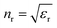The factors L_j are determined by the geometry of the NP, and given by the analytical expression,

For the general case these integrals must be solved numerically, but closed-form solutions exist when at least two of the semi-axes are identical, i.e. for prolate and oblate spheroids, as well as spheres.³⁵

For metallic NPs, ε₁ becomes increasingly negative above the plasma wavelength, resulting in a vanishing real part of the denominator in eqn (2) at a specific wavelength, for which

Reε_NP(λ) = ε_m(1 − L_j⁻¹), (4)

leading to a large polarizability α_i. This effect is called the localised surface plasmon resonance (LSPR) of the NP, and for a sphere, for which L_j = 1/3, it occurs at Reε_NP(λ) = −2ε_m. Accordingly, for increasing ε_m, the LSPR wavelength increases, and by way of example, for a spherical gold NP embedded in n_m = 1.52 silicone oil, the LSPR occurs at λ ≈ 530 nm. For large a/b, L_a becomes smaller, placing the LSPR at a more negative Reε_NP, which in turn results in a red-shift of the LSPR. We refer to the induced polarisation along the long axis a as the longitudinal mode. The LSPR of the longitudinal mode is generally sharper and stronger than in the spherical case, since the ratio between the real and imaginary parts of ε_NP increases with increasing wavelengths in this range for gold and other metals. The polarisabilities along the minor axes are instead less affected.

Since a NP can have an arbitrary orientation in the measurement instrument, we need to transform eqn (1) into the measurement frame,³⁴ yielding [small alpha, Greek, circumflex]. In the NP's reference frame, the polarization induced by a field, , incident on an NP with polarisability, [small alpha, Greek, circumflex]′, is given by

For the measurement frame, we label the axes of the Cartesian coordinates, ι∈{x, y, z}, with unit vectors , where is along the optical path, and , are spanning the sample plane, as illustrated in Fig. 1. A vector in the NP frame is transformed into in the measurement frame as,

with the rotation matrix, R̂, so that for the NP polarization we haveand hence the NP polarizability in the measurement frame is given by

[small alpha, Greek, circumflex] = R̂[small alpha, Greek, circumflex]′R̂^T, (8)

where we have used that for rotations the inverse matrix, R̂⁻¹, is equal to the transposed matrix R̂^T. In general, [small alpha, Greek, circumflex] will therefore have non-zero off-diagonal elements. It can be shown³⁴ that σ_abs and σ_sca are given byandwith the wavenumber in the medium k = 2πn_m/λ, the star indicating the complex conjugation, and a time dependence proportional to exp(−iωt) of the field with ω = 2πc₀/λ and the light velocity c₀ in vacuum. The square moduli and the dot product in eqn (9) and (10) imply a summation over the different components of the NP polarisation, so that the cross-section depends on the orientation of the NP in the measurement system.

Fig. 1 A sketch of the geometry of the NP in the measurement reference system, with the +z pointing away from the objective. Note, and are in the x–y plane. a, b, and c are mutually orthogonal and refer to the semi-axes of the NP, which are ordered so that a ≥ b ≥ c. Circular arrows with angles ϕ, θ, and ψ indicate the action of the rotation matrices R_ϕ, R_θ, R_ψ, respectively.

The resulting extinction cross-section spectra are given in Fig. 2 for a gold NP of a volume given by that of a sphere of 30 nm diameter, and different aspect ratios, for fields along the NP semi-axes. Here, and in the remainder of this work, we took ε_NP from the tabulated values for gold from ref. 36, interpolated in 2 nm steps over the range λ = 400 nm to 800 nm. For prolate NPs, the σ_ext for fields along the long axis (Fig. 2a top) shows the longitudinal LSPR shifting to longer wavelength and increasing in amplitude, reaching 600 nm and 10⁵ nm² for aspect ratios b/a around 1/2. For oblate NPs, similarly, 600 nm and 10⁵ nm² are reached for b/a ≈ 3 (Fig. 2b bottom). The geometrical cross-section of the sphere is about 707 nm², which is similar to the calculated extinction cross-sections at λ = 400 nm, where gold is strongly absorptive. For NPs with three different semi-axes lengths, shown in Fig. 2c–e, the qualitative behaviour is similar, with the LSPR for a polarization along each semi-axis red-shifting with increasing axis length, but also affecting the LSPRs along the other two axes.

Fig. 2 Extinction cross-section spectra σ_ext for a GNP of constant volume equal to a D = 30 nm sphere, in n = 1.52 homogeneous environment, with varying aspect ratios. Logarithmic grey-scale from 10 to 10⁵ nm² as given on the right. For illustration purposes, the NP semi-axis directions are taken as vertical (a), horizontal (b), and out of drawing plane (c), and the size ordering a ≥ b ≥ c is disregarded. The incident field directions are given by the arrows, along a in (a) and (c), along b in (b) and (d), and along c in (e). GNPs in (a and b) are prolate (top) and oblate (bottom) with varying b/a = c/a, while in (c), (d), and (e) they have varying c/a for b/a = 0.5 (top), and b/a = 2 (bottom).

A specific rotational formalism must be chosen in order to calculate R̂ in a consistent way. For computational reasons, we wish to remove the angle γ_P as an explicit parameter (as described in the ESI section S.II†), which can be achieved by having the first rotation in R̂^T given by a rotation about the z axis. We therefore define R̂ as

R̂ = R_ψR_θR_ϕ, R̂^T = R_ϕ^TR_θ^TR_ψ^T (11)

where,


so that in eqn (7), R_ψ^T is the first multiplier of . The rotations R_ψ, R_θ, R_ϕ when acting in the measurement frame are illustrated in Fig. 1. The unique angular ranges are given by ϕ ∈ [0, π], θ ∈ [−π/2, π/2], and ψ ∈ [0, π], as discussed in the ESI section S.IIA.†

We can now calculate, in the dipole limit, for a given field , the cross-sections for an elliptical NP of orientation Ω = (ψ, θ, ϕ), described by the semi axes a ≥ b ≥ c, NP permittivity ε_NP, and medium permittivity ε_m.

The illumination in the experiment employs a polarizer at an angle γ_P to the x axis in the back focal plane of the condenser, and a given numerical aperture range. As a result, the field in the sample plane is a superposition of incoherent contributions of a range of incident directions and polarizations. To approximate this illumination, excitation fields of three orthogonal directions are considered. These are the two fields in the sample plane, one along the polarizer , and one orthogonal to it, given by

as well as a field normal to the sample plane,

To treat the illumination approximately, we consider an average of cross-sections for fields in the three directions , , , with weights given by the corresponding field intensities created by the illumination (see eqn (3.16) in ref. 24). Briefly, the illumination rays are projected into the respective polarization directions, and their intensity is integrated over the illumination range. For typical illuminations, the highest intensity is along , followed by 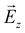, and then . Specifically, for illumination with NA = 0.95 in a medium of n = 1.52, the corresponding relative field strengths are E_‖ = 0.999, E_⊥ = 0.044, E_z = 0.321, while for NA = 1.34, they are E_‖ = 0.996, E_⊥ = 0.092, E_z = 0.449, with the normalization E_‖² + E_⊥² = 1. The normalization does not consider E_z since this component is propagating orthogonal to z and is thus not contributing to the measured reference intensity. The corresponding long shadow effect is discussed in ref. 33. As a result, the illumination probes not only the response for in-plane polarization, but also to some extent the response for a polarization along the microscope axis. The expected measured absorption cross-section is then calculated as

and equivalent for the scattering cross-section σ_sca(γ_P). In a measurement, the cross-section will be determined as a power loss for different illumination spectra Λ, called “colour channels” in the following, having a normalized spectral intensity I_Λ(λ), with , defining spectrally averaged absorption cross-sectionsand equivalently scattering cross-sections σ_sca,Λ. To model the bandpass filters, we assume a constant value of I_Λ over the passband and zero outside, and identify them in Λ by their center wavelength in nm. For the LED illumination, identified by their nominal wavelength in nm, we used the measured LED spectrum, shown in Fig. S1,† to determine I_Λ.

The resulting extinction cross-sections for various polarizer angles γ_P and colour channels Λ are then compared with the corresponding measured quantities σ_Λ (γ_P), defining the normalized error

where N is the number of measurements used in the sum, and [small sigma, Greek, circumflex]_Λ(γ_P) is the measurement noise of σ_Λ(γ_P). The parameter η accounts for the fact that a fraction of the scattered light is collected by the objective. In the present model, we approximate this fraction by the one for scattering by a spherical NP in a homogeneous medium, for unpolarized illumination, in the dipole limit. Using a NA of 0.95 for both illumination and collection, the fraction of scattered light collected is 13.6%,³⁷ so that we use η = 0.864. We note that this is a small correction, and that accordingly the approximation used is appropriate. Minimising S² over the NP parameters, we determine the most likely parameters describing the NP. We use MatLab R2018b to perform this fitting procedure, which is described in more detail in the ESI section S.II.† Typical computational times are around 1 second per NP fit on a modern CPU (AMD Ryzen Threadripper 2950X).

3. Experiment

3.1. Optical measurements

The optical measurements reported in this work were performed on a Nikon Ti-U inverted microscope, using as illumination source either a 100 W halogen lamp with bandpass filters (center wavelengths 450 nm, 550 nm, 600 nm, 650 nm, or 750 nm) of 40 nm width, or a light emitting diode (LED) source (Thorlabs LED4D106) providing two independent LEDs of center wavelengths 530 nm and 660 nm (for their spectrum see ESI Fig. S1†) coupled via a liquid light guide (Thorlabs AD5LLG). The microscope was setup with a 1.34 numerical aperture (NA) oil-immersion condenser (Nikon MEL41410) limited to NA = 0.95 to match the 0.95NA 40× dry objective (Nikon MRD00405) used with the 1.5× tube-lens. The image data was recorded using a scientific-CMOS (sCMOS) camera (PCO Edge 5.5), capable of acquiring 100 frames per second (FPS) at 2560 × 2160 pixels with 16 bit digitization, 0.54 electrons per count, and a full well capacity of N_fw = 30 000 electrons. The illumination intensity and exposure time was chosen to be close to N_fw without entering the range of non-linear response. A sketch of the setup is given in Fig. 3.

Fig. 3 Sketch of the imaging setup used. The transmission of a sample under Köhler illumination of a defined linear polarization and selectable wavelength range is imaged onto a sCMOS camera, using a condenser and an objective of matched high numerical apertures. The sample position is laterally shifted by a piezoelectric stage for referencing.

3.2. Structural characterization

Transmission electron microscopy (TEM) was performed on a JEOL-JEM 2100 TEM operating at 200 kV, with samples prepared on 300 Mesh holey carbon. High-angle annular dark-field scanning transmission electron microscope (HAADF-STEM) images and tomography series were acquired using a FEI Osiris microscope operated at 200 kV. The tomography series were acquired over the tilt range of ±75° with a tilt increment of 3° using a Fischione 2020 single-tilt tomography holder and a pixel dwell time of 6 μs. After alignment of the projection images by using a cross correlation, the stacks of aligned projection images served as inputs for 20 iterations of the expectation maximization reconstruction algorithm implemented in the ASTRA toolbox 1.9.0 using Matlab 2019a.^38,39 Amira 5.4.0 was used for the 3D visualization.

3.3. Samples and their preparation for optical measurements

GNPs of nominal spherical shape and mean diameters of 20 nm (GNSs) were obtained from BBI Solutions. Branded ‘ultra-uniform GNPs’ of nominal spherical shape and mean diameter of 30 nm (UGNSs) were obtained from NanoComposix. Finally, gold nanorods (GNRs) of nominal dimensions (30 × 10 × 10) nm³ were obtained from NanoPartz. Glass slides and coverslips (Menzel-Gläser, #1.5) were cleaned by sequential sonication phases in toluene to remove non-polar substances, acetone to clear the toluene, and then rinsed and boiled in deionised (DI) water. Slides and coverslips were then left in 30% hydrogen peroxide until needed, allowing oxidation of remaining surface contaminants, as well as hydrophilising the glass surfaces. Prior to NP deposition, any required glass was washed with DI water. The NP colloid was diluted with water to a final concentration of 10⁸ NP per ml, and a volume of 200 μl was spin-coated onto the coverslips at 2000 RPM for 2 minutes, with an acceleration time of 30 seconds. This procedure provided an areal density of NPs of (0.1–0.4) NP per μm², such that most NPs visible in the image are resolved individuals with well-separated point spread functions (PSF). The NP side of the coverslip was coated in 18 μl of refractive index n = 1.52 silicone oil, and covered with a slide. The samples were then sandwiched between two pieces of cleanroom grade optical paper and two more glass slides. The unsealed construction was then slowly pressed in a table vice and the oil allowed to leave for a few minutes soaking into the optical paper. This process was continued until the outer glass slides exhibited a subtle, but audible, crack. The outer slides and paper were removed, and the original coverslip and slide were then sealed with clear nail varnish. This process resulted in an oil layer below 1 μm thickness, so that the slide surface and the NPs on the coverslip surface were close to focus at the same time. As a result, debris on the slide surface creates a spatially localized perturbation, affecting only a small fraction of the total sample area.

3.4. Measurement of extinction

We use a method to quantitatively measure σ_ext, which has been described in ref. 31, 32 and 37. Briefly, two offset-subtracted brightfield images are obtained; the signal, I₁, with NPs in focus at position, P₁ = (x₁, y₁), and the reference, I₂, with the sample laterally shifted to position, P₂ = (x₂, y₂) = (x₁ + δx, y₁ + δy), with the magnitude of the shift, . Generally, I₁ and I₂ are averaged over a number, N_i, of individual acquisitions, reducing shot noise in the final image. The normalised transmission is obtained bywith + indicating we have chosen the signal to refer to the sample at P₁. Thus, T₋ = T₊⁻¹ can be obtained as well by choosing the signal to refer to the sample at P₂. To further reduce shot noise, while simultaneously reducing systematic noise due to sensor electronic drift, we repeat this procedure, moving the sample between the two positions at a rate, ν_s. We then determine the extinction imageswith the number of repetitions N_r. The shift rate is limited by the number N_i and the framerate, ν_F, with typical values of N_i = 128, ν_F about 400 Hz, and ν_s about 3 Hz. As mentioned above, a single NP appears twice in Δ_±, as a bright and dark PSF pair, with flipped contrast between Δ₊ and Δ₋. An example can be seen in Fig. 4, for a selected region of Δ₊. The corresponding full field of view of Δ₊, seen in the ESI Fig. S2,† contains around a hundred simultaneously measured NPs.

Fig. 4 Examples of Δ₊ (right, triple colour channel overlay) and σ_Λ (γ_P) (left) for different polarizer angles γ_P and three colour channels Λ, along with fits using eqn (21). (a) GNR, colour channel range in Δ₊ is ±0.76%. Imaging parameters were N_i = 128, N_r = 10, such that [small sigma, Greek, circumflex]_ext = (49.7, 51.5, 92.5) nm² for Λ = (550, 650, 750). (b) UGNS, colour channel range in Δ₊ is ±0.8%. Imaging parameters were N_i = 128, N_r = (4, 4, 16), such that [small sigma, Greek, circumflex]_ext = (57.5, 53.1, 30.9)nm² for Λ = (450, 550, 600). The total acquisition time for the 18 Δ images covering all polariser angles and wavelengths was about 4 min. The full acquired field of Δ₊ is given in the ESI Fig. S2.†

3.5. Analysis of σ_ext

To measure the cross-section of a NP at P₁ in Δ₊, we integrate Δ₊ over an area, A_i, of radius, r_i, centred at P₁, and Δ₋ over the corresponding area at P₂, such that the extinction cross-section is given by

The shot-noise limited noise in the measurement of σ_ext is given by³²

with the magnification M from sample to detector, the number of acquired frames N_a ≈ N_iN_r, and d_px = 6.5 μm the pixel pitch of the sensor. We use r_i = 3λ/(2NA) unless otherwise stated. For typical values of N_i = 128 and N_r = 4, we can achieve [small sigma, Greek, circumflex]_ext of about 50 nm², and are shot-noise limited with increasing N_a down to about 4 nm². Below this value, surface roughness, debris, residual sensor fluctuations etc. are affecting the results for our setup and samples. To achieve [small sigma, Greek, circumflex]_ext < 1 nm², we can employ additional procedures as described in ref. 32, which were not used in the present work.

When measuring σ_ext as a function of the excitation polarizer angle γ_p, we fit the data with

σ(γ_p) = σ[1 + α cos{2(γ_p − γ)}], (21)

to extract the average given by σ, and the polarisation dependence given by the relative amplitude parameter α > 0, and the angle γ∈[0,π] of maximum σ_ext. α is a measure of the observed NP asymmetry, with α = 0 corresponding to absence of dipolar asymmetry. γ gives the observed orientation of the NP dipolar asymmetry in the sample plane. We denote the measured extinction cross-section for a certain filter Λ and polariser orientation γ_P by σ_Λ(γ_p).

Examples of this analysis are given in Fig. 4, where Fig. 4a shows results for a NP with strong asymmetry, from the GNRs. For Λ = (550, 650, 750), this NP is described by α_Λ = (0.042, 0.84, 0.94), σ_Λ = (290, 427, 1087) nm², and γ_Λ = (138.9, 1.1, 177.8)°, hence we can infer an orientation of the long axis of the NP with γ ≈ 0 considering both Λ = 650 and Λ = 750 which are considerably red-shifted with respect to the resonance of a spherical GNP in the dipole limit. Conversely, the NP is nearly invisible for γ_P ≈ 90°. Additionally, we can see a significant polarisation-dependence for Λ = 650 and Λ = 750, but not for Λ = 550. This is consistent with the redshift of the LSPR polarized along the long axis.

Fig. 4b instead shows a NP with low asymmetry, from the UGNSs. For Λ = (550, 650, 750), this NP is described by α_Λ = (0.067, 0.043, 0.048), σ_Λ = (614, 1172, 217) nm², and γ_Λ = (75.5, 64.4, 79.1)°. A weak polarisation dependence is observed for all three Λ, and the NP is visible in Δ₊ at both polariser angles shown. It exhibits the largest cross-section for Λ = 550, consistent with the expected wavelength dependence discussed in section 2.

4. Results and discussion

Here we discuss the results of the analysis of σ_ext for hundreds of individual NPs of different types. Particular care needs to be taken in understanding the meaning of the statistical distribution of the cross-sections across a set of NPs. Information related to the size and shape distributions is contained within the NP set. Yet, each measured quantity on an individual NP will be affected by the error due to the measurement noise. The evaluation of these effects is discussed below.

4.1. Distributions of σ_Λ and α_Λ

The distribution of α_Λversus σ_Λ is shown in Fig. 5 for three sets of NPs, together with batch-representative TEM images. We call the mean of the polarisation-averaged cross-sections for a given colour channel [small sigma, Greek, macron]_Λ, and the associated standard deviation [small sigma, Greek, circumflex]_Λ,m. We call the analogous properties of the α parameter [small alpha, Greek, macron]_Λ and [small alpha, Greek, circumflex]_Λ,m. For each NP, we determine the error of the fitted parameters σ, α, and γ, using a Monte Carlo-like simulation. In detail, we add random noise to the measured data, from a Gaussian distribution with a root mean square (RMS) given by the experimentally determined noise [small sigma, Greek, circumflex]_ext for each γ_P and Λ, refit the data, and use the RMS of the resulting parameter distribution as error. Let us in particular denote the standard deviation of the per-NP fitted parameter σ_i by [small sigma, Greek, circumflex]_Λ,i, where i numbers the N NPs. To remove the measurement noise from [small sigma, Greek, circumflex]_Λ,m, we define , which represents only the distribution of NP cross-sections across the various NPs, due to their different sizes and shapes. Note that for [small alpha, Greek, circumflex]_{Λ, m} this correction has not been done, since the corresponding standard deviations [small alpha, Greek, circumflex]_Λ,i vary strongly depending on [small alpha, Greek, circumflex]_Λ,m and [small sigma, Greek, macron]_Λ, and we use [small alpha, Greek, circumflex]_Λ = [small alpha, Greek, circumflex]_Λ,m.

Fig. 5 Asymmetry α_Λversus cross-section σ_Λ for sets of different NPs and channels Λ as given, with representative TEM images of the investigated NP batch on the right. Left inset: σ_Λvs. σ_Λ′ as labelled. Right inset: α_Λvs. α_Λ′ as labelled. Both on a range as indicated. In all cases, N_i = 128. (a) 223 UGNSs using N_r = (4, 4, 16) for Λ as labelled, yielding [small sigma, Greek, circumflex]_ext = (57.5, 53.1, 30.9) nm². (b) 129 GNSs using N_r = 4 for both Λ as labelled, yielding [small sigma, Greek, circumflex]_ext = (44.1, 45.8) nm². (c) 95 GNRs, using N_r = 10 for all Λ as labelled, yielding [small sigma, Greek, circumflex]_ext = (49.7, 51.5, 92.5) nm². The error bars are showing the error of σ_Λ of the respective colour channels, given by . The grey areas indicate the noise in the fitted α of the red channels due to [small sigma, Greek, circumflex]_ext, estimated as .

4.1.1 Nominally spherical gold NPs. We have investigated two types of nominally spherical NPs, the UGNSs of nominal 30 nm diameter, and the GNSs of nominal 20 nm diameter (see section 3). Fig. 5a presents the measured σ_Λ and α_Λ of a set of UGNSs, which exhibit narrow distributions of both σ_Λ and α_Λ. We find α₆₀₀ to be below 0.2 (apart from some outliers accounting for 4.7% of the population) with a mean and standard deviation [small alpha, Greek, macron]₆₀₀ ± [small alpha, Greek, circumflex]₆₀₀ = 0.058 ± 0.031, indicating NPs of very low ellipticity. [small sigma, Greek, circumflex]₄₅₀/[small sigma, Greek, macron]₄₅₀ and [small sigma, Greek, circumflex]₅₅₀/[small sigma, Greek, macron]₅₅₀ are both about 18%. At these wavelengths the cross-section is roughly proportional to the NP volume, hence 18% relative volume distribution corresponds to 6% radius distribution. [small sigma, Greek, circumflex]₆₀₀/[small sigma, Greek, macron]₆₀₀ instead is larger, about 41%, consistent with the fact that the variability of σ_ext at a wavelength above the LSPR of a spherical NP is sensitive to shape deviations, in fact elliptical shapes result in a red-shifted σ_ext as shown in Fig. 2. This can also be seen in the correlation of increasing σ₆₀₀ with α₆₀₀ for the outliers having larger deviations from the spherical shape in Fig. 5a. Notably, correlating σ₆₀₀ with σ₅₅₀ (see inset), two groups can be identified, with different ratios σ₆₀₀/σ₅₅₀, identifying two distinct shapes. Qualitatively, these observations are consistent with TEM, where most of these ultra-uniform NPs are defect-free and have a faceted shape, while a few NPs contain defects and hence vary from these shapes, as shown in the ESI section S.III.† Additionally, we see that [small sigma, Greek, macron]₅₅₀ > [small sigma, Greek, macron]₄₅₀ > [small sigma, Greek, macron]₆₀₀ as expected for spherical gold NPs with a LSPR at λ ≈ 530 nm in a homogeneous environment of n_r = 1.52.

Fig. 5b shows the results for a set of GNSs, which we measured using LED illuminations centred at 530 nm and 660 nm. For this sample, the TEM indicates a large variability in shape, dominated by multicrystalline roundish NPs, and monocrystalline triangular plates with rounded edges. The plates are seen also side-on, where they appear rod-shaped. Indeed, we find that the measured σ_Λ is highly distributed for both available Λ, with [small sigma, Greek, macron]₅₃₀ ± [small sigma, Greek, circumflex]₅₃₀ = (645 ± 469) nm², and [small sigma, Greek, macron]₆₆₀ ± [small sigma, Greek, circumflex]₆₆₀ = (298 ± 482) nm². For many NPs in this sample, σ₆₆₀ is comparable to the noise level, with [small sigma, Greek, circumflex]_ext = 43 nm², resulting in a large error of α₆₆₀, as estimated by the dashed line. Nonetheless, for NP with larger σ₆₆₀, also a large α₆₆₀ is observed, consistent with the presence of plate-like shapes in TEM. Likewise, α₅₃₀ ranges from about 0 to 0.4, with most values below 0.25 ([small alpha, Greek, macron]₅₃₀ ± [small alpha, Greek, circumflex]₅₃₀ = 0.12 ± 0.18), indicating that on average the NPs have some distinct non-sphericity. The large value of [small sigma, Greek, circumflex]₅₃₀/[small sigma, Greek, macron]₅₃₀ ≈ 57% suggests a wide distribution in average size as well. However, [small sigma, Greek, macron]₅₃₀ > [small sigma, Greek, macron]₆₆₀, showing that most NPs do not have an aspect ratio above 1.5 (see Fig. 2), consistent with TEM analysis (see also Table 1 and ESI Table S1†).

Table 1 TEM derived mean and standard deviation of parameters p_i. Here we consider the two main semi-axes seen in plane-view TEM, and assign the longer to a, and the shorter to b and c

NP type	p̄ D v ± p̂Dv (nm)	p̄ b/a ± p̂b/a
30 nm UGNS	28.59 ± 1.77	0.973 ± 0.024
20 nm GNS	17.84 ± 1.25	0.865 ± 0.091
30 × 10 × 10 nm^3 GNR	15.36 ± 2.86	0.394 ± 0.135

---

4.1.2. Rod-shaped gold NPs. Results for the GNRs are shown in Fig. 5c. Considering the large nominal aspect ratio, we performed measurements with an additional channel in the red part of the spectrum, at 750 nm. Looking at Fig. 2, we find the longitudinal resonance for b/a = c/a = 1/3 around 700 nm. We therefore expect [small sigma, Greek, macron]₆₅₀ > [small sigma, Greek, macron]₅₅₀, and a ratio [small sigma, Greek, macron]₆₅₀/[small sigma, Greek, macron]₇₅₀ around one, increasing with aspect ratio. We find that [small sigma, Greek, macron]₆₅₀ = 867 nm² and [small sigma, Greek, macron]₇₅₀ = 935 nm² are indeed larger than [small sigma, Greek, macron]₅₅₀ = 580 nm². The variabilities of σ_Λ and α_Λ are large, with [small sigma, Greek, circumflex]_Λ/[small sigma, Greek, macron]_Λ > 83% and [small alpha, Greek, circumflex]_Λ,m/[small alpha, Greek, macron]_Λ > 43% for all Λ, indicating a significant distribution of both shapes and sizes. Additionally, [small alpha, Greek, macron]₅₅₀ = 0.2, [small alpha, Greek, macron]₆₅₀ = 0.62, and [small alpha, Greek, macron]₇₅₀ = 0.72 indicate that the NPs have a large optical asymmetry. This is consistent with the TEM for this batch, which shows nanorods in the size range indicated by the manufacturer (nominal (30 × 10 × 10) nm³) alongside quasi-spherical NPs smaller than 10 nm, rods with aspect ratios as large as 10 : 1, and some other shapes.

4.2. NP geometry determined by fits

The primary goal of this work is to determine NP size and shape by comparing the data with a parameterized model, and determine the most likely parameters by minimizing the weighted error between model and experimental data, as given in eqn (16). We implemented this minimization in MatLab R2018b. To best use the optimized vector/matrix operations of Matlab, portions of the various equations described in section 2, such as constants defined as integrals over spectral ranges, were brought outside the parameterized parts of calculations. A gridded multi-dimensional parameter space was created, allowing for two rotation angles (note that the angle ψ is contained in the polarizer angle γ_P), and two shape parameters via semi-axes aspect ratios b/a ∈ [ι₁, ι₂] and c/a ∈ [ι₁, ι₂]. We used ι₁ = 0.25 to ι₂ = 1.43 for the UGNSs, and ι₁ = 0.1 to ι₂ = 1.75 for the GNSs and GNRs to cover the broader spread in shapes. We then calculated σ_abs(γ_P,Λ)/V and σ_sca(γ_P,Λ)/V² at each grid point, and obtained an interpolant of their values between the grid points using an Akima piecewise cubic function. The experimental data were compared to all calculated values on the grid viaeqn (16). The right side of eqn (16) is a fourth order polynomial in the volume, V. We therefore minimized S²versus V using the analytical roots of the third-order polynomial equation , yielding S and V for all points on the grid. The points which are local minima of S on the grid, and have an error below a threshold, S < σ_c, were then used as initial guesses for a gradient descent minimizing S² using the interpolation. Initial guesses with equal error within the numerical precision were considered to be rotational redundancies, and only one of each of these degenerate cases was used to reduce computational effort. The resulting set of errors and parameters obtained over all gradient descents is called the minimized set. Assuming we have no further information at hand, the element of the minimized set exhibiting the minimum error S is the most likely to describe the size, shape, and orientation of the NP.

Firstly, we checked the validity of this fitting procedure using synthetic data of gold NPs with given size and shape, and verified that the fit was converging to the expected values. Then, we examined the distribution of fitted parameters when adding the experimental noise to synthetic data. An example of this analysis is shown for prolate gold NPs in Fig. 6. The data are calculated matching the experimental conditions, including Λ and γ_P, of the UGNSs in Fig. 5a. The cross-section data to be fitted were calculated for a NP of a volume characterized by the sphere-equivalent diameter D_V = 25.6 nm (taken from the average of the fitted in Fig. 7), and of an orientation ψ = θ = ϕ = 0, so that a and b are in the measurement x, y plane. The distribution of fitted parameters results from the set of noise realizations, with [small sigma, Greek, circumflex]_ext = (57.5, 53.1, 30.9) nm² for Λ = (450, 550, 600), respectively. These values of [small sigma, Greek, circumflex]_ext correspond to the measurements in Fig. 5a, and amount to 2–20% of the respective σ_ext. The different colors in the plots show different simulated aspect ratios b/a = c/a as indicated. The fit parameter space is 6-dimensional (three orientation angles and three semi-axis lengths), and we have 18 simulated measurements (6 γ_P at 3 Λ). Notably, measuring a spherical NP (b/a = c/a = 1), the noise results in fitted values of aspect ratios between 1 and 0.8. For a strongly prolate NP instead (e.g. b/a = c/a = 0.6), the average aspect ratio is rather well defined (see right inset, e.g. magenta histogram), while b/a and c/a still vary significantly. The retrieved volume (see histogram in left inset) shows a smaller dependence on the aspect ratio, while still being of decreasing variation with decreasing aspect ratio. Reducing the measurement noise, the distributions narrow, as shown in the ESI Fig. S3.† Equivalent simulations for the oblate and general cases are discussed in the ESI section S.IIC.† Generally, the interplay between NP orientation, aspect ratios, and probed colour channels goes beyond an intuitive understanding for all but the simplest cases. Nevertheless, we see that a suited choice of colour channels and measurement noise allows retrieval of NP shapes and sizes. Notably, the colour channel choice can be informed by this type of simulation, by evaluating the errors of fitted sizes and shapes for a given measurement noise for different combinations of available colour channels.

Fig. 6 . Evaluation of fit results for synthetic data. Fitted c/a and b/a using 1000 measurement noise realizations for a prolate gold NP with constant volume equivalent to a sphere of diameter, D_V = 25.6 nm, for various b/a = c/a as indicated(see also circle symbols), and ψ = θ = ϕ = 0. The polarization averaging (eqn (14)) was done for an illumination NA of 0.95. A noise of [small sigma, Greek, circumflex]_ext = (57.5, 53.1, 30.9) nm², was used for the color channels Λ = (450, 550, 650), respectively, taken from the UGNS experiment in Fig. 5a. Top inset: Extinction spectra at γ_P = 0, for b/a = 1 (black), b/a = 0.6 (magenta). The bands indicate the spectral ranges Λ used. Right inset: Histograms of fitted for b/a as colour coded. Left inset: Histogram of the fitted volume V for b/a as colour coded.

Fig. 7 Fitted parameters for UGNSs using the channels Λ = 450, 550 from the measurements shown in Fig. 5a. (a) c/a versus b/a, with the colour scale indicating the volume equivalent diameter D_V. (b) magenta points: geometric average aspect ratio, , versus D_V. Black points: b/a versus, for 30 NPs examined using TEM. The magenta bars give the histogram of the magenta points. In both (a) and (b), the size of the points is given by S⁻ = 1/(1 + S), so larger points indicated lower error, as shown in (a). Inset in (b) shows the fitted NP orientation angles θ versus ϕ, with the colour indicating . (c) For the measured NPs indicated by stars in (a and b), fit results for 10 000 realizations (1000 shown by filled circles) of added random measurement noise. Contours are the boundaries of regions of highest density containing 68% (black) and 95% (grey) of the data. Insets show the distributions of D_V, and provide the symbol colour scale. The inset in the red starred plot is a TEM tomographic reconstruction of an exemplary NP (see also ESI section S.III†) from the same sample stock with similar D_V as the fitted NP.

Prior knowledge, such as ensemble size specifications from the NP manufacturer, can also be taken into account to determine the most likely NP geometry. We perform such a selection as a post-fit routine, comparing the fitted parameters in the minimized set with those of prior knowledge for each NP. We then select the parameter set exhibiting the minimum “combined error” after this comparison. Using the mean p̄_i and variance p̂_i for the parameters i ∈ {D_V, b/a, c/a} taken from TEM, we add an error related to the deviation from expected values to arrive at the combined error S_c given by

The values of p̄_i and p̂_i used for the different NP types are given in Table 1. Since TEM is measuring only two sizes, we set p̄_b/a = p̄_c/a and p̂_b/a = p̂_c/a.

4.2.1. Geometrical parameters from measured nominally spherical gold NPs. The fit results are presented below for the investigated nominally spherical NPs. Let us start discussing the UGNSs, using the colour channels {Λ} = {450, 550}. The resulting values of c/a and b/a are shown in Fig. 7a, with the colour indicating the ellipsoid average diameter , and the symbol size indicating the fit error S. We find that c/a and b/a are mostly above 0.9, and the D_V ranges between 24 and 27 nm. Fig. 7b shows the average aspect ratio versus D_V, and a histogram of D_V. Notably, the values of D_V are about 10% smaller than measured in TEM, the latter shown as black points in Fig. 7b (see also ESI Fig. S14† for a comparison with 2D projection HAADF-STEM). A possible explanation of this small discrepancy is the fact that in TEM we measure only the NP size in plane, and the corresponding values in Fig. 7b are calculated using .

To appraise the measured parameter distributions, it is again important to understand the effect of the measurement noise characterized by [small sigma, Greek, circumflex]_ext. To this end, four measured NPs were selected, indicated by (black, red, blue, magenta) stars in Fig. 7a, which have α₅₅₀ = (0.092, 0.026, 0.023, 0.203), and σ₅₅₀ = (1150, 1117, 2566, 1473) nm², respectively. Random Gaussian noise of standard deviation [small sigma, Greek, circumflex]_ext was added to the experimental data, and the NP parameters were retrieved from the resulting data. This was repeated for 10 000 noise realizations, and the results are shown in Fig. 7c, each NP in a separate panel. The contours indicate the regions of highest probability density containing 68% and 95% of the data, which for a Gaussian distribution are the σ and 2σ confidence intervals, respectively. The results show that, depending on the NP size and shape, the measurement noise results in about 1 nm full-width-at-half maximum (FWHM) in D_V, and 10% in b/a and c/a. These values account for about half the parameter spread in the set of investigated UGNSs, confirming that the size and shape distribution of these NPs is indeed very uniform.

The NPs indicated by the black and red stars show a confinement of the data to b ≈ c, which is consistent with the simulated result in Fig. 6 for a spherical NP. The blue star NP shows a tighter distribution due to its high cross-section, reducing the effect of noise. The measured in-plane anisotropy is very small (2.3%) for this NP, and the fit shows a slightly oblate particle with b/a > 0.95, c/a ≈ 0.92, and the c semi-axis along z in the measurement system, as in Fig. S4.† The magenta star NP has a sizeable anisotropy (20.3%) and three different semi-axes, with c/a ≈ 0.71 and b/a ≈ 0.82. Overall, we see that the measurements give detailed information about these nominally 30 nm diameter NPs, with diameter precision around 1 nm and anisotropy precision in the 10% range for a measurement noise around 50 nm². Decreasing the measurement noise by about an order of magnitude would increase the precision, as seen in Fig. S3,† and is possible with the experimental technique.³² Notably, the precision of the diameter would increase by the same factor, while for the asymmetry, the situation is more complex. For an isotropic case, the degeneracy of all semi-axes allows for a larger parameter space resulting in similar cross-sections, while for a significantly asymmetric NP, this degeneracy is at least partially lifted, reducing the resulting parameter uncertainty. This is exemplified in the simulated cases seen in Fig. S4 and S5† comparing c/a = 1.0 with c/a = 0.6, and for three distinct semi-axes in the ESI Fig. S6.†

The fitted angles are shown in the inset of Fig. 7b. In particular we plot θ and ϕ, the two angles which rotate the NP out of the substrate plane. The in-plane rotation ψ creates only a shift in the measured dependence of σ_Λ(γ_P) on γ_P, and thus does not change the measured cross-section set. The observed angular distribution is spread over the full ranges of ϕ and θ, consistent with the near spherical shape of the NPs. Some reduction around |θ − π/2| = 0, and around |ϕ| = π/2 is visible, which we can understand considering that as soon as there is some asymmetry, the NP is more likely to lie down on the substrate plane, so that a and b are in the substrate plane, corresponding to θ = ϕ = 0, as opposed to standing on end, which is either θ ≈ π/2 (a normal to substrate), or θ ≈ 0 and |ϕ| ≈ π/2 (b normal to substrate).

To determine the full three-dimensional NP shape with EM, going beyond 2D projection TEM as shown in Fig. 5, we have performed high-angle annular dark-field scanning transmission electron microscope (HAADF-STEM) tomography for a few of the UGNSs, as described in the ESI section S.III.† We found that most NPs are mono-crystalline and nearly spherical, consistent with our optical measurements and discussed fitting results. The aspect ratios of two NPs obtained from tomography are 0.99 and 0.96. For illustration one 3D rendering is shown in the inset of Fig. 7c.

We note that the selection of color channels Λ influences the results to some extent, as different channels are sensitive to different NP parameters and shape ranges, as discussed in detail in the ESI section S.II E.† Using {Λ} = {450, 600} is found to produce oblate NPs in the fit, which shows that the model underestimates the cross-section in the Λ = 600 channel. This can be attributed to the neglected surface damping^20,25 in the gold permittivity used in our model, and the absence of surface faceting in the ellipsoidal shape assumed.

We now move to the more conventional GNSs, which, as we have seen in Fig. 5b, have a more variable shape. This is visible also in the fit results shown in Fig. 8, where there are rod-shaped NPs with b/a ≈ c/a < 0.6, plates with b/a > 0.8 and c/a < 0.5, and reasonably spherical NPs with c/a > 0.7, as indicated in Fig. 8a. The distribution of the diameter results in a mean D̄ = 21.8 ± 5.8 nm. We see a narrow mode around 18 nm, in good agreement with the observations from TEM (black dots in Fig. 8b). The comparison with results of 2D projection HAADF-STEM are given in the ESI Fig. S13.† A tail of outliers to higher volume with a small aspect ratio is also found. Such NPs are not obvious in the TEM data, which mainly show roundish NPs with defects, and triangular plates in either side or top view. They could be thin plates of larger size, which are sporadically seen in TEM, and possibly NP dimers formed by aggregation. We also note that by dropping the Λ = 450 channel compared to the UGNS data shown in Fig. 7, the NP volume is less constrained. The orientation of the NPs (inset in Fig. 8b) shows again a broad distribution, but with a stronger tendency to lie flat (θ ≈ 0, | ϕ − π/2| ≈ π/2), consistent with the larger deviation from spherical shape. To assess the effect of the measurement error, also in this case four measured NPs were selected, indicated by (black, red, blue, magenta) stars. Random Gaussian noise of standard deviation [small sigma, Greek, circumflex]_ext was added to the experimental data, and the NP parameters were retrieved. The corresponding distributions are shown in Fig. 8c. We find an uncertainty in the diameter of about 2 nm FWHM in D_V and 20% in b/a and c/a, larger than in the case of Fig. 7c, because the NPs, and therefore the cross-sections, are smaller, resulting in a lower signal to noise ratio. Nonetheless, the method clearly separates different NPs, and highlights the fairly broad distribution of NP sizes and shapes in this sample. Also here, we have performed tomographic TEM for a few of the GNSs, as described in the ESI section III.† We found, consistent with the above fitting results, that the NPs look rather irregular, with some pentatwinned NPs but also many other spherical-like irregular shapes. Almost all NPs contain lattice defects. Note that lattice defects provide additional scattering sites for the free electrons of the metal, affecting ε_NP, as discussed in the ESI sec. II.D.† The aspect ratios obtained from tomography for two GNSs are 0.9 and 0.813. For illustration, one 3D rendering is shown in the inset of Fig. 8c.

Fig. 8 As Fig. 7, but for GNSs, and Λ = 530, 660.

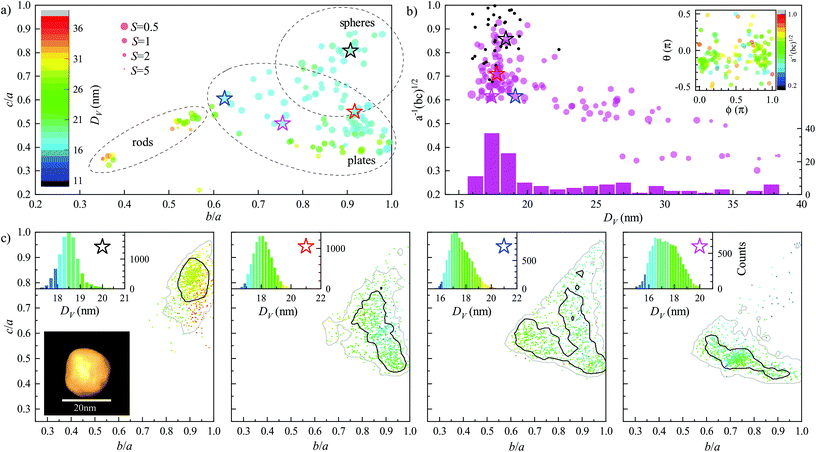
4.2.2. Rod-shaped gold NPs. The fit results for the GNRs are shown in Fig. 9, and are highly distributed in D_V, b/a, and c/a, while quite well defined in the average aspect ratio . The volume has been calculated assuming a cylindrical shape. These findings are in line with observations from TEM, and the optical results in Fig. 5d. We do see a large proportion of cases with b/a and c/a around 1/3, as expected from the nominal specifications, and TEM (see also ESI Fig. S14† for a comparison with 2D projection HAADF-STEM). Importantly, the individual NP fits shown in the lower four panels exhibit narrow bands at small values of c/a and b/a, similarly to the synthetic cases seen in Fig. 6. The NP orientations (see inset Fig. 9b) are distributed in ϕ but concentrated around θ = 0, as expected for rods, where ϕ is rotating around the rod axis, having little effect, and θ is tilting the rod axis out of plane. Additionally, a fraction of NPs, such as the black star one, are plate-like, with c/a < 0.25 and b/a > 0.5. Again we have performed tomographic TEM for a few of the GNRs, as described in the ESI section S.III.† We found, consistent with the above fitting results, that almost all NPs are defect free, and rod-shaped NPs are dominating. The aspect ratios obtained from tomography for two NPs are 0.36 and 0.42. For illustration, one 3D rendering is shown in the inset of Fig. 9c.

Fig. 9 As Fig. 7, but for the GNRs and Λ = 550, 650, 750. Considering a cylindrical shape, the equivalent diameter (black points) was determined as .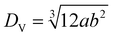

5. Conclusions and outlook

To summarise, we have demonstrated a rapid, quantitative and accurate method to “optically size” hundreds of individual nanoparticles, by measuring their optical cross-sections in widefield extinction microscopy for different light wavelengths and excitation polarizations, and solving the inverse problem of determining the particle size, shape and orientation from the measurements.

We have shown examples for three different gold nanoparticle samples, nominally spherical and rod-like, in practice exhibiting various sizes and shapes, which were fitted using an ellipsoid model in the dipole limit. The results are, in general, in good agreement with non-correlative 2D projection TEM and HAADF-STEM, and HAADF-STEM tomography of the same batches. Depending on the experimental noise and the choice of colour channels in the measurements, we have quantified the sensitivity of the method. We show an uncertainty down to about 1 nm in mean diameter, and 10% in aspect ratios when using two or three colour channels and an experimental noise of about [small sigma, Greek, circumflex]_ext = 50 nm². Notably, the precision can be increased by decreasing the measurement noise.

As an outlook, further advances in the method on the experimental side could include the direct probing of the nanoparticle axial direction, through the addition of a radial polarizer and a high numerical aperture illumination lens to generate an axial polarization component. This would improve the capability of the technique to measure particle geometries in 3D, presently originating from the interplay between particle shapes and plasmon resonance shifts. On the modelling side, calculating the response using a fully numerical solver, e.g. via COMSOL as presented in ref. 25 and 40, and optimizing the material permittivity used, would enable a more accurate and general description of essentially arbitrary shapes and material types. Combined, these future developments are poised to provide a powerful nanoparticle sizing method by optical means, presenting an alternative to complex and expensive TEM tomography analysis, merging accuracy with simplicity of use, easy access to statistics over large particle sets, and applicability to any nanoparticle size, shape, and composition.

Author contributions

L.P., W.L. and P.B. conceived the work. L.P. prepared the samples for the optical measurements and performed the related measurements and data analysis. W.A. prepared the samples for the STEM tomography, and performed the related measurements and data analysis. L.P, P.B. and W.L. developed the numerical model and fitting methods. L.P. performed the numerical simulations and data fitting. All authors contributed to the data interpretation and writing of the manuscript.

Data availability

Information on the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2020.0107215015.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a Welsh Government Life Sciences Bridging Fund (grant LSBF/R6-005) and by the UK EPSRC (grant no. EP/I005072/1 and EP/M028313/1). PB acknowledges the Royal Society for her Wolfson research merit award (grant WM140077). The authors acknowledge funding from the European Commission (Grant EUSMI E191000350). WA acknowledges an Individual Fellowship from the Marie Sklodowska-Curie actions (MSCA) under the EU's Horizon 2020 program (Grant 797153, SOPMEN), and Sara Bals for supporting the STEM measurements. The bright-field TEM was performed by Thomas Davies at Cardiff University. We acknowledge Attilio Zilli for helpful discussions and contributions in calculating the relative field strengths in the illumination and finite-element simulation of cross-sections shown in the ESI.† We acknowledge Iestyn Pope for technical support of the optical equipment.

References

1. T. Sun, Y. S. Zhang, B. Pang, D. C. Hyun, M. Yang and Y. Xia, Angew. Chem., Int. Ed., 2014, 53, 12320–12364.
2. X. Han, K. Xu, O. Taratulab and K. Farsadc, Nanoscale, 2019, 11, 799–819.
3. J. Kneipp, ACS Nano, 2017, 11, 1136–1141.
4. R. M. Pallares, N. T. K. Thanh and X. Su, Nanoscale, 2019, 11, 22152–22171.
5. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
6. H. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213.
7. W. D. Pyrz and D. J. Buttrey, Langmuir, 2008, 24, 11350–11360.
8. R. Vogel, G. Wilmott, D. Kozak, G. S. Roberts, W. Anderson, L. Groenewegen, B. Glossop, A. Barnett, A. Turner and M. Trau, Anal. Chem., 2011, 83, 3499–3506.
9. R. R. Henriquez, T. Ito, L. Sun and R. M. Crooks, Analyst, 2004, 129, 478–482.
10. F. Caputo, J. Clogston, L. Calzolai, M. Rösslein and A. Prina-Mello, J. Controlled Release, 2019, 299, 31–43.
11. L. Calzolai, D. Gilliland and F. Rossi, Food Addit. Contam., Part A, 2012, 29, 1183–1193.
12. S. Gioria, F. Caputo, P. Urbán, C. M. Maguire, S. Bremer-Hoffmann, A. Prina-Mello, L. Calzolai and D. Mehn, Nanomedicine, 2018, 13, 539–554.
13. M. Wagner, S. Holzschuh, A. Traeger, A. Fahr and U. Schubert, Anal. Chem., 2014, 86, 5201–5210.
14. K. S. Silmore, X. Gong, M. S. Strano and J. W. Swan, ACS Nano, 2019, 13, 3940–3952.
15. D. Boyer, P. Tamarat, A. Maali, B. Lounis and M. Orrit, Science, 2002, 297, 1160–1163.
16. M. Husnik, S. Linden, R. Diehl, J. Niegemann, K. Busch and M. Wegener, Phys. Rev. Lett., 2012, 109, 233902.
17. A. Tcherniak, J. Ha, S. Dominguez-Medina, L. Slaughter and S. Link, Nano Lett., 2010, 10, 1398–1404.
18. S. Berciaud, D. Lasne, G. Blab, L. Cognet and B. Lounis, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–8.
19. A. Arbouet, D. Christofilos, N. Del Fatti, F. Vallée, J. R. Huntzinger, L. Arnaud, P. Billaud and M. Broyer, Phys. Rev. Lett., 2004, 93, 127401.
20. O. L. Muskens, P. Billaud, M. Broyer, N. Del Fatti and F. Vallée, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205410.
21. P. Kukura, M. Celebrano, A. Renn and V. Sandoghdar, J. Phys. Chem. Lett., 2010, 1, 3323–3327.
22. M. Celebrano, P. Kukura, A. Renn and V. Sandoghdar, Nat. Photonics, 2011, 5, 95–98.
23. A. Crut, P. Maioli, N. D. Fatti and F. Vallée, Chem. Soc. Rev., 2014, 43, 3921–3956.
24. A. Zilli, PhD thesis, Cardiff University, 2018.
25. A. Zilli, W. Langbein and P. Borri, ACS Photonics, 2019, 6, 2149–2160.
26. I. Pope, L. Payne, G. Zoriniants, E. Thomas, O. Williams, P. Watson, W. Langbein and P. Borri, Nat. Nanotechnol., 2014, 9, 940–946.
27. J. Zhu, S. K. Ozdemir, Y.-F. Xiao, L. Li, L. He, D.-R. Chen and L. Yang, Nat. Photonics, 2009, 4, 46–49.
28. O. Avci, C. Yurdakul and M. S. Ünlü, Appl. Opt., 2017, 56, 4238–4242.
29. K. S. B. Culver, T. Liu, A. J. Hryn, N. Fang and T. W. Odom, J. Phys. Chem. Lett., 2018, 9, 2886–2892.
30. L. M. Payne, W. Langbein and P. Borri, Appl. Phys. Lett., 2013, 102, 131107–131101.
31. L. Payne, G. Zoriniants, F. Masia, K. P. Arkill, P. Verkade, D. Rowles, W. Langbein and P. Borri, Faraday Discuss., 2015, 184, 305–320.
32. L. Payne, W. Langbein and P. Borri, Phys. Rev. Appl., 2018, 9, 034006.
33. L. Payne, A. Zilli, Y. Wang, W. Langbein and P. Borri, Proc. SPIE 10892, Colloidal Nanoparticles for Biomedical Applications XIV, 2019.
34. C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-Interscience, New York, New York, U.S.A, 1983.
35. C. F. Bohren and D. R. Huffman, Absorption and scattering of light by small particles, John Wiley & Sons, New York, 1983.
36. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379.
37. L. Payne, PhD thesis, Cardiff University, 2016.
38. T. Moon, IEEE Signal Process. Mag., 1996, 13, 47–60.
39. W. van Aarle, W. J. Palenstijn, J. D. Beenhouwer, T. Altantzis, S. Bals, K. J. Batenburg and J. Sijbers, Ultramicroscopy, 2015, 157, 35–47.
40. Y. Wang, A. Zilli, Z. Sztranyovszky, W. Langbein and P. Borri, Nanoscale Adv., 2020, 2, 2485.

---

Footnote

† Electronic supplementary information (ESI) available: 8 pages, Fig. S1–S13. See DOI: 10.1039/D0NR03504A

---