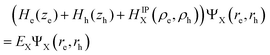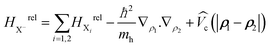Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning trion binding energy and oscillator strength in a laterally finite 2D system: CdSe nanoplatelets as a model system for trion properties†
Sabrine
Ayari
a,
Michael T.
Quick
b,
Nina
Owschimikow
b,
Sotirios
Christodoulou
 c,
Guillaume H. V.
Bertrand
c,
Guillaume H. V.
Bertrand
 d,
Mikhail
Artemyev
d,
Mikhail
Artemyev
 e,
Iwan
Moreels
e,
Iwan
Moreels
 f,
Ulrike
Woggon
b,
Sihem
Jaziri
ag and
Alexander W.
Achtstein
f,
Ulrike
Woggon
b,
Sihem
Jaziri
ag and
Alexander W.
Achtstein
 *b
*b
aLaboratoire de Physique des Materiaux, Faculte des Sciences de Bizerte, Universite de Carthage, Jarzouna 7021, Tunisia
bInstitute of Optics and Atomic Physics, Technische Universität Berlin, Strasse des 17. Juni 135, 10623 Berlin, Germany. E-mail: achtstein@tu-berlin.de
cICFO-Institut de Ciencies Fotoniques, 08860 Castelldefels, Barcelona, Spain
dCEA Saclay, 91191 Gif-sur-Yvette, France
eResearch Institute for Physical Chemical Problems of Belarusian State University, 220006 Minsk, Belarus
fDepartment of Chemistry, Ghent University, Krijgslaan 281 - S3, 9000 Gent, Belgium
gLaboratoire de Physique de la Matiere Condensee, Departement de Physique, Faculte des Sciences de Tunis, Campus Universitaire, 1060 Tunis, Tunisia
First published on 22nd June 2020
Abstract
We present a theoretical study combined with experimental validations demonstrating that CdSe nanoplatelets are a model system to investigate the tunability of trions and excitons in laterally finite 2D semiconductors. Our results show that the trion binding energy can be tuned from 36 meV to 18 meV with the lateral size and decreasing aspect ratio, while the oscillator strength ratio of trions to excitons decreases. In contrast to conventional quantum dots, the trion oscillator strength in a nanoplatelet at low temperature is smaller than that of the exciton. The trion and exciton Bohr radii become lateral size tunable, e.g. from ∼3.5 to 4.8 nm for the trion. We show that dielectric screening has strong impact on these properties. By theoretical modeling of transition energies, binding energies and oscillator strength of trions and excitons and comparison with experimental findings, we demonstrate that these properties are lateral size and aspect ratio tunable and can be engineered by dielectric confinement, allowing to suppress e.g. detrimental trion emission in devices. Our results strongly impact further in-depth studies, as the demonstrated lateral size tunable trion and exciton manifold is expected to influence properties like gain mechanisms, lasing, quantum efficiency and transport even at room temperature due to the high and tunable trion binding energies.
1. Introduction
II–VI semiconductor nanoplatelets (NPLs) are colloidal analogues to epitaxial quantum wells, yet with a finite lateral size.1–24 Compared to zero-dimensional (0D) quantum dots (QDs) and one-dimensional (1D) nanorods (NRs), two-dimensional (2D) zinc blende CdSe NPLs have sharper absorption and emission peaks, larger absorption cross-sections and radiative decay rates allowing high quantum yields, and they also exhibit directed and polarized emission.1–3,22,25–30 Similar to 2D transition metal dichalcogenides (TMDCs)31–33 and perovskites34–36 showing strong confinement in z-direction and dielectric mismatch to the surroundings, CdSe NPL excitons exhibit high exciton binding energies making them stable even at room temperature.2,5,23,37–39 In laterally infinite TMDCs, trionic states with high binding energies have been predicted and observed.40–48 In contrast to TMDCs, there is a precise synthesis based control over the finite lateral size4,49 and thickness of CdSe nanoplatelets reported in ref. 50. The controlled monolayer (ML) thickness precission results in narrow PL emission.1,2,22 The excitonic optical properties and dynamics of NPLs interpolate between the Coulomb correlation- and confinement-dominated limits known from ideal quantum wells and quantum dots. As a consequence, the optical response of excitons in CdSe NPLs can be tuned strongly by the lateral size and thickness,2,18,51 as they are a system between quantum well-like (weak lateral confinement) and quantum dot-like (strong confinement) regimes.7,51 Until now, the influence of the finite lateral size on the electronic properties of trions has not been investigated comprehensively in theory and experiment.Based on theoretical modeling of the exciton and trion energies, we investigate the properties of trions and excitons in CdSe nanoplatelets. We study the tunability of the radiative rate, oscillator strength, binding energy and Bohr radius of trions and excitons in the nanoplatelets. We show that nanoplatelets are a model system for laterally finite 2D semiconductors to study their size tunable trion and exciton physics. We show that e.g. the trion binding energy and oscillator strength can be tuned in a way that at room temperature a large fraction or no trions are present, paving the way e.g. to an effective control of the emission efficiency of devices. We substantiate our theory results by comparison with experiments.
An exemplary low temperature photoluminescence (PL) spectrum of 4.5 monolayer (ML) CdSe nanoplatelets (NPS) is shown in Fig. 1(a) along with a sketch of the chemical platelet structure (inset in c). The PL shows a double emission.5,14,16,17,52–55 (Details on the samples, preparation and time-resolved and integrated PL spectroscopy can be found in sections S2 and S3 of (ESI†).) A lower state (LS) trion emission and an upper state (US) exciton emission have been identified.54,55 The energy spacing ΔE strongly depends on the lateral platelet size and varies from 38 to 18 meV, see Fig. S3 in the ESI† and Table 1. We investigate in this paper the properties of trions and excitons and the tunability of their properties by the lateral size.
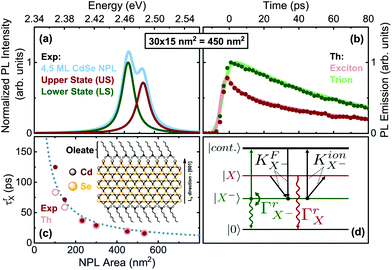 | ||
| Fig. 1 (a) Time-integrated PL emission of 4.5 monolayer (ML) CdSe NPLs for exemplary lateral size at 4 K and ∼0.2 W cm−2 (CW equivalent) 420 nm excitation, showing a lower state (LS, trion) and upper state (US, exciton) emission. (b) Transient PL decay under the same conditions. (c) Exciton radiative rates from Table 1. Inset: Structure of CdSe NPLs with ligands. (d) Level scheme of the trion model: Crystal ground state |0〉 (no excitation), trion |X−〉, exciton |X〉 and e–h pair continuum states, as well as allowed transitions, see ESI section S3† for details. | ||
| Size (nm2) | 17 × 6 | 21 × 7 | 29 × 8 | 30 × 10 | 30 × 15 | 41 × 13 |
| Area (nm2) | 102 | 147 | 232 | 300 | 450 | 533 |
| ΔE (meV) | 36 | 32 | 26 | 24 | 20 | 18 |
| Γ rX (ns−1) | 8 | 14 | 27 | 35 | 53 | 64 |
| Γ X− r (ns−1) | 1.6 | 1.9 | 2.5 | 3.3 | 4.1 | 4.6 |
| γ X− 0 (ns−1) | 62 | 77 | 111 | 96 | 78 | 32 |
| Γ rX,theo (ns−1) | 11 | 16 | 26 | 34 | 50 | 62 |
2. Results and discussion
Charged excitons (trions) appear frequently in 2D transition metal dichalcogenides (TMDCs) and are demonstrated in CdSe platelets.15,17,55 For a negative trion, the two opposite-spin electrons of an X− trion can be in a triplet state S = 1 or singlet state S = 0. We refer to their singlet configurations in which they appear as bound states (generally below the energies of neutral excitons). The observation of triplet trions is more elusive.56–59 In the ESI†, we evaluate experimental time resolved and integrated PL data (Fig. S3–S5†) for CdSe platelet samples of varying lateral size at low temperature (T = 4 K). Using a numerical model, which accounts for population transfer between exciton and trion states under pulsed excitation we fit the experimental transients numerically (section S3 of the ESI†). The model (Fig. 1(d)) takes four levels into consideration: the crystal ground state |0〉, the electron state |continuum〉 (from e–h continuum), the excitonic state |X〉, and trion state |X−〉. We also compare the resultant power dependence of the time-integrated PL intensity from the rate equation model with the experimental findings in Fig. S5† and obtain also good agreement between the model and experiment. The electron for trion formation is assumed to originate from a residual background doping (see ESI section S3 A†).From the fits to the rate equation model (section S3 A of the ESI†) we obtain three fit parameters, the exciton radiative rate ΓrX, the trion radiative rate ΓX−r, and scattering rate γX−0. Hence, for low T the PL decay is a function of only these parameters for fits. Table 1 summarizes the fit results displayed in Fig. S4 (ESI†) for different sizes.
At first we analyze the trends in Table 1 phenomenologically and then provide an in-depth theoretical modeling. With increasing lateral platelet size, the radiative rate of the exciton increases. This leads to measured exciton lifetimes (τrX) in the range of tens of picoseconds (37 ps for 29 × 8 nm2, and 16 ps for 41 × 13 nm2, see also Fig. 1(c)). These are about two orders of magnitude shorter than those for spherical CdSe nanocrystals60,61 and a consequence of the so-called giant oscillator strength (GOST) effect.62 The radiative rate of a 2D exciton is proportional to the ratio of the area of the exciton coherent in-plane motion to the exciton Bohr radius aB squared.6,13,62,63 First indications for such a behavior have been found.2,3,5,27,28,64 For NPLs, much smaller than the wavelength and much larger than aB (the weak and intermediate confinement regime), the exciton oscillator strength can be given by (see also further below for detailed calculations):13,57
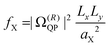 | (1) |
Here Ω(R)QP is the vacuum Rabi coupling and aX is the exciton spatial extension, equal to the exciton Bohr radius aB.13,31,57 The equation shows, that the exciton oscillator strength increases with the ratio of the NPL area to the effective Bohr radius. For large NPLs, aB is equal to the two-dimensional limit a2DB.13 Hence, for a fixed value of aB for larger platelets, the oscillator strength should approximately increase e.g. by a factor of 2.28, with increasing lateral size from 232 nm2 (29 × 8 nm2) NPLs to 533 nm2 (41 × 13 nm2), in good agreement with our experimental results from Table 1, where a ratio of 2.37 is found. Extrapolating the radiative exciton lifetime (Table 1) towards a (much) larger platelet area (Fig. 1(c)), few ps lifetimes can be achieved,13,28,64 being also comparable in order of magnitude with some TMDC materials (1 ps for WS265,66 and ∼10 ps for MoSe267). This sets the CdSe NPLs among the fastest nano emitters.
Moreover, Table 1 shows that the exciton radiative rate is much greater than the trion rate, resulting in ΓrX/ΓX−r ∼ 5–14. This is a general trend also observed in III–V,68 II–VI69 and TMDC65,66 semiconductor quantum wells, where e.g. about 15 times longer trion emission time in TMDC materials is ascribed to a lowering of the oscillator strength due to a stronger localization. For CdSe quantum dots the trion lifetime is comparable to that of the exciton in the strong confinement regime,70 while for large QDs it can be longer than that of the excitons.71 In 2D systems the trion lifetime can be comparable or longer than the exciton lifetime.72
Actually, in 2D systems, when a photon transforms into a correlated exciton, the photon wave vector Qp transforms into the exciton center-of-mass plane wave with the same in-plane momentum projection providing good matching. When a trion is formed, two plane waves – one for the free electron and the photon – transform into one plane wave, the trion center of mass motion. The electron (Ke), originally delocalized over the sample volume LD, with D the dimensionality, ends up being localized in the trion (in a volume of the order of the trion volume aX−D), while the whole trion is delocalized again over the sample volume. The mentioned localization leads to a 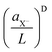 reduction of the trion oscillator strength, as seen by the trend in Table 1 for the associated radiative rate. For larger NPLs in the weak/intermediate confinement regime (L ≥ aB),
reduction of the trion oscillator strength, as seen by the trend in Table 1 for the associated radiative rate. For larger NPLs in the weak/intermediate confinement regime (L ≥ aB), 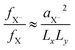 is valid, with aX−, the trion Bohr radius (calculated later in Fig. 2(d)).57 The trion oscillator strength fX− (being calculated later numerically) is far smaller than the exciton oscillator strength fX (as Lx,y ≫ aX−), except for very poor samples having coherence lengths or sample size L of the order of the trion spatial extension, which we do not have. Hence, the trion radiative rate is much less than the exciton rate in Table 1, with predictions in ref. 57, while in a strong confined quantum dot (Lx,y ∼ aX−) it is near to one, as discussed above. We also notice an LO-phonon bottleneck in the scattering rate γX−0, showing its maximum for platelets with energy spacing near to the 25 meV (ref. 73) LO-phonon energy.5,18
is valid, with aX−, the trion Bohr radius (calculated later in Fig. 2(d)).57 The trion oscillator strength fX− (being calculated later numerically) is far smaller than the exciton oscillator strength fX (as Lx,y ≫ aX−), except for very poor samples having coherence lengths or sample size L of the order of the trion spatial extension, which we do not have. Hence, the trion radiative rate is much less than the exciton rate in Table 1, with predictions in ref. 57, while in a strong confined quantum dot (Lx,y ∼ aX−) it is near to one, as discussed above. We also notice an LO-phonon bottleneck in the scattering rate γX−0, showing its maximum for platelets with energy spacing near to the 25 meV (ref. 73) LO-phonon energy.5,18
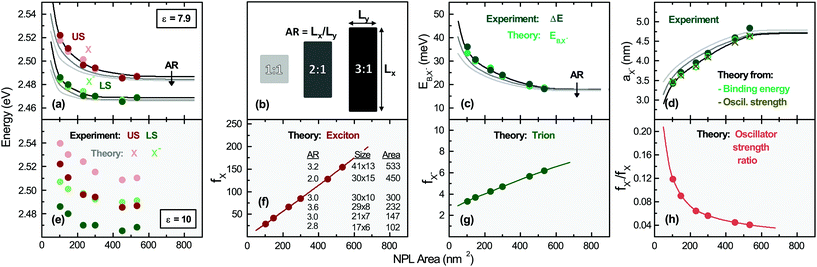 | ||
| Fig. 2 (a) (US) and (LS) energies obtained from Fig. 1 (darker color data points) and theoretical model for (X) and (X−), (pale color data points). Additionally the variation of exciton and trion energy with respect to the lateral NPL aspect ratio (AR) is shown, (lines of different brightness, see the legend in (b)). The energy of the trion and exciton is obtained by the numerical diagonalization of the matrix resulting from the projection of the Hamiltonian HX− and HX for a fixed surrounding dielectric constant εenv = 2.07 and two different CdSe dielectric constants in (a) and (e). Partially single data points indicate that the data and model fall on top of each other. (b) Definition of the lateral aspect ratio, which varies from sample to sample, as given in (f). (c) Trion binding energy from the experiment and theory. The theoretical value dependence on the lateral NPL AR is also shown. (d) Trion Bohr radius from the experiment and theory. (f) Exciton and (g) trion oscillator strength and inverse oscillator strength ratio (h) for the samples. Different AR curves fall on top of each other. | ||
While the rate equation model does not take into account some features such as an exciton fine structure, which plays a minor role (see ESI section S3 C† for detailed discussion) or higher excited states,51 it describes consistently the key features and trends of the size tunable trion and exciton properties. In-depth theoretical modeling is performed in the next section and compared with these results.
Theory for trions and excitons
The NPLs are modeled as quantum box like structures with a strong z-confinement to 4.5 ML (coordinates ze,h) and variable lateral confinement (Lx, Ly). Within the effective-mass and envelope-function approximation, the Schrödinger equation of a neutral exciton in a NPL readswhere ri = (ρi,zi). The total exciton wave function ΨX(re, rh) is split into two parts: (i) the confinement wave functions ϕe(ze), (ϕh(zh)) of the lowest electron (heavy-hole) sublevel, which are solutions of the single electron (hole) Hamiltonian in the z-direction Hi(zi) = −ħ2/2m⊥i(∂2/∂zi2) + Vi(zi). Here Vi(zi) is the sum of all possible single-particle potentials affecting particle i (i = e, h), and m⊥i is the mass of carrier i along the strongly confined z-direction ([001]), taken from ref. 37. (ii) The in-plane wave function ψIPX(ρe, ρh) (index IP for in-plane) is the solution of the following in-plane Schrödinger equation:
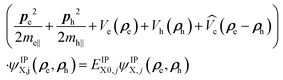 | (2) |
For the negative trions within the effective-mass approximation, the Schrödinger equation can be written as: 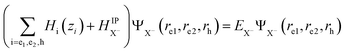 . The total wave function of the trion solution of HX− can be factorized into: ΨX−(re1, re2, rh) = ϕe1(ze1)ϕe2(ze2)ϕh(zh)ψX−,jIP(ρe1, ρe2, ρh), where ϕi(zi) are the confinement functions of the lowest electron (i = e1, e2) and heavy-hole sublevel (i = h) and ψX−,jIP(ρe1,ρe2,ρh) is the wave function solution of the in-plane trion Hamiltonian:
. The total wave function of the trion solution of HX− can be factorized into: ΨX−(re1, re2, rh) = ϕe1(ze1)ϕe2(ze2)ϕh(zh)ψX−,jIP(ρe1, ρe2, ρh), where ϕi(zi) are the confinement functions of the lowest electron (i = e1, e2) and heavy-hole sublevel (i = h) and ψX−,jIP(ρe1,ρe2,ρh) is the wave function solution of the in-plane trion Hamiltonian:
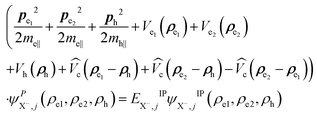 | (3) |
To investigate the negative trion binding energy of CdSe NPLs, we adopt the same formalism as for the exciton using the relative ρi = ρei − ρh and the center of mass RX− = (meρe1 + meρe2 + mhρh)/MX− trion coordinates. Hence the trion in-plane Hamiltonian is the sum of center of mass and relative Hamiltonian HX−IP = HX−CM + HX−rel, where the eigenenergy and eigenvector solutions of the in-plane Hamiltonian can be written as 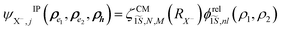 and
and 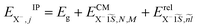 , with
, with 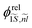 and
and 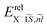 the wave function and the energy solution of the relative Hamiltonian HX−rel given by:
the wave function and the energy solution of the relative Hamiltonian HX−rel given by:
Here HXirel is the relative Hamiltonian of the neutral exciton and MX− = 2me + mh is the trion mass. To solve the eigenvalue equation, we use a wave function expansion technique. (See Methods for further details.)
Fig. 2(a) reports the theory results of the exciton and trion energies for different platelet sizes. The experimental values (obtained from Fig. S3†) are also included for comparison, showing very good agreement. We can clearly notice that the exciton and trion energy for using the high-frequency CdSe dielectric constant (εCdSe,∞ = 7.9) in the calculations for the treatment of screening provides a very good agreement, while the use of the static dielectric constant (nCdSe,s = 10, Fig. 2(e)) provides an overestimate of the transition energies, known in the literature and in line with trends in ref. 37. (See also Methods.) Further recent studies also suggest an effective dielectric constant of 6.478 (averaging over the field components inside the platelet and outside in the ligands for the screened lowest exciton state). It has to be slightly lower than the inside dielectric constant we use, since the outside dielectric constant is near to two. Hence this further substantiates our ε = 7.9 value.
Increasing the lateral platelet confinement results in a blue shift of about ∼18 meV for the trion and ∼35 meV for the exciton, while the lateral size is reduced from 533 to 102 nm2. (See also the Methods section for more details.) Theory curves for varying lateral aspect ratio (AR, see (b) for definition) are also displayed. We remark that our calculations are further substantiated as they result e.g. in an exciton binding energy of 201 meV for 533 nm2 (41 × 13 nm2) platelets in good agreement with experiments in refs 28 and 39. We will analyze the dependence of the binding energy and other parameters in Fig. 3.
In panel (c) of Fig. 2 the trion binding energy, corresponding to the energy separation between X and X−, is plotted vs. platelet area. It decreases from 33 meV for 102 nm2 (17 × 6 nm2 to 19 meV for 533 nm2 (41 × 13 nm2)) platelets. Going from laterally extended platelets to smaller ones, the calculated trion binding energies in our 2D system start with comparable values as e.g. for large quantum dots (14–22 meV)79,80 and get higher with decreased lateral size approaching the range of strong confined CdSe quantum dots (30–50 meV).71 A slight deviation for the smallest platelets considered (102 nm2, 17 × 6 nm2) is explained by the increasingly quantum dot like nature, while the model is exact for weak to intermediate lateral confinement. The continuous lines in Fig. 2(a) and (c), obtained from our calculations, show that the transition energies also depend on the lateral aspect ratio (AR).
In panel (f) and (g) of Fig. 2 we plot the calculated exciton and trion oscillator strength fi ∝ |〈Ψ|δre, rh|Ψ〉|2, see ESI section S1 B.† Both exciton and trion oscillator strengths increase with the NPL area, consistent with the theory of giant oscillator strength in quantum wells62 and weakly confined quantum dots. Theory curves for different AR values fall on top of each other. fX− is far smaller than that of the exciton (fX−/fX < 1), consistent with our assumption of a more quantum well like than quantum dot like system for the lowest state. This is a result of the weaker localization of the trion compared to the exciton and in line with expectations based on Combescot et al.57 The variation of the oscillator strength of both species with the lateral size and the relative trion to exciton oscillator strength ratio (Fig. 2(h)) support our fitting parameters presented in Table 1. The trion oscillator strength is an order of magnitude lower as for the excitons, also reflected in the experimental radiative rates in Table 1. In line with our results, much lower radiative rates of trions in quantum wells as compared to excitons have been predicted56,81 at low temperatures and found in epitaxial II–VI and III–V wells.82 If the predicted oscillator strength of the exciton is translated to a radiative rate,13,26,83,84 we obtain 12 ns−1 to 62 ns−1 for the exciton transition. (See Table 1, Fig. 1(c); see also the ESI† for the method of calculation.) These values are in agreement with our experimental results validating the model. A slight deviation for the smallest sample is attributed to its increasingly quantum dot like nature.
Fig. 2(d) displays the relative motion extension of the trion85 (Bohr radius) 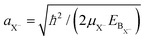 , deduced from theory, as a function of the platelet area. As in (a), the specific sample lateral aspect ratio (given in (f)) is used for the calculations (data points), while the continuous lines represent the theory for different lateral aspect ratios. For the experimental data, the energy spacing in Table 1 is used with the formula above. μX− = MXme/(MX + me) is the trion relative motion mass. In order to validate our theoretical calculations, we plot in the same figure aX− calculated using the oscillator strength ratio in (h):
, deduced from theory, as a function of the platelet area. As in (a), the specific sample lateral aspect ratio (given in (f)) is used for the calculations (data points), while the continuous lines represent the theory for different lateral aspect ratios. For the experimental data, the energy spacing in Table 1 is used with the formula above. μX− = MXme/(MX + me) is the trion relative motion mass. In order to validate our theoretical calculations, we plot in the same figure aX− calculated using the oscillator strength ratio in (h): 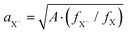 ('Oscill. strength’).57,85,86 Further we deduce aX− from the experimental results (trion–exciton energy difference) using the first mentioned equation and making use of ref. 85 and 86. The trion extension aX− calculated using our models is consistent with the experimental result, substantiating our model. Slight deviations occur for the 102 nm2, (17 × 6 nm2) platelets, which are increasingly quantum dot like.
('Oscill. strength’).57,85,86 Further we deduce aX− from the experimental results (trion–exciton energy difference) using the first mentioned equation and making use of ref. 85 and 86. The trion extension aX− calculated using our models is consistent with the experimental result, substantiating our model. Slight deviations occur for the 102 nm2, (17 × 6 nm2) platelets, which are increasingly quantum dot like.
We remark that we decided to plot all trion and exciton properties in Fig. 2versus the platelet area, as with varying lateral aspect ratio AR only the shortest length (Ly) impacts the properties. A detailed discussion of the dependence of trion energy, binding energy and oscillator strength on the shortest platelet length Ly, which dominates the lateral confinement for platelets with higher lateral aspect ratios, is presented in section S1 C of the ESI.†
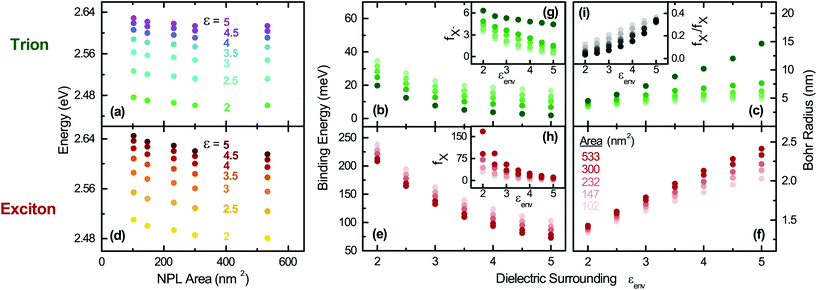
In order to provide further insight into the optical properties of the CdSe NPLs, we investigate in Fig. 3 the effect of the dielectric environment on the transition energies, binding energies, Bohr radii and oscillator strength of trions and excitons by varying the surroundings (ligand) εenv and the platelet area. Therefore, the former parameter is varied in the calculations between ε = εenv = 2 and ε = 5 to cover a large span of potential dielectric surroundings from strong dielectric contrast to weak dielectric contrast to the inside dielectric constant of 7.9 (as in Fig. 2(a)). As shown in Fig. 3, it is clear that the optical properties of the exciton and trion are sensitive to the dielectric environment and subsequently to the choice of the surrounding (e.g. organic ligands). E.g. for a fixed NPL size (41 × 13 nm2 or 533 nm2) the absolute trion and exciton transition energies (Fig. 3(a) and (d) are only weakly altered. This is due to the decrease of the exciton and trion binding energy subtracted from the sum of the high bandgap (1.766 eV for CdSe) and confinement energy (∼0.9 eV). The exciton binding energy decreases by 135 meV from 208 meV to 73 meV while εenv is increased from 2 to 5, see Fig. 3(e). Our calculations result in an exciton binding energy of 201 meV for 41 × 13 nm2 platelets and εenv = 2.07 (oleic acid), in good agreement with experimental determinations in ref. 28 and 39. The trion binding energy is more sensitive to the environment and drops from 20 to 2 meV (Fig. 3(b)). However, most organic ligands (including oleic acid used here with εenv = 2.07) have high frequency dielectric constants near to 2, so that in an experiment only minor shifts would be observed upon ligand exchange. In contrast, a variation of the dielectric surrounding is possible using (colloidal) atomic layer deposition (ALD) methods87 for controlled deposition of a few monolayers of a high bandgap semiconductor or dielectric. In line with the trend in Fig. 3(e) the binding energy can be reduced considerably, e.g. upon CdS coating.9
Using our ∼200 meV exciton binding energy and an about ∼20 meV trion binding energy for the larger platelets we obtain an EBX−/EBX ratio of 0.1. This is in good agreement with predictions for trions in ideal quantum wells54,88,89 predicting a ratio of 0.12. Hence, it further confirms our calculations. From our trion binding energy of the largest platelet we can calculate in Fig. 3(c) a trion Bohr radius of 4.6 nm (for εenv = 2.07) using the previously mentioned equation. It is in good agreement with the experimental value (Fig. 2(d)) calculated from the double peak energy spacing (4.8 nm). The corresponding exciton Bohr radius of 1.6 nm (compare Fig. 3(f)), calculated using aX = (ħ2/2μEXB)1/2, is in line with the trend in Brumberg et al.,39 having measured about 1.15 to 1.4 nm, for smaller sizes (17–65 nm2). The Bohr radius increases in Fig. 3(f) with the lateral size. An increase of εenv leads to an increase of the Bohr radius ((c) and (f)) and a reduction of the spatial overlap between the electron and hole in their relative motion. This results in reduced oscillator strength ((g) and (h)) for both trions and excitons.
Notably, our results in Fig. 3(g) and (h) emphasize that in line with the binding energy, the negatively charged exciton oscillator strength is less sensitive to the dielectric environment5,18 compared to the exciton oscillator strength for a given lateral size. Both fX− and fX increase by trend with the lateral size of the NPLs (brightness coded area scale in (f)), in line with the trends shown in Table 1, where a fastening of the radiative rates is observed.
Transferring the exciton oscillator strength e.g. in a radiative rate (see section S1 B of the ESI†) results in good agreement with experiments. As the change of oscillator strength with increasing lateral platelet size is different for trions and excitons, this results in a reduction of the trion to exciton oscillator strength ratio with increasing lateral size shown in (i). For a fixed size, the ratio increases with εenv as fX is more sensitive compared to fX−, see (g) and (h). A further important aspect is that using low dielectric constant ligands or atomic layer deposition high dielectric constant coating the trion emission can be suppressed or enhanced with respect to the exciton emission and its oscillator strength. Furthermore, our results imply that the trion binding energy can be tuned strongly above and below the room temperature thermal energy (Fig. 3(b)), while the exciton binding energy (Fig. 3(f)) is always above the room temperature thermal energy. As a consequence, either no trions or a considerable amount is present e.g. in devices, where the former is desired to enhance the emission efficiency.
Summing up our theoretical results for the trion and exciton properties, they are consistent with our experimental results on CdSe platelet PL dynamics and time-integrated and power-dependent PL as well as the energy separation and state energies. Our results show that especially the trion binding energies, Bohr radii and oscillator strength can be tuned by the lateral size and dielectric environment. Nanoplatelets are thus a model system to study the tunability of trion properties in a laterally finite 2D system. The trion plus exciton model is also fully compatible with reported findings in the literature. (See section S5 of the ESI† for a detailed discussion.)
3. Conclusion
In summary, we demonstrated that CdSe nanoplatelets are a model system to study the presence and tunability of trions and excitons in laterally finite 2D semiconductors. Based on theoretical modeling of transition energies, trion binding energies and oscillator strength of trions and excitons we showed that these properties can be tuned via the lateral size and aspect ratio. We further demonstrated that dielectric screening by the high frequency dielectric constant of the surroundings strongly changes e.g. the trion Bohr radius and oscillator strength. Using low dielectric constant ligands or atomic layer deposition high dielectric constant coating e.g. either trion emission can be suppressed or enhanced with respect to the exciton emission. Furthermore, our results imply that the trion binding energy can be tuned strongly above and below the room temperature thermal energy. Combining both effects, no trions or a considerable amount is present paving the way e.g. to an effective control of the emission efficiency of devices. Built on the 2D effective-mass approximation and solving the full four dimensional Schrödinger equation for anisotropic platelets, we have investigated the lateral size tunability of the exciton (upper state) and trion (lower state) energies in CdSe NPLs including dielectric confinement. The trion binding energy becomes tunable and increases from 18 meV to 36 meV with lateral platelet quantization. The obtained size tunable trion Bohr radius (∼3.5–4.8 nm) is in excellent agreement with experiments. Using the exciton and trion wave function from modeling, we calculated the oscillator strengths of excitons and trions and demonstrated that the trion oscillator strength is far smaller and tunable. This seems to be a general trend, in line with strong confined conventional quantum dots. All these data are in good agreement and allow for our model to consistently describe the experimentally observed dependencies. Our theoretical model is further substantiated by the good agreement of the calculated very short radiative exciton lifetimes with the experimental results. The short lifetimes or high transition oscillator strength, being strongly tunable by the lateral size and lateral aspect ratio, set the nanoplatelets among the fastest nano emitters.The presented results lay the foundation for further in-depth studies of the photophysics of CdSe nanoplatelets and related structures (e.g. 2D perovskites, TMDCs), as the demonstrated exciton and trion manifold is expected to impact properties like gain mechanisms, lasing or transport strongly. Especially interesting is that systematic studies of the trion physics in a system with tunable, strongly anisotropic confinement become feasible. This e.g. opens up the possibility to investigate to which extent localization impacts trion formation and decay and relevant understanding also for MBE grown devices, where a finite coherence length or disorder potentials localize excitons and impact the detrimental trion formation, which limits the quantum yield and device performance for instance. Nanoplatelets are a system in-between the yet studied extrema of 0D quantum dots and laterally infinite quantum wells and allow strong tuning of the optical and dynamical properties, while the transition energies remain nearly constant. These unique properties feature nanoplatelets as an excellent model system to study trion and exciton properties.
4. Methods
Theoretical simulations
As discussed platelets have strong z-confinement (coordinates ze and zh) and tunable lateral confinement. The Schrödinger equation of a neutral exciton in a NPL reads within the effective-mass and the envelope-function approximation: (He(ze) + Hh(zh) + HIPX(ρe, ρh))ΨX(re, rh) = EXΨX(re, rh), where ri = (ρi, zi). The total exciton wave function ΨX(re, rh) is split into two parts: (i) the confinement wave functions ϕe(ze) (ϕh(zh)) of the lowest electron (heavy-hole) sublevel, which are solutions of the single electron (hole) Hamiltonian in the z direction (perpendicular to the layers of the NPLs).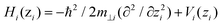 . Here Vi(zi) is the sum of all possible single-particle potentials affecting particle (i = e, h), and m⊥i, is the mass of carrier i along the strongly confined z-direction ([001]), the latter are taken from ref. 37. (ii) The in-plane wave function ψIPX(ρe, ρh) (index IP for in-plane) is the solution of the following in-plane Schrödinger equation:
. Here Vi(zi) is the sum of all possible single-particle potentials affecting particle (i = e, h), and m⊥i, is the mass of carrier i along the strongly confined z-direction ([001]), the latter are taken from ref. 37. (ii) The in-plane wave function ψIPX(ρe, ρh) (index IP for in-plane) is the solution of the following in-plane Schrödinger equation: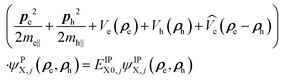 | (4) |
It takes into account the defined platelet extent (Lx, Ly) and aspect ratios of our samples. ρi are the in plane electron (i = e), hole (i = h) position vectors, pi = −iħ∇ρi is the in plane momentum operator, mi|| is the in-plane mass of carrier i used from ref. 37, and Vi(ρi) are the confinement potentials of the electron and hole. NPLs are embedded within organic ligands having a relatively small dielectric constant (εenv = 2.07 for oleic acid ligands5).
Actually, the electric force lines emerging from charges within a semiconductor nanoparticle pass through the surrounding medium, having a smaller dielectric constant than the semiconductor. Therefore, in order to take the dielectric screening of coulomb interaction properly into account, the electron–hole direct Coulomb interaction is treated here using a Rytova–Keldysh potential 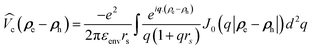 according to the widely accepted approach.7,31,32,51,74–77 However to avoid the divergence of the integral of the Bessel function in the Keldysh potential J0(q|ρe − ρh|), we can construct an approximate expression for
according to the widely accepted approach.7,31,32,51,74–77 However to avoid the divergence of the integral of the Bessel function in the Keldysh potential J0(q|ρe − ρh|), we can construct an approximate expression for 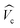 in terms of elementary functions
in terms of elementary functions 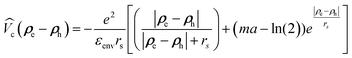 (see ref. 77 for details). This potential is better than using an unscreened vacuum Coulomb potential together with envelope functions in z-direction, the standard approach for quantum wells. Here, rs = εCdSeZ0/(2nenv) is the dielectric screening length, Z0 = (a0/2) × 4.5 ML is the platelet thickness and γ is the Euler constant.
(see ref. 77 for details). This potential is better than using an unscreened vacuum Coulomb potential together with envelope functions in z-direction, the standard approach for quantum wells. Here, rs = εCdSeZ0/(2nenv) is the dielectric screening length, Z0 = (a0/2) × 4.5 ML is the platelet thickness and γ is the Euler constant.
CdSe NPLs can be in a weak (quantum well-like), intermediate or strong confinement regime (quantum dot-like), depending on their lateral size.7,13,51 However, based on the recent results of ref. 7 and 51 the lowest energy exciton state can be described well by a weak confinement regime for the x and y directions, where the platelets have finite extent Lx and Ly. Since larger platelets are in the focus of this paper (Lx, Ly > a3DB ∼ 4 nm, calculated using ref. 5) and we are interested in the lowest energy exciton state, the theoretical model for excitons will be built with the assumption of a weak (lateral) confinement regime, i.e. considering NPLs as a more quantum well like than quantum dot like structure. In this context, to target the weak confinement limit, we will at first (i) ignore the confinement potential and solve the Schrödinger equation including only Coulomb interaction besides the kinetic terms and (ii) use the center of mass approximation. In fact, by transforming ρe and ρh into 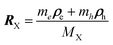 and ρ = ρe − ρh, which are the position vector of the center of mass of the exciton and relative distance of the electron from the hole, respectively, the Hamiltonian in eqn (4) can be separated in center of mass HcmX and relative motion HrelX Hamiltonians, which are solved numerically using the finite lateral size (Lx, Ly) of the NPLs.
and ρ = ρe − ρh, which are the position vector of the center of mass of the exciton and relative distance of the electron from the hole, respectively, the Hamiltonian in eqn (4) can be separated in center of mass HcmX and relative motion HrelX Hamiltonians, which are solved numerically using the finite lateral size (Lx, Ly) of the NPLs.
M
X = me + mh is the exciton mass. The solutions of the resulting Schrödinger equation of the system satisfy the eigenequation (HCMX + HrelX)ψIPX,j(RX, ρ) = EIPX,jψIPX,j(RX, ρ) and are given by 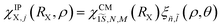 ,
, 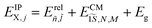 . Here, Eñ,
. Here, Eñ,![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) and ξñ,
and ξñ,![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) (ρ, θ) are the eigenenergy and the eigenvalue, respectively, obtained by numerical diagonalization of the relative Hamiltonian. ξñ,
(ρ, θ) are the eigenenergy and the eigenvalue, respectively, obtained by numerical diagonalization of the relative Hamiltonian. ξñ,![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) (ρ) can be expanded using an auxiliary basis along with
(ρ) can be expanded using an auxiliary basis along with 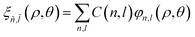 , where φn,l(ρ, θ) are the wave functions of the 2D-hydrogenic states given in terms of orthogonal associated Laguerre polynomials.
, where φn,l(ρ, θ) are the wave functions of the 2D-hydrogenic states given in terms of orthogonal associated Laguerre polynomials. 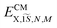 and
and 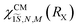 are the solution of the center of mass Hamiltonian, obtained by multiplying eqn (4) by
are the solution of the center of mass Hamiltonian, obtained by multiplying eqn (4) by 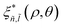 and integrating the full Schrödinger equation over ρ. (For more details see e.g.ref. 7 and 51). Eg is the energy gap between conduction and valence bands at the Γ point, taken from ref. 90.
and integrating the full Schrödinger equation over ρ. (For more details see e.g.ref. 7 and 51). Eg is the energy gap between conduction and valence bands at the Γ point, taken from ref. 90.
Excitons can form charged excitons (trions) with excess charges. For negative trions the Schrödinger equation can be written as: 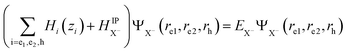 . The total trion wave function of the Hamitonian HX− can be factorized into: ΨX−(re1, re2, rh) = ϕe1(ze1)ϕe2(ze2)ϕh(zh)ψX−,jIP(ρe1, ρe2, ρh), where ϕi(zi) are the confinement functions of the lowest electron (i = e1, e2) and heavy-hole sublevel (i = h), respectively, and ψX−,jIP(ρe1, ρe2, ρh) is the wave function solution of the in plane trion Hamiltonian:
. The total trion wave function of the Hamitonian HX− can be factorized into: ΨX−(re1, re2, rh) = ϕe1(ze1)ϕe2(ze2)ϕh(zh)ψX−,jIP(ρe1, ρe2, ρh), where ϕi(zi) are the confinement functions of the lowest electron (i = e1, e2) and heavy-hole sublevel (i = h), respectively, and ψX−,jIP(ρe1, ρe2, ρh) is the wave function solution of the in plane trion Hamiltonian:
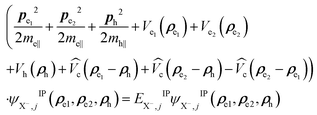 | (5) |
To investigate the negative trion binding energy in CdSe NPLs, we adopt the same formalism as for the exciton i.e. neglecting the confinement potential and using the relative ρi = ρei − ρb and the center of mass 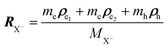 trion coordinates. Hence the trion in-plane Hamiltonian can be rewritten as a sum of center of mass and relative Hamiltonians HX−IP = HX−CM + HX−rel, where the eigen energy and eigen vector solution of the in plane Hamiltonian can be rewritten as
trion coordinates. Hence the trion in-plane Hamiltonian can be rewritten as a sum of center of mass and relative Hamiltonians HX−IP = HX−CM + HX−rel, where the eigen energy and eigen vector solution of the in plane Hamiltonian can be rewritten as 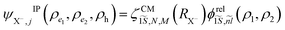 and
and 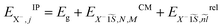 , where
, where 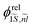 and
and 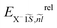 are the wave function and the energy solution of the relative Hamiltonian HX−rel given by
are the wave function and the energy solution of the relative Hamiltonian HX−rel given by 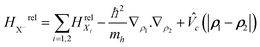 . Here HrelXi is the relative Hamiltonian of the neutral exciton and MX− = 2me + mh is the trion mass.
. Here HrelXi is the relative Hamiltonian of the neutral exciton and MX− = 2me + mh is the trion mass.
To solve the eigenvalue equation, we use a wave function expansion technique. It is factorized into 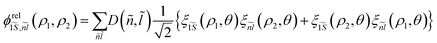 , where
, where 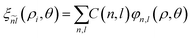 is the eigenvalue solution of the exciton Hamiltonian HrelXi (see ESI section S1 A† for more details on the choice of relative basis functions). As for the exciton, the center of mass eigenvalue and eigenenergy are obtained by multiplying eqn (3) with
is the eigenvalue solution of the exciton Hamiltonian HrelXi (see ESI section S1 A† for more details on the choice of relative basis functions). As for the exciton, the center of mass eigenvalue and eigenenergy are obtained by multiplying eqn (3) with 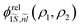 and integrating the full Schrödinger eqn (3) over ρ1 and ρ2. Table 2 reports the used material constants applied in the theoretical simulations.
and integrating the full Schrödinger eqn (3) over ρ1 and ρ2. Table 2 reports the used material constants applied in the theoretical simulations.
A comment on surrounding dielectric constant's high and low frequency values: in panel (e) of Fig. 2 we plot the exciton and trion energies for the static dielectric constant of CdSe NPLs εCdSe,s = 10. We notice that the use of εCdSe,s = 10 instead of εCdSe,∞ = 7.9 (panel (a)) would increase EX and EX− significantly. In the case of the exciton the calculated binding energies (∼200 meV, see the discussion in the main text) are much larger than the optical phonon energies in CdSe (25 meV). This implies that a high frequency dielectric constant should be used to calculate the NPL exciton ground state. However, in the case of the trion and for a sufficiently large NPL area (e.g. 41 × 13 nm2 (533 nm2)), the binding energy of the trion (∼18 meV) is smaller than the optical phonon energy. Hence, choosing between the static and high-frequency dielectric constants is a subtle problem when one wishes to calculate the trion states in CdSe NPLs. In our case, since the high dielectric constant gives a very good agreement with the experimental finding for both states (trion and exciton) we employ the high-frequency dielectric constant of CdSe. We should note that the energy shift (trion binding energy) is completely independent of these parameters. This can be reasoned directly from Fig. 2, e.g. for 21 × 7 nm2 (147 nm2) and 30 × 15 nm2 (450 nm2) platelets, where for the latter the trion binding energy is 29 meV for both dielectric constants, while it is 19.6 and 19.2 meV for the two different dielectric constants and 30 × 15 nm2 platelets.
Author contributions
S.A., A.W.A., and S.J. developed and performed modeling and calculations. A.W.A. designed and performed measurements. S.C., G.H.V.B., I.M., and M.A. provided samples and conducted their characterization. N.O. and U.W. contributed to the discussion. A.W.A., S.A., and M.T.Q. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. W. A. acknowledges funding by DFG projects AC290/2-1 and AC290/2-2 and I. M. by the European Research Council (ERC) Horizon 2020 research and innovation programme (grant no. 714876 PHOCONA).References
- S. Ithurria and B. Dubertret, J. Am. Chem. Soc., 2008, 130, 16504–16505 CrossRef CAS PubMed.
- A. W. Achtstein, A. Schliwa, A. Prudnikau, M. Hardzei, M. V. Artemyev, C. Thomsen and U. Woggon, Nano Lett., 2012, 12, 3151–3157 CrossRef CAS PubMed.
- S. Ithurria, M. D. Tessier, B. Mahler, R. P. S. M. Lobo, B. Dubertret and A. L. Efros, Nat. Mater., 2011, 10, 936–941 CrossRef CAS PubMed.
- G. H. V. Bertrand, A. Polovitsyn, S. Christodoulou, A. H. Khan and I. Moreels, Chem. Commun., 2016, 52, 11975–11978 RSC.
- A. W. Achtstein, R. Scott, S. Kickhöfel, S. T. Jagsch, S. Christodoulou, G. H. Bertrand, A. V. Prudnikau, A. Antanovich, M. Artemyev, I. Moreels, A. Schliwa and U. Woggon, Phys. Rev. Lett., 2016, 116, 116802 CrossRef PubMed.
- J. Planelles, A. W. Achtstein, R. Scott, N. Owschimikow, U. Woggon and J. I. Climente, ACS Photonics, 2018, 5, 3680–3688 CrossRef CAS.
- M. Richter, Phys. Rev. Mater., 2017, 1, 016001 CrossRef.
- D. P. Morgan, C. J. A. Maddux and D. F. Kelley, J. Phys. Chem. C, 2018, 122, 23772–23779 CrossRef CAS.
- A. W. Achtstein, O. Marquardt, R. Scott, M. Ibrahim, T. Riedl, A. V. Prudnikau, A. Antanovich, N. Owschimikow, J. K. N. Lindner, M. Artemyev and U. Woggon, ACS Nano, 2018, 12, 9476–9483 CrossRef CAS PubMed.
- B. Mahler, B. Nadal, C. Bouet, G. Patriarche and B. Dubertret, J. Am. Chem. Soc., 2012, 134, 18591–18598 CrossRef CAS PubMed.
- M. Nasilowski, P. Spinicelli, G. Patriarche and B. Dubertret, Nano Lett., 2015, 15, 3953–3958 CrossRef CAS PubMed.
- V. Dzhagan, A. G. Milekhin, M. Y. Valakh, S. Pedetti, M. Tessier, B. Dubertret and D. R. T. Zahn, Nanoscale, 2016, 8, 17204–17212 RSC.
- F. Rajadell, J. I. Climente and J. Planelles, Phys. Rev. B, 2017, 96, 035307 CrossRef.
- M. D. Tessier, B. Mahler, B. Nadal, H. Heuclin, S. Pedetti and B. Dubertret, Nano Lett., 2013, 13, 3321–3328 CrossRef CAS PubMed.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, D. Feng, V. F. Sapega, N. Flipo, A. A. Golovatenko, M. A. Semina, A. V. Rodina, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, Y. G. Kusrayev, M. Nasilowski, B. Dubertret and M. Bayer, Nano Lett., 2018, 18, 373–380 CrossRef CAS PubMed.
- L. Biadala, F. Liu, M. D. Tessier, D. R. Yakovlev, B. Dubertret and M. Bayer, Nano Lett., 2014, 14, 1134–1139 CrossRef CAS PubMed.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, V. F. Sapega, Y. G. Kusrayev, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, V. V. Belykh, M. V. Kochiev, N. N. Sibeldin, A. A. Golovatenko, A. V. Rodina, N. A. Gippius, A. Kuntzmann, Y. Jiang, M. Nasilowski, B. Dubertret and M. Bayer, Nanoscale, 2018, 10, 646–656 RSC.
- R. Scott, A. V. Prudnikau, A. Antanovich, S. Christodoulou, T. Riedl, G. H. V. Bertrand, N. Owschimikow, J. K. N. Lindner, Z. Hens, I. Moreels, M. Artemyev, U. Woggon and A. W. Achtstein, Nanoscale, 2019, 11, 3958–3967 RSC.
- C. J. A. Maddux, D. F. Kelley and A. M. Kelley, J. Phys. Chem. C, 2018, 122, 27100–27106 CrossRef CAS.
- R. Scott, A. W. Achtstein, A. Prudnikau, A. Antanovich, S. Christodoulou, I. Moreels, M. Artemyev and U. Woggon, Nano Lett., 2015, 15, 4985–4992 CrossRef CAS PubMed.
- J. Heckmann, R. Scott, A. V. Prudnikau, A. Antanovich, N. Owschimikow, M. Artemyev, J. I. Climente, U. Woggon, N. B. Grosse and A. W. Achtstein, Nano Lett., 2017, 17, 6321–6329 CrossRef CAS PubMed.
- C. She, I. Fedin, D. S. Dolzhnikov, A. Demortière, R. D. Schaller, M. Pelton and D. V. Talapin, Nano Lett., 2014, 14, 2772–2777 CrossRef CAS PubMed.
- J. Q. Grim, S. Christodoulou, F. Di Stasio, R. Krahne, R. Cingolani, L. Manna and I. Moreels, Nat. Nanotechnol., 2014, 9, 891–895 CrossRef CAS PubMed.
- M. T. Quick, N. Owschimikow, A. H. Khan, A. Polovitsyn, I. Moreels, U. Woggon and A. W. Achtstein, Nanoscale, 2019, 11, 17293–17300 RSC.
- Q. A. Akkerman, G. Rainò, M. V. Kovalenko and L. Manna, Nat. Mater., 2018, 17, 394–405 CrossRef CAS PubMed.
- A. W. Achtstein, A. Antanovich, A. Prudnikau, R. Scott, U. Woggon and M. Artemyev, J. Phys. Chem. C, 2015, 119, 20156–20161 CrossRef CAS.
- L. T. Kunneman, M. D. Tessier, H. Heuclin, B. Dubertret, Y. V. Aulin, F. C. Grozema, J. M. Schins and L. D. A. Siebbeles, J. Phys. Chem. Lett., 2013, 4, 3574–3578 CrossRef CAS.
- A. Naeem, F. Masia, S. Christodoulou, I. Moreels, P. Borri and W. Langbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121302 CrossRef.
- R. Scott, J. Heckmann, A. V. Prudnikau, A. Antanovich, A. Mikhailov, N. Owschimikow, M. Artemyev, J. I. Climente, U. Woggon, N. B. Grosse and A. W. Achtstein, Nat. Nanotechnol., 2017, 17, 1155–1160 CrossRef PubMed.
- D.-E. Yoon, W. D. Kim, D. Kim, D. Lee, S. Koh, W. K. Bae and D. C. Lee, J. Phys. Chem. C, 2017, 121, 24837–24844 CrossRef CAS.
- S. Ayari, A. Smiri, A. Hichri, S. Jaziri and T. Amand, Phys. Rev. B, 2018, 98, 205430 CrossRef CAS.
- A. Hichri, I. B. Amara, S. Ayari and S. Jaziri, J. Phys.: Condens. Matter, 2017, 29, 435305 CrossRef CAS PubMed.
- L. Waldecker, A. Raja, M. Rösner, C. Steinke, A. Bostwick, R. J. Koch, C. Jozwiak, T. Taniguchi, K. Watanabe, E. Rotenberg, T. O. Wehling and T. F. Heinz, Phys. Rev. Lett., 2019, 123, 206403 CrossRef CAS PubMed.
- V. A. Hintermayr, L. Polavarapu, A. S. Urban and J. Feldmann, ACS Nano, 2018, 12, 10151–10158 CrossRef CAS PubMed.
- Q. Wang, X.-D. Liu, Y.-H. Qiu, K. Chen, L. Zhou and Q.-Q. Wang, AIP Adv., 2018, 8, 025108 CrossRef.
- J. A. Sichert, Y. Tong, N. Mutz, M. Vollmer, S. Fischer, K. Z. Milowska, R. García Cortadella, B. Nickel, C. Cardenas-Daw, J. K. Stolarczyk, A. S. Urban and J. Feldmann, Nano Lett., 2015, 15, 6521–6527 CrossRef CAS PubMed.
- R. Benchamekh, N. A. Gippius, J. Even, M. Nestoklon, J.-M. Jancu, S. Ithurria, B. Dubertret, A. L. Efros and P. Voisin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035307 CrossRef.
- R. Scott, A. W. Achtstein, A. V. Prudnikau, A. Antanovich, L. D. A. Siebbeles, M. Artemyev and U. Woggon, Nano Lett., 2016, 16, 6576–6583 CrossRef CAS PubMed.
- A. Brumberg, S. M. Harvey, J. P. Philbin, B. T. Diroll, B. Lee, S. A. Crooker, M. R. Wasielewski, E. Rabani and R. D. Schaller, ACS Nano, 2019, 13, 8589–8596 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045318 CrossRef.
- K. F. Mak, K. He, C. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Nat. Mater., 2013, 12, 207–211 CrossRef CAS PubMed.
- B. Ganchev, N. Drummond, I. Aleiner and V. Fal'ko, Phys. Rev. Lett., 2015, 114, 107401 CrossRef PubMed.
- G. Plechinger, P. Nagler, A. Arora, R. Schmidt, A. Chernikov, A. G. del Águila, P. C. M. Christianen, R. Bratschitsch, C. Schüller and T. Korn, Nat. Commun., 2016, 7, 12715 CrossRef CAS PubMed.
- S. Helmrich, R. Schneider, A. W. Achtstein, A. Arora, B. Herzog, S. M. de Vasconcellos, M. Kolarczik, O. Schöps, R. Bratschitsch, U. Woggon and N. Owschimikow, 2D Mater., 2018, 5, 045007 CrossRef CAS.
- A. Arora, T. Deilmann, T. Reichenauer, J. Kern, S. Michaelis de Vasconcellos, M. Rohlfing and R. Bratschitsch, Phys. Rev. Lett., 2019, 123, 167401 CrossRef CAS PubMed.
- F. Cadiz, S. Tricard, M. Gay, D. Lagarde, G. Wang, C. Robert, P. Renucci, B. Urbaszek and X. Marie, Appl. Phys. Lett., 2016, 108, 251106 CrossRef.
- A. Singh, G. Moody, K. Tran, M. E. Scott, V. Overbeck, G. Berghäuser, J. Schaibley, E. J. Seifert, D. Pleskot, N. M. Gabor, J. Yan, D. G. Mandrus, M. Richter, E. Malic, X. Xu and X. Li, Phys. Rev. B, 2016, 93, 041401 CrossRef.
- K. Hao, L. Xu, P. Nagler, A. Singh, K. Tran, C. K. Dass, C. Schüller, T. Korn, X. Li and G. Moody, Nano Lett., 2016, 16, 5109–5113 CrossRef CAS PubMed.
- F. Gerdes, C. Navío, B. H. Juárez and C. Klinke, Nano Lett., 2017, 17, 4165–4171 CrossRef CAS PubMed.
- S. Christodoulou, J. I. Climente, J. Planelles, R. Brescia, M. Prato, B. Martín-Garcí, A. H. Khan and I. Moreels, Nano Lett., 2018, 18, 6248–6254 CrossRef CAS PubMed.
- J. F. Specht, R. Scott, M. C. Castro, S. Christodoulou, G. H. Bertrand, A. Prudnikau, A. Antanovich, L. Siebbeles, N. Owschimikow and I. Moreels, et al. , Nanoscale, 2019, 11, 12230–12241 RSC.
- B. T. Diroll, W. Cho, I. Coropceanu, S. M. Harvey, A. Brumberg, N. Holtgrewe, S. A. Crooker, M. R. Wasielewski, V. B. Prakapenka, D. V. Talapin and R. D. Schaller, Nano Lett., 2018, 18, 6948–6953 CrossRef CAS PubMed.
- O. Erdem, M. Olutas, B. Guzelturk, Y. Kelestemur and H. V. Demir, J. Phys. Chem. Lett., 2016, 7, 548–554 CrossRef CAS PubMed.
- E. V. Shornikova, D. R. Yakovlev, L. Biadala, S. A. Crooker, V. V. Belykh, M. V. Kochiev, A. Kuntzmann, M. Nasilowski, B. Dubertret and M. Bayer, Nano Lett., 2020, 20, 1370–1377 CrossRef CAS PubMed.
- D. Kudlacik, V. F. Sapega, D. R. Yakovlev, I. V. Kalitukha, E. V. Shornikova, A. V. Rodina, E. L. Ivchenko, G. S. Dimitriev, M. Nasilowski, B. Dubertret and M. Bayer, Nano Lett., 2020, 20, 517–525 CrossRef CAS PubMed.
- A. Esser, E. Runge, R. Zimmermann and W. Langbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8232 CrossRef CAS.
- M. Combescot and S.-Y. Shiau, Excitons and Cooper pairs: two composite bosons in many-body physics, Oxford University Press, 2015 Search PubMed.
- A. M. Jones, H. Yu, N. J. Ghimire, S. Wu, G. Aivazian, J. S. Ross, B. Zhao, J. Yan, D. G. Mandrus and D. Xiao, et al. , Nat. Nanotechnol., 2013, 8, 634 CrossRef CAS PubMed.
- D. Andronikov, V. Kochereshko, A. Platonov, T. Barrick, S. Crooker and G. Karczewski, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165339 CrossRef.
- P. P. Jha and P. Guyot-Sionnest, ACS Nano, 2009, 3, 1011–1015 CrossRef CAS PubMed.
- V. I. Klimov, Annu. Rev. Phys. Chem., 2007, 58, 635–673 CrossRef CAS PubMed.
- J. Feldmann, G. Peter, E. Göbel, P. Dawson, K. Moore, C. Foxon and R. Elliott, Phys. Rev. Lett., 1987, 59, 2337 CrossRef CAS PubMed.
- H. Akiyama, S. Koshiba, T. Someya, K. Wada, H. Noge, Y. Nakamura, T. Inoshita, A. Shimizu and H. Sakaki, Phys. Rev. Lett., 1994, 72, 924–927 CrossRef CAS PubMed.
- D. P. Morgan and D. F. Kelley, J. Phys. Chem. C, 2019, 123, 18665–18675 CrossRef CAS.
- C. Robert, D. Lagarde, F. Cadiz, G. Wang, B. Lassagne, T. Amand, A. Balocchi, P. Renucci, S. Tongay and B. Urbaszek, et al. , Phys. Rev. B, 2016, 93, 205423 CrossRef.
- S. Ayari and S. Jaziri, Phys. Status Solidi B, 2019, 256, 1800682 CrossRef.
- H. H. Fang, B. Han, C. Robert, M. A. Semina, D. Lagarde, E. Courtade, T. Taniguchi, K. Watanabe, T. Amand, B. Urbaszek, M. M. Glazov and X. Marie, Phys. Rev. Lett., 2019, 123, 067401 CrossRef CAS PubMed.
- E. Vanelle, M. Paillard, X. Marie, T. Amand, P. Gilliot, D. Brinkmann, R. Lévy, J. Cibert and S. Tatarenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 2696 CrossRef CAS.
- G. Finkelstein, V. Umansky, I. Bar-Joseph, V. Ciulin, S. Haacke, J.-D. Ganiere and B. Deveaud, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 12637 CrossRef CAS.
- B. Patton, W. Langbein and U. Woggon, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125316 CrossRef.
- M. Califano, A. Franceschetti and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115401 CrossRef.
- J.-h. Wang, G.-j. Liang and K.-f. Wu, Chin. J. Chem. Phys., 2017, 30, 649–656 CrossRef CAS.
- S. A. Cherevkov, M. V. Artemyev, A. V. Prudnikau and A. V. Baranov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 041303 CrossRef.
- A. Hichri, I. Ben Amara, S. Ayari and S. Jaziri, J. Appl. Phys., 2017, 121, 235702 CrossRef.
- N. S. Rytova, arXiv preprint arXiv:1806.00976, 2018.
- A. Chernikov, T. C. Berkelbach, H. M. Hill, A. Rigosi, Y. Li, O. B. Aslan, D. R. Reichman, M. S. Hybertsen and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 076802 CrossRef PubMed.
- P. Cudazzo, I. V. Tokatly and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085406 CrossRef.
- F. García Flórez, A. Kulkarni, L. D. A. Siebbeles and H. T. C. Stoof, Phys. Rev. B, 2019, 100, 245302 CrossRef.
- Y. Louyer, L. Biadala, P. Tamarat and B. Lounis, Appl. Phys. Lett., 2010, 96, 203111 CrossRef.
- S. R. Stock, Microcomputed tomography: methodology and applications, CRC press, 2018 Search PubMed.
- A. Esser, R. Zimmermann and E. Runge, Phys. Status Solidi B, 2001, 227, 317–330 CrossRef CAS.
- G. V. Astakhov, V. P. Kochereshko, D. R. Yakovlev, W. Ossau, J. Nürnberger, W. Faschinger and G. Landwehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10345–10352 CrossRef CAS.
- Z. Hens and I. Moreels, J. Mater. Chem., 2012, 22, 10406 RSC.
- P. Geiregat, R. Tomar, K. Chen, S. Singh, J. M. Hodgkiss and Z. Hens, J. Phys. Chem. Lett., 2019, 10, 3637–3644 CrossRef CAS PubMed.
- M. Combescot and J. Tribollet, Solid State Commun., 2003, 128, 273–277 CrossRef CAS.
- M. Combescot and O. Betbeder-Matibet, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205313 CrossRef.
- S. Ithurria and D. V. Talapin, J. Am. Chem. Soc., 2012, 134, 18585–18590 CrossRef CAS PubMed.
- R. A. Sergeev, R. A. Suris, G. V. Astakhov, W. Ossau and D. R. Yakovlev, Eur. Phys. J. B, 2005, 47, 541–547 CrossRef CAS.
- E. Courtade, M. Semina, M. Manca, M. M. Glazov, C. Robert, F. Cadiz, G. Wang, T. Taniguchi, K. Watanabe, M. Pierre, W. Escoffier, E. L. Ivchenko, P. Renucci, X. Marie, T. Amand and B. Urbaszek, Phys. Rev. B, 2017, 96, 085302 CrossRef.
- W. Shan, J. Song, H. Luo and J. Furdyna, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 8012 CrossRef CAS PubMed.
- S.-H. Wei and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 5404 CrossRef CAS.
- Y. Kim, M. Klein, S. Ren, Y. Chang, H. Luo, N. Samarth and J. Furdyna, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7262 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details on theoretical model, samples and experimental results. See DOI: 10.1039/D0NR03170D |
| This journal is © The Royal Society of Chemistry 2020 |