Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selective magnetometry of superparamagnetic iron oxide nanoparticles in liquids†
Juliusz
Kuciakowski
 ab,
Angelika
Kmita
ab,
Angelika
Kmita
 a,
Dorota
Lachowicz
a,
Dorota
Lachowicz
 a,
Magdalena
Wytrwal-Sarna
a,
Magdalena
Wytrwal-Sarna
 a,
Krzysztof
Pitala
a,
Krzysztof
Pitala
 ab,
Sara
Lafuerza
ab,
Sara
Lafuerza
 c,
Dorota
Koziej
c,
Dorota
Koziej
 d,
Amélie
Juhin
d,
Amélie
Juhin
 e and
Marcin
Sikora
e and
Marcin
Sikora
 *a
*a
aAGH University of Science and Technology, Academic Centre for Materials and Nanotechnology, Al. Mickiewicza 30, 30-059 Krakow, Poland. E-mail: marcin.sikora@agh.edu.pl
bAGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Al. Mickiewicza 30, 30-059 Krakow, Poland
cEuropean Synchrotron Radiation Facility, CS40220, 38043 Grenoble Cedex 9, France
dInstitute of Nanostructure- and Solid State Physics, Center for Hybrid Nanostructures, University of Hamburg, Luruper Chaussee 149, 22607 Hamburg, Germany
eInstitut de Minéralogie, de Physique des Matériaux et de Cosmochimie (IMPMC), Sorbonne Université, UMR CNRS 7590, Muséum National d'Histoire Naturelle, 4 Place Jussieu, 75005 Paris, France
First published on 3rd August 2020
Abstract
We show that the properties of superparamagnetic iron oxide nanoparticles suspended in liquids can be effectively studied using Magnetic Circular Dichroism in Resonant Inelastic X-ray Scattering. Analysis of the spectral shape and magnetic contrast produced by this experiment enables an assessment of the site distribution and magnetic state of metal ions in the spinel phase. The selective magnetization profile of particles as derived from the field dependence of dichroism empowers an estimation of particle size distribution. Furthermore, the new proposed methodology discriminates sizes that are below the detection limits of X-ray and light scattering probes and that are difficult to spot in TEM.
The efficient control of the magnetic response1,2 of synthesized3,4 or filtered5 suspensions of nanoparticles is essential for effective and safe use in biomedical and environmental applications.6,7 Over the past few decades, significant progress has been made in understanding the physical and chemical properties of the smallest magnetic species,8 establishing robust methodology for the analysis of surface effects, magnetic anisotropy and inter-particle interactions.9–13
The majority of these studies, however, were performed on dry nanoparticles, which greatly simplifies the estimation of particle size, chemical composition and magnetic properties. However, in a suspension, the native environment for colloidal synthesis and storage of superparamagnetic iron oxide nanoparticles (SPION),14,15 this approach is insufficient due to the uncertainty in separation of paramagnetic response of small particles from that of the diamagnetic background of carrier liquid. Therefore, it is usually not possible to determine the density of the smallest particles. In addition, uncertain concentration, morphology and magnetization of particles, and possible chemical ageing also results in significant ambiquity.16–18 Hence, it is clear that the analysis of in situ magnetization of SPION in suspensions is needed for accurately ascertaining the functionality of magnetic liquids.5,6,14,15,19–24
In response to these needs, several new methods based on photon scattering and resonant spectroscopies have recently been developed.25–30 In parallel, methodology for the interpretation of volume magnetic data has advanced significantly and become indispensable for the precise determination of particle size distribution.31–34
Spectroscopic methods, which are capable of probing individual magnetic components by taking advantage of their element and site selectivity, are indispensable to unravel the response of particles from that of the carrier liquid. 57Fe Mössbauer spectroscopy (MS), magnetic particle spectroscopy (MPS) and X-ray magnetic circular dichroism (XMCD) are often used for characterization of iron oxide nanoparticles.9,16,23,35–41 Although the XMCD spectra has a lower energy resolution and the experimental setup is more involved than that of MS and MPS, XMCD has the advantage that it can be applied to any magnetic element. Moreover, the XMCD spectral shape is not prone to relaxation effects. It reflects the time and spatial average of the net magnetization in the ensemble of particles, because it is characterized by significantly shorter characteristic time defined by core-hole lifetime.42 Thus, it can be directly used to derive magnetization profiles of a selected element or crystal site in iron-oxide nanoparticles.38,43
Element specificity and versatile detection modes, namely transmission, fluorescence and electron yield, make XMCD especially advantageous for separation of volume- and surface-related properties of core/shell nanoparticles and multi-component nanoscale materials.44,45 Nevertheless, except from experiments performed on magnetotactic bacteria (particle radius R > 15 nm) using transmission X-ray microscopy,40 XMCD studies are limited to dry samples due to instrumental difficulties related to the use of soft X-rays in probing inhomogeneous liquids.46,47 However, it has been recently shown that selective magnetization profiles can be probed on frozen SPION suspensions by means of hard X-ray Magnetic Circular Dichroism combined with Resonant Inelastic X-ray Scattering (RIXS-MCD).48
Here we report on the feasibility of using 1s2p RIXS-MCD, a photon-in/photon-out spectroscopy that probes intensity of 2p emission upon resonant excitation of 1s electrons, for the selective characterization of structural and magnetic properties of SPION in suspensions.
RIXS-MCD reveals a strong magnetic contrast at the K pre-edge of transition metals in ferrimagnetic spinel oxides and garnets.49,50 The RIXS-MCD plane comprises of several pairs of high energy resolution fluorescence detected X-ray absorption spectra (HERFD-XAS) probed with opposite circular polarisation of incident light (Fig. 1). As such, our method inherits the main advantages of HERFD-XAS, namely high selectivity to chemical environment of the probed metal, and background-free detection.51
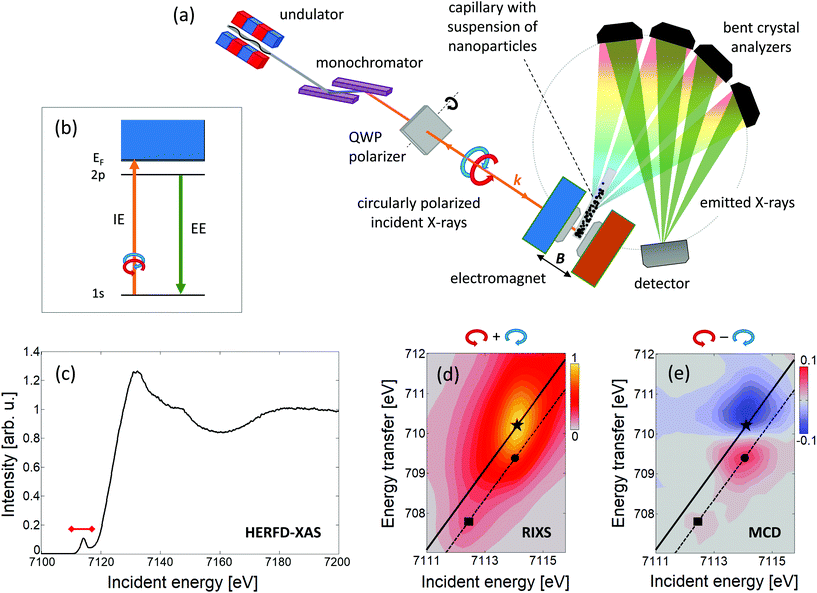 | ||
| Fig. 1 (a) Sketch of the experimental setup used for selective magnetic probing of SPION in suspensions† and (b) a schematic diagram of the energy levels involved, namely 1s absorption (IE, incidence energy) followed by 2p decay (EE, emitted energy). Results of the measurements performed on the suspension of γ-Fe2O3 nanoparticles in benzyl alcohol: (c) HERFD-XAS collected at EE = 6403.8 eV, red mark indicates the IE range covered by RIXS-MCD spectra; (d) 1s2p3/2 RIXS plane, and (e) 1s2p3/2 RIXS-MCD plane. Energy transfer is the difference between IE and EE. Solid and dashed lines represent the linear scans collected at constant EE corresponding to the pre-edge maximum (marked with star, EE = 6403.8 eV) and the pronounced Fe2+/Fe3+ features of MCD (marked with square/circle, EE = 6404.7 eV), respectively. | ||
The experiments were performed at room temperature on the suspensions of spinel iron oxide and cobalt ferrite nanoparticles dispersed in benzyl alcohol (BnOH) as well as zinc-doped iron oxide nanoparticles dispersed in water.† Measurements were performed at ID26 beamline at the European Synchrotron Radiation Facility. SPION suspensions were embedded into thin-walled Kapton capillaries and placed in the geometrical centre of an electromagnet which produced a magnetic field aligned parallel to the monochromatic, circularly polarized incident X-ray beam. Emitted photons were resolved in energy using a multianalyzer spectrometer and detected by a single-photon-counting detector. A sketch of the experimental setup, the schematic diagram of the transitions involved, and the results acquired on suspension of iron oxide nanoparticles are shown in Fig. 1.
The Fe 1s2p HERFD-XAS spectrum and the 1s2p3/2 RIXS and RIXS-MCD planes collected from suspension of spinel iron oxide nanoparticles (Fig. 1(c–e)) closely resemble the characteristic shape of spectra previously collected at the iron K pre-edge on powders, thin films and nanoparticles of spinel ferrites.45,49,50,52,53 The strong magnetic contrast and the good signal-to-noise ratio are sufficient for quantitative study. Noticeably, the weak feature at IE ≈ 7112.5 eV (marked with a square in Fig. 1), arising from Fe2+ Oh site54 is present in the RIXS-MCD plane. This indicates that the particles contain both Fe3+ and Fe2+ ions. However, the position of the pre-edge maximum in 1s2p3/2 RIXS, which is due to the contribution of tetrahedrally coordinated Fe3+ ions, is shifted to higher incident energy by approx. 0.5 eV with respect to that of magnetite (Fe3O4, Fig. 2(a)). Such a small shift is also observed in maghemite (γ-Fe2O3).54 Both the RIXS and RIXS-MCD spectral shapes are compatible with a spinel structure of particles and the expected iron oxide stoichiometry being close to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.55 The peak-to-peak amplitude of RIXS-MCD measured for this sample (approx. 23%) is in line with the presence of tetrahedral Fe3+ ions. It is reduced proportionally to volume magnetization with respect to bulk magnetite (30%).56
3.55 The peak-to-peak amplitude of RIXS-MCD measured for this sample (approx. 23%) is in line with the presence of tetrahedral Fe3+ ions. It is reduced proportionally to volume magnetization with respect to bulk magnetite (30%).56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡ This is clear evidence that RIXS-MCD spectra of SPION suspensions are not affected by magnetization flipping and other relaxation phenomena observed in hyperfine probes.
‡ This is clear evidence that RIXS-MCD spectra of SPION suspensions are not affected by magnetization flipping and other relaxation phenomena observed in hyperfine probes.
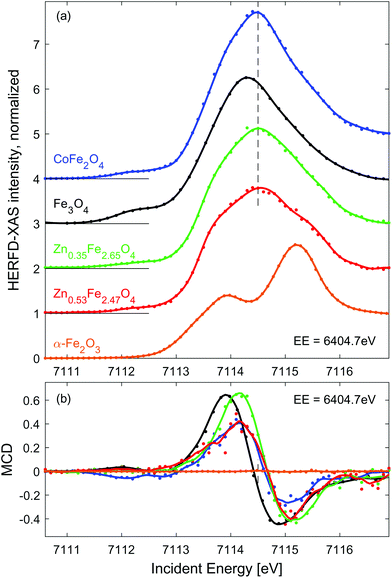 | ||
| Fig. 2 Line scans through the RIXS (a) and RIXS-MCD (b) plane at EE = 6404.7 eV (dashed line in Fig. 1(d and e)). Dots show experimental points, solid lines represent spectra smoothed using Savitzky-Golay filter. Spectra in panel (a) are shifted vertically for clarity. The dashed vertical line in (a) marks the position of the pre-edge maximum in CoFe2O4 and Zn doped iron oxides, which is clearly shifted up from that of Fe3O4, as expected for spinel oxides with high concentration of Fe3+. | ||
Fe 1s2p3/2 HERFD-XAS and MCD spectra measured for the other three SPION suspensions and solid reference samples are shown in Fig. 2. For the sake of comparison, they are normalized to equal intensity at IE = 7116.8 eV. In order to enhance the MCD signal characteristic to Fe2+ Oh sites,49 these spectra were probed at emission energy of 6404.7 eV (dashed line in Fig. 1(e)). As expected, HERFD-XAS of spinel ferrites is dominated by strong peak originating from Fe3+ Td sites, while the α−Fe2O3 reference reveals a separated double peak structure characteristic for Fe3+ Oh sites.55 The peak intensity in CoFe2O4 is the largest due to the largest fraction of tetrahedral Fe3+ in population of iron ions, i.e. 1/2 for perfectly inverse spinel. The second highest pre-edge feature is observed for magnetite reference, i.e. 1/3 of iron sites is tetrahedral. As expected, the pre-edge peak is further decreasing and broadens when Fe3+ is replaced by Zn2+ in Td sites, which is due to emerging intensity of the double-peak Fe3+ Oh features.
Based on the results of previous experiments and Ligand Field Multiplet calculations50,54 it can be derived that the amplitude of the Fe K pre-edge peak is proportional to 7NTd + 2NOh, where NTd and NOh denotes the occupation of Td and Oh sites by iron ions, respectively.† Quantification of the spectral intensity in Zn doped iron oxides provides an estimate of the population of metal sites by iron ions, which equals NTd ≈ 0.99 (0.88) and NOh ≈ 1.66 (1.59) for Zn0.35Fe2.65O4 (Zn0.53Fe2.47O4) particles. However, to fully confirm these numbers as accurate indicators of site occupancy simultaneous measurement should be performed at the Zn K edge. Nevertheless, we show that quantitative analysis of Fe 1s2p HERFD-XAS indicates a preferential substitution site, which is predominantly Oh, inverse spinel, at low Zn content and partially Td, mixed spinel, at high Zn content.
RIXS-MCD spectra shown in Fig. 2(b) are dominated by net magnetization of Fe3+ Td site, which is approximately 3-times stronger and opposite in sign than that of Fe3+ Oh site.50 The strongest magnetic dichroism is observed for pristine magnetite. However, the peak-to-peak amplitude of the RIXS-MCD signal probed in the dispersion of Zn0.35Fe2.65O4 nanoparticles is nearly the same as Fe3O4. It is in line with the scenario of predominant substitution of Oh sites by Zn. A significant (approx. 20%) reduction of the magnetic contrast in the case of Zn0.53Fe2.47O4 agrees with the relative decrease in occupation of Fe3+ Td sites. Surprisingly, the weakest RIXS-MCD amplitude among SPION samples is detected for the CoFe2O4 suspension. Since the relative distributions of Fe3+ ions between available crystal sites is identical in this inverse spinel and Fe3O4, identical amplitude of magnetic spectra is expected in both samples. Otherwise, the reduction of MCD must be related to lack of magnetic saturation. Indeed, magnetization of CoFe2O4 suspension is strongly decreased at room temperature as confirmed by ex situ measurements shown in ESI, Fig. S1.† As expected for antiferromagnetic materials, the amplitude of magnetic contrast in the spectrum of α-Fe2O3 is negligible.
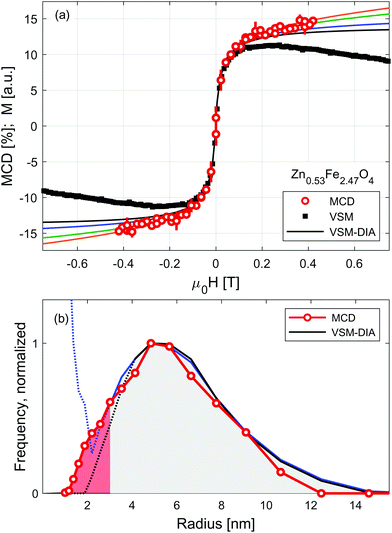
Sensitivity of RIXS-MCD spectra to different elements and crystal sites provides a straightforward way to disentangle individual contributions to magnetization, which has been recently used for the selective determination of magnetic anisotropy in core/shell and mixed ferrite nanoparticle systems.45,48,57 Here we verify whether it can be applied to separate magnetization profiles of SPION from that of the carrier liquid. Results of the measurements performed at room temperature on Zn0.53Fe2.47O4 nanoparticles suspended in water are shown in Fig. 3. Dependence of the strongest positive feature of RIXS-MCD marked with a circle in Fig. 1(e) is probed versus the magnetic field varied in the full magnetization loop. As expected for particles suspended in liquid, no indication of magnetic hysteresis is observed. The profile resembles that of small nanoparticles of weak magnetic anisotropy. To confirm that it is not affected by experimental artefacts related to instabilities of the liquid under intense X-ray irradiation, such as slow particle agglomeration, convection, concentration changes etc., we performed independent volume magnetization measurements by means of vibrating sample magnetometry (VSM). Comparison of RIXS-MCD derived magnetization profiles with that of VSM reveals a significant difference at moderate and large magnetic fields. There the VSM curve exhibits a diamagnetic contribution of carrier liquid, which results in a negative slope of volume magnetization.
Equilibrium magnetization curve of superparamagnetic particles can be fitted by Langevin function,58 leading to the determination of a magnetic dipole moment. However, the magnetic response of SPION suspensions may deviate significantly from the Langevin function in the range of magnetic field in which the magnetic anisotropy energy is comparable to the thermal fluctuation energy. Therefore, magnetic saturation of SPION requires magnetic fields sufficiently high to distinguish the diamagnetic contribution of carrier liquid from that of nanoparticles. To overcome this limitation several models have been recently developed, which allow us to derive the distribution of magnetic moments from medium-field magnetization curves.16,33,59,60
For the sake of comparison to RIXS-MCD data, diamagnetic contribution is subtracted from VSM data using MINORIM software.60 Depending on the cut-off field used, ranging from 0.1 T to 0.4 T, the resulting profiles of the inferred superparamagnetic component (VSM-DIA) lies between the black and blue line in Fig. 3(a). The agreement with particle selective data is thereby better, but not perfect. To further improve the equivalence between MCD and VSM-DIA profiles, the strength of the diamagnetic contribution must be artificially increased by approx. 40% as revealed by the green and orange lines in Fig. 3(a). In this way, the border estimates of the magnetization profile of the particles in Zn0.53Fe2.47O4 suspension are derived. Paramagnetic response is tentatively ascribed to the smallest particles in the further discussion, but may also originate from strong inter-particle interactions.
The distribution of magnetic dipole moments, μ, are derived from the MCD and VSM-DIA profiles by means of a non-regularized inversion method implemented in MINORIM software. To facilitate the analysis these are transformed to magnetic volumes assuming particles have a spherical shape and volume magnetization of 350 kA m−1.37 Resulting distribution is presented in Fig. 3(b) as a function of particle radius, R. It reveals negligible effect of the subtraction of linear distribution in the limit of large particles/dipoles (R > 4 nm, μ > 8 × 10−20 A m2). However, for smaller particles (at the limit of R < 2.5 nm, μ < 5 × 10–20 A m2, shaded red in Fig. 3(b)), the distributions derived from VSM-DIA data strongly depends upon the linear contribution of the cut-off field.
Despite being experimentally more challenging due to lower statistics, particle selective RIXS–MCD magnetometry provides an ample approximation of the dipole moment distribution in the entire particle size range. It confirms the profile derived from VSM data for the large particles and remains valid at the paramagnetic limit. With the expanding availability of high energy resolution spectrometers, such experiments may become readily available at many synchrotron sources which generate hard X-ray photons. Ultimately, RIXS-MCD experiments could be performed under high magnetic fields generated by superconducting magnets. This opens up the possibility of being able to probe the magnetic saturation of the smallest (weakly magnetic) particles in solution.
Conclusions
We have successfully probed 1s2p RIXS-MCD in BnOH and water suspensions of superparamagnetic iron oxide nanoparticles. Four different SPION systems were studied revealing strong magnetic contrast and good signal-to-noise ratio. No indication of spectral shape modification due to magnetization fluctuation, such as broadening, intensity loss, etc. is observed. Spectral variations related to the instability of the suspensions under hard X-ray irradiation are effectively filtered out. Based on the quantitative spectral analysis, the distribution of metal ions between spinel sites is assessed.Following the field dependence of RIXS-MCD amplitude, selective magnetization profiles of Zn-doped magnetite nanoparticles suspended in water is derived. This enables us to uncover a paramagnetic response of particles in the suspension and to reliably estimate the size distribution profile of the smallest particles, which are below the detection limit of scattering probes and difficult to spot in TEM images.
The methodology presented here can be used as selective magnetometry of SPION in liquids as long as the magnetic suspension remains spatially and temporary homogeneous. This method could possibly also be extended to more sophisticated sample environments allowing for in situ experiments,4,15,61,62 also at ultralow concentration and small volume.63
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Andrzej Kozłowski for providing reference sample of magnetite single crystal as well as Jan Żukrowski, Wojciech Szczerba, Uwe Steinhoff, Philipp Jaker, Mauro Rovezzi, Pieter Glatzel, James Ablett, and Philippe Sainctavit for stimulating discussions. This project was supported by National Science Centre, Poland, grant number 2014/14/E/ST3/00026 (JK, DL, MW, KP, MS) and 2016/23/D/ST8/00013 (AK). The access to ESRF was financed by the Polish Ministry of Science and High Education - decision number: DIR/WK/2016/19. AJ acknowledges financial support from the French ANR under grant agreement 17-CE30-0010-01. This project (DK) has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme Grant agreement No. 818941-LINCHPIN-ERC-2018-COG.Notes and references
- M. Shuai, A. Klittnick, Y. Shen, G. P. Smith, M. R. Tuchband, C. Zhu, R. G. Petschek, A. Mertelj, D. Lisjak, M. Čopič, J. E. Maclennan, M. A. Glaser and N. A. Clark, Nat. Commun., 2016, 7, 10394 CrossRef CAS PubMed.
- D. Hoffelner, M. Kundt, A. M. Schmidt, E. Kentzinger, P. Bender and S. Disch, Faraday Discuss., 2015, 181, 449–461 RSC.
- M. Unni, A. M. Uhl, S. Savliwala, B. H. Savitzky, R. Dhavalikar, N. Garraud, D. P. Arnold, L. F. Kourkoutis, J. S. Andrew and C. Rinaldi, ACS Nano, 2017, 11, 2284–2303 CrossRef CAS PubMed.
- D. Koziej, Chem. Mater., 2016, 28, 2478–2490 CrossRef CAS.
- C. M. Schumacher, I. K. Herrmann, S. B. Bubenhofer, S. Gschwind, A.-M. Hirt, B. Beck-Schimmer, D. Günther and W. J. Stark, Adv. Funct. Mater., 2013, 23, 4888–4896 CrossRef CAS.
- N. Lee, D. Yoo, D. Ling, M. H. Cho, T. Hyeon and J. Cheon, Chem. Rev., 2015, 115, 10637–10689 CrossRef CAS PubMed.
- C. T. Yavuz, J. T. Mayo, W. W. Yu, A. Prakash, J. C. Falkner, S. Yean, L. Cong, H. J. Shipley, A. Kan, M. Tomson, D. Natelson and V. L. Colvin, Science, 2006, 314, 964–967 CrossRef PubMed.
- S. Mørup, M. F. Hansen and C. Frandsen, in Comprehensive Nanoscience and Technology, Elsevier, 2011, pp. 437–491 Search PubMed.
- J. M. D. Coey, Phys. Rev. Lett., 1971, 27, 1140–1142 CrossRef CAS.
- S. Mørup and E. Tronc, Phys. Rev. Lett., 1994, 72, 3278–3281 CrossRef PubMed.
- E. Lima, A. L. Brandl, A. D. Arelaro and G. F. Goya, J. Appl. Phys., 2006, 99, 083908 CrossRef.
- A. Demortière, P. Panissod, B. P. Pichon, G. Pourroy, D. Guillon, B. Donnio and S. Bégin-Colin, Nanoscale, 2011, 3, 225–232 RSC.
- M. Estrader, A. López-Ortega, I. V. Golosovsky, S. Estradé, A. G. Roca, G. Salazar-Alvarez, L. López-Conesa, D. Tobia, E. Winkler, J. D. Ardisson, W. A. A. Macedo, A. Morphis, M. Vasilakaki, K. N. Trohidou, A. Gukasov, I. Mirebeau, O. L. Makarova, R. D. Zysler, F. Peiró, M. D. Baró, L. Bergström and J. Nogués, Nanoscale, 2015, 7, 3002–3015 RSC.
- P. Yang, H. Li, S. Zhang, L. Chen, H. Zhou, R. Tang, T. Zhou, F. Bao, Q. Zhang, L. He and X. Zhang, Nanoscale, 2016, 8, 19036–19042 RSC.
- A. Feld, A. Weimer, A. Kornowski, N. Winckelmans, J.-P. Merkl, H. Kloust, R. Zierold, C. Schmidtke, T. Schotten, M. Riedner, S. Bals and H. Weller, ACS Nano, 2019, 13, 152–162 Search PubMed.
- H. Sharifi Dehsari, V. Ksenofontov, A. Möller, G. Jakob and K. Asadi, J. Phys. Chem. C, 2018, 122, 28292–28301 CrossRef.
- L. K. Bogart, C. Blanco-Andujar and Q. A. Pankhurst, Appl. Phys. Lett., 2018, 113, 133701 CrossRef.
- C. Schmitz-Antoniak, Rep. Prog. Phys., 2015, 78, 062501 CrossRef PubMed.
- I. Torres-Díaz and C. Rinaldi, Soft Matter, 2014, 10, 8584–8602 RSC.
- Y. Li, J. Zhao, W. You, D. Cheng and W. Ni, Nanoscale, 2017, 9, 3925–3933 RSC.
- D. Eberbeck, F. Wiekhorst, S. Wagner and L. Trahms, Appl. Phys. Lett., 2011, 98, 182502 CrossRef.
- P. Dames, B. Gleich, A. Flemmer, K. Hajek, N. Seidl, F. Wiekhorst, D. Eberbeck, I. Bittmann, C. Bergemann, T. Weyh, L. Trahms, J. Rosenecker and C. Rudolph, Nat. Nanotechnol., 2007, 2, 495–499 CrossRef PubMed.
- J. Lohr, A. A. de Almeida, M. S. Moreno, H. Troiani, G. F. Goya, T. E. Torres Molina, R. Fernandez-Pacheco, E. L. Winkler, M. Vásquez Mansilla, R. Cohen, L. C. C. M. Nagamine, L. M. Rodríguez, D. E. Fregenal, R. D. Zysler and E. Lima, J. Phys. Chem. C, 2019, 123, 1444–1453 CrossRef CAS.
- D. Shi, M. E. Sadat, A. W. Dunn and D. B. Mast, Nanoscale, 2015, 7, 8209–8232 RSC.
- S. Disch, E. Wetterskog, R. P. Hermann, D. Korolkov, P. Busch, P. Boesecke, O. Lyon, U. Vainio, G. Salazar-Alvarez, L. Bergström and T. Brückel, Nanoscale, 2013, 5, 3969–3975 RSC.
- S. Biederer, T. Knopp, T. F. Sattel, K. Lüdtke-Buzug, B. Gleich, J. Weizenecker, J. Borgert and T. M. Buzug, J. Phys. D: Appl. Phys., 2009, 42, 205007 CrossRef.
- J. Landers, S. Salamon, H. Remmer, F. Ludwig and H. Wende, Nano Lett., 2016, 16, 1150–1155 CrossRef CAS PubMed.
- W. Szczerba, R. Costo, S. Veintemillas-Verdaguer, M. del P. Morales and A. F. Thünemann, J. Appl. Crystallogr., 2017, 50, 481–488 CrossRef CAS PubMed.
- Y. Sun and Y. Ren, Part. Part. Syst. Charact., 2013, 30, 399–419 CrossRef CAS.
- B. Gleich and J. Weizenecker, Nature, 2005, 435, 1214–1217 CrossRef CAS PubMed.
- J. Leliaert, A. Coene, M. Liebl, D. Eberbeck, U. Steinhoff, F. Wiekhorst, B. Fischer, L. Dupré and B. V. Waeyenberge, Appl. Phys. Lett., 2015, 107, 222401 CrossRef.
- K. Wu, K. Schliep, X. Zhang, J. Liu, B. Ma and J.-P. Wang, Small, 2017, 13, 1604135 CrossRef PubMed.
- P. Bender, C. Balceris, F. Ludwig, O. Posth, L. K. Bogart, W. Szczerba, A. Castro, L. Nilsson, R. Costo, H. Gavilán, D. González-Alonso, I. de Pedro, L. F. Barquín and C. Johansson, New J. Phys., 2017, 19, 073012 CrossRef.
- J. van Rijssel, B. W. M. Kuipers and B. H. Erné, J. Magn. Magn. Mater., 2015, 380, 325–329 CrossRef CAS.
- L. Rebbouh, R. P. Hermann, F. Grandjean, T. Hyeon, K. An, A. Amato and G. J. Long, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 174422 CrossRef.
- X. Li, L. Yuan, J. Wang, L. Jiang, A. I. Rykov, D. L. Nagy, C. Bogdán, M. A. Ahmed, K. Zhu, G. Sun and W. Yang, Nanoscale, 2016, 8, 2333–2342 RSC.
- W. Szczerba, J. Żukrowski, M. Przybylski, M. Sikora, O. Safonova, A. Shmeliov, V. Nicolosi, M. Schneider, T. Granath, M. Oppmann, M. Straßer and K. Mandel, Phys. Chem. Chem. Phys., 2016, 18, 25221–25229 RSC.
- J. F. Hochepied, P. Bonville and M. P. Pileni, J. Phys. Chem. B, 2000, 104, 905–912 CrossRef CAS.
- J. F. Hochepied, Ph. Sainctavit and M. P. Pileni, J. Magn. Magn. Mater., 2001, 231, 315–322 CrossRef CAS.
- X. Zhu, A. P. Hitchcock, D. A. Bazylinski, P. Denes, J. Joseph, U. Lins, S. Marchesini, H.-W. Shiu, T. Tyliszczak and D. A. Shapiro, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E8219–E8227 CrossRef CAS PubMed.
- V. S. Coker, C. I. Pearce, R. A. D. Pattrick, G. van der Laan, N. D. Telling, J. M. Charnock, E. Arenholz and J. R. Lloyd, Am. Mineral., 2008, 93, 1119–1132 CrossRef CAS.
- L. Braicovich, G. Ghiringhelli, A. Tagliaferri, G. van der Laan, E. Annese and N. B. Brookes, Phys. Rev. Lett., 2005, 95, 267402 CrossRef CAS PubMed.
- S. Brice-Profeta, M.-A. Arrio, E. Tronc, N. Menguy, I. Letard, C. Cartier dit Moulin, M. Noguès, C. Chanéac, J.-P. Jolivet and Ph. Sainctavit, J. Magn. Magn. Mater., 2005, 288, 354–365 CrossRef CAS.
- D. Nolle, E. Goering, T. Tietze, G. Schütz, A. Figuerola and L. Manna, New J. Phys., 2009, 11, 033034 CrossRef.
- A. Juhin, A. López-Ortega, M. Sikora, C. Carvallo, M. Estrader, S. Estradé, F. Peiró, M. D. Baró, P. Sainctavit, P. Glatzel and J. Nogués, Nanoscale, 2014, 6, 11911–11920 RSC.
- C. Antoniak, A. Warland, M. Darbandi, M. Spasova, A. Trunova, K. Fauth, E. F. Aziz, M. Farle and H. Wende, J. Phys. D: Appl. Phys., 2010, 43, 474007 CrossRef.
- F. M. F. de Groot, Nat. Chem., 2012, 4, 766 CrossRef CAS PubMed.
- N. Daffé, M. Sikora, M. Rovezzi, N. Bouldi, V. Gavrilov, S. Neveu, F. Choueikani, P. Ohresser, V. Dupuis, D. Taverna, A. Gloter, M.-A. Arrio, P. Sainctavit and A. Juhin, Adv. Mater. Interfaces, 2017, 2017, 1700599 CrossRef.
- M. Sikora, A. Juhin, T.-C. Weng, P. Sainctavit, C. Detlefs, F. de Groot and P. Glatzel, Phys. Rev. Lett., 2010, 105, 037202 CrossRef PubMed.
- A. Juhin, P. Sainctavit, K. Ollefs, M. Sikora, A. Filipponi, P. Glatzel, F. Wilhelm and A. Rogalev, J. Phys.: Condens. Matter, 2016, 28, 505202 CrossRef PubMed.
- P. Glatzel, T.-C. Weng, K. Kvashnina, J. Swarbrick, M. Sikora, E. Gallo, N. Smolentsev and R. A. Mori, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 17–25 CrossRef CAS.
- M. Sikora, A. Juhin, G. Simon, M. Zając, K. Biernacka, Cz. Kapusta, L. Morellon, M. R. Ibarra and P. Glatzel, J. Appl. Phys., 2012, 111, 07E301 CrossRef.
- N. Kawamura, E. Ikenaga, M. Mizumaki, N. Hiraoka, H. Yanagihara and H. Maruyama, J. Electron Spectrosc. Relat. Phenom., 2017, 220, 81–85 CrossRef CAS.
- T. E. Westre, P. Kennepohl, J. G. DeWitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314 CrossRef CAS.
- M. Wilke, F. Farges, P.-E. Petit, G. E. Brown and F. Martin, Am. Mineral., 2001, 86, 714–730 CrossRef CAS.
- J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge University Press, New York, 2010 Search PubMed.
- N. Daffé, J. Zečević, K. N. Trohidou, M. Sikora, M. Rovezzi, C. Carvallo, M. Vasilakaki, S. Neveu, J. D. Meeldijk, N. Bouldi, V. Gavrilov, Y. Guyodo, F. Choueikani, V. Dupuis, D. Taverna, P. Sainctavit and A. Juhin, Nanoscale, 2020, 12, 11222–11231 RSC.
- R. Chantrell, J. Popplewell and S. Charles, IEEE Trans. Magn., 1978, 14, 975–977 CrossRef.
- D.-X. Chen, A. Sanchez, E. Taboada, A. Roig, N. Sun and H.-C. Gu, J. Appl. Physiol., 2009, 105, 083924 CrossRef.
- J. van Rijssel, B. W. M. Kuipers and B. H. Erné, J. Magn. Magn. Mater., 2014, 353, 110–115 CrossRef CAS.
- S. G. Kwon, S. Chattopadhyay, B. Koo, P. C. dos Santos Claro, T. Shibata, F. G. Requejo, L. J. Giovanetti, Y. Liu, C. Johnson, V. Prakapenka, B. Lee and E. V. Shevchenko, Nano Lett., 2016, 16, 3738–3747 CrossRef CAS PubMed.
- S. G. Kwon, G. Krylova, P. J. Phillips, R. F. Klie, S. Chattopadhyay, T. Shibata, E. E. Bunel, Y. Liu, V. B. Prakapenka, B. Lee and E. V. Shevchenko, Nat. Mater., 2015, 14, 215–223 CrossRef CAS PubMed.
- R.-J. Yang, H.-H. Hou, Y.-N. Wang and L.-M. Fu, Sens. Actuators, B, 2016, 224, 1–15 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the synthesis procedure, details of the experimental setup and data collection procedure, comments on stability of magnetic liquids under X-ray irradiation, quantitative estimation of site occupancy. See DOI: 10.1039/d0nr02866e |
| ‡ RIXS-MCD signal is calculated as the difference of RIXS signals collected with left- and right-handed circularly polarized light divided by the maximum intensity of the averaged RIXS signals.50 |
| This journal is © The Royal Society of Chemistry 2020 |