Exploring the limits of sensitivity for strain gauges of graphene and hexagonal boron nitride decorated with metallic nanoislands†
Julian
Ramírez‡
,
Armando D.
Urbina‡
,
Andrew T.
Kleinschmidt
,
Mickey
Finn
III
,
Samuel J.
Edmunds
,
Guillermo L.
Esparza
and
Darren J.
Lipomi
 *
*
Department of NanoEngineering, University of California, San Diego, 9500 Gilman Drive, Mail Code 0448, La Jolla, CA 92093-0448, USA. E-mail: dlipomi@eng.ucsd.edu
First published on 8th May 2020
Abstract
The purpose of this work is to clarify the mechanism of piezoresistance in a class of ultra-sensitive strain gauges based on metallic films on 2D substrates (“2D/M” films). The metals used are gold or palladium deposited as ultrathin films (≤16 nm). These films transition from a regime of subcontiguous growth to a percolated morphology with increasing nominal thickness. The 2D substrates are either single-layer graphene or hexagonal boron nitride (hBN). By using either a conductor (graphene) or an insulator (hBN), it is possible to de-couple the relative contributions of the metal and the 2D substrate from the overall piezoresistance of the composite structure. Here, we use a combination of measurements including electron microscopy, automated image analysis, temperature-dependent conductivity, and measurements of gauge factor of the films as they are bent over a 1 μm step edge (0.0001% or 1 ppm). Our observations are enumerated as follows: (1) of the four permutations of metal and 2D substrate, all combinations except hBN/Au are able to resolve 1 ppm strain (considered extraordinary for strain gauges) at some threshold thickness of metal; (2) for non-contiguous (i.e., unpercolated) films of metal on hBN, changes in resistance for these small step strains cannot be detected; (3) for percolated films on hBN, changes in resistance upon strain can be resolved only for palladium and not for gold; (4) graphene does not exhibit detectable changes in resistance when subjected to step strains of either 1 or 10 ppm, but does so upon the deposition of any amount of gold or palladium, even for nominal thicknesses below the threshold for percolation. Our observations reveal unexpected complexity in the properties of these simple composite materials, and ways in which these materials might be combined to exhibit even greater sensitivity.
Introduction
Strain gauges are ubiquitous components of instruments used in research and technology, from wearable sensors,1 to structural health monitors.2 The majority of commercial strain gauges are based on solid, unstructured materials—e.g., metallic foils and semiconductor slabs—which undergo a change in electrical resistance when mechanically deformed.3 The resistance of an isotropic conductor can be defined as: | (1) |
For strain gauges based on semiconductors, the change in the resistivity is due to shifts in the electronic band structure.9 The most common type of semiconductor devices are microelectromechanical systems (MEMS) strain gauges based on silicon. They can resolve strains of ∼0.01% (100 microstrains or 100 ppm strain) with gauge factors ranging from 20 to 40, but are used only in applications where the total strain is ≤0.3% due to the rigidity of crystalline semiconductors.10–12
To overcome these challenges, a variety of strain gauges based on nanostructured materials have been developed.4,13–16 For example, our laboratory has introduced the use of single-layer graphene decorated with ultrathin metallic films laminated to flexible or stretchable substrates.16 On graphene, metals deposited with low nominal thicknesses (e.g., less than approximately 10 nm) adopt a highly granular structure (“nanoislands”). These metal-graphene composite gauges exhibit a large piezoresistive response and, when paired with the proper instrumentation, are capable of resolving strains on the order of 0.001% (10 ppm). Moreover, these sensors can be tuned to exhibit a near-zero temperature coefficient of resistance (TCR) with the proper balance of metal (which has a positive TCR) on graphene (which has a negative TCR).17 The mechanism responsible for the piezoresistance of these composite films has not been straightforward to establish, largely because graphene,1,18,19 metallic films,5,20,21 and closely spaced metallic particles22–24 have been shown to exhibit sensitivity to strain when used alone (though usually in response to strains larger than the ones explored here). It was our belief that we could obtain a refined understanding of the piezoresistance by systematically changing the metal, the nominal thickness (and thus the interconnectivity of the nanoislands), and the identity of the 2D substrate (i.e., graphene or hexagonal boron nitride). While the morphologies of metallic films on graphene and hBN have been the subject of previous work,25–27 here, our goal was to use these 2D substrates for their conductive and insulating properties in order to compare the difference in piezoresistance performance of various 2D/M films. With this empirical comparison, we sought to narrow the range of possible mechanisms which could account for the piezoresistance of the composite films. This investigation of the ways in which the structure influences the electrical performance would enable the fabrication of strain gauges with even greater sensitivity, the ability to resolve even lower strains, and greater reproducibility than is now possible.
Background
Figures of merit
The tensile or compressive deformation of a strain gauge is referred to as the engineering strain, which is the change in length of the strained axis divided by its length at equilibrium. Engineering strain (hereafter strain) is expressed as either a percent or a fraction (0.01 = 1% = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm = 10
000 ppm = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 microstrains). In this paper, the performance of a strain gauge is quantified using two interrelated metrics: gauge factor (i.e., “sensitivity”), and lowest resolvable strain (the resolution where the initial state of the specimen is at mechanical equilibrium).
000 microstrains). In this paper, the performance of a strain gauge is quantified using two interrelated metrics: gauge factor (i.e., “sensitivity”), and lowest resolvable strain (the resolution where the initial state of the specimen is at mechanical equilibrium).
The relative change in the electrical resistance of a material due to applied strain is quantified by the gauge factor (GF):
 | (2) |
| GFnp = 1 + 2ν | (3) |
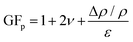 | (4) |
This term is called the piezoresistive coefficient; it describes the relative strain-induced change in the resistivity of the material. The gauge factor can be thought of as describing the “sensitivity” of the electrical resistance of a strain gauge to deformation. When the gauge factor is greater than two, piezoresistance must be a contributing factor. While the gauge factor captures how responsive a material is to strain, it does not describe the range of strain over which the piezoresistive response is reproducible, i.e., the dynamic range. The gauge factor need not be constant over this range; for nanoparticle-based strain gauges, it usually is not. The minimum deformation necessary to create a signal that is differentiable from the noise is called the “resolution”. Given that the resolution is dependent on the noise, the resolution is also dependent on the apparatus used to measure the resistance, and thus resolution—and hence gauge factor—is a system-level quantity. From an experimental standpoint, it is important to establish a robust contact between the wires used for measurement and the sensor film, as a poor contact can lead to large variation under strain and provide sensitivity values that are misleading. In this paper, we were particularly interested in determining the lowest strain that can be resolved by the system. While not specifically discussed in this work, other aspects of strain sensor performance, such as multi-directional sensitivity, are also critical aspects of future technologies based on strain gauges.29
Graphene
Single-layer graphene exhibits reproducible piezoresistance and can thus be used as a strain gauge, with gauge factors ranging from 2–4, as reported by multiple groups.19,30,31 The piezoresistance of single-layer graphene at strains approximately ≥0.4% is generally attributed to scattering effects stemming from unscreened charge impurities or random pseudomagnetic fields due to random strain fluctuations in the film.30,32 Others have attributed the piezoresistance of single-layer graphene to an opening in the band gap due to the break in sublattice symmetry when C–C bonds are elongated.33,34 The strain at which the band structure opening of graphene occurs, however, has been calculated to be above 20% by using various mathematical models and computational simulations.30,35–37 Such calculations, however, assume pristine, single-crystal, and defect-free graphene, which is difficult to obtain on scales larger than hundreds of microns.38,39 Strain gauges for practical applications usually require lengths >1 mm, and will thus nearly always contain grain boundaries and defects not considered in simulations of pristine materials. Strain gauges based on graphene flakes, supported on flexible and stretchable substrates, are capable of detecting strains from 0.1%–0.4% with wide ranging gauge factors (100–106) while maintaining compatibility with the substrate.18,40,41Ultrathin metallic films
One type of structure which has been exploited for its piezoresistive qualities are ultrathin metallic films on elastomeric substrates. In these composite structures, the increase in resistance upon mechanical strain has been attributed to the formation of nanoscale cracks, around which the electrical current must travel in a tortuous pathway. Upon release of the strain, the cracks close (wholly or in part), and conductivity is restored. These processes result in a type of strain gauge characterized by ultra-high sensitivity and reversibility.15 Metallic thin film sensors, with thicknesses of tens of nanometers, have demonstrated notable sensitivity, with gauge factors up to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; at strains of 2%, the film tends to form cracks and eventually bifurcates and forms an open circuit.15,42,43 The combination of these films with self-healing polymers have led to the development of nanoscale metallic film sensors capable of withstanding 106 cycles under 2% strain, as the polymer is able to assist in closing the gaps formed by mechanical deformation.14 These devices possess a greater dynamic range than that of silicon-based MEMS device but cannot resolve strains as low as the ones tested on MEMS devices (∼0.3%). Applications requiring both mechanical deformability and high sensitivity require materials that can offer both a wide dynamic range of operation and the ability to detect the lowest strains possible.
000; at strains of 2%, the film tends to form cracks and eventually bifurcates and forms an open circuit.15,42,43 The combination of these films with self-healing polymers have led to the development of nanoscale metallic film sensors capable of withstanding 106 cycles under 2% strain, as the polymer is able to assist in closing the gaps formed by mechanical deformation.14 These devices possess a greater dynamic range than that of silicon-based MEMS device but cannot resolve strains as low as the ones tested on MEMS devices (∼0.3%). Applications requiring both mechanical deformability and high sensitivity require materials that can offer both a wide dynamic range of operation and the ability to detect the lowest strains possible.
Ultrathin metallic films on 2D graphene
Our laboratory has been exploring an approach that combines the advantages of strain gauges based on single-layer graphene and those based on ultrathin metallic films. These composite structures can detect lower strains, have higher sensitivities, and exhibit wider dynamic range than either component alone. At low nominal thicknesses (≤10 nm), the morphology of gold and palladium on single-layer graphene progresses from separated island-like clusters (subcontiguous coverage) to a film of contiguous nanoscale grains. We have used these composite materials as strain gauges in a variety of applications. For example, as the active component of a wearable sensor to monitor swallowing activity when attached to the neck,44 pulse and respiration waveforms simultaneously when attached to the ribcage,45 and monitoring the pulse waveform on the wrist while minimizing signal drift stemming from thermal effects.17 The composite material was also useful in a number of cellular biophysical measurements, in vitro. For example, the films have been used to monitor the mechanical activity of rat cardiomyocytes,16 and when embedded in the sidewalls of microfluidic channels could be used to detect cells and particles as they transitted.46 In another example, the strain-dependent variations in near-field coupling between adjacent gold nanoislands on graphene made it possible to detect (optically) the contractions of a 2D layer of myoblast cells as they were stimulated (electrically).47Experimental design
Framework
The central goal of this study was to establish the range of possible mechanisms consistent with the high sensitivity of strain gauges based on ultrathin, granular metallic films (“nanoislands”) supported by 2D materials. For example, both graphene and thin metallic films exhibit piezoresistance when measured in isolation, but it is unclear which material dominates the electrical properties of the composite. (Moreover, it is unclear the extent to which mechanisms such as tunneling between closely spaced islands, increased scattering of electrons in necked regions, formation of microcracks, and quantization of electron transport due to confinement in the height axis play a role.) To tease out the relative contributions of the graphene and the metallic film to the overall piezoresistance of the graphene/metal composite, we compared results obtained with single-layer graphene (Gr) with those obtained with hexagonal boron nitride (hBN). The use of hBN as a substrate removes the conductivity and piezoresistivity possessed by graphene while retaining the island-like morphology of the metallic films, along with the ability to transfer these composite films to a variety of flexible and stretchable substrates. For the metallic films, we used both palladium and gold, which exhibit drastically different morphologies but similar piezoresistive effects when deposited on graphene at low nominal thicknesses. Thus, the four permutations of 2D substrate/metal composites (2D/M) used were Gr/Pd, Gr/Au, hBN/Pd, hBN/Au. In addition to the elemental makeup of the composites, the nominal thickness of metal deposited also has a profound effect on the interconnectivity and thus transport behavior of the films. We chose a narrow range (2 nm and 10 nm for palladium, and 2 nm and 16 nm for gold) and visualized the morphology by scanning electron microscopy (SEM, for gold, which exhibited relatively large islands and gaps) and transmission electron microscopy (TEM, for palladium, which exhibited smaller ones). The interconnectivity of the nanoislands were quantified by image analysis. When testing the piezoresistance of the four composites, we used small step strains of 1 ppm and 10 ppm to eliminate possible effects based on buckling, delamination, and large-scale cracking, which occur when films are subjected to larger strains. To shed light on transport pathways activated thermally (e.g., tunneling), we obtained temperature-dependent conductivity measurements.Selection of materials
Results
Fabrication of 2D/M films
A summary of the process used for fabrication of the 2D/M films is shown in Fig. 1. Described in further detail in the Methods section, a thin film of gold or palladium (metal, M) was thermally evaporated with varying nominal thickness on top of graphene or hBN (two-dimensional substrate, 2D) supported on copper foil (step 1). After depositing the metal film, poly(methyl methacrylate) (PMMA) was deposited on the Cu/2D/M composite by spin coating (step 2). The copper foil was then etched by floating the Cu/2D/M/PMMA sample in ammonium persulfate, and the 2D/M/PMMA film was transferred by a water bath onto a final receiving substrate of a glass coverslip (step 3). The PMMA in the 2D/M/PMMA film was then dissolved in heated acetone (step 4). The 2D/M film, now supported by glass, was addressed with copper wires attached by carbon paint. A TEM micrograph depicting of a sample of a film of palladium islands on single-layer graphene can be seen in Fig. S1.†Connectivity of gold nanoislands on graphene and hBN
Thermal evaporation of gold at low nominal thicknesses produced islands and gaps of a size large enough to be visualized by scanning electron microscopy. We obtained SEM images for Gr/Au and hBN/Au films for nominal thicknesses of gold from 2 to 16 nm in increments of 2 nm (Fig. 2). This range of nominal thicknesses was selected in order to produce a gradual reduction in interparticle spacing and change in morphology from disconnected to percolated as more metal is evaporated. Using image analysis, it was possible to determine both the fraction of the surface that was covered by islands along with the interconnectivity of the metal. The interconnectivity was quantified by measuring the number of “discrete islands” per square micron. A discrete island is one for which it is possible to trace an uninterrupted path from one side of the image to the other. Plots of fractional coverage and discrete islands are plotted as a function of nominal thickness for both graphene (top) and hBN (bottom). Deposition of gold on either graphene or hBN produces a similar increase in surface coverage. The relatively steep increase in coverage between 8 and 12 nm possibly corresponds to increased favorability of lateral spreading as opposed to vertical growth in this range of nominal thickness. Films of gold on both 2D substrates appear to be mostly percolated at nominal thicknesses ≥12 nm, as determined by size of the large island in the SEM images for nominal thicknesses of 14 nm (e.g., “all white”, indicating a large size of the island). When comparing graphene to hBN as a substrate, it appears that gold spreads more readily on graphene than on hBN, as the grains have a greater fractional coverage and are more highly connected at lower nominal thicknesses for graphene as opposed to hBN. A set of SEM micrographs of Gr/Au and hBN/Au with different nominal thicknesses (from 2–10 nm) can be seen in Fig. S2.†Connectivity of palladium nanoislands on graphene and hBN
We then performed a similar analysis for palladium as opposed to gold, seen in Fig. 3. However, the morphology of palladium—consisting of small (∼12 nm) quasi-spherical grains separated by nanoscale gaps much smaller than those exhibited by gold made it necessary to use TEM as opposed to SEM (Fig. 2). Compared to gold, palladium exhibits a notably higher surface coverage at every nominal thickness, with coverage reaching approximately 90% at 10 nm (Fig. 3). Moreover, percolation (i.e., presumed electrical contiguity of metal based on image analysis) appears to occur at a nominal thickness of 4 nm on graphene and 6 nm on hBN, i.e., at lower nominal thicknesses compared to gold on either substrate. The earlier onset of percolation in palladium can partially be attributed to the inherently higher surface coverage and a greater number of islands per area at low nominal thicknesses. A set of TEM micrographs of Gr/Pd and hBN/Pd for different nominal thicknesses (from 2–10 nm) can be seen in Fig. S3.†The evolution in surface coverage of the metallic films of low nominal thickness is influenced by two parameters: the binding energy (the minimum energy required to disassemble a system of particles) of the metal atom to the substrate and its activation barrier to diffusion. For gold and palladium on graphene and hBN, palladium has the greater binding energy while both possess similar diffusion barriers.26,63 Our observations of the progression of the surface coverage as a function of nominal thickness of both metals on either 2D substrate are consistent with these parameters. For example, at similar nominal thicknesses, palladium exhibits greater fractional surface coverage and a larger number of discrete islands than gold on either graphene or hBN. This behavior is likely a consequence of the greater binding energy of palladium to graphene, and also to hBN, than gold to graphene. Comparing 2D substrates, surface coverage is somewhat greater on graphene, but number of islands is greater on hBN.
In considering the differences in morphology of the metals when changing the 2D substrates, we observed that the number and size of islands for palladium is similar when the metal is deposited on either graphene or hBN (for the same nominal thicknesses). In the case of gold, however, the number of islands is notably greater in the case of hBN while the size of the islands is much greater on graphene, starting from a nominal thickness of 6 nm until the islands percolate. Considering that the binding energy of gold is low (∼0.09 eV) when compared to palladium (∼1 eV) on either 2D substrate and the activation barrier for diffusion of gold is also low (∼0.4 eV on Gr and ∼0.13 eV on hBN), the differences in morphology between Gr/Au and hBN/Au can potentially stem from the small amount of energy required to disassemble and diffuse gold adatoms on the 2D surfaces.26,27,63,64
Sheet resistance measurements
To support the microscopy results which identified the onset of percolation (visually), we measured the sheet resistances of the composite films as a function of nominal thickness (Fig. 4). In the case of hBN/Pd, nominal thicknesses ≥6 nm of palladium affected a transition from insulating to conductive, while for hBN/Au, ≥12 nm of gold on hBN transitioned from insulating to conductive. (Data points for hBN/M which registered as open circuits are not shown.) These findings are consistent with the image analysis of Fig. 2 and 3 where the number of islands per square centimeter decreases to zero at the same nominal thickness that the sheet resistance became measurable. Gr/M films gave measurable sheet resistances at all nominal thicknesses, which can be attributed to the conductivity inherent to single-layer graphene. A curious feature of Gr/M (black squares in Fig. 4) is the initial increase in sheet resistance (for palladium, 4a) or roughly constant value (for gold, 4a) for the first few nanometers of metal deposited. The increase in sheet resistance in the metal films supported on graphene can possibly be due to the introduction of defect or scattering sites that can alter the band structure of pristine graphene.25,65–68 | ||
| Fig. 4 Sheet resistance of 2D/M films. Sheet resistance measurements of (a) 2D/Pd and (b) 2D/Au as a function of nominal thickness of metal deposited. Data for (a) Gr/Pd reprinted with permission from ref. 45. | ||
Piezoresistive response
The films were tested for their piezoresistive response by subjecting them to 0.001% (10 ppm) and 0.0001% (1 ppm) bending strains using the cantilever setup shown in Fig. 5. Among all four permutations of 2D/M films tested, Gr/Pd, hBN/Pd, and Gr/Au were able to detect strains of 1 ppm. Films consisting of hBN/Au showed open circuits for all nominal thicknesses ≤10 nm (and thus no piezoresistance) owing to the insulating behavior of hBN and the lack of interconnectivity of gold. For higher nominal thicknesses, at which gold formed a percolated network, the films were conductive but did not undergo a measurable change in resistance for either 1 ppm or 10 ppm strain. In the case of hBN/Pd, the unpercolated films gave open circuits, while the percolated films (≥6 nm nominal thickness) exhibited relatively large changes in resistance for both the 1 ppm and 10 ppm step strain, confirming that the highly granular film of palladium alone can be responsible for the piezoresistance. Interestingly, the gauge factor was larger for the smaller step strain, suggesting that much of the effects leading to the piezoresistive response occurred upon the early stages of deformation. We attribute the lack of piezoresistive sensitivity in hBN/Au films to greater ductility and thicker connections (e.g., “isthmuses”) between adjacent islands which, compared to palladium, are less likely to break at small strains. It should be noted that previous work by our group has demonstrated the reliability of these films under cyclical strain.44,45In contrast to films of either gold or palladium supported by hBN, all metallic films supported by graphene—even unpercolated ones—exhibited a measurable change in the resistance at 1 ppm strain. The resistance of graphene alone, however, was insensitive to strains of either 1 ppm or 10 ppm (Fig. 5). Coincidentally, the deposition of an unpercolated film onto graphene did not decrease its resistance (Fig. 4a and b), yet these films exhibited a measurable gauge factor, whereas graphene alone did not, at least at the very small step strains tested. Thus, a reduction in conductivity with small nominal thicknesses corresponded to the onset of piezoresistive sensitivity. The mechanism for this transition is not entirely clear, though, several changes in the graphene occur at the initial stages of metallization, which could be envisioned to affect the evolution in electrical resistance with strain. For example, palladium is known to react with graphene—forming palladium carbide bonds—which degrades its conductivity.65,66 The effect of mechanical deformation on the electronic structure of so-modified graphene is not clear. Moreover, the adhesion of metal islands to the surface of graphene would also produce an inhomogeneous strain field whose effects on the electromechanical behavior are not straightforward to predict. Plots of the Gr/M responses to 1 ppm strain for a case of a disconnected metal film and a percolated subcontiguous film can be seen in Fig. S4.†
Temperature coefficient of resistance
To elucidate the mechanism of conductivity in the 2D/M composites that produced a piezoresistive response, we measured the temperature coefficient of resistance (TCR). In particular, we were looking for evidence of decreased resistance with increasing temperature, especially in hBN/M, which would be consistent with a contribution of tunneling to the overall conductivity (which would also implicate a piezoresistive mechanism mediated, at least in part, by tunneling). To obtain the measurements, samples were placed on heating stage and the temperature was raised from 20 °C to 70 °C, in increments of 5 °C. The data points corresponding to hBN/Pd were measured here for the first time, while those corresponding to Gr/M were obtained from our previous work69 (Fig. 6a and b). In the case of the hBN/Pd composites, all nominal thicknesses of palladium tested gave a positive TCR. Increased resistance in metals at high temperature is generally attributed to scattering.70,71 We conclude from these measurements—along with the fact that these films appear to be percolated by TEM (Fig. 3)—that tunneling is not dominant and does not appreciably contribute to the piezoresistive mechanism of hBN/Pd films. | ||
| Fig. 6 Temperature coefficient of resistance of 2D/M films. (a and b) TCR measurements of Gr/M systems from previous work (top row, reprinted with permission from ref. 69) and (c) hBN/Pd systems capable of detecting 1 ppm strain. | ||
The temperature-dependent resistivity of Gr/M films is complicated by the fact that graphene itself has a negative TCR, which could be erroneously interpreted as evidence for tunneling between metallic particles. Previous work from our group (reproduced in Fig. 6) has demonstrated that the negative TCR of graphene can be overcome with the deposition of a sufficient nominal thickness of metal. It should be noted however, that depositing an excessive amount of metal on single-layer graphene can create a film with a TCR of sufficient magnitude to interfere with the ability of the film to respond reliably to strain. For example, the transition from negative to positive TCR for Gr/Au occurs at nominal thicknesses of approximately 8 nm while the transition for Gr/Pd occurs at 0.9 nm.17 Given the morphology of these films seen in Fig. 2 and 3 we can deduce that the transition of TCR from negative to positive happens approximately at the onset of percolation, where the conductive pathway changes from dominated by graphene to dominated by metal. It should be noted that a higher metal deposition rate of 0.05 Å s−1 was used in previous TCR measurements (Fig. 6a and b) compared to a rate of 0.03 Å s−1 for this study, which could account for morphological differences (namely different nominal thicknesses at which percolation occurs) between the studies. Nevertheless, we can infer that the TCR values of our samples measured in Fig. 5 can be either negative due to the negative TCR of pristine graphene (i.e. Au ≤8 nm) or near-zero/positive (i.e. Pd ≥0.9 nm). Regardless of the TCR, all graphene samples with any amount of metal (even unpercolated coverages) registered sensitivity to 1 ppm strain. These observations highlight the importance of both the graphene and the metal in producing the piezoresistive response, though they also point away from tunneling as a dominant mechanism of either conductance or piezoresitance.72Table 1 tabulates comparisons of the gauge factor and the lowest resolvable strain of the 2D/M composites.
| 2D/M | Sheet resistance (Ω sq−1) | Gauge factor at 1 ppm strain | Lowest resolvable strain (ppm strain) |
|---|---|---|---|
| Gr | 521 | 0 | >10 |
| Gr/Pd (d, 2–4 nm) | 1001–2100 | 81.5–82 | 1 |
| Gr/Pd (p, 6–10 nm) | 72–251 | 74–80 | 1 |
| Gr/Au (d, 2–8 nm) | 213–737 | 123–126 | 1 |
| Gr/Au (p, 10–16 nm) | 12–137 | ∼116 | 1 |
| hBN | N/A | 0 | N/A |
| hBN/Pd (d, 2–4 nm) | N/A | 0 | N/A |
| hBN/Pd (p, 6–10 nm) | 240–1087 | 118–178 | 1 |
| hBN/Au (d, 2–8 nm) | N/A | 0 | N/A |
| hBN/Au (p, 10–16 nm) | 13–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 620 |
0 | >10 |
Conclusions
These experiments have shed light on the mechanism of piezoresistance of ultrasensitive strain gauges based on metallic films on 2D substrates. In particular, the use of hexagonal boron nitride as an alternative to graphene to separate the intrinsic piezoresistance of the 2D substrate from that of the metal highlighted the profound effect of the substrate. Indeed, unpercolated films of metal on hBN produced no piezoresistive response at strains ≤10 ppm; physical continuity of the metallic film was necessary to achieve sensitivity, and only in the case of palladium, for the regime of small strains tested. In contrast, the electrical resistance of even disconnected films of metal on graphene could resolve strains ≥1 ppm. Interestingly, however, the electrical resistance of graphene alone did not have a resolution high enough to detect small strains. The fact that morphologies on hBN in which the metal was disconnected produced open circuits—along with the fact that the resistance of these films increased with temperature—also point to the absence of tunneling as a dominant mode of either conductance or piezoresistivity. We highlight the low strains detectable (≥1 ppm) by several entries in Table 1. These strains are among the smallest ever tested for nanostructured strain gauges, and could thus be useful in measuring small effects in structural health monitoring and biomechanics (particularly of cells, which produce small forces and displacements). Shortcomings of our approach are that it is empirical and does not consider electronic coupling between the metal and the 2D substrates or quantization of charge transport in the metallic films given their extremely small thicknesses. For example, a simple thought experiment, described in the ESI,† suggests that dissimilar densities of states between continuous regions of different thicknesses could lead to significant backscattering of conduction electrons; this effect would in principle be augmented with tensile strains, when stress may be concentrated in the thinner regions.73–78 Other differences between the 2D substrates, such as the mechanical properties and adhesion to metal adatoms, could possibly contribute to the differences in piezoresistive performance when comparing the Gr/M to its hBN/M counterpart. In sum, however, we believe that the phenomenological approach used here—especially the use of hBN as an alternative to graphene—helps to elucidate the mechanism by which piezoresistance arises so that such systems can be made more reliable and sensitive in a variety of applications in engineering and healthcare.Methods
Fabrication
The following steps refer to those indicated in Fig. 1. Step 1: the nominal thickness of palladium or gold nanoislands was deposited on top of single layer-graphene or single-layer hexagonal boron nitride on copper foil (GrollTex, Inc.) using thermal evaporation (Orion System, AJA International) at a rate of 0.03 Å s−1. Step 2: 4% PMMA (by mass, product no. 43982, Alfa Aesar) in anisole (Acros Organics) was deposited on top of the copper foil/2D substrate/metal by spin coating (4000 rpm, 4000 rpm s−1, 60 s). The film was then heated to 150 °C for 5 min to remove residual solvent. Step 3: the copper foil/2D substrate/metal/PMMA was cut into 0.5 cm × 1 cm strips and the supporting copper foil was etched away in 0.05 g mL−1 ammonium persulfate (Acros Organics) in water. The film of 2D substrate/metal/PMMA was transferred out of the ammonium persulfate by adhering the edge of the film to a glass slide, lifting out the film from the ammonium persulfate, and plunging the glass slide into a water bath, releasing the film on the surface of the water.The 2D substrate/metal/PMMA film was then transferred onto a 2.54 cm × 2.54 cm glass coverslip (Sail Brand, 130–170 μm thickness), resulting in glass coverslip/2D substrate/metal/PMMA. Step 4: after transferring the obtaining the glass coverslip/2D substrate/metal/PMMA architecture, the PMMA was dissolved in a hot acetone bath of around 40 °C for three repetitions of 5 min. The After the bath, the sample was immediately rinsed with IPA and placed under vacuum to dry. After allowing the composite film to dry, the sensor was addressed with copper wire; carbon paint was painted on the contact area (DAG-T-502, Ted Pella, Inc.) and left to dry in a fume hood, resulting in the finished device (glass coverslip/2D substrate/metal/copper wire). This fabrication technique was used to create devices for cantilever and TCR experiments.
Imaging and image analysis
The imaging of the gold nanoisland samples on graphene and hBN were done on a Zeiss Sigma 500 SEM. All samples were imaged at accelerating voltages ≤1 kV, with an aperture size of 30μm. Imaging of the palladium samples on graphene and hBN were done on a JEOL 1200 EX II TEM. All samples were images at an accelerating voltage of 80 kV.For the analysis of the SEM and TEM images, the raw image files were edited by Adobe Photoshop CC 2019 Software by increasing the contrast, and in the case of TEM images, converting pixels stemming from the islands to white and gaps were converted to black pixels. The edited SEM and TEM images were analyzed using a custom python code, which extensively used the mahotas computer vision and image processing library.79 An iteration of this code is available freely at (https://github.com/juramire1/SEM_TEM_Image_Analysis). An overview of the analysis is given previous work.17
Measurements of gauge factor
For the cantilever strain experiment, where the materials were strained to 0.0001% (1 ppm, seen in Fig. 5), the device on the coverslip was partially suspended, clamped with a 1.27 cm overlap, over a silicon step edge of ∼1 μm. The step edge in silicon was created by spinning a layer SU8 photoresist over a silicon wafer and developing half of the wafer to define a straight edge across the wafer diameter. The exposed silicon surface was etched using reactive ion etching (RIE ICP – Oxford Plasmalab 100) for 4 min. A radio frequency source at 30 W and an inductively coupled plasma (ICP) source at1200 W was used, with 25 sccm of SF6 and 50 sccm of C4F8 at a chamber pressure of 15 mTorr. After etching the silicon surface, the remaining photoresist was removed. In the case of 0.0001% (1 ppm) strain, the device on the coverslip was partially suspended, clamped with a 1.27 cm overlap, over a Si step edge of ∼1 μm, made by adhering polyimide tape (Caplinq, product no. PIT0.5S UT/25.4) to a 7.62 cm × 5.08 cm glass slide. The resistance measurements were recorded using two-point measurements using a Keithley 2611B SourceMeter and custom LabView software. The tensile strain applied to the sensor device was calculated by FEA analysis of our experimental setup, described below. Signal drift in the sensors, due to thermal effects, were corrected using OriginPro 8.1.Finite-element modeling
All finite element analysis models were done using Fusion360 (Autodesk). A force was applied to the edge of the glass coverslip overhanging the respective cantilever steps. The force applied corresponded to the vertical displacement between the hanging coverslip edge and the supporting substrate.Sheet resistance
Samples for sheet-resistance measurements were prepared using the evaporation and polymer-coating technique indicated above, then cut into 2.54 cm × 2.54 cm squares and mounted on 5.08 cm × 7.62 cm glass slides. The sheet resistance was measured using a 4-point probe attachment on a Keithley 2400 SourceMeter and confirmed with contact-free resistance measurement (Delcom 20J3).Temperature coefficient of resistance (TCR)
To determine the thermal coefficient of resistance, samples (of 2D substrate/metal) were cut into 0.5 cm × 1 cm strips, mounted onto a 2.54 cm × 2.54 cm glass coverslip (Sail Brand, 130–170 μm thickness), and copper wire contacts were addressed using carbon paint (DAG-T-502, Ted Pella, Inc.). These devices were heated from room temperature to 70 °C, in 5 °C increments using an Instec mK2000 high precision temperature controller. The resistance of each device was recorded using a Keithley 2611B after a steady-state resistance was reached (<1% change).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Institutes of Health Director's New Innovator Award, Grant 1DP2EB022358. J. R. acknowledges support provided by the National Science Foundation Graduate Research Fellowship Program under Grant DGE-1144086. A. U. acknowledges support provided by the San Diego Nanotechnology Infrastructure REU summer program, supported by National Science Foundation (Grant ECCS-1542148). Additional support was provided by the Center for Wearable Sensors in the Jacobs School of Engineering at the University of California, San Diego, and member companies Sabic, Cubic, Dexcom, Honda, Samsung, Gore, Huami, Kureha, Merck KGaA, Pepsico, and Sony. This work was performed in part at the San Diego Nanotechnology Infrastructure (SDNI), a member of the National Nanotechnology Coordinated Infrastructure, which is supported by the National Science Foundation (Grant ECCS-1542148).References
- T. Yang, X. Jiang, Y. Zhong, X. Zhao, S. Lin, J. Li, X. Li, J. Xu, Z. Li and H. Zhu, A Wearable and Highly Sensitive Graphene Strain Sensor for Precise Home-Based Pulse Wave Monitoring, ACS Sens., 2017, 2(7), 967–974 CrossRef CAS PubMed.
- M. Segev-Bar and H. Haick, Flexible Sensors Based on Nanoparticles, ACS Nano, 2013, 7(10), 8366–8378 CrossRef CAS PubMed.
- J. P. Lynch, A Summary Review of Wireless Sensors and Sensor Networks for Structural Health Monitoring, Shock Vib. Dig., 2006, 38(2), 91–128 CrossRef.
- L. Jibril, J. Ramírez, A. V. Zaretski and D. J. Lipomi, Single-Nanowire Strain Sensors Fabricated by Nanoskiving, Sens. Actuators, A, 2017, 263, 702–706 CrossRef CAS PubMed.
- Y. S. Kim, J. Lu, B. Shih, A. Gharibans, Z. Zou, K. Matsuno, R. Aguilera, Y. Han, A. Meek and J. Xiao, et al., Scalable Manufacturing of Solderable and Stretchable Physiologic Sensing Systems, Adv. Mater., 2017, 29(39), 1–11 Search PubMed.
- L. E. Hollander, G. L. Vick and T. J. Diesel, The Piezoresistive Effect and Its Applications, Rev. Sci. Instrum., 1960, 31(3), 323–327 CrossRef CAS.
- R. He and P. Yang, Giant Piezoresistance Effect in Silicon Nanowires, Nat. Nanotechnol., 2006, 1(1), 42–46 CrossRef CAS PubMed.
- C. S. Smith, Piezoresistance Effect in Germanium and Silicon, Phys. Rev., 1954, 94(1), 42–49 CrossRef CAS.
- J. Bardeen and W. Shockley, Deformation Potentials and Mobilities in Non-Polar Crystals, Phys. Rev., 1950, 80(1), 72–80 CrossRef CAS.
- L. Cao, T. S. Kim, S. C. Mantell and D. L. Polla, Simulation and Fabrication of Piezoresistive Membrane Type MEMS Strain Sensors, Sens. Actuators, A, 2000, 80(3), 273–279 CrossRef CAS.
- A. A. S. Mohammed, W. A. Moussa and E. Lou, Development and Experimental Evaluation of a Novel Piezoresistive MEMS Strain Sensor, IEEE Sens. J., 2011, 11(10), 2220–2232 CAS.
- C. Hautamaki, S. Zurn, S. C. Mantell and D. L. Polla, Experimental Evaluation of MEMS Strain Sensors Embedded in Composites, J. Microelectromech. Syst., 1999, 8(3), 272–279 CrossRef.
- H. Jeon, S. K. Hong, M. S. Kim, S. J. Cho and G. Lim, Omni-Purpose Stretchable Strain Sensor Based on a Highly Dense Nanocracking Structure for Whole-Body Motion Monitoring, ACS Appl. Mater. Interfaces, 2017, 9(48), 41712–41721 CrossRef CAS PubMed.
- B. Park, S. Lee, H. Choi, J. U. Kim, H. Hong, C. Jeong, D. Kang and T. l. Kim, A Semi-Permanent and Durable Nanoscale-Crack-Based Sensor by on-Demand Healing, Nanoscale, 2018, 10(9), 4354–4360 RSC.
- D. Kang, P. V. Pikhitsa, Y. W. Choi, C. Lee, S. S. Shin, L. Piao, B. Park, K. Y. Suh, T. I. Kim and M. Choi, Ultrasensitive Mechanical Crack-Based Sensor Inspired by the Spider Sensory System, Nature, 2014, 516(7530), 222–226 CrossRef CAS PubMed.
- A. V. Zaretski, S. E. Root, A. Savchenko, E. Molokanova, A. D. Printz, L. Jibril, G. Arya, M. Mercola and D. J. Lipomi, Metallic Nanoislands on Graphene as Highly Sensitive Transducers of Mechanical, Biological, and Optical Signals, Nano Lett., 2016, 16(2), 1375–1380 CrossRef CAS PubMed.
- B. C. Marin, S. E. Root, A. D. Urbina, E. Aklile, R. Miller, A. V. Zaretski and D. J. Lipomi, Graphene–Metal Composite Sensors with Near-Zero Temperature Coefficient of Resistance, ACS Omega, 2017, 2(2), 626–630 CrossRef CAS PubMed.
- J. Zhao, C. He, R. Yang, Z. Shi, M. Cheng, W. Yang, G. Xie, D. Wang, D. Shi and G. Zhang, Ultra-Sensitive Strain Sensors Based on Piezoresistive Nanographene Films, Appl. Phys. Lett., 2012, 101(6), 063112-1–063112-5 Search PubMed.
- A. D. Smith, F. Niklaus, A. Paussa, S. Schröder, A. C. Fischer, M. Sterner, S. Wagner, S. Vaziri, F. Forsberg and D. Esseni, et al., Piezoresistive Properties of Suspended Graphene Membranes under Uniaxial and Biaxial Strain in Nanoelectromechanical Pressure Sensors, ACS Nano, 2016, 10(11), 9879–9886 CrossRef CAS PubMed.
- S. U. Jen, C. C. Yu, C. H. Liu and G. Y. Lee, Piezoresistance and Electrical Resistivity of Pd, Au, and Cu Films, Thin Solid Films, 2003, 434(1–2), 316–322 CrossRef CAS.
- Z. H. Meiksin and R. A. Hudzinski, A Theoretical Study of the Effect of Elastic Strain on the Electrical Resistance of Thin Metal Films, J. Appl. Phys., 1967, 38(11), 4490–4494 CrossRef CAS.
- I. S. Beloborodov, A. V. Lopatin, V. M. Vinokur and K. B. Efetov, Granular Electronic Systems, Rev. Mod. Phys., 2007, 79(2), 469–518 CrossRef CAS.
- J. Lee, S. Kim, J. Lee, D. Yang, B. C. Park, S. Ryu and I. Park, A Stretchable Strain Sensor Based on a Metal Nanoparticle Thin Film for Human Motion Detection, Nanoscale, 2014, 6(20), 11932–11939 RSC.
- B. Xie, P. Mao, M. Chen, Z. Li, C. Liu, Y. Qin, L. Yang, M. Wei, M. Liu and X. Wang, et al., A Tunable Palladium Nanoparticle Film-Based Strain Sensor in a Mott Variable-Range Hopping Regime, Sens. Actuators, A, 2018, 272, 161–169 CrossRef CAS.
- M. Manadé, F. Viñes and F. Illas, Transition Metal Adatoms on Graphene: A Systematic Density Functional Study, Carbon, 2015, 95, 525–534 CrossRef.
- O. V. Yazyev and A. Pasquarello, Metal Adatoms on Graphene and Hexagonal Boron Nitride: Towards Rational Design of Self-Assembly Templates, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(4), 1–5 CrossRef.
- K. T. Chan, J. B. Neaton and M. L. Cohen, First-Principles Study of Metal Adatom Adsorption on Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(23), 235430-1–235430-12 CrossRef.
- D. Roylance, Mechanical Properties of Materials, Massachusetts Institute of Technology, Cambridge, MA, 2008 Search PubMed.
- K. K. Kim, S. Hong, H. M. Cho, J. Lee, Y. D. Suh, J. Ham and S. H. Ko, Highly Sensitive and Stretchable Multidimensional Strain Sensor with Prestrained Anisotropic Metal Nanowire Percolation Networks, Nano Lett., 2015, 15(8), 5240–5247 CrossRef CAS PubMed.
- M. Huang, T. A. Pascal, H. Kim, W. A. Goddard and J. R. Greer, Electronic−Mechanical Coupling in Graphene from in Situ Nanoindentation Experiments and Multiscale Atomistic Simulations, Nano Lett., 2011, 11(3), 1241–1246 CrossRef CAS PubMed.
- A. D. Smith, F. Niklaus, A. Paussa, S. Vaziri, A. C. Fischer, M. Sterner, F. Forsberg, A. Delin, D. Esseni and P. Palestri, et al., Electromechanical Piezoresistive Sensing in Suspended Graphene Membranes, Nano Lett., 2013, 13(7), 3237–3242 CrossRef CAS PubMed.
- N. J. G. Couto, D. Costanzo, S. Engels, D.-K. Ki, K. Watanabe, T. Taniguchi, C. Stampfer, F. Guinea and A. F. Morpurgo, Random Strain Fluctuations as Dominant Disorder Source for High-Quality on-Substrate Graphene Devices, Phys. Rev. X, 2014, 4(4), 1–13 Search PubMed.
- R. Skomski, P. A. Dowben, M. Sky Driver and J. A. Kelber, Sublattice-Induced Symmetry Breaking and Band-Gap Formation in Graphene, Mater. Horiz., 2014, 1(6), 563–571 RSC.
- J. Hicks, A. Tejeda, A. Taleb-Ibrahimi, M. S. Nevius, F. Wang, K. Shepperd, J. Palmer, F. Bertran, P. Le Fèvre and J. Kunc, et al., A Wide-Bandgap Metal-Semiconductor-Metal Nanostructure Made Entirely from Graphene, Nat. Phys., 2013, 9(1), 49–54 Search PubMed.
- V. M. Pereira, A. H. Castro Neto and N. M. R. Peres, Tight-Binding Approach to Uniaxial Strain in Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(4), 1–8 CrossRef.
- Z. H. Ni, T. Yu, Y. H. Lu, Y. Y. Wang, Y. P. Feng and Z. X. Shen, Uniaxial Strain on Graphene: Raman Spectroscopy Study and Band-Gap Opening, ACS Nano, 2008, 2(11), 2301–2305 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Large-Scale Pattern Growth of Graphene Films for Stretchable Transparent Electrodes, Nature, 2009, 457(7230), 706–710 CrossRef CAS PubMed.
- X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung and E. Tutuc, et al., Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils, Science, 2009, 324(5932), 1312–1314 CrossRef CAS PubMed.
- A. V. Zaretski, H. Moetazedi, C. Kong, E. J. Sawyer, S. Savagatrup, E. Valle, T. F. O'Connor, A. D. Printz and D. J. Lipomi, Metal-Assisted Exfoliation (MAE): Green, Roll-to-Roll Compatible Method for Transferring Graphene to Flexible Substrates, Nanotechnology, 2015, 26(4), 045301-1–045301-7 CrossRef PubMed.
- Y. Wang, L. Wang, T. Yang, X. Li, X. Zang, M. Zhu, K. Wang, D. Wu and H. Zhu, Wearable and Highly Sensitive Graphene Strain Sensors for Human Motion Monitoring, Adv. Funct. Mater., 2014, 24(29), 4666–4670 CrossRef CAS.
- N. Hu, Y. Karube, C. Yan, Z. Masuda and H. Fukunaga, Tunneling Effect in a Polymer/Carbon Nanotube Nanocomposite Strain Sensor, Acta Mater., 2008, 56(13), 2929–2936 CrossRef CAS.
- T. Yang, X. Li, X. Jiang, S. Lin, J. Lao, J. Shi, Z. Zhen, Z. Li and H. Zhu, Structural Engineering of Gold Thin Films with Channel Cracks for Ultrasensitive Strain Sensing, Mater. Horiz., 2016, 3(3), 248–255 RSC.
- B. Park, J. Kim, D. Kang, C. Jeong, K. S. Kim, J. U. Kim, P. J. Yoo and T. Kim, Dramatically Enhanced Mechanosensitivity and Signal-to-Noise Ratio of Nanoscale Crack-Based Sensors: Effect of Crack Depth, Adv. Mater., 2016, 28(37), 8130–8137 CrossRef CAS PubMed.
- J. Ramírez, D. Rodriquez, F. Qiao, J. Warchall, J. Rye, E. Aklile, A. S-C. Chiang, B. C. Marin, P. P. Mercier and C. K. Cheng, et al., Metallic Nanoislands on Graphene for Monitoring Swallowing Activity in Head and Neck Cancer Patients, ACS Nano, 2018, 12(6), 5913–5922 CrossRef PubMed.
- J. Ramírez, D. Rodriquez, A. D. Urbina, A. M. Cardenas and D. J. Lipomi, Combining High Sensitivity and Dynamic Range: Wearable Thin-Film Composite Strain Sensors of Graphene, Ultrathin Palladium, and PEDOT:PSS, ACS Appl. Nano Mater., 2019, 2(4), 2222–2229 CrossRef.
- C. Dhong, S. J. Edmunds, J. Ramirez, L. Kayser, F. Chen, J. Jokerst and D. J. Lipomi, Optics-Free, Non-Contact Measurements of Fluids, Bubbles and Particles in Microchannels Using Metallic Nanoislands on Graphene, Nano Lett., 2018, 18(8), 5306–5311 CrossRef CAS PubMed.
- B. C. Marin, J. Liu, E. Aklile, A. D. Urbina, A. S. C. Chiang, N. Lawrence, S. Chen and D. J. Lipomi, SERS-Enhanced Piezoplasmonic Graphene Composite for Biological and Structural Strain Mapping, Nanoscale, 2017, 9(3), 1292–1298 RSC.
- M. Pozzo, D. Alfè, P. Lacovig, P. Hofmann, S. Lizzit and A. Baraldi, Thermal Expansion of Supported and Freestanding Graphene: Lattice Constant versus Interatomic Distance, Phys. Rev. Lett., 2011, 106(13), 135501(1)–135501(4) CrossRef PubMed.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim and K. L. Shepard, et al., Boron Nitride Substrates for High-Quality Graphene Electronics, Nat. Nanotechnol., 2010, 5(10), 722–726 CrossRef CAS PubMed.
- A. Govind Rajan, M. S. Strano and D. Blankschtein, Ab Initio Molecular Dynamics and Lattice Dynamics-Based Force Field for Modeling Hexagonal Boron Nitride in Mechanical and Interfacial Applications, J. Phys. Chem. Lett., 2018, 9(7), 1584–1591 CrossRef PubMed.
- G. Giovannetti, P. A. Khomyakov, G. Brocks, P. J. Kelly and J. Van Den Brink, Substrate-Induced Band Gap in Graphene on Hexagonal Boron Nitride: Ab Initio Density Functional Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(7), 2–5 Search PubMed.
- K. Watanabe, T. Taniguchi and H. Kanda, Direct-Bandgap Properties and Evidence for Ultraviolet Lasing of Hexagonal Boron Nitride Single Crystal, Nat. Mater., 2004, 3(6), 404–409 CrossRef CAS PubMed.
- J. Rafiee, X. Mi, H. Gullapalli, A. V. Thomas, F. Yavari, Y. Shi, P. M. Ajayan and N. A. Koratkar, Wetting Transparency of Graphene, Nat. Mater., 2012, 11(3), 217–222 CrossRef CAS PubMed.
- H. Li and X. C. Zeng, Wetting and Interfacial Properties of Water Nanodroplets in Contact with Graphene and Monolayer Boron-Nitride Sheets, ACS Nano, 2012, 6(3), 2401–2409 CrossRef CAS PubMed.
- R. L. Parker and A. Krinsky, Electrical Resistance-Strain Characteristics of Thin Evaporated Metal Films, J. Appl. Phys., 1963, 34(9), 2700–2708 CrossRef CAS.
- C. A. Neugebauer and M. B. Webb, Electrical Conduction Mechanism in Ultrathin, Evaporated Metal Films, J. Appl. Phys., 1962, 33(1), 74–82 CrossRef CAS.
- R. M. Hill, Electrical Conduction in Ultra Thin Metal Films. II. Experimental, Proc. R. Soc. A, 1969, 309(1498), 397–417 CAS.
- L. L. Kazmerski and D. M. Racine, Growth, Environmental, and Electrical Properties of Ultrathin Metal Films, J. Appl. Phys., 1975, 46(2), 791–795 CrossRef CAS.
- P. A. Tick and F. P. Fehlner, Electrical Behavior of Composite Discontinuous Films, J. Appl. Phys., 1972, 43(2), 362–368 CrossRef CAS.
- B. Xie, P. Mao, M. Chen, Z. Li, C. Liu, Y. Qin, L. Yang, M. Wei, M. Liu and X. Wang, et al., Sensors and Actuators A: Physical A Tunable Palladium Nanoparticle Film-Based Strain Sensor in a Mott Variable-Range Hopping Regime, Sens. Actuators. A, 2018, 272, 161–169 CrossRef CAS.
- J. van Lith, A. Lassesson, S. A. Brown, M. Schulze, J. G. Partridge and A. Ayesh, A Hydrogen Sensor Based on Tunneling between Palladium Clusters, Appl. Phys. Lett., 2007, 91(18), 1–3 CrossRef.
- S. Wagner and A. Pundt, Conduction Mechanisms during the Growth of Pd Thin Films: Experiment and Model, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(15), 1–14 CrossRef.
- X. Liu, C. Z. Wang, M. Hupalo, H. Q. Lin, K. M. Ho and M. C. Tringides, Metals on Graphene: Interactions, Growth Morphology, and Thermal Stability, Crystals, 2013, 3(1), 79–111 CrossRef CAS.
- P. A. Pandey, G. R. Bell, J. P. Rourke, A. M. Sanchez, M. D. Elkin, B. J. Hickey and N. R. Wilson, Physical Vapor Deposition of Metal Nanoparticles on Chemically Modified Graphene: Observations on Metal-Graphene Interactions, Small, 2011, 7(22), 3202–3210 CrossRef CAS PubMed.
- C. Gong, S. McDonnell, X. Qin, A. Azcatl, H. Dong, Y. J. Chabal, K. Cho and R. M. Wallace, Realistic Metal-Graphene Contact Structures, ACS Nano, 2014, 8(1), 642–649 CrossRef CAS PubMed.
- Q. M. Ramasse, R. Zan, U. Bangert, D. W. Boukhvalov, Y. W. Son and K. S. Novoselov, Direct Experimental Evidence of Metal-Mediated Etching of Suspended Graphene, ACS Nano, 2012, 6(5), 4063–4071 CrossRef CAS PubMed.
- F. Xia, V. Perebeinos, Y. M. Lin, Y. Wu and P. Avouris, The Origins and Limits of Metal-Graphene Junction Resistance, Nat. Nanotechnol., 2011, 6(3), 179–184 CrossRef CAS PubMed.
- K. Pi, K. M. McCreary, W. Bao, W. Han, Y. F. Chiang, Y. Li, S. W. Tsai, C. N. Lau and R. K. Kawakami, Electronic Doping and Scattering by Transition Metals on Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(7), 1–5 CrossRef.
- B. C. Marin, S. E. Root, A. D. Urbina, E. Aklile, R. Miller, A. V. Zaretski and D. J. Lipomi, Graphene-Metal Composite Sensors with Near-Zero Temperature Coefficient of Resistance, ACS Omega, 2017, 2(2), 626–630 CrossRef CAS PubMed.
- W. F. Leonard and R. L. Ramey, Temperature Coefficient of Resistance in Thin Metal Films, J. Appl. Phys., 1966, 37(9), 3634–3635 CrossRef CAS.
- Q. G. Zhang, X. Zhang, B. Y. Cao, M. Fujii, K. Takahashi and T. Ikuta, Influence of Grain Boundary Scattering on the Electrical Properties of Platinum Nanofilms, Appl. Phys. Lett., 2006, 89(11), 2004–2007 Search PubMed.
- Y. Namba, Resistivity and Temperature Coefficient of Thin Metal Films with Rough Surface, Jpn. J. Appl. Phys., 1970, 9(11), 1326–1329 CrossRef CAS.
- T. C. Chiang, Quantum Physics of Thin Metal Films, AAPPS Bull., 2008, 18(2), 2–10 CAS.
- C. Kittel, Introduction to Solid State Physics, Wiley & Sons, New York, NY, 8th edn, 2004 Search PubMed.
- J. R. Hook and H. E. Hall, Solid State Physics, Wiley & Sons, New York, NY, 2nd edn, 1995 Search PubMed.
- R. Landauer, Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction, IBM J. Res. Dev., 1957, 1(3), 223–231 Search PubMed.
- D. A. Wharam, T. J. Thornton, R. Newbury, M. Pepper, H. Ahmed, J. E. F. Frost, D. G. Hasko, D. C. Peacock, D. A. Ritchie and G. A. C. Jones, One-Dimensional Transport and the Quantisation of the Ballistic Resistance, J. Phys. C: Solid State Phys., 1988, 21, L209–L214 CrossRef.
- B. J. Van Wees, H. Van Houten, C. W. J. Beenakker, J. G. Williamson, L. P. Kouwenhoven, D. Van Der Marel and C. T. Foxon, Quantized Conductance of Point Contacts in a Two-Dimensional Electron Gas, Phys. Rev. Lett., 1988, 60(9), 848–850 CrossRef CAS PubMed.
- L. P. Coelho, Mahotas: Open Source Software for Scriptable Computer Vision, J. Open Res. Softw., 2013, 1(1), e3 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr02270e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |




