Open Access Article
Open Access ArticleHalf-hedgehog spin textures in sub-100 nm soft magnetic nanodots†
Eider
Berganza
 *ab,
Miriam
Jaafar
*ab,
Miriam
Jaafar
 *ac,
Jose A.
Fernandez-Roldan
*ac,
Jose A.
Fernandez-Roldan
 ad,
Maite
Goiriena-Goikoetxea
ad,
Maite
Goiriena-Goikoetxea
 ef,
Javier
Pablo-Navarro
g,
Alfredo
García-Arribas
ef,
Javier
Pablo-Navarro
g,
Alfredo
García-Arribas
 fh,
Konstantin
Guslienko
ij,
César
Magén
gkl,
José M.
De Teresa
fh,
Konstantin
Guslienko
ij,
César
Magén
gkl,
José M.
De Teresa
 gkl,
Oksana
Chubykalo-Fesenko
a and
Agustina
Asenjo
gkl,
Oksana
Chubykalo-Fesenko
a and
Agustina
Asenjo
 a
a
aInstituto de Ciencia de Materiales de Madrid, CSIC, 28049 Madrid, Spain
bInstitute of Nanotechnology, KIT Campus North, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: eider.eguiarte@kit.edu
cDepartamento de Física de la Materia Condensada and Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
dDepartamento de Física, Universidad de Oviedo, Federico García Lorca s/n, Oviedo 33007, Spain
eDepartment of Electrical Engineering and Computer Science, University of California, Berkeley, CA 94720, USA
fDepartamento de Electricidad y Electrónica, Universidad del País Vasco (UPV/EHU), 48940 Leioa, Spain
gLaboratorio de Microscopías Avanzadas (LMA) - Instituto de Nanociencia de Aragón (INA), Universidad de Zaragoza, 50018 Zaragoza, Spain
hBasque Center for Materials, Applications and Nanostructures (BCMaterials), UPV/EHU Science Park, 48940 Leioa, Spain
iDepartment of Materials Physics, University of the Basque Country (UPV/EHU), 20018 Donostia, Spain
jIKERBASQUE, the Basque Foundation for Science, 48013 Bilbao, Spain
kInstituto de Ciencia de Materiales de Aragón (ICMA), Universidad de Zaragoza-CSIC, 50009 Zaragoza, Spain
lDepartamento de Física de la Materia Condensada, Universidad de Zaragoza, 50009 Zaragoza, Spain
First published on 19th June 2020
Abstract
Topologically non-trivial structures such as magnetic skyrmions are nanometric spin textures of outstanding potential for spintronic applications due to their unique features. It is well known that Néel skyrmions of definite chirality are stabilized by the Dzyaloshinskii–Moriya exchange interaction (DMI) in bulk non-centrosymmetric materials or ultrathin films with strong spin–orbit coupling at the interface. In this work, we show that soft magnetic (permalloy) hemispherical nanodots are able to host three-dimensional chiral structures (half-hedgehog spin textures) with non-zero tropological charge. They are observed at room temperature, in absence of DMI interaction and they can be further stabilized by the magnetic field arising from the Magnetic Force Microscopy probe. Micromagnetic simulations corroborate the experimental data. Our work implies the existence of a new degree of freedom to create and manipulate complex 3D spin-textures in soft magnetic nanodots and opens up future possibilities to explore their magnetization dynamics.
Introduction
Magnetic skyrmions, topologically protected inhomogeneous spin textures on the nanoscale, named after T. Skyrme, who predicted similar non-linear configurations in quantum field theory,1 are widely investigated due to their potential spintronic applications in memory storage devices,2 or sensors,3 as well as due to their unusual fundamental physical properties.Most of the published papers report on magnetic skyrmions in systems with broken inversion symmetry, that display Dzyaloshinskii–Moriya exchange interaction (DMI) either in ultra-thin multilayers of transition metals4 and materials with strong spin–orbit coupling5,6 or in non-centrosymmetric B20 compounds. Both Néel (hedgehog) and Bloch skyrmions can be stabilized in the above-mentioned cases due to the interplay of exchange interaction, DMI and uniaxial perpendicular magnetic anisotropy.7,8 DMI can also induce skyrmions in materials with easy-plane magnetic anisotropy.9,10 Moreover, the magnetization configuration of Néel and Bloch skyrmions is chiral, i.e., only one rotation sense of the magnetization direction is energetically favourable, depending on the DMI nature. A separate question is the stabilization of the Néel and Bloch skyrmions in nanostructured materials such as nanodots, where the confinement plays a very important role and changes the skyrmion stability conditions.11
On the other hand, the so-called curvature driven effects in nanomagnetic systems constitute a very active research field.12,13 It has been established that the sample curvature can be considered as a source of an effective magnetic anisotropy and trigger magnetochiral effects.14,15 In 1D systems as magnetic nanowires, for instance, the curvature and geometrical confinement have proved to stabilize skyrmionics textures with no need of DMI.16,17
Planar soft magnetic permalloy (Py, NiFe alloy) dots are believed to host magnetic vortices only.18 However, the shape and curvature may produce additional effects as the theoretically predicted 3D Bloch-type skyrmions in hemispherical or spherical nanoparticles.19 Nevertheless, hemispherical shaped soft nanomagnets have not been investigated systematically. Despite the existence of Néel-like skyrmions in thick films with out-of plane anisotropy has been recently reported,20 so far nobody has observed the stabilization of chiral structures in confined systems with neither DMI nor perpendicular magnetic anisotropy.
During the last decade, essential progress of the experimental techniques enabled the detection of magnetic vortices,21 bubbles22 or skyrmions23 by using various imaging techniques on the nanoscale. The importance of imaging individual nano-objects lies in its capability to directly visualize these spin textures or even to control them.24,25 Several techniques such as Photo Emission Electron Microscopy (PEEM)5 or Electron Holography (EH)26 are commonly used to study magnetic configurations of individual nano-objects. Nevertheless, the family of Scanning Probe Microscopy techniques (Spin Polarized Scanning Tunneling Microscopy, SP-STM,27 Magnetic Exchange Force Microscopy, MExFM,28,29 Magnetic Force Microscopy, MFM,30 and NV-magnetometry31) provide higher resolution images as well as remarkable sensitivity.
In this article, we study sub-100 nm diameter Py (Ni80Fe20) hemispherical shaped nanodots with no uniaxial out-of-plane magnetic anisotropy or DMI. Many previous works studying cylindrical Py nanodots reported the stabilization of flux-closure vortex state or a single domain state due to the low magnetocrystalline anisotropy.18,32 However, half-skyrmionic (Néel-type) spin textures were unexpectedly detected in the present study using MFM. The evolution of the magnetic configuration under externally applied in-plane (IP) fields, together with micromagnetic simulations leave no doubts of the existence of stable three-dimensional configurations with non-zero topological charge, which behave as chiral radial vortices in such Py nanodots.
Results and discussion
Ruling out vortex configuration
For the present experiments, Py hemispherical-shaped nanodots with a diameter of 70 nm and height of 30 nm were grown by hole mask colloidal lithography (HCL) using preparation conditions that guarantee the absence of out-of-plane magnetic anisotropy, as explained elsewhere.33 The studied nanodots were distributed onto a silicon substrate far enough from neighbouring nanodots in such way that they can be considered as non-interacting with each other. Their shape and size were assessed by Scanning Electron Microscopy (SEM) and High-Resolution Transmission Electron Microscopy (HR-TEM), which confirmed polycrystalline nature of the nanodots and reveal a dome-shape, close to a hemisphere (see ESI1† for further details on the morphological characterization).As a first approach, magnetic imaging was performed after subjecting the sample to a saturating out-of-plane (OOP) magnetic field. The resulting MFM image, shown in Fig. 1a, resembles a magnetic vortex because their core can clearly distinguished from the surrounding area. Magnetic vortices present in-plane (IP) closed-flux magnetization with a core at the centre, where the OOP magnetization component can be either positive or negative and their chirality can be clock- or counter-clockwise.34,35
In the vortex configuration, since the MFM signal is mainly sensitive to the OOP component of the magnetization, a repulsive (bright) or attractive (dark) contrast is expected at the vortex core when the tip stray field and the core polarization are antiparallel (repulsive interaction) or parallel (attractive interaction), respectively, as Fig. 1b illustrates. Thus, the core contrast could be simply reversed by changing the magnetization of the MFM tip.
Keeping this in mind, MFM experiments were repeatedly performed on a previously saturated sample, whose magnetic state is left unchanged during the imaging process. Surprisingly, despite changing the MFM probe polarization, the contrast at the centre of the Py nanodots is always positive (corresponding to an antiparallel tip-core configuration, as illustrated in Fig. 1c). Moreover, the contour of the magnetic configuration of the sample is quite intense, considering that the MFM in-plane configuration should lead to a faint contrast. All in all, the results point at the existence of an alternative configuration to the expected magnetic vortex. Further experiments (presented in ESI2†) were done in order to discard any crosstalk with electrostatic interactions, given that they are also strong at the scale of a few tens of nanometers.
Half-hedgehog spin texture
The fingerprint of the vortex spin texture is the perpendicular displacement of its core with respect to an IP applied magnetic field direction, until the critical field is reached and the magnetic moments completely align with the in-plane field.Moreover, the final movement direction of the core depends entirely on the vortex chirality and it is therefore independent of its core magnetization direction.36,37
The application of in situ magnetic field during MFM measurements is frequently used to shed light upon the magnetic configuration and its dynamic behaviour. In this case, Variable Field-MFM (VF-MFM) is performed applying the field along the in-plane direction. The results display an unexpected behaviour where the movement of the core is parallel or antiparallel to the external magnetic field. These results are incompatible with the conventional vortex configuration and they necessarily imply the presence of some radial magnetization component.
In order to investigate the kind of magnetic configurations that fulfil such condition, micromagnetic simulations have been performed. Similarly to conventional vortices, where the combination of the two possible core polarities plus the two chiralities give rise to 4 energy degenerate states, one might also expect to find 4 stable states in the system that concerns us, combining the two polarities and two radial components. To reveal the stability of the magnetic configurations, micromagnetic simulations were carried out using Object Oriented Micromagnetic Framework (OOMMF).38 Hemispherical Py nanoparticles were modelled choosing a configuration with a core pointing perpendicular to the plane, an outer part pointing opposite to the core magnetization and a radially magnetized shell as initial condition. To mimic the existence of internal tensions generated by the dot fabrication process, a radial magnetic anisotropy of 2.5 × 105 J m−3 was chosen.
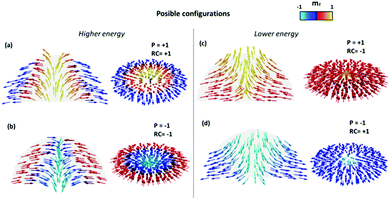
As a matter of fact, micromagnetic simulations show that 4 different states are stable states-resulting from the combination of 2 different core polarities P and 2 radial chiralities RC- (see Fig. 2, where cross sectional and basal planes of the nanodot magnetic configurations are shown). However, due to the lack of cylindrical symmetry of the nanodot, they do not present equal energy values. Micromagnetic simulations estimate that the total energy of the configurations displayed in Fig. 2a and b is E = 1.934 × 10−17 J, while those in 2c and d present E = 1.701 × 10−17 J value. Therefore, they do reveal the existence of 3D chiral magnetization configurations, hereinafter referred to as half-hedgehog spin textures, with a half-Néel skyrmion in the dot basal plane.39
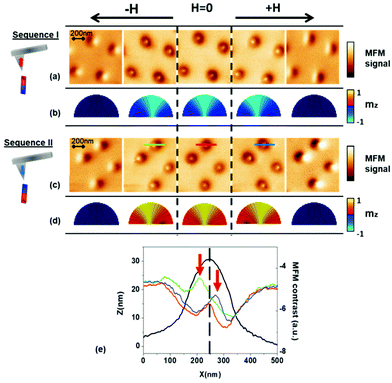
VF-MFM imaging shows, however, that not all the simulated configurations are possible in the studied system. In the two sequences shown below, the magnetization of the tip is fixed in up or down direction, while the sample is initially demagnetized in both cases. As it was previously mentioned, the MFM images display the same contrast (bright core, corresponding to repulsive interaction) in both sequences where all the cores are antiparallel to the tip magnetization. When magnetic in-plane field is applied along the x direction (see Fig. 3a and b), the white cores move antiparallel to the field direction (sequence I). In sequence II, the experiment is repeated with opposite tip polarity (Fig. 3d), which gives a different result, since the core moves parallel to the magnetic field. The combination of the two sequences proves that the displacement of the core (antiparallel or parallel to the applied field) depends on the polarity of the tip. The core displacement can be better seen on the profiles of the MFM data displayed in Fig. 3e.
Simulations in Fig. 3b and d reproduce the magnetic configurations with a radial vortex on the base plane as a minimum energy state and prove that the configuration is stable in hemispheres of 70 nm in diameter. Notice that the out-of-plane (mz) magnetization component is represented in a colour scale and that a transversal dot cross section is shown to emphasize the movement of the core. The stability of both positive (and negative) polarity half-hedgehog configurations is proven, with the radial component of the magnetization pointing in (and out), in good agreement with the observations. Results unveil that the core diameter is narrow at the base and it grows in size approaching the nanodot surface. Additionally, when it is subjected to external field, the magnetic moments of the base respond later than the ones closer to the dot upper surface.
Therefore, the comparison of simulations and experiment shows that only structures with one chirality are observed.40
A similar coupling effect between polarity and the domain wall chirality was reported for vortex-like structures in spherical dots.19
At this point we can claim that the stray field of the tip plays a critical role on the definition of the magnetic configuration of the nanodots, considering that a positive or negative core structure can be induced by applying an out-of-plane field in the appropriate direction. This explains why the images obtained in the MFM measurements (i.e., faint core and dark contour, on Fig. 1c) stay the same regardless of the magnetization direction of the tip: the relative orientation of sample–tip magnetization remains always the same. Notice that in this system, the MFM tip does not produce the usual reversible process where the sample magnetization aligns parallel to the tip magnetic moment. The tip creates a perturbation that induces a metastable state, where the dot external part keeps the radial component of the tip stray field while the core is magnetized antiparallel to it.
More importantly, it should be made clear that despite all four configurations in Fig. 2 being energy minimum states, only the two lower energy configurations have been experimentally detected (Fig. 2c and d). This conclusion can be extracted through careful interpretation of the VF-MFM images in Fig. 3. A more detailed explanation can be found in ESI3.†
Topological charge
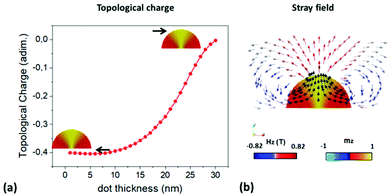
Systems with topological defects have attracted much attention due to their rich physics that serve as extensible models for condensed matter systems beyond the scope of magnetism. A topological whirl is a region of singular field distribution, which mathematically represents a soliton solution for a continuous field described by a partial differential equation. Vortices and radial vortices can be considered as solitons of topological charge 1/2, instead of 1. At the same time, it is known that exactly integer and half-integer topological charges can exist in infinite thin films only, while the confined geometry of dots imposes additional boundary conditions, which render the topological charge to be non-integer.We also note that the widely used concept of the topological charge (skyrmion number or degree of mapping) in 2D spin systems is not directly applicable to our dots because the magnetization depends on the thickness coordinate z, m (x, y, z). Despite this issue, several works in literature report 2D topological charge analysis in nanowires as a function of z dimension.17,41
In order to understand the evolution of the topological charge as a function of the dot thickness, we have calculated the 2D topological charge a function of the dot thickness coordinate in the dot, according to the following equation:
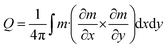 | (1) |
The 2D topological charge (eqn (1)) is approximately equal to 0.4 at the base of the nanodot and it decreases when approaching the dot surface (Fig. 4a). A more rigorous approach to the topological charge in 3D case assumes calculation of the flux of the gyrocoupling density vector over the sample surface or introducing a Hopf invariant.42
At this point, the interpretation of the MFM images might be controversial due to the high intensity measured in the contour of the nanodots. For deep analysis of the MFM contrast, the intensities of the signal from the remnant state and the signal from the saturated nanodot are compared in ESI4.† At first sight, this might lead us to think that the topological charge of the configuration is higher than what we calculated. However, considering the stray field generated by the nanodot (Fig. 4b), with strong OOP field component close to the nanodot contour, a strong attractive interaction (dark contrast) between the MFM tip and the nanodot edge is expected.
Stability of the magnetic configuration
The stabilization of these chiral 3D configurations, resembling 2D hedgehog Néel half-skyrmions in soft sub-100 nm nanodots, is herein reported for the first time. Two parameters, namely the nanodot geometry and the tip stray field, seem to play a key role in the stabilization and the determination of the half-hedgehog magnetization configuration chirality.The previous experiments shown in Fig. 1c and 3 have demonstrated that the MFM tip stray field nucleates the chiral structure. Johnson et al. already predicted the possibility of stabilizing skyrmionic spin textures in curved nanostructures assisted by an external stray field.43 In fact, the direction of the core can be chosen by selecting the polarization of the tip prior to scanning. Furthermore, none of the MFM images obtained so far present any kind of sudden changes or “jumps”, where the stability of the induced configuration might to some extent be questioned. Conversely, they seem to remain always stable during the scan, even if the retrace distance is on purpose enlarged (see ESI5†).
However, the influence of the MFM tip over the stability of the configuration is not yet clear. For further experiments addressing this topic, lower moment MFM tips were designed and characterized44,45 (see Table 1 and ESI6† for more details), which give us a gradient of tip stray fields with tuned intensity.
Making use of the series of VF-MFM based methods,46 the critical fields of the structures creation and annihilation have been determined, repeating the experiment with each one of the tips. In Fig. 5a, the field intervals for the half-hedgehog structure existence are depicted as a function of the stray field contrast of the probes.
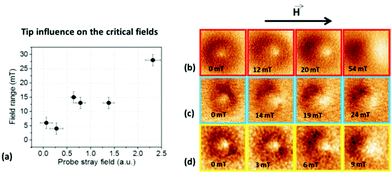 | ||
| Fig. 5 Assessment of the half-hedgehog stability as a function of the magnetic force gradient. (a) Correlation between OOP magnetic probe stray field (x axis) and the field range where the structure is stable (y axis). The black dots represent the experimental data obtained from the MFM based measurements described in ESI7.† Field sequences performed ith different tips show the decreasing saturating in-plane magnetic fields from (b)–(d). Image size is 250 × 250 nm. | ||
Notice that the stray field contrast value is given in Hz units, as the observable of the MFM contrast is the oscillation frequency channel due to the use of the Phase Locked Loop. Fig. 5b–d display representative standard MFM images of the structures under in situ applied magnetic fields, performed with probes of different stray field values. The colour code of frames of the MFM images in Fig. 5 is in accordance with that shown in Table 1. Interestingly, the annihilation field is almost 5 times larger when a commercial probe is used (tip 1, Fig. 5b) as compared to the values obtained for the nanorod probe (tip 3, Fig. 5d).
Thus, the larger stray fields lead to the stabilization of the half hedgehog 3D structures, turning it into a magnetically harder configuration. This phenomenon has been observed in previous works, where the local field of the MFM tip was used to manipulate the magnetic charges.47,48 In this work, the tip stray field serves as a tool to create and enhance the stability of the configurations. The set of images from Fig. 5d, which were scanned with the smallest possible stray field tip (4 Hz) speak for themselves, remarkably showing how just a very small stray field is needed to nucleate the half-hedgehog spin texture. Moreover, the configuration still stays relatively stable, i.e. it does not immediately vanish upon applied field.
On the other hand, in simulations, the configuration is stabilized specifically for 70 nm diameter hemispheres. However, additional experiments with slightly different samples show that the stabilization of the studied configuration is closely related to a specific dot geometry and aspect ratio. Some examples are shown in ESI7,† where a sample with a bigger size dispersion presents also single domain configurations, additionally to the here studied magnetic configurations.
Experimental
Materials and methods
Conclusions
In summary, in the present work we achieve to induce 3D half-hedgehog configurations with radial vortices in the base plane on permalloy hemispherical nanodots with neither DMI nor perpendicular magnetocrystalline anisotropy. Remarkably, a single chirality of the structures is observed in the absence of DMI, induced by the hemispherical shape of the nanodots. This is a non-expected magnetization configuration in permalloy nanoparticles, where only two magnetic configurations have been previously reported as possible ground states in numerous phase diagrams, i.e. single domain and vortex configuration. The magnetic force microscopy results are supported by micromagnetic simulations. Under in-plane applied magnetic field, the observed magnetic configurations behave as half-Neél skyrmion (radial vortices) as it is theoretically predicted, i.e. their core moves parallel or antiparallel to the field in agreement with its radial component direction. The chirality of the structures seems to be further stabilized by the fact that they are created in the presence of stray field coming from the MFM tip.We believe that the possibility of stabilizing chiral structures in permalloy nanodots without magnetic anisotropy and DMI opens new perspectives for the exploration of topologically non-trivial spin textures in soft magnetic systems that have not been yet considered, or novel magnetic configurations arising from curvature in nanoscale magnetic systems.
Author contribution
E. B., M. J. and A. A. conceived the project. M. G-G. and A. G-A. fabricated the samples. E. B. and M. J. performed the MFM measurements. E. B. and J. A. F. R. carried out the micromagnetic simulations with the help of O. C-F. K. G. contributed to the interpretation of the data. E. B. and J. P.-N. fabricated the MFM tips. J. P.-N. and C. M. performed the TEM measurements. J. M. D. T. and C. M. supervised the growth of the MFM tips by FEBID, the lamellae preparation by FIB-SEM and the TEM experiments. E. B., M. J. O. C-F. and A. A. wrote the manuscript. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. J., E. B., J. A. F. R and A. A. acknowledge the support from the Spanish Ministerio de Economia y Competitividad (MINECO) under projects no. S2018/NMT 4321, MAT2015-73775-JIN and MAT2016-76824-C3-1-R. E. B. acknowledges the financial support from the Alexander von Humboldt Foundation. M. G-G. and A.G-A. acknowledge the financial support from the Spanish MINECO project MAT2017-83632-C3 and from the Basque Government through IT1245-19 project and M. G. G. postdoctoral fellowship. M. J. also acknowledges financial support from the Spanish Ministry of Economy and Competitiveness, through The “María de Maeztu” Programme for Units of Excellence in R&D (MDM-2014-0377) and from Universidad Autónoma de Madrid and Comunidad Autónoma de Madrid through the project SI1/PJI/2019-00055. J. P.-N., C. M. and J. M. D. T. acknowledge financial support from the Spanish Ministry of Economy and Competitiveness through Projects MAT2018-102627-T and MAT2017-82970-C2, and from the Aragon Regional Government (Construyendo Europa desde Aragón) through Project E13_20R, with European Social Fund funding. A grant to J. P.-N. was funded by the Ayuda para Contratos Predoctorales para la Formación de Doctores, Convocatoria Res. 05/06/15 (BOE 12/06/15) of the Secretaría de Estado de Investigación, Desarrollo e Innovación in the Subprograma Estatal de Formación of the Spanish Ministry of Economy and Competitiveness with the participation of the European Social Fund. K. G. acknowledges support by IKERBASQUE (the Basque Foundation for Science). The work of K. G. and O. C.-F. was supported by the Spanish Ministry of Economy and Competitiveness under the project FIS2016-78591-C3-3-R.References
- T. H. R. Skyrme, A Unified Field Theory of Mesons and Baryons, Nucl. Phys., 1962, 31, 556–569 CrossRef CAS.
- G. Yu, P. Upadhyaya, Q. Shao, H. Wu, G. Yin, X. Li, C. He, W. Jiang, X. Han, P. K. Amiri and K. L. Wang, Room-Temperature Skyrmion Shift Device for Memory Application, Nano Lett., 2017, 17(1), 261–268 CrossRef CAS PubMed.
- F. Garcia-Sanchez, J. Sampaio, N. Reyren, V. Cros and J. V. Kim, A skyrmion-based spin-torque nano-oscillator, New J. Phys., 2016, 18, 075011 CrossRef.
- U. K. Rössler, A. N. Bogdanov and C. Pfleiderer, Spontaneous Skyrmion Ground States in Magnetic Metals, Nature, 2006, 442(7104), 797–801 CrossRef PubMed.
- O. Boulle, J. Vogel, H. Yang, S. Pizzini, D. de Souza Chaves, A. Locatelli, T. O. Menteş, A. Sala, L. D. Buda-Prejbeanu and O. Klein, et al., Room-Temperature Chiral Magnetic Skyrmions in Ultrathin Magnetic Nanostructures, Nat. Nanotechnol., 2016, 11(5), 449–454 CrossRef CAS PubMed.
- C. Moreau-Luchaire, C. Moutafis, N. Reyren, J. Sampaio, C. A. F. Vaz, N. Van Horne, K. Bouzehouane, K. Garcia, C. Deranlot and P. Warnicke, et al., Additive Interfacial Chiral Interaction in Multilayers for Stabilization of Small Individual Skyrmions at Room Temperature, Nat. Nanotechnol., 2016, 11(5), 444–448 CrossRef CAS PubMed.
- I. Kezsmarki, S. Bordacs, P. Milde, E. Neuber, L. M. Eng, J. S. White, H. M. Rønnow, C. D. Dewhurst, M. Mochizuki, K. Yanai, H. Nakamura, D. Ehlers, V. Tsurkan and A. Loidl, Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8, Nat. Mater., 2015, 14, 1116–1122 CrossRef CAS PubMed.
- S. D. Pollard, J. A. Garlow, J. Yu, Z. Wang, Y. Zhu and H. Yang, Observation of stable Néel skyrmions in cobalt/palladium multilayers with Lorentz transmission electron microscopy, Nat. Commun., 2017, 8, 14761 CrossRef PubMed.
- M. Vousden, M. Albert, M. Beg, M. A. Bisotti, R. Carey, D. Chernyshenko, D. Cortés-Ortuño, W. Wang, O. Hovorka, C. H. Marrows and H. Fangohr, Skyrmions in thin films with easy-plane magnetocrystalline anisotropy, Appl. Phys. Lett., 2016, 108, 132406 CrossRef.
- S. Zhang, J. Zhang, Y. Wen, Y. Peng, Z. Qiu, T. Matsumoto and X. Zhang, Deformation of Néel-type skyrmions revealed by Lorentz transmission electron microscopy, Appl. Phys. Lett., 2020, 116, 142402 CrossRef.
- K. Y. Guslienko, Skyrmion State Stability in Magnetic Nanodots With Perpendicular Anisotropy, IEEE Magn. Lett., 2015, 6, 4000104 Search PubMed.
- R. Streubel, P. Fischer, F. Kronast, V. P. Kravchuk, D. D. Sheka, Y. Gaididei, O. G. Schmidt and D. Makarov, Magnetism of curved geometries, J. Phys. D: Appl. Phys., 2016, 49, 363001 CrossRef.
- A. Fernández-Pacheco, R. Streubel, O. Fruchart, R. Hertel, P. Fischer and R. P. Cowburn, Three-dimensional nanomagnetis, Nat. Commun., 2017, 8, 15756 CrossRef PubMed.
- Y. Gaididei, V. P. Kravchuk and D. D. Sheka, Curvature Effects in Thin Magnetic Shells, Phys. Rev. Lett., 2014, 112, 257203 CrossRef PubMed.
- O. V. Pylypovskyi, V. P. Kravchuk, D. D. Sheka, D. Makarov, O. G. Schmidt and Y. Gaididei, Coupling of Chiralities in Spin and Physical Spaces: The Möbius Ring as a Case Study, Phys. Rev. Lett., 2015, 114(19), 197204 CrossRef PubMed.
- J. A. Fernandez-Roldan, R. Perez del Real, C. Bran, M. Vazquez and O. Chubykalo-Fesenko, Magnetization pinning in modulated nanowires: from topological protection to the “corkscrew” mechanism”, Nanoscale, 2018, 10, 5923–5927 RSC.
- J. A. Fernandez-Roldan, Y. P. Ivanov and O. Chubykalo-Fesenko, Micromagnetic modelling of magnetic domain walls and domains in cylindrical nanowires, in Magnetic Nano- and Microwires, Elsevier, 2020, pp. 403–426 Search PubMed.
- K. Y. Guslienko and V. Novosad, Vortex State Stability in Soft Magnetic Cylindrical Nanodots, J. Appl. Phys., 2004, 96(8), 4451–4455 CrossRef CAS.
- V. P. Kravchuk, D. D. Sheka, R. Streubel, D. Makarov, O. G. Schmidt and Y. Gaididei, Out-of-surface vortices in spherical shells, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144433 CrossRef.
- S. A. Montoya, R. Tolley, I. Gilbert, S. G. Je, M. Y. Im and E. E. Fullerton, Spin-orbit torque induced dipole skyrmion motion at room temperature, Phys. Rev. B, 2018, 98, 104432 CrossRef CAS.
- E. Pinilla-Cienfuegos, S. Mañas-Valero, A. Forment-Aliaga and E. Coronado, Switching the Magnetic Vortex Core in a Single Nanoparticle, ACS Nano, 2016, 10(2), 1764–1770 CrossRef CAS PubMed.
- C. Moutafis, S. Komineas, C. A. F. Vaz, J. A. C. Bland, T. Shima, T. Seki and K. Takanashi, Magnetic Bubbles in FePt Nanodots with Perpendicular Anisotropy, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(10), 104426 CrossRef.
- X. Zhao, C. Jin, C. Wang, H. Du, J. Zang, M. Tian, R. Che and Y. Zhang, Direct Imaging of Magnetic Field-Driven Transitions of Skyrmion Cluster States in FeGe Nanodisks, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(18), 4918–4923 CrossRef CAS PubMed.
- S. Zhang, J. Zhang, Q. Zhang, C. Barton, V. Neu, Y. Zhao, Z. Hou, Y. Wen, C. Gong, O. Kazakova, W. Wang, Y. Peng, D. A. Garanin, E. M. Chudnovsky and X. Zhang, Direct writing of room temperature and zero field skyrmion lattices by a scanning local magnetic field, Appl. Phys. Lett., 2018, 112, 132405 CrossRef.
- J. Li, A. Tan, K. W. Moon, A. Doran, M. A. Marcus, A. T. Young, E. Arenholz, S. Ma, R. F. Yang and C. Hwang, et al., Tailoring the Topology of an Artificial Magnetic Skyrmion, Nat. Commun., 2014, 5, 4704 CrossRef CAS PubMed.
- C. Jin, Z. A. Li, A. Kovács, J. Caron, F. Zheng, F. N. Rybakov, N. S. Kiselev, H. Du, S. Blügel and M. Tian, et al., Control of Morphology and Formation of Highly Geometrically Confined Magnetic Skyrmions, Nat. Commun., 2017, 8, 15569 CrossRef CAS PubMed.
- N. Romming, C. Hanneken, M. Menzel, J. E. Bickel, B. Wolter, K. Von Bergmann, A. Kubetzka and R. Wiesendanger, Writing and Deleting Single Magnetic Skyrmions, Science, 2013, 341(6146), 636–639 CrossRef CAS PubMed.
- J. Grenz, A. Köhler, A. Schwarz and R. Wiesendanger, Probing the Nano-Skyrmion Lattice on Fe/Ir(111) with Magnetic Exchange Force Microscopy, Phys. Rev. Lett., 2017, 119(4), 047205 CrossRef PubMed.
- N. Hauptmann, J. W. Gerritsen, D. Wegner and A. A. Khajetoorians, Sensing Noncollinear Magnetism at the Atomic Scale Combining Magnetic Exchange and Spin-Polarized Imaging, Nano Lett., 2017, 17(9), 5660–5665 CrossRef CAS PubMed.
- A. Soumyanarayanan, M. Raju, A. L. G. Oyarce, A. K. C. Tan, M. Y. Im, A. P. Petrovic, P. Ho, K. H. Khoo, M. Tran and C. K. Gan, et al., Tunable Room-Temperature Magnetic Skyrmions in Ir/Fe/Co/Pt Multilayers, Nat. Mater., 2017, 16(9), 898–904 CrossRef CAS PubMed.
- W. Akhtar, A. Hrabec, S. Chouaieb, A. Haykal, I. Gross, M. Belmeguenai, M. S. Gabor, B. Shields, P. Maletinsky, A. Thiaville, S. Rohart and V. Jacques, Current-Induced Nucleation and Dynamics of Skyrmions in a Co-based Heusler Alloy, Phys. Rev. Appl., 2019, 11, 034066 CrossRef CAS.
- M. Goiriena-Goikoetxea, K. Guslienko, M. Rouco, I. Orue, E. Berganza, M. Jaafar, A. Asenjo, M. Fdez-Gubieda, L. Fernández Barquín and A. García-Arribas, Magnetization Reversal in Circular Vortex Dots of Small Radius, Nanoscale, 2017, 9, 11269–11278 RSC.
- M. Goiriena-Goikoetxea, A. García-Arribas, M. Rouco, A. V. Svalov and J. M. Barandiaran, High-yield fabrication of 60 nm Permalloy nanodiscs in well-defined magnetic vortex state for biomedical applications, Nanotechnology, 2016, 27, 175302 CrossRef CAS PubMed.
- T. Shinjo, T. Okuno, R. Hassdorf, K. Shigeto and T. Ono, Magnetic Vortex Core Observation in Circular Dots of Permalloy, Science, 2000, 289(5481), 930–932 CrossRef PubMed.
- A. Wachowiak, J. Wiebe, M. Bode, O. Pietzsch, M. Morgenstern and R. Wiesendanger, Direct Observation of Internal Spin Structure of Magnetic Vortex Cores, Science, 2002, 298(5593), 577–580 CrossRef CAS PubMed.
- M. Jaafar, R. Yanes, A. Asenjo, O. Chubykalo-Fesenko, M. Vázquez, E. M. González and J. L. Vicent, Field induced vortex dynamics in magnetic Ni nanotriangles, Nanotechnology, 2008, 19, 1–8 CrossRef PubMed.
- R. P. Cowburn, D. K. Koltsov, A. O. Adeyeye, M. E. Welland and D. M. Tricker, Single-Domain Circular Nanomagnets, Phys. Rev. Lett., 1999, 83(5), 1042–1045 CrossRef CAS.
- M. J. Donahue and D. G. Porter, OOMMF User's Guide, Version 1.0 Interagency Report NISTIR 6376, 2002 Search PubMed.
- J. Zang, V. Cros and A. Hoffmann, Topology in Magnetism., Springer series in solid state sciences, 192, Springer Nature, Switzerland, 2018 Search PubMed.
- Z. Luo, T. P. Dao, A. Hrabec, J. Vijayakumar, A. Kleibert, M. Baumgartner, E. Kirk, J. Cui, T. Savchenko, G. Krishnaswamy, L. J. Heyderman and P. Gambardella, Chirally coupled nanomagnets, Science, 2019, 363(6434), 1435–1439 CrossRef CAS PubMed.
- M. Charilaou, H. B. Braun and J. F. Loeffler, Monopole-Induced Emergent Electric Fields in Ferromagnetic Nanowires, Phys. Rev. Lett., 2018, 121, 097202 CrossRef PubMed.
- S. Komineas and N. Papanicolaou, Topology and dynamics in ferromagnetic media, Phys. D, 1996, 99, 81–107 CrossRef.
- P. Johnson, A. K. Gangopadhyay, R. Kalyanaraman and R. Nussinov, Demagnetization-borne microscale skyrmions, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 064427 CrossRef.
- J. Pablo-Navarro, C. Magén and J. M. De Teresa, Three-Dimensional, Core-Shell Ferromagnetic Nanowires Grown by Focused Electron Beam Induced Deposition, Nanotechnology, 2016, 27(28), 285302 CrossRef PubMed.
- M. Jaafar, J. Pablo-Navarro, E. Berganza, P. Ares, C. Magén, A. Masseboeuf, C. Gatel, E. Snoeck, J. Gómez-Herrero, J. M. de Teresa and A. Asenjo, Customized MFM probes based on magnetic nanorods, Nanoscale, 2020, 12, 10090–10097 RSC.
- M. Jaafar, L. Serrano-Ramón, O. Iglesias-Freire, A. Fernández-Pacheco, M. R. Ibarra, J. M. de Teresa and A. Asenjo, Hysteresis Loops of Individual Co Nanostripes Measured by Magnetic Force Microscopy, Nanoscale Res. Lett., 2011, 6, 1–6 CrossRef PubMed.
- J. C. Gartside, D. M. Burn, L. F. Cohen and W. R. Branford, A Novel Method for the Injection and Manipulation of Magnetic Charge States in Nanostructures, Sci. Rep., 2016, 6, 32864 CrossRef CAS PubMed.
- Y. L. Wang, Z. L. Xiao, A. Snezhko, J. Xu, L. E. Ocola, R. Divan, J. E. Pearson, G. W. Crabtree and W. K. Kwok, Rewritable Artificial Magnetic Charge Ice, Science, 2016, 352(6288), 962–966 CrossRef CAS PubMed.
- O. Iglesias-Freire, M. Jaafar, E. Berganza and A. Asenjo, Customized MFM probes with high lateral resolution, Beilstein J. Nanotechnol., 2016, 7, 1068–1074 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Morphological and structural characterization (ESI1), study of the electrostatic contribution to the frequency shift (ESI2), MFM data interpretation (ESI3), topological charge (ESI4), imaging at different heights (ESI5), determination of critical fields and tip stray field values (ESI6), influence of geometrical parameters (ESI7). See DOI: 10.1039/d0nr02173c |
| This journal is © The Royal Society of Chemistry 2020 |