Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Difference frequency generation in monolayer MoS2
Yadong
Wang
 ab,
Masood
Ghotbi
ab,
Masood
Ghotbi
 *c,
Susobhan
Das
*c,
Susobhan
Das
 b,
Yunyun
Dai
b,
Yunyun
Dai
 b,
Shisheng
Li
b,
Shisheng
Li
 d,
Xuerong
Hu
d,
Xuerong
Hu
 be,
Xuetao
Gan
be,
Xuetao
Gan
 a,
Jianlin
Zhao
a,
Jianlin
Zhao
 *a and
Zhipei
Sun
*a and
Zhipei
Sun
 *b
*b
aMOE Key Laboratory of Material Physics and Chemistry under Extraordinary Conditions, and Shaanxi Key Laboratory of Optical Information Technology, School of Physical Science and Technology, Northwestern Polytechnical University, Xi'an 710129, China. E-mail: jlzhao@nwpu.edu.cn
bDepartment of Electronics and Nanoengineering, Aalto University, Fi-00076 Aalto, Finland. E-mail: zhipei.sun@aalto.fi
cDepartment of Physics, University of Kurdistan, P.O. Box 66177-15175, Sanandaj, Iran. E-mail: m.ghotbi@uok.ac.ir
dInternational Center for Young Scientists (ICYS), National Institute for Materials Science (NIMS), Tsukuba, Japan
eInstitute of Photonics and Photon Technology, Northwest University, Xi'an 710069, China
First published on 28th May 2020
Abstract
Difference frequency generation has long been employed for numerous applications, such as coherent light generation, sensing and imaging. Here, we demonstrate difference frequency generation down to atomic thickness in monolayer molybdenum disulfide. By mixing femtosecond optical pulses at wavelength of 406 nm with tunable pulses in the spectral range of 1300–1520 nm, we generate tunable pulses across the spectral range of 550–590 nm with frequency conversion efficiency up to ∼2 × 10−4. The second-order nonlinear optical susceptibility of monolayer molybdenum disulfide, χ(2)eff, is calculated as ∼1.8 × 10−8 m V−1, comparable to the previous results demonstrated with second harmonic generation. Such a highly efficient down-conversion nonlinear optical process in two-dimensional layered materials may open new ways to their nonlinear optical applications, such as coherent light generation and amplification.
Introduction
Nonlinear optics, in particular nonlinear frequency conversions, have significantly expanded the applications of the lasers in many fields.1,2 Widely tunable laser systems in different spectral ranges are provided by nonlinear frequency conversion schemes using second- and third-order nonlinear optical processes. Among the second-order nonlinear optical processes, difference frequency generation (DFG), as a building block for a large range of applications, is of great significance. It plays the main role for generating coherent light at longer wavelengths and acts as the base for other second-order nonlinear parametric interactions such as optical parametric generation (OPG), amplification (OPA) and oscillation (OPO),1,2 which enable to produce tunable light sources across different spectral regions for a large variety of applications including material characterizations,3 laser spectroscopy,4 and molecular sensing.5Currently, there are major obstacles in scaling down the nonlinear frequency conversion systems to micro- and nano-scale regimes for various emerging applications, mainly due to the relatively low optical nonlinearity coefficients of the traditional bulk nonlinear optical materials. Introducing the two-dimensional (2D) layered materials with extraordinarily strong nonlinear optical responses for frequency conversions, has created new possibilities for potential on-chip applications.6,7 For example, monolayer transition-metal dichalcogenides (TMDs) have been demonstrated with strong second-, third- and high-order nonlinearities.8–12
Among the second-order frequency conversion nonlinear interactions, second harmonic generation (SHG) and sum frequency generation (SFG) are the common processes that generate light with wavelengths shorter than that of input beams (i.e., up-conversion interactions). Because of its simple implementation, by applying only one input light component as the fundamental beam, SHG has been performed widely in different 2D materials including MoS2,11–16 MoSe2,17,18 WS2,19,20 WSe2,21 and MoTe2.22 Similarly, SFG in TMDs has also been reported in recent years.23–25
In contrast to the SHG and SFG processes, DFG is a frequency down-conversion second-order nonlinear interaction, thus extending the application range of nonlinear processes to various fields. The exploration of such a process in nanoscale is highly important,26 especially in 2D materials. Thus far, DFG in graphene has been observed in terahertz region.27,28 For example, with assistance of graphene plasmon, the photon efficiency of DFG can be as high as 10–5 under specific in-plane phase-matching conditions.28
Here, we report the DFG by using monolayer MoS2 to produce tunable femtosecond pulses in the visible spectral range of 550–590 nm. Such a nonlinear optical interaction can also be a foundation for other down-conversion interactions, including OPG, OPA, as well as OPO.
Sample characterization and experimental setup
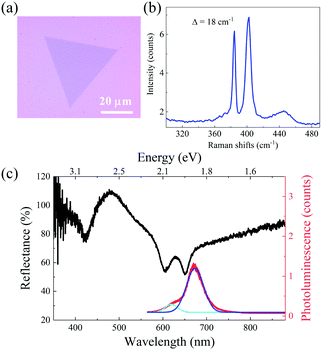
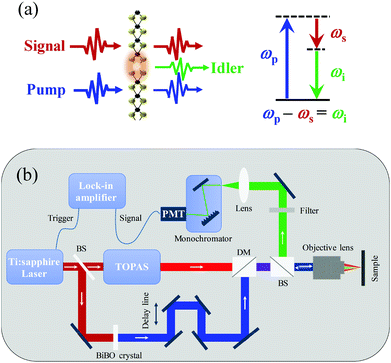
In this work, we employ monolayer MoS2 as a typical representative of TMDs. Monolayer MoS2 was grown on a SiO2/Si substrate (the thickness of SiO2: 285 nm) via vapor–liquid–solid method. First, ∼2 mg mL−1 Na2MoO4 aqueous solution was spin-coated on the substrate at 6000 rpm for 30 seconds. Then, the Na2MoO4 coating was sulfurized in sulphur vapor to obtain monolayer MoS2 at 750 °C for 5 min.29,30 As shown in Fig. 1(a), the MoS2 flake is typically with a triangle shape. The Raman measurement (Fig. 1(b)) shows peaks of an in-plane mode (E2g) located at ∼384 cm−1, and an out-of-plane mode (A1g) at ∼402 cm−1. The difference of these two modes is around ∼18 cm−1, indicating the monolayer structure. Further, the monolayer MoS2 flake is characterized by linear optical reflection and photoluminescence measurements. As shown in Fig. 1(c), the three dips at ∼421 nm, 604 nm, 650 nm, appear in the reflection spectrum (black curve), corresponding to the C, B, A excitons respectively. In the meantime, the photoluminescence spectrum (red curve) is also plotted in Fig. 1(c). Two photoluminescence peaks (∼619 nm and ∼673 nm, corresponding to B, A excitons) are obtained by Lorentz fitting, shown as the light- and dark-blue curves. The peak positions are slightly red-shifted comparing with the dips of reflection spectrum, because of large binding energy in the confined structure.31 The above-mentioned sample characterization experiments indicate that our CVD-grown MoS2 flakes are typically monolayer with relatively high quality.Fig. 2(a) shows an illustration of the DFG process in monolayer MoS2, where a pump photon stimulated by a signal photon, generates two photons at different frequencies (the one with same frequency of signal photon is called signal and the other one is called idler). Therefore, this process typically results in the generation of the idler beam at new wavelengths and the amplification of the incident signal beam. The frequencies of newly generated photons follow the law of energy conservation (i.e., ωidler=ωpump−ωsignal). The right panel in Fig. 2(a) shows the energy level diagram of DFG.
To perform the DFG interaction, we built an experimental setup as shown in Fig. 2(b). The femtosecond (∼150 fs) pulses from an amplified Ti:sapphire laser system at the wavelength of 812 nm with a repetition rate of 2 kHz is employed as the light source. The output beam is first divided into two beams, one is applied for the generation of pump pulses at 406 nm via frequency doubling in a BiBO crystal and the other for generating the tunable near-infrared pulses (1300 to 1550 nm) by pumping a TOPAS system (Light conversion). The pump and signal beams are combined by a dichroic mirror (DM) and then focused by an objective (40×, NA. 0.75) on the target sample. The full width at half maximum of the pump and signal beam spots is ∼2.5 μm. A delay line is employed in order to synchronize pump and signal pulses. The generated idler is then collected with the same objective lens by a reflection configuration and finally focused into a monochromator followed by a photomultiplier tube (PMT). Colour filters are also used in order to get rid of the residual pump and signal pulses before the monochromator. It should be noted that the repetition rate of our applied laser source (2 kHz) is much lower than the ones (∼tens of MHz) typically applied in the previously reported SHG experiments. While such a low repetition rate will not affect the conversion efficiency, it allows advantages including the reduction of the photon-excited luminescence and the thermal effects.
Results and discussion
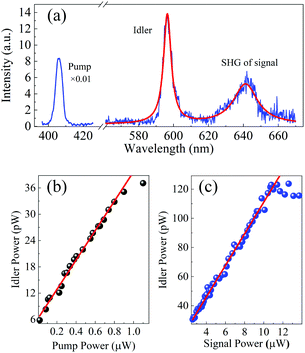
Fig. 3(a) shows the three-wave mixing spectrum corresponding to the pump pulses with the wavelength of 406 nm and the average power of ∼0.9 μW (peak intensity at the focus spot: ∼21.18 GW cm−2) and the input signal pulses with the wavelength of 1280 nm and average power of ∼3.5 μW (peak intensity at the focus spot: ∼82.37 GW cm−2). There are two peaks at wavelengths of ∼595 nm and 640 nm, corresponding to the DFG idler and SHG of the signal, respectively. The third peak at 406 nm is the residual pump light after colour filters. The whole spectrum shows the clear evidence of the DFG interaction in monolayer MoS2. To investigate the DFG at different incident intensities, we measured the power dependence of the output idler as a function of the pump and signal powers. Note that the detected idler power is calibrated with a standard light source. In Fig. 3(b), the power of the generated idler at 595 nm is shown as a function of the pump power, while the signal power is fixed at ∼2.5 μW and the pump power is increased from ∼0.02 to 0.9 μW. The degradation of sample happens when the pump power is higher than ∼0.9 μW. As it is expected from the theoretical formula for the generated DFG idler, the idler power increases linearly, from ∼6 to 35 pW. The idler power dependence on the input signal power was measured by increasing the signal power from ∼2.5 to 14 μW and fixing the pump power at 0.9 μW as shown in Fig. 3(c). In these conditions, the power of DFG idler also increases linearly with the signal power till 11 μW. However, when the signal power is higher than 11 μW, it becomes saturated which could be attributed to the unbalanced photons of the two input beams. In this regime, the photon number ratio (the signal power of 11 μW and the pump power of 0.9 μW) is about 38 signal photons to 1 pump photon. The participating pump photons are much less than the signal photons at these power levels, limiting the interaction efficiency. Note that all results are repeatable during the measurements.In order to estimate the effective second-order nonlinear susceptibility χ(2)effof monolayer MoS2, we simulated the nonlinear optical process in monolayer flake with the coupled-wave equations. Since the thickness of monolayer MoS2 (L=∼0.65 nm) is much smaller than the interacting wavelengths and the DFG is generated within only one layer of molecules, no phase matching consideration is needed. By solving the coupled-wave equations, the χ(2)effin the DFG process can be written as2
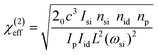 | (1) |
As shown in Fig. 3(c), the generated idler power at 595 nm can be as high as 120 pW, when the signal power is ∼10.5 μW and pump power is ∼0.9 μW. This corresponds to a second-order nonlinear susceptibility χ(2)effof ∼1.8 × 10−8 m V−1, which is comparable to the reported values for MoS2 in earlier works.12,14 It should be mentioned that the imperfect temporal and spatial overlaps between the two interacting input pulses in the DFG interaction will notably reduce the interaction efficiency in comparison to the SHG process. In addition, we assume that the substrate introduced doping,33 strain,18 and interference34 effects are to be small in our experiment. In the current condition, the maximum quantum conversion efficiency from the pump to the idler in our DFG process is calculated as ∼2 × 10−4.
We also investigated the relations among polarization directions of the interacting components in the DFG interaction. The structural symmetry group of bulk MoS2 is D6h with inversion symmetry which leads to zero second-order nonlinearity. While the structural symmetry group of monolayer MoS2 is D3h with broken inversion symmetry and having strong χ(2) supporting highly efficient second-order nonlinear optical responses.13,16 In the x′y′z′ crystalline coordinates, the four nonzero elements of χ(2) tensor for monolayer MoS2 are −χ(2)y′x′x′ = χ(2)y′y′y′ = −χ(2)x′y′x′ = −χ(2)x′x′y′. In the case of SHG process, the scenario for the polarizations of the interacting beams is simple because of the presence of only one input beam and one output beam as the SHG: the SH radiation components detected in directions parallel and perpendicular to the polarization of the fundamental field are highly dependent on the azimuthal angle.13
Regarding that the DFG interaction is a three-wave interaction: with the pump and signal incident pulses as the input beams and idler as the output, the situation is more complicated and the possible combinations of the relative polarization orientations between each interacting beam and the crystalline axes are increased. In order to check the compatibility of the obtained results with the symmetrical constraints imposed by the D3h symmetry of MoS2, we performed the analytical calculations for determining the dependence of the generated DFG polarization on the polarization orientations of the input (pump and signal) beams. Supposing the crystal surface in the xy plane and the -z as the propagation direction of the input pump and signal beams in the lab frame xyz, we consider β as the angle between the x direction and the crystal armchair direction x′, and also αid, αp and αsi as the angles between the idler, pump and signal polarizations, relative to the x direction, respectively. After calculating the components of the generated DFG idler in x′y′z′ (z′ = z) coordinates we will have
| (Eid)x′ ∝ − sin(2β + αsi + αp) | (2a) |
| (Eid)y′ ∝ − cos(2β + αsi + αp) | (2b) |
| (Eid)x ∝ − sin(3β + αsi + αp) | (3a) |
| (Eid)y ∝ − cos(3β + αsi + αp) | (3b) |
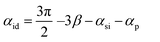 | (4) |
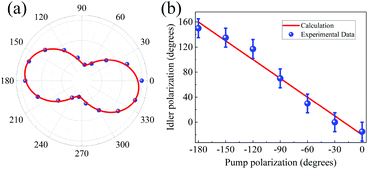
To investigate the generated idler polarization experimentally, we measured the polarization dependence of the generated DFG pulses on the polarization orientations of two input beams. Both the idler and pump polarization orientations were measured relative to the fixed signal polarization which is supposed to be along the x direction (αsi=0). The angular dependence of the idler power for each pump polarization direction was measured by using a linear polarizer before the detector. The results of such measurement at the pump polarization angle of αp = 0° are shown in Fig. 4(a) which also confirms the linear polarization of the generated idler pulse. As shown in Fig. 4(b), the linear polarization angles of the idler for different pump polarization orientations are measured. The polarization angles of the idler light (blue dots) show a good agreement with the calculation (eqn (4), red curve). The results confirm the linear dependence of the polarization orientation of the idler beam on the angle between the polarization of each input beam and the crystalline axis x′ as demonstrated in eqn (4).
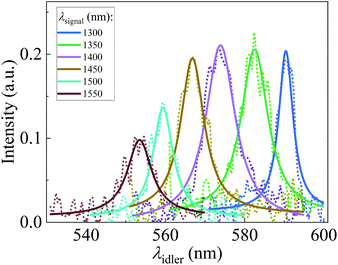
The corresponding behaviour of the MoS2 monolayers for the DFG at different wavelengths across our available spectral range is also investigated. With the advantage of independence from the limiting phase-matching conditions, in monolayer MoS2 the nonlinear interactions can be performed across a broad spectral bandwidth. The wavelength of the DFG idler was tuned from 550 to 590 nm by changing the wavelength of signal from 1520 to 1300 nm with the pump wavelength fixed at 406 nm. The experimental data of the generated idler spectra and the Lorentz fitting curves at each wavelength are shown in Fig. 5. The higher generated idler intensities in the spectral region of 570–590 nm could be attributed to the presence of the resonant excitonic effects in this region.35,36
Performing the DFG process is a confirmation for the possibility of realizing effective optical parametric interactions. In our experiment, the quantum conversion efficiency is about 2 × 10−4, which is much higher than that of the most nonlinear responses in monolayer structures. However, because of the practical difficulties, the demonstration of a more efficient OPA process is still far from the reach. In order to improve the conversion efficiency, the exciton enhancement in single-layer TMDs could be employed as an effective solution in the future explorations.21 While the atomic thickness of monolayer TMDs (∼0.65 nm for MoS2) physically limits the light–matter interaction length, 3R-type bulk MoS2 with broken inversion symmetry enables strong second-order nonlinear processes, offering a possible method for efficiency improvement.16,37 On the other hand, integrating monolayer TMDs and other 2D materials with external cavities (such as photonic-crystal nanocavity, micro-ring resonator, whispering-gallery cavity and metallic plasmonics), or waveguides (including microfibers, on-chip waveguides) is also promising for further improvements,6,38 due to the easy and flexible integration advantages of 2D materials. Furthermore, with assistance of the cavities, OPO operation with 2D materials could be achieved.39
Conclusions
We have reported the experimental demonstration of the DFG nonlinear interaction with a second-order nonlinear susceptibility of ∼1.8 × 10−8 m V−1 in monolayer MoS2. The generated idler pulses are tunable across the optical spectral range of 550–590 nm by tuning the input signal beam wavelength. The results of this work will pave the way for performing the optical parametric interactions in 2D materials and introducing new tunable light sources in nanoscale.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from Aalto Centre for Quantum Engineering, China Scholarship Council (Grant No.: 201606290190), Academy of Finland (Grant No.: 276376, 284548, 295777, 304666, 312297, 312551, and 314810), Academy of Finland Flagship Program (Grant No.: 320167, PREIN), Business Finland (OPEC, A-Photonics), ERC (ATOP), the European Union's Horizon 2020 research and innovation program (Grant No.: 820423, S2QUIP) and the National Natural Science Foundation of China (Grant No.: 11634010, 61775183).Notes and references
- Y. R. Shen, The principles of nonlinear optics, J. Wiley & Sons, New York, 1984 Search PubMed.
- R. W. Boyd, Nonlinear Optics, Academic press, 2007 Search PubMed.
- K. G. Lubic and T. Amano, J. Chem. Phys., 1984, 81, 1655–1660 CrossRef CAS.
- D. Richter, A. Fried and P. Weibring, Laser Photonics Rev., 2009, 3, 343–354 CrossRef CAS.
- F. Che, S. A. Ponomarenko, M. Cada and N. Nguyen-Huu, IEEE Photonics J., 2017, 9, 4800511 Search PubMed.
- A. Autere, H. Jussila, Y. Dai, Y. Wang, H. Lipsanen and Z. Sun, Adv. Mater., 2018, 30, 1705963 CrossRef PubMed.
- Z. Sun, A. Martinez and F. Wang, Nat. Photonics, 2016, 10, 227–238 CrossRef CAS.
- A. Saynatjoki, L. Karvonen, H. Rostami, A. Autere, S. Mehravar, A. Lombardo, R. A. Norwood, T. Hasan, N. Peyghambarian, H. Lipsanen, K. Kieu, A. C. Ferrari, M. Polini and Z. Sun, Nat. Commun., 2017, 8, 893 CrossRef PubMed.
- A. Autere, H. Jussila, A. Marini, J. R. M. Saavedra, Y. Dai, A. Säynätjoki, L. Karvonen, H. Yang, B. Amirsolaimani, R. A. Norwood, N. Peyghambarian, H. Lipsanen, K. Kieu, F. J. G. de Abajo and Z. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 115426 CrossRef CAS.
- H. Liu, Y. Li, Y. S. You, S. Ghimire, T. F. Heinz and D. A. Reis, Nat. Phys., 2016, 13, 262–265 Search PubMed.
- D. J. Clark, V. Senthilkumar, C. T. Le, D. L. Weerawarne, B. Shim, J. I. Jang, J. H. Shim, J. Cho, Y. Sim, M. J. Seong, S. H. Rhim, A. J. Freeman, K. H. Chung and Y. S. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 121409 CrossRef.
- L. M. Malard, T. V. Alencar, A. P. M. Barboza, K. F. Mak and A. M. de Paula, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 201401 CrossRef.
- Y. Li, Y. Rao, K. F. Mak, Y. You, S. Wang, C. R. Dean and T. F. Heinz, Nano Lett., 2013, 13, 3329 CrossRef CAS PubMed.
- N. Kumar, S. Najmaei, Q. Cui, F. Ceballos, P. M. Ajayan, J. Lou and H. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 161403 CrossRef.
- X. Yin, Z. Ye, D. A. Chenet, Y. Ye, K. O'Brien, J. C. Hone and X. Zhang, Science, 2014, 344, 488 CrossRef CAS PubMed.
- M. Zhao, Z. Ye, R. Suzuki, Y. Ye, H. Zhu, J. Xiao, Y. Wang, Y. Iwasa and X. Zhang, Light: Sci. Appl., 2016, 5, 16131 CrossRef PubMed.
- G. Wang, I. C. Gerber, L. Bouet, D. Lagarde, A. Balocchi, M. Vidal, T. Amand, X. Marie and B. Urbaszek, 2D Mater., 2015, 2, 045005 CrossRef.
- J. Liang, J. Zhang, Z. Li, H. Hong, J. Wang, Z. Zhang, X. Zhou, R. Qiao, J. Xu, P. Gao, Z. Liu, Z. Liu, Z. Sun, S. Meng, K. Liu and D. Yu, Nano Lett., 2017, 17, 7539–7543 CrossRef CAS PubMed.
- X. Fan, Y. Jiang, X. Zhuang, H. Liu, T. Xu, W. Zheng, P. Fan, H. Li, X. Wu, X. Zhu, Q. Zhang, H. Zhou, W. Hu, X. Wang, L. Sun, X. Duan and A. Pan, ACS Nano, 2017, 11, 4892–4898 CrossRef CAS PubMed.
- X. Lin, Y. Liu, K. Wang, C. Wei, W. Zhang, Y. Yan, Y. J. Li, J. Yao and Y. S. Zhao, ACS Nano, 2018, 12, 689–696 CrossRef CAS PubMed.
- G. Wang, X. Marie, I. Gerber, T. Amand, D. Lagarde, L. Bouet, M. Vidal, A. Balocchi and B. Urbaszek, Phys. Rev. Lett., 2015, 114, 097403 CrossRef CAS PubMed.
- Y. Song, R. Tian, J. Yang, R. Yin, J. Zhao and X. Gan, Adv. Opt. Mater., 2018, 6, 1701334 CrossRef.
- D. Li, W. Xiong, L. Jiang, Z. Xiao, H. R. Golgir, M. Wang, X. Huang, Y. Zhou, Z. Lin, J. Song, S. Ducharme, L. Jiang, J. F. Silvain and Y. Lu, ACS Nano, 2016, 10, 3766–3775 CrossRef CAS.
- L. Fang, Q. Yuan, H. Fang, X. Gan, J. Li, T. Wang, Q. Zhao, W. Jie and J. Zhao, Adv. Opt. Mater., 2018, 6, 1800698 CrossRef.
- K. Yao, E. Yanev, H. J. Chuang, M. R. Rosenberger, X. Xu, T. Darlington, K. M. McCreary, A. T. Hanbicki, K. Watanabe, T. Taniguchi, B. T. Jonker, X. Zhu, D. N. Basov, J. C. Hone and P. J. Schuck, ACS Nano, 2020, 14, 708–714 CrossRef CAS PubMed.
- Y. Zhang, A. Manjavacas, N. J. Hogan, L. Zhou, C. Ayala-Orozco, L. Dong, J. K. Day, P. Nordlander and N. J. Halas, Nano Lett., 2016, 16, 3373–3378 CrossRef CAS PubMed.
- B. Yao, Y. Liu, S.-W. Huang, C. Choi, Z. Xie, J. F. Flores, Y. Wu, M. Yu, D.-L. Kwong, Y. Huang, Y. Rao, X. Duan and C. W. Wong, Nat. Photonics, 2017, 12, 22–28 CrossRef.
- T. J. Constant, S. M. Hornett, D. E. Chang and E. Hendry, Nat. Phys., 2015, 12, 124–127 Search PubMed.
- S. S. Li, Y. C. Lin, W. Zhao, J. Wu, Z. Wang, Z. H. Hu, Y. D. Shen, D. M. Tang, J. Y. Wang, Q. Zhang, H. Zhu, L. Q. Chu, W. J. Zhao, C. Liu, Z. P. Sun, T. Taniguchi, M. Osada, W. Chen, Q. H. Xu, A. T. S. Wee, K. Suenaga, F. Ding and G. Eda, Nat. Mater., 2018, 17, 535–542 CrossRef CAS PubMed.
- S. S. Li, Y. C. Lin, X. Y. Liu, Z. H. Hu, J. Wu, H. Nakajima, S. Liu, T. Okazaki, W. Chen, T. Minari, Y. Sakuma, K. Tsukagoshi, K. Suenaga, T. Taniguchi and M. Osada, Nanoscale, 2019, 11, 16122–16129 RSC.
- A. Chernikov, T. C. Berkelbach, H. M. Hill, A. Rigosi, Y. Li, O. B. Aslan, D. R. Reichman, M. S. Hybertsen and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 076802 CrossRef PubMed.
- W. Li, A. G. Birdwell, M. Amani, R. A. Burke, X. Ling, Y.-H. Lee, X. Liang, L. Peng, C. A. Richter, J. Kong, D. J. Gundlach and N. V. Nguyen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195434 CrossRef.
- A. Raja, A. Chaves, J. Yu, G. Arefe, H. M. Hill, A. F. Rigosi, T. C. Berkelbach, P. Nagler, C. Schuller, T. Korn, C. Nuckolls, J. Hone, L. E. Brus, T. F. Heinz, D. R. Reichman and A. Chernikov, Nat. Commun., 2017, 8, 15251 CrossRef PubMed.
- Y. Tang, K. C. Mandal, J. A. McGuire and C. W. Lai, Phys. Rev. B, 2016, 94 Search PubMed.
- G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001 CrossRef CAS.
- J. Xiao, M. Zhao, Y. Wang and X. Zhang, Nanophotonics, 2017, 0, 1309–1328 CAS.
- J. Shi, P. Yu, F. Liu, P. He, R. Wang, L. Qin, J. Zhou, X. Li, J. Zhou, X. Sui, S. Zhang, Y. Zhang, Q. Zhang, T. C. Sum, X. Qiu, Z. Liu and X. Liu, Adv. Mater., 2017, 29, 1701486 CrossRef PubMed.
- Z. Sun, Nat. Photonics, 2018, 12, 378–385 CrossRef.
- A. Ciattoni, A. Marini, C. Rizza and C. Conti, Light: Sci. Appl., 2018, 7, 5 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2020 |