Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Near-field mechanism of the enhanced broadband magneto-optical activity of hybrid Au loaded Bi:YIG†
Spiridon D.
Pappas
 *a,
Philipp
Lang
a,
Tobias
Eul
a,
Michael
Hartelt
a,
Antonio
García-Martín
*a,
Philipp
Lang
a,
Tobias
Eul
a,
Michael
Hartelt
a,
Antonio
García-Martín
 b,
Burkard
Hillebrands
a,
Martin
Aeschlimann
b,
Burkard
Hillebrands
a,
Martin
Aeschlimann
 a and
Evangelos Th.
Papaioannou
a and
Evangelos Th.
Papaioannou
 *ac
*ac
aDepartment of Physics and Research Center OPTIMAS, University of Kaiserslautern, 67663 Kaiserslautern, Germany. E-mail: pappas@rhrk.uni-kl.de
bInstituto de Micro y Nanotecnología IMN-CNM, CSIC, CEI UAM+CSIC, Isaac Newton 8, E-28760 Tres Cantos, Madrid, Spain
cInstitute of Physics, Martin-Luther University Halle-Wittenberg, Von-Danckelmann-Platz 3, 06120 Halle, Germany. E-mail: evangelos.papaioannou@physik.uni-halle.de
First published on 18th March 2020
Abstract
We unravel the underlying near-field mechanism of the enhancement of the magneto-optical activity of bismuth-substituted yttrium iron garnet films (Bi:YIG) loaded with gold nanoparticles. The experimental results show that the embedded gold nanoparticles lead to a broadband enhancement of the magneto-optical activity with respect to the activity of the bare Bi:YIG films. Full vectorial near- and far-field simulations demonstrate that this broadband enhancement is the result of a magneto-optically enabled cross-talking of orthogonal localized plasmon resonances. Our results pave the way to the on-demand design of the magneto-optical properties of hybrid magneto-plasmonic circuitry.
Introduction
The field of magneto-plasmonics has attracted a lot of scientific interest, both for its importance in potential technological applications, and for its fundamental scientific relevance.1–4 Towards these directions, various ideas like using external magnetic fields to control the dispersion relation of plasmonic resonances (active magneto-plasmonics),5 or using plasmonic resonances for spin current generation in adjacent magnetic insulators,6,7 and the implementation of a magneto-plasmonic interferometer,8 have been realized and explored.Magneto-optical studies on magneto-plasmonic nanostructures, composed of magnetic and/or plasmonic materials, have revealed new exciting effects: nanopatterned hybrid heterostructures,9–16 pure ferromagnetic films,17–24 and noble metal/magnetic dielectric systems25,26 exhibit plasmon-induced enhancement of their magneto-optical activity. Recently, the correlation of near- and far-field effects of a patterned magneto-plasmonic array has been shown with the aid of Photoemission Electron Microscopy (PEEM),27 paving the way for tailoring the magneto-optical response of these systems: the spatial distribution of the polarization- and energy-dependent electric near-field of the propagating plasmon polaritons has been connected to the enhancement of the magneto-optical Kerr effect. As a further matter, the nature of the plasmonic resonances (localized or propagating surface plasmons28,29) can alter differently the response of the magneto-optically active material in a magneto-plasmonic structure. From the wider family of the hybrid magneto-plasmonic structures,14–16,25,30,31 the system composed of ferrimagnetic dielectric layers of bismuth-substituted yttrium iron garnet (Bi:YIG) with embedded Au nanoparticles (AuNPs) that support localized plasmon resonances (LPRs), has attracted little attention for its importance.26,32,33 The underlying near-field mechanism is not clarified yet, while there is lack of studies on the plasmon-induced magneto-optical response in the Longitudinal Magneto-optical Kerr Effect (L-MOKE) configuration.
In this paper, we explore the microscopic origin of the magneto-plasmonic coupling in bismuth-substituted yttrium iron garnet films (Bi:YIG), loaded with self-assembled Au nanoparticles (AuNPs). We can unambiguously prove that the features in the enhanced magneto-optical activity are the result of two coupled orthogonal LPRs. The coupling is mediated by the magneto-optical activity of the underlying Bi:YIG matrix, for both polarization states of incident light.
Results and discussion
Hybrid Au loaded Bi:YIG films
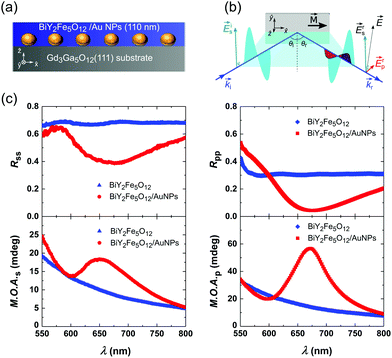
In Fig. 1(a), the structure of the investigated hybrid sample (Bi:YIG/AuNPs) is presented. Scanning electron microscopy (SEM) images of the sample (see ref. 6) reveal that the AuNPs are randomly distributed close to the interface between Bi:YIG and gadolinium gallium garnet (GGG), and that they are embedded in the Bi:YIG film. Furthermore, they have the shape of oblate spheroids, with an in-plane diameter ranging from 30 to 90 nm and a height ranging from 20 to 50 nm. The optical properties of this sort of system are mainly determined by localized plasmon resonances (LPRs), rather than by geometrical-lattice resonances. A second sample, having exactly the same structure, but containing no AuNPs (BiY2Fe5O12), was used as a reference. The reader is referred to the ESI† for further details on the fabrication of the samples.The L-MOKE configuration
The magneto-optical response of the samples was experimentally probed in the L-MOKE configuration, which is schematically depicted in Fig. 1(b). In the L-MOKE geometry, the magnetization (M) of the sample lies in the sample plane, as well as in the plane of incidence of the incident light. The incident light can either be s- or p-polarized. In Fig. 1(b) only the case of a measurement performed with s-polarized light is presented for simplicity. Superscripts r and i denote the reflected and incident light, respectively. The reflected light contains a p-polarized component which causes a change in the polarization state. The polarization state of the reflected light is then given by: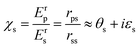 | (1) |
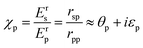 | (2) |
Measured magneto-optical response
In Fig. 1(c) (top graphs), we present the measured reflectance spectra for both incident s- (Rss plot) and p-polarized (Rpp plot) light. It is apparent, that the reflectance of the sample containing no AuNPs, retains a constant value in the spectral region of 550–800 nm. In the case of the sample containing AuNPs, a broad drop in the Rss and Rpp spectra is located in the spectral region 550–900 nm, reaching a minimum at ∼675 nm. The reflectance reduction in this spectral region, where the electronic transitions of Bi:YIG34,35 have no relevant influence, is solely attributed to localized plasmon resonances (LPRs) in the AuNPs, for sizes smaller than ∼100 nm.Our interest is particularly focused on the influence of the LPRs on the magneto-optical response in the L-MOKE configuration. The L-MOKE configuration is easy to be implemented, and therefore quite attractive for technological applications, as well. In order to obtain a direct insight into the effect, we extracted the modulus of the complex Kerr angle χs(p), which is also called the magneto-optical activity 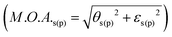 , for applied external magnetic fields sufficiently large to saturate the sample along the film in-plane direction. The spectral dependence of M.O.A. for s- and p-incident polarized light is shown in the bottom graphs of Fig. 1(c) for both samples. The increased M.O.A. of Bi:YIG in the low-wavelength spectral region is attributed to the wings of the magneto-optical transitions located at photon energies of 2.8 and 3.3 eV (442 and 378 nm respectively).35 It becomes apparent that the magneto-optical response of the Bi:YIG layer, for the sample containing AuNPs, is strongly modified in the broad optical region where the resonant localized surface plasmon phenomena occur. Furthermore, by observation it can be deduced that the enhancement of the M.O.A. is larger in the case of incident p-polarized light. The experimental results clearly show a significant broadband enhancement of the magneto-optical response of Bi:YIG in a spectral regime far from the inherent Bi:YIG magneto-optical transitions, which originates from LPRs in the hybrid sample.
, for applied external magnetic fields sufficiently large to saturate the sample along the film in-plane direction. The spectral dependence of M.O.A. for s- and p-incident polarized light is shown in the bottom graphs of Fig. 1(c) for both samples. The increased M.O.A. of Bi:YIG in the low-wavelength spectral region is attributed to the wings of the magneto-optical transitions located at photon energies of 2.8 and 3.3 eV (442 and 378 nm respectively).35 It becomes apparent that the magneto-optical response of the Bi:YIG layer, for the sample containing AuNPs, is strongly modified in the broad optical region where the resonant localized surface plasmon phenomena occur. Furthermore, by observation it can be deduced that the enhancement of the M.O.A. is larger in the case of incident p-polarized light. The experimental results clearly show a significant broadband enhancement of the magneto-optical response of Bi:YIG in a spectral regime far from the inherent Bi:YIG magneto-optical transitions, which originates from LPRs in the hybrid sample.
Near-field simulations & analysis
In order to gain insight into the deeper mechanism of the enhanced magneto-optical activity of the hybrid BiY2Fe5O12/AuNPs structure, we performed numerical simulations with the aid of Computer Simulation Technology (CST) software package and analyzed both the electric near-field features, as well as the far-field magneto-optical behaviour (see ESI† for further details on the Method). To perform these simulations, the dielectric tensor of BiY2Fe5O12 was used. For the L-MOKE geometry and the vector directions as they are defined in Fig. 1(b), the dielectric tensor of Bi:YIG has the following form: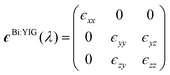 | (3) |
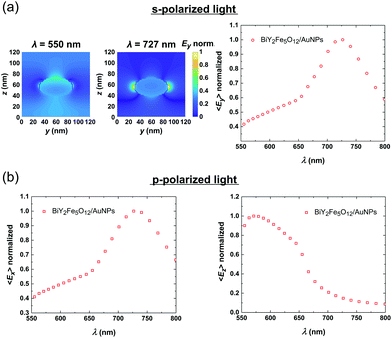
In Fig. 2(a) (left side) the maps of the spatial y component (Ey) of the local electric field E is presented at two characteristic spectral positions: λ = 550 nm, and 727 nm. In this case the incident electric field is s-polarized. The maps reveal the spectral position of the electric near-field enhancement which emanate from the localized plasmon resonances in AuNPs. As it can be observed, at λ = 727 nm a big volume of the hosting Bi:YIG is exposed to the enhanced near-field around the AuNP. In order to quantify these near-field results in a more comprehensive way, and reveal the exact spectral positions of the plasmonic resonances, we calculate the induced dipole moment in the AuNP. In the small particle limit, the dipole moment induced in the AuNP, which is embedded in the dielectric Bi:YIG, is given by the following formula:40,41
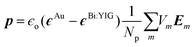 | (4) |
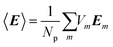 is the average electric field in the AuNP. The calculated y component of the averaged field (〈Ey〉) as a function of the wavelength of the incident light, in the case of s-incident light, is shown in the right hand side plot of Fig. 2(a). The results show a clear intensification of the average field along the y direction, with the peak of 〈Ey〉 located at 727 nm. All of the values have been normalized to the maximum value of the curve. In the case of p-polarized light, the vector of the oscillating incident electric field can be analyzed along the x and the vertical z direction. Therefore, in Fig. 2(b), we choose to show both 〈Ex〉 and 〈Ez〉. The plots reveal the existence of a clear intensification along the x direction (where 〈Ex〉 is considered), as well as a clear but more feature-complicated intensification spectrum along the z direction (where 〈Ez〉 is considered). By comparison, we can deduce that the 〈Ey〉 plot in the case of s-polarized incident light, and the 〈Ex〉 plot in the case of p-polarized incident light, have identical shapes. This can be clearly explained from the symmetry of the geometrical shape of the simulated nanoparticle on the xy plane. From the 〈Ez〉 plot in Fig. 2(b), we can observe a field intensification close to the lower limit of the simulated spectral region. A clear peak is shown at λ = 575 nm, with an extra feature at about λ = 625 nm. In the case of p-polarized incident light, 〈Ez〉 becomes enhanced at a much smaller wavelength value than the component 〈Ex〉 does. This, can be understood by the fact that the dimension of the nanoparticle along the z direction is smaller than that along the x or y direction. Therefore, the resonant mode along z is shifted at lower wavelength values, as it is compared to the resonances along the x or y direction. Furthermore, the fact that the 〈Ez〉 curve has a more complex shape, in comparison to the 〈Ex〉 curve, could be explained by the geometric complexityof the oblate spheroid shape.
is the average electric field in the AuNP. The calculated y component of the averaged field (〈Ey〉) as a function of the wavelength of the incident light, in the case of s-incident light, is shown in the right hand side plot of Fig. 2(a). The results show a clear intensification of the average field along the y direction, with the peak of 〈Ey〉 located at 727 nm. All of the values have been normalized to the maximum value of the curve. In the case of p-polarized light, the vector of the oscillating incident electric field can be analyzed along the x and the vertical z direction. Therefore, in Fig. 2(b), we choose to show both 〈Ex〉 and 〈Ez〉. The plots reveal the existence of a clear intensification along the x direction (where 〈Ex〉 is considered), as well as a clear but more feature-complicated intensification spectrum along the z direction (where 〈Ez〉 is considered). By comparison, we can deduce that the 〈Ey〉 plot in the case of s-polarized incident light, and the 〈Ex〉 plot in the case of p-polarized incident light, have identical shapes. This can be clearly explained from the symmetry of the geometrical shape of the simulated nanoparticle on the xy plane. From the 〈Ez〉 plot in Fig. 2(b), we can observe a field intensification close to the lower limit of the simulated spectral region. A clear peak is shown at λ = 575 nm, with an extra feature at about λ = 625 nm. In the case of p-polarized incident light, 〈Ez〉 becomes enhanced at a much smaller wavelength value than the component 〈Ex〉 does. This, can be understood by the fact that the dimension of the nanoparticle along the z direction is smaller than that along the x or y direction. Therefore, the resonant mode along z is shifted at lower wavelength values, as it is compared to the resonances along the x or y direction. Furthermore, the fact that the 〈Ez〉 curve has a more complex shape, in comparison to the 〈Ex〉 curve, could be explained by the geometric complexityof the oblate spheroid shape.
Far-field simulations & analysis
Subsequently, we want to compare the near-field simulations with the obtained far-field data. Therefore, we initially calculated the reflectivity for incident s- and p-polarized light, Rss and Rpp respectively. Additionally, the polarization conversion efficiencies Rps and Rsp have been calculated in the L-MOKE geometry. These values are defined as follows: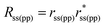 and
and 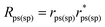 . The Fresnel coefficients rss, rpp, rps and rsp have been calculated with the aid of CST by calculating the scattering matrix elements in the defined waveguide port above the simulated structure. The simulating method is based on the calculation of the power of the electromagnetic waves impinging on the defined waveguide port (see ESI† for further details), and provides very useful qualitative information about the reflectivity and the polarization conversion efficiency.
. The Fresnel coefficients rss, rpp, rps and rsp have been calculated with the aid of CST by calculating the scattering matrix elements in the defined waveguide port above the simulated structure. The simulating method is based on the calculation of the power of the electromagnetic waves impinging on the defined waveguide port (see ESI† for further details), and provides very useful qualitative information about the reflectivity and the polarization conversion efficiency.
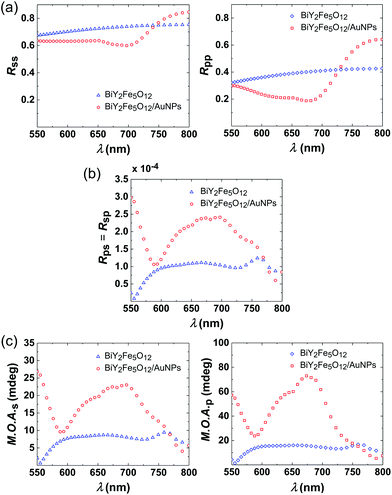
The simulated Rss and Rpp for the corresponding oblique angle of incidence of θi = 55 deg, are presented in Fig. 3(a). For incident s-polarized light (Rss), in the case of the film containing AuNPs, the characteristic minimum in the reflectivity associated with plasmon excitation is observed at ∼700 nm. Plasmon excitation is further verified by the spectral position of the maximum of the near-field 〈Ey〉 (Fig. 2(a)), which is also very close to the minimum of the measured reflectance spectrum at ∼675 nm. Furthermore, the simulated Rss plot reproduces the corresponding experimental one, also very well. In the case of incident p-polarized light (Rpp), the modification due to the LPRs is stronger than in the case of incident s-polarized, as observed in the experimental Rpp curve in Fig. 1(c). It is worthwhile to notice that the influence of the two resonances associated to 〈Ex〉 and 〈Ez〉 appearing at two distinct spectral positions (see in Fig. 2(b)), becomes visible in the Rpp curve. This distinction is not clear in the experimental curves, we surmise, due to the dispersion of the aspect ratios of the AuNPs and other typical imperfections in the actual samples. To account for this distribution of the sizes and the aspect ratios, a large number of simulations over different configurations would be required, leading to an unaffordable time-scale for each numerical spectrum.
In Fig. 3(b), we show the simulated polarization conversion efficiencies Rps or Rsp for each sample. The polarization conversion efficiency expresses quantitatively the part of the intensity of the incident light which is converted from one polarization state to the other, upon reflection from the sample. These appear always to be identical in every case, namely Rps = Rsp. The latter is dictated by the symmetry imposed by the material itself (ϵyz = −ϵzy). The simulations show that Rps(sp) clearly exhibits a broadband enhancement in the spectral region of 600–800 nm where the plasmonic resonances are located, and it is independent of the incident light polarization. This proves that even in the case of incident s-polarized light, there is a resonance along the z direction. This resonance is the result of polarization coupling, and it is mediated through the magneto-optical properties of Bi:YIG, giving rise to the broadband enhancement of the polarization conversion.40,41 Indeed, if we express the complex oscillating electric dipole in the AuNP as p = αAuEi, where Ei stands for the electric field of the incident light, then it can be shown that in linear response of ϵyz:
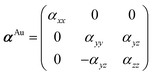 | (5) |
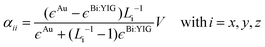 | (6) |
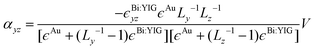 | (7) |
Conclusions
In summary, we have experimentally demonstrated a broad-band enhancement of the magneto-optical activity of hybrid Bi:YIG/AuNPs systems induced by localized plasmon resonances, by analyzing the longitudinal magneto-optical Kerr configuration. In order to unravel the role played by the localized plasmon resonances on the magneto-optical behaviour of the host Bi:YIG, we performed near-field simulations, and correlated the obtained results with the numerical far-field spectra. We have unambiguously shown that the features in the enhanced magneto-optical activity are the result of two orthogonal localized plasmon resonances that are coupled by the magneto-optical activity of the underlying Bi:YIG matrix, and are presented for both polarization states of the incident light. Our results pave the way to the design on-demand of the magneto-optical response of hybrid magneto-plasmonic circuitry, by controlling the localized resonances through the size and the aspect ratio of the nanoparticles.Experimental
The Kerr rotation (θ) spectra measured with the aid of a spectroscopic Kerr effect setup operating in the longitudinal geometry (L-MOKE). A Wollaston prism, combined with a balanced photodiode setup mounted on a motorized rotational stage, was used to detect the rotation of the polarization axis. The Kerr ellipticity (ϵ) has been recorded as a function of wavelength, by incorporating into the detection path a superachromatic quarter-wave prism from Thorlabs. The setup is fully automated and, with proper calibration, can provide Kerr rotation and ellipticity in absolute values. The probing light in the range of 550–800 nm was produced by a supercontinuum laser light source (SuperK Extreme) and was properly monochromatized by an acousto-optical tunable filter. The reader is referred to the ESI† for an indicative example of Kerr rotation and ellipticity measurements.The specular reflectance spectra were recorded with the aid of the same setup, by replacing the balanced photodiode module with an integrating sphere photodiode power sensor. The power sensor was read by a PM400 power and energy meter from Thorlabs. An aluminium mirror was used as a reference for all of the recorded reflectance spectra.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – TRR 173 – 268565370. E. Th. P. and S. D. P. acknowledge the Carl Zeiss Foundation. Ken-ichi Uchida (NIMS, Japan) is acknowledged for providing the Bi:YIG/AuNPs samples. Dipl.-Phys. Marc Vogel – AG von Freymann – TU Kaiserslautern is acknowledged for the introduction to CST software and his help with the installation of the package.References
- G. Armelles, A. Cebollada, A. García-Martín and M. U. Gonzalez, Adv. Opt. Mater., 2013, 1, 10–35 CrossRef.
- D. O. Ignatyeva, G. A. Knyazev, P. O. Kapralov, G. Dietler, S. K. Sekatskii and V. I. Belotelov, Sci. Rep., 2016, 6, 28077 CrossRef CAS.
- N. Maccaferri, E. K. Gregorczyk, T. V. A. G. de Oliveira, M. Kataja, S. van Dijken, Z. Pirzadeh, A. Dmitriev, J. Åkerman, M. Knez and P. Vavassori, Nat. Commun., 2015, 6, 6150 CrossRef CAS PubMed.
- B. Caballero, A. García-Martín and J. C. Cuevas, ACS Photonics, 2016, 3, 203 CrossRef CAS.
- V. V. Temnov, G. Armelles, U. Woggon, D. Guzatov, A. Cebollada, A. García-Martín, J.-M. Garcia-Martin, T. Thomay, A. Leitenstorfer and R. Bratschitsch, Nat. Photonics, 2010, 4, 107 CrossRef CAS.
- K. Uchida, H. Adachi, D. Kikuchi, S. Ito, Z. Qiu, S. Maekawa and E. Saitoh, Nat. Commun., 2015, 6, 5910 CrossRef CAS PubMed.
- S. Ishii, K.-i. Uchida, T. D. Dao, Y. Wada, E. Saitoh and T. Nagao, APL Photonics, 2017, 2, 106103 CrossRef.
- C. J. Firby and A. Y. Elezzabi, Appl. Phys. Lett., 2016, 109, 011101 CrossRef.
- B. Sepúlveda, J. B. González-Díaz, A. García-Martín, L. M. Lechuga and G. Armelles, Phys. Rev. Lett., 2010, 104, 147401 CrossRef PubMed.
- J. F. Torrado, E. T. Papaioannou, G. Ctistis, P. Patoka, M. Giersig, G. Armelles and A. García-Martín, Phys. Status Solidi RRL, 2010, 4, 271 CrossRef CAS.
- N. Maccaferri, X. Inchausti, A. García-Martín, J. C. Cuevas, D. Tripathy, A. O. Adeyeye and P. Vavassori, ACS Photonics, 2015, 2, 1769 CrossRef CAS.
- E. T. Papaioannou, T. Meyer and B. Hillebrands, J. Surf. Interfaces Mater., 2014, 2, 40–45 CrossRef.
- I. Razdolski, D. G. Gheorghe, E. Melander, B. Hjörvarsson, P. Patoka, A. V. Kimel, A. Kirilyuk, E. T. Papaioannou and T. Rasing, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 075436 CrossRef.
- G. Armelles, A. Cebollada, F. García, A. García-Martín and N. de Sousa, ACS Photonics, 2016, 3, 2427 CrossRef CAS.
- B. Caballero, A. García-Martín and J. C. Cuevas, Opt. Express, 2015, 23, 22238 CrossRef CAS PubMed.
- D. Martin-Becerra, J. B. Gonzalez-Diaz, V. V. Temnov, A. Cebollada, G. Armelles, T. Thomay, A. Leitenstorfer, R. Bratschitsch, A. García-Martín and M. U. Gonzalez, Appl. Phys. Lett., 2010, 97, 183114 CrossRef.
- H. Fang, B. Caballero, E. M. Akinoglu, E. T. Papaioannou, A. García-Martín, J. C. Cuevas, M. Giersig and P. Fumagalli, Appl. Phys. Lett., 2015, 106, 153104 CrossRef.
- M. Kataja, T. K. Hakala, A. Julku, M. J. Huttunen, S. van Dijken and P. Torma, Nat. Commun., 2015, 6, 7072 CrossRef CAS PubMed.
- E. Melander, E. Östman, J. Keller, J. Schmidt, E. T. Papaioannou, V. Kapaklis, U. B. Arnalds, B. Caballero, A. García-Martín, J. C. Cuevas and B. Hjörvarsson, Appl. Phys. Lett., 2012, 101, 063107 CrossRef.
- L. Chen, J. Gao, W. Xia, S. Zhang, S. Tang, W. Zhang, D. Li, X. Wu and Y. Du, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 214411 CrossRef.
- V. Bonanni, S. Bonetti, T. Pakizeh, Z. Pirzadeh, J. Chen, J. Nogués, P. Vavassori, R. Hillenbrand, J. Åkerman and A. Dmitriev, Nano Lett., 2011, 11, 5333 CrossRef CAS.
- E. T. Papaioannou, V. Kapaklis, E. Melander, B. Hjörvarsson, S. D. Pappas, P. Patoka, M. Giersig, P. Fumagalli, A. García-Martín and G. Ctistis, Opt. Express, 2011, 19, 23867 CrossRef CAS PubMed.
- H. M. Luong, B. Ai, Y. Zhao and T. D. Nguyen, J. Magn. Magn. Mater., 2018, 468, 79 CrossRef CAS.
- N. Maccaferri, A. Berger, S. Bonetti, V. Bonanni, M. Kataja, Q. H. Qin, S. van Dijken, Z. Pirzadeh, A. Dmitriev, J. Noguós, J. Åkerman and P. Vavassori, Phys. Rev. Lett., 2013, 111, 167401 CrossRef PubMed.
- V. I. Belotelov, I. A. Akimov, M. Pohl, V. A. Kotov, S. Kasture, A. S. Vengurlekar, A. V. Gopal, D. R. Yakovlev, A. K. Zvezdin and M. Bayer, Nat. Nanotechnol., 2011, 6, 370 CrossRef CAS PubMed.
- S. Tomita, T. Kato, S. Tsunashima, S. Iwata, M. Fujii and S. Hayashi, Phys. Rev. Lett., 2006, 96, 167402 CrossRef PubMed.
- M. Rollinger, P. Thielen, E. Melander, E. Östman, V. Kapaklis, B. Obry, M. Cinchetti, A. García-Martín, M. Aeschlimann and E. T. Papaioannou, Nano Lett., 2016, 16, 2432 CrossRef CAS PubMed.
- T. A. Kelf, Y. Sugawara, R. M. Cole, J. J. Baumberg, M. E. Abdelsalam, S. Cintra, S. Mahajan, A. E. Russell and P. N. Bartlett, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245415 CrossRef.
- E. T. Papaioannou, H. Fang, B. Caballero, E. M. Akinoglu, M. Giersig, A. García-Martín and P. Fumagalli, Opt. Express, 2017, 25, 32792 CrossRef CAS.
- O. Borovkova, A. Kalish and V. Belotelov, Opt. Lett., 2016, 41, 4593 CrossRef CAS PubMed.
- I. S. Maksymov, J. Hutomo and M. Kostylev, Opt. Express, 2014, 22, 8720 CrossRef CAS PubMed.
- E. Almpanis, P. Pantazopoulos, N. Papanikolaou, V. Yannopapas and N. Stefanou, J. Opt. Soc. Am. B, 2016, 33, 2609 CrossRef CAS.
- H. Uchida, Y. Masuda, R. Fujikawa, A. Baryshev and M. Inoue, J. Magn. Magn. Mater., 2009, 321, 843 CrossRef CAS.
- V. Doormann, J. P. Krumme, C. P. Klages and M. Erman, Appl. Phys. A, 1984, 34, 223 CrossRef.
- S. Wittekoek, T. J. A. Popma, J. M. Robertson and P. F. Bongers, Phys. Rev. B: Solid State, 1975, 12, 2777 CrossRef CAS.
- V. Doormann, J. Krumme and H. Lenz, J. Appl. Phys., 1990, 68, 3544 CrossRef CAS.
- A. D. Rakić, A. B. Djurišić, J. M. Elazar and M. L. Majewski, Appl. Opt., 1998, 37, 5271 CrossRef PubMed.
- E. D. Palik and G. Ghosh, Handbook of optical constants of solids, Academic Press, San Diego, 1998 Search PubMed.
- V. G. Andrianova, V. S. Dozhdikov, O. Yu. Obukhov, V. A. Petrov, V. Yu. Reznik and O. N. Sevryukov, Teplofiz. Vys. Temp., 1983, 21(4), 680 CAS ; High Temperature, 1983, 21(4), 513.
- N. de Sousa, L. S. Froufe-Pérez, J. J. Sáenz and A. García-Martín, Sci. Rep., 2016, 6, 30803 CrossRef CAS PubMed.
- S. Albaladejo, R. Gómez-Medina, L. S. Froufe-Pérez, H. Marinchio, R. Carminati, J. F. Torrado, G. Armelles, A. García-Martín and J. J. Sáenz, Opt. Express, 2010, 18, 3556 CrossRef CAS.
- K. Lodewijks, N. Maccaferri, T. Pakizeh, R. K. Dumas, I. Zubritskaya, J. Åkerman, P. Vavassori and A. Dmitriev, Nano Lett., 2014, 14, 7207 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr00198h |
| This journal is © The Royal Society of Chemistry 2020 |