Intrinsic ferromagnetism with high temperature, strong anisotropy and controllable magnetization in the CrX (X = P, As) monolayer†
Abstract
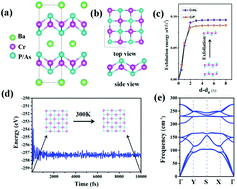
2D ferromagnetic (FM) materials with high temperature, large magnetocrystalline anisotropic energy (MAE), and controllable magnetization are highly desirable for novel nanoscale spintronic applications. Herein by using DFT and Monte Carlo simulations, we demonstrate the possibility of realizing intrinsic ferromagnetism in 2D monolayer CrX (X = P, As), which are stable and can be exfoliated from their bulk phase with a van der Waals layered structure. Following the Goodenough–Kanamori–Anderson (GKA) rule, the long-range ferromagnetism of CrX is caused via a 90° superexchange interaction along Cr–P(As)–Cr bonds. The Curie temperature of CrP is predicted to be 232 K based on a Heisenberg Hamiltonian model, while the Berezinskii–Kosterlitz–Thouless transition temperature of CrAs is as high as 855 K. In contrast to other 2D magnetic materials, the CrP monolayer exhibits a significant uniaxial MAE of 217 μeV per Cr atom originating from spin–orbit coupling. Analysis of MAE reveals that CrP favors easy out-of-plane magnetization, while CrAs prefers easy in-plane magnetization. Remarkably, hole and electron doping can switch the magnetization axis in between the in-plane and out-of-plane direction, allowing for the effective control of spin injection/detection in 2D structures. Our results offer an ideal platform for realizing 2D magnetoelectric devices such as spin-FETs in spintronics.
- This article is part of the themed collection: Editor’s Choice: Controlling anisotropy in nanomaterials


 Please wait while we load your content...
Please wait while we load your content...