Temperature-induced nanostructural evolution of hydrogen-rich voids in amorphous silicon: a first-principles study†
Abstract
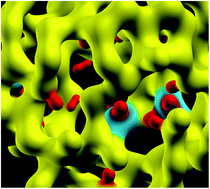
The paper presents an ab initio study of temperature-induced nanostructural evolution of hydrogen-rich voids in amorphous silicon. By using large a-Si models, obtained from classical molecular-dynamics simulations, with a realistic void-volume density of 0.2%, the dynamics of Si and H atoms on the surface of the nanometer-size cavities were studied and their effects on the shape and size of the voids were examined using first-principles density-functional simulations. The results from ab initio calculations were compared with those obtained from using the modified Stillinger–Weber potential. The temperature-induced nanostructural evolution of the voids was examined by analyzing the three-dimensional distribution of Si and H atoms on/near void surfaces using the convex-hull approximation, and computing the radius of gyration of the corresponding convex hulls. A comparison of the results with those from the simulated values of the intensity in small-angle X-ray scattering of a-Si/a-Si:H in the Guinier approximation is also provided, along with a discussion on the dynamics of bonded and non-bonded hydrogen in the vicinity of voids.


 Please wait while we load your content...
Please wait while we load your content...