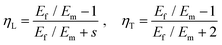Open Access Article
Open Access ArticleMechanisms of mechanical reinforcement by graphene and carbon nanotubes in polymer nanocomposites
Dimitrios G.
Papageorgiou
 *,
Zheling
Li
,
Mufeng
Liu
,
Ian A.
Kinloch
and
Robert J.
Young
*,
Zheling
Li
,
Mufeng
Liu
,
Ian A.
Kinloch
and
Robert J.
Young
 *
*
Department of Materials and National Graphene Institute, The University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: d.papageorgiou@qmul.ac.uk; robert.young@manchester.ac.uk
First published on 13th January 2020
Abstract
Polymer nanocomposites reinforced with carbon-based nanofillers are gaining increasing interest for a number of applications due to their excellent properties. The understanding of the reinforcing mechanisms is, therefore, very important for the maximization of performance. This present review summarizes the current literature status on the mechanical properties of composites reinforced with graphene-related materials (GRMs) and carbon nanotubes (CNTs) and identifies the parameters that clearly affect the mechanical properties of the final materials. It is also shown how Raman spectroscopy can be utilized for the understanding of the stress transfer efficiency from the matrix to the reinforcement and it can even be used to map stress and strain in graphene. Importantly, it is demonstrated clearly that continuum micromechanics that was initially developed for fibre-reinforced composites is still applicable at the nanoscale for both GRMs and CNTs. Finally, current problems and future perspectives are discussed.
1. Introduction
Polymer nanocomposites reinforced with graphene-related materials (GRMs) or carbon nanotubes (CNTs) have been explored extensively for use as engineering materials in a number of demanding application as a result of their low mass density and exceptional mechanical properties. In addition to their excellent inherent properties, the individual morphological characteristics of CNTs1 and GRMs2 play a major role on determining the ultimate properties of polymer nanocomposites.Graphene is comprised of an atomically thin sheet of sp2 carbon and constitutes the basic building block of carbon nanotubes, as shown in Fig. 1. Single-walled CNTs can be viewed as a rolled-up graphene sheet, with its one-dimensional geometry providing efficient reinforcement only along the length direction. Double-walled CNTs consist of two layers of rolled up graphene and multi-walled CNTs consist of many rolled-up graphene layers. In contrast to CNTs, the two-dimensional nature of graphene and GRMs, ensure that reinforcement takes place along all its in-plane directions. Moreover, as a result of the 2D geometry, graphene displays a larger surface to volume ratio, highly important for the creation of larger interfaces and production of stronger composites. In the present review, we will report in detail the parameters that affect strongly the reinforcing effects of both CNTs and GRMs and discuss the advantages and disadvantages of both types of filler for the production of high-performance polymer nanocomposites.
The majority of the early studies on nanocarbon composites were conducted using CNTs with research upon graphene and graphene-based nanocomposites having taken place only since its first identification and isolation in 2004.3 Nevertheless, the extensive research studies on the GRM-based materials have now led to a better understanding of the fundamental properties for all of these sp2 materials. In particular, GRMs have lateral dimensions of the order of microns that makes them amenable to study by a wider range of analytical techniques than in the case of CNTs. For example flakes of monolayer graphene can be easily resolved in an optical microscope,4 unlike individual nanotubes. Hence, this review of the literature will not be undertaken chronologically. GRMs will be discussed first of all and the findings on these materials will be then related to earlier studies upon CNTs.
A number of scientific challenges have risen over the last years as a result of the rapid expansion of polymer nanocomposites, with the understanding of the elastic properties being one of the most important. There are generally two approaches for the evaluation of the mechanical properties of polymer nanocomposites. A number of researchers have suggested that the mechanics of polymer nanocomposites are similar to polymer composites reinforced with continuous reinforcements such as carbon or glass fibres.5 In this case, the composite micromechanics, using concepts firstly introduced by Cox6 and Kelly7 through the use of shear-lag theory, is employed to predict the distribution of stress and strain in discontinuous fillers within a low-modulus matrix. Raman spectroscopy is a very useful tool towards the application of shear-lag theory in nanocomposites and the monitoring of the stresses within a nanofiller in a matrix, especially for carbon-based fillers with strong resonance Raman scattering.8 On the other hand, other researchers have taken an opposing viewpoint and have suggested that polymer nanocomposites should be considered as molecular composites or self-reinforced composites, as they are actually quasi-homogeneous molecular blends.9,10 In this case, composite micromechanics should not be applied to polymer nanocomposites since the properties are controlled by interactions between the fillers and the matrix on the molecular scale. On these terms, important indicators of interaction between the matrix and nanoparticles such as molecular nucleation and confinement (which are not taken into account by micromechanical models) may play a major role on the ultimate properties of polymer nanocomposites.
In this present review, the inherent mechanical properties of both GRMs and CNTs are discussed along with the criteria that determine the effective reinforcement from both nanofillers in polymer nanocomposites. The understanding and prediction of the mechanisms of reinforcement in such systems holds the key for the successful implementation of both nanofillers and we will subsequently explore this direction through the use of analytical models and micromechanical theories. Moreover, the application of Raman spectroscopy for monitoring the deformation of GRMs and CNTs both individually and within polymer nanocomposites through the study of the frequency shifts of the stress-sensitive Raman bands is thoroughly reviewed. Finally, this review is concluded by emphasizing the current challenges and future research directions for both GRM- and CNT-based polymer nanocomposites.
2. Mechanical properties of nanocarbons
2.1 Graphene
However, it should be noted that quite a few discrepancies exist in the graphene literature regarding the modulus of graphene, most possibly originating from the inherent and inevitable crumpling of graphene and the presence of different types of defects, both of which can decrease significantly the stiffness. For example, Ruiz-Vargas et al.12 have reported decreased stiffness or crumpled CVD graphene by using nanoindentation. The same conclusion was taken from the work of Nicholl et al.,13 where graphene was softened significantly as a result of cross-plane crumpling. On the other hand, the López-Polín et al.14 used Ar+ ions to introduce a controlled density of defects into mechanically exfoliated monolayer flakes deposited onto Si/SiO2 substrates with predefined circular wells and used AFM indentation experiments to obtain the mechanical properties of their samples. Counter-intuitively, the defect-free samples showed a significantly lower stiffness than the ones with defects, when the mean distance of defects was up to ∼5 nm (0.2% defect content). Various experimental methods have been utilized for the evaluation of the mechanical properties of graphene and they have been summarized well in a recent review by Kim et al.15 Moreover, in Section 5, we will identify the usefulness of Raman spectroscopy for the study of the mechanical properties of both graphene and carbon nanotubes and their composites.
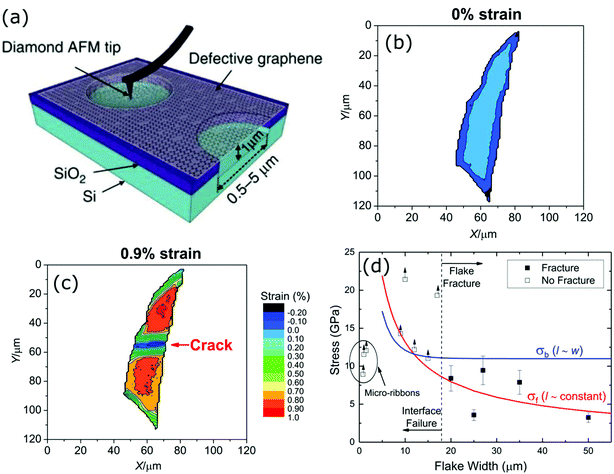 | ||
| Fig. 2 (a) AFM nanoindentation on suspended graphene sheets with defects17 (Copyright 2014, Nature Publishing Group), (b) strain contour map of a mechanically-exfoliated monolayer graphene flake before deformation (0% strain), (c) strain contour map of the same flake after fracture (0.9% strain), (d) graph of the graphene failure strength versus the flake width for various monolayer graphene flakes (Reproduced from ref. 18 with permission from The Royal Society of Chemistry). | ||
In a recent report from our group,18 the strength of mechanically exfoliated monolayer graphene was studied in detail through in situ Raman mapping at different strain levels (Fig. 2b and c). It was found that after the deposition of the monolayers onto a flexible polymeric substrate the failure mechanisms were either flake fracture or failure of the graphene/polymer interface. The strength of large flakes, was measured to be less than ∼10 GPa (Fig. 2d) (more than one order of magnitude lower than the values reported in ref. 11), as a result of the presence of defects that locally concentrated stress.
2.2 Carbon nanotubes
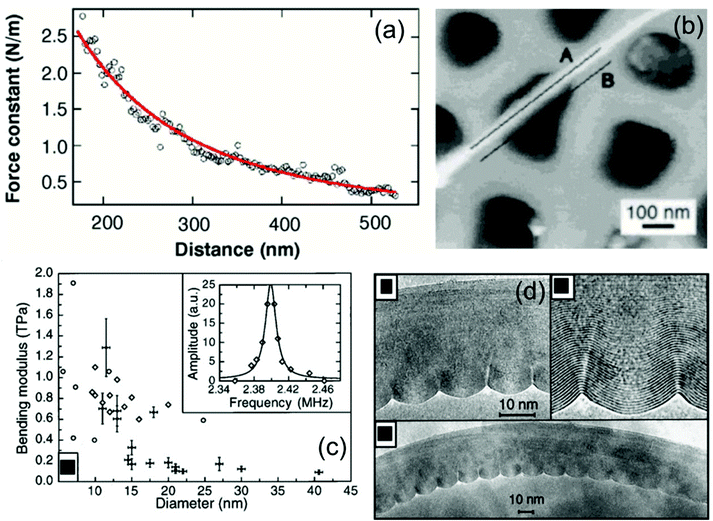 | ||
| Fig. 3 (a) Graph of the force constant versus distance along the axis of a MWCNT22 (Reprinted with permission from AAAS). (b) AFM image of a MWCNT adhered on an ultrafiltration membrane, with a part of it bridging a port of the membrane25 (Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission). (c) Bending modulus of MWCNTs as a function of nanotube diameter, (d) high resolution TEM images of bent nanotubes, showing a wave-like distorsion (radius of curvature ≈400 nm)26 (Reprinted with permission from AAAS). | ||
The bending modulus (Eb) of MWCNTs has been studied by Poncharal et al.26 by transmission electron microscope and MWCNTs with a diameter higher than 8 nm. It is known from elements of vibration analysis that a beam bends by elongation of the outer arc and compression of the inner arc. Thus, by applying this equation to CNTs, Eb can be associated with the Young's modulus of the material. The authors found that the bending modulus of MWCNTs decreases significantly from 1 TPa to almost 0.1 TPa with an increase in the diameter of the nanotubes (from 8 to 40 nm) (Fig. 3c), as a result of a different bending mode of the nanotube from a uniform elastic mode to a mode that is observed as a wave-like distortion mode (Fig. 3d). Given that the frequency of the excitation (vj) is known, the bending modulus (Eb) can be obtained from eqn (1):
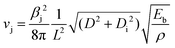 | (1) |
Overall, it can be seen that although there are some variations in the estimates of the stiffness particularly of CNTs, it is safe to assume that, to a first approximation, both few-layer graphene and small diameter CNTs have a Young's modulus approaching 1 TPa. Multi-layer graphene and MWCNTs have lower Young's modulus values as the result of inter-layer slippage and the hole down the centre of CNTs will reduce their modulus further.
Ruoff and coworkers in a set of pioneering experiments24,27 attached the ends of MWCNTs27 and SWCNT ropes24 onto the opposing tips of AFM cantilever probes and then the nanotube sections were stress-loaded and observed in situ in an SEM chamber. The deflection of the soft cantilever and the length change of the nanotubes were simultaneously recorded. The results revealed that the outermost layer of MWCNTs was the one that fractured via a “sword-in-sheath” mechanism, as the fragment lengths were significantly longer than the initial length of the nanotubes (Fig. 4a, b and c). The measured tensile strengths of the outer layer of MWCNTs in this work ranged from ∼11 GPa to ∼63 GPa, with no apparent dependence on the outer shell diameter. These values are lower than the theoretical predictions of SWCNTs,28 as a result of structural defects, diameter reduction during elongation and the presence of small twists and/or shear loads.
 | ||
| Fig. 4 SEM images of the fracture of MWCNTs under tensile load:27 (a) a MWCNT gripped onto the AFM cantilever probes having a section length of ∼6.9 μm, just before breaking, (b) a fragment of the same MWCNT just after breaking, displaying a length of ∼6.6 μm, (c) the other fragment of the starting MWCNT, that was attached on the bottom AFM cantilever probe, exhibiting a length of ∼5.9 μm (Reprinted with permission from AAAS), (d) the lateral force on a SWCNT rope suspended across a trench.31 Data from four consecutive measurements on the same rope (Reprinted with permission from IOP). | ||
In the case of the SWCNT bundles,24 the average tensile strength ranged from ∼13 GPa to ∼52 GPa, while the maximum tensile strain achieved in this work was ∼5.3%, which is in accordance with earlier theoretical predictions.29 Falvo et al.30 managed to strain MWCNTs up to 16% without observing a separation of the nanotube even after repeated application of bending stresses, revealing once again the high strength and flexibility of carbon nanotubes. In another study, Walters et al.31 also obtained the tensile strength of SWCNT ropes, by applying force via an AFM tip to a length of the rope that was freely suspended across a trench and by subsequently measuring the AFM tip displacement. They calculated the breaking strain to be 5.8 ± 0.9% (Fig. 4d) and the tensile strength to be 45 ± 7 GPa. Demczyk et al.32 utilized a piezoelectric manipulation holder within a TEM, in order to apply tension to MWCNTs. The authors observed a tensile force at failure of 18 μN and a tensile stress to breakage of 150 GPa, which is higher than previous reports, most probably as a result of the outer walls of MWCNTs breaking almost simultaneously.
Wagner et al.33 followed a different approach for the measurement of the strength of SWCNTs and embedded them into thin polymeric films to perform fragmentation tests, similar to the ones that are routinely performed for the study of the stress transfer ability of fibre-reinforced polymers. The authors found out that the tensile strength was in the order of 55 GPa by using a simple isostress model and the stress is effectively transferred from the matrix to the fibre through the nanotube ends, and the stress transfer efficiency was estimated to be at least one order of magnitude larger than conventional fibre-based composites.
The majority of experimental studies on the strength of carbon nanotubes have not achieved the strength values predicted by theoretical analyses (>100 GPa)34–36 as a result of the presence of a number of defects along the CNTs, the inadequate measurement procedures and artefacts introduced during sample preparation. However, the important study of Peng et al.37 reported measurements of MWCNTs with mean fracture strength in the order of 100 GPa, in-line with the theoretical expectations. The authors achieved these values by limiting the formation of defects via omitting chemical treatments during sample preparation. The nanotubes were then welded to the nanomanipulator probe and transported to a microelectromechanical stage that was placed within a TEM system. Electron irradiation induced crosslinking was achieved by focusing the TEM beam on the suspended portion of MWCNTs, a fact that led to concomitant dramatic increases in sustainable loads, while the stiffness and failure strain of the MWCNTs were only decreased slightly.
In summary, it is clear that both graphene and CNTs are capable in certain circumstances of realising strengths in excess of 100 GPa; however, in practice this is invariably reduced by the presence of either intrinsic or extrinsic defects.
3. Mechanical properties of nanocarbon-based polymer composites
3.1 Graphene nanocomposites
The exceptional mechanical properties of graphene have been one of the most important reasons for the introduction of graphene-related materials into polymers. The proficiency of the scientific community developed for the preparation of high-performance carbon nanotube nanocomposites has been subsequently extended for the preparation of multifunctional graphene-reinforced nanocomposites. We will now describe some of the most important aspects of graphene-based polymer composites for the improvement of their mechanical properties, such as the preparation methods of graphene-based composites, the dispersion and the orientation of the two-dimensional fillers, the lateral dimensions and the thickness of graphene, the waviness of the flakes and the interactions with the matrix.Solution blending is most probably the most widely used method for the preparation of polymer nanocomposites on the laboratory scale as a result of its versatility with the use of various solvents and the possibilities for functionalization of the flakes along with its speed and simplicity.42–46 In this process, the polymer is initially dissolved in a suitable solvent. The GRMs are then subsequently dispersed in a solvent that is compatible with the solvent that the polymer has already been dissolved. Graphene-related materials can be produced very successfully via liquid exfoliation since the energy that is required to exfoliate graphene is balanced by the solvent–graphene interaction (when the surface energy of graphene matches the one of the solvent).47 The two elements are then mixed together (by simple mixing or shear mixing or ultrasonication) and during this process, the polymer adsorbs onto the graphene flakes. It is of utmost importance to ensure a full evaporation of the solvent, since the formation of the nanocomposite and the homogeneous dispersion of the flakes take place during this process while additionally, the ultimate properties are highly sensitive to the presence of any solvent, as it can plasticize the matrix and tends to stay at the surface. Additional limiting factors for the use of solution blending include the absence of solubility of some polymers in common solvents and the eco-friendliness of this process, as usually large quantities of solvents are used. Despite these factors, solution processing is widely used in some industries, notably in coatings and some epoxy formulations.
Melt mixing is an industrially-friendly process for the production of (mainly) thermoplastic-based nanocomposites since it is fast and inexpensive. During melt mixing, the polymer is heated above its melting/softening point and then GRMs are added into the polymer melt.48–54 Mixing can take place by using an internal mixer with different rotor designs (Sigma, Banbury, cam or roller blades) or single-, twin-, triple- or even quad-screw extruders. Various parameters can affect significantly the dispersion of the GRMs within the polymer during melt mixing, including the temperature of mixing, the selection of the appropriate rotors or screw configuration, the feeding rates and the mixing rates. After melt mixing, additional processing steps usually take place such as hot pressing, injection moulding etc. which can also affect significantly the dispersion, the structure and the orientation of the fillers. The polymer nanocomposites that are produced by melt mixing can display an adequate dispersion of the fillers; however, the high shear forces that are required for the efficient mixing of the components of the system can lead to the formation of folds/wrinkles or even breaking of the nanoplatelets that lead to the reduction of their effective modulus.55 An additional problem that is associated with the use of melt mixing is the fact that the high temperatures, particularly for high performance systems such as PEEK, can lead to the decomposition of the functional groups on the surface of the GRMs or even the decomposition of the polymer. The group of Paiva has also explored the concept of re-agglomeration, where a small-scale mixer with a relaxation chamber was utilized56–58 for the production of GNP-reinforced polypropylene nanocomposites. The results have shown that re-agglomeration takes place in the relaxation chamber since an increase of the agglomerate area takes place, affecting significantly the subsequent dispersion rate of GNPs in the second mixing zone. A gradual decrease of the number and size of GNP agglomerates was also observed and at low shear rates, interparticle interactions induced re-agglomeration.58 As expected, the surface modification of GNPs delayed re-agglomeration and enhanced the mechanical properties and the electrical conductivity.57
Furthermore, in situ polymerization allows grafting of the filler onto the polymer, which subsequently leads to an increase in the compatibility between the components of the system and an improved interface.59–62 In this method, the GRMs are mixed with the monomer and then polymerization is initiated by heating or radiation after a suitable initiator is diffused in the liquid monomer. Once the reaction is initiated, the monomer that is present in and out of the layered material polymerizes and the filler nanoplatelets can be delaminated within the final polymer nanocomposites. The specific process is not easily scalable compared to melt mixing or solution blending, while additional problems include the increase of viscosity during the polymerization that prevents the production of nanocomposites at high filler loadings and leads to the creation of agglomerates.
Finally, layer by layer (LbL) assembly is another useful technique that can be used for the production of multifunctional and highly ordered graphene-based composites. In LbL assembly oppositely charged polyelectrolytes and graphene-related materials can be deposited on a substrate to create desired nano-architectures, multilayer thin films of specific thickness or hierarchical nanostructures. Usually, the interactions between the components of the assembly can be tuned by applying coordination chemistry, electrostatic and charge-transfer interactions, or simply hydrogen and covalent bonding. The 2D geometry of GRMs that provides high surface area makes them ideal for the preparation of such composites, while additionally the epoxy and hydroxyl groups in the basal plane of GO offer opportunities for the increase of the electrostatic attractive interactions and hydrogen bonding. The work of Zhao et al.63 revealed that the modulus of (PVA/GO)300 multilayer films with a bilayer thickness of 3 nm was doubled compared to the neat PVA, while more recently Vallés et al.64 reported that the combination of a positively charged polyelectrolyte (PEI) and electrochemically reduced GO (PEI/GO)10 (6 μm thick) led to very high electromagnetic interference (EMI) shielding values, in the order of ∼29 dB. The review from Xiao et al.65 has nicely summarized the current literature status on the LbL assembly of various nanoarchitectures.
A combination of the above-mentioned techniques has been applied in a number of studies in order to counterbalance some disadvantages from each method and ensure better dispersion of the nanofillers. For example, the group of Fina has prepared graphene-reinforced poly(butylene terephthalate) nanocomposites by inducing ring-opening polymerization within a twin screw micro-extruder.66,67 The nanocomposites produced displayed enhanced mechanical properties and improved thermal and electrical conductivities. In a different study, Maio et al.68 used a combined wet phase inversion method and melt mixing in order to produce GO-reinforced ethylene vinyl acetate (EVA) and nylon 6 (PA6) nanocomposites. The combined approach led to an efficient removal of the solvent and improved mechanical properties.
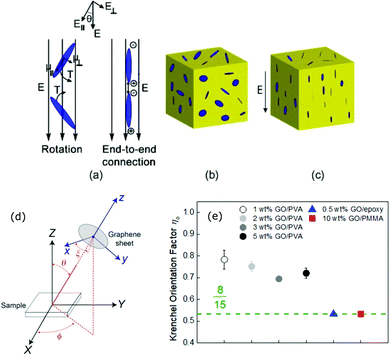 | ||
| Fig. 5 Two different alignment mechanisms of the GNPs by an AC electric field through: (a) rotation (left) and end-to-end connection (right) of polarized GNPs, (b) initial random orientation of GNPs within an epoxy resin, (c) oriented GNPs along the electric field direction within the resin71 (Copyright 2015, with permission from Elsevier), (d) the relationship between the local coordinate system of a graphene sheet (x, y, z) and the nanocomposite (X, Y, Z) defined by the three Euler angles (θ, φ, ξ),77 (e) Krenchel orientation factor of the composites studied in ref. 77 (the dashed line represents the Krenchel factor of 8/15 for the materials reinforced with randomly distributed GNPs (Copyright 2016, with permission from Elsevier). | ||
Another interesting method has been reported by Li et al.72 who used multilayer coextrusion for the fabrication of composites made of alternating layers of polymer and polymer/graphene composites. A modulus reinforcement of 118% was reported at 2 wt% of graphene as a result of the planar orientation of graphene in the individual polymer layers. The formation of other layered graphene/polymer structure, where graphene is essentially oriented in the in-plane direction, has been explored in the works of Vlassiouk et al.73 and Liu et al.74 In the two separate studies, CVD graphene has been sandwiched between two polymer layers of poly(methyl methacrylate) and polycarbonate. Vlassiouk et al.73 clearly showed that the preparation of these model composites might be a viable method to realise the unique mechanical properties of monolayer graphene in the macroscale, as the effective modulus of graphene (Eeff) in the structures was found equal to 1.2 ± 0.5 TPa. However, the value of Eeff that was calculated in the work of Liu et al.74 was significantly lower, in the order of 360 GPa. This can originate from the higher number of consecutive graphene/polycarbonate layers, where graphene within the structure can form ripples or it can also bend, something that is very difficult to monitor during the preparation procedure. Either way, this is a promising method that can utilise several of the unique properties of graphene such as the electrical or mechanical properties and the upscaling of this method can provide solutions for a number of applications.
The use of a magnetic field, which has been extensively explored for the preparation of oriented GNP-based composites was also employed for a set of polyimide/graphene composites.75 The authors decorated graphene with supermagnetic, tethered nickel nanoparticles, oriented their fillers by applying high and low magnetic field and it was found that the tensile modulus of the highly oriented nanocomposites was increased significantly.
Finally, 3D printing for the production of polymer nanocomposites is another technique that can induce orientation of graphene-related materials within a polymer. In the work of Yang et al.,76 the authors used electrically assisted 3D printing for the production of graphene-based, nacre-inspired structures with enhanced properties. The use of the electric field led to the achievement of a nanoscale-to-microscale assembly of the GNPs, while the use of 3D printing induced a microscale-to-macroscale assembly. The alignment of GNPs led to anisotropic conductivity and also creates a “bridge and interlock” phenomenon within the composites, essential to confer a stress-induced damage. Overall this is an exceptional study, taking advantage of a very strong, nature-inspire structure and modern composite fabrication techniques which led to excellent final results, revealing that the produced materials can take advantage of the multifunctional properties of graphene for the creation of smart and lightweight structures.
Polarised Raman spectroscopy has been identified as a technique that can be used to quantify the spatial orientation of graphene, which has a large effect upon its ability to reinforce nanocomposites.78 Li et al.74 applied the method to a number of GO-reinforced systems and obtained the Krenchel orientation factor (ηo), which can be subsequently substituted in a number of micromechanical equations such as the modified rule of mixtures. The local orientation of graphene is defined by its surface normal and can be seen in Fig. 5d as the z direction in the x, y plane. The Raman scattering intensity under VV laser polarization can then be expressed as a function of the polarization angle Φ:
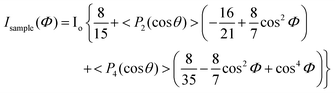 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is the Legendre polynomial of the i-th degree and <Pi(cos
θ) is the Legendre polynomial of the i-th degree and <Pi(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> is the average value. The Herman's orientation factor (S) is the <P2(cos
θ)> is the average value. The Herman's orientation factor (S) is the <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)>, while the higher the <P2(cos
θ)>, while the higher the <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> and <P4(cos
θ)> and <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> values, the higher the orientation of graphene in a composite. After substitution on the orientation distribution function, the Krenchel orientation factor can be obtained by:
θ)> values, the higher the orientation of graphene in a composite. After substitution on the orientation distribution function, the Krenchel orientation factor can be obtained by: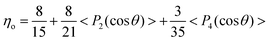 | (3) |
For a composite with a perfect orientation of the flakes <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> = <P4(cos
θ)> = <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> = 1, while for random orientation <P2(cos
θ)> = 1, while for random orientation <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> = <P4(cos
θ)> = <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> = 0. Finally, for a composite where the nanoplatelets are randomly aligned, ηo = 8/15 (Fig. 5e). The important implication of this study to the general field of composites comes from the conclusion that the reinforcing efficiency of 2-dimensional materials is significantly higher than fibre or nanotube-based materials. This is because the Krenchel orientation factor for randomly oriented 1-dimensional fillers reduces the modulus by a factor of 5 (ηo = 1/5), while for 2-dimensional fillers it is only reduced in less than half. The values of <P2(cos
θ)> = 0. Finally, for a composite where the nanoplatelets are randomly aligned, ηo = 8/15 (Fig. 5e). The important implication of this study to the general field of composites comes from the conclusion that the reinforcing efficiency of 2-dimensional materials is significantly higher than fibre or nanotube-based materials. This is because the Krenchel orientation factor for randomly oriented 1-dimensional fillers reduces the modulus by a factor of 5 (ηo = 1/5), while for 2-dimensional fillers it is only reduced in less than half. The values of <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> and <P4(cos
θ)> and <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> also enable the reconstruction of the full orientation distribution function of graphene flakes in composites.
θ)> also enable the reconstruction of the full orientation distribution function of graphene flakes in composites.
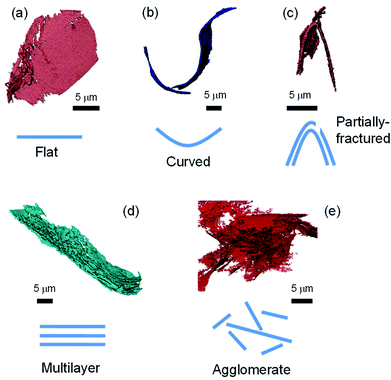 | ||
| Fig. 6 The taxonomy of individual GNP flakes as obtained from X-ray computed tomography in an epoxy/GNP composite. (a) A flat flake, (b) two curved GNP flakes, (c) a curved GNP flake that fractured partially in the middle, (d) a multi-layer flake with a large number of layers, (e) an agglomerate of flakes82 (Copyright 2019, with permission from Elsevier). | ||
The emergence of X-ray computed tomography now enables the visualization of the “real” structure and morphology of the nanofillers within composites and provide important information regarding the effect of processing on the fillers. The recent study of Li et al.82 has shed some light to this crucial issue of mechanical reinforcement from GNPs and the authors suggested that a size reduction of at least a factor of two should be expected for epoxy/GNP composites prepared by stirring and sonication of GNPs within the resin. Very long flakes are clearly more prone to bending and agglomeration/restacking than smaller ones, so a balance of the lateral dimensions should always be kept in mind. This effect can be observed more commonly in materials with low shear modulus (i.e. elastomers) since the stress transfer is less effective than stiffer materials and the interfacial strength of the filler/matrix interface is small. For example, in the case of natural rubber reinforced by GNPs83 or GO84 with different lateral dimensions, the Young's modulus of the composites with the smaller flakes was higher than that with the largest flakes.
Moriche et al.90 demonstrated that the composite preparation method can alter the morphology of the nanoplatelets significantly and consequently, their properties. The authors studied epoxy/GNP composites prepared by different methods and found out that when GNPs are firstly dispersed by sonication, they retain their wrinkled morphology, which leads to higher residual stress in the nanocomposites. On the other hand, the calendering method enabled the separation and exfoliation of the nanoplatelets and their extension via flattening (Fig. 7). The number of calendering cycles is important as at higher cycles number a higher residual stress was observed. According to Wang et al.91 the amplitude (A) (eqn (4)) and wavelength (λ) (eqn (5)) of a wrinkle is directly proportional to the flake dimensions (length and thickness):
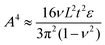 | (4) |
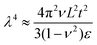 | (5) |
 | ||
| Fig. 7 Schematics of the morphology of GNPs within an epoxy resin after using different preparation techniques90 (Copyright 2015, with permission from Elsevier). | ||
3.2 Carbon nanotube nanocomposites
Even though the intrinsic properties of carbon nanotubes can ensure the good performance of the produced CNT-based nanocomposites, there are several parameters, the control of which can ensure the maximization of performance of CNTs in the composites. Some of the most important parameters include the dispersion and orientation of CNTs, the length of the CNTs, the waviness, the interfacial interaction between CNTs and the matrix and the chirality. Several investigators have attempted to evaluate those parameters individually and in combination and they will be discussed in the following section.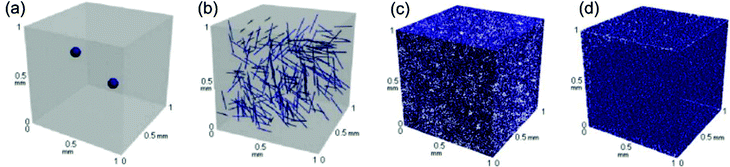 | ||
| Fig. 8 Distribution of micro- and nano-scale fillers (filler content: 0.1 vol% in a reference volume of 1 mm3) (a: Al2O3 particle; b: carbon fibre; c: GNP; d: CNT)98 (Copyright 2010, with permission from Elsevier). | ||
Various techniques can be employed for the melt processing of nanocomposites, such as extrusion,103 injection moulding,104 calendaring,105 compression moulding106 and others. One of the most popular approaches for the production of CNT-based composites is the blending of the polymers with nanotubes at high filler content to form a masterbatch that is subsequently diluted by adding pure polymer during production. The specimens are then produced by either injection or compression moulding. This process is also favoured by industry since handling of nanomaterials for direct incorporation into composites at varying filler loadings can be challenging. The majority of studies that have followed this approach have reported excellent mechanical properties at even high filler loadings.107–112 The group of Potschke has investigated extensively the effect of CNTs in a number of polymeric matrices via melt mixing and masterbatch dilution. In their research, they evaluated a number of important characteristics for the efficient dispersion of CNTs within a polymer matrix such as the screw profile, the temperature profile, the rotation speed, the injection moulding parameters and the specific mechanical energy.113–118 In general, higher extrusion/rotation speeds are known to lead to smaller agglomerates and better dispersion due to the higher level of shear stress that is acting on the primary agglomerates; this fact can, however, lead to a decrease of the nanotube length and a subsequent deterioration of their intrinsic properties. The dispersion of the initial agglomerates through the creation of secondary agglomerates (or clusters) of CNTs via thermal annealing in the quiescent melt as well as under shear deformation is certainly an interesting one, as it has been shown to lead to a significant increase in electrical conductivity due to the formation of a network of interconnected agglomerates.119,120 The overall process takes place during the mixing and includes the initial wetting of the primary agglomerates by the polymer, the weakening of the agglomerates from the infiltration of the polymer chains, then the dispersion of agglomerates by erosion and rupture and finally the distribution of the individual nanotubes in the polymer. The manipulation of shear and the elongational flow during the preparation procedure is critical in this case since it can either lead to a build-up or a destruction of the secondary agglomerates, which is subsequently reflected on the ultimate properties.119
Solution blending is also one of the most popular methods for the production of polymer nanocomposites and for the dispersion of fillers that are known to form agglomerates readily. This method involves the dispersion of CNTs within a polymer or solvent by some form of energetic agitation, the mixing of CNTs and the polymer and the subsequent evaporation of the solvent for the production of a composite film. The functionalization of CNTs is known to improve the dispersion of CNTs significantly. Critical parts of this process for the production of the nanocomposite are the correct selection of the solvent for the dispersion of the CNTs, the time and energy applied to the CNT/solvent suspension, the efficient mixing of the polymer/CNT blend and the full evaporation of the solvent. In addition, the final step of the solution blending process can commonly induce re-agglomeration of the CNTs so strategies such as the coagulation have been applied where the CNT/polymer suspension is poured into an excess of nonsolvent. This approach has as a result of the entrapment of the precipitation of CNTs from the polymer chains, preventing them from bundling.121,122
In situ polymerization involves the dispersion of nanotubes in monomers and the subsequent polymerization of the monomers.123 This process is quite useful for the preparation of nanocomposites when the polymer matrix is resistant to chemicals or possesses properties that make melt mixing difficult (i.e. high melting point, high viscosity etc.). The functionalization of the CNTs prior to the mixing with the liquid monomer or solvent can induce better dispersion within the composites. It should be noted, though, that at higher CNT contents there is a lack of polymerization reactions as well as the major increase of viscosity. Nevertheless, in situ polymerization enables grafting of the polymer molecules onto CNTs and the formation of covalent bonding between the CNTs and the matrix by various condensation reactions, leading to significantly improved mechanical properties.
As mentioned earlier, LbL assembly is a versatile technique that can enable the creation of high performing, multifunctional nanocomposite materials. In the early work of Mamedov et al.,124 the authors fabricated free-standing single-walled CNT/polyelectrolyte membranes with enhanced strength, as a result of the minimization of structural defects originating from phase segregation. Since then, a number of works have dealt with the preparation and the properties of CNT-based LbL assemblies and the enhanced performance of the nanocomposites in terms of the mechanical, electrical and other properties have been clearly exhibited.125–128
Combinations of the above-mentioned techniques have also been employed by a number of groups for the efficient preparation of high-performing CNT-based composites. For example, CNTs have been coated with polyethylene by in situ polymerization of ethylene catalyzed directly from the nanotube surface and they have been subsequently melt-blended with HDPE,129 ethylene-co-vinyl acetate (EVA)130 or polycarbonate.131 Another combination that has been applied is the use of solution blending and extrusion such as in the studies of Thostenson and Chu where CVD-MWCNTs were dispersed in a solution of polystyrene in tetrahydrofuran (THF) to form a nanocomposite film, which was subsequently chopped and extruded. The resultant nanocomposites showed improved tensile modulus, yield strength and ultimate strength.132
Electric fields have been utilized in a number of creative ways in order to induce alignment of CNTs within a matrix. Importantly, the behaviour of CNTs can be controlled by adjusting the gap between the electrodes of the AC or DC electric fields and it is highly dependent on the surface charge and the type and frequency of electric field. More specifically, in the application of an AC electric field the alignment of CNTs takes place due to their dielectrophoretic behaviour, since the electrophoretic mobility of the field is zero and CNTs essentially disrupt the homogeneity in the electric field. Thus, the use of AC electric fields has been reported to be more effective in the production of uniform and aligned networks, such as in the work of Martin et al.134 The parameters of the AC electric field, such as the field voltage and frequency are vital for inducing orientation of CNTs; it should be noted, however, that increased voltage can also promote a degree of agglomeration, so a fine balance has to be maintained.135 Moreover, as the research of Ma et al. has shown, oxidized MWCNTs were dispersed and aligned in PMMA at a higher degree than their un-functionalized counterparts due to a higher amount of charges and a larger dipole moment.136
On the other hand, on the application of a DC electric field, the CNTs move towards the electrodes of opposite charge as a result of their electrophoretic mobility and the surface charge. The alignment in this case can be controlled by the level of applied potential. The important work of Kim and coworkers137 evaluated the orientation of MWCNTs in an epoxy matrix as a function of the DC electric field. As well as an exceptionally-low electrical percolation threshold of about 0.0031 vol% in the direction of alignment, the tensile modulus of the oriented composites at 0.3 wt% CNTs was 40% higher than for the neat epoxy, while the fracture toughness was 51% higher at the same filler content. For higher filler loadings, the Young's modulus was reduced, as a result of a reduced degree of alignment; the increased loadings also lead to an increase in the viscosity of the epoxy resin, thus making it more difficult for the CNTs to move and orient under the DC field. It should also be noted that the transverse storage modulus obtained by dynamic mechanical analysis for the aligned CNT composites was lower than that of the randomly-oriented CNT composites due to the lower restriction of the macromolecular chains of the resin in the transverse direction, similar to the work of Zhu et al.138
The application of a magnetic field is another method for the fabrication of oriented MWCNT-based nanocomposites.139,140 The fabrication of MWCNTs commonly involves the use of metal catalysts such as Fe, Co or Ni, an amount of which can remain in the MWCNTs after the preparation procedure and subsequently respond to the application of low magnetic fields. Ma et al. aligned CNTs with Ni particles as a residual catalyst in an epoxy under a low magnetic field of 0.4 T.141 The authors reported that the alignment of CNTs perpendicular to the crack plane resulted to significantly higher fracture toughness and energy compared to the randomly oriented CNT samples or to the samples where CNTs were oriented parallel to the crack plane. Another similar method involves the coating of CNTs with superparamagnetic particles, which can facilitate the orientation of the nanotubes.142 Kimura et al.143 first reported on the use of a magnetic field of 10 T for the polymerization of a polyester resin and MWCNTs. The storage modulus measurements revealed that the alignment of the MWCNTs attributed a higher increase of the modulus in the parallel direction compared to that for the perpendicular direction. There are also reports where the orientation of MWCNTs in an epoxy matrix by magnetic field has also been shown to degrade the mechanical properties of the system due to a decoupled orientation of the polymer chains due to the inhibition of the macromolecular chain movement and the formation of a highly-disordered complex microstructure.144 This fact once again reveals that the alignment of CNTs in an epoxy resin is highly dependent on the cross-linking molecules and the core polymer component of the resin.
The alignment of CNTs can also be attained by the use of mechanical force during the processing of the nanocomposites. For example, flow-induced alignment of MWCNTs has been achieved by the application of intense drag/shear forces during the moulding process in a variety of polymer matrices.145–148 Mechanical stretching is also a technique that has been proven to produce aligned CNTs.149,150 Jin et al.151 followed this procedure for CNTs in a polymerized matrix, however, it is important to understand that the large draw ratio can lead to unfavourable interface binding between CNTs and the matrix. Also, Schulte and coworkers aligned high loadings of CNTs in an epoxy matrix, at a MWCNT fraction of 68 wt% by applying hot-press infiltration through a semi-permeable membrane. The Young's modulus in the direction parallel to the alignment was in the order of 36 GPa, while the electrical conductivity was 3.7 × 104 S m−1.
Finally, electrospinning is another method, amongst many, that can be used for the production of aligned CNT-based nanocomposites.152,153 A number of studies, such as the one of Cheng and coworkers154 on polyacrylonitrile/MWCNT composite nanofibre sheets produced by electrospinning have reported an improvement in the mechanical properties.155–157 More recently King et al.158 managed to engineer single- and double-walled CNTs into highly aligned arrays by electrospinning poly(ethylene oxide) and functionalized CNTs solutions (Fig. 9). Mechanical testing revealed that at a CNT loading of 3.9 wt%, the strength and ductility were improved by a factor of 3, while the modulus increased by a factor of 4. The process can be further optimized in order to allow a higher control of the nanotube orientation, by using a magnetic field. Magnetic field assisted electrospinning is easy to set up by using just two magnets added to conventional electrospinning, the CNTs are highly-aligned and the resultant fibres can be easily transferred to other substrates.159,160
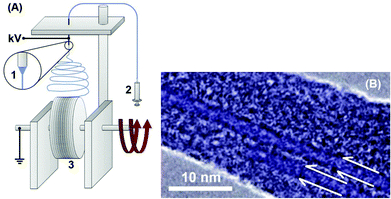 | ||
| Fig. 9 (A) Schematic diagram of the electrospinning setup used by King et al.158 showing (1) the single needle spinneret, (2) the pumped syringe and (3) the grounded high speed collector where full alignment of the CNTs takes place within the fibres. (B) The coloured TEM micrograph shows the CNTs embedded within the PEO electrospun nanofibre (Copyright 2018, with permission from Elsevier). | ||
The quantification of the spatial orientation of CNTs was made firstly by Liu et al.161 by adjusting the theory developed earlier to quantify the orientation of polymer chains, including liquid crystals.162 The orientation of a carbon nanotube is defined by its axial direction in a coordinate system. The Raman scattering intensity, obtained from the products of the tensors of the CNT and the vectors of Raman laser representing its polarisation directions, can be expressed as a function of the polarization angle Φ for the VV polarisation configuration:
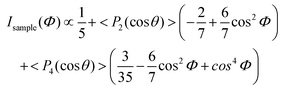 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is the Legendre polynomial of the i-th degree and <Pi(cos
θ) is the Legendre polynomial of the i-th degree and <Pi(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> is the average value. Specifically, the definition of <P2(cos
θ)> is the average value. Specifically, the definition of <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> is the same as the well-known Herman's orientation factor (S) commonly used in polymer field. From eqn (6) it can be understood that the higher the <P2(cos
θ)> is the same as the well-known Herman's orientation factor (S) commonly used in polymer field. From eqn (6) it can be understood that the higher the <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> and <P4(cos
θ)> and <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> values, the better the orientation of CNTs in a composite. <P2(cos
θ)> values, the better the orientation of CNTs in a composite. <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> and <P4(cos
θ)> and <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> being equal to unity stands for the unidirectional orientation of CNTs, while <P2(cos
θ)> being equal to unity stands for the unidirectional orientation of CNTs, while <P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> and <P4(cos
θ)> and <P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)> being equal to 0 means that all the CNTs are randomly oriented three-dimensionally in bulk. This, as calculated by Krenchel163 for the case of fibres, reduces the reinforcement efficiency to only 1/5, as compared to unidirectionally-oriented CNTs in composites.
θ)> being equal to 0 means that all the CNTs are randomly oriented three-dimensionally in bulk. This, as calculated by Krenchel163 for the case of fibres, reduces the reinforcement efficiency to only 1/5, as compared to unidirectionally-oriented CNTs in composites.
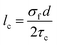 | (7) |
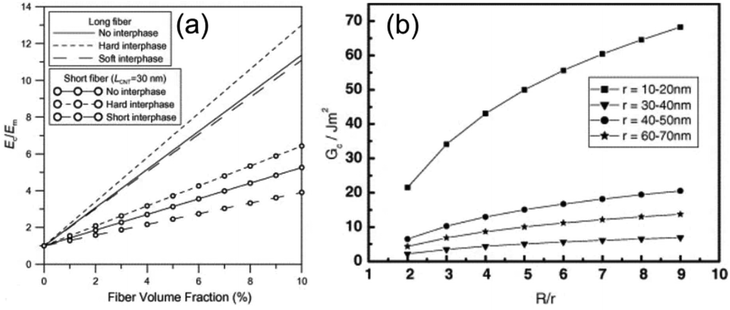 | ||
| Fig. 10 (a) Effect of fibre length and quality of the interphase on the effective Young's modulus of the composite166 (Copyright 2005, with permission from Elsevier). (b) Calculated interfacial fracture energy for the pullout of a single MWCNT from a polyethylene–butene matrix for various R/r values, where R/r is a stress transfer parameter, r is the fibre radius and R is the matrix radial distance from the axis of the fibre, at which shear tends to be zero170 (Copyright 2004, with permission from Elsevier). | ||
The diameter of the tubes is another important parameter for the reinforcement of polymeric matrices. SWCNTs possess smaller diameters and larger specific surface areas than MWCNTs. This large surface area can be beneficial for good stress transfer; however, it induces strong attractive forces between CNTs, which subsequently leads to excessive agglomeration. Multi-walled CNTs display larger diameters and as a result can be dispersed more efficiently but their shorter length can lead to the formation of a smaller interface for stress transfer and lower aspect ratio, thus poorer mechanical properties. Larger diameter nanotubes can also exhibit a lower effective modulus due to inter-wall slippage.168 It is clear, therefore, that a fine balance need to be maintained between the number of walls and the specific surface area in order to compromise between mechanical reinforcement and homogeneous dispersion. Cadek et al. showed that the low diameter MWCNTs were more efficient for reinforcing poly(vinyl alcohol) (PVA) since SWCNTs formed a number of agglomerates and DWCNTs were able to reinforce the matrix only up to 1 wt%.169 Wagner and coworkers have identified that smaller diameter nanotubes formed a stronger interface with a polyethylene-butene matrix, a fact that led to a higher fracture energy, as measured by single fibre pullout tests (Fig. 10b).170 Finally, the work of Thostenson and Chou has clearly shown that larger nanotube diameters leads to a lower effective modulus and to the occupation of a greater volume fraction in the composite, compared to lower diameter nanotubes.171
4. Composite micromechanics
4.1 Rule of mixtures
The simplest and most straightforward relationship that was developed originally for the description of the reinforcement of a low modulus matrix by a high modulus fibre, for stress parallel to the fibre direction, is the rule of mixtures. The Young's modulus of a composite Ec consisting of infinitely long and aligned fibres is given by:| Ec = EfVf + Em(1 − Vf) | (8) |
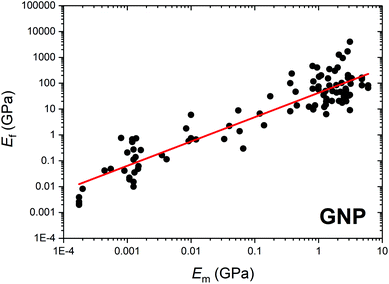 | ||
| Fig. 11 Filler modulus (Ef) versus matrix modulus (Em) for a number of different literature reports where polymers of varying degrees of stiffness were reinforced by graphene nanoplatelets. The solid line represents the linear fit of the data and has a slope of unity2 (Copyright 2017, with permission from Elsevier). | ||
However, given the fact that the above equation does not take into account important factors such as the orientation, the length (or aspect ratio) and the agglomeration of the fibres (which are all very important in the case of nanocomposites), it should be mainly used as an approximation for the modulus of the filler or of the composite. Based on this, a modified rule of mixtures has also been proposed for the calculation of the Young's modulus of a composite:
| Ec = EeffVfηoηl + Em(1 − Vf) | (9) |
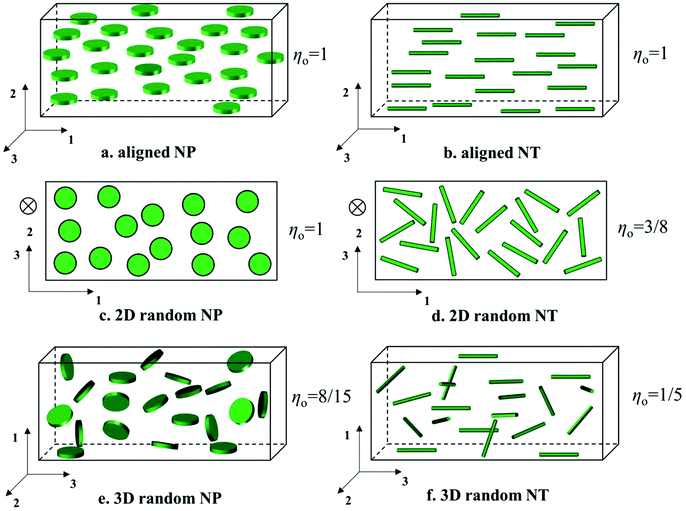 | ||
| Fig. 12 Schematics of nanoplatelet (NP) and nanotube (NT) nanocomposites with different orientation of the nanofillers: (a and b) aligned, (a, c and d) randomly oriented, in-plane and (e and f) 3D randomly oriented (Adapted from ref. 187). | ||
The length factor (or fibre length distribution factor) can be calculated by using the Cox equation:
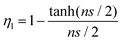 | (10) |
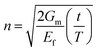 . The main assumption behind the use of the length factor is that the matrix and the filler remain elastic during deformation, the interfacial bonding is perfect, while on the basis of the shear-lag theory the shear stress at the ends of the fibre is maximum and falls to zero after half the critical length.
. The main assumption behind the use of the length factor is that the matrix and the filler remain elastic during deformation, the interfacial bonding is perfect, while on the basis of the shear-lag theory the shear stress at the ends of the fibre is maximum and falls to zero after half the critical length.
Li et al.188 included an agglomeration factor (ηa) within the modified rule of mixtures, taking values between 0 and 1. It is 1 for perfect dispersion and effective stress transfer from the matrix to the filler and 0 is for major agglomeration, so that the effect from the nanoscale dimensions of the filler is diminished and thus nearly no stress transfer takes place. The modified Rule of Mixtures (mROM) in this case takes the form:
| Ec = ηoηlEeffηaVf + Em(1 − Vf) | (11) |
For the case of CNT-based composites, Omidi et al.189 also modified the classical rule of mixtures, in order to account for the non-linearity in the modulus at higher loadings of CNTs (VNT), in an epoxy-MWCNT composite with filler contents up to 10 wt%. The proposed equation involves several parameters that are crucial for effective reinforcement in CNT-based composites such as an exponential shape function, a length efficiency parameter (κl), an orientation factor (κo) and a waviness parameter (κw). The final form of the modified rule of mixtures proposed by Omidi et al.189 is:
| EC/M = (κlκoκwENT/M − 1)VNTeaVNT | (12) |
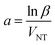 and
and 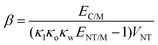 .
.
The results from the application of eqn (12) reveal that the fitting is quite good when the waviness parameter (κw) is 0.4, showing high degree of waviness, given the fact that for straight nanotubes κw = 1.
The rule of mixtures gives a simple yet reliable estimation of the Young's modulus of composites based on the modulus and volume fraction of each component. It considers the major factors that determine the performance of the composites, which is particularly useful for industrial applications so, during development, major issues can be prioritised.
4.2 Shear-lag analysis
The rule of mixtures was derived originally for continuous fibres, hence some assumptions were made for simplification, such as perfect/elastic interfacial bonding, infinitely long fillers, unidirectional alignment of fillers etc.190 For continuous fibres these assumptions are valid, but when the size of fillers decreases, e.g. discontinuous or chopped fibres, modification of those assumption has to be considered. As the interfacial adhesion is related closely to the size of filler, when the filler has a finite size, the stress transfer through interfacial adhesion is reduced. Kelly191 discussed how stress can be transferred from matrix to fillers with finite length in his book Strong Solids, where the interfacial shear stress on the filler is balanced by the axial stress. In this scenario, the deformation of both filler and matrix can be depicted schematically in Fig. 13.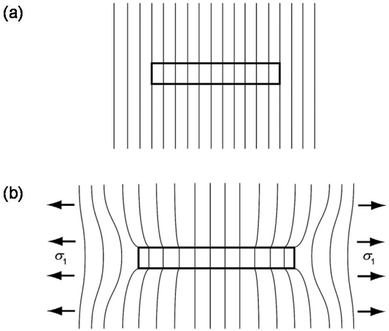 | ||
| Fig. 13 Single filler with finite size and matrix at the (a) undeformed and (b) deformed state with a tensile stress σ1. The vertical lines represent the positions perpendicular to the stress. | ||
It can be seen that under axial deformation, the filler deforms the most in the central part while deforms the least at the edges, which leads to a high interfacial shear stress at the edges of filler as a result of the large displacement between filler and matrix around filler edge.
This stress distribution can be quantified by using the ‘Kelly–Tyson’ model,7 assuming a constant shear stress at the ends of fillers. A more accurate model was proposed by Cox,6i.e. the ‘shear-lag’ model, for fibres in paper science which has been widely studied and applied since then.192 For 1D fibres, it has the form as below, while detailed discussion of the ‘shear-lag’ theory can be found elsewhere:193
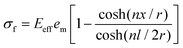 | (13) |
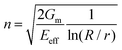 | (14) |
In eqn (13), σf is the stress on the filler, Eeff is the Young's modulus of the filler, and em is the strain applied to the matrix. R and r stand for the radius of the representative volume element and the filler, respectively. l is the length of filler in the strain direction, along which the position is defined as x. Although not mathematically rigorous, eqn (13) presents a way of estimating the stress distribution of the filler along the strain direction. Dividing both sides by the modulus of fillers one can obtain the strain distribution as well. On this basis, the shear stress τi along the filler can be derived by differentiating eqn (13) to give:
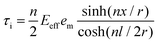 | (15) |
Eqn (15) shows one of the major differences from the Kelly–Tyson model, i.e. the non-constant interfacial shear stress. Likewise, for 2D fillers such as graphene, the shear-lag model has been revisited recently and modified as:5
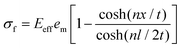 | (16) |
where
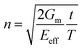 | (17) |
Apart from t and T denoting for the thickness of the 2D filler and the representative volume element, other parameters have the same physical meaning as eqn (17) for a 1D filler. Similarly, the shear stress along a 2D filler can be written as:
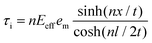 | (18) |
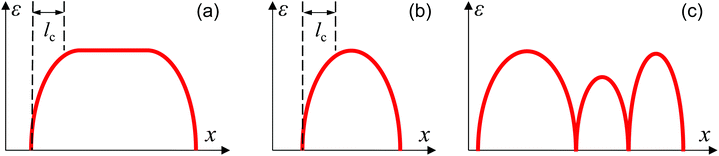
Both the ‘Kelly–Tyson model’ and the ‘Shear-lag model’ depict the stress transfer efficiency from matrix to fillers in composites where the strain in fillers starts to build up from the edge and reaches the strain applied to the matrix at a distance from the filler edge (Fig. 14a), and 90% of this distance is defined as the ‘critical length-lc’. The region in the critical length reinforces the composite poorly while the central part delivers an effective reinforcement, in accordance with Fig. 4. The size of lc has been found to be several hundred μm for fibres194 and 2–4 μm for graphene,5 though it can vary with the level of strain even for one system. In order to give an effective reinforcement, it is usually considered that the size of fillers needs to be 10 times of lc.5 Fillers with size below this value are still able to provide reinforcement, however with a significantly reduced reinforcement efficiency, especially when the size of filler is comparable to lc (Fig. 14b).
When the applied strain is over a critical value, fragmentation of the fillers occurs, e.g. ∼1.0% for fibres.194 Its strain distribution as found by using the stress/strain sensitive Raman band position shows that strain in each fragmented fibre is very low as a result of the length of the fragments being shorter than or comparable to the critical length of fibres. Similar behaviour has been found on graphene which is equivalent to having a significantly reduced ‘length factor’.195
The discussion above highlights the great importance of the interfacial adhesion in composites as the load is normally applied only to the matrix and not the fillers. Interface modification can be employed to strength the interface, and typical techniques include physical approach (interface roughening) and chemical modification (plasma, functionalisation etc.).196 The levels of interfacial adhesion can be evaluated by using several techniques such as pull-out, push-out, microdroplet and fragmentation test.197 Regarding the stress/strain distribution of filler, Raman spectroscopy has been demonstrated as a powerful and quantitative tool by simply monitoring the stress/strain sensitive Raman band position198 and will examined in detail in the next section.
Micromechanical models can be combined to deliver a more accurate and rigorous prediction and estimation of the mechanical properties of composites. For example, the rule of mixtures can be modified by implementing the ‘shear-lag’ theory with more factors being taken into consideration such as the size and spatial orientation of the fillers. In our previous study we combined the shear lag theory with the modified rule of mixtures in order to understand the mechanisms of reinforcement of polymers from graphene nanoplatelets.195 Thus, starting from the mean stress along an aligned individual nanoplatelet:
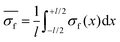 | (19) |
If we substitute x in the shear-lag equation with the aspect ratio of a graphene nanoplatelet (l/t) then the eqn (16) can be rewritten as:
 | (20) |
For uniform strain, after combining eqn (16) and (20) and performing a series of substitutions and Taylor series, the final equation for the modulus of graphene nanoplatelets within a composite is given:
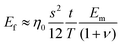 | (21) |
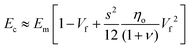 | (22) |
As can be understood, the value of the Ef (and subsequently of Ec) depends upon the degree of orientation (ηo), the interfacial parameter t/T which is essentially an indication of the strength of the interface and most importantly, of the aspect ratio s of the nanofiller. It is also interesting to notice that on first observation the composite modulus is essentially independent of the filler modulus (at least for soft polymers where Em < 500 MPa) and depends mostly on the above-mentioned parameters.
Another very important parameter in the use of the shear-lag theory and the subsequent derivation of eqn (21), which explains the mechanism of reinforcement of polymers from graphene-related materials is the interfacial parameter t/T. This parameter depends upon how fast the stress decays into the matrix away from the nanofiller and it is controlled generally by the volume fraction of the filler and the strength of the interface between the filler and the matrix. In a bulk nanocomposite, the t/T ratio is associated strongly with the proximity of neighbouring particles and hence the volume fraction of the filler. Liu et al.199 proposed a mechanical percolation mechanism for the reinforcement of a thermoplastic elastomer by graphene. The authors designed a set of equations for Vf below and above the percolation threshold volume fraction (Vp). Below Vp the reinforcement originates from the inherent ability of individual GNPs to transfer stress effectively (Fig. 15a and b), while above Vp, accelerated stiffening is observed due to the reduction of the distance between adjacent flakes (Fig. 15c and d). The proposed equations are:
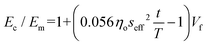 | (23) |
| Ec/Em = 1 − Vf + 0.056ηoseff2Vf2 | (24) |
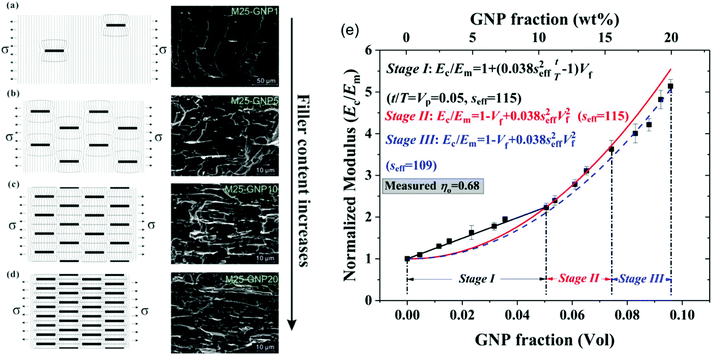 | ||
| Fig. 15 Schematic illustration of shear lag units at low filler contents (a and b) below the percolation threshold volume fraction Vp and at higher contents (c and d) above Vp. (e) Fittings of normalized modulus against Vf with eqn (23) and (24) for a TPE-GNP nanocomposite.199 | ||
4.3 Semi-empirical models
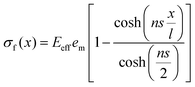
In addition, there are also other micromechanical models that one can adopt to predict the Young's modulus of composites, such as Halpin–Tsai model200 and the Mori–Tanaka model.201 The Halpin–Tsai model can be shown as below: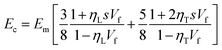 | (25) |
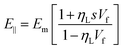 | (26) |
Ec and E∥ are the Young's modulus of composite with randomly-oriented and unixially-aligned fillers, respectively. Eqn (25) and (26) can be applied for both the 1D and 2D fillers but it is worth noting that the definition of s is sometimes slightly different.202,203 The parameter s is generally dependent on both the geometry and the boundary conditions of the reinforcement. Thostenson and Chou171 modified the equations of Halpin and Tsai by considering s for an aligned short fibre composite to be equal to
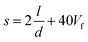 and for low volume fractions
and for low volume fractions 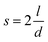 . The authors also showed that the effective fibre modulus is dependent on the nanotube modulus according to the equation:
. The authors also showed that the effective fibre modulus is dependent on the nanotube modulus according to the equation: 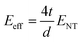 . This approach takes into account that the outer shell of the CNTs carries the majority (if not all) load that is applied, since the bonding between the outer layer and the inner layers was thought to be relatively poor. Thus, when substituting the above equations to the original Halpin–Tsai equation, the final equation that can express the nanocomposite modulus in terms of both the matrix and carbon nanotube properties is:171
. This approach takes into account that the outer shell of the CNTs carries the majority (if not all) load that is applied, since the bonding between the outer layer and the inner layers was thought to be relatively poor. Thus, when substituting the above equations to the original Halpin–Tsai equation, the final equation that can express the nanocomposite modulus in terms of both the matrix and carbon nanotube properties is:171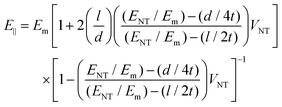 | (27) |
The nanotube diameter must be known for the application of the above equation, as it is very important to the reinforcement efficiency of CNTs, while it should also be noted that eqn (27) is valid only for l > d > 4t.
The excellent work of Liu and Brinson187 has clearly identified that the amount of interface in carbon nanotube-based composites, compared to nanoplatelet-based composites (assuming perfect dispersion and equal ability for polymer-filler interactions), is significantly larger. Thus, the mechanical reinforcing efficiency of nanotubes is higher than that of nanoplatelets of the same aspect ratio, for longitudinal properties of the aligned composites. Given the fact that for commercially-available CNTs and GRMs, the aspect ratio of GRMs is significantly lower than CNTs, the later are expected to perform better towards modulus reinforcement, when oriented along the tensile axis.
4.4 Other factors
From the micromechanical models discussed above, it can be seen that the size and spatial orientation of fillers play significant roles in determining the Young's modulus of composites, hence their quantification is of paramount value. However, it is worth pointing out that other factors are also influential. In particular, the waviness and wrinkling induced during manufacturing especially for fillers at nano- or micro-scale. They are thought to be the reason why the experimental values are lower than the ones predicted from theoretical models. Furthermore, agglomeration is another reason that many studies in the literature have used to interpret the deviation between the measured and estimated Young's modulus of composites. Due to their different scale and hence much large surface area than macroscale fibres, nanofillers are prone to agglomerate. Although practically difficult, attempts have been made to use models to predict the effect of agglomeration on the mechanical properties of composites.2045. Analysis of GRM- and CNT-based composites using Raman spectroscopy
Raman spectroscopy is a non-destructive experimental technique that can be used to characterise in detail all sp2 carbons from zero to three dimensions such as fullerenes (0D),205,206 carbon nanotubes (1D),207 graphene (2D)208 and graphite (3D).209 The physical properties of sp2 carbons that are correlated to electrons and phonons can be obtained through Raman spectroscopy, along with unique crystallographic and vibrational information.210 The usefulness of Raman spectroscopy in the study of sp2 carbons lies in the combination of the Raman process with optical absorption to (or emission from) an excited state; in this case the Raman intensity signal can be enhanced by several orders of magnitude by resonance.211 The specific effect is the reason why the one-atom-thick graphene can provide a strong and well-defined Raman signal or why individual single walled carbon nanotubes can be clearly identified. In this review, we will focus on the Raman spectroscopy of carbon-based nanocomposites and the information we can obtain through the application of this technique, since the use of Raman for the study of graphene or carbon nanotubes has been well documented and presented in detail in a number of highly-cited reports.212–2155.1 GRM-based nanocomposites
As in the case of carbon fibres or carbon nanotubes, Raman spectroscopy has been employed extensively for the study of the micromechanics of reinforcement by graphene-related materials (GRMs) in nanocomposites. The strong resonant Raman scattering, even from a one-atom-thick graphene flake, produces a well-defined Raman signal and enables the observation of a number of very interesting phenomena under various conditions (Fig. 16). One of the parameters that enhance the usefulness of Raman spectroscopy in the study of GRMs is the fact that pronounced differences can be observed between flakes with a different number of layers. For the case of monolayer graphene, the intensity of the characteristic 2D (or G′) (∼2690 cm−1) band is twice the intensity of the G band (∼ 1580 cm−1), while in the case of bilayer graphene flakes, the 2D band is comparable or even weaker than the G band. Furthermore, a change of shape can be seen due to the resonance effects in the electronic structure of the two-layer material, while also a shift of the 2D band towards higher wavenumbers can be observed for bilayer graphene.216 With increasing number of layers the 2D band shifts to even higher wavenumbers and more asymmetric/broader shape, while for more than 5 layers, the signal resembles the one of graphite. The defect-induced D band, which is usually found in different forms of graphitic carbon is most commonly observed in the case of imperfect graphene prepared by methods such as chemical vapour deposition (CVD) and thermal expansion, while it is very prominent in graphene oxide as a result of defects, vacancies and distortions induced during oxidation.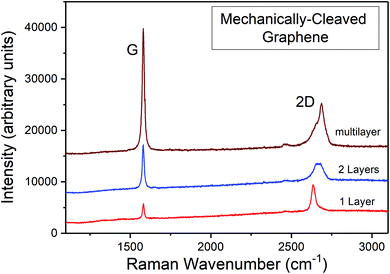 | ||
| Fig. 16 Raman spectra of graphene showing the difference in spectra between monolayer, bilayer and multilayer samples.198 | ||
Raman spectroscopy can be used for the detailed study of both free-standing graphene-related materials, graphene deposited on a flexible substrate or graphene-filled polymer nanocomposites. For this reason, this section will be divided into two parts: the investigation of the mechanical properties of (i) graphene flakes on a substrate and (ii) graphene-based polymer nanocomposites and “model” nanocomposites.
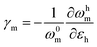 | (28) |
After a series of substitutions and transformations the final form of the Grüneisen parameter for the graphene bands takes the form:
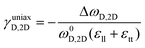 | (29) |
The Grüneisen parameters obtained were γG = 1.99, γD′ = 1.61, γD = 3.55 and βG = 0.99. Galiotis and coworkers218 further confirmed the original findings of Mohiuddin et al.219 when they deformed monolayer graphene flakes under tension and compression. The high flexibility of graphene was revealed by the buckling of the material at about 0.7% strain. Also, the ∂ω/∂ε was reduced from +25 cm−1 %−1 strain to zero at ∼0.7 strain, indicating the presence of residual strain. It should be noted that in the case of nanocomposites, the rate of decrease should be smaller, as simply deposited and uncoated flakes are more prone to detachment under compressive forces.
Polyzos et al.220 managed to suspend monolayer flakes for the evaluation of the “true” uniaxial deformation. This was achieved by sandwiching the monolayer flake between two PMMA layers and by suspending its central part by the removal of a section of PMMA with e-beam lithography. The authors reported on the splitting of both G and 2D bands of graphene and the results of the G band were in accordance with the ones obtained by Mohiuddin et al.219 for graphene suspended in air (Fig. 17a and b). On the other hand, the reported strain sensitivities of −84 cm−1 %−1 strain for the 2D1 and −94 cm−1 %−1 strain for the 2D2 components of the 2D peak are the largest values of phonon shifts reported for uniaxial deformation (Fig. 17c and d). This study reveals the difficulties in the application of uniaxial strain in 2D materials deposited on a flexible substrate and proposes a good practice for the manipulation of graphene on the nanoscale and the implementation of experimental mechanical measurements.
 | ||
| Fig. 17 (a) The G-peak of a suspended monolayer graphene flake at various strain levels; the splitting of the G− and G+ components are clearly seen. Each strain level corresponds to a different lateral position across graphene. (b) The two components of G peak (G− and G+) and the respective downshift of the G peak as a function of strain. The straight lines are least-squares-fitted to the experimental data. (c) The 2D-peak of suspended monolayer graphene in air at various strain levels (d) 2D sub-peaks as a function of strain. The straight lines in figures (b) and (d) are least-squares-fitted to the experimental data (Reproduced from ref. 220 with permission from The Royal Society of Chemistry). | ||
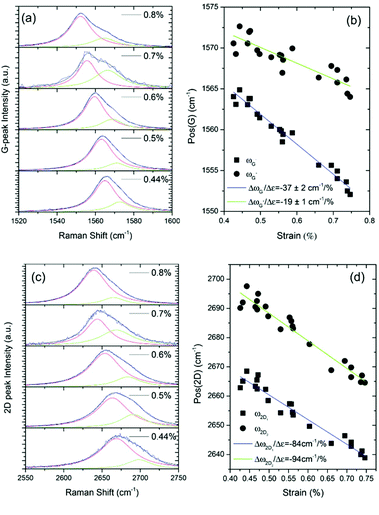
In addition to monolayer graphene, the investigation of graphene with a larger number of layers is of utmost importance for practical applications, since the inherent properties and behaviour of few- and many-layer graphene should be identified, as they will be used mostly for the fabrication of bulk nanocomposites. Gong et al.221 undertook a study on the effect of the number of layers on the downshift of the characteristic Raman bands and it was found that there is a decrease in the band shift rate with increasing layer number (Fig. 18a). Monolayer and bilayer graphene display almost the same redshift rate, while from that point on the shift of the 2D band decreases as a result of weak van der Waals forces between the layers and lower internal stress transfer. Additionally, the G band of trilayer graphene was reported to split into the G− and G+ components at higher strains in tension (Fig. 18b), while as expected, in compression, both Raman peaks (G and 2D) blue-shift up to a critical compressive strain (Fig. 18c and d).222
 | ||
| Fig. 18 Shifts with strain of the 2D band for adjacent monolayer, bilayer, and trilayers regions on a graphene flake showing monolayer, bilayer and trilayer regions, along with the shift with strain for the 2D band of a multilayer flake (all 2D bands were force fitted to a single Lorentzian peak)221 (Copyright 2012 by the American Chemical Society). (b) Evolution of the G Raman peak under uniaxial tensile strain in a trilayer part of a flake displaying regions with different thickness. The evolution of (c) G and (d) 2D Raman peaks under uniaxial compression for a trilayer flake.222 | ||
The trilayer graphene possesses a higher bending rigidity compared to the monolayer, however it has been reported that its critical strain is 4 times smaller than the one found in single layer graphene. Since earlier studies established that shear at the graphene-substrate interface is the mechanism of stress transfer, Anagnostopoulos et al.223 investigated the effect of the edges of graphene upon axial stress transfer by Raman mapping near the edges of a monolayer that was supported onto a SU-8/PMMA matrix. The authors revealed that the presence of unintentional doping, residual stresses (from the preparation procedure) and/or edge defects lead to a deviation from the classic shear-lag prediction for a region of ∼2 μm from the edge. This should be taken into account, especially in studies where mapping of graphene flakes is performed by Raman spectroscopy and the experimental results of stress versus position are (commonly) fitted with the shear-lag equation.
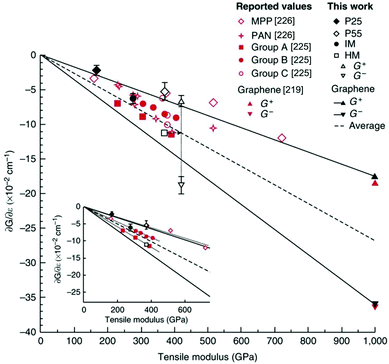
Raman spectroscopy can be also applied for monitoring the response of the G band of monolayer graphene in relation to the response of carbon fibres to the application of strain.224 A universal value of average phonon shift rate with axial stress has been proposed to be −5ω0−1 (cm−1 MPa−1) where ω0 is the G peak position at zero stress for both graphene and carbon fibres with an annular morphology. Another very important aspect of this work was the construction of a universal plot for the downshift of the G band that enables the quantification of the shift for all graphitic materials (Fig. 19).
 | ||
| Fig. 19 The characteristic downshift of the G band of graphene and carbon fibres versus the tensile modulus of the respective materials. The black solid and dashed lines correspond to fits to experimental data for graphene. The graphene G sub-bands values measured in this study and in ref. 219, are represented by black and red triangles, respectively. Also, from ref. 225 where a number of different types of fibres were studied, in red, the solid square points correspond to group A fibres, the solid circles correspond to group B, the open circles to group C, whereas the diamonds to MPP-CFs and the stars to various PAN-CFs from the work of Huang and Young.226 In black, data points for high modulus (HM) (open square), intermediate modulus (IM – full circle), P25 (full diamond) and P55 (open diamond) CFs measured in this work.224 The high modulus carbon fibre G band splitting and its projection onto the graphene average line are represented by the black open triangles. The inset shows the ∂ωG/∂σ least-squares line fits for group A (∂ωG/∂σ = 3 cm−1 GPa−1), B (2.3 cm−1 GPa−1) and MPP-CFs (1.5 cm−1 GPa−1) as dotted lines. The other symbols in the inset have the same meaning as in the main plot. The error bars represent the standard deviation from all measurements on the given fibre224 (Copyright 2011, Springer Nature Publishing Group). | ||
Chemical functionalization is considered to be one of the most prominent methods for the improvement of the interactions between a nanomaterial and a polymer. In this context, Zhang and coworkers227 functionalized monolayer graphene deposited onto a PMMA beam in order to improve the interactions between the two materials. The authors utilized an O3/H2O gaseous mixture in order to oxidize the monolayer under a controlled functionalization procedure. The strain distribution (εg) can be plotted as a function the position (x) along the length direction based on the shear lag model (eqn (16)). As mentioned earlier, the shear-lag equation suggests that the strain is maximized at the centre of the flake (x = 0) and the maximum interfacial shear stress occurs at the edges (x = ±L/2). From Fig. 20a it can be seen that eqn (16) fits well the experimental results at low strains, while beyond the critical sliding strain (εc) it is not able to predict the strain distribution as a result of interfacial sliding at the edges.
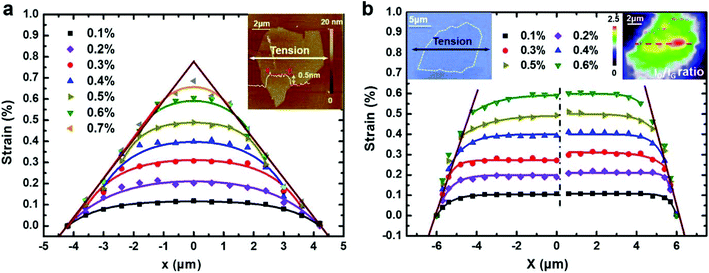 | ||
| Fig. 20 The strain distribution across the tensile axis of (a) a monolayer, pristine graphene and (b) oxidized graphene, at different strain levels. The inset in (a) shows the AFM image of the monolayer, while in (b, left panel) the optical image of the monolayer graphene and (b, right panel) the corresponding Raman contour map of ID/IG of the specific flake. The solid lines represent the fits based on the nonlinear shear-lag model (Reprinted (adapted) with permission from ref. 227. Copyright 2016 American Chemical Society). | ||
The results revealed that the stress transfer is more effective for functionalized monolayers (Fig. 20b), leading to enhanced mechanical properties due to the formation of hydrogen bonds at the interface. The interfacial shear strength (τc) was also derived based on the linear slope of the strain distribution according to:
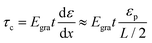 | (30) |
The majority of publications dealing with of strain in graphene and the in situ evaluation of the Raman spectra follow the uniaxial deformation of graphene-related materials. The application of biaxial strain and the study of the Raman spectra is also of utmost importance as this procedure is highly related to the performance of graphene in thin films, membranes and pressure sensors. A few studies have made an attempt to evaluate the behaviour of 2D materials under biaxial strain. Casiraghi and coworkers228 created graphene bubbles (or balloons) where monolayer and bilayer graphene was strained biaxially. The Grüneisen parameter was obtained and was in agreement with the report of Mohiuddin, while the small strain (∼1.2%) did not affect the stacking configuration. It was also reported that doping and strain caused by the interactions of graphene with the substrate, can also affect the Grüneisen parameters and these are the most important reasons why there are variations in the literature regarding the Grüneisen parameters of graphene. For example, in the work of Ding et al.,229 piezoelectric actuators were used for the application of biaxial strain but the Grüneisen parameters of the D and 2D bands were different than the ones obtained from Casiraghi and coworkers228 (γD = 2.3 and γ2D = 2.98). In a manner similar to the previous study, Lee et al. applied pressure to graphene suspended over round holes and measured the strain after inducing a bulging of the samples, similar to balloons. The Grüneisen parameter were taken to be equal to γ = 2.2 ± 0.1 and the shear deformation potential was taken equal to β = 0.93 ± 0.04; thus, the strain was calculated by: Δωb = −2ω0γεb, where ω0 is the frequency of unstrained graphene and εb is the biaxial strain. The G peak shift was in the order of −13 cm−1 %−1 strain, while the biaxial modulus of monolayer graphene was equal to 2.4 ± 0.4 TPa, while for bilayer was equal to 2.0 ± 0.5 TPa. It should be noted that these values might be slightly higher than the usual values of the biaxial modulus of graphene, as the authors managed to apply a maximum strain of only 0.19%, while higher strains lead to softening of the material and a subsequent reduction of the modulus.
Androulidakis et al. utilized a cross-type shaped apparatus for the application of biaxial strain where the as 2D materials are deposited on the centre of the cross.230 The authors subjected a number of graphene related materials to controlled biaxial deformation and the mean values of ∂ω2D/∂ε and ∂ωG/∂ε for a monolayer graphene membrane were found to be equal to −148 ± 6 cm−1 %−1 strain and −62.3 ± 5 cm−1 %−1 strain respectively. Similar to the results from the application of uniaxial strain, bilayer graphene showed very similar shifts to monolayer graphene, while the increasing layer number led to a reduction of the shift rates as a result of cohesive failure within the flakes. Finally, Metzger et al.231 investigated graphene membranes that were deposited over a patterned substrate with shallow depressions. The authors observed that the membranes did not remain free-standing but adhered to the substrate despite the biaxial strain. The Grüneisen parameters obtained were close to the ones of Mohiuddin, while the downshift of the 2D band was slightly higher than the values reported by Androulidakis, of the order of 203 ± 20 cm−1 %−1 strain.
Most of the investigations discussed earlier were undertaken upon the deformation characteristics of flat graphene, but the case of wrinkled graphene presents a lot of interest as the majority of the graphene nanoplatelets that are commonly used as reinforcements in polymer composites display wrinkles and folds that reduce the reinforcing efficiency. Li et al.232 deposited CVD graphene on a poly(ethylene terephthalate) substrate and followed the uniaxial deformation mechanics of wrinkled graphene by Raman spectroscopy. It was found that the wrinkles separated the flat graphene into isolated islands with a size of ∼1 μm and the downshift of the 2D band was in the order of −12.8 cm−1 %−1 strain, less than 25% of the reference 2D band shift rate of ∼ −60 cm−1 %−1 strain (Fig. 21a). It should be noted though that the wrinkles examined in this case have little to do with the performance of wrinkled material in bulk composites, as the stress transfer length (1.2 μm) is probably lower than the critical length and this can explain the low shift rates. Moreover, this work deals with wrinkles constrained from flat graphene areas, a compression of 2–3% is developed upon cooling from ∼ 1000 °C, which leads to the formation of wrinkles, but such CVD material is highly unlikely to be used in composites.
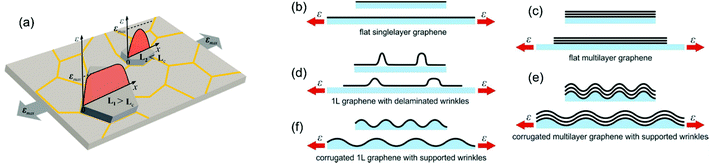 | ||
| Fig. 21 Schematic diagram (a) explaining the proposed stress transfer mechanism in wrinkled CVD graphene (li is the length of the i-crystallite and lc the critical transfer length) (Reprinted (adapted) with permission from ref. 232. Copyright 2015 American Chemical Society). Schematic of the morphology and qualitative stress transfer of a flat (b) mono- and (c) few-layer graphene, (d) wrinkled CVD graphene on polymer, and wrinkled (e) few- and (f) monolayer graphene (Reprinted (adapted) with permission from ref. 86. Copyright 2017 American Chemical Society). | ||
Anagnostopoulos et al.233 developed a similar CVD graphene/epoxy system and the redshift of the 2D band displayed a rate of ∼−18 cm−1 %−1 strain up to 1.4% strain, that is less than 30% than the one expected for a flat monolayer graphene. As shown in a study234 the group of Galiotis managed to create similar mosaic patterns to those observed in CVD graphene by means of lateral wrinkling induced by tension and Euler buckling resulting from uniaxial compression upon unloading. The same group has also provided evidence86 that the “corrugation” of flat graphene enhances the load bearing capability of few-layer graphene, as compared to flat specimen (Fig. 21b–e). The authors commented that the interfacial shear stress between the graphene and the polymer increased due to wrinkling and the downshift of the characteristic 2D band was in the order of −57 cm−1 %−1 strain for both monolayer, bilayer and trilayer graphene (Table 1). This was unexpected since it is known that for increasing layer number, the interlayer coupling cannot transfer the load efficiently. The exceptional performance of the wrinkled material was attributed to the small amplitude wrinkled morphology due to the enhanced shear strength of the interface. It should be noted at this point that the definition of wrinkling is very broad thus its effect is difficult to quantify. Finally, in a very recent study, Li et al.235 came up with an analytical equation to quantity the effect of different types of wrinkles and folds on graphene, after applying strain engineering to wrinkled and folded graphene. It was found that wrinkles do not reduce the reinforcement efficiency significantly when majority of graphene still conforms to substrate, while when graphene detaches from substrate its efficiency drops significantly as a result of delamination.
| Thickness (no. of layers) | ∂Pos (2D)/∂ε (cm−1 %−1) | ∂Pos (G+)/∂ε (cm−1 %−1) | ∂Pos (G−)/∂ε (cm−1 %−1) | |
|---|---|---|---|---|
| Wrinkled flakes | 1 | −57.4 ± 3.0 | −9.7 ± 0.8 | −29.6 ± 1.1 |
| 2 | −57.1 ± 1.5 | −11.4 ± 1.5 | −28.2 ± 1.3 | |
| 3 | −57.1 ± 2.8 | −12.7 ± 1.1 | −29.8 ± 1.0 | |
| ≪Flat≫ flakes | 2 | −48.6 ± 2.5 | −11.6 ± 0.7 | −27.9 ± 1.0 |
| 3 | −28.6 ± 1.4 | −6.5 ± 1.8 | −18.3 ± 1.2 |
Another material that presents a highly-wrinkled, 2D morphology is graphene oxide (GO). Generally, the study of the application of strain to GO and the in situ Raman measurements presents a number of challenges due to the presence of the functional groups that damage the graphene lattice and give rise to the defect-activated 2D band. In addition, GO is also vulnerable to damage from the laser beam as thermal- or photo-reduction of the material can take place. Additionally, the absence of the strain-sensitive 2D band is another limiting factor for the study of GO with Raman. Young and coworkers analysed the deformation micromechanics of GO by strain engineering.236 Interestingly, the results showed that the number of GO layers does not affect the reinforcement efficiency of GO; this effect is possibly associated with the enhanced interlayer adhesion GO due to the functionalisation, which is already too large even for few-layer GO and as a consequence the interlayer stress transfer is not effective. Moreover, the degree of layer exfoliation is not expected to play any role on the mechanical reinforcement in GO-based nanocomposites. The application of strain (up to 1%) led to a downshift of the D band in the order of −14.9 cm−1 %−1 strain. Interestingly, when the authors mapped the strain distribution in a GO flake, the strain profile remained constant along the flake, which is in contrast to what is observed for monolayer graphene, where the strain increases from the edges and remains constant only at the centre of the flake, in accordance with the expectation from the shear-lag theory. This observation, along with the poor resolution of the GO edges under the microscope and the spatial resolution of Raman spectrometer (1–2 μm) do not allow the determination of the critical length for reinforcement, making the classical shear-lag theory not applicable for this specific material.
The product ns depends on both the degree of interaction of the graphene flake with the matrix and the morphology of the flake and of the strain mapping at 0.4% strain it was found to be equal to 20, showing that the behaviour could be modelled. Furthermore, the critical length (lc) for the evaluation of the quality of reinforcement from graphene flakes was obtained, and according to its definition, it is the product of 2× the distance over which the strain rises from the fibre ends to the plateau. In this case, it is ∼3 μm, while it is generally thought that the fibre length in order to obtain good reinforcement should be ∼10lc, revealing that flakes of around 30 μm diameter are needed to reinforce a polymer significantly.
The same group also reported on the use of Raman spectroscopy for mapping the strain in a model nanocomposite consisting of graphene sandwiched between two thin layers of SU-8 and deposited onto a PMMA beam.237 Once again, the strong resonance from graphene enabled the authors to monitor the stress-induced band shifts and map the strain distribution. The mapping procedure revealed clearly the development of cracks as a result of fragmentation at 0.8% strain (Fig. 22). As this strain is very low for a graphene monolayer to undergo fragmentation, it is quite possible that cracking took place only in the SU-8 coatings. Moreover, the authors showed that the interfacial shear stress (IFSS) in the fragments was only ∼0.25 MPa, an order of magnitude lower than the IFSS before fragmentation. A further study of model nanocomposites where graphene was deposited onto a PMMA beam and then coated with an epoxy resin, revealed that the rate of band shift per unit strain for monolayer graphene is independent of whether the coating exists or not221 (Fig. 23a). On the other hand, for the case of bilayer graphene, the poor stress transfer between the graphene layers led to a lower rate of band shift for the uncoated specimen (Fig. 23b). For bulk composites, this means that bilayer graphene is equally effective for mechanical reinforcement, to monolayer graphene, while only 15% of the efficiency is lost with trilayer graphene, while according to the authors for more than 7 layers of graphene, the reinforcing efficiency drops to half that of monolayer graphene.
 | ||
| Fig. 22 Strain contour mapping through Raman spectroscopy over the coated graphene monolayer in the relaxed states and reloaded to 0.8% and 0.6% strain (Reprinted (adapted) with permission from ref. 237. Copyright 2011 American Chemical Society). | ||
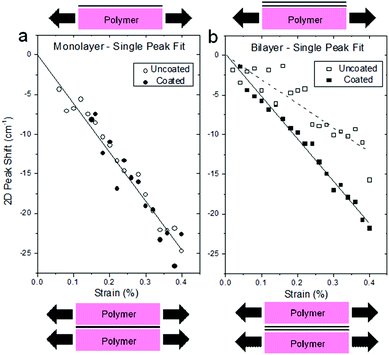 | ||
| Fig. 23 Downshift of the 2D Raman band of graphene during deformation upon the PMMA beam (laser excitation 633 nm). (a) A monolayer graphene flake deformed before and after coating with SU-8 epoxy-based negative photoresist. (b) A graphene bilayer deformed before and after coating with SU-8. (Schematic diagrams of the deformation of the uncoated (above) and coated (below) graphene are also included). (Reprinted (adapted) with permission from ref. 221. Copyright 2012 American Chemical Society). | ||
In a recent, interesting study of Eichorn and coworkers, the authors created a model bilayer graphene/nanocellulose composite and studied the deformation behaviour by applying strain.238 A quite high stress transfer efficiency of 66% was derived at the cellulose/graphene interface, while the splitting of the G band enabled the calculation of shear strain in the graphene. Moreover, the stress uptake and the compression buckling strain in model graphene monolayer nanocomposites was evaluated by Frank et al. by monitoring the shift of the G or 2D Raman bands.239 The compression strain led to a decrease in the values of ∂ωG,2D/∂ε up to a point where the slope started to increase, indicative of progressive buckling which leads to the collapse of the flakes. The critical buckling strain, as expected, depends on the size of the flakes and their geometrical characteristics.
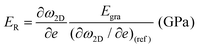 | (31) |
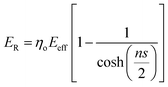 | (32) |
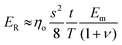 | (33) |
The application of both equations Ef and ER in the study of Liu et al.55 enabled the effective aspect ratio of the graphene nanoplatelets in bulk nanocomposites to be quantified, while as was expected the modulus from Raman spectroscopy was higher than that obtained from the tensile measurements. This comes as a result of the application of Raman spectroscopy to flakes that are axially aligned to the surface of the sample (so that ηo = 1), while the GNPs were partially aligned in the bulk composites. In the same study it is also clearly shown that the effective aspect ratio (seff) is pronouncedly reduced with increased filler loading due to agglomeration between graphene nanoplatelets.
5.2 CNT-based composites
The combination of the versatility of Raman spectroscopy along with the strong resonance from carbon nanotubes8 can provide a wealth of information regarding the effect of CNTs in polymer nanocomposites. A number of research investigations have applied Raman for the evaluation of the nanotube-polymer interactions, the dispersion characteristics, the orientation of nanotubes and the response of CNTs during the application of strain by following the Raman band shifts or the peak width changes.Polarized Raman spectroscopy has been proven very useful for the evaluation of the orientation of carbon nanotubes within a polymer matrix.241 The intensity of the Raman G band of CNTs is known to decrease monotonously with increasing angle between the polarization direction of the polarizer and the nanotube axis.242 Chang et al.243 used polarized Raman spectroscopy for the evaluation of orientation in a SWCNT/polypropylene fibre composite and observed that the scattering intensity of the G band decreased significantly when the angle between the fibre axis and the polarization of light changed from 0 to 90°, revealing an orientation of SWCNTs along the fibre direction. In addition, in an excellent study by Peijs and coworkers244 on oriented PVA/SWCNT tapes, the authors also used polarised Raman spectroscopy for the characterisation of the orientation of the nanotubes. They reported that when the scattered light is analysed parallel to the incident laser polarisation (VV geometry), the intensity of the Raman peaks is proportional to cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ where θ is the angle between the direction of the polariser and the fibre. The intensity as a function of the angle between the drawing direction and incident polarization (Ψ) is given by:
θ where θ is the angle between the direction of the polariser and the fibre. The intensity as a function of the angle between the drawing direction and incident polarization (Ψ) is given by:
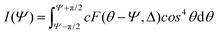 | (34) |
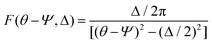 | (35) |
 | ||
| Fig. 24 (a) Raman spectra of oriented SWCNT-PVA composites, at different tape orientations, with respect to the incident polarization, (b) relative Raman intensity versus the angle between the polarization direction and the sample axis Ψ (0–π/2), at draw ratio 5, revealing a high degree of orientation of the SWCNTs.244 | ||
It should be noted that the deviations from linearity in the downshift of the characteristic Raman bands are indicators of an interface failure and thus, a less effective load transfer. Slippage of the CNTs (or the respective filler) takes place at the interface because the generally weak interfacial interactions cannot bear the shear stress, reducing this way the load transfer efficiency. Another important aspect of the study of Cooper et al. was the establishment of a method to calculate the effective modulus of nanotubes by using the universal calibration rate of −5 cm−1 %−1 GPa−1 for the 2D (G′) band in carbon fibres and assuming that this value was also valid for CNT composites. However, their approach led to wide bounds in terms of modulus calculation for the nanotubes since they did not take into account the polarization of the laser in their analysis. Deng et al.248 in a subsequent study modelled the effective modulus of the nanotubes in PVA/SWCNT composite by suggesting that the effective modulus Eeff can be obtained by:
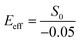 | (36) |
| S0 = 1.3 × SVV (0) | (37) |
| S0 = 3.3 × SVH (0) | (38) |
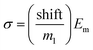 | (39) |
The effect of temperature on the Raman spectra of a CNT-based nanocomposite is also important, as a result of the differences in the coefficient of thermal expansion (CTE) and the rigidity of the polymer. For example, the CTE of SWCNTs is in the order of 10−6 °C−1, while the CTE of an epoxy resin is ∼6.5 × 10−5 °C−1.249 This difference leads to a large thermal stress in the filler-matrix interface. When the interfacial bonding is strong, then the interatomic distance of C atoms in the nanotube will increase due to thermal stress; this will cause a decrease of bonding potentials and a decline of the Raman vibration frequency. The work of Wang et al.250 clearly exhibited that thermal loading in epoxy composites reinforced with neat and functionalised SWCNTs leads to a downshift of the Raman G+ band with increasing temperature. Interestingly, pure SWCNTs (not mixed with the epoxy resin) showed a very small change in their Raman spectra, while all composite samples displayed a downshift, with the functionalized-SWCNT composites demonstrating a more efficient stress transfer (and a larger downshift) (Fig. 25a). On the other hand, it is well known that the modulus of the polymers is a temperature-dependent parameter. Thus, increasing the temperature can lead to a higher mobility of the macromolecular chains and subsequent decrease of the efficiency of stress transfer, while as expected, a decrease of the temperature leads to a restriction of the movement of the chains and to a stiffer matrix, which in turn contributes in a more efficient load transfer. This has been clearly demonstrated in the study of Zhao and Wagner,251 where the authors prepared a polyurethane acrylate (PUA)-SWCNT composite and measured the Raman band shifts under different temperatures. As expected, the slope of the 2D (G′) band at small strains (up to 2%) was higher at 235 K (−9.09 cm−1 %−1 strain) than 298 K (−4.67 cm−1 %−1 strain) (Fig. 25b). It is clear that the two phenomena are competitive to each other, thus the contributions from both should be taken into account when performing in situ Raman tests of carbon nanomaterials-reinforced composites at various temperatures.
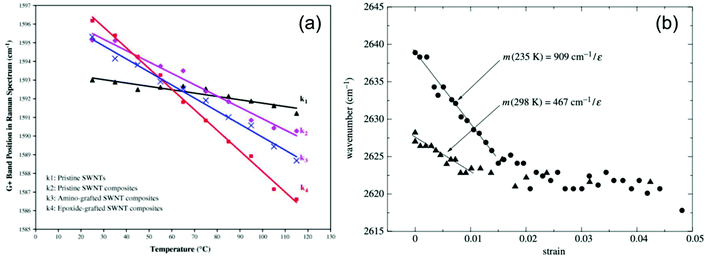 | ||
| Fig. 25 (a) G+ Raman band shift of the SWCNT-epoxy composites when heated250 (Copyright 2008, with permission from Elsevier), (b) Raman band shift of the SWCNT-PUA composites under different temperatures.251 | ||
In a more recent study by Young et al.252 the authors studied the interfacial and internal stress transfer in nanocomposites reinforced with different types of carbon nanotubes (SWCNTs and MWCNTs). As expected, the downshift of the 2D (G′) band in SWCNT-based composites was over four times higher than MWCNT composites (−14.1 ± 3.3 cm−1 %−1 strain over −3.4 ± 1.3 cm−1 %−1 strain) (Fig. 26a). Interfacial slippage took place for the SWCNTs at 0.5% strain. In the case of MWCNTs, it is the inner-wall slippage that delays the epoxy/MWCNT slippage at the interface, thus the interfacial stress transfer is considerably better. The authors modelled the deformation of the two types of nanotubes in the nanocomposites by introducing a stress transfer efficiency factor ki (0 ≤ ki ≤ 1), where for perfect stress transfer ki = 1 and for no stress transfer ki = 0. For the MWCNT/epoxy nanocomposites ki was found to be around 0.7, attributed to imperfect bonding between layers, while ki decreases with increasing number of layers (Fig. 26b). Importantly, the authors suggested that the load in MWCNT-based nanocomposites is taken mainly by the outside layer and the inner layers actually decrease the reinforcement efficiency. It should be pointed out that a similar stress transfer efficiency factor of around 0.7 was found for few-layer graphene (Fig. 18a),221 showing the similarity of the interlayer stress transfer phenomenon for the different carbon nanomaterials.
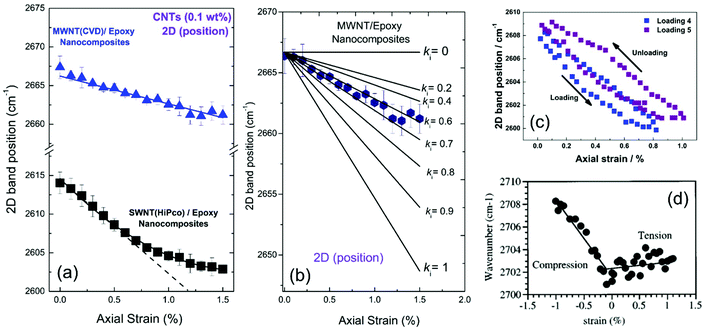 | ||
| Fig. 26 (a) Shift of the 2D (G′) band positions of SWCNT- and MWCNT-reinforced epoxy nanocomposites, (b) shift of the Raman 2D (G′) band (hexagons) and theoretical simulation as a function of strain (straight lines) at different values of stress transfer efficiency parameters252 (Copyright 2016, Springer Nature Publishing Group), (c) shift of the Raman 2D (G′) band for cyclic deformation for 0.8 and 1% maximum loading strain for an epoxy-SWCNT nanocomposite. Data showing both loading (blue squares) and unloading (purple squares) procedures254 (Copyright 2016, Springer Nature Publishing Group), (d) Raman Wavenumber shift as a function of strain for a MWCNT-epoxy nanocomposite168 (Reprinted with permission from AIP). | ||
Winey and coworkers253 on their study on SWCNT/PMMA fibres reported a downshift of the G band of −7.5 cm−1 %−1 strain for small strains (up to 0.2% strain). The authors also identified that during the unloading procedure the G peak position recovered back linearly at the same rate, while after the second loading, the G peak displayed the characteristic downshift at the same rate with the initial loading procedure, revealing the reversibility of load transfer. Kao and Young254 also looked into the cyclic deformation of epoxy/SWCNT composites and as expected, the maximum loading strain and loading cycles affected significantly the interfacial adhesion. A hysteresis loop was obtained from the mismatch between the loading and unloading processes, due to the damage at the nanotube-epoxy interface, which enabled the authors to calculate the energy dissipation and modelling of the interface damage (Fig. 26c).
The deformation of a MWCNT/epoxy nanocomposite under tension and compression was investigated in the work of Schadler et al.168 (Fig. 26d). The 2D (G′) band shifted upwards by ∼7 cm−1 under 1% compressive strain, while under tension, a slightly downward shift was reported. This observation was in contrast with the bulk mechanical properties of the composites, which indicated a ∼24% improvement of compression modulus and a ∼20% improvement in tension modulus. The difference arises from the different modes of deformation in the two experimental techniques. The MWCNTs are expected to carry the load from their outer tube to the inner tubes, but in practice this is difficult due to weak van der Waals interactions between the tubes. Therefore, under tension, the deformation of the inner walls is small. Thus, since the Raman signal is averaged for the whole MWCNT, the overall peak shift is insignificant. On the other hand, during compression the load is transferred effectively to the inner tubes through buckling and bending of the nanotubes, while slippage under compression is prevented due to seamless structure of MWCNTs and geometrical constrains the outer layers impose on the inner layers. This has as a result pronounced upward shifts of the 2D (G′) band.
The functionalization of CNTs for the improvement of both the dispersion and interfacial properties can also lead to a differentiation of the Raman band shifts, compared to the un-functionalized materials. For example, the work of Liu et al.255 revealed that the functionalization of SWCNTs with hydroxyl groups (SWCNT-OH) led to a more efficient stress transfer than neat SWCNTs in a PVA matrix; thus, the band shift of the PVA/0.5 wt% SWCNTs was in the order of −2.61 cm−1 %−1 strain, while the band shift of the PVA/0.6wt% SWCNT-OH was in the order of −36.9 cm−1 %−1 strain. The same conclusion comes out of the study of Lachman et al.256 where carboxylated SWCNTs (SWCNT-COOH) within a PVA matrix, displayed higher shifts at low strains, than the neat SWCNT-PVA composites, as a result of the better interfacial adhesion. However, the bulk mechanical properties of the SWCNT-PVA fibres were better than the COOH-SWCNT/PVA fibres, as a result of the carboxylation procedure, which is known to degrade the wall structure of nanotubes.
Even though the deformation of individual carbon nanotubes cannot be followed via the application of strain in combination with Raman spectroscopy as a result of their nanoscale dimensions, they can be used as coatings of different types of fibres and the local stress can then be studied by using Raman spectroscopy. The works of Jin et al.257,258 revealed that the coating of low- and high-modulus carbon fibres with carboxylated SWCNTs enabled them to analyse the fibre fragmentation during the deformation process and to follow the 2D Raman band shifts along the fibre length. The presence of the SWCNTs led to very high interfacial shear stress, in the order of 50 MPa and >30 MPa for low- and high-modulus carbon fibres, respectively, as a result of the additional bonding caused by the presence of the functional groups.
6. Conclusions and outlook
Graphene-related materials and carbon nanotubes offer unique opportunities for the evolution of polymer nanocomposites towards enhanced performance and multifunctionality. The reinforcement mechanisms of both types of nanocomposites have been reviewed thoroughly in the present manuscript by evaluating the inherent properties of the nanofillers and the parameters that affect significantly the ultimate properties of the polymer nanocomposites. Various well-established micromechanical theories that were developed initially for continuous composites have been examined for their applicability in polymer nanocomposites and there is overwhelming evidence that the elastic deformation of graphene- or nanotube-reinforced polymers can be modelled using classical composite micromechanics. Finally, the usefulness of Raman spectroscopy on the assessment of the mechanical properties of both nanofillers has been highlighted; numerous qualities and characteristics of sp2 carbon allotropes can be identified through the use of Raman spectroscopy. The shift rates of the Raman bands are highly dependent on the Young's modulus of the nanocarbons and thus, it has been shown how they can be used as universal stress sensors for the study of the mechanics of polymer nanocomposites.Overall it can be concluded that both types of nanofillers can reinforce low-modulus polymers significantly as a result of their inherent properties. Obviously, they display different reinforcement characteristics as a result of their completely different geometry and various parameters that originate from processing. The CNT-related materials, when aligned, display a remarkably-high aspect ratio that contributes to the creation of a large polymer-filler interface, which subsequently leads to very high levels of mechanical reinforcement. Thus, in this case the CNTs perform better than GRMs; however, alignment of CNTs even at a laboratory scale is quite challenging to achieve and scaling up of these processes at an industrial level is still uncertain. On the other hand, when CNTs are randomly oriented, they reinforce polymers less effectively than GRMs, because of their 1D geometry, which leads to a reduction of their effective modulus by 5, as can be concluded from their Krenchel orientation factor. In comparison, when GRMs are randomly oriented within a polymer, their effective modulus drops to less than half (8/15) as a consequence of their 2D geometry. Another major disadvantage of CNTs in the production of high-performing polymer nanocomposites is the very large increase in the viscosity of the final materials, which comes as a result of the formation of entanglements between CNTs, leading to a significantly poorer dispersion and a reduction of the effective aspect ratio of nanotubes. On the other hand, graphene related materials are much easier to process at higher loadings, as the viscosity of the polymer-graphene mixture is commonly significantly lower. One additional advantage of nanoplatelet-type materials such as GRMs, is that they can display an increased ability to alter a larger zone of polymer than nanotubes as a result of their micron-size lateral dimensions, through the creation of cooperating regions of altered dynamics, which can interact with each over above a certain percolation threshold volume fraction.
Despite the relatively high level of understanding of the mechanical reinforcement mechanisms of polymer nanocomposites with GRMs or CNTs, the impressive mechanical properties of both nanofillers still have not been fully realised in composite structures. The creation of continuous composites with lightweight spun fibres produced by CNTs or GRMs can be a solution to this problem, where both the unique multifunctional properties of both nanocarbons could be employed along with enhanced performance at very high filler loadings. Obviously the 1D materials (CNTs) are more appropriate than 2D materials (GRMs) for the creation of continuous fibres, leading to high inter-tube stress transfer and so far, CNT-based fibres seem to outperform GRM-based ones. Another critical aspect for the maximization of the performance of both nanocarbons in polymer nanocomposites is the precise engineering of the polymer-filler interface, that contributes significantly to the mechanical properties of the composites. Direct growth of CNTs or graphene onto macroscale glass/carbon fibres can lead to an increased cross-plane improvement in interlaminar shear stress, while evidently, the chemical modification of both fillers can enhance the polymer-filler interactions and as a consequence, the mechanical properties.
Even though the mechanical reinforcement characteristics of both nanocarbons has been explored for numerous polymer matrices, a number of challenges still exist and prevent full understanding of the reinforcement mechanisms, maximization of the performance of the composites and production of such composites extensively in an industrial scale. For example, the scale-up of the production of high-quality and low-cost GRMs is a major issue that reflects on both the commercialization and ultimate properties of the materials. From a modelling viewpoint, the mechanical strength of the polymer nanocomposites and the extent of the interfacial zone for both nanofillers should be analysed, while in terms of production the effective toughening of various polymers at low filler contents and the formation of composites with hybrid (1D:2D) nanofillers should be explored.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 Research and Innovation Programme under grant agreement no. 785219, the Royal Academy of Engineering and Morgan Advanced Materials.References
- E. T. Thostenson, Z. Ren and T.-W. Chou, Advances in the science and technology of carbon nanotubes and their composites: a review, Compos. Sci. Technol., 2001, 61(13), 1899–1912 CrossRef CAS.
- D. G. Papageorgiou, I. A. Kinloch and R. J. Young, Mechanical properties of graphene and graphene-based nanocomposites, Prog. Mater. Sci., 2017, 90, 75–127 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. Morozov, D. Jiang, Y. Zhang, S. Dubonos, I. Grigorieva and A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306(5696), 666–669 CrossRef CAS PubMed.
- R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. Peres and A. K. Geim, Fine structure constant defines visual transparency of graphene, Science, 2008, 320(5881), 1308 CrossRef CAS PubMed.
- L. Gong, I. A. Kinloch, R. J. Young, I. Riaz, R. Jalil and K. S. Novoselov, Interfacial stress transfer in a graphene monolayer nanocomposite, Adv. Mater., 2010, 22(24), 2694–2697 CrossRef CAS PubMed.
- H. Cox, The elasticity and strength of paper and other fibrous materials, Br. J. Appl. Phys., 1952, 3(3), 72 CrossRef.
- A. Kelly and W. Tyson, Tensile properties of fibre-reinforced metals: copper/tungsten and copper/molybdenum, J. Mech. Phys. Solids, 1965, 13(6), 329–350 CrossRef CAS.
- R. Saito, M. Hofmann, G. Dresselhaus, A. Jorio and M. S. Dresselhaus, Raman spectroscopy of graphene and carbon nanotubes, Adv. Phys., 2011, 60(3), 413–550 CrossRef CAS.
- G. Marom and H. D. Wagner, Should polymer nanocomposites be regarded as molecular composites?, J. Mater. Sci., 2017, 52(14), 8357–8361 CrossRef CAS.
- P. Calvert, Strength in disunity, Nature, 1992, 357(6377), 365–366 CrossRef.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321(5887), 385–388 CrossRef CAS PubMed.
- C. S. Ruiz-Vargas, H. L. Zhuang, P. Y. Huang, A. M. Van Der Zande, S. Garg, P. L. McEuen, D. A. Muller, R. G. Hennig and J. Park, Softened elastic response and unzipping in chemical vapor deposition graphene membranes, Nano Lett., 2011, 11(6), 2259–2263 CrossRef CAS PubMed.
- R. J. Nicholl, H. J. Conley, N. V. Lavrik, I. Vlassiouk, Y. S. Puzyrev, V. P. Sreenivas, S. T. Pantelides and K. I. Bolotin, The effect of intrinsic crumpling on the mechanics of free-standing graphene, Nat. Commun., 2015, 6, 8789 CrossRef CAS PubMed.
- G. López-Polín, C. Gómez-Navarro, V. Parente, F. Guinea, M. I. Katsnelson, F. Pérez-Murano and J. Gómez-Herrero, Increasing the elastic modulus of graphene by controlled defect creation, Nat. Phys., 2014, 11, 26 Search PubMed.
- J. H. Kim, J. H. Jeong, N. Kim, R. Joshi and G.-H. Lee, Mechanical properties of two-dimensional materials and their applications, J. Phys. D: Appl. Phys., 2018, 52(8), 083001 CrossRef.
- A. Shekhawat and R. O. Ritchie, Toughness and strength of nanocrystalline graphene, Nat. Commun., 2016, 7, 10546 CrossRef CAS PubMed.
- A. Zandiatashbar, G.-H. Lee, S. J. An, S. Lee, N. Mathew, M. Terrones, T. Hayashi, C. R. Picu, J. Hone and N. Koratkar, Effect of defects on the intrinsic strength and stiffness of graphene, Nat. Commun., 2014, 5, 3186 CrossRef PubMed.
- X. Zhao, D. G. Papageorgiou, L. Zhu, F. Ding and R. J. Young, The strength of mechanically-exfoliated monolayer graphene deformed on a rigid polymer substrate, Nanoscale, 2019, 11(30), 14339–14353 RSC.
- P. Zhang, L. Ma, F. Fan, Z. Zeng, C. Peng, P. E. Loya, Z. Liu, Y. Gong, J. Zhang and X. Zhang, Fracture toughness of graphene, Nat. Commun., 2014, 5, 3782 CrossRef CAS PubMed.
- G. Jung, Z. Qin and M. J. Buehler, Molecular mechanics of polycrystalline graphene with enhanced fracture toughness, Extreme Mech. Lett., 2015, 2, 52–59 CrossRef.
- M. J. Treacy, T. Ebbesen and J. Gibson, Exceptionally high Young's modulus observed for individual carbon nanotubes, Nature, 1996, 381(6584), 678 CrossRef CAS.
- E. W. Wong, P. E. Sheehan and C. M. Lieber, Nanobeam mechanics: elasticity, strength, and toughness of nanorods and nanotubes, Science, 1997, 277(5334), 1971–1975 CrossRef CAS.
- A. Krishnan, E. Dujardin, T. W. Ebbesen, P. N. Yianilos and M. M. J. Treacy, Young's modulus of single-walled nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(20), 14013–14019 CrossRef CAS.
- M.-F. Yu, B. S. Files, S. Arepalli and R. S. Ruoff, Tensile loading of ropes of single wall carbon nanotubes and their mechanical properties, Phys. Rev. Lett., 2000, 84(24), 5552 CrossRef CAS PubMed.
- J. P. Salvetat, A. J. Kulik, J. M. Bonard, G. A. D. Briggs, T. Stöckli, K. Méténier, S. Bonnamy, F. Béguin, N. A. Burnham and L. Forró, Elastic modulus of ordered and disordered multiwalled carbon nanotubes, Adv. Mater., 1999, 11(2), 161–165 CrossRef CAS.
- P. Poncharal, Z. Wang, D. Ugarte and W. A. De Heer, Electrostatic deflections and electromechanical resonances of carbon nanotubes, Science, 1999, 283(5407), 1513–1516 CrossRef CAS PubMed.
- M.-F. Yu, O. Lourie, M. J. Dyer, K. Moloni, T. F. Kelly and R. S. Ruoff, Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load, Science, 2000, 287(5453), 637–640 CrossRef CAS PubMed.
- B. I. Yakobson, Fullerenes, in Recent advances in the chemistry and physics of fullerenes and related materials, ed. K. M. Kadish and R. S. Ruoff, Electrochemical Society, Pennington, NJ, 1997, pp. 549–560 Search PubMed.
- M. B. Nardelli, B. I. Yakobson and J. Bernholc, Brittle and ductile behavior in carbon nanotubes, Phys. Rev. Lett., 1998, 81(21), 4656 CrossRef CAS.
- M. R. Falvo, G. J. Clary, R. M. Taylor II, V. Chi, F. P. Brooks Jr., S. Washburn and R. Superfine, Bending and buckling of carbon nanotubes under large strain, Nature, 1997, 389, 582 CrossRef CAS PubMed.
- D. Walters, L. Ericson, M. Casavant, J. Liu, D. Colbert, K. Smith and R. Smalley, Elastic strain of freely suspended single-wall carbon nanotube ropes, Appl. Phys. Lett., 1999, 74(25), 3803–3805 CrossRef CAS.
- B. G. Demczyk, Y. M. Wang, J. Cumings, M. Hetman, W. Han, A. Zettl and R. O. Ritchie, Direct mechanical measurement of the tensile strength and elastic modulus of multiwalled carbon nanotubes, Mater. Sci. Eng., A, 2002, 334(1), 173–178 CrossRef.
- H. Wagner, O. Lourie, Y. Feldman and R. Tenne, Stress-induced fragmentation of multiwall carbon nanotubes in a polymer matrix, Appl. Phys. Lett., 1998, 72(2), 188–190 CrossRef CAS.
- S. Ogata and Y. Shibutani, Ideal tensile strength and band gap of single-walled carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(16), 165409 CrossRef.
- T. Dumitrică, T. Belytschko and B. I. Yakobson, Bond-breaking bifurcation states in carbon nanotube fracture, J. Chem. Phys., 2003, 118(21), 9485–9488 CrossRef.
- G. G. Samsonidze, G. G. Samsonidze and B. I. Yakobson, Kinetic theory of symmetry-dependent strength in carbon nanotubes, Phys. Rev. Lett., 2002, 88(6), 065501 CrossRef PubMed.
- B. Peng, M. Locascio, P. Zapol, S. Li, S. L. Mielke, G. C. Schatz and H. D. Espinosa, Measurements of near-ultimate strength for multiwalled carbon nanotubes and irradiation-induced crosslinking improvements, Nat. Nanotechnol., 2008, 3(10), 626 CrossRef CAS PubMed.
- Y. Li, Z. Feng, L. Huang, K. Essa, E. Bilotti, H. Zhang, T. Peijs and L. Hao, Additive Manufacturing High Performance Graphene-based Composites: A Review, Composites, Part A, 2019, 105483 CrossRef.
- W. Chee, H. Lim, N. Huang and I. Harrison, Nanocomposites of graphene/polymers: a review, RSC Adv., 2015, 5(83), 68014–68051 RSC.
- V. Mittal, Functional polymer nanocomposites with graphene: a review, Macromol. Mater. Eng., 2014, 299(8), 906–931 CrossRef CAS.
- D. G. Papageorgiou, I. A. Kinloch and R. J. Young, Graphene/elastomer nanocomposites, Carbon, 2015, 95, 460–484 CrossRef CAS.
- E. Lago, P. S. Toth, G. Pugliese, V. Pellegrini and F. Bonaccorso, Solution blending preparation of polycarbonate/graphene composite: boosting the mechanical and electrical properties, RSC Adv., 2016, 6(100), 97931–97940 RSC.
- S. Park, S. He, J. Wang, A. Stein and C. W. Macosko, Graphene-polyethylene nanocomposites: Effect of graphene functionalization, Polymer, 2016, 104, 1–9 CrossRef CAS.
- H. Xu, L.-X. Gong, X. Wang, L. Zhao, Y.-B. Pei, G. Wang, Y.-J. Liu, L.-B. Wu, J.-X. Jiang and L.-C. Tang, Influence of processing conditions on dispersion, electrical and mechanical properties of graphene-filled-silicone rubber composites, Composites, Part A, 2016, 91, 53–64 CrossRef CAS.
- X. Cheng, V. Kumar, T. Yokozeki, T. Goto, T. Takahashi, J. Koyanagi, L. Wu and R. Wang, Highly conductive graphene oxide/polyaniline hybrid polymer nanocomposites with simultaneously improved mechanical properties, Composites, Part A, 2016, 82, 100–107 CrossRef CAS.
- C. Vallés, F. Beckert, L. Burk, R. Mülhaupt, R. J. Young and I. A. Kinloch, Effect of the C/O ratio in graphene oxide materials on the reinforcement of epoxy-based nanocomposites, J. Polym. Sci., Part B: Polym. Phys., 2016, 54(2), 281–291 CrossRef.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'Ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, High-yield production of graphene by liquid-phase exfoliation of graphite, Nat. Nanotechnol., 2008, 3, 563 CrossRef CAS PubMed.
- E.-C. Cho, J.-H. Huang, C.-P. Li, C.-W. Chang-Jian, K.-C. Lee, Y.-S. Hsiao and J.-H. Huang, Graphene-based thermoplastic composites and their application for LED thermal management, Carbon, 2016, 102, 66–73 CrossRef CAS.
- D. G. Papageorgiou, I. A. Kinloch and R. J. Young, Hybrid multifunctional graphene/glass-fibre polypropylene composites, Compos. Sci. Technol., 2016, 137, 44–51 CrossRef CAS.
- Y. Liu and J. Feng, An attempt towards fabricating reduced graphene oxide composites with traditional polymer processing techniques by adding chemical reduction agents, Compos. Sci. Technol., 2017, 140, 16–22 CrossRef CAS.
- P. Bhawal, S. Ganguly, T. K. Das, S. Mondal, S. Choudhury and N. C. Das, Superior electromagnetic interference shielding effectiveness and electro-mechanical properties of EMA-IRGO nanocomposites through the in situ reduction of GO from melt blended EMA-GO composites, Composites, Part B, 2018, 134, 46–60 CrossRef CAS.
- D. G. Papageorgiou, Z. Terzopoulou, A. Fina, F. Cuttica, G. Z. Papageorgiou, D. N. Bikiaris, K. Chrissafis, R. J. Young and I. A. Kinloch, Enhanced thermal and fire retardancy properties of polypropylene reinforced with a hybrid graphene/glass-fibre filler, Compos. Sci. Technol., 2018, 156, 95–102 CrossRef CAS.
- M. Liebscher, M.-O. Blais, P. Pötschke and G. Heinrich, A morphological study on the dispersion and selective localization behavior of graphene nanoplatelets in immiscible polymer blends of PC and SAN, Polymer, 2013, 54(21), 5875–5882 CrossRef CAS.
- D. G. Papageorgiou, M. Liu, Z. Li, C. Vallés, R. J. Young and I. A. Kinloch, Hybrid poly(ether ether ketone) composites reinforced with a combination of carbon fibres and graphene nanoplatelets, Compos. Sci. Technol., 2019, 175, 60–68 CrossRef CAS.
- M. Liu, D. G. Papageorgiou, S. Li, K. Lin, I. A. Kinloch and R. J. Young, Micromechanics of reinforcement of a graphene-based thermoplastic elastomer nanocomposite, Composites, Part A, 2018, 110, 84–92 CrossRef CAS.
- R. Santos, S. Mould, P. Formánek, M. Paiva and J. Covas, Effects of particle size and surface chemistry on the dispersion of graphite nanoplates in polypropylene composites, Polymers, 2018, 10(2), 222 CrossRef PubMed.
- R. Santos, C. Vilaverde, E. Cunha, M. Paiva and J. Covas, Probing dispersion and re-agglomeration phenomena upon melt-mixing of polymer-functionalized graphite nanoplates, Soft Matter, 2016, 12(1), 77–86 RSC.
- C. Vilaverde, R. M. Santos, M. C. Paiva and J. A. Covas, Dispersion and re-agglomeration of graphite nanoplates in polypropylene melts under controlled flow conditions, Composites, Part A, 2015, 78, 143–151 CrossRef CAS.
- Z. Xu and C. Gao, In situ polymerization approach to graphene-reinforced nylon-6 composites, Macromolecules, 2010, 43(16), 6716–6723 CrossRef CAS.
- X. Wang, Y. Hu, L. Song, H. Yang, W. Xing and H. Lu, In situ polymerization of graphene nanosheets and polyurethane with enhanced mechanical and thermal properties, J. Mater. Chem., 2011, 21(12), 4222–4227 RSC.
- N. D. Luong, U. Hippi, J. T. Korhonen, A. J. Soininen, J. Ruokolainen, L.-S. Johansson, J.-D. Nam and J. Seppälä, Enhanced mechanical and electrical properties of polyimide film by graphene sheets via in situ polymerization, Polymer, 2011, 52(23), 5237–5242 CrossRef.
- M. A. Milani, D. González, R. Quijada, N. R. Basso, M. L. Cerrada, D. S. Azambuja and G. B. Galland, Polypropylene/graphene nanosheet nanocomposites by in situ polymerization: synthesis, characterization and fundamental properties, Compos. Sci. Technol., 2013, 84, 1–7 CrossRef CAS.
- X. Zhao, Q. Zhang, Y. Hao, Y. Li, Y. Fang and D. Chen, Alternate Multilayer Films of Poly(vinyl alcohol) and Exfoliated Graphene Oxide Fabricated via a Facial Layer-by-Layer Assembly, Macromolecules, 2010, 43(22), 9411–9416 CrossRef CAS.
- C. Vallés, X. Zhang, J. Cao, F. Lin, R. J. Young, A. Lombardo, A. C. Ferrari, L. Burk, R. Mülhaupt and I. A. Kinloch, Graphene/Polyelectrolyte Layer-by-Layer Coatings for Electromagnetic Interference Shielding, ACS Appl. Nano Mater., 2019, 2(8), 5272–5281 CrossRef.
- F.-X. Xiao, M. Pagliaro, Y.-J. Xu and B. Liu, Layer-by-layer assembly of versatile nanoarchitectures with diverse dimensionality: a new perspective for rational construction of multilayer assemblies, Chem. Soc. Rev., 2016, 45(11), 3088–3121 RSC.
- S. Colonna, M. M. Bernal, G. Gavoci, J. Gomez, C. Novara, G. Saracco and A. Fina, Effect of processing conditions on the thermal and electrical conductivity of poly (butylene terephthalate) nanocomposites prepared via ring-opening polymerization, Mater. Des., 2017, 119, 124–132 CrossRef CAS.
- S. Colonna, O. Monticelli, J. Gomez, C. Novara, G. Saracco and A. Fina, Effect of morphology and defectiveness of graphene-related materials on the electrical and thermal conductivity of their polymer nanocomposites, Polymer, 2016, 102, 292–300 CrossRef CAS.
- A. Maio, R. Fucarino, R. Khatibi, S. Rosselli, M. Bruno and R. Scaffaro, A novel approach to prevent graphene oxide re-aggregation during the melt compounding with polymers, Compos. Sci. Technol., 2015, 119, 131–137 CrossRef CAS.
- N. Yousefi, M. M. Gudarzi, Q. Zheng, X. Lin, X. Shen, J. Jia, F. Sharif and J.-K. Kim, Highly aligned, ultralarge-size reduced graphene oxide/polyurethane nanocomposites: Mechanical properties and moisture permeability, Composites, Part A, 2013, 49, 42–50 CrossRef CAS.
- P.-G. Ren, D.-X. Yan, T. Chen, B.-Q. Zeng and Z.-M. Li, Improved properties of highly oriented graphene/polymer nanocomposites, J. Appl. Polym. Sci., 2011, 121(6), 3167–3174 CrossRef CAS.
- S. Wu, R. B. Ladani, J. Zhang, E. Bafekrpour, K. Ghorbani, A. P. Mouritz, A. J. Kinloch and C. H. Wang, Aligning multilayer graphene flakes with an external electric field to improve multifunctional properties of epoxy nanocomposites, Carbon, 2015, 94, 607–618 CrossRef CAS.
- X. Li, G. B. McKenna, G. Miquelard-Garnier, A. Guinault, C. Sollogoub, G. Regnier and A. Rozanski, Forced assembly by multilayer coextrusion to create oriented graphene reinforced polymer nanocomposites, Polymer, 2014, 55(1), 248–257 CrossRef CAS.
- I. Vlassiouk, G. Polizos, R. Cooper, I. Ivanov, J. K. Keum, F. Paulauskas, P. Datskos and S. Smirnov, Strong and Electrically Conductive Graphene-Based Composite Fibers and Laminates, ACS Appl. Mater. Interfaces, 2015, 7(20), 10702–10709 CrossRef CAS PubMed.
- P. Liu, Z. Jin, G. Katsukis, L. W. Drahushuk, S. Shimizu, C.-J. Shih, E. D. Wetzel, J. K. Taggart-Scarff, B. Qing, K. J. Van Vliet, R. Li, B. L. Wardle and M. S. Strano, Layered and scrolled nanocomposites with aligned semi-infinite graphene inclusions at the platelet limit, Science, 2016, 353(6297), 364 CrossRef CAS PubMed.
- M. Yoonessi, J. R. Gaier, J. A. Peck and M. A. Meador, Controlled direction of electrical and mechanical properties in nickel tethered graphene polyimide nanocomposites using magnetic field, Carbon, 2015, 84, 375–382 CrossRef CAS.
- Y. Yang, X. Li, M. Chu, H. Sun, J. Jin, K. Yu, Q. Wang, Q. Zhou and Y. Chen, Electrically assisted 3D printing of nacre-inspired structures with self-sensing capability, Sci. Adv., 2019, 5(4), eaau9490 CrossRef CAS PubMed.
- Z. Li, R. J. Young, N. R. Wilson, I. A. Kinloch, C. Vallés and Z. Li, Effect of the orientation of graphene-based nanoplatelets upon the Young's modulus of nanocomposites, Compos. Sci. Technol., 2016, 123, 125–133 CrossRef CAS.
- Z. Li, R. J. Young, I. A. Kinloch, N. R. Wilson, A. J. Marsden and A. P. A. Raju, Quantitative determination of the spatial orientation of graphene by polarized Raman spectroscopy, Carbon, 2015, 88, 215–224 CrossRef CAS.
- C. Vallés, A. M. Abdelkader, R. J. Young and I. A. Kinloch, The effect of flake diameter on the reinforcement of few-layer graphene–PMMA composites, Compos. Sci. Technol., 2015, 111, 17–22 CrossRef.
- C. Vallés, A. M. Abdelkader, R. J. Young and I. A. Kinloch, Few layer graphene–polypropylene nanocomposites: the role of flake diameter, Faraday Discuss., 2014, 173(0), 379–390 RSC.
- S. G. Prolongo, A. Jiménez-Suárez, R. Moriche and A. Ureña, Graphene nanoplatelets thickness and lateral size influence on the morphology and behavior of epoxy composites, Eur. Polym. J., 2014, 53, 292–301 CrossRef CAS.
- Z. Li, T. J. A. Slater, X. Ma, Y. Yu, R. J. Young and T. L. Burnett, The taxonomy of graphite nanoplatelets and the influence of nanocomposite processing, Carbon, 2019, 142, 99–106 CrossRef CAS.
- S. Li, Z. Li, T. L. Burnett, T. J. A. Slater, T. Hashimoto and R. J. Young, Nanocomposites of graphene nanoplatelets in natural rubber: microstructure and mechanisms of reinforcement, J. Mater. Sci., 2017, 52(16), 9558–9572 CrossRef CAS.
- X. Wu, T. Lin, Z. Tang, B. Guo and G. Huang, Natural rubber/graphene oxide composites: Effect of sheet size on mechanical properties and strain-induced crystallization behavior, eXPRESS Polym. Lett., 2015, 9(8), 672–685 CrossRef CAS.
- V. M. Pereira, A. H. Castro Neto, H. Y. Liang and L. Mahadevan, Geometry, Mechanics, and Electronics of Singular Structures and Wrinkles in Graphene, Phys. Rev. Lett., 2010, 105(15), 156603 CrossRef PubMed.
- C. Androulidakis, E. N. Koukaras, J. Rahova, K. Sampathkumar, J. Parthenios, K. Papagelis, O. Frank and C. Galiotis, Wrinkled Few-Layer Graphene as Highly Efficient Load Bearer, ACS Appl. Mater. Interfaces, 2017, 9(31), 26593–26601 CrossRef CAS PubMed.
- M. A. Rafiee, J. Rafiee, I. Srivastava, Z. Wang, H. Song, Z.-Z. Yu and N. Koratkar, Fracture and Fatigue in Graphene Nanocomposites, Small, 2010, 6(2), 179–183 CrossRef CAS PubMed.
- T. Ramanathan, A. A. Abdala, S. Stankovich, D. A. Dikin, M. Herrera-Alonso, R. D. Piner, D. H. Adamson, H. C. Schniepp, X. Chen, R. S. Ruoff, S. T. Nguyen, I. A. Aksay, R. K. Prud'Homme and L. C. Brinson, Functionalized graphene sheets for polymer nanocomposites, Nat. Nanotechnol., 2008, 3, 327 CrossRef CAS PubMed.
- M. A. Rafiee, J. Rafiee, Z. Wang, H. Song, Z.-Z. Yu and N. Koratkar, Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content, ACS Nano, 2009, 3(12), 3884–3890 CrossRef CAS PubMed.
- R. Moriche, S. G. Prolongo, M. Sánchez, A. Jiménez-Suárez, M. J. Sayagués and A. Ureña, Morphological changes on graphene nanoplatelets induced during dispersion into an epoxy resin by different methods, Composites, Part B, 2015, 72, 199–205 CrossRef CAS.
- Z. Wang and M. Devel, Periodic ripples in suspended graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(12), 125422 CrossRef.
- S.-H. Liao, P.-L. Liu, M.-C. Hsiao, C.-C. Teng, C.-A. Wang, M.-D. Ger and C.-L. Chiang, One-Step Reduction and Functionalization of Graphene Oxide with Phosphorus-Based Compound to Produce Flame-Retardant Epoxy Nanocomposite, Ind. Eng. Chem. Res., 2012, 51(12), 4573–4581 CrossRef CAS.
- V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zboril and K. S. Kim, Functionalization of Graphene: Covalent and Non-Covalent Approaches, Derivatives and Applications, Chem. Rev., 2012, 112(11), 6156–6214 CrossRef CAS PubMed.
- N. Rubio, H. Au, H. S. Leese, S. Hu, A. J. Clancy and M. S. P. Shaffer, Grafting from versus Grafting to Approaches for the Functionalization of Graphene Nanoplatelets with Poly(methyl methacrylate), Macromolecules, 2017, 50(18), 7070–7079 CrossRef CAS.
- B. Shen, W. Zhai, M. Tao, D. Lu and W. Zheng, Chemical functionalization of graphene oxide toward the tailoring of the interface in polymer composites, Compos. Sci. Technol., 2013, 77, 87–94 CrossRef CAS.
- S. Quiles-Díaz, P. Enrique-Jimenez, D. G. Papageorgiou, F. Ania, A. Flores, I. A. Kinloch, M. A. Gómez-Fatou, R. J. Young and H. J. Salavagione, Influence of the chemical functionalization of graphene on the properties of polypropylene-based nanocomposites, Composites, Part A, 2017, 100, 31–39 CrossRef.
- Y.-J. Wan, L.-X. Gong, L.-C. Tang, L.-B. Wu and J.-X. Jiang, Mechanical properties of epoxy composites filled with silane-functionalized graphene oxide, Composites, Part A, 2014, 64, 79–89 CrossRef CAS.
- P.-C. Ma, N. A. Siddiqui, G. Marom and J.-K. Kim, Dispersion and functionalization of carbon nanotubes for polymer-based nanocomposites: a review, Composites, Part A, 2010, 41(10), 1345–1367 CrossRef.
- M. Moniruzzaman and K. I. Winey, Polymer Nanocomposites Containing Carbon Nanotubes, Macromolecules, 2006, 39(16), 5194–5205 CrossRef CAS.
- Z. Spitalsky, D. Tasis, K. Papagelis and C. Galiotis, Carbon nanotube–polymer composites: chemistry, processing, mechanical and electrical properties, Prog. Polym. Sci., 2010, 35(3), 357–401 CrossRef CAS.
- N. G. Sahoo, S. Rana, J. W. Cho, L. Li and S. H. Chan, Polymer nanocomposites based on functionalized carbon nanotubes, Prog. Polym. Sci., 2010, 35(7), 837–867 CrossRef CAS.
- J. N. Coleman, U. Khan, W. J. Blau and Y. K. Gun'ko, Small but strong: a review of the mechanical properties of carbon nanotube–polymer composites, Carbon, 2006, 44(9), 1624–1652 CrossRef CAS.
- L. Wang, J. Qiu, E. Sakai and X. Wei, The relationship between microstructure and mechanical properties of carbon nanotubes/polylactic acid nanocomposites prepared by twin-screw extrusion, Composites, Part A, 2016, 89, 18–25 CrossRef CAS.
- M. Arjmand, T. Apperley, M. Okoniewski and U. Sundararaj, Comparative study of electromagnetic interference shielding properties of injection molded versus compression molded multi-walled carbon nanotube/polystyrene composites, Carbon, 2012, 50(14), 5126–5134 CrossRef CAS.
- F. H. Gojny, M. H. G. Wichmann, U. Köpke, B. Fiedler and K. Schulte, Carbon nanotube-reinforced epoxy-composites: enhanced stiffness and fracture toughness at low nanotube content, Compos. Sci. Technol., 2004, 64(15), 2363–2371 CrossRef CAS.
- D. Xiang, E. Harkin-Jones, D. Linton and P. Martin, Structure, mechanical, and electrical properties of high-density polyethylene/multi-walled carbon nanotube composites processed by compression molding and blown film extrusion, J. Appl. Polym. Sci., 2015, 132(42), 42665 CrossRef.
- M. A. L. Manchado, L. Valentini, J. Biagiotti and J. M. Kenny, Thermal and mechanical properties of single-walled carbon nanotubes–polypropylene composites prepared by melt processing, Carbon, 2005, 43(7), 1499–1505 CrossRef CAS.
- M. T. Müller, B. Krause, B. Kretzschmar and P. Pötschke, Influence of a supplemental filler in twin-screw extruded PP/CNT composites using masterbatch dilution, AIP Conf. Proc., 2019, 2055(1), 090006 CrossRef.
- M. Hoikkanen, M. Poikelispää, A. Das, U. Reuter, W. Dierkes and J. Vuorinen, Evaluation of mechanical and dynamic mechanical properties of multiwalled carbon nanotube-based ethylene–propylene copolymer composites mixed by masterbatch dilution, J. Compos. Mater., 2016, 50(29), 4093–4101 CrossRef CAS.
- I. Burmistrov, N. Gorshkov, I. Ilinykh, D. Muratov, E. Kolesnikov, E. Yakovlev, I. Mazov, J. P. Issi and D. Kuznetsov, Mechanical and electrical properties of ethylene-1-octene and polypropylene composites filled with carbon nanotubes, Compos. Sci. Technol., 2017, 147, 71–77 CrossRef CAS.
- G. Vaganov, V. Yudin, J. Vuorinen and E. Molchanov, Influence of multiwalled carbon nanotubes on the processing behavior of epoxy powder compositions and on the mechanical properties of their fiber reinforced composites, Polym. Compos., 2016, 37(8), 2377–2383 CrossRef CAS.
- F. F. Alves, A. A. Silva and B. G. Soares, Epoxy—MWCNT composites prepared from master batch and powder dilution: Effect of ionic liquid on dispersion and multifunctional properties, Polym. Eng. Sci., 2018, 58(10), 1689–1697 CrossRef CAS.
- T. Villmow, B. Kretzschmar and P. Pötschke, Influence of screw configuration, residence time, and specific mechanical energy in twin-screw extrusion of polycaprolactone/multi-walled carbon nanotube composites, Compos. Sci. Technol., 2010, 70(14), 2045–2055 CrossRef CAS.
- P. Pötschke, A. R. Bhattacharyya and A. Janke, Melt mixing of polycarbonate with multiwalled carbon nanotubes: microscopic studies on the state of dispersion, Eur. Polym. J., 2004, 40(1), 137–148 CrossRef.
- T. Villmow, P. Pötschke, S. Pegel, L. Häussler and B. Kretzschmar, Influence of twin-screw extrusion conditions on the dispersion of multi-walled carbon nanotubes in a poly(lactic acid) matrix, Polymer, 2008, 49(16), 3500–3509 CrossRef CAS.
- T. McNally, P. Pötschke, P. Halley, M. Murphy, D. Martin, S. E. J. Bell, G. P. Brennan, D. Bein, P. Lemoine and J. P. Quinn, Polyethylene multiwalled carbon nanotube composites, Polymer, 2005, 46(19), 8222–8232 CrossRef CAS.
- T. Villmow, S. Pegel, P. Pötschke and U. Wagenknecht, Influence of injection molding parameters on the electrical resistivity of polycarbonate filled with multi-walled carbon nanotubes, Compos. Sci. Technol., 2008, 68(3), 777–789 CrossRef CAS.
- P. Pötschke, S. M. Dudkin and I. Alig, Dielectric spectroscopy on melt processed polycarbonate—multiwalled carbon nanotube composites, Polymer, 2003, 44(17), 5023–5030 CrossRef.
- I. Alig, P. Pötschke, D. Lellinger, T. Skipa, S. Pegel, G. R. Kasaliwal and T. Villmow, Establishment, morphology and properties of carbon nanotube networks in polymer melts, Polymer, 2012, 53(1), 4–28 CrossRef CAS.
- I. Alig, T. Skipa, D. Lellinger, M. Bierdel and H. Meyer, Dynamic percolation of carbon nanotube agglomerates in a polymer matrix: comparison of different model approaches, Phys. Status Solidi B, 2008, 245(10), 2264–2267 CrossRef CAS.
- F. Du, J. E. Fischer and K. I. Winey, Coagulation method for preparing single-walled carbon nanotube/poly (methyl methacrylate) composites and their modulus, electrical conductivity, and thermal stability, J. Polym. Sci., Part B: Polym. Phys., 2003, 41(24), 3333–3338 CrossRef CAS.
- R. Haggenmueller, J. E. Fischer and K. I. Winey, Single wall carbon nanotube/polyethylene nanocomposites: nucleating and templating polyethylene crystallites, Macromolecules, 2006, 39(8), 2964–2971 CrossRef CAS.
- K. Wiemann, W. Kaminsky, F. H. Gojny and K. Schulte, Synthesis and Properties of Syndiotactic Poly(propylene)/Carbon Nanofiber and Nanotube Composites Prepared by in situ Polymerization with Metallocene/MAO Catalysts, Macromol. Chem. Phys., 2005, 206(15), 1472–1478 CrossRef CAS.
- A. A. Mamedov, N. A. Kotov, M. Prato, D. M. Guldi, J. P. Wicksted and A. Hirsch, Molecular design of strong single-wall carbon nanotube/polyelectrolyte multilayer composites, Nat. Mater., 2002, 1(3), 190–194 CrossRef CAS PubMed.
- K. J. Loh, J. Kim, J. P. Lynch, N. W. S. Kam and N. A. Kotov, Multifunctional layer-by-layer carbon nanotube–polyelectrolyte thin films for strain and corrosion sensing, Smart Mater. Struct., 2007, 16(2), 429 CrossRef CAS.
- M. Olek, J. Ostrander, S. Jurga, H. Möhwald, N. Kotov, K. Kempa and M. Giersig, Layer-by-Layer Assembled Composites from Multiwall Carbon Nanotubes with Different Morphologies, Nano Lett., 2004, 4(10), 1889–1895 CrossRef CAS.
- B. S. Shim and N. A. Kotov, Single-walled carbon nanotube combing during layer-by-layer assembly: From random adsorption to aligned composites, Langmuir, 2005, 21(21), 9381–9385 CrossRef CAS PubMed.
- D. E. Bergbreiter and K.-S. Liao, Covalent layer-by-layer assembly—an effective, forgiving way to construct functional robust ultrathin films and nanocomposites, Soft Matter, 2009, 5(1), 23–28 RSC.
- D. Bonduel, M. Mainil, M. Alexandre, F. Monteverde and P. Dubois, Supported coordination polymerization: a unique way to potent polyolefin carbon nanotube nanocomposites, Chem. Commun., 2005,(6), 781–783 RSC.
- S. Peeterbroeck, B. Lepoittevin, E. Pollet, S. Benali, C. Broekaert, M. Alexandre, D. Bonduel, P. Viville, R. Lazzaroni and P. Dubois, Polymer layered silicate/carbon nanotube nanocomposites: The catalyzed polymerization approach, Polym. Eng. Sci., 2006, 46(8), 1022–1030 CrossRef CAS.
- P. Pötschke, S. Pegel, M. Claes and D. Bonduel, A Novel Strategy to Incorporate Carbon Nanotubes into Thermoplastic Matrices, Macromol. Rapid Commun., 2008, 29(3), 244–251 CrossRef.
- E. T. Thostenson and T.-W. Chou, Aligned multi-walled carbon nanotube-reinforced composites: processing and mechanical characterization, J. Phys. D: Appl. Phys., 2002, 35(16), L77 CrossRef CAS.
- R. Beigmoradi, A. Samimi and D. Mohebbi-Kalhori, Engineering of oriented carbon nanotubes in composite materials, Beilstein J. Nanotechnol., 2018, 9(1), 415–435 CrossRef CAS PubMed.
- C. Martin, J. Sandler, A. Windle, M.-K. Schwarz, W. Bauhofer, K. Schulte and M. Shaffer, Electric field-induced aligned multi-wall carbon nanotube networks in epoxy composites, Polymer, 2005, 46(3), 877–886 CrossRef CAS.
- A. I. Oliva-Avilés, F. Avilés and V. Sosa, Electrical and piezoresistive properties of multi-walled carbon nanotube/polymer composite films aligned by an electric field, Carbon, 2011, 49(9), 2989–2997 CrossRef.
- C. Ma, W. Zhang, Y. Zhu, L. Ji, R. Zhang, N. Koratkar and J. Liang, Alignment and dispersion of functionalized carbon nanotubes in polymer composites induced by an electric field, Carbon, 2008, 46(4), 706–710 CrossRef CAS.
- S. U. Khan, J. R. Pothnis and J.-K. Kim, Effects of carbon nanotube alignment on electrical and mechanical properties of epoxy nanocomposites, Composites, Part A, 2013, 49, 26–34 CrossRef CAS.
- Y.-F. Zhu, C. Ma, W. Zhang, R.-P. Zhang, N. Koratkar and J. Liang, Alignment of multiwalled carbon nanotubes in bulk epoxy composites via electric field, J. Appl. Phys., 2009, 105(5), 054319 CrossRef.
- M. Abdalla, D. Dean, M. Theodore, J. Fielding, E. Nyairo and G. Price, Magnetically processed carbon nanotube/epoxy nanocomposites: Morphology, thermal, and mechanical properties, Polymer, 2010, 51(7), 1614–1620 CrossRef CAS.
- Y. He, S. Yang, H. Liu, Q. Shao, Q. Chen, C. Lu, Y. Jiang, C. Liu and Z. Guo, Reinforced carbon fiber laminates with oriented carbon nanotube epoxy nanocomposites: Magnetic field assisted alignment and cryogenic temperature mechanical properties, J. Colloid Interface Sci., 2018, 517, 40–51 CrossRef CAS PubMed.
- C. Ma, H.-Y. Liu, X. Du, L. Mach, F. Xu and Y.-W. Mai, Fracture resistance, thermal and electrical properties of epoxy composites containing aligned carbon nanotubes by low magnetic field, Compos. Sci. Technol., 2015, 114, 126–135 CrossRef CAS.
- C. Du, M. Li, M. Cao, S. Feng, H. Guo and B. Li, Enhanced thermal and mechanical properties of polyvinlydene fluoride composites with magnetic oriented carbon nanotube, Carbon, 2018, 126, 197–207 CrossRef CAS.
- T. Kimura, H. Ago, M. Tobita, S. Ohshima, M. Kyotani and M. Yumura, Polymer composites of carbon nanotubes aligned by a magnetic field, Adv. Mater., 2002, 14(19), 1380–1383 CrossRef CAS.
- E. Camponeschi, R. Vance, M. Al-Haik, H. Garmestani and R. Tannenbaum, Properties of carbon nanotube–polymer composites aligned in a magnetic field, Carbon, 2007, 45(10), 2037–2046 CrossRef CAS.
- M. Arjmand, M. Mahmoodi, G. A. Gelves, S. Park and U. Sundararaj, Electrical and electromagnetic interference shielding properties of flow-induced oriented carbon nanotubes in polycarbonate, Carbon, 2011, 49(11), 3430–3440 CrossRef CAS.
- Y. A. Kim, T. Hayashi, M. Endo, Y. Gotoh, N. Wada and J. Seiyama, Fabrication of aligned carbon nanotube-filled rubber composite, Scr. Mater., 2006, 54(1), 31–35 CrossRef CAS.
- T. H. Nam, K. Goto, K. Oshima, E. V. A. Premalal, Y. Shimamura, Y. Inoue, K. Naito and S. Ogihara, Mechanical property enhancement of aligned multi-walled carbon nanotube sheets and composites through press-drawing process, Adv. Compos. Mater., 2016, 25(1), 73–86 CrossRef CAS.
- P. Pötschke, H. Brünig, A. Janke, D. Fischer and D. Jehnichen, Orientation of multiwalled carbon nanotubes in composites with polycarbonate by melt spinning, Polymer, 2005, 46(23), 10355–10363 CrossRef.
- Q. Wang, J. Dai, W. Li, Z. Wei and J. Jiang, The effects of CNT alignment on electrical conductivity and mechanical properties of SWNT/epoxy nanocomposites, Compos. Sci. Technol., 2008, 68(7), 1644–1648 CrossRef CAS.
- C. Jolowsky, R. Sweat, J. G. Park, A. Hao and R. Liang, Microstructure evolution and self-assembling of CNT networks during mechanical stretching and mechanical properties of highly aligned CNT composites, Compos. Sci. Technol., 2018, 166, 125–130 CrossRef CAS.
- L. Jin, C. Bower and O. Zhou, Alignment of carbon nanotubes in a polymer matrix by mechanical stretching, Appl. Phys. Lett., 1998, 73(9), 1197–1199 CrossRef CAS.
- S. D. McCullen, D. R. Stevens, W. A. Roberts, S. S. Ojha, L. I. Clarke and R. E. Gorga, Morphological, Electrical, and Mechanical Characterization of Electrospun Nanofiber Mats Containing Multiwalled Carbon Nanotubes, Macromolecules, 2007, 40(4), 997–1003 CrossRef CAS.
- L. Jiang, H. Tu, Y. Lu, Y. Wu, J. Tian, X. Shi, Q. Wang, Y. Zhan, Z. Huang and H. Deng, Spherical and rodlike inorganic nanoparticle regulated the orientation of carbon nanotubes in polymer nanofibers, Chem. Phys. Lett., 2016, 650, 82–87 CrossRef CAS.
- H. Hou, J. J. Ge, J. Zeng, Q. Li, D. H. Reneker, A. Greiner and S. Z. D. Cheng, Electrospun Polyacrylonitrile Nanofibers Containing a High Concentration of Well-Aligned Multiwall Carbon Nanotubes, Chem. Mater., 2005, 17(5), 967–973 CrossRef CAS.
- F. Ko, Y. Gogotsi, A. Ali, N. Naguib, H. Ye, G. Yang, C. Li and P. Willis, Electrospinning of continuous carbon nanotube-filled nanofiber yarns, Adv. Mater., 2003, 15(14), 1161–1165 CrossRef CAS.
- R. Sen, B. Zhao, D. Perea, M. E. Itkis, H. Hu, J. Love, E. Bekyarova and R. C. Haddon, Preparation of Single-Walled Carbon Nanotube Reinforced Polystyrene and Polyurethane Nanofibers and Membranes by Electrospinning, Nano Lett., 2004, 4(3), 459–464 CrossRef CAS.
- Y. Song, Z. Sun, L. Xu and Z. Shao, Preparation and Characterization of Highly Aligned Carbon Nanotubes/Polyacrylonitrile Composite Nanofibers, Polymers, 2017, 9(1), 1 CrossRef PubMed.
- S. G. King, N. J. Terrill, A. J. Goodwin, R. Stevens, V. Stolojan and S. R. P. Silva, Probing of polymer to carbon nanotube surface interactions within highly aligned electrospun nanofibers for advanced composites, Carbon, 2018, 138, 207–214 CrossRef CAS.
- L.-Y. Mei, P. Song and Y.-Q. Liu, Magnetic-field-assisted electrospinning highly aligned composite nanofibers containing well-aligned multiwalled carbon nanotubes, J. Appl. Polym. Sci., 2015, 132(22), 41995 CrossRef.
- N. Shehata, E. Elnabawy, M. Abdelkader, A. H. Hassanin, M. Salah, R. Nair and S. Ahmad Bhat, Static-Aligned Piezoelectric Poly (Vinylidene Fluoride) Electrospun Nanofibers/MWCNT Composite Membrane: Facile Method, Polymers, 2018, 10(9), 965 CrossRef PubMed.
- T. Liu and S. Kumar, Quantitative characterization of SWNT orientation by polarized Raman spectroscopy, Chem. Phys. Lett., 2003, 378(3–4), 257–262 CrossRef CAS.
- M. Van Gurp, The use of rotation matrices in the mathematical description of molecular orientations in polymers, Colloid Polym. Sci., 1995, 273(7), 607–625 CrossRef CAS.
- H. Krenchel, Fibre reinforcement; theoretical and practical investigations of the elasticity and strength of fibre-reinforced materials, Akademisk Forlag, Copenhagen, 1964 Search PubMed.
- J. B. Bai and A. Allaoui, Effect of the length and the aggregate size of MWNTs on the improvement efficiency of the mechanical and electrical properties of nanocomposites—experimental investigation, Composites, Part A, 2003, 34(8), 689–694 CrossRef.
- K. Lu, R. Lago, Y. Chen, M. Green, P. Harris and S. Tsang, Mechanical damage of carbon nanotubes by ultrasound, Carbon, 1996, 34(6), 814–816 CrossRef CAS.
- H. Wan, F. Delale and L. Shen, Effect of CNT length and CNT-matrix interphase in carbon nanotube (CNT) reinforced composites, Mech. Res. Commun., 2005, 32(5), 481–489 CrossRef.
- X. Wang, Q. Jiang, W. Xu, W. Cai, Y. Inoue and Y. Zhu, Effect of carbon nanotube length on thermal, electrical and mechanical properties of CNT/bismaleimide composites, Carbon, 2013, 53, 145–152 CrossRef CAS.
- L. Schadler, S. A. Giannaris and P. Ajayan, Load transfer in carbon nanotube epoxy composites, Appl. Phys. Lett., 1998, 73(26), 3842–3844 CrossRef CAS.
- M. Cadek, J. N. Coleman, K. P. Ryan, V. Nicolosi, G. Bister, A. Fonseca, J. B. Nagy, K. Szostak, F. Béguin and W. J. Blau, Reinforcement of Polymers with Carbon Nanotubes: The Role of Nanotube Surface Area, Nano Lett., 2004, 4(2), 353–356 CrossRef CAS.
- A. H. Barber, S. R. Cohen, S. Kenig and H. D. Wagner, Interfacial fracture energy measurements for multi-walled carbon nanotubes pulled from a polymer matrix, Compos. Sci. Technol., 2004, 64(15), 2283–2289 CrossRef CAS.
- E. T. Thostenson and T.-W. Chou, On the elastic properties of carbon nanotube-based composites: modelling and characterization, J. Phys. D: Appl. Phys., 2003, 36(5), 573 CrossRef CAS.
- L. H. Shao, R. Y. Luo, S. L. Bai and J. Wang, Prediction of effective moduli of carbon nanotube–reinforced composites with waviness and debonding, Compos. Struct., 2009, 87(3), 274–281 CrossRef.
- J. Nafar Dastgerdi, G. Marquis and M. Salimi, The effect of nanotubes waviness on mechanical properties of CNT/SMP composites, Compos. Sci. Technol., 2013, 86, 164–169 CrossRef CAS.
- A. Alian and S. Meguid, Molecular dynamics simulations of the effect of waviness and agglomeration of CNTs on interface strength of thermoset nanocomposites, Phys. Chem. Chem. Phys., 2017, 19(6), 4426–4434 RSC.
- U. A. Joshi, S. C. Sharma and S. P. Harsha, Effect of carbon nanotube orientation on the mechanical properties of nanocomposites, Composites, Part B, 2012, 43(4), 2063–2071 CrossRef CAS.
- U. A. Joshi, S. C. Sharma and S. P. Harsha, Effect of waviness on the mechanical properties of carbon nanotube based composites, Phys. E, 2011, 43(8), 1453–1460 CrossRef CAS.
- R. Rafiee, Influence of carbon nanotube waviness on the stiffness reduction of CNT/polymer composites, Compos. Struct., 2013, 97, 304–309 CrossRef.
- A. Y. Matveeva, S. V. Pyrlin, M. M. D. Ramos, H. J. Böhm and F. W. J. van Hattum, Influence of waviness and curliness of fibres on mechanical properties of composites, Comput. Mater. Sci., 2014, 87, 1–11 CrossRef.
- C. Li and T.-W. Chou, Failure of carbon nanotube/polymer composites and the effect of nanotube waviness, Composites, Part A, 2009, 40(10), 1580–1586 CrossRef.
- F. T. Fisher, R. D. Bradshaw and L. C. Brinson, Fiber waviness in nanotube-reinforced polymer composites—I: Modulus predictions using effective nanotube properties, Compos. Sci. Technol., 2003, 63(11), 1689–1703 CrossRef CAS.
- R. D. Bradshaw, F. T. Fisher and L. C. Brinson, Fiber waviness in nanotube-reinforced polymer composites—II: modeling via numerical approximation of the dilute strain concentration tensor, Compos. Sci. Technol., 2003, 63(11), 1705–1722 CrossRef CAS.
- D. Tasis, N. Tagmatarchis, A. Bianco and M. Prato, Chemistry of Carbon Nanotubes, Chem. Rev., 2006, 106(3), 1105–1136 CrossRef CAS PubMed.
- H. Kim and C. W. Macosko, Processing-property relationships of polycarbonate/graphene composites, Polymer, 2009, 50(15), 3797–3809 CrossRef CAS.
- S. Uchida, T. Murakami, T. Iwamura, R. Ishige and S. Ando, Enhanced thermal conductivity in immiscible polyimide blend composites with needle-shaped ZnO particles, RSC Adv., 2017, 7(25), 15492–15499 RSC.
- T. Fornes and D. R. Paul, Modeling properties of nylon 6/clay nanocomposites using composite theories, Polymer, 2003, 44(17), 4993–5013 CrossRef CAS.
- X. Lin, X. Shen, Q. Zheng, N. Yousefi, L. Ye, Y.-W. Mai and J.-K. Kim, Fabrication of highly-aligned, conductive, and strong graphene papers using ultralarge graphene oxide sheets, ACS Nano, 2012, 6(12), 10708–10719 CrossRef CAS PubMed.
- H. Liu and L. C. Brinson, Reinforcing efficiency of nanoparticles: A simple comparison for polymer nanocomposites, Compos. Sci. Technol., 2008, 68(6), 1502–1512 CrossRef CAS.
- Z. Li, J. Chu, C. Yang, S. Hao, M. A. Bissett, I. A. Kinloch and R. J. Young, Effect of functional groups on the agglomeration of graphene in nanocomposites, Compos. Sci. Technol., 2018, 163, 116–122 CrossRef CAS.
- M. Omidi, H. Rokni D. T., A. S. Milani, R. J. Seethaler and R. Arasteh, Prediction of the mechanical characteristics of multi-walled carbon nanotube/epoxy composites using a new form of the rule of mixtures, Carbon, 2010, 48(11), 3218–3228 CrossRef CAS.
- R. J. Young and P. A. Lovell, Introduction to polymers, CRC Press, 2011 Search PubMed.
- A. Kelly, Strong Solids, Clarendon Press, 1966 Search PubMed.
- J. A. Nairn, On the use of shear-lag methods for analysis of stress transfer in unidirectional composites, Mech. Mater., 1997, 26(2), 63–80 CrossRef.
- R. Young, Composite micromechanics: From carbon fibres to graphene, Structural Integrity and Durability of Advanced Composites, Elsevier, 2015, pp. 3–23 Search PubMed.
- M. Andrews and R. Young, Fragmentation of aramid fibres in single-fibre model composites, J. Mater. Sci., 1995, 30(22), 5607–5616 CrossRef CAS.
- R. J. Young, M. Liu, I. A. Kinloch, S. Li, X. Zhao, C. Vallés and D. G. Papageorgiou, The mechanics of reinforcement of polymers by graphene nanoplatelets, Compos. Sci. Technol., 2018, 154, 110–116 CrossRef CAS.
- M. Terrones, O. Martín, M. González, J. Pozuelo, B. Serrano, J. C. Cabanelas, S. M. Vega-Díaz and J. Baselga, Interphases in Graphene Polymer-based Nanocomposites: Achievements and Challenges, Adv. Mater., 2011, 23(44), 5302–5310 CrossRef CAS PubMed.
- M. Piggott, Why interface testing by single-fibre methods can be misleading, Compos. Sci. Technol., 1997, 57(8), 965–974 CrossRef CAS.
- R. J. Young, I. A. Kinloch, L. Gong and K. S. Novoselov, The mechanics of graphene nanocomposites: a review, Compos. Sci. Technol., 2012, 72(12), 1459–1476 CrossRef CAS.
- M. Liu, I. A. Kinloch, R. J. Young and D. G. Papageorgiou, Modelling mechanical percolation in graphene-reinforced elastomer nanocomposites, arXiv preprint arXiv:1903.10224, 2019.
- J. C. Halpin and J. Kardos, The Halpin-Tsai equations: a review, Polym. Eng. Sci., 1976, 16(5), 344–352 CrossRef CAS.
- T. Mori and K. Tanaka, Average stress in matrix and average elastic energy of materials with misfitting inclusions, Acta Metall., 1973, 21(5), 571–574 CrossRef.
- J. Liang, Y. Huang, L. Zhang, Y. Wang, Y. Ma, T. Guo and Y. Chen, Molecular-level dispersion of graphene into poly (vinyl alcohol) and effective reinforcement of their nanocomposites, Adv. Funct. Mater., 2009, 19(14), 2297–2302 CrossRef CAS.
- X. Zhang, T. Liu, T. Sreekumar, S. Kumar, V. C. Moore, R. H. Hauge and R. E. Smalley, Poly (vinyl alcohol)/SWNT composite film, Nano Lett., 2003, 3(9), 1285–1288 CrossRef CAS.
- X.-Y. Ji, Y.-P. Cao and X.-Q. Feng, Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites, Modell. Simul. Mater. Sci. Eng., 2010, 18(4), 045005 CrossRef.
- D. S. Bethune, G. Meijer, W. C. Tang, H. J. Rosen, W. G. Golden, H. Seki, C. A. Brown and M. S. de Vries, Vibrational Raman and infrared spectra of chromatographically separated C60 and C70 fullerene clusters, Chem. Phys. Lett., 1991, 179(1–2), 181–186 CrossRef CAS.
- M. Dresselhaus, G. Dresselhaus and P. Eklund, Raman scattering in fullerenes, J. Raman Spectrosc., 1996, 27(3–4), 351–371 CrossRef CAS.
- M. S. Dresselhaus, G. Dresselhaus, R. Saito and A. Jorio, Raman spectroscopy of carbon nanotubes, Phys. Rep., 2005, 409(2), 47–99 CrossRef.
- A. C. Ferrari, J. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. Novoselov and S. Roth, Raman spectrum of graphene and graphene layers, Phys. Rev. Lett., 2006, 97(18), 187401 CrossRef CAS PubMed.
- F. Tuinstra and J. L. Koenig, Raman spectrum of graphite, J. Chem. Phys., 1970, 53(3), 1126–1130 CrossRef CAS.
- L. Malard, M. Guimaraes, D. Mafra and A. Jorio, Group-theory analysis of electrons and phonons in N-layer graphene systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(12), 125426 CrossRef.
- A. Rao, E. Richter, S. Bandow, B. Chase, P. Eklund, K. Williams, S. Fang, K. Subbaswamy, M. Menon and A. Thess, Diameter-selective Raman scattering from vibrational modes in carbon nanotubes, Science, 1997, 275(5297), 187–191 CrossRef CAS PubMed.
- A. C. Ferrari, Raman spectroscopy of graphene and graphite: disorder, electron–phonon coupling, doping and nonadiabatic effects, Solid State Commun., 2007, 143(1–2), 47–57 CrossRef CAS.
- A. C. Ferrari and D. M. Basko, Raman spectroscopy as a versatile tool for studying the properties of graphene, Nat. Nanotechnol., 2013, 8(4), 235 CrossRef CAS PubMed.
- M. S. Dresselhaus, A. Jorio, M. Hofmann, G. Dresselhaus and R. Saito, Perspectives on carbon nanotubes and graphene Raman spectroscopy, Nano Lett., 2010, 10(3), 751–758 CrossRef CAS PubMed.
- R. J. Young and S. J. Eichhorn, Deformation mechanisms in polymer fibres and nanocomposites, Polymer, 2007, 48(1), 2–18 CrossRef CAS.
- A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Raman Spectrum of Graphene and Graphene Layers, Phys. Rev. Lett., 2006, 97(18), 187401 CrossRef CAS PubMed.
- T. M. G. Mohiuddin, A. Lombardo, R. R. Nair, A. Bonetti, G. Savini, R. Jalil, N. Bonini, D. M. Basko, C. Galiotis, N. Marzari, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(20), 205433 CrossRef.
- G. Tsoukleri, J. Parthenios, K. Papagelis, R. Jalil, A. C. Ferrari, A. K. Geim, K. S. Novoselov and C. Galiotis, Subjecting a graphene monolayer to tension and compression, Small, 2009, 5(21), 2397–2402 CrossRef CAS PubMed.
- T. M. G. Mohiuddin, A. Lombardo, R. R. Nair, A. Bonetti, G. Savini, R. Jalil, N. Bonini, D. M. Basko, C. Galiotis, N. Marzari, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Gruneisen parameters, and sample orientation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(20), 205433 CrossRef.
- I. Polyzos, M. Bianchi, L. Rizzi, E. N. Koukaras, J. Parthenios, K. Papagelis, R. Sordan and C. Galiotis, Suspended monolayer graphene under true uniaxial deformation, Nanoscale, 2015, 7(30), 13033–13042 RSC.
- L. Gong, R. J. Young, I. A. Kinloch, I. Riaz, R. Jalil and K. S. Novoselov, Optimizing the reinforcement of polymer-based nanocomposites by graphene, ACS Nano, 2012, 6(3), 2086–2095 CrossRef CAS PubMed.
- G. Tsoukleri, J. Parthenios, C. Galiotis and K. Papagelis, Embedded trilayer graphene flakes under tensile and compressive loading, 2D Mater., 2015, 2(2), 024009 CrossRef.
- G. Anagnostopoulos, C. Androulidakis, E. N. Koukaras, G. Tsoukleri, I. Polyzos, J. Parthenios, K. Papagelis and C. Galiotis, Stress transfer mechanisms at the submicron level for graphene/polymer systems, ACS Appl. Mater. Interfaces, 2015, 7(7), 4216–4223 CrossRef CAS PubMed.
- O. Frank, G. Tsoukleri, I. Riaz, K. Papagelis, J. Parthenios, A. C. Ferrari, A. K. Geim, K. S. Novoselov and C. Galiotis, Development of a universal stress sensor for graphene and carbon fibres, Nat. Commun., 2011, 2, 255 CrossRef.
- N. Melanitis, P. L. Tetlow and C. Galiotis, Characterization of PAN-based carbon fibres with laser Raman spectroscopy, J. Mater. Sci., 1996, 31(4), 851–860 CrossRef CAS.
- Y. Huang and R. J. Young, Effect of fibre microstructure upon the modulus of PAN- and pitch-based carbon fibres, Carbon, 1995, 33(2), 97–107 CrossRef CAS.
- G. Wang, Z. Dai, L. Liu, H. Hu, Q. Dai and Z. Zhang, Tuning the Interfacial Mechanical Behaviors of Monolayer Graphene/PMMA Nanocomposites, ACS Appl. Mater. Interfaces, 2016, 8(34), 22554–22562 CrossRef CAS PubMed.
- J. Zabel, R. R. Nair, A. Ott, T. Georgiou, A. K. Geim, K. S. Novoselov and C. Casiraghi, Raman spectroscopy of graphene and bilayer under biaxial strain: bubbles and balloons, Nano Lett., 2012, 12(2), 617–621 CrossRef CAS PubMed.
- F. Ding, H. Ji, Y. Chen, A. Herklotz, K. Dörr, Y. Mei, A. Rastelli and O. G. Schmidt, Stretchable graphene: a close look at fundamental parameters through biaxial straining, Nano Lett., 2010, 10(9), 3453–3458 CrossRef CAS PubMed.
- C. Androulidakis, E. N. Koukaras, J. Parthenios, G. Kalosakas, K. Papagelis and C. Galiotis, Graphene flakes under controlled biaxial deformation, Sci. Rep., 2015, 5, 18219 CrossRef CAS PubMed.
- C. Metzger, S. Rémi, M. Liu, S. V. Kusminskiy, A. H. Castro Neto, A. K. Swan and B. B. Goldberg, Biaxial strain in graphene adhered to shallow depressions, Nano Lett., 2009, 10(1), 6–10 CrossRef PubMed.
- Z. Li, I. A. Kinloch, R. J. Young, K. S. Novoselov, G. Anagnostopoulos, J. Parthenios, C. Galiotis, K. Papagelis, C.-Y. Lu and L. Britnell, Deformation of wrinkled graphene, ACS Nano, 2015, 9(4), 3917–3925 CrossRef CAS PubMed.
- G. Anagnostopoulos, G. Paterakis, I. Polyzos, P.-N. Pappas, K. Kouroupis-Agalou, N. Mirotta, A. Scida, V. Palermo, J. Parthenios and K. Papagelis, Strain Engineering in Highly Wrinkled CVD Graphene/Epoxy Systems, ACS Appl. Mater. Interfaces, 2018, 10(49), 43192–43202 CrossRef CAS PubMed.
- M. G. P. Carbone, A. C. Manikas, I. Souli, C. Pavlou and C. Galiotis, Mosaic pattern formation in exfoliated graphene by mechanical deformation, Nat. Commun., 2019, 10(1), 1572 CrossRef PubMed.
- Z. Li, R. J. Young, D. Papageorgiou, I. Kinloch, X. Zhao, C. Yang and S.-J. Hao, Interfacial stress transfer in strain engineered wrinkled and folded graphene, 2D Mater., 2019, 6(4), 045026 CrossRef.
- Z. Li, I. A. Kinloch and R. J. Young, The role of interlayer adhesion in graphene oxide upon its reinforcement of nanocomposites, Philos. Trans. R. Soc., A, 2016, 374(2071), 20150283 CrossRef PubMed.
- R. J. Young, L. Gong, I. A. Kinloch, I. Riaz, R. Jalil and K. S. Novoselov, Strain mapping in a graphene monolayer nanocomposite, ACS Nano, 2011, 5(4), 3079–3084 CrossRef CAS PubMed.
- J. Morgan, M. Craciun and S. Eichhorn, Quantification of stress transfer in a model cellulose nanocrystal/graphene bilayer using Raman spectroscopy, Compos. Sci. Technol., 2019, 177, 34–40 CrossRef CAS.
- O. Frank, G. Tsoukleri, J. Parthenios, K. Papagelis, I. Riaz, R. Jalil, K. S. Novoselov and C. Galiotis, Compression behavior of single-layer graphenes, ACS Nano, 2010, 4(6), 3131–3138 CrossRef CAS PubMed.
- A. Ferrari, J. Robertson, A. Jorio, R. Saito, G. Dresselhaus and M. S. Dresselhaus, Determination of nanotubes properties by Raman spectroscopy, Philos. Trans. R. Soc., A, 2004, 362(1824), 2311–2336 CrossRef PubMed.
- J. Wood, Q. Zhao and H. Wagner, Orientation of carbon nanotubes in polymers and its detection by Raman spectroscopy, Composites, Part A, 2001, 32(3–4), 391–399 CrossRef.
- H. Gommans, J. Alldredge, H. Tashiro, J. Park, J. Magnuson and A. Rinzler, Fibers of aligned single-walled carbon nanotubes: Polarized Raman spectroscopy, J. Appl. Phys., 2000, 88(5), 2509–2514 Search PubMed.
- T. E. Chang, L. R. Jensen, A. Kisliuk, R. B. Pipes, R. Pyrz and A. P. Sokolov, Microscopic mechanism of reinforcement in single-wall carbon nanotube/polypropylene nanocomposite, Polymer, 2005, 46(2), 439–444 CrossRef CAS.
- Z. Wang, P. Ciselli and T. Peijs, The extraordinary reinforcing efficiency of single-walled carbon nanotubes in oriented poly (vinyl alcohol) tapes, Nanotechnology, 2007, 18(45), 455709 CrossRef.
- S. Iijima and T. Ichihashi, Single-shell carbon nanotubes of 1 nm diameter, Nature, 1993, 363(6430), 603 CrossRef CAS.
- C. A. Cooper, R. J. Young and M. Halsall, Investigation into the deformation of carbon nanotubes and their composites through the use of Raman spectroscopy, Composites, Part A, 2001, 32(3), 401–411 CrossRef.
- M. Frogley, Q. Zhao and H. Wagner, Polarized resonance Raman spectroscopy of single-wall carbon nanotubes within a polymer under strain, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(11), 113413 CrossRef.
- L. Deng, S. J. Eichhorn, C.-C. Kao and R. J. Young, The effective Young's modulus of carbon nanotubes in composites, ACS Appl. Mater. Interfaces, 2011, 3(2), 433–440 CrossRef CAS PubMed.
- S. Wang, Z. Liang, P. Gonnet, Y. H. Liao, B. Wang and Z. Zhang, Effect of Nanotube Functionalization on the Coefficient of Thermal Expansion of Nanocomposites, Adv. Funct. Mater., 2007, 17(1), 87–92 CrossRef CAS.
- S. Wang, R. Liang, B. Wang and C. Zhang, Load-transfer in functionalized carbon nanotubes/polymer composites, Chem. Phys. Lett., 2008, 457(4), 371–375 CrossRef CAS.
- Q. Zhao and H. D. Wagner, Raman spectroscopy of carbon–nanotube–based composites, Philos. Trans. R. Soc., A, 2004, 362(1824), 2407–2424 CrossRef CAS PubMed.
- R. J. Young, L. Deng, T. Z. Wafy and I. A. Kinloch, Interfacial and internal stress transfer in carbon nanotube based nanocomposites, J. Mater. Sci., 2016, 51(1), 344–352 CrossRef CAS.
- M. Mu, S. Osswald, Y. Gogotsi and K. I. Winey, An in situ Raman spectroscopy study of stress transfer between carbon nanotubes and polymer, Nanotechnology, 2009, 20(33), 335703 CrossRef PubMed.
- C.-C. Kao and R. J. Young, Assessment of interface damage during the deformation of carbon nanotube composites, J. Mater. Sci., 2010, 45(6), 1425–1431 CrossRef CAS.
- L. Liu, A. H. Barber, S. Nuriel and H. D. Wagner, Mechanical properties of functionalized single-walled carbon-nanotube/poly (vinyl alcohol) nanocomposites, Adv. Funct. Mater., 2005, 15(6), 975–980 CrossRef CAS.
- N. Lachman, C. Bartholome, P. Miaudet, M. Maugey, P. Poulin and H. D. Wagner, Raman Response of Carbon Nanotube/PVA Fibers under Strain, J. Phys. Chem. C, 2009, 113(12), 4751–4754 CrossRef CAS.
- S. Y. Jin, R. J. Young and S. J. Eichhorn, Controlling and mapping interfacial stress transfer in fragmented hybrid carbon fibre–carbon nanotube composites, Compos. Sci. Technol., 2014, 100, 121–127 CrossRef CAS.
- S. Y. Jin, R. J. Young and S. J. Eichhorn, Hybrid carbon fibre–carbon nanotube composite interfaces, Compos. Sci. Technol., 2014, 95, 114–120 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |