Mercury adsorption in the gas phase by regenerable Au-loaded activated carbon foams: a kinetic and reaction mechanism study

Abstract

Mercury has been the focus of environmental concern and scientific research for decades due to the risks associated with its use, release and emission. An international agreement established in 2017 during the UN Minamata Convention highlighted the need for innovative approaches and technology to tackle these problems. The use of regenerable sorbents for mercury removal in the gas phase is a possible solution that can avoid the generation of new mercury-contaminated waste. However, to make significant progress in this field, it is necessary to develop efficient, economic and environmentally friendly sorbents, for which, a good understanding of the mechanism of adsorption in this type of process is needed. In this study, several kinetic models were applied to determine the rate-controlling step in the adsorption process of elemental mercury by regenerable sorbents based on gold. Three diffusional models (Weber and Morris, Bangham and pseudo-first order models) and two adsorptive models (pseudo-second order and Elovich models) were tested. The results of this study show that external diffusion from the gaseous phase to the sorbent particles is the rate-limiting step. The complexity of the process is also reflected in the results obtained, which indicate that pore diffusion plays a significant role over most of the mass transfer zone, while adsorption itself becomes determinant only when the saturation of the sorbent is near.

---

1. Introduction

Mercury is a global and devastating threat to the environment and human health, and has been listed in the top ten chemicals of public concern by the World Health Organization (WHO). The growing interest in the problem of mercury contamination and the awareness in reducing its use and in the control of anthropogenic emissions is reflected in the global Minamata Agreement¹ of 2017, which contemplates the protection of human health and the environment from the adverse effects of mercury. The treaty includes specific guidelines for the emissions of mercury to the atmosphere from its main industrial sources: coal-fired power plants, coal-fired industrial boilers, smelting and roasting processes used in the production of non-ferrous metals, waste incineration facilities and cement clinker production. The gases emitted that contain mercury are frequently enriched in CO₂, and this has to be taken into account in the development of processes for the mitigation of mercury emissions.

Presumably, significant cuts in CO₂ emissions will be reached by 2050, due to energy policies and the application of carbon capture and storage (CCS) strategies.² In such CCS technologies, the presence of elemental mercury (Hg⁰) in gases enriched in CO₂ is not only an environmental risk but also a technological problem: it needs to be controlled in the compression stage,³ which is carried out, in many cases, in cryogenic aluminum plate fin exchangers. If the Hg⁰ reaches these heat exchangers, it can form an amalgam with Al, which may cause deterioration or even destruction of the installation. The final part of the CCS process, the storage of CO₂ in geological environments, is also negatively affected by the presence of Hg, not only due to the reduction of the volume occupied by CO₂, but also as a result of some chemical reactions that could decrease its injectivity.⁴

Hg⁰ is significantly difficult to capture even by using the most advanced technologies already developed for industrial gases. This problem is being addressed through the development of specific sorbents.^5–7 By using regenerable sorbents, the mercury that is retained may be desorbed and condensed to be confined and isolated. The sorbents studied so far for this purpose are mainly metal oxides and porous solids impregnated with noble metals such as gold, silver, palladium and platinum.^8–16

The sorbents based on metal oxides have the ability to capture mercury and other trace elements at high temperatures (200–400 °C), and have even been tested for the retention of toxic metals in gasification processes.^17,18 Studies carried out with regenerable sorbents based on manganese oxide showed a good capability for mercury capture up to 300 °C and were completely regenerated at 500 °C.¹⁴ No decrease in mercury retention capacity over repeated cycles of mercury adsorption/desorption was observed. Metal oxides and composites have also been evaluated as regenerable sorbents for the treatment of gaseous steams generated in industrial processes such as energy generation or non-ferrous metal smelting.^15,16 They capture elemental mercury by catalytic oxidation and adsorption with great efficiency and can be regenerated by thermal decomposition.

On the other hand, the regenerable materials loaded with noble metals (Au, Ag, Cu, Pd or Pt),^{8,11,14,19–21} are able to retain elemental mercury by amalgamation between the metal and the mercury, both in an elemental state.^9,10,22 Subsequently, the amalgam can be decomposed by heating at 450 °C to detach and recover the mercury, leaving the sorbent ready for the next adsorption cycle.

Regenerable sorbents based on activated carbon foams impregnated with nanodispersed gold, developed and tested for gaseous Hg⁰ capture, are the focus of this work.²³ Activated carbon foams offer enhanced mechanical strength and easy manageability, which makes it possible to manufacture carbon structures of any monolithic shape. Furthermore, the physical and chemical characteristics of their surfaces can be modified to meet the needs of any particular industrial adsorption process.

The adsorption process surely depends on the capacity of sorbents to retain pollutants, but also on the adsorption kinetics.^24–27 A number of kinetic models have been studied to describe heavy metal adsorption processes, mainly from the liquid phase,^28,29 and most of them by means of batch experiments. Pseudo-first-order, pseudo-second-order and Elovich equations have been used most often.^30–35

There is only a limited amount of information available in the literature on the adsorption kinetics of gas-phase mercury,^26,36 and the pseudo-second order model appears to be the most accurate to describe the process, indicating the rate-limiting influence of the adsorption itself; however, the good behaviour of other models suggests that the whole process is complex, and that the diffusion of the sorbate to and into the sorbent may also pose a significant influence.

This study attempts to improve the current level of understanding of the adsorption of elemental mercury in a new kind of sorbent, by applying several simplified kinetic models, namely Weber and Morris (intraparticle diffusion), Bangham, pseudo-first order, pseudo-second order and Elovich models. The models are applied to the experimental data obtained from the capture of Hg⁰ in the gas phase by adsorption with gold-impregnated activated carbon foams, which have proven to capture mercury with 100% capacity over several adsorption–desorption cycles.²³

2. Materials and methods

The activated coal-based carbon foams have been prepared from a demineralized high volatile bituminous coal from the USA (Pondfork), using the procedure described elsewhere.^23,37 Chemical activation was carried out simultaneously to the foaming of the precursor, using ZnCl₂ as an activating agent, at the temperature of coal maximum fluidity (450 °C).³⁷ The “green” foam thus obtained was subsequently carbonized at 500 °C obtaining the CF500 foam. The heat treatment of CF500 at 800 °C under a flow of CO₂ gave rise to the activated carbon foam CF800.²³ The properties of the final activated carbon foams CF500 and CF800 have been evaluated using the techniques and procedures previously reported.²³ The textural properties of these activated carbon foams used as the Au supports are given in Table 1. The N₂ isotherms and the distributions of micro- and macropores are shown in the ESI† (Fig. S1–S3). Moreover, the presence of oxygen functional groups in their surface, identified by temperature programmed desorption (TPD), has revealed the presence of phenolic and etheric groups.²³

Table 1 Textural properties of the activated carbon foams²³

	CF500	CF800
Surface area (SBET, m^2 g^−1)	880	738
Micro-porosity volume (VDR-N2, cm^3 g^−1)	0.36	0.28
Narrow porosity volume (VDR-CO2, cm^3 g^−1)	0.30	0.19
True density (ρHe, g cm^−3)	1.52	1.91
Apparent density (ρHg, g cm^−3)	0.42	0.31
Open porosity (s, %)	72.3	83.7
Total pore volume (VHg, cm^3 g^−1)	1.71	2.69

---

The activated carbon foams were impregnated with 1, 2, 3, 4 and 5 wt% Au, following the THPC (tetrakis(hydroxymethyl)-phosphonium chloride) method, which is based on the formation of Au colloids. The detailed procedure has been previously reported.^23,38 The actual amount of Au loaded in the sorbent is determined by analysing the Au in the solution, after the foam impregnation, by inductively coupled plasma mass spectrometry (ICP-MS). The sorbents prepared with Au contents of 1 to 5 wt% were labelled CF500-1%, CF500-2%, CF500-3%, CF500-4% and CF500-5% and CF800-1%, CF800-2%, CF800-3%, CF800-4% and CF800-5%.

The average size of the Au particles in the Au-loaded carbon foams, estimated using SEM and TEM,²³ increases with Au-loading, from 5 nm in CF500-1% to 23 nm in CF500-5%, and from 16 nm in CF800-1% to 116 nm in CF800-5%. The deposited Au in the surface is in its elemental state as demonstrated via XPS analysis, by the presence of two Au 4f peaks corresponding to the binding energy of metallic Au (84.0 eV and 87.7 eV) in the XPS spectrum.²³ It was observed that the loading of elemental Au on the activated carbon foam does not exert a significant influence on the surface area and pore diameter of the adsorbent, as it was previously reported.³⁹

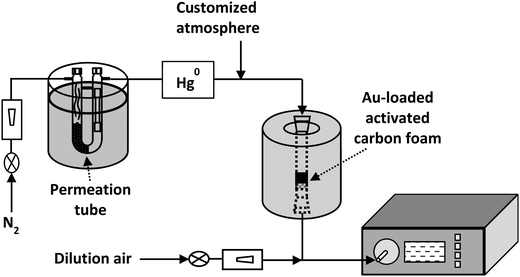
The laboratory scale device used for the retention of Hg was described in previous works.^23,39 A general schematic is depicted in Fig. 1. The gas composition used in the experiments was 80% CO₂ and 20% N₂, with 100 μg m⁻³ of Hg⁰ being incorporated to the gas stream. The sorbent was kept at 40–50 °C and the total volume of the gas flow through it was 500 mL min⁻¹. Hg⁰ was monitored at the exit of the sorbent bed, using a continuous elemental mercury analyser (VM 3000). In the case of an eventual oxidation of elemental mercury,^40,41 the Hg²⁺ originated would be captured with a Dowex® 1 × 8 ion exchanger resin. The total amount of Hg retained in the sorbent and the Hg²⁺ captured in the resin were analysed using a mercury analyser (Advanced Mercury Analyser, AMA 254).

Fig. 1 General schematic of the Hg retention device.

3. Results and discussion

In the adsorption experiments, the concentration of Hg⁰ at the exit of the adsorption reactor was recorded at 3 minute intervals, and the cumulative concentration of Hg⁰ in the sorbent (q_t, μg g⁻¹) at an adsorption time t (min) was calculated with the following equation:^42,43
where Q is the volumetric gas flow rate (N m³ min⁻¹), m is the mass of the adsorbent (g), and C₀ (μg m⁻³) and C (μg m⁻³) are the Hg⁰ concentrations in the flue gas at the inlet and outlet of the fixed-bed reactor, respectively.

To study the kinetics of the adsorption process, the interval taken into consideration is the mass transfer zone, beginning just at the breakthrough time (considered as zero time), when the period of 100% Hg adsorption ends. The cumulative adsorbed mercury curves in this mass transfer zone after breakthrough for the studied adsorbents are shown in Fig. 2. In general, it can be observed that an increasing concentration of Au in the adsorbent gives rise to slower adsorption rates (longer times needed for saturation) and higher amounts of Hg captured. The latter does not mean a higher capacity of the adsorbent for mercury capture, but suggests that a higher amount of Au has remained untouched in the zone of 100% adsorption (before the breakthrough point). This therefore means a lower efficiency of the sorbent. The adsorption capacity of these Au-loaded carbon foams has been studied previously by the authors,²³ and has been proven to be influenced by the amount, dispersion and particle size of the elemental Au incorporated, and by the chemical nature of the carbon foam surface.

Fig. 2 Cumulative Hg⁰ captured by Au-impregnated carbon foams after the breakthrough time: (a) Au-loaded CF500 samples; (b) Au-loaded CF800 samples.

Adsorption on the surface of a porous material is considered to take place via three steps:^29,43,44 (i) diffusion through the fluid surrounding the solid particles to the external surface of the adsorbent, controlled by external mass transfer, (ii) diffusion through the fluid within the pores of the sorbent particles to the sorption sites, in a pore diffusion mechanism, and (iii) adsorption at the active sites on the surface of the sorbent.

The mechanism of adsorption can be described by various mathematical models, with approaches that differ according to which step is considered as the rate-limiting one. The deviation between the calculated and experimental data are expressed by correlation coefficient R² and the sum of squares due to error (SSE), which will be used in this study for model comparison. The kinetic models may be roughly classified as diffusional and adsorption models.

3.1. Diffusional models

They consider the mass transfer to the sorption sites as the slowest step. Three models will be considered here: the Weber and Morris model (broadly known as the intra-particle diffusion model), the Bangham model and the pseudo-first order model.

3.1.1. Weber and Morris or intra-particle diffusion model⁴⁵. The adsorption process is considered to be influenced by diffusion in the sorbent. The amount of the species adsorbed at time t is expressed by the following equation:^46,47

q_t = k_idt^1/2 + θ

where k_id is the intra-particle diffusion rate constant (μg g⁻¹ min^−1/2), and θ (μg g⁻¹) is a constant that increases with the thickness of the boundary layer.⁴⁸

This model contemplates the adsorption process as controlled by external mass transfer (boundary layer diffusion) and internal pore diffusion.⁴⁹ Among multiple stages of adsorption, the process can be considered as controlled by intra-particle diffusion only if the plot of q_tversus t^1/2 produces a straight line.⁴⁵

Fig. S4 and S5 (ESI†) display the cumulative capture of Hg with different Au loadings of the carbon foams and the corresponding curves derived from the Weber and Morris model. The kinetic parameters obtained for the adsorption curves of the ten sorbents tested are listed in Tables 2 and 3. The values of R² are rather low, revealing poor fits between the experimental curves and the theoretical ones derived from the model. The value of the constant k_id, on the other hand, increases with the increasing amount of Au loaded in the carbon foams, according to the evolution of the cumulated Hg⁰ in the mass transfer zone.

Table 2 Kinetic parameters obtained for the adsorption curves of the Au-loaded CF500 carbon foams with several models

		CF500-1%	CF500-2%	CF500-3%	CF500-4%	CF500-5%
Weber and Morris	SSE	1942	3005	6816	28 830	281 100
	R ^2	0.9496	0.9478	0.9359	0.9278	0.9077
	k id (mg g^−1 min^−1/2)	3.214	3.912	4.300	5.006	9.226
	θ (mg g^−1)	1.509 × 10^−12	3.439 × 10^−13	2.742 × 10^−12	0.000083	9.784
Bangham	SSE	1345	2956	6787	27 270	247 800
	R ^2	0.9651	0.9487	0.9362	0.9317	0.9186
	k (mg g^−1 s^−α)	1.916	3.494	4.568	6.370	14.95
	α	0.5989	0.5206	0.4891	0.4604	0.432
Pseudo-first order	SSE	270.4	313.8	821.6	1947	18 960
	R ^2	0.9930	0.9946	0.9923	0.9951	0.9938
	q e (μg g^−1)	62.57	77.41	83.89	124.4	282.7
	k 1 (min^−1)	0.007006	0.007136	0.007593	0.004876	0.003669
Pseudo-second order	SSE	445.6	757.4	1918	6293	58 010
	R ^2	0.9884	0.9869	0.9820	0.9842	0.9810
	q e (μg g^−1)	91.81	106.7	113.0	163.6	364.1
	k 2 (g μg^−1 s^−1)	5.648 × 10^−5	5.527 × 10^−5	5.812 × 10^−5	2.703 × 10^−5	9.56 × 10^−6
Elovich	SSE	638.7	1318	3291	12450	117800
	R ^2	0.9834	0.9771	0.9691	0.9688	0.9613
	α (μg g^−1 s^−1)	0.5278	0.7478	0.9152	0.9310	1.7057
	β (g μg^−1)	0.0316	0.0300	0.0296	0.0213	0.0100

---

Table 3 Kinetic parameters obtained for the adsorption curves of the Au-loaded CF800 carbon foams with several models

		CF800-1%	CF800-2%	CF800-3%	CF800-4%	CF800-5%
Weber and Morris	SSE	3311	4160	19 400	10 420	64 260
	R ^2	0.9486	0.9410	0.9454	0.9528	0.9402
	k id (mg g^−1 min^−1/2)	2.897	2.912	5.235	3.957	6.634
	θ (mg g^−1)	1.157 × 10^−12	0.008725	2.386 × 10^−10	7.371 × 10^−8	3.496 × 10^−9
Bangham	SSE	2142	3920	8052	10 420	20 970
	R ^2	0.9668	0.9444	0.9773	0.9528	0.9805
	k (mg g^−1 s^−α)	1.547	3.632	2.090	3.933	2.173
	α	0.6084	0.4630	0.6525	0.5010	0.6765
Pseudo-first order	SSE	356.3	146.1	1319	522.4	3903
	R ^2	0.9945	0.9979	0.9963	0.9976	0.9964
	q e (μg g^−1)	75.14	68.48	166.4	108.4	258.5
	k 1 (min^−1)	0.003942	0.005398	0.002625	0.003796	0.001762
Pseudo-second order	SSE	629.1	696.1	2238	1931	6102
	R ^2	0.9902	0.9901	0.9937	0.9913	0.9943
	q e (μg g^−1)	110.9	90.18	249.0	146.8	400.6
	k 2 (g μg^−1 s^−1)	2.603 × 10^−5	5.432 × 10^−5	7.598 × 10^−6	2.212 × 10^−5	2.996 × 10^−6
Elovich	SSE	937.3	1587	3218	4053	8493
	R ^2	0.9855	0.9774	0.9909	0.9816	0.9921
	α (μg g^−1 s^−1)	0.3526	0.5694	0.4980	0.5822	0.5086
	β (g μg^−1)	0.0259	0.0386	0.0108	0.0225	0.0066

---

The plots corresponding to the linear form of the model are shown in Fig. 3. Again, the correlation coefficients (R²) obtained are low, indicating a poor description of the process of adsorption of Hg⁰ by the Au-loaded activated carbon foams, and that the intra-particle diffusion is hardly the adsorption rate-controlling step.

Fig. 3 Plots corresponding to the linear form of the Weber and Morris model for the adsorption of Hg⁰ by the Au-impregnated carbon foams with different loadings: (a) Au-loaded CF500 samples; (b) Au-loaded CF800 samples.

3.1.2. Bangham model. The Bangham model assumes that the kinetics of the adsorption process is determined by the pore diffusion. The equation is as follows:

q_t = kt^α

where k and α are constants of the model.

The kinetic coefficients indicate correlations slightly better than those observed with the Weber and Morris model (Tables 2 and 3). However, the plots show that the correlations are far from the experimental results (Fig. S6 and S7, ESI†). According to these results, the present Hg adsorption process is not determined by the diffusion of the adsorbate inside the sorbent particles.

The model can also be represented by a linear equation:^50,51

where V is the volume of the sample. The corresponding plots are shown in Fig. 4. For all the samples, the global correlation coefficients are generally better that those obtained with the Weber and Morris model (Fig. 3), with the exception of CF800-5%. It can also been observed that most of the points adjust to a straight line, and they only get far from the linear correlation at the end of the adsorption process, when saturation is near. This means that the adsorption process of Hg in the Au-loaded activated carbon foams could be pore-diffusion controlled up to the proximity of the saturation of the sorbent.

Fig. 4 Plots corresponding to the linear form of the Bangham model for the adsorption of Hg by the Au-impregnated carbon foams with different loadings: (a) Au-loaded CF500 samples; (b) Au-loaded CF800 samples.

3.1.3. Pseudo-first order model⁵². This model is described by the following equation:^53–56
where q_e is the concentration of the adsorbate at equilibrium time (μg g⁻¹) and k₁ is the rate constant of the first order equation (min⁻¹). Integrating the equation in the boundary conditions t = 0 to t = t and q_t = 0 to q_t = q_t, the following expression is obtained:

q_e = q_t(1 − e^−k₁t)

or, in linear form:

ln(q_e − q_t) = ln q_e − k₁t

This model is a good simulation when mass transfer to the active sites is a controlling factor during the adsorption process. The correlations found in this case (Fig. S8 and S9, ESI,† and Tables 2 and 3) are considerably better than those observed in the previous models.

With this model, the estimated values of the accumulated concentration of Hg⁰ in the sorbents in equilibrium (q_e) increases from 62.57 and 75.14 μg g⁻¹ for CF500-1% and CF800-1%, to 282.7 and 258.5 μg g⁻¹ for CF500-5% and CF800-5%, respectively (Tables 2 and 3). The adsorption constant provided by the model ranges from 1.762 × 10⁻³ s⁻¹ (CF800-5%, Table 3) to 7.593 × 10⁻³ s⁻¹ (CF500-3%, Table 2).

Fig. 5 displays the plots corresponding to the linear equation of the first-order model. They show good correlation coefficients, especially in the case of adsorbent CF800-2% (R² = 0.9989). The correlations are similar to or better than those of the Bangham model. The correlation also becomes worse as saturation approaches. These results, together with those of the non-linear plots (Fig. S8 and S9, ESI†) indicate that the mass transfer between the adsorbate and the adsorption sites plays a significant role in the process of adsorption of Hg by Au-loaded activated carbon foams. The pseudo-first order equation accurately predicts the initial period of adsorption^57–59 and, for that reason, fast Hg⁰ adsorption processes can be better adjusted to pseudo-first order kinetics.⁵³

Fig. 5 Plots corresponding to the linear form of the pseudo-first order model for the adsorption of Hg⁰ by the Au-impregnated carbon foams with different loadings: (a) Au-loaded CF500 samples; (b) Au-loaded CF800 samples.

3.2. Adsorption models

In these models, the adsorption itself is considered to be the slowest stage of the process. This is usually the case when the adsorbate uptake on the adsorbent is of a chemical nature (chemisorption). Two models of this kind will be considered here: (i) the pseudo-second order model, and (ii) the Elovich model.

3.2.1. Pseudo-second order model⁶⁰. This model assumes that the sorption process is a pseudo-chemical reaction process, i.e., adsorption takes place mainly by chemisorption. In the kinetic rate equation is the following:⁶¹
where k₂ represents the adsorption reaction rate constant (g μg⁻¹ s⁻¹). Integrating between the boundary conditions t = 0 to t = t and q_t = 0 to q_t = q_t, the last equation transforms into:
with the following linear form:

Good correlations are also obtained with this model for the experimental data (Fig. S10 and S11, ESI,† and Tables 2 and 3). However, the values of R² are slightly lower and the values of SSE are slightly higher than those of the pseudo-first order model indicating that the latter reflects the mechanism of adsorption more accurately in this particular case.

The plots corresponding to the linear equation of the model are displayed in Fig. 6. The best match with the experimental results is that of sample CF800-2%, and the worst corresponds to CF800-1%. It is evident that the distribution of the experimental results is closer to a straight line as adsorption time increases, suggesting that the adsorption, presumably by Hg–Au amalgamation, become the limiting step as the adsorption process proceeds and approaches the saturation of the sorbent.

Fig. 6 Plots corresponding to the linear form of the pseudo-second order model for the adsorption of Hg⁰ by the Au-impregnated carbon foams with different loadings: (a) Au-loaded CF500 samples; (b) Au-loaded CF800 samples.

3.2.2. Elovich model⁶². This model also considers the adsorption as a process limited by the linking of the adsorbate in the active sites, with the rate of adsorption exponentially decreasing with the increase in the amount of the species adsorbed. The equation is as follows:
where constants α (μg g⁻¹ s⁻¹) and β (g μg⁻¹) are related to the initial adsorption rate and to the number of sites available for adsorption, respectively. This expression, integrated between the boundary conditions: q_t = 0 at t = 0 and q_t = q_t at t = t, gives rise to the equation:
or, in linear form, assuming that αβt ≫ 1:⁶³

The non-linear and linear plots in Fig. S12 and S13 (ESI†) and Fig. 7 and the values in Tables 2 and 3 indicate a worse correlation than those observed for the pseudo-first order and the pseudo-second order models.

Fig. 7 Plots corresponding to the linear form of the Elovich model for the adsorption of Hg⁰ by the Au-impregnated carbon foams with different loadings: (a) Au-loaded CF500 samples; (b) Au-loaded CF800 samples.

3.3. General discussion

A comparison of the kinetic parameters, R² and SSE (Tables 2 and 3), indicates that the pseudo-first order model delivers the most accurate match with the experimental results. This is the model that describes the capture of Hg⁰ by Au-loaded activated carbon foams most accurately, suggesting that external diffusion is the rate-limiting step in the process,³⁶ especially in the case of the lowest Au-loaded sample. However, the pseudo-second order adsorption model also displays good correlations, indicating that the entire capture process is complex and that either amalgam formation between Au and Hg and plain adsorption in appropriate active sites can also play a significant role. The surface reaction and diffusion-controlled kinetic models, which match the experimental data to different degrees, lend support to the assumption that both the surface reaction and diffusion steps control the overall rate of the sorption process simultaneously, although the predominant role belongs to surface diffusion.

When the non-linear correlations are considered, the pseudo-first order and Bangham models provide the best matches, and so it is the external diffusion that controls the global adsorption process from the beginning to the point where the sorbent is saturated. The linear plots support this assertion, but they also show that: (i) the Bangham model matches the experimental results in the first stages of the process and only deviates from them when the sorbent is close to the saturation point, and (ii) the pseudo-second order model approaches the experimental results more closely in the last stages of the process, including the saturation of the sorbent. The results confirm that, although external diffusion seems to control the entire process, pore diffusion is also determinant in the initial stages, whereas adsorption acquires importance towards the end, when saturation of the sorbent is imminent.

4. Conclusions

The results of this study contribute to a much better understanding of the gas phase-mercury adsorption mechanism by solid sorbents. The regenerable sorbents developed using carbon foams impregnated with Au show that, in the mass transfer zone, after breakthrough time, an increase in the amount of gold provides slower kinetics and an enhanced cumulative capture of Hg⁰. Among the kinetic models studied, the best correlation with the experimental results is achieved, in all cases, with the pseudo-first order model. In spite of this, the behaviour of other models over the whole mass transfer zone suggests that the mechanism of mercury adsorption is a complex process, in which mass transfer to the active sites is the rate-controlling step over the whole process, but the actual capture of Hg⁰ (either by Au–Hg amalgam formation or by plain adsorption) plays an important role in the final stages near the saturation of the sorbent.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank the Spanish Ministry of Economy and Competitiveness (research project CTQ2014-58110-R) and PCTI Asturias (Spain) (research project IDI/2018/000234) for financial support.

References

1. United Nations Environment Programme, Minamata Convention on Mercury, http://www.mercuryconvention.org/, (accessed 7 February 2020).
2. European Commission, Energy, Climate change, Environment, Climate Action, EU Action, Climate strategies & targets, 2050 long-term strategy, https://ec.europa.eu/clima/policies/strategies/2050_en, (accessed 7 February 2020).
3. Y. Mitsui, N. Imada, H. Kikkawa and A. Katagawa, Int. J. Greenhouse Gas Control, 2011, 5, S143–S150.
4. C. M. Oldenburg and N. Spycher, Greenhouse Gases: Sci. Technol., 2015, 5, 64–71.
5. G. Li, Q. Wu, S. Wang, Z. Duan, H. Su, L. Zhang, Z. Li, Y. Tang, M. Zhao, L. Chen, K. Liu and Y. Zhang, Environ. Sci. Technol., 2018, 52, 1940–1945.
6. J. H. Pavlish, L. L. Hamre and Y. Zhuang, Fuel, 2010, 89, 838–847.
7. W. Liu, H. Xu, Y. Guo, Y. Yuan, Y. Liao, Z. Qu and N. Yan, Fuel, 2019, 254, 115641.
8. Y. Liu, D. J. A. Kelly, H. Yang, C. C. H. Lin, S. M. Kuznicki and Z. Xu, Environ. Sci. Technol., 2008, 42, 6205–6210.
9. J. P. Baltrus, E. J. Granite, H. W. Pennline, D. Stanko, H. Hamilton, L. Rowsell, S. Poulston, A. Smith and W. Chu, Fuel, 2010, 89, 1323–1325.
10. J. P. Baltrus, E. J. Granite, E. C. Rupp, D. C. Stanko, B. Howard and H. W. Pennline, Fuel, 2011, 90, 1992–1998.
11. D. Ballestero, C. Gómez-Giménez, E. García-Díez, R. Juan, B. Rubio and M. T. Izquierdo, J. Hazard. Mater., 2013, 260, 247–254.
12. J. Dong, Z. Xu and S. M. Kuznicki, Environ. Sci. Technol., 2009, 43, 3266–3271.
13. C. L. Munson, P. Indrakanti, M. Ramezan, E. Granite and J. Tennant, 31st Annual International Pittsburgh Coal Conference: Coal - Energy, Environment and Sustainable Development, PCC 2014, International Pittsburgh Coal Conference, 2014, vol. 3, pp. 65–76.
14. F. Scala, C. Anacleria and S. Cimino, Fuel, 2013, 108, 13–18.
15. H. Xu, J. Jia, Y. Guo, Z. Qu, Y. Liao, J. Xie, W. Shangguan and N. Yan, J. Hazard. Mater., 2018, 342, 69–76.
16. J. Mei, C. Wang, L. Kong, P. Sun, Q. Hu, H. Zhao, Y. Guo and S. Yang, J. Hazard. Mater., 2020, 381, 120967.
17. J. W. Portzer, J. R. Albritton, C. C. Allen and R. P. Gupta, Fuel Processing Technology, Elsevier, 2004, vol. 85, pp. 621–630.
18. S. Poulston, E. J. Granite, H. W. Pennline, C. R. Myers, D. P. Stanko, H. Hamilton, L. Rowsell, A. W. J. Smith, T. Ilkenhans and W. Chu, Fuel, 2007, 86, 2201–2203.
19. C. Gómez-Giménez, D. Ballestero, R. Juan, B. Rubio and M. T. Izquierdo, Chem. Eng. Sci., 2015, 122, 232–239.
20. M. T. Izquierdo, D. Ballestero, R. Juan, E. García-Díez, B. Rubio, C. Ruiz and M. R. Pino, J. Hazard. Mater., 2011, 193, 304–310.
21. Y. Li, P. Murphy and C. Y. Wu, Fuel Process. Technol., 2008, 89, 567–573.
22. H. W. Granite and E. J. Pennline, US Pat., 7033419, 2006.
23. C. Antuña-Nieto, E. Rodríguez, M. A. Lopez-Anton, R. García and M. R. Martínez-Tarazona, Energy, 2018, 159, 630–637.
24. W. Liu, P. Yin, X. Liu, X. Dong, J. Zhang and Q. Xu, Chem. Eng. Res. Des., 2013, 91, 2748–2758.
25. M. S. Shafeeyan, W. M. A. Wan Daud and A. Shamiri, Chem. Eng. Res. Des., 2014, 92, 961–988.
26. C. L. M. Camargo, N. S. De Resende, A. G. De Oliveira, V. M. M. Salim and F. W. Tavares, Fuel, 2014, 129, 129–137.
27. S. T. Chung, K. Il Kim and Y. R. Yun, Powder Technol., 2009, 192, 47–53.
28. J. R. V. Flora, R. A. Hargis, W. J. O’Dowd, H. W. Pennline and R. D. Vidic, J. Air Waste Manage. Assoc., 2003, 53, 478–488.
29. B. Zhao, Z. Zhang, J. Jin and W. P. Pan, J. Hazard. Mater., 2009, 170, 1179–1185.
30. Y. S. Ho, Scientometrics, 2004, 59, 171–177.
31. Y. S. Ho and G. McKay, Process Biochem., 1999, 34, 451–465.
32. X. Wang, Z. Zhang, Y. Zhao, K. Xia, Y. Guo, Z. Qu and R. Bai, Nanomaterials, 2018, 8, 673–693.
33. Y. Zhao, K. Xia, Z. Zhang, Z. Zhu, Y. Guo and Z. Qu, Nanomaterials, 2019, 9, 455–475.
34. K. Xia, Y. Guo, Q. Shao, Q. Zan and R. Bai, Nanomaterials, 2019, 9, 1532–1554.
35. Z. Zhang, K. Xia, Z. Pan, C. Yang, X. Wang, G. Zhang, Y. Guo and R. Bai, Appl. Surf. Sci., 2020, 500, 143970.
36. G. Skodras, I. Diamantopoulou, G. Pantoleontos and G. P. Sakellaropoulos, J. Hazard. Mater., 2008, 158, 1–13.
37. E. Rodríguez and R. García, Energy Fuels, 2012, 26, 3703–3710.
38. J. Rodríguez-Pérez, M. A. López-Antón, M. Díaz-Somoano, R. García and M. R. Martínez-Tarazona, Energy Fuels, 2011, 25, 2022–2027.
39. N. Fernández-Miranda, E. Rodríguez, M. A. Lopez-Anton, R. García and M. R. Martínez-Tarazona, Energies, 2017, 10, 1311–1321.
40. A. Fuente-Cuesta, M. Diaz-Somoano, M. A. Lopez-Anton and M. R. Martinez-Tarazona, Fuel, 2014, 122, 218–222.
41. N. Fernández-Miranda, M. A. Lopez-Anton, M. Díaz-Somoano and M. R. Martínez-Tarazona, Environ. Sci. Technol., 2014, 48, 7164–7170.
42. M. Auta and B. H. Hameed, Chem. Eng. J., 2012, 198–199, 219–227.
43. B. Shen, Z. Li, J. Chen, S. Singh and C. He, Can. J. Chem. Eng., 2015, 93, 2168–2176.
44. H. Qiu, L. Lv, B. C. Pan, Q. J. Zhang, W. M. Zhang and Q. X. Zhang, J. Zhejiang Univ., Sci., A, 2009, 10, 716–724.
45. W. J. Weber and J. C. Morris, J. Sanit. Eng. Div., 1963, 89, 31–60.
46. L. Cáceres, M. Escudey, E. Fuentes and M. E. Báez, J. Hazard. Mater., 2010, 179, 795–803.
47. F. C. Wu, R. L. Tseng and R. S. Juang, Chem. Eng. J., 2009, 153, 1–8.
48. N. Kannan and M. M. Sundaram, Dyes Pigm., 2001, 51, 25–40.
49. N. Asasian, T. Kaghazchi and M. Soleimani, J. Ind. Eng. Chem., 2012, 18, 283–289.
50. C. Aharoni, S. Sideman and E. Hoffer, J. Chem. Technol. Biotechnol., 2007, 29, 404–412.
51. A. Derylo-Marczewska, M. Blachnio, A. W. Marczewski, M. Seczkowska and B. Tarasiuk, Chemosphere, 2019, 214, 349–360.
52. S. Lagergren, Handlingar, 1898, 24, 1–39.
53. A. Fuente-Cuesta, I. Diamantopoulou, M. A. Lopez-Anton, M. Diaz-Somoano, M. R. Martínez-Tarazona and G. P. Sakellaropoulos, Ind. Eng. Chem. Res., 2015, 54, 5572–5579.
54. L. Largitte and R. Pasquier, Chem. Eng. Res. Des., 2016, 109, 495–504.
55. H. C. Hsi, C. Y. Tsai, T. H. Kuo and C. S. Chiang, Bioresour. Technol., 2011, 102, 7470–7477.
56. I. D. Mall, V. C. Srivastava and N. K. Agarwal, J. Hazard. Mater., 2007, 143, 386–395.
57. Y. S. Ho and G. McKay, Process Saf. Environ. Prot., 1998, 76, 332–340.
58. Y. S. Ho, J. Hazard. Mater., 2006, 136, 681–689.
59. S. Wang and H. Li, Dyes Pigm., 2007, 72, 308–314.
60. C. F. Ho, Y.-S. Wase and D. A. J. Forster, Water SA, 1996, 22, 219–224.
61. S. Kumar, K. V. Ramamurthi and V. Sivanesan, J. Colloid Interface Sci., 2005, 284, 14–21.
62. O. G. Elovich and S. Y. Larinov, Izv. Akad. Nauk SSSR, Otd. Khim. Nauk, 1962, 2, 209–216.
63. S. H. Chien and W. R. Clayton, Soil Sci. Soc. Am. J., 1980, 44, 265–268.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nj00898b

---