Open Access Article
Open Access Article3D texturing of the air–water interface by biomimetic self-assembly†
Erik
Bergendal
 a,
Richard A.
Campbell
a,
Richard A.
Campbell
 bc,
Georgia A.
Pilkington
bc,
Georgia A.
Pilkington
 a,
Peter
Müller-Buschbaum
a,
Peter
Müller-Buschbaum
 de and
Mark W.
Rutland
de and
Mark W.
Rutland
 *af
*af
aKTH Royal Institute of Technology, School of Engineering Sciences in Chemistry, Biotechnology and Health, Department of Chemistry, Drottning Kristinas väg 51, 10044 Stockholm, Sweden. E-mail: mark@kth.se
bInstitut Laue-Langevin, 71 avenue des Martyrs, 38042 Grenoble, France
cDivision of Pharmacy and Optometry, University of Manchester, Manchester M21 9PT, UK
dPhysik-Department, Lehrstuhl für Funktionelle Materialen, Technische Universität München, James-Franck-Str.1, 85748 Garching, Germany
eHeinz Maier-Leibnitz Zentrum (MLZ), Technische Universität München, Lichtenbergstr. 1, 85748 Garching, Germany
fRISE Research Institutes of Sweden, Chemistry, Materials and Surfaces, Box 5607, SE-114 86 Stockholm, Sweden
First published on 24th December 2019
Abstract
A simple, insoluble monolayer of fatty acid is shown to induce 3D nanotexturing of the air–water interface. This advance has been achieved through the study of monolayers of a methyl-branched long chain fatty acid, analogous to those found on the surface of hair and wool, directly at the air–water interface. Specular neutron reflectometry combined with AFM probing of deposited monolayers shows pronounced 3D surface domains, which are absent for unbranched analogues and are attributed to hydrocarbon packing constraints. The resulting surface topographies of the water far exceed the height perturbation that can be explained by the presence of capillary waves of a free liquid surface. These have hitherto been considered the only source of perturbation of the flatness of a planar water interface under gravity in the absence of topographical features from the presence of extended, globular or particulate matter. This amounts to a paradigm shift in the study of interfacial films and opens the possibility of 3D texturing of the air–water interface.
New conceptsThe air–water interface has long been used to study the self-assembly of amphiphilic molecules that is ubiquitous in nature. Langmuir–Blodgett deposition of such films is used in semiconductor and OLED manufacture where homogeneous, nanometre thick films are required; the underlying science that supports this field is mature. Assumptions about self-assembly at the air–water interface over the last 100 years are here shown to have been too simple. The novelty of this work is to demonstrate that the air–water interface can be shaped and textured according to the architecture and interfacial properties of the molecules adsorbed. The current paradigm is that water is flat (apart from capillary waves) and that surface adsorbed molecules arrange in a 2D morphology in response to this criterion. In fact, the water can be forced to bend to accommodate the interfacial structures and their respective packing parameters. This new insight opens up the possibility of novel, endlessly tuneable nano-architectures which can be simply deposited from a surface which is anything other than flat. These structures are subject to the same design criteria as self-assembly structures in bulk (micelles, microemulsions etc.), are robust towards deposition and are stable with time. |
In the study of monolayers at the air–water interface, long chain fatty acids have been of interest as model systems for two-dimensional ordering as well as for carboxylic acid–metal ion interactions of biological interest.1–3 The straight chain fatty acid eicosanoic acid (EA, also called arachidic acid) has been the most studied monolayer system due to its simplicity, chain saturation, and subphase insolubility.4–6 The structure and stability of floating and deposited fatty acid monolayers have thus been extensively studied at varying temperature, pH, and subphase composition and concentration.1,7–10 By far the most common technique to study monolayers at the air–liquid interface is the Langmuir technique,11–13 which allows the study of how surface pressure (derived from surface tension measurement) varies as a function of the area available to the monolayer.
The air–water interface is conventionally considered either as flat (i.e. a planar surface under gravity) or curved (e.g. in bubbles, droplets, and foams). In the former case, various 2D phases of the monolayer (e.g. gaseous, tilted expanded, and untilted expanded) can be inferred from surface pressure–area isotherms, analogous to conventional phase changes with pressure and volume,13,14 and a surface roughness is imparted from the presence of capillary waves.15,16 Frequently used complementary techniques for monolayer studies at planar water interfaces are ellipsometry and X-ray scattering,17–19 neutron reflectometry,20,21 spectroscopy,22,23 and, indirectly, atomic force microscopy (AFM) studies of the films deposited from the air–water interface onto solid substrates.24,25 The extension of fundamental studies of the air–water interface, using the Langmuir–Blodgett technique26 to deposit monolayers has led to recent advances in nanofabrication,27,28 device applications,29 life science,30 and semi-conductors.31,32
Formation of 2D surface domains in monolayers, indicating lateral inhomogeneity in the plane of the interface, has been shown for several small molecular weight surfactants.33–36 Domains resolved to date consist of several hundred semi-fluorinated fatty acid or alkane molecules, where deposited monolayers have also been studied with AFM and scattering techniques. The inherent insolubility of the molecules restricts them to a 2D film at the air–water interface, whereas the internal density mismatch imposes both the domain structure and its size. Typically, aside from the roughness originating from the capillary waves, any interfacial topography on a planar water interface under gravity has been assigned only to species present at the interface, such as extended, globular or particular matter in the form of polymer brushes, proteins or nanoparticles, respectively.37–40
A recent study using non-linear spectroscopy and AFM on the ordering of (unbranched) EA and its iso- and antiso-methyl branched derivatives challenged the assumption that the structures at the liquid–air interface are flat, and led to the hypothesis of 3D texturing of the air–water interface itself due to aggregate curvature imposed by tail group packing constraints.41 The unbranched alkyl chains of EA are capable of adopting a uniform, parallel packing, allowing the molecules to form a continuous, flat monolayer on the water surface. The addition of a branch, for example at the iso position imposes a packing strain since the maximum packing densities at the two ends of the alkyl chain are different. To maintain optimal packing densities and surface tension, it was proposed41 that the water–headgroup interface adopted a curvature to accommodate the branch packing, thus locally raising the water interface. This inference, however, was formed indirectly as a result of measurements on deposited films rather than by in situ measurements at the air–water interface itself. Thus, the hypothesis remained to be tested directly at the air–water interface. Here, specular neutron reflectometry (NR) at this interface is used to investigate the veracity of the hypothesis and demonstrate how (branched) 19-methyl eicosanoic acid (19-MEA) induces a texturing of the water surface that far exceeds that explicable by the roughness induced by capillary waves. The addition of a methyl branch, such as the one for 19-MEA, is characteristic of the biological molecules forming the outer barrier of hair and wool,42–44 though in that case the branch is at the C18 carbon (18-MEA). 19-MEA was selected in this case since a larger radius of curvature of the aggregates would be expected for interfacial aggregates from a consideration of packing constraints,41 and is thus biomimetic rather than a biomolecule per se. To the best knowledge of the authors, this system provides the first in situ evidence of 3D ordering of the air–water interface, where only 2D representations or lateral diffraction have previously been invoked.45 This approach will shed light on the possible curvature moderation of biomolecules in the palisade layers of hair and wool,42–44 as well as whether planar water interfaces can be templated against gravity by the combination of surface energy considerations and appropriate choice of self-assembly structures, providing a simple bottom-up approach for 3D nanotexturing.
Results and discussion
Atomic force microscopy
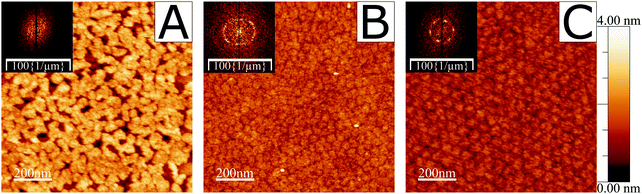
A verification was performed to demonstrate the existence of ordered domains of the fatty acid under study in this work, 19-MEA, when deposited from the air–water interface onto solid substrates. The depositions were carried out at various surface pressures. Fig. S1 in the ESI† shows examples of such surface pressure–area isotherms. A pH-buffered cadmium chloride solution was used as subphase for all depositions and during NR measurements. The cadmium(II) interacts strongly with the carboxylate headgroup to condense the monolayer,7,9 and maintaining a pH of 6.0 (or pD for NR measurements) stabilises the monolayer.46 AFM imaging of deposited monolayers of 19-MEA onto silicon wafers can be seen in Fig. 1, which clearly reveals the formation of domains at all surface pressures. At 0 mN m−1 (A) the fatty acids self-assemble into irregular shapes of around 40 nm in diameter. The height of the domains is roughly 25 Å above the silicon substrate, which corresponds well to the theoretical extended chain length of an all-trans C20 hydrocarbon chain (26.8 Å).47 At increased surface deposition pressure, the surface is completely covered in domains of more homogenous size distribution, as shown for 10 mN m−1 (B) and emphasised by the Fourier transform (FT) inset. At the highest surface pressure of deposition of 40 mN m−1 (C), the domains can be seen to be monodisperse and closely packed with hexagonal order. This increased order is clearly reflected in the corresponding FT inset. From the FT and line profiles, the domain size was determined to vary between 40 to 50 nm at 10 mN m−1 and close to 50 nm at 40 mN m−1. For comparison, monolayers of the unbranched analogue eicosanoic acid, EA, were also deposited under equivalent conditions. They display a featureless monolayer with no evidence of domain formation (see Fig. S2 in ESI†), in agreement with a wealth of studies on this species.24,25,41,48,49Thus far the observations are consistent with ref. 34 and imply a markedly different interfacial packing of the branched and unbranched species, although it cannot be proven that this structure reflects the packing at the air–water interface. To address this issue, neutron reflectometry measurements were performed to directly probe the air–water interface in situ.
Neutron reflectometry
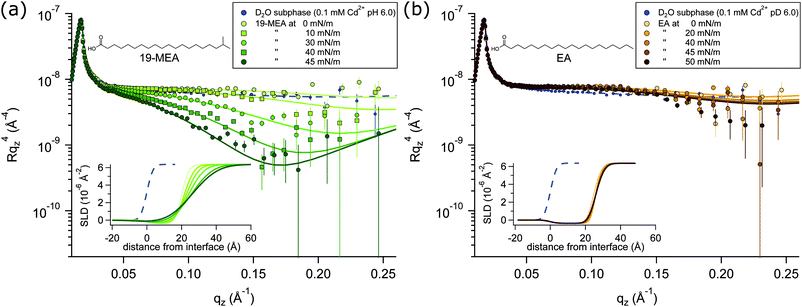
NR profiles of 19-MEA (a) and EA (b) at the air–water interface are shown in Fig. 2 as a function of wave vector transfer qz for several consecutive surface pressures, measured on a single monolayer in each case. With increasing surface pressure, the specular reflectivity for 19-MEA decreases significantly above 0.05 Å−1 in qz. This effect is not seen for EA, where only very small changes in reflectivity are observed with increasing surface pressure. As a reference, a measurement of the neat D2O subphase salt solution is included in Fig. 2, with a fit to the data (dashed line) corresponding to a roughness of 2.8 Å, in good agreement with what is expected from capillary wave theory.15 Neutron reflectivity was measured at two angles of incidence for a monolayer of 19-MEA and EA, both at zero surface pressure and at the highest measured surface pressure for each system. For all other surface pressures, the monolayer was measured only at the higher angle of incidence since these data contained the primary region of interest (qz ≥ 0.05 Å−1)All experiments were carried out with hydrogenous fatty acids on a pH buffered D2O salt solution subphase, which is only one of the possible isotopic contrast combinations of the surfactant and subphase. This provides the optimal contrast to specifically probe the flatness of the planar water interface itself, rather than structural aspects of the monolayer. (The scattering length density of hydrocarbon is close to that of air, which renders it effectively invisible to neutrons). For NR, this lack of contrast is normally seen as a drawback because of the lack of sensitivity to chain length determination. However, thanks to this weak scattering of the aliphatic tails, the reflectivity signal is dominated by the texturing of the D2O surface.
According to capillary wave theory, an increase in surface pressure of a fluid monolayer at the air–water interface should lead to an increased capillary wave amplitude. This is not observed in the reflectivity of EA, however, where the roughness in fact first decreases, before then increasing only slightly over the applied surface pressure range. Such behaviour has been observed earlier, and was explained by the increasing monolayer rigidity suppressing the capillary wave roughness for the straight chain fatty acid behenic acid.50 Analogously, this should explain the observed behaviour for EA since it enters the untilted condensed phase directly upon lift-off51 of the pressure–area isotherm (shown in Fig. S1 in ESI†—where this is further discussed together with Fig. S4, ESI†). Lateral fluctuations in the scattering length density of the interface due to domain formation on the scale shown in Fig. 1, would be far below the neutron coherence length, which is on the micrometre scale in these experiments. The implication is that the measured neutron reflectivity is determined from the scattering length density (SLD) depth profile that is averaged across the whole sample. This in turn allows fitting of the data using a slab model based on the reflection of neutrons at stratified media20,21 where a roughness term can be used to account for any inhomogeneity across the surface as well as the roughness due to capillary waves.
A two-layer model was required to fit the data, separating the distinctly different scattering properties of the fatty acid headgroups and the aliphatic tails. Fitting parameters and a detailed explanation of the fitting procedures for 19-MEA and EA are presented in the ESI.† Note that conventional 2D monolayer fitting approaches need to be adapted somewhat to model a textured surface, the details of which are given in the Methods section. Attempts to fit the system with a one-layer model of smeared SLD did not give satisfactory correlation with the data. Moreover, it has recently been shown that the use of a one-layer model to fit neutron reflectivity data from surfactant monolayers in a limited number of isotopic contrasts can result in erroneous interpretations, particularly when unsupported by data from other isotopic contrasts, and this problem is avoided through use of a two-layer model.52 Such a two-layer model with low roughness (corresponding to the amplitude of capillary waves) provides an excellent fit to the EA data (see Table S1 in ESI†) since it is known that the monolayer forms a homogeneous 2D monolayer. To fit the 19-MEA data, however, it was necessary to invoke a significantly higher surface roughness, consistent with the idea of a 3D textured water interface.
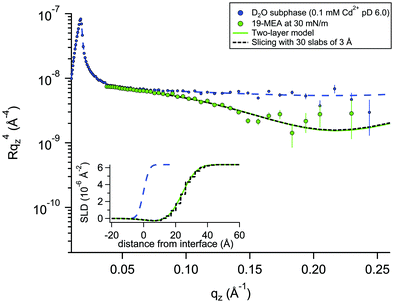
For a system modelled with layers of varying scattering length density, the introduction of a roughness parameter is used to describe interfacial mixing of the two layers as a Gaussian error function. In a system of stratified media with an interfacial roughness on the order of the layer thickness itself, the error functions between layers can overlap, leading to unphysical calculated densities in the interfacial region. It has been shown that this problem is avoided, however, by choosing identical roughness values at all interfaces.52 To verify that not only is the SLD calculation physically reasonable, but also that the reflectivity calculations used to fit the data (based on roughness-modified stratified media with Fresnel reflectivity) are valid, one dataset was fitted in two different ways. The premise for this verification is described in more depth in the Neutron Reflectivity Fitting section. Approach 1 is a conventional fit using a two-layer model (as for EA) but employing higher, identical, interfacial roughness at each interface. Approach 2 involves the generation of a SLD profile using almost the same physical density distribution of the material at the interface, but which is instead sliced into 30 layers of 3 Å thickness with zero interfacial roughness to eliminate the possibility of artefacts in the data from the relatively high roughness. Fig. 3 shows an example of these two data fitting approaches for the case of 19-MEA on the D2O subphase at a surface pressure of 30 mN m−1. For the two-layer model, the (identically constrained) interfacial roughness was fitted as 7.0 Å, with headgroup and tail region thicknesses of 4.5 Å and 23.5 Å, respectively. The solid line represents the two-layer model fit and the dashed black line represents the slicing fit with zero roughness. The inset shows the resulting SLD-profiles. The fits overlap to the point of being almost indistinguishable. This demonstrates that the Fresnel reflectivity calculation with the added Gaussian error function is valid and equivalent to the standard Fresnel calculation of stratified media, even when the topographic variation far exceeds the layer thickness. This empirical validation of the use of identically constrained high roughness values, should be generally applicable to multiple stratified systems, for example phospholipid monolayers where both tail is deuterated and headgroup is partially deuterated.52
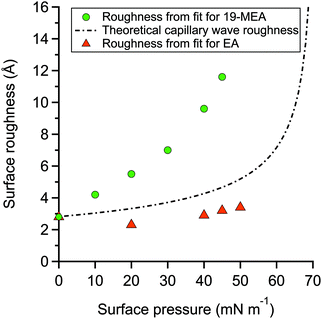
The fitting parameters for 19-MEA, extracted from the two-layer slab model, are shown in Table S2 of the ESI.† The large range of surface pressures measured were accessed through rather minor changes of surface area (and resulting area per molecule), due to the steepness of the surface pressure–area isotherm, and thus it would not be expected that there should be significant changes in any of the density or thickness parameters corresponding to the fatty acid. Therefore, the only fitting parameter was the roughness of all the interfaces in the slab model, which were constrained to be equal to each other. For 19-MEA, the hydrocarbon region thickness was also varied slightly and systematically based on the isotherm data. The SLD values of the hydrocarbon and headgroup region were calculated, and the headgroup region thickness was constrained to the same calculated value for both EA and 19-MEA. The only parameter capable of inducing the observed decrease in intensity in Fig. 2 is the interfacial roughness parameter (constrained to be identical at each of the three interfaces in the two-layer model). The roughness parameters for the model fits to the experimental data for EA and 19-MEA are presented in Fig. 4 with respect to the surface pressure, together with a theoretical prediction of capillary wave roughness based on the assumption of a fluid monolayer.15,53 As noted earlier, the data from EA demonstrates that its surface roughness is less than the model predicts, which is attributed to the bending rigidity of the molecule. Importantly, the increased roughness of the air–water interface observed for 19-MEA far exceeds that which can be argued to originate exclusively from the presence of capillary waves, even ignoring the damping effect. Therefore, these results together provide the first direct in situ evidence for 3D texturing of the air–water interface using a simple surfactant monolayer.
Curvature of the spherical cap
The AFM images reveal that the aggregates, which exist already at 0 mN m−1 are further organised into monodisperse domains of hexagonal ordering at 40 mN m−1. There is no observable coalescence between domains. Their monodispersity suggests an optimal size corresponding to an energy minimum, analogous to the monodispersity of other surfactant self-assembly structures such as micelles and microemulsions, where the aggregate curvature is determined by the so-called packing parameter.54,55 To extend this self-assembly analogy, to the air–water interface, this optimal size would then correspond to a spherical cap with a radius of curvature governed by the fatty acid tail group packing. The presence of the methyl group prevents the close parallel packing of the alkyl chains, which leads to a flat monolayer in the case of the unbranched molecules, and imposes a negative curvature for the branched molecules. The larger topography (measured as increased surface roughness) at higher surface pressure implies that closer packing of the monolayer yields a larger perturbation—or lifting—of the water surface. Thus, it can be concluded that self-assembly of surface domains alone does not perturb the water surface, but that compression of the domain-containing monolayer is also necessary if three-dimensional texturing is to be achieved, and the rule of a flat planar water interface under gravity is to be broken.So far, AFM measurements indicate the lateral size of the domains (but no height information since the monolayers are deposited on a rigid solid interface) and the NR studies indicate a measure of their height (or texturing), but with no explicit information on their lateral extent. While compelling, these independent observations do not completely prove the hypothesis of self-assembly based curvature. If the suggested mechanism is correct, however, it should then be possible to use equations describing the geometry of a spherical cap to predict the radius of curvature from the normal and lateral dimensions, respectively, provided by the two completely independent techniques. Such a calculation is performed in the ESI.† Using the diameter of 50 nm for the 45 mM m−1 case, and assuming that the Gaussian roughness in fact is an estimation of the average height of the spherical caps, h = 11.5 Å at the same pressure, a curvature radius of 2.2 μm is obtained. In ref. 41 a simple estimation of the curvature is proposed based on molecular areas. Using the areas per molecule at 45 mN m−1 from that paper, a radius of curvature is calculated with no free parameters, corresponding to 2.4 μm. These values differ by only 9% which is extraordinarily good agreement given the simplicity of the calculations in each case, and provides categorical support for the self-assembly model.
Conclusions
The notion of a planar water interface under gravity has been challenged. In the present work, it has been directly shown that the biomimetic, methyl-branched long chain fatty acid 19-MEA perturbs the flatness of the air–water interface by several Ångströms to create 3D surface domains with a height modulation that far exceeds that expected for capillary waves. The straight chain analogue EA on the other hand does not exhibit this behaviour and in fact displays a lower surface roughness than capillary wave theory predicts for a fluid, disordered monolayer, which is explained by its high bending rigidity. The novel 3D surface texturing for the 19-MEA system is attributed to packing constraints imposed by its branched, saturated chains. This advance thus provides the opportunity to template the air–water interface itself with nanosized, regularly ordered asperities through control of the surfactant packing parameter; via chain branching, chain substitution, unsaturation or multiple chains, which was not apparent before. Controlled nano-structuring of sol–gel polymerisation at the water–monolayer interface, or UV-initiated monolayer polymerisation, are two potential pathways of exploitation, utilising either side of the textured surface. Further, while the applications of deposited Langmuir–Blodgett films generally require homogeneous monolayers, there is a clear opportunity to tune the architecture of such films. Regular patterns can be generated, of nanometre thickness, nanoscale-microscale lateral dimensions with uniform size over areas which could be on the scale of square metres. These 3D species could then be used to decorate a solid surface with regular patterns on the nanometre scale, transformed to 2D due to the rigidity of the solid. As is known from 100 years or so of research into microemulsions and micellar aggregates, self-assembly is exquisitely tuneable in terms of curvature and thus lateral dimensions. Both the polar headgroup area and the non-polar region can be independently tuned in size and anisotropy and these tools already exist. Since metal ions are associated with the fatty acids (in this case) it should be feasible to deposit nanometre size islands consisting of a few hundred metal ions in each which could then be reduced to form metallic nanodots, avoiding costly printing and nanotechnology solutions, which are usually feasible only over smaller areas. Unlike many soft nanomaterial breakthroughs, requiring sophisticated equipment, printers, advanced lithography and so on, these large-scale patterns on nanometre scale could be generated by undergraduates in the laboratory on the first attempt, using chemicals they buy from a catalogue.A planar air–water interface under gravity is thus not necessarily a self-levelling two-dimensional environment, supporting self-assembly structures and moderated only by the presence of capillary waves, as previously believed, but can support a significant degree of static topography.
Materials and methods
All chemicals were used as received. The fatty acids were provided by Sigma Aldrich (EA ≥99%, 19-MEA >98%). Chloroform (Sigma Aldrich, ≥99.5%, stabilised with 100–200 ppm amylene) was used to spread fatty acid monolayers on a water and D2O subphase for Langmuir–Blodgett depositions and NR measurements, respectively. In both cases, the subphase contained 0.1 mM CdCl2, 0.1 mM NaHCO3, and was buffered to pH (or pD) 6.0 with HCl (or DCl). The addition of cadmium salt condenses the monolayer as cadmium(II) interacts covalently with the carboxylate headgroup, while the pH (or pD) was regulated to 6.0 to stabilise the monolayer.7,9,46 A KSV NIMA 5000 PTFE (polytetrafluoroethylene) trough with hydrophilic POM (polyoxymethylene) barriers was used for depositions. For NR measurements a similar, but smaller trough was used, which was stabilised on-line by an active anti-vibration table. Barriers were symmetrically compressed at 4.5 cm2 min−1. Wilhelmy plates of paper were used to monitor surface pressure and the subphase was temperature controlled to 22 °C. Monolayers were deposited at 1 mm min−1 onto silicon wafers, cleaned by immersion in chromosulfuric acid (5% Cr(VI) in H2SO4) and thoroughly rinsed with MilliQ water. AFM imaging of deposited monolayers was done with a Bruker Multimode Microscope LN in tapping mode, using silicon cantilevers (HQ:NSC35/AL BS, MikroMasch) with a typical radius of 8 nm. The nominal resonance frequency and force constant of the cantilevers were 150 kHz and 5.4 N m−1, respectively. Analysis of representative 1 μm by 1 μm AFM images was performed in WSxM 5.0.56 NR measurements were performed at the horizontal time-of-flight reflectometer FIGARO at Institut Laue-Langevin (ILL) in Grenoble, France.57 Reflectivity was acquired at two angles of incidence, θ = 0.62° and θ = 3.8° with a wavelength resolution of 7% dλ/λ, and 2D detector at 2890 mm from the sample stage, situated in an evacuated flight tube. The intensity of specular reflected neutrons was normalized to the incident neutron beam as a function of angle and neutron wavelength according to the momentum transfer qz along the surface normal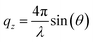 | (1) |
Neutron reflectivity fitting
The application of a slab, or layer, model where the topographic variation or roughness is large compared to the layer thickness is not without controversy.52,59–61Ref. 52 demonstrated conservation of material in the SLD-profile through application of relatively high but identical roughness values at the three interfaces present in the two-layer model of a surfactant monolayer at the air–water interface (water–headgroups, headgroups–tails, and tails–air). This conservation of material may not be maintained if different roughness values that are significantly large with respect to the smallest layer thickness are applied at the respective interfaces because an artefact in the form of a region of negative density can appear in the density profiles normal to the interface. Therefore, it was concluded that application of roughness values as large as the smallest layer thickness is a physically reasonable approach. The work, however, stopped short of demonstrating that the application of such relatively high, but identical roughness values results in physically realistic reflectivity calculations. This point is now addressed by examining whether the reflectivity calculations are correctly described by a model where the “roughness” (the factor accounting for the smearing of the SLD in the vertical direction by the topography variation) is as large as—or ever larger than—the smallest layer thickness. The Fresnel coefficients in eqn (2) are used to describe reflection and refraction in stratified media. Due to interdiffusion or surface perturbations, or both, a Gaussian error function is added to account for the deviation from homogeneous slab behaviour62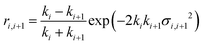 | (2) |
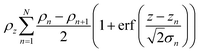 | (3) |
Conflicts of interest
The authors declare no competing interests.Acknowledgements
We thank the ILL for the provision of neutron beam time on FIGARO (DOI: 10.5291/ILL-DATA.9-10-1487). MR and EB acknowledge support from the Swedish Research Council via grant VR 2013-04384. PMB acknowledges funding from the Excellence Cluster Nanosystems Initiative Munich (NIM) and the Center for NanoScience (CeNS). We thank Gustavo Luengo, Deborah Wakeham, Anna Oleshkevych, Philipp Gutfreund, and Adrian Rennie for useful discussions.References
- V. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779–819 CrossRef CAS.
- G. Brezesinski and H. Möhwald, Adv. Colloid Interface Sci., 2003, 100–102, 563–584 CrossRef CAS PubMed.
- M. D. King, A. R. Rennie, K. C. Thompson, F. N. Fisher, C. C. Dong, R. K. Thomas, C. Pfrang and A. V. Hughes, Phys. Chem. Chem. Phys., 2009, 11, 7699–7707 RSC.
- E. Pezron, P. M. Claesson, J. M. Berg and D. Vollhardt, J. Colloid Interface Sci., 1990, 138, 245–254 CrossRef CAS.
- L. M. Eng, C. Seuret, H. Looser and P. Gunter, J. Vac. Sci. Technol., B: Microelectron. Process. Phenom., 1996, 14, 1386 CrossRef CAS.
- K. Kjaer, J. Als-Nielsen, R. Kenn, C. Böhm, P. Tippman-Krayer, C. A. Helm, H. Möhwald, F. Leveiller, D. Jacquemain, M. Lahav, L. Leiserowitz and M. Deutsch, in Proceedings of the 2nd International Conference, Physik Zentrum, Bad Honnef, Fed. Rep. of Germany, 1991, pp. 143–146.
- B. P. Binks, Adv. Colloid Interface Sci., 1991, 34, 343–432 CrossRef CAS.
- S. Kundu, A. Datta and S. Hazra, Langmuir, 2005, 21, 5894–5900 CrossRef CAS PubMed.
- J. Kmetko, PhD thesis, Northwestern University, 2002.
- J. B. Peng, G. T. Barnes and I. R. Gentle, Adv. Colloid Interface Sci., 2001, 91, 163–219 CrossRef CAS PubMed.
- A. Pockels, Nature, 1891, 43, 437–439 Search PubMed.
- G. L. Gaines, Insoluble Monolayers at Liquid-gas Interfaces, Interscience Publishers, 1966 Search PubMed.
- G. Barnes and I. Gentle, Interfacial science: an introduction, Oxford University Press, 2011 Search PubMed.
- E. Matijević, J. Colloid Interface Sci., 1979, 70, 399 CrossRef.
- A. Braslau, P. S. Pershan, G. Swislow, B. M. Ocko and J. Als-Nielsen, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 2457–2470 CrossRef PubMed.
- S. K. Sinha, E. B. Sirota and S. Garoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 2297–2311 CrossRef PubMed.
- J. G. Petrov, T. Pfohl and H. Möhwald, J. Phys. Chem. B, 1999, 103, 3417–3424 CrossRef CAS.
- T. M. Bohanon, B. Lin, M. C. Shih, G. E. Ice and P. Dutta, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 4846–4849 CrossRef CAS PubMed.
- J. B. Peng, G. T. Barnes, I. R. Gentle and G. J. Foran, J. Phys. Chem. B, 2000, 104, 5553–5556 CrossRef CAS.
- J. Bradley, E. Lee, R. Thomas, J. Penfold and R. Ward, Langmuir, 1988, 80, 821–826 CrossRef.
- C. Pfrang, F. Sebastiani, C. O. M. Lucas, M. D. King, I. D. Hoare, D. Chang and R. A. Campbell, Phys. Chem. Chem. Phys., 2014, 16, 13220–13228 RSC.
- E. Tyrode, M. W. Rutland and C. D. Bain, J. Am. Chem. Soc., 2008, 130, 17434–17445 CrossRef CAS PubMed.
- G. Ma and H. C. Allen, Langmuir, 2006, 22, 5341–5349 CrossRef CAS PubMed.
- D. K. Schwartz, R. Viswanathan, J. Garnaes and J. A. Zasadzinski, J. Am. Chem. Soc., 1993, 115, 7374–7380 CrossRef CAS.
- J. B. Peng and G. T. Barnes, Thin Solid Films, 1994, 252, 44–48 CrossRef CAS.
- K. B. Blodgett, J. Am. Chem. Soc., 1934, 56, 495 CrossRef CAS.
- K. Ariga, Y. Yamauchi, T. Mori and J. P. Hill, Adv. Mater., 2013, 25, 6477–6512 CrossRef CAS PubMed.
- K. A. Svit and K. S. Zhuravlev, J. Phys. Chem. C, 2015, 119, 19496–19504 CrossRef CAS.
- Z. Tong, S. Liu, X. Li, J. Zhao and Y. Li, Nanoscale Horiz., 2018, 3, 261–292 RSC.
- J. D. Mangadlao, C. M. Santos, M. J. L. Felipe, A. C. C. de Leon, D. F. Rodrigues and R. C. Advincula, Chem. Commun., 2015, 51, 2886–2889 RSC.
- T. J. Reece, A. Gerber, H. Kohlstedt and S. Ducharme, J. Appl. Phys., 2010, 108, 024109 CrossRef.
- S. Acharya, A. B. Panda, N. Belman, S. Efrima and Y. Golan, Adv. Mater., 2006, 18, 210–213 CrossRef CAS.
- T. Kato, M. Kameyama, M. Ehara and K.-I. Iimura, Langmuir, 1998, 7463, 1786–1798 CrossRef.
- M. P. Krafft, Acc. Chem. Res., 2012, 45, 514–524 CrossRef CAS PubMed.
- L. De Viguerie, R. Keller, U. Jonas, R. Berger, C. G. Clark, C. O. Klein, T. Geue, K. Müllen, H. J. Butt and D. Vlassopoulos, Langmuir, 2011, 27, 8776–8786 CrossRef CAS PubMed.
- S. M. Malone, S. Trabelsi, S. Zhang, T. R. Lee and D. K. Schwartz, J. Phys. Chem. B, 2010, 114, 8616–8620 CrossRef CAS PubMed.
- S. Micciulla, Y. Gerelli, R. A. Campbell and E. Schneck, Langmuir, 2018, 34, 789–800 CrossRef CAS PubMed.
- J. Reguera, E. Ponomarev, T. Geue, F. Stellacci, F. Bresme and M. Moglianetti, Nanoscale, 2015, 7, 5665–5673 RSC.
- J. R. Lu, T. J. Su, R. K. Thomas, J. Penfold and J. Webster, J. Chem. Soc. – Faraday Trans., 1998, 94, 3279–3287 RSC.
- P. J. Atkinson, E. Dickinson, D. S. Horne and R. M. Richardson, J. Chem. Soc., Faraday Trans., 1995, 91, 2847–2854 RSC.
- J. F. D. Liljeblad, E. Tyrode, E. Thormann, A.-C. Dublanchet, G. Luengo, C. Magnus Johnson and M. W. Rutland, Phys. Chem. Chem. Phys., 2014, 16, 17869–17882 RSC.
- P. W. Wertz and D. T. Downing, Lipids, 1988, 23, 878–881 CrossRef CAS PubMed.
- L. N. Jones and D. E. Rivett, Micron, 1997, 28, 469–485 CrossRef CAS PubMed.
- A. Negri, H. Cornell and D. Rivett, Aust. J. Agric. Res., 2004, 42, 1285 CrossRef.
- P. Fontaine, M. Goldmann, P. Muller, M. C. Fauré, O. Konovalov and M. P. Krafft, J. Am. Chem. Soc., 2005, 127, 512–513 CrossRef CAS PubMed.
- J. Peltonen, M. Linden, H. Fagerholm, E. Györvary and F. Eriksson, Thin Solid Films, 1994, 242, 88–91 CrossRef CAS.
- C. Tanford, J. Phys. Chem., 1972, 76, 3020–3024 CrossRef CAS.
- K. S. Birdi and D. T. Vu, Surf. Coat. Technol., 1994, 67, 183–191 CrossRef CAS.
- K. Das and S. Kundu, Colloids Surf., A, 2016, 492, 54–61 CrossRef CAS.
- J. Daillant, L. Bosio, J. J. Benattar and J. Meunier, Eur. Lett., 1989, 8, 453–458 CrossRef CAS.
- M. L. Kurnaz and D. K. Schwartz, J. Phys. Chem., 1996, 100, 11113–11119 CrossRef CAS.
- R. A. Campbell, Y. Saaka, Y. Shao, Y. Gerelli, R. Cubitt, E. Nazaruk, D. Matyszewska and M. J. Lawrence, J. Colloid Interface Sci., 2018, 531, 98–108 CrossRef CAS PubMed.
- A. Braslau, M. Deutsch, P. S. Pershan, A. H. Weiss, J. Als-Nielsen and J. Bohr, Phys. Rev. Lett., 1985, 54, 114–117 CrossRef CAS PubMed.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- R. Nagarajan, Langmuir, 2002, 18, 31–38 CrossRef CAS.
- I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef CAS PubMed.
- R. A. Campbell, H. P. Wacklin, I. Sutton, R. Cubitt and G. Fragneto, Eur. Phys. J. Plus, 2011, 126, 107 CrossRef.
- A. Nelson, J. Appl. Crystallogr., 2006, 39, 273–276 CrossRef CAS.
- B. Vidal and P. Vincent, Appl. Opt., 2009, 23, 1794 CrossRef PubMed.
- D. K. G. De Boer, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5817–5820 CrossRef CAS PubMed.
- D. Jia, K. Tao, J. Wang, C. Wang, X. Zhao, M. Yaseen, H. Xu, G. Que, J. R. P. Webster and J. R. Lu, Langmuir, 2011, 27, 8798–8809 CrossRef CAS PubMed.
- L. Névot and P. Croce, Rev. Phys. Appl., 1980, 15, 761–779 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00722a |
| This journal is © The Royal Society of Chemistry 2020 |