A new approach for an ultrasensitive tactile sensor covering an ultrawide pressure range based on the hierarchical pressure-peak effect†
Congyi
Wu
ab,
Tian
Zhang
a,
Jian
Zhang
a,
Jin
Huang
*c,
Xing
Tang
a,
Tingting
Zhou
a,
Youmin
Rong
b,
Yu
Huang
b,
Songxin
Shi
b and
Dawen
Zeng
 *ad
*ad
aState Key Laboratory of Materials Processing and Die Mould Technology, Huazhong University of Science and Technology (HUST), Wuhan 430074, China. E-mail: dwzeng@mail.hust.edu.cn
bState Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology (HUST), Wuhan 430074, China
cChongqing Key Laboratory of Soft-Matter Material Chemistry and Function Manufacturing, School of Chemistry and Chemical Engineering, Southwest University, Chongqing 400715, China. E-mail: huangjin2015@swu.edu.cn
dHubei Collaborative Innovation Center for Advanced Organic Chemical Materials, Hubei University, Wuhan 430074, China
First published on 10th December 2019
Abstract
Flexible tactile sensors that imitate the skin tactile system have attracted extensive research interest due to their potential applications in medical diagnosis, intelligent robots and so on. However, it is still a great challenge to date to fabricate tactile sensors with both high sensitivity and wide detection range due to the difficulties in modulating the resistance variation in the sensing materials in a wide pressure range. Here, a tactile sensor with a novel design based on the hierarchical pressure-peak effect (HPPE) consisting of PVP nanowires and electroless deposition (ELD) silver PDMS micro-pyramids is reported. The HPPE can effectively modulate the resistance change rate by adjusting the change of contact area during compression deformation, and the HPPE tactile sensor was demonstrated to have both ultrahigh sensitivity (11.60–1108.75 kPa−1) and ultrawide pressure range (0.04–600 kPa). The designed HPPE tactile sensor is successfully utilized in detecting multi-level pressures including respiration, finger heart rate, pulse and foot pressures. Moreover, it is used to sense a subtle clamping force in the Leonardo Da Vinci surgical robot demonstrating the potential of the sensor in surgical robot applications. In all these cases, the sensor exhibits enough capability to respond quickly to ultrawide-range pressures with high accuracy and stability.
New conceptsA new approach based on the hierarchical pressure-peak effect (HPPE) has been employed to fabricate a flexible piezoresistive tactile sensor, which can effectively modulate the resistance change rate during compression and thereby broaden the pressure testing range while ensuring higher sensitivity. Ultrahigh sensitivity (11.60–1108.75 kPa−1) and ultrawide pressure range (0.04–600 kPa) can be simultaneously achieved in such best-performing HPPE tactile sensor. More importantly, a quantitative summary of how resistance changes can be adjusted by controlling the contact area and sensitive materials in the peak pressure effect (PPE) is given. It provides a new approach and calculation basis for the subsequent design and manufacture of flexible tactile sensors with controllable pressure range, sensitivity and signal linearity. The HPPE tactile sensor was first applied to the Leonardo Da Vinci surgical robot to detect tiny clamping pressures. |
1. Introduction
The human tactile system can detect a diverse range of environmental changes by sensing a wide range of pressure stimuli1–3 such as a breeze (<1 kPa), water flow (1–100 kPa) and griping (50–600 kPa). In designing products imitating the human tactile system, such as electronic skin,4–10 wearable electronics11–15 and human-computer interactive systems,16–19 a flexible tactile sensor is required to have high sensitivity, wide detection range, quick response and high stability. Based on these requirements, flexible capacitive,7,20–23 piezoelectric,24,25 triboelectric26 and piezoresistive27–31 tactile sensors have been intensively studied. Among these sensor types, the piezoresistive tactile sensors, which convert the mechanical pressure into a resistance signal, have been widely investigated due to their simple structure, low manufacturing cost and easy signal processing.29,31–35 However, due to the limitations of the combined design of structures and materials, it is a great challenge to fabricate flexible tactile sensors with both a wide pressure range and high sensitivity.In recent years, a variety of ordered micro-nano structures (such as pillars,29,33 semi-spheres,33–36 pyramids,27,33,37 and metal nanowires38) and conductive materials (such as carbon materials27,30,37) have been adopted to improve the sensitivity of the piezoresistive tactile sensors. For instance, a flexible piezoresistive tactile sensor has been demonstrated to have high sensitivity of 5.5 kPa−1 in a low pressure range of <100 Pa by introducing pyramid microstructures and sensitive graphene layers,27 high sensitivity of ≤2 kPa−1 and a larger pressure range of 0.2–1 kPa by combining Au-deposited PDMS micropillars with polyaniline nanofibers,29 and ultra-high sensitivity of 28.34 kPa−1 in a wider pressure range of 3–10 kPa by the use of wrinkled graphene film/interconnected polyvinyl alcohol nanowires/interdigital electrodes.30 However, these tactile sensors are unable to detect pressures greater than 10 kPa.27,31 Nevertheless, the detection range of pressure can be further improved by controlling the contact area change during compression deformation, which would lead to resistance variation at higher pressures. For instance, a piezoresistive tactile sensor with multilayer microstructures in which sequential contact occurred over a wide detection range of 0.01–400 kPa achieved excellent sensitivity of 2.5–1051 kPa−1.31 However, in this case, the irregular surface morphology led to the instability of device performance. In an innovative work by Kim et al., an all-fabric sensor based on the multi-layer geometry and the contact area change of the fabric showed high sensitivity of 26.13 kPa−1 over a wide pressure range of 0.2–982 kPa, but the substrate was too thick, which may limit its applications.28 Furthermore, a foam-like piezoresistive tactile sensor based on laser-scribed graphene showed large contact area changes during compression and hence achieved a large pressure detection range of up to 113 kPa, but the sensitivity (<1 kPa−1) was too low due to a small resistance variation range.39 Although the measurement range of pressure can be improved by controlling the contact area, more innovative combination design is still a mainstream approach to optimizing the performance of piezoresistive tactile sensors. In summary, to design a high-performance flexible piezoresistive tactile sensor with a wide pressure range and high sensitivity, the following conditions should be met: (1) innovative structural design should be adopted to ensure stable and controllable contact change over a wide pressure range and the substrate must be as thin as possible, (2) as a kind of sensing material, a highly conductive material should have small saturation resistance and large package resistance, and then higher sensitivity could be obtained by combining a novel structural design.
In this work, we demonstrate a new approach to fabricate a flexible piezoresistive tactile sensor with ultrahigh sensitivity (11.60–1108.75 kPa−1) in an ultrawide detection range (0.04–600 kPa) based on the hierarchical pressure-peak effect (HPPE). The sensor consists of insulating polyvinyl-pyrrolidone (PVP) nanowires (NWs) and ELD-Ag PDMS micro-pyramids. On the one hand, the HPPE can ensure a stable change of contact area during compression deformation. On the other hand, a silver film with high-adhesion and high-conductivity can be obtained by an intensified ELD method, ensuring the stability of the sensitive material while obtaining large package resistance and small saturation resistance. During the compression of the sensor, the contact between the micro-pyramid and the plate electrode forms the first-stage pressure-peak effect (PPE) and ensures a stable contact area change at the top of the micro-pyramid. The contact between the conductive film and the plate electrode in the PVPNW mesh forms the second-stage PPE and ensures a stable contact area change in the PVPNW mesh. This HPPE can effectively modulate the resistance change rate during compression and thereby broaden the pressure testing range while ensuring higher sensitivity. In addition, the sensor demonstrated a short response time (<60 ms) and excellent repeatability with more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles even when tested at a high pressure of 100 kPa. Significantly, the experimental results showed that the variation of resistance in the piezoresistive tactile sensor was mainly caused by the compression deformation of sensitive materials with peak-like structure, which is termed as the pressure-peak effect (PPE). Meanwhile, the PPE of the flexible piezoresistive tactile sensor was investigated in detail by analyzing the resistance change of the ELD-Ag PDMS micro-pyramids during compression deformation. The experimental results showed that a small number of pyramids of silver and a thinner silver film by magnetron sputtering resulted in a smaller change in resistance rate. To demonstrate this concept, the as-prepared HPPE tactile sensor was utilized in detecting multi-level pressure stimuli including respiration, finger heart rate, pulse and foot pressures. Moreover, by attaching this sensor to the clamp on a Leonardo Da Vinci surgical robot, it was shown that the variation of clamping force can be easily measured, demonstrating the potential of the sensor in intelligent robot applications.
000 cycles even when tested at a high pressure of 100 kPa. Significantly, the experimental results showed that the variation of resistance in the piezoresistive tactile sensor was mainly caused by the compression deformation of sensitive materials with peak-like structure, which is termed as the pressure-peak effect (PPE). Meanwhile, the PPE of the flexible piezoresistive tactile sensor was investigated in detail by analyzing the resistance change of the ELD-Ag PDMS micro-pyramids during compression deformation. The experimental results showed that a small number of pyramids of silver and a thinner silver film by magnetron sputtering resulted in a smaller change in resistance rate. To demonstrate this concept, the as-prepared HPPE tactile sensor was utilized in detecting multi-level pressure stimuli including respiration, finger heart rate, pulse and foot pressures. Moreover, by attaching this sensor to the clamp on a Leonardo Da Vinci surgical robot, it was shown that the variation of clamping force can be easily measured, demonstrating the potential of the sensor in intelligent robot applications.
2. Results and discussion
2.1. Preparation of the HPPE tactile sensor
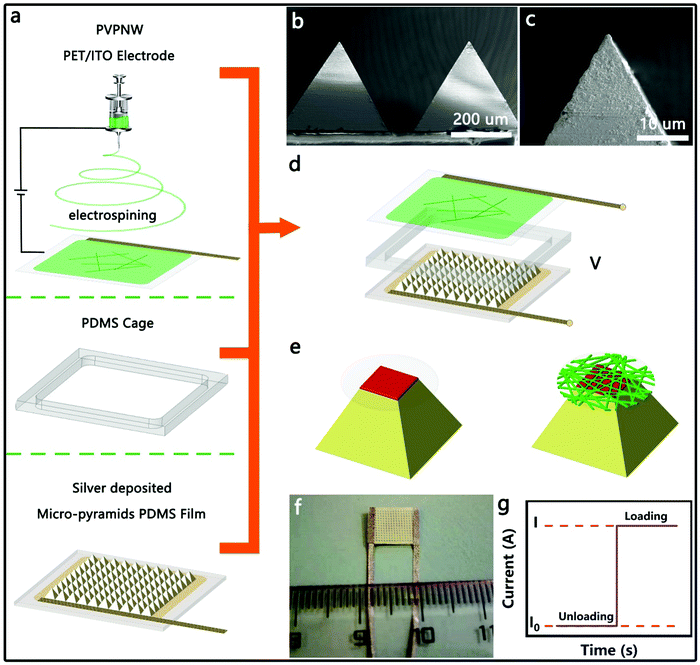
Fig. 1 illustrates the process of manufacturing a HPPE tactile sensor and the testing mechanism. The insulating PVPNW networks were formed on a PET/ITO sheet by an electrospinning process (Fig. 1a). The electrospinning solution was composed of a PVP ethanol solution at a weight ratio of 15%. By varying the time of electrospinning (0, 20 s, 40 s, 60 s, 80 s), PVPNW meshes with different densities (PVP-0, PVP-20, PVP-40, PVP-60, PVP-80) were obtained. Curing at 120 °C for 10 min was then necessary to ensure that the PVPNW mesh was firmly formed on the PET/ITO sheet. The PDMS cage was prepared by laser cutting, and was hollow inside to accommodate the pyramid array. The upper surface of the PDMS cage was cemented with PET/ITO electrode, and the lower surface was cemented with the micro-pyramid PDMS film. As shown in Fig. S1 (ESI†), the micro-pyramid PDMS film was fabricated via a two-step soft lithography replication process with metal micro-pyramids as the original template, which was manufactured by a milling machining with computerized numerical control (CNC) (Fig S2, ESI†). A 190 nm thick silver film was then formed on the surface of the PDMS micro-pyramid film by electroless silver plating (Fig. S3 and S4, ESI†). Measured by the four-probe method, the electroless plated silver layer exhibited a high conductivity of 3.9 × 107 S m−1, which was the premise for ensuring a small saturation resistance. As shown in Fig. 1b and c and Fig. S5 and S6 (ESI†), the surfaces of the prepared ELD-Ag micro-pyramids were smooth and the tops were sharp with a top platform no larger than 2 × 2 μm2. The HPPE tactile sensor was obtained (Fig. 1f) by assembling the micro-pyramid PDMS film, PDMS cage and PVPNW PET/ITO electrode in order, as shown in Fig. 1d. During the compression of the sensor, the contacts between the micro-pyramids and the plate electrode formed the first-stage PPE and ensured a stable contact area change at the top of the micro-pyramids (Fig. 1e). The contact between the conductive film and the plate electrode in the PVPNW mesh formed the second-stage PPE and ensured a stable contact area change in the PVPNW mesh. At a test voltage of 0.1 V, the external pressure deformed the pyramid and caused a change in the contact area at the top of the micro-pyramids and inside the PVPNW meshes, resulting in an increase in current as shown in Fig. 1g.2.2. Characterization of the piezoresistance properties
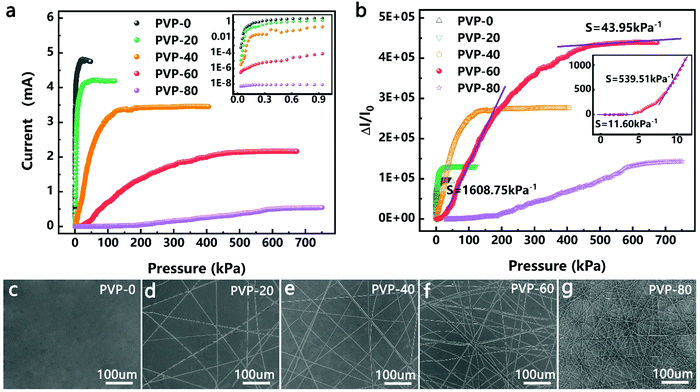
The effects of the density of the PVPNW mesh on the performance of the HPPE tactile sensor were investigated by comparing the performance of devices made using different electrospinning times. In Fig. 2c–g, the samples produced using electrospinning times of 0, 20 s, 40 s, 60 s, and 80 s were designated as PVP-0, PVP-20, PVP-40, PVP-60 and PVP-80, respectively. The straight PVPNWs were evenly distributed on the PET/ITO sheet with an average diameter of 300 nm (Fig. 2d–g). Obviously, the size of the PVPNW meshes became smaller as the electrospinning time was increased (Fig. 2d–g).The size of the PVPNW meshes can regulate the performance of the HPPE tactile sensor (Fig. 2a and b). Fig. 2a shows the current–pressure curves of the HPPE tactile sensor with different sizes of PVPNW meshes at a test voltage of 0.1 V. It was observed that the initial current of the device was larger when the size of the PVPNW meshes was bigger, which was caused by the pre-pressure of device packaging. In the cases where pre-pressure was constant, a larger mesh size resulted in a weaker isolation effect on the sensing material, and hence a larger initial current. In addition, as the size of the PVPNW meshes became smaller, the pressure range that the sensor can detect gradually increased and the saturation current steadily decreased.
The effect of the PVPNW meshes on the performance of the HPPE tactile sensor can be described quantitatively by the sensitivity of the piezoresistive tactile sensor (S), which is given by the slope of the curve:
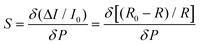 | (1) |
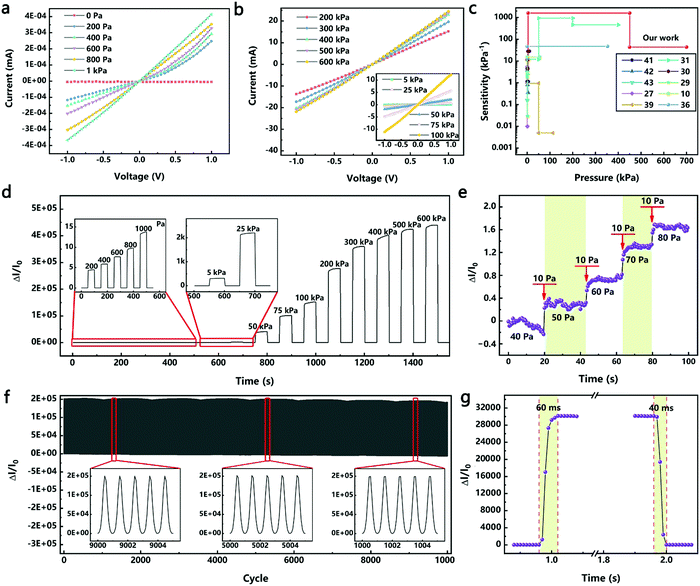
For testing the current–voltage (I–V) characteristics of the device, the voltage was increased from −1 V to 1 V at a step of 0.05 V. As shown in Fig. 3a and b, in the pressure range of 0.2–600 kPa, the resistance of the device decreased as the pressure increased. When the pressure was greater than 0.8 kPa, the linear characteristics of the I–V curves indicated that the devices obeyed Ohm's law. When the pressure was less than 0.8 kPa, the I–V curves exhibited nonlinear characteristics; however, the linear characteristics remain in the test range of −0.2 to 0.2 V. This nonlinear characteristic was due to the “point-to-face” contact mode between the sensitive material and the electrode under low pressures.32,40 Further increasing the pressure, this “point-to-face” contact mode will translate into a “face-to-face” contact mode, resulting in linear characteristics of the I–V curves. When the test voltage was less than 0.2 V, linear characteristics of the I–V curves were maintained. Therefore, a voltage of 0.1 V was used in all the following tests unless otherwise stated.
Fig. 3c compares the performances of the HPPE tactile sensor of this study with those of the recently reported piezoresistive flexible tactile sensors (see Table S1, ESI† for specific values). Metal nanowires were often used to fabricate high sensitivity flexible pressure sensors. Thereinto, an efficient, low-cost fabrication strategy was reported to construct a highly sensitive (>1.14 kPa−1), flexible pressure sensor by sandwiching ultrathin gold nanowire-impregnated tissue paper between two thin polydimethylsiloxane sheets.41 Besides, the principles of spontaneous buckle formation of the PDMS surface and the embedding of silver nanowires were used to fabricate the multiscale-structured pressure sensor, which showed high sensitivity (>3.8 kPa−1), fast response and relaxation time (<150 ms), high bending stability and high cycling stability.42 Furthermore, ultralight flexible pressure sensors with tunable sensitivities (0.02 kPa−1 to 0.7 kPa−1) were fabricated from the Cu NW based aerogels through a one-pot method.43 Carbon materials were also widely used in the fabrication of flexible pressure sensors. By virtue of the pyramid microstructures and sensitive graphene layers, the pressure sensor demonstrated an ultrahigh sensitivity at a low pressure range (−5.5 kPa−1, <100 Pa), a very low detection limit of 1.5 Pa, and an ultra-fast response time (0.2 ms).27 Benefitting from the large spacing between the graphene layers and the unique v-shaped microstructure, the sensitivity of another pressure sensor was as high as 0.96 kPa−1 in a wide pressure range (50 kPa).39 Furthermore, a unique multilevel microstructure via a two-step sandpaper-molding method led to an ultrahigh sensitivity (2.5–1051 kPa−1) and could detect subtle and large pressures over an ultrawide range (0.01–400 kPa), which covers the overall pressure regime in daily life.31 The combination of highly conductive materials and elastic biology was also used to fabricate flexible pressure sensors, such as GO/PVA,30 Au/PPY,29 rGO/PVDF,10,36etc., which also provided high sensitivity and measurement ranges (Table S1, ESI†). However, due to the limitations of the combined design of structures and materials, it is still a great challenge to fabricate flexible tactile sensors with both a wide pressure range and high sensitivity. On the basis of these studies, the pioneering introduction of the HPPE produced a flexible tactile sensor with an ultra-high sensitivity of 11.60–1108.75 kPa−1 in a wide pressure range of 0.02–700 kPa.
The dynamic response of the HPPE tactile sensor was studied by loading and unloading pressure from 0.2 to 600 kPa. The sensitivity of the sensor remained basically the same during the 5 cyclic tests under the same pressure (Fig. S7, ESI†), demonstrating an excellent resolution and reliability in the whole tested pressure range. As shown in Fig. 3d, when the load was increased in the low pressure range (0.2–1 kPa), the sensitivity increased gradually, and the current increased and became stable rapidly, indicating that the sensor had a high resolution and reliability in detecting tiny pressures. This excellent performance also occurred at higher pressure ranges. The relative change in current showed a stable switch-off ratio signal, indicating that the HPPE tactile sensor was reliable under various pressures. In addition, the detection limit of the sensor was also investigated using tiny dynamic pressure loadings. As shown in Fig. 3e, the sensor clearly responded to a pressure as low as 40 Pa, proving that the sensor was capable of detecting tiny pressure signals such as those generated by human pulse (<5 kPa) and respiration (5–50 kPa) as well as large pressure signals such as foot pressure signals (>50 kPa).31,44
The HPPE tactile sensor must have excellent reliability and fast response in order to ensure that it can be widely used. Fig. 3f corroborates that the HPPE tactile sensor had favorable stability under a pressure of 100 kPa for more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loading and unloading cycles, and the detailed images of each test phase were compatible with the stability requirements of the sensor. It should be emphasized that a better combination of the metal layer and the flexible substrate helped improve the stability of the device performance, and the ELD process used in this work enabled high adhesion of the silver layer on the PDMS film.17 As shown in Fig. S8 (ESI†), after 10
000 loading and unloading cycles, and the detailed images of each test phase were compatible with the stability requirements of the sensor. It should be emphasized that a better combination of the metal layer and the flexible substrate helped improve the stability of the device performance, and the ELD process used in this work enabled high adhesion of the silver layer on the PDMS film.17 As shown in Fig. S8 (ESI†), after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compression deformation tests, there are microcracks on the silver layer but no obvious shedding. The modulus mismatch between the PDMS and the silver layer leads to microscopic cracks, and the high-adhesion between the PDMS and the silver layer makes sure the silver layer does not fall off, which helps to improve the stability of the device performance. As shown in Fig. 3g, at a test speed of 50 mm s−1 under a pressure of 50 kPa, the response and the recovery time of the HPPE tactile sensor were 60 ms and 40 ms, respectively. Considering the time required for the press distance, the inherent response time of the tactile sensor should be less than 60 ms. To demonstrate the generality of this approach, a magnetron sputtered Au/PET electrode was used instead of a PET/ITO electrode, as shown in Fig. S9 (ESI†), and the HPPE tactile sensor still showed good sensitivity and favorable stability under 100 kPa for more than 10
000 compression deformation tests, there are microcracks on the silver layer but no obvious shedding. The modulus mismatch between the PDMS and the silver layer leads to microscopic cracks, and the high-adhesion between the PDMS and the silver layer makes sure the silver layer does not fall off, which helps to improve the stability of the device performance. As shown in Fig. 3g, at a test speed of 50 mm s−1 under a pressure of 50 kPa, the response and the recovery time of the HPPE tactile sensor were 60 ms and 40 ms, respectively. Considering the time required for the press distance, the inherent response time of the tactile sensor should be less than 60 ms. To demonstrate the generality of this approach, a magnetron sputtered Au/PET electrode was used instead of a PET/ITO electrode, as shown in Fig. S9 (ESI†), and the HPPE tactile sensor still showed good sensitivity and favorable stability under 100 kPa for more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. In addition, as shown in Fig. S10 (ESI†), when the magnetron sputtering Ag process was used instead of the ELD-Ag process, the HPPE tactile sensor still showed good sensitivity but less stability, which was caused by the lower adhesion between the silver layer and the PDMS film. Furthermore, when using the polyvinyl alcohol nanowire (PVANW) insulating network instead of the PVPNW insulating network, it is also observed that excellent performance sensitivity and repeatability are obtained (Fig. S11, ESI†).
000 cycles. In addition, as shown in Fig. S10 (ESI†), when the magnetron sputtering Ag process was used instead of the ELD-Ag process, the HPPE tactile sensor still showed good sensitivity but less stability, which was caused by the lower adhesion between the silver layer and the PDMS film. Furthermore, when using the polyvinyl alcohol nanowire (PVANW) insulating network instead of the PVPNW insulating network, it is also observed that excellent performance sensitivity and repeatability are obtained (Fig. S11, ESI†).
2.3. Hierarchical pressure-peak effect
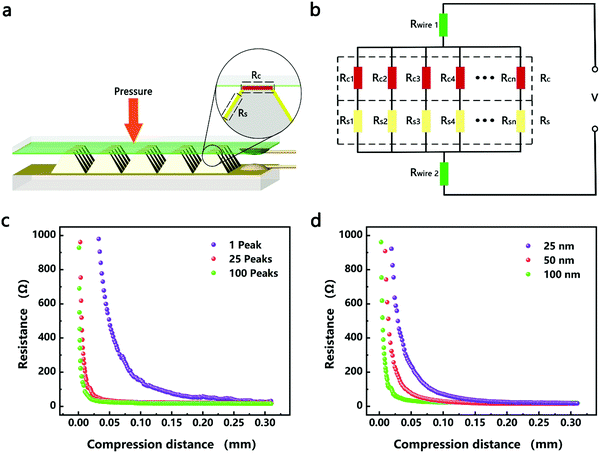
The resistance variation of the piezoresistive tactile sensor is mainly caused by the change in contact area of the sensor material with peak structure during the compression deformation process, which is termed as PPE. As shown in Fig. 4a and b, the resistance in the whole test circuit mainly consisted of wire resistance (Rwire), pyramid surface resistance (Rs) and top contact resistance (Rc). The resistances due to different pyramids were connected in parallel, and Rs was connected in series with Rc on the same pyramid, which was finally connected in series with Rwire. As shown in Fig. 4c, when the compressed sensor contains only one pyramid, its resistance value gradually decreases as the compression distance increases, and finally becomes saturated. It can be seen from the calculations that Rs has a maximum value when the sensor is not under pressure, but it is not higher than 0.15 Ω (calculation S1, ESI†). Therefore, Rs has little effect on the change of the overall resistance of the single pyramid during compression. Since Rwire remains constant, the change in Rc at the top of the pyramid is the most important reason for the change in the resistance of the sensor. In the PPE, the change in compression force causes a change in the compression distance, which results in a change in contact area and resistance. In order to quantitatively explore the relationship between contact area and resistance, an experimental device as shown in Fig. S12 (ESI†) was fabricated to simultaneously detect changes in the compression force, displacement, contact area and resistance during compression. A FET/ITO plate electrode is fixed on the outer surface of the quartz glass at the bottom of the cavity, and the cavity moves downward at a speed of 0.2 mm min−1. It is important to emphasize that the magnetron sputtering process was used to ensure the evenness of the thickness of the silver film, and the PDMS film with regular pyramid shape was used as the pressure-sensing component to ensure verifiable calculation of the contact area.The relationship between changes in the contact area and in the resistance satisfies the classical circuit theory. The distance-contact area curve measured by a CCD camera is shown in Fig. S14 (ESI†). In order to quantify the change in contact area, the cross-sectional area and the rule of constant volume are used to calculate the contact area (Fig. S13 and calculation S2, ESI†).45,46 The comparison results (Fig. S14b, ESI†) show that the rule of constant volume can better simulate the change of contact area and the revised formula is as follows:
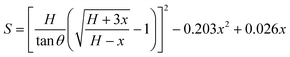 | (2) |
| R = ρl/S | (3) |
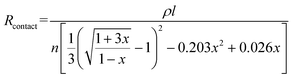 | (4) |
According to eqn (4), the change in the resistance in the pressure-peak effect can be effectively adjusted by changing the number of pyramids and the thickness of the sensor material. As shown in Fig. 4c, when the number of compressed pyramids gradually increased, the rate of the resistance change gradually increased, and the compression distance corresponding to the saturation resistance gradually decreased, which was consistent with the predictions of eqn (4). At the same time, the resistance–displacement curves for different numbers of pyramids can also be fitted by eqn (4) (Fig. S16 and Table S2, ESI†), confirming once again the applicability of eqn (4). As shown in Fig. 4d, when the electrode thickness of the magnetron sputtered silver film gradually decreases, the rate of the resistance changes according to eqn (4) should gradually decrease, which is opposite to the experimental results. This inconsistency is considered to be due to the fact that the resistivity of the electrode can be affected by its thickness, which in turn influences the rate of the resistance change of the sensor. As shown in Fig. S17 and Table S3 (ESI†), the thinner the electrode, the larger the coefficient A (A = ρl/n) as determined by fitting the data to eqn (4), and the greater the change in resistance after compression.
The change of the contact area during compression can be effectively controlled by HPPE to expand the detection range of the sensor. As shown in Fig. 1e, the second-stage PPE was formed in the PVPNW meshes during compression. Due to the change of the contact area of the first-stage pyramid, the number of peaks in the mesh will increase during compression. In the case of a single mesh, its resistance will be reduced due to the increase of the contact surface area during compression. Furthermore, as the mesh size reduces, the contact surface area will be smaller at resistance saturation, and accordingly the saturation resistance will be larger in a single mesh. By using the electrostatic spinning method to reduce the size of the PVPNW mesh, the pressure required for reaching a constant contact surface area in a single mesh will increase, and so will its saturation resistance, which effectively expands the pressure measurement range of the sensor. This is consistent with the performance changes observed for the samples PVP-0, PVP-20, PVP-40, and PVP-60 as shown in Fig. 2b. As shown by the result for the sample PVP-80 in Fig. 2b, when the size of the mesh was further reduced, the isolation effect caused by the large saturation resistance in the PVPNW mesh played a leading role in modulating the resistance change. Although the pressure measurement range was expanded, the sensitivity of the sensor was reduced.
2.4. Applications in detecting physiological signals on the body surface
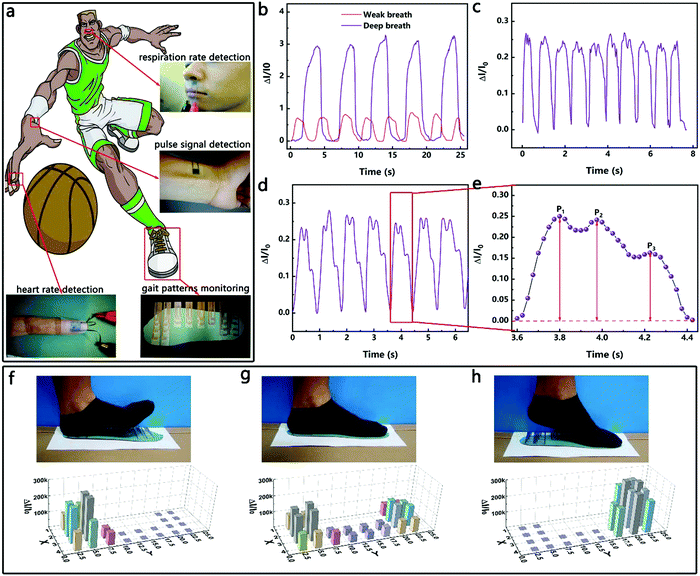
Since the HPPE tactile sensor has high sensitivity and wide pressure sensing range, the sensor can be placed in different positions to detect physiological signals of different pressures. Whether the respiratory rate is normal is an important reference for the diagnosis of asthma, sleep apnea and other illnesses.47–50 As shown in Fig. 5a, the sensor fixed between the upper lip and the nose of a 28 year old male adult weighing 65 kg was used to detect pressure signals generated by weak and deep breaths. As shown in Fig. 5b, the measured respiratory rate during calm periods was about 18 breaths per minute, which was within the range of the respiratory rate of healthy adults. Furthermore, conscious deep breaths led to an obvious increase in current signal and a decrease in respiratory frequency, indicating that the sensor can effectively detect weak pressures and thus has potential applications in respiratory monitoring.In addition, heart rate is another important signal for assessing physical condition. The most common way to detect it is to measure the finger heart rate and pulse heart rate.11,31,51 As shown in Fig. 5c–e, the HPPE tactile sensor was taped on the forefinger and the radial artery of the wrist, and the heart rate signals of an adult male were clearly captured. The heart rate detected in real-time by affixing the sensor on the forefinger was about 70 bpm, which was within the range of the heart rate of healthy adults. According to the test results of the pulse heart rate, the heart rate of the adult tested was consistent with the former finger heart rate signals. Moreover, the peaks P1 (early systolic peak pressure), P2 (late systolic peak pressure), and P3 (peak diastolic pressure) were clearly detected. The results illustrate the potential application of the sensor in heart rate monitoring.
Furthermore, the measurement of plantar pressure distribution has potential applications in the areas of health surveillance, motion analysis and footwear design.36,52 Few flexible tactile sensors have been reported that can be used for detecting plantar pressures due to their small pressure measurement limits. As a proof of concept, the HPPE tactile sensor was fabricated as an insole as shown in Fig. 5a and was used to detect the plantar pressure while walking (left foot). As shown in Fig. 5f–h, three typical stages of normal walking were identified, namely the heel striking, the midfoot striking and the forefoot striking, which corresponded to three distinct three-dimensional bar graphs of the pressure distribution. Clearly, various gaits can be monitored from the measurements based on the sensor. Once again, the excellent performance of the tactile sensor and its potential application in intelligent motion detection were demonstrated.
2.5. Applications in a Leonardo Da Vinci surgical robot
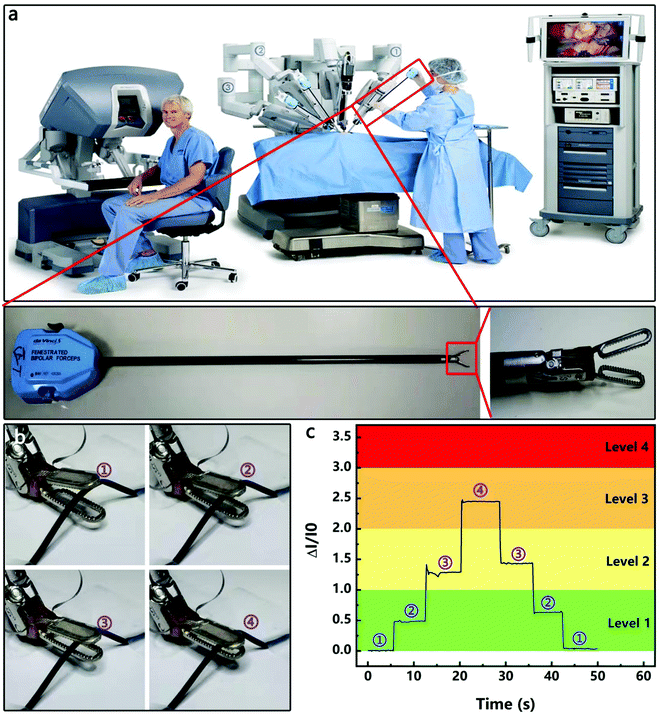
The HPPE tactile sensor was also evaluated in the fixture on a Leonardo Da Vinci surgical robot for sensing the variation of its grasping force. The Leonardo Da Vinci surgical robot is widely used in the laparoscopic radical prostatectomy program,53 total mesorectal excision for rectal cancer,54 laparoscopic hysterectomy,55etc., due to its advantages of high accuracy, high stability and small wound. However, in soft tissue surgery, inadequate clamping forces can cause tissue slippage during surgery and interfere with surgery, and excessive clamping forces can produce irreparable damage to the tissue. Therefore, the effective monitoring of the magnitude and variation of the clamping force is critical for precise surgical procedures. Fig. 6a shows the mechanical system of the Leonardo Da Vinci surgical robot, which controls the movement of the fixture through rope transmission. As shown in Fig. 6b, the HPPE tactile sensor was encapsulated on the fixture, and a silicone hose (diameter 1.2 mm, wall thickness 0.1 mm) was used as a clamping object to simulate blood vessels. As shown in Fig. 6c and Supporting Video 1 (ESI†), four clamping states of the fixture were observed during the test, and the change of the clamping force caused by the real time movement of the fixture was displayed on the test equipment. As the clamping force increased, the sensitivity gradually increased and was quickly stabilized, and the sensitivity was fully recovered after unloading the pressure. Furthermore, by dividing the clamping force into different levels, the clamping force can be quickly fed back to assist the operation, demonstrating the potential of the sensor in surgical robot applications.3. Conclusions
A new approach to fabricating a flexible piezoresistive tactile sensor with high sensitivity (11.60–1108.75 kPa−1) in a wide detection range of 0.04–600 kPa was demonstrated. The sensor was based on the HPPE, and consisted of insulating PVPNWs and ELD-Ag PDMS micro-pyramids. Under compression, the contact between the micro-pyramids and the plate electrode of the sensor formed the first-stage PPE and ensured a stable contact area change (eqn (2)) at the top of the micro-pyramids. The contact between the conductive film and the plate electrode in the PVPNW mesh formed the second-stage PPE and ensured a stable contact area change in the PVPNW mesh. This HPPE effectively adjusted the rate of resistance change during compression, which increased the pressure test range while ensuring test sensitivity. In addition, the PPE of the flexible piezoresistive tactile sensor was investigated in detail by analyzing the resistance change of the ELD-Ag PDMS micro-pyramids during compression. The experimental results showed that the rate of resistance change was smaller for sensors with a smaller number of magnetron sputtered silver pyramids and a thinner magnetron sputtered silver film. The as-prepared HPPE tactile sensor was utilized in detecting multi-level pressures generated by different pressure stimuli such as respiration, finger heart rate, pulse and foot pressures. Moreover, by applying this sensor to the clamp on the Leonardo Da Vinci surgical robot, the variation of clamping force was effectively monitored, showing the potential of the sensor in intelligent robot applications.4. Experimental section
4.1 Materials
PDMS prepolymer and curing agent were obtained from Dow Corning. PPY with an average molecular weight of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 was purchased from Sigma Aldrich. Different thicknesses of PDMS film were purchased from Hangzhou Bald Advanced Materials CO., Ltd. Conductive silver paint was purchased from Supplies (SPI) China. All the other chemical reagents applied in this work were of analytical grade from Aladdin.
000 was purchased from Sigma Aldrich. Different thicknesses of PDMS film were purchased from Hangzhou Bald Advanced Materials CO., Ltd. Conductive silver paint was purchased from Supplies (SPI) China. All the other chemical reagents applied in this work were of analytical grade from Aladdin.
4.2 Preparation of the silver deposited micro-pyramid PDMS film
The micro-pyramid PDMS film was fabricated via a two-step soft lithography replication process with the micro-pyramid metal block as the original template, which was manufactured by CNC milling machine manufacturing with the same external dimensions (300 μm high, 60° between the surface and the bottom). Firstly, the PDMS prepolymer and the curing agent at a weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were fully blended and then the bubbles were removed in a vacuum desiccator. Secondly, the prepolymer was poured on the micro-pyramid metal block, and after curing at 70 °C for 2 hours, the micro-concave PDMS film was peeled off from the metal template. It should be emphasized that all PDMS in this study was prepared by this process to avoid affecting the sensor performance due to different elastic modulus of PDMS. Thirdly, a silver film with a thickness of 20 nm was magnetron-sputtered on the micro-concave PDMS film to isolate PDMS that will be cast later. Then, using the Ag-deposited micro-concave PDMS film as a template, the process of the second step was repeated to produce the micro-pyramid PDMS film. Finally, a layer of ELD-Ag was coated on the micro-pyramid film, and the ELD-Ag process used was the same as that described in a previous report:17
1 were fully blended and then the bubbles were removed in a vacuum desiccator. Secondly, the prepolymer was poured on the micro-pyramid metal block, and after curing at 70 °C for 2 hours, the micro-concave PDMS film was peeled off from the metal template. It should be emphasized that all PDMS in this study was prepared by this process to avoid affecting the sensor performance due to different elastic modulus of PDMS. Thirdly, a silver film with a thickness of 20 nm was magnetron-sputtered on the micro-concave PDMS film to isolate PDMS that will be cast later. Then, using the Ag-deposited micro-concave PDMS film as a template, the process of the second step was repeated to produce the micro-pyramid PDMS film. Finally, a layer of ELD-Ag was coated on the micro-pyramid film, and the ELD-Ag process used was the same as that described in a previous report:17
Pretreatment of the micro-pyramid PDMS film: firstly, dopamine and (3-aminopropyl)triethoxysilane (APTES) were coated on the film. The PDMS film was placed on top of Tris–HCl buffer (10 mg of dopamine per milliliter of 50 mM Tris, pH 8.5) for 24 h under slight stirring. After washing with DI water, the film was immersed in a 1 wt% APTES-ethanol solution for 12 h at room temperature, and then dried in an oven at 110 °C for 20 min. Secondly, the ELD solution was prepared. Ammonia solution (30 wt%) was added to silver nitrate aqueous solution (30 mL, 2 wt%) until the solution was clear. After that, 20 mL of silver nitrate solution (6 wt%) was added. Then, 7 mL of ammonia solution (6 wt%) was added and the solution became transparent, and was then mixed with 10 mL of glucose solution (35 wt%). Thirdly, the PDMS film was sensitized and activated. The PDMS film was immersed in a sensitizing solution (10 g L−1 SnCl2) and an activating solution (25 mL L−1 HCl, 0.5 g L−1 Pd) for 10 min in sequence, and then rinsed with DI water slowly. Finally, the pretreated film was placed on the ELD solution for the ELD process.
4.3 Preparation of the PDMS cage
PDMS films were cut into the required flat patterns by the laser cutting method. The laser model was LNS-532-40 [Pro-III] from Logan laser (Wuhan, China). The PDMS cage played the role of packaging the device. The PDMS cage was hollow inside to accommodate the pyramid array, the upper surface was cemented with the PET/ITO electrode, and the lower surface was cemented with the micro-pyramid PDMS film.4.4 Preparation of the insulating PVPNW covered PET/ITO electrode
The PVP particles were dissolved in ethanol at a mass fraction of 15% and then electromagnetically stirred until a clear gel was formed. Next, the PET/ITO sheet was then cleaned by deionized water and ethanol respectively, and dried in an oven at 60 °C. Then, a copper wire was fixed on the PET/ITO sheet by conductive silver paint. Finally, by controlling the time of electrostatic spinning (0, 20, 40, 60 and 80 s), insulating PVPNW covered PET/ITO electrodes with different densities of PVPNWs were obtained. The electrospinning process was carried out at a high direct current (DC) voltage of 14 kV with a collection distance of 15 cm and a solution feed rate of 2 mL h−1.4.5 Fabrication of the tactile sensor device
The ELD-Ag micro-pyramid PDMS film and the PDMS cage were bonded by oxygen plasma treatment. The treatment time, power and oxygen flow rate used were 70 s, 150 W and 200 mL min−1, respectively. Then, the PDMS cage was bonded to the PVPNW covered PET/ITO electrode using an epoxy resin. The HPPE tactile sensor used in the routine tests of this work was of the size of 10 × 10 mm2. The HPPE tactile sensor used in the Leonardo Da Vinci surgical robot was tailor-designed to fit the size of the fixture.4.6 Testing
The structures of the Au-deposited micro-pyramid PDMS film and the PVPNW covered PET/ITO electrode were characterized by field-emission scanning electron microscopy (FE-SEM) (Nova NanoSEM 450from FEIC). The pressure and displacement signals in the sensor testing came from the Dynamic and Static Electronic Fatigue Testing Machine (ElectroPuls E1000 from INSTRON). The resistance signal was collected with an Agilent B1500A. The contact surface images of the sensor were collected by a Charge Coupled Device (CCD) industrial digital camera (U3CMOS1800 from COSSIM).Funding sources
This work was supported by the National Nature Science Foundation of China (No. 61971204, No. 51902114, No. 51572075, No. 51905191 and No. 51603171).Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the technology support by the Analytic Testing Center and the Experiment Center for Advanced Manufacturing and Technology in School of Mechanical Science &Engineering of HUST for carrying out FESEM.References
- A. Gescheider, S. J. Bolanowski and K. R. Hardick, Somatosens. Res., 2001, 18, 191–201 CrossRef PubMed.
- Å. Vallbo, H. Olausson and J. Wessberg, J. Neurophysiol., 1999, 81, 2753–2763 CrossRef.
- R. S. Snider and A. J. J. O. N. Stowell, J. Neurophysiol., 1944, 7, 331–357 CrossRef.
- U. Khan, T. H. Kim, H. Ryu, W. Seung and S. W. J. A. M. Kim, Adv. Mater., 2017, 29, 1603544 CrossRef PubMed.
- G. Y. Bae, S. W. Pak, D. Kim, G. Lee, D. H. Kim, Y. Chung and K. J. A. M. Cho, Adv. Mater., 2016, 28, 5300–5306 CrossRef CAS PubMed.
- J. Duan, X. Liang, J. Guo, K. Zhu and L. J. A. M. Zhang, Adv. Mater., 2016, 28, 8037–8044 CrossRef CAS PubMed.
- D. Kwon, T.-I. Lee, J. Shim, S. Ryu, M. S. Kim, S. Kim, T.-S. Kim and I. J. A. A. M. Park, ACS Appl. Mater. Interfaces, 2016, 8, 16922–16931 CrossRef CAS PubMed.
- D. Y. Park, D. J. Joe, D. H. Kim, H. Park, J. H. Han, C. K. Jeong, H. Park, J. G. Park, B. Joung and K. J. J. A. M. Lee, Adv. Mater., 2017, 29, 1702308 CrossRef PubMed.
- I. You, B. Kim, J. Park, K. Koh, S. Shin, S. Jung and U. J. A. M. Jeong, Adv. Mater., 2016, 28, 6359–6364 CrossRef CAS PubMed.
- Z. Lou, S. Chen, L. Wang, K. Jiang and G. J. N. E. Shen, Nano Energy, 2016, 23, 7–14 CrossRef CAS.
- Y. Khan, A. E. Ostfeld, C. M. Lochner, A. Pierre and A. C. J. A. M. Arias, Adv. Mater., 2016, 28, 4373–4395 CrossRef CAS PubMed.
- C. G. Núñez, W. T. Navaraj, E. O. Polat and R. J. A. F. M. Dahiya, Adv. Funct. Mater., 2017, 27, 1606287 CrossRef.
- S. Sundaram, P. Kellnhofer, Y. Li, J.-Y. Zhu, A. Torralba and W. J. N. Matusik, Nature, 2019, 569, 698 CrossRef CAS PubMed.
- H. Hwang and U. J. A. F. M. Jeong, Adv. Funct. Mater., 2019, 1901810 CrossRef.
- K. Meng, J. Chen, X. Li, Y. Wu, W. Fan, Z. Zhou, Q. He, X. Wang, X. Fan and Y. J. A. F. M. Zhang, Adv. Funct. Mater., 2019, 29, 1806388 Search PubMed.
- Y. Zang, H. Shen, D. Huang, C. A. Di and D. Zhu, Adv. Mater., 2017, 29, 1606088 CrossRef PubMed.
- C. Wu, X. Tang, L. Gan, W. Li, J. Zhang, H. Wang, Z. Qin, T. Zhang, T. Zhou and J. J. A. A. M. Huang, ACS Appl. Mater. Interfaces, 2019, 11, 20535–20544 CrossRef CAS PubMed.
- O. O. Ojuroye, R. N. Torah, A. O. Komolafe and S. P. Beeby, IEEE Sens. J., 2019, 19, 6975–6985 Search PubMed.
- H. Cheng, Y. Huang, L. Qu, Q. Cheng, G. Shi and L. J. N. E. Jiang, Nano Energy, 2018, 45, 37–43 CrossRef CAS.
- S. Y. Kim, S. Park, H. W. Park, D. H. Park, Y. Jeong and D. H. J. A. M. Kim, Adv. Mater., 2015, 27, 4178–4185 CrossRef CAS PubMed.
- A. P. Gerratt, H. O. Michaud and S. P. J. A. F. M. Lacour, Adv. Funct. Mater., 2015, 25, 2287–2295 CrossRef CAS.
- X. Guo, Y. Huang, X. Cai, C. Liu and P. J. M. S. Liu, Meas. Sci. Technol., 2016, 27, 045105 CrossRef.
- Z. Qiu, Y. Wan, W. Zhou, J. Yang, J. Yang, J. Huang, J. Zhang, Q. Liu, S. Huang and N. J. A. F. M. Bai, Adv. Funct. Mater., 2018, 28, 1802343 CrossRef.
- Z. Chen, Z. Wang, X. Li, Y. Lin, N. Luo, M. Long, N. Zhao and J.-B. J. A. N. Xu, ACS Nano, 2017, 11, 4507–4513 CrossRef CAS PubMed.
- W. Wu, X. Wen and Z. L. J. S. Wang, Science, 2013, 340, 952–957 CrossRef CAS PubMed.
- F.-R. Fan, L. Lin, G. Zhu, W. Wu, R. Zhang and Z. L. J. N. L. Wang, Nano Lett., 2012, 12, 3109–3114 CrossRef CAS PubMed.
- B. Zhu, Z. Niu, H. Wang, W. R. Leow, H. Wang, Y. Li, L. Zheng, J. Wei, F. Huo and X. J. S. Chen, Small, 2014, 10, 3625–3631 CrossRef CAS PubMed.
- S. Pyo, J. Lee, W. Kim, E. Jo and J. J. A. F. M. Kim, Adv. Funct. Mater., 2019, 1902484 CrossRef.
- Q. Shao, Z. Niu, M. Hirtz, L. Jiang, Y. Liu, Z. Wang and X. J. S. Chen, Small, 2014, 10, 1466–1472 CrossRef CAS PubMed.
- W. Liu, N. Liu, Y. Yue, J. Rao, F. Cheng, J. Su, Z. Liu and Y. J. S. Gao, Small, 2018, 14, 1704149 CrossRef PubMed.
- X. Tang, C. Wu, L. Gan, T. Zhang, T. Zhou, J. Huang, H. Wang, C. Xie and D. J. S. Zeng, Small, 2019, 15, 1804559 CrossRef PubMed.
- C. Luo, N. Liu, H. Zhang, W. Liu, Y. Yue, S. Wang, J. Rao, C. Yang, J. Su and X. J. N. E. Jiang, Nano Energy, 2017, 41, 527–534 CrossRef CAS.
- J. Park, J. Kim, J. Hong, H. Lee, Y. Lee, S. Cho, S.-W. Kim, J. J. Kim, S. Y. Kim and H. J. N. A. M. Ko, NPG Asia Mater., 2018, 10, 163 CrossRef CAS.
- Y. Zhang, Y. Hu, P. Zhu, F. Han, Y. Zhu, R. Sun and C.-P. J. A. A. M. Wong, ACS Appl. Mater. Interfaces, 2017, 9, 35968–35976 CrossRef CAS PubMed.
- Z. Wang, L. Zhang, J. Liu, H. Jiang and C. J. N. Li, Nanoscale, 2018, 10, 10691–10698 RSC.
- Y. Lee, J. Park, S. Cho, Y.-E. Shin, H. Lee, J. Kim, J. Myoung, S. Cho, S. Kang and C. J. A. N. Baig, ACS Nano, 2018, 12, 4045–4054.
- J. Zhang, L. Zhou, H. Zhang, Z. Zhao, S. Dong, S. Wei, J. Zhao, Z. Wang, B. Guo and P. J. N. Hu, Nanoscale, 2018, 10, 7387–7395 RSC.
- X. Fu, H. Dong, Y. Zhen and W. J. S. Hu, Small, 2015, 11, 3351–3356 CrossRef CAS.
- H. Tian, Y. Shu, X.-F. Wang, M. A. Mohammad, Z. Bie, Q.-Y. Xie, C. Li, W.-T. Mi, Y. Yang and T.-L. J. S. R. Ren, Sci. Rep., 2015, 5, 8603 CrossRef CAS.
- L. Sheng, Y. Liang, L. Jiang, Q. Wang, T. Wei, L. Qu and Z. J. A. F. M. Fan, Adv. Funct. Mater., 2015, 25, 6545–6551 CrossRef CAS.
- S. Gong, W. Schwalb, Y. Wang, Y. Chen, Y. Tang, J. Si, B. Shirinzadeh and W. Cheng, Nat. Commun., 2014, 5, 3132 CrossRef.
- Y. Joo, J. Byun, N. Seong, J. Ha, H. Kim, S. Kim, T. Kim, H. Im, D. Kim and Y. Hong, Nanoscale, 2015, 7, 6208–6215 RSC.
- X. Xu, R. Wang, P. Nie, Y. Cheng, X. Lu, L. Shi and J. Sun, ACS Appl. Mater. Interfaces, 2017, 9, 14273–14280 CrossRef CAS PubMed.
- S. H. Cho, S. W. Lee, S. Yu, H. Kim, S. Chang, D. Kang, I. Hwang, H. S. Kang, B. Jeong and E. H. J. A. A. M. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 10128–10135 CrossRef CAS.
- A. Abdollahi, D. Millan, C. Peco, M. Arroyo and I. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104103 CrossRef.
- J. Wang, J. Lian, J. R. Greer, W. D. Nix and K.-S. Kim, Acta Mater., 2006, 54, 3973–3982 CrossRef CAS.
- Y. Khan, A. E. Ostfeld, C. M. Lochner, A. Pierre and A. C. Arias, Adv. Mater., 2016, 28, 4373–4395 CrossRef CAS.
- O. Atalay, W. R. Kennon and E. Demirok, IEEE Sens. J., 2014, 15, 110–122 Search PubMed.
- E. M. Tennyson, C. Gong and M. S. Leite, ACS Energy Lett., 2017, 2761–2777, DOI:10.1021/acsenergylett.7b00944.
- O. Atalay, W. R. Kennon and E. Demirok, IEEE Sens. J., 2015, 15, 110–122 Search PubMed.
- X. Wang, Z. Liu and T. J. S. Zhang, Small, 2017, 13, 1602790 CrossRef PubMed.
- Y. Pang, K. Zhang, Z. Yang, S. Jiang, Z. Ju, Y. Li, X. Wang, D. Wang, M. Jian and Y. J. A. N. Zhang, ACS Nano, 2018, 12, 2346–2354 CrossRef CAS PubMed.
- E. J. Trabulsi, R. A. Linden, L. G. Gomella, D. E. McGinnis, S. E. Strup and C. D. Lallas, Can. J. Urol., 2008, 15, 3994–3999 Search PubMed.
- L. Morelli, G. Di Franco, S. Guadagni, L. Rossi, M. Palmeri, N. Furbetta, D. Gianardi, M. Bianchini, G. Caprili and C. D’Isidoro, Surg. Endosc., 2018, 32, 589–600 CrossRef PubMed.
- C. Nezhat, E. Balassiano, C. H. Nezhat and A. Nezhat, Hysterectomy, 2018, pp. 979–990 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00671k |
| This journal is © The Royal Society of Chemistry 2020 |