DOI:
10.1039/D0NA00655F
(Minireview)
Nanoscale Adv., 2020,
2, 5504-5515
Transparent thermal insulation silica aerogels
Received
8th August 2020
, Accepted 31st October 2020
First published on 31st October 2020
Abstract
Silica aerogels have received much attention due to their unique nanoporous networks, which consist of nanoscale connective silica particles and high-volume nanoscale pores. This lightweight superinsulation solid materials are synthesized by a ‘sol–gel’ process involving precursor preparation, gelation, aging and drying. By controlling their synthesis and processing, silica aerogels demonstrate good thermal and acoustic insulation, mechanical strength and optical transparency. In recent years, incorporating transparent and thermal insulation silica aerogels in energy-saving windows is of great interest for both scientific and technological applications. This review introduces the basic principles of thermal and optical properties of silica aerogels and highlights their tunability via synthetic and processing control. In addition, the use of silica aerogels in transparent thermal insulation windows is discussed.
 Jieyu Wang | Jieyu Wang obtained her bachelor's degree in Chemistry from both Nanjing Tech University and the University of Sheffield in 2019. She joined the lab of Prof. Shenqiang Ren at the University at Buffalo as a master student in 2019. Her research interests focus on the thermal insulating aerogels. |
 Donald Petit | Donald Petit obtained his bachelor's degree in Mechanical Engineering from the City College of New York in 2019. He joined Prof. Shenqiang Ren's group in 2019 as a master's student at the University at Buffalo. His research interests focus on improving the energy efficiency of structural materials and health-monitoring devices. |
 Shenqiang Ren | Dr Shenqiang Ren is Professor of Mechanical and Aerospace Engineering, Chemistry and RENEW institute at SUNY-Buffalo, with research interests in emerging functional materials and devices. |
1. Introduction
The aerogel was invented by Steven Kistler who named it ‘aerogel’ because the aerogel network is prepared by replacing the liquid phase in the gel with air.1 This so-called ‘sol–gel’ process makes aerogels the lightest solid materials with high porosity (∼90%), large specific surface area (∼1600 m2 g−1) and low density (∼0.01 g cm−3).2–5 The type of aerogel material is termed according to the input precursors, such as silica, metal oxides, and polymers.6–8 In this context, silica aerogels are particularly attractive due to their abundance, high performance and ease of manufacturing.9 Silica aerogels have been used in emerging applications because of their high performance in thermal insulation, mechanical strengthening and noise-proofing.10–13 Among these properties, thermal insulation is the most attractive option since this is the most powerful component of the aerogel, allowing it to be used in building materials and protective clothes.14 The optical properties of silica aerogels also make the materials suitable candidates for applications utilizing electromagnetic (EM) radiations, such as superinsulation windows and Cherenkov radiator.15–17 In many cases, silica aerogels are transparent, which is unique because majority of the porous materials are opaque (Fig. 1a–c show silica aerogels with difference transparency).18 Due to the nanoscale pore size (few nanometers), which is far smaller than the wavelength of visible light (390–760 nm), aerogel pores can act as Rayleigh scattering centers and the transparency occurs (discussed below).19 There are a large number of studies on transparent and thermal insulating silica aerogels for use in building double-layered windows, suggesting a great prospect.16,20,21 However, an overview illustrating the theory and existing works of optical and thermal insulation properties of silica aerogels is absent. Based on a broad survey of recent research works on aerogels, this review provides an overview of transparent and low-thermal conductivity silica aerogels. These two properties strongly correlate with the manufacturing of silica aerogels, and therefore, we present a discussion of ‘sol–gel’ chemistry in the preparation of aerogel materials (scanning electron microscopic images of silica aerogels are shown in Fig. 1d).22 Silica aerogels are synthesized with silicon alkoxide or silica salts as precursors by a ‘sol–gel’ process, which involves hydrolysis, gelation, aging and drying.23,24 There are three drying methods for silica aerogel: supercritical drying (SD), ambient pressure drying (APD), and freeze drying.25–27 Besides the basic introduction to transparent and thermal insulation silica aerogels, relevant mechanical and acoustic properties are included. The process of thermal isolation window fabrication based on silica aerogel glazing, which is the central application of aerogels these years, is presented in this review. A few comments on present challenges and future directions in this field are also given.
 |
| | Fig. 1 Optical images of: (a) silica aerogel with refractive indices of 1.0149 (left) and 1.0026 (right) showing a great transparency. (b) Semi-transparent silica aerogel prepared through APD. (c) Opaque silica aerogel monolith with ultra-low density. (d) Scanning electron microscopic (SEM) images of trimethoxymethylsilane (MTMS) aerogels. Reproduced from ref. 4, 18, 22 and 84 with the permission of Elsevier, American Chemical Society and John Wiley and Sons. | |
2. Synthesis of silica aerogels: a sol–gel process
Silica aerogels are solid materials manufactured by a ‘sol–gel’ process.28 It is an economic and effective way for the synthesis of aerogel materials, which usually gives high-quality materials with uniform and small-size particles.29 There are few steps involved in this sol–gel process, including precursor preparation, gelation (hydrolysis and condensation), aging, surface modification (solvent exchange), and drying.3,24
2.1 Precursor preparation and gelation
The aerogel precursors are liquid ‘solvents’, which contain colloidal suspensions of nanometer-scale silica particles.9 Commonly used precursors are silicon alkoxide, including tetramethoxysilane (TMOS), tetraethoxysilane (TEOS), methyltrimethoxysilane (MTMS) and sodium silicate (waterglass).30–33 Wagh et al. compared several basic properties of silica aerogels prepared with different kinds of precursor, shown in Table 1, in which polyethoxydisiloxane (PEDS) with optimal properties prohibited its large-scale applications due to its high cost. Waterglass is more attractive due to its abundance and low cost ($0.02 per kg, reagent grade).30 In 2015, He et al. prepared a low-density (0.089 g cm−3), high-surface area (680 m2 g−1) and superhydrophobic (contact angle of 161°) waterglass-based aerogel through ambient pressure drying.34 However, the process is complex and an ion exchange step is necessary due to its strongly basic nature, which is a result of the large amount of sodium ions contained in the solution.35
Table 1 Effect of five precursors on the basic properties of silica aerogels. Partly reproduced from ref. 30 with the permission of Elsevier
| Precursor |
Molar ratio of precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
Catalyst and concentration |
Gelation time (Tg) |
Bulk density (ρb) (kg m−3) |
Porosity% |
Surface area (m2 gm−1) |
Thermal conductivity (W m−1 K−1) |
| TEOS |
TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1 H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
Citric acid 0.001 M |
2.2 days |
230 |
87.89 |
800 |
0.060 |
| TMOS |
TMOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1 H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
NH4OH 0.05 M |
30 min |
129 |
93.21 |
1000 |
0.020 |
| PEDS |
PEDS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1 H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
HF 0.01 M |
10 min |
98 |
96.84 |
1100 |
0.015 |
| Waterglass |
Waterglass![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH 1 EtOH 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
HCl 5 M to pH 6.2 |
15 min |
89 |
∼95 |
680 |
— |
| MTMS |
MTMS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O H2O |
Oxalic acid 0.1 M |
8 h |
42 |
— |
— |
— |
The gelation of silica aerogel starts from hydrolysis of silica precursors and then condensation of hydrolyzed nanoparticles, while the chemical equation for precursor hydrolysis and condensation is given as follows:23
| Hydrolysis: Si–(OR)4 + 4H2O ⇌ Si–(OH)4 + 4ROH |
Water condensation: ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–(OH) + Si–(OH) Si–(OH) + Si–(OH)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ⇌ ⇌ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) + H2O + H2O |
Alcohol condensation: ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–(OH) + Si–(OR) Si–(OH) + Si–(OR)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ⇌ ⇌ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) + ROH + ROH |
A pH treatment under a room temperature and normal pressure is essential towards increasing the viscosity, thus allowing the ‘sol’ phase to transform into the ‘gel’ phase: nanoparticles in solvents are connected via networks, and solvents are trapped in voids formed by the cross of silica chains, as shown in Fig. 2a.23,36 Few research works have proved the vital role of the pH value in both hydrolysis and condensation. Stolarski et al. used TEOS as a silica precursor, and the experimental data showed that the kinetics of hydrolysis reaction is under a first-order relationship with the reaction time when the pH is relatively low, as shown in Fig. 2b.37 Brinker and Scherer further found that when the pH was around 2.4, primary silica oligomers could grow into a cluster–cluster model, which showed a high surface area and low pore volume.38 The boundary between hydrolysis and condensation is hazy because after hydrolysis, Si–O–Si links begin to form, leading to condensation, which prefers a slightly basic environment.39 Stolarski et al. investigated the influence of pH on precursor condensation by adding different amounts of ammonia water, and the results are shown in Fig. 2c.37 It presented that the efficiency of condensation reached the maximum when the pH was a little larger than 7: obtaining the largest surface area of 1082 m2 g−1 when the pH was 7.3 and the largest pore volume of 12.2 cm3 g−1 when the pH was 7.7. However, a further increase in pH led to a drop in both surface area and pore volume.
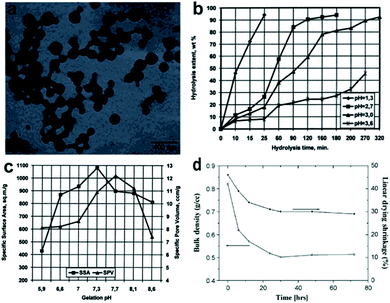 |
| | Fig. 2 (a) Transmission electron microscopic (TEM) image of silica nanoparticles during gelation. (b) Effect of pH on the hydrolysis of silica precursor. (c) Effect of condensation pH on aerogel specific surface area and pore volume. (d) Plot of bulk density and linear drying shrinkage of silica aerogel changing with aging time. Reproduced from ref. 9, 37 and 44 with the permission of Elsevier. | |
2.2 Aging
After its hydrolysis and condensation, a gel point is going to be reached and the primary Si–O–Si silica networks are constructed. However, this represents the silica networks that just take up the container shape, which leaves the potential for collapse during drying due to the existence of numerous unreacted silica alkoxide groups that need further strengthening. This consolidation process is called ‘aging’, greatly influenced by the aging time, temperature and solvent.40–42 Smitha et al. prepared a TEOS aerogel through effective supercritical drying before reaching the optimal time (48 h), and with the increase in aging time, density and the degree of drying, shrinkage decreased (seeing Fig. 2d) due to the introduction of more silica precursor monomers into the aerogel networks.43,44Table 2 concludes Omranpour et al., He et al. and Reichenauer's work studying the effect of the aging temperature on the silica aerogel.40,42,45 A rise in temperature promotes the dissolution and reprecipitation of silica alkoxides in water and thus enhances the silica skeletal strength, reduces bulk density and increases pore diameter, which further reduces the degree of shrinkage during drying. Different aging solvents play an important role in the thermal and mechanical properties of silica aerogels. Omranpour concluded that organic solvents such as n-hexane and ethanol could reduce the degree of shrinkage during drying due to the lower surface tension of organic matters.42 Chang et al. used ethanol as an aging solvent to obtain well-integrated silica aerogels with a low thermal conductivity of 0.036 W m−1 K−1.46 Lei et al. successfully enhanced the transparency (light transmittance up to 70% at 550 nm) and mechanical strength (Young's modulus up to 4.33 MPa) of polymethylsilsesquioxane aerogels by a developed aging process with ethanol as the solvent.47
Table 2 Comparison of the basic properties for aerogels that are affected by the aging temperature: S1 and S2 are TEOS aerogels aged at 50 °C and 75 °C respectively in water; S3 and S4 are TEOS aerogels aged at 25 °C and 100 °C respectively in ethanol; S5 and S6 are TMOS aerogels
| Sample |
Aging time (h) |
Aging temperature (°C) |
Solvent |
Bulk density (g cm−3) |
Shrinkage (%) |
Surface area (cm3 g−1) |
Mean pore diameter (nm) |
| 1 |
24 |
50 |
Water |
0.731 |
93.84 |
535 |
3.19 |
| 2 |
24 |
75 |
Water |
0.560 |
91.96 |
534 |
3.05 |
| 3 |
60 |
25 |
Ethanol |
0.32 |
62.29 |
1084 |
19 |
| 4 |
60 |
100 |
Ethanol |
0.18 |
48.07 |
983 |
36 |
| 5 |
46 |
30 |
Methanol |
0.223 |
— |
580 |
8 |
| 6 |
46 + 1 |
46 hours at 30 °C and 1 hour at 70 °C |
Methanol |
0.115 |
— |
420 |
9.6 |
2.3 Drying
Drying is the last step in the ‘sol–gel’ process to remove contained solvents and dry wet gels. However, there is still a great potential for silica networks to crack due to the hydrophilic nature of silica aerogel itself and the capillary forces existing in the liquid–vapor interface during the removal of the solvent.48 Furthermore, according to the Laplace equation (eqn (1)), a smaller pore radius results in a larger hydrostatic pressure.49 The meniscus in pores and surface tension forces could pull particles together to overcome this pressure, leading to the collapse of the network structure.23| | 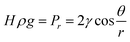 | (1) |
2.3.1 Supercritical drying.
The supercritical drying was assumed to be the primary method to prepare low-density and highly transparent aerogels. It is a feasible way to dry aerogels without network collapse because it works at a critical temperature and pressure, where the liquid in pores are transformed into a ‘supercritical’ phase allowing for liquid particles to be removed freely without leading to surface tension. However, there are few drawbacks for supercritical drying. It is energy-intensive and time-consuming (2 to 3 days), which operates at high temperatures (∼270 °C) and high pressures (∼1800 PSI). To improve the efficiency of supercritical drying, Tewari et al. used liquid carbon dioxide as the drying fluid instead of traditional alcohol due to its relatively low critical temperature (31.1 °C). The whole process was shortened to 6–8 hours and the operation temperature was decreased to 40 °C.50 García-González further improved low-temperature CO2 under a lower pressure of 11 MPa (∼1600 PSI), as shown in Fig. 3a.51 The liquid CO2 would diffuse into the gel via its flow to replace the original solvent. Then, the system temperature increases to 40 °C and remains for 90 min to ensure the vaporization of CO2. Then, the temperature and pressure slowly return to normal over a certain period and the aerogel sample could be taken out. Lee et al. used methanol as the drying fluid, although the operation temperature was still high (265 °C); by pressurizing with dry N2, the pressure was reduced to 5 MPa (∼725 PSI) and the entire process was reduced to 4 h.52
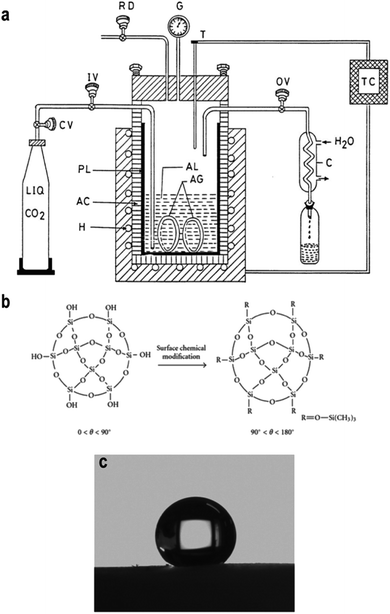 |
| | Fig. 3 (a) A scheme illustrating the process of supercritical drying using CO2 as the medium fluid: H is heater, AC is autoclave, PL is pyrex liner, CV is carbon dioxide cylinder valve, IV is inlet valve, OV is outlet valve, C is condenser, RD is rupture disk, G is pressure gauge, T is thermocouple and TC is the temperature controller. (b) Scheme describing the organic surface modification of the silica aerogel. (c) Hydrophobicity of the well-modified silica aerogel. Reproduced from ref. 6, 30 and 55 with the permission of Hindawi and Elsevier. | |
2.3.2 Surface modification and ambient pressure drying.
In 1990, Brinker developed surface modification-induced ambient pressure drying (APD), through which to replace hydrophilic silanol groups on the surface of the aerogel with hydrophobic alkyl groups (Fig. 3b) to overcome the potential cracking of silica network during APD.37 Until now, there are numerous papers proving that silylating agents and organic solvents perform well in surface modification.53 Schwertfeger et al. utilized trimethylchlorosilane (TMCS) as a modification agent and found that with the addition of more TMCS, the aerogel density decreased due to the well-modified silica network.54 Wang et al. further improved and quantified Schwertfeger's conclusion: when using EtOH and n-hexane as a co-solvent with TMCS, the hydrophobicity of silica aerogel could be improved while also making it possible to increase the contact angle to 157.8° (Fig. 3c).55 Although the pressure was greatly decreased, high drying temperature was still used.56 Kang et al. investigated the effect of heat treatment on the properties of silica aerogel and the conclusion was that when the drying temperature went beyond 300 °C, negative influence came due to the oxidation of Si–H groups into hydrophilic Si–OH groups.57 Meanwhile, the rate of heat treatment is also important and only a slow temperature-rise period can obtain crack-free aerogels. This ‘low temperature gradual drying’ idea is widely applied in APD, as shown in Table 3.58–60
Table 3 Illustration of the effects of drying techniques on the properties of different kinds of silica aerogels
| Precursor |
Surface treatment |
Drying technique |
Specific surface area (m2 g−1) |
Pore volume (cm3 g−1) |
Density (g cm−3) |
Thermal conductivity (W m−1 K−1) |
| TEOS |
TMCS/hexane |
65 °C for 4 h, 80 °C for 2 h, 120 °C for 2 h and 200 °C for 1 h |
1108 |
4.7 |
0.06 |
— |
| TEOS |
HMDZ/hexane |
50 °C for 6 h, 150 °C for 24 h and 200 °C for 12 h |
— |
— |
0.075 |
0.09 |
| Water-glass |
TMCS/hexane |
50 °C for 3 h, 100 °C for 3 h, 150 °C for 3 h and 200 °C for 3 h |
— |
24.5 |
0.04 |
— |
2.3.3 Freeze drying.
Freeze drying, which has rapidly developed in recent years, is another feasible drying method for aerogel synthesis. Using this drying technique, the solvent trapped in pores can be frozen and then sublimed in vacuum, so that the capillary pressure can be neglected.27 However, there are few drawbacks for this drying process: first, in order to ensure the stability of the silica aerogel under very low freezing temperatures and low sublimation rates that lead to relatively long sublimation time, an aging step is necessary for full condensation and polymerization of silica nanoparticles. Moreover, a solvent exchange step is vital before drying to exchange the solvent for a low thermal expansion coefficient one.61,62 Another potential danger of freeze drying is that the silica network tends to be destroyed during freezing by crystallization of the liquid contained in pores.
3. Optical properties of silica aerogels
The silica aerogel became attractive in the optics due to its great transparency in the visible region (as shown in Fig. 4a).30 The optical properties of the silica aerogel are the ways that the light interacts with silica aerogel nanoparticles and voids. Due to the nanoscale particles, connective network structures and voids, pure silica aerogels do not absorb light, so the transmittance ratio is very high.63 Previous studies have proved that silica aerogels present a bluish haze (Fig. 4b) due to the Rayleigh scattering.64 Moreover, due to the non-absorbance of light, the silica aerogel acts as air whose refractive index is 1, which makes the refractive index an important factor while considering the optical properties of the silica aerogel. When the refractive index is closer to 1, the aerogel is more transparent.
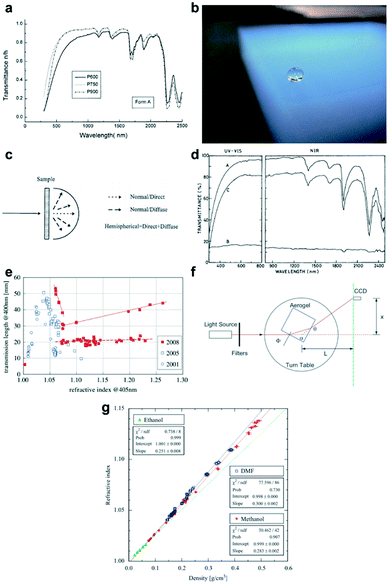 |
| | Fig. 4 (a) Transmittance spectra of the silica aerogel: P600: molar ratio of water to TEOS is 1.2; P750: molar ratio of water to TEOS is 1.5; P900: molar ratio of water to TEOS is 1.8. (b) Rayleigh scattering silica aerogel monolith, which presents a bluish haze. (c) Diagram showing normal direct and normal diffuse transmittance. (d) UV-visible-NIR transmittance spectra of MTMS/TMOS aerogels in a 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (A is the normal-hemispherical transmittance, B is the normal-diffuse transmittance and C is the normal-direct transmittance). (e) Plot showing the refractive index of the silica aerogel achieved in 2001, 2005 and 2008. (f) The prism method for the measurement of the silica aerogel refractive index, n. (g) A plot showing the refractive index n as a first-order function of silica aerogel density ρ. Reproduced from ref. 4, 61, 64, 66 and 68 with the permission of Degruyter and Elsevier. 1 ratio (A is the normal-hemispherical transmittance, B is the normal-diffuse transmittance and C is the normal-direct transmittance). (e) Plot showing the refractive index of the silica aerogel achieved in 2001, 2005 and 2008. (f) The prism method for the measurement of the silica aerogel refractive index, n. (g) A plot showing the refractive index n as a first-order function of silica aerogel density ρ. Reproduced from ref. 4, 61, 64, 66 and 68 with the permission of Degruyter and Elsevier. | |
3.1 Transmittance
The transmittance ratio measures the efficiency of the material surface in transmitting radiant energy. Silica aerogels show a great transparency when measured at 750 nm for 1 cm thickness with the transmittance greater than 90%.65 The transmittance ratio of silica aerogel can be measured using an ultraviolet-visible-NIR spectrophotometer containing an integrating sphere, which produces spectra of both normal direct and normal diffuse (τnd) transmittance, as shown in Fig. 4c.66 The normal hemispherical transmittance (τnh) is the sum of direct and diffuse transmittance. According to eqn (2), the direct-to-hemispherical transmittance ratio (T.R.) can be calculated as follows:| | | T.R. = (τnh − τnd)/τnh | (2) |
3.2 Refractive index
The silica aerogels can be applied as the medium of the Cherenkov radiator due to their extremely low refractive index, and specifically, only silica aerogel can fill the refractive index gap between the gas and liquid materials.67 The refractive index reflects how much the incoming light would be refracted when entering the interface of the medium. As more than 90% volume of silica aerogel consists of air, the refractive index of the silica aerogel is very close to air (vacuum and air refractive index is 1 and 1.00029), which means that a small amount of light scattering could occur at the surface of the silica aerogel. As shown in Fig. 4e, it can be seen that when measured at 400 nm, the refractive index of the silica aerogel varies between 1.005 and 1.26. Fig. 4f shows that the refractive index of the silica aerogel can be measured by the prism method.68 The resulting index can be calculated according to eqn (3) by assuming the refractive index of air to be 1:| | 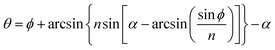 | (3) |
where θ is the deflection angle, ϕ is the angle of incidence to the surface of aerogel, n is the refractive index of the silica aerogel and α is the angle between the two adjacent sides of the aerogel and is assumed as 90°.
The refractive index of the silica aerogel depends mainly on its bulk density, given as eqn (4):
where
k is a coefficient depending on the light wavelength. Therefore, researchers can optimize the refractive index by decreasing the density
ρ of the silica aerogel. Several people have proved this theory and Tabata plotted a first-order function of refractive index verse density, as shown in
Fig. 4g.
69,70 In 2010, Tabata's group reduced the silica aerogel refractive index to 1.0026 by synthesizing extremely low-density hydrophobic sample (0.01 g cm
−3).
4 Details about the optimization will be given as follows.
3.3 Rayleigh scattering and haze
Due to the difference in the refractive index between the silica aerogel and the air, light scattering, the interaction between light and any materials arranged in an inhomogeneous way, occurs. The actual entity leading to the light scattering is called the scatter, the efficiency of which could reach the maximum when the size of the particle is closer to the wavelength of the incoming light. For the silica aerogel, nanoscale particles are the scatters. Although the average size of them varies with the reaction conditions, aerogel particles are smaller than 50 nm, so they contribute to exhibit Rayleigh scattering when light comes in ref. 71. Zhao et al. used a modelling method to prove that the scattering property of silica aerogels depends on its intrinsic nanostructure rather than the exterior geometry.72 Rayleigh scattering intensity I can be calculated according to eqn (5):| | 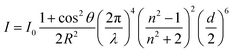 | (5) |
In this equation, d is the diameter of scatter and n is its refractive index; λ is the wavelength of incoming light and I0 is its intensity; R is the distance to scatter and θ is the scattering angle. The relationship between the scattering density and wavelength (I ∝ λ−4) can also be proved by the transmittance spectra of the silica aerogel: this is due to the Rayleigh scattering, as shown in Fig. 4d.
It is well known that the Rayleigh scattering effect of sunlight is the sky blue during the daytime. When light and radiation travel through silica aerogels, the Rayleigh scattering occurs due to the inhomogeneity of silica nano-particles, which leads to a reddening effect of the transmission light and a bluish appearance of the reflective light that is known as haze.15,64 Haze is defined as the ratio of the normal-diffuse transmittance and the normal-total transmittance, shown as eqn (6):
| | | Haze = τdiffuse/τtotal = τdiffuse/(τdiffuse + τdirect) | (6) |
Opposite to the transmittance, the Rayleigh scattering and haze both degrade the transparency of the silica aerogel.73 Thus it is important to minimize the aerogel particle size in order to reduce them for better transparency.
3.4 Tunable optical properties of silica aerogel
The transparency of silica aerogels depends strongly on their average pore diameter, pore size distribution and the bulk density. These can be controlled by tuning the reaction conditions during the ‘sol–gel’ process. Wagh's group investigated the effect of the precursor on the transparency of silica aerogels (Fig. 5a).29 Waterglass is attractive due to its low price; however, Rao et al. found that even a highly concentrated waterglass-precursor could not give a fully transparent product (Fig. 5b).74 Khedkar et al. investigated the pH effect on aerogel gelation, where colloidal nanoparticles connect into primary silica networks.75 Gel aging is the step that further strengthens silica networks, narrows the pore diameter and decreases the bulk density. In 2004, Rao concluded the role of aging: with the extension of aging time, silica aerogel becomes transparent, as shown in Fig. 5c. In 2018, Lei investigated the role of aging solvent and successfully enhanced the transparency of polymethylsilsesquioxane aerogels by a controlling shrinkage method (CS method) with ethanol as an aging solvent.44 Compared with the conventional method that uses water as the aging solvent, the CS method gave low density (0.25 g cm−3), low average pore diameter (∼12 nm) and high transmittance sample (transparency up to 70% at 550 nm), as shown in Fig. 5d. Supercritical drying usually contributes to a much lower pore size and stiff skeletal structure, resulting in good optical properties in the visible range. Tewari et al. compared the conventional supercritical drying and novel ambient-temperature supercritical drying and both contributed to great transparency in the visible range, as shown in Fig. 5e.47 Tabata et al. developed a time-gradual supercritical drying (80 °C, 15.7 MPa) with 2-proponal and CO2 as the drying fluid and attained a refractive index of 1.045 for a large-scale aerogel sample (18 cm × 18 cm × 2 cm).76 Liu et al. added a thermal treatment step following low-pressure acetonitrile supercritical drying (at 274.7 °C and only 4.83 MPa) and the applied high temperature (600 °C) optimized the optical transmittance of the silica aerogel to 91.5% at 800 nm due to the loss of micropores and mesopores, which contribute to the Rayleigh scattering.77 Ambient pressure drying can attain transparent silica aerogels as well when applying surface modification. Kim et al. found that when using 2% TMCS as a modification agent before ambient pressure drying, an optical transmittance of 85% at 700 nm can be obtained.78 Rao comprehensively studied parameters in the ‘sol–gel’ process and concluded that when the molar ratio of TEOS (precursor)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH
EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acidic H2O
acidic H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) basic H2O
basic H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oxalic acid
oxalic acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH4OH
NH4OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMDZ (surface modification agent) is kept at 1
HMDZ (surface modification agent) is kept at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.75
3.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.25
2.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.23 × 10−5
6.23 × 10−5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04
0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.36, TEOS-based transparent aerogels (transmittance > 90%) can be obtained.56
0.36, TEOS-based transparent aerogels (transmittance > 90%) can be obtained.56
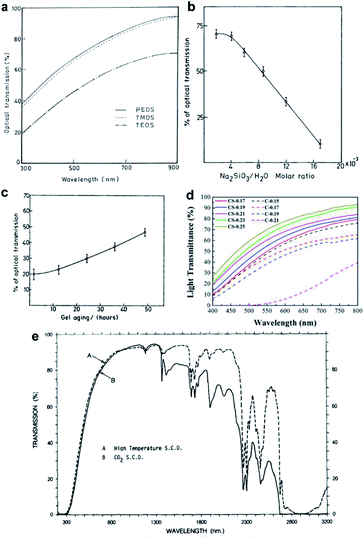 |
| | Fig. 5 (a) Plot of optical transmittance vs. wavelength for three precursors: PEDS, TMOS and TEOS. (b) Optical transmission of silica aerogel varies with the waterglass concentration. (c) Optical transmittance of silica aerogel (0.8 cm thickness at 750 nm) increasing with the aging time. (d) Transmittance of the aerogels prepared by the controllable shrinkage method (CS method) and the conventional method (C method). (e) Transmission spectra of TEOS aerogels (3 mm thickness) dried at (A) conventional high-temperature supercritical drying and (B) low-temperature supercritical drying. Reproduced from ref. 30, 47, 50 and 69 with the permission of Elsevier. | |
4. Thermal insulation of silica aerogels
Due to its high porosity, nanoscale pore size and crosslinking silica networks, silica aerogels are distinguished thermal insulating materials. Because up to 90% volume of the aerogel is air, its thermal conductivity (which is measured with the equipment shown in Fig. 6a) can be similar or even less than air (0.021 W m−1 K−1 at 0 °C under 1 bar).79 In this section, theories explaining the thermal insulating ability of silica aerogels and methods to further reduce their thermal conductivity are included.
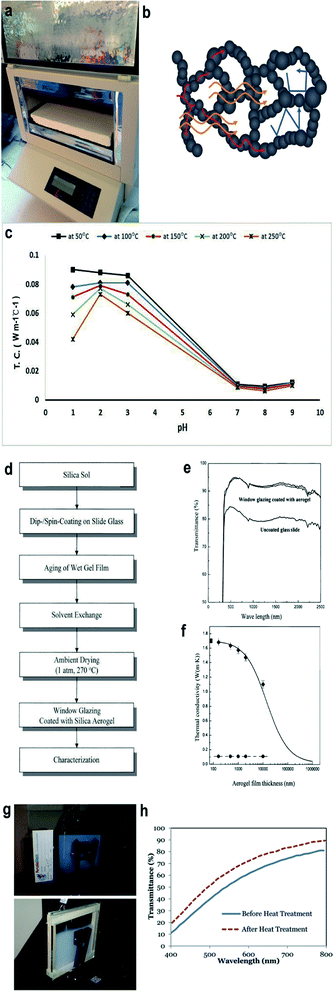 |
| | Fig. 6 (a) Bulk silica aerogel for the thermal conductivity test. The test equipment is called the Fox 314 HFM apparatus and the test method is the steady-state hot plane. (b) Three different mechanisms of silica aerogel heat transfer: red, yellow and blue lines represent solid, radiative and gaseous heat conduction respectively. (c) Thermal conductivity of the silica aerogel with different aging temperatures varying with the pH. (d) An overall flow chart for the experiment of window coated with the silica aerogel. (e) Optical transmittance spectra of the window coated with and without aerogels. (f) Plot illustrating the trend of thermal conductivity versus aerogel film thickness. (g) Assembling of monolith silica aerogel (up) and granular silica aerogel (down). (h) Transmittance spectra of 1.27 cm-thick silica aerogel monolith before and after heat treatment. Reproduced from ref. 10, 21, 77, 79, 85 and 96 with the permission of University of Baghdad, American Chemical Society, MDPI, Royal Society of Chemistry and Elsevier. | |
4.1 Mechanisms of heat transfer in silica aerogels
Excellent thermal insulating property of silica aerogels results from their high porosity and network structure, which almost nullifies three or four kinds of heat transfer, as shown in Fig. 6b.80,81 Specifically, convection heat transfer is first neglected when the average pore size is smaller than 4 mm (average pore size of the aerogel is around few nanometers).81,82 A tortuous structure and high connectivity network of aerogels, which can hinder heat transport in air and solid, also contribute to the low thermal conductivity. Radiative thermal transfer depends on electromagnetic waves related to photon's mean free path, and thus, it varies with the temperature and can be neglected at room temperature.83 Several scientists have proved this by measuring the thermal conductivity, which increases at high temperatures due to the existence of radiative heat transfer.84 In most cases, silica aerogels work as functional materials at room temperature, so their radiative thermal conductivity is neglected.
4.2 Controlling the thermal conductivity of the silica aerogel
All steps in the ‘sol–gel’ process tend to affect the thermal conductivity of silica aerogels. In 1999, Wagh's group compared the thermal conductivity of silica aerogels prepared with TEOS, TMOS and PEDS, respectively.29 PEDS-based aerogels were low in density with high porosity (96.84%) and surface area (1100 m2 g−1), and therefore showed a low thermal conductivity of 0.015 W m−1 K−1. As mentioned in Section 2.1, the pH would greatly affect precursor gelation and thus affect the pore size and surface area of silica aerogel, which then further affect the thermal insulation ability of the aerogel sample. Israa investigated the relationship between the pH and aerogel thermal property in 2019 (shown in Fig. 6c), which greatly correspond to Stolarski's find.85 The thermal conductivity of silica aerogel can be as low as 0.01 W m−1 C−1 when the pH is between 7 and 8.
In 2016, Pisal and Rao prepared silica aerogels through ambient pressure drying and found that the thermal conductivity of the waterglass- and TMOS-based sample (0.025 W m−1 K−1 and 0.030 W m−1 K−1 respectively) was lower than that of the TEOS-based aerogel (0.050 W m−1 K−1).86 Aging can dictate the aerogel properties to a great extent because it is the step where silica skeleton forms. There are few works investigating the effect of aging on the aerogel thermal conductivity. In 2009, Nadargi found that the optimal aging time is two days.87 Beyond that time, the thermal conductivity would increase due to the over-condensation of hydroxyl groups.
In addition, supercritical drying and freeze drying can obtain low-thermal conductivity silica aerogels. In 2014, Wong et al. prepared polyethoxydisiloxane aerogels through CO2 supercritical drying and obtained a sample of 0.0135 W m−1 K−1.88 Moreover, in 2016, Pan's group synthesized MTMS/waterglass (molar ratio is 5.1) aerogels with a thermal conductivity of 0.0226 W m−1 K−1via freeze and vacuum drying.26 Ambient pressure drying can also obtain silica aerogels good thermal insulation if accompanied by enough surface modification because a well-modified surface usually contributes to the hydrophobic silica aerogel, whose silica networks are less likely to collapse during drying. Thus, the connectivity of the silica skeleton is well maintained and heat transfer is significantly hindered. Kwon et al. prepared a very low-thermal conductivity TEOS aerogel (0.0136 W m−1 K−1) by immersing the sample in TMCS/n-hexane for 4 days at 30 °C before ambient pressure drying.84 Ge's group modified silica aerogels with epoxy powders by varying the ratio of aerogel and epoxy, resulting in an increase in the contact angle of the sample from 117 to 140° and a decrease in thermal conductivity from 0.044 to 0.011 W m−1 K−1 correspondingly.89 Wei et al. investigated the effects of surface modification on the thermal conductivity of silica aerogels, which are given in Table 4. It is clear that the thermal conductivity can be greatly reduced when the surface of silica aerogel is well modified.46
Table 4 Effect of MSM (multiple surface modification), SSM (single surface modification) and NSM (no surface modification) on the thermal conductivity of TEOS-based aerogels
| Sample |
Bulk density (g cm−3) |
Porosity (%) |
Contact angle (°) |
Thermal conductivity (W m−1 K−1) |
| NSM |
0.624 ± 0.022 |
72.0 ± 1.5 |
— |
0.417 ± 0.006 |
| SSM |
0.502 ± 0.007 |
77.2 ± 0.3 |
114 |
0.079 ± 0.002 |
| MSM |
0.069 ± 0.004 |
96.8 ± 0.2 |
143 |
0.036 ± 0.001 |
5. Mechanical and acoustic properties of silica aerogels
5.1 Mechanical property
Usually, the mechanical property of the silica aerogel is its mechanical strength, which is usually measured by a three-point flexural and a compression test. Woignier et al. investigated the mechanical strength of TMOS aerogel in 1988 and the resulting stress–strain curve shows an elastic behavior with a flexural strength smaller than 0.01 MPa, which indicates the brittleness of the conventional aerogel.90 This can be understood according to the relationship between the bulk density of the silica aerogel ρb and Young's modulus E: E ∝ ρbβ with β ranging from 3.2 to 3.8.91 In order to further optimize the mechanical properties of the silica aerogel, researchers tried heat treatment and changing parameters in aging. Hæreid et al. found that with a temporal aging time at higher temperatures, the mechanical strength and stiffness of the TMOS-based aerogels can be increased with a shear modulus of 1.6 MPa.92 In 2019, Yang and co-workers synthesized hierarchical aerogel forms and when annealing the sample at 400 °C, Young's modulus is further increased to 89.85 MPa, showing a great mechanical strength.18
5.2 Acoustic property
Monolith aerogels also perform well in acoustic insulation across audible (20–2500 Hz) and low ultrasonic range (20–200 kHz) due to their great ability in sound absorption, which comes from the greatly connective silica network, high porosity and strong mechanical durability.18,93 Due to the wide application of silica aerogels in building materials, researchers are trying to optimize the acoustic property. Buratti et al. mixed plaster with 90 wt% silica aerogel and obtained a maximum of sound absorption coefficient for 18% at 900 Hz.79 In 2018, Cao's group synthesized the silica aerogel with a noise reduction coefficient of 41% by a freeze-drying method and found that when the porosity decreases and the density increases, the coefficient of sound absorption for the silica aerogel increases due to the rise in the aerogel density, airflow resistivity and the tortuosity of the transmission path for the sound waves.94
6. Thermal insulation silica aerogel windows
The glass window shows a great optical transparency with the refractive index of ∼1.52. However, the energy lost is a long-standing challenge of the glass window due to its high thermal conductivity (usually more than 1 W m−1 K−1) and high thermal transmittance U-value (∼3–5 W m−2 K−1). The silica aerogels which are transparent and do well in thermal insulation thus become a strong candidate of the window raw materials.95
6.1 Fabrication of aerogel windows
In the beginning of this century, scientists started to incorporate silica aerogels onto a window through a dip or spin-coating/glazing. In order to increase the efficiency of gel coating, Kim et al. operated the coating and aging step in a saturated isopropanol atmosphere and isopropanol solvent respectively.20 The overall operation flow chat is shown in Fig. 6d. Fig. 6e shows the optical transparency of the glass window coated with the silica aerogel. The impact of the coated aerogel film on the overall glazing window is shown in Fig. 6f, while the increase in the aerogel film thickness can largely decrease the thermal conductivity. In 2004, Jensen et al. sealed silica aerogels between two pieces of windows and dried them by the CO2 supercritical method. The final thermal transmittance U-value was reduced to 0.72 W m−2 K−1 and a transmittance of 76% was obtained with a 15 mm-thick aerogel monolith.15 Although the product properties are great, the preparation process was complicated and not suitable in scalable fabrication. In 2012, as shown in Fig. 6g, Buratti and Moretti glazed windows with the silica aerogel and the U-value was reduced to 0.6 W m−2 K−1.10 One year later, Cha et al. incorporated 20 wt% silica aerogels onto a glass window and 32% thermal conductivity was reduced, compared with the net glass window.20 In 2016, Bhuiya et al. used hot press to seal the TMOS aerogel solution in the mold and when the thickness is 0.8 mm, the U-value of the corresponding glazing window is as low as 0.5 W m−2 K−1.96 In 2019, Zinzi et al. followed Bhuiya's recipe and studied optical properties of the assembled 15 mm-thick aerogel monolith, which was sealed between two 4.7 mm glasses. The transmittance of the glazing aerogel window in the light and the solar spectra was 0.69 and 0.62 respectively.97 The same year, Buratti's team developed a rapid process: combining hot press and supercritical fluid cooling to prepare an aerogel glazing window in 6.5 hours. The corresponding thermal transmittance U-value could be as low as 0.99 W m−2 K−1.98
6.2 Present challenges and future direction of aerogel windows
The biggest challenge now for the aerogel window manufacturing is that the great thermal insulation and high transparency cannot be ensured at the same time. This contradiction is shown in a few works. In the winter of 2013, Cotana et al. performed an in-field experiment to analyze the thermal, optical and acoustic properties of the glazing aerogel, and they found that compared with the normal air-filled double-glazing window, the aerogel windows could decrease the heating up energy consumption to 50% and increase the acoustic insulation level by 3 dB. However, they lowered the cloudy day and sunny day luminance level to 47% and 10% respectively.99 Berardi's group assessed the thermal resistance of glazing silica aerogel windows in 2015×.100 The corresponding thermal resistance was reduced to 0.6 W m−2 K−1 when a 12 mm aerogel pane was sealed between two 4.0 mm glasses. However, the transmittance was just 50%. Garnier et al. used a modeling method to investigate the impact of the aerogel window on daylight and thermal energy and they found that the thermal transmittance value could be as low as 0.3 W m−2 K−1, but the corresponding light transmittance is reduced to ∼0.3 at the same time.101
Thus, in the near future, it is necessary to find a feasible method to improve the thermal and optical aerogel window at the same time. Heat treatment maybe a potential way and extensive research has proved that it could increase the light transmittance to some extent. As shown in Fig. 6h, Bhuiya found that 10% more light would transmit through the aerogel after heat treatment. However, as discussed in the section above, increasing the temperature would increase the relevant thermal conductivity due to the collapse of nanoscale silica networks. Therefore, the temperature of heat treatment would not be high. In 2017, Strobach et al. found that the optimal annealing time for 400 °C is 24 hours where the transmittance of the pure TMOS aerogel is above 98% and its thermal conductivity is 0.06 W m−1 K−1. They predicted that in the same annealing way, aerogel coated windows can be optimized.102
7. Conclusions
Silica aerogels are one of the lightest solid materials in the world, with extremely high porosity and nanoscale pore size, which contribute to distinguished practical properties, including thermal insulation and optical transparency. Silica aerogels are synthesized by a ‘sol–gel’ process and by tuning the parameters of it, silica networks can be strengthened, and pores can be narrowed and uniformed. Drying is of vital importance in the ‘sol–gel’ process, and nowadays, ambient pressure drying is preferred these years when considering commercial problems. A surface modification step is necessary before ambient drying and there have been a number of works investigating this from the perspective of efficiency, cost and environmental-protection. Due to the low thermal conductivity and high optical transmittance, the silica aerogel is one of the most potential candidates of energy-saving window materials. Via a dip/spin-coating step, wet aerogels can be well incorporated into glass windows and the resulted thermal transmittance U-value can be as low as 0.3 W m−2 K−1. However, the corresponding light transmittance would be low as well, which makes the fabrication difficult. Therefore, it is expected that in the nearest future, manufacturing both thermal insulating and transparent integrated silica aerogel windows will be of core interest in the area of aerogel.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work at University at Buffalo is supported by the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Building Technology Office (BTO) Award Number DE-EE0008675.
Notes and references
- A. Du, B. Zhou, Z. Zhang and J. Shen, Materials, 2013, 6, 941–968 CrossRef CAS.
- S. B. Riffat and G. Qiu, Int. J. Low-Carbon Technol., 2013, 8, 1–6 CrossRef CAS.
-
M. A. Aegerter, N. Leventis and M. M. Koebel, Aerogels handbook, Springer Science & Business Media, 2011 Search PubMed.
- M. Tabata, I. Adachi, Y. Ishii, H. Kawai, T. Sumiyoshi and H. Yokogawa, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 623, 339–341 CrossRef CAS.
- N. Hüsing and U. Schubert, Angew. Chem., Int. Ed., 1998, 37, 22–45 CrossRef.
- J. L. Gurav, I.-K. Jung, H.-H. Park, E. S. Kang and D. Y. Nadargi, J. Nanomater., 2010, 409310 Search PubMed.
- R. C. Mehrotra, J. Non-Cryst. Solids, 1992, 145, 1–10 CrossRef CAS.
- Y. J. Lee, G.-P. Kim, Y. Bang, J. Yi, J. G. Seo and I. K. Song, Mater. Res. Bull., 2014, 50, 240–245 CrossRef CAS.
- A. S. Dorcheh and M. Abbasi, J. Mater. Process. Technol., 2008, 199, 10–26 CrossRef.
- C. Buratti and E. Moretti, Appl. Energy, 2012, 98, 396–403 CrossRef CAS.
- A. Shaid, M. Fergusson and L. Wang, Chem. Mater. Eng., 2014, 2, 37–43 Search PubMed.
- B. C. Dunn, P. Cole, D. Covington, M. C. Webster, R. J. Pugmire, R. D. Ernst, E. M. Eyring, N. Shah and G. P. Huffman, Appl. Catal., A, 2005, 278, 233–238 CrossRef CAS.
- S. Cao, K. L. Yeung and P.-L. Yue, Appl. Catal., B, 2007, 76, 64–72 CrossRef CAS.
- E. Moretti, M. Zinzi, F. Merli and C. Buratti, Energy Build., 2018, 166, 407–417 CrossRef.
- J. M. Schultz, K. I. Jensen and F. H. Kristiansen, Sol. Energy Mater. Sol. Cells, 2005, 89, 275–285 CrossRef CAS.
- K. I. Jensen, J. M. Schultz and F. H. Kristiansen, J. Non-Cryst. Solids, 2004, 350, 351–357 CrossRef CAS.
- I. Adachi, Y. Ishii, H. Kawai, A. Kuratani and M. Tabata, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 595, 180–182 CrossRef CAS.
- R. Yang, F. Hu, L. An, J. N. Armstrong, Y. Hu, C. Li, Y. Huang and S. Ren, Nano Lett., 2020, 20(2), 1110–1116 CrossRef CAS.
- G. M. Pajonk, Colloid Polym. Sci., 2003, 281, 637–651 CrossRef CAS.
- J. Cha, S. Kim, K.-W. Park, D. R. Lee, J.-H. Jo and S. Kim, J. Therm. Anal. Calorim., 2014, 116, 219–224 CrossRef CAS.
- G.-S. Kim and S.-H. Hyun, J. Non-Cryst. Solids, 2003, 320, 125–132 CrossRef CAS.
- S. D. Bhagat, C.-S. Oh, Y.-H. Kim, Y.-S. Ahn and J.-G. Yeo, Microporous Mesoporous Mater., 2007, 100, 350–355 CrossRef CAS.
- M. Moner-Girona, A. Roig, E. Molins and J. Llibre, J. Sol-Gel Sci. Technol., 2003, 26, 645–649 CrossRef CAS.
- J. L. Gurav, I.-K. Jung, H.-H. Park, E. S. Kang and D. Y. Nadargi, J. Nanomater., 2010, 409310 Search PubMed.
- M. Van Bommel and A. De Haan, J. Non-Cryst. Solids, 1995, 186, 78–82 CrossRef CAS.
- F. Shi, L. Wang and J. Liu, Mater. Lett., 2006, 60, 3718–3722 CrossRef CAS.
- Y. Pan, S. He, L. Gong, X. Cheng, C. Li, Z. Li, Z. Liu and H. Zhang, Mater. Des., 2017, 113, 246–253 CrossRef CAS.
- P. C. Thapliyal and K. Singh, J. Mater., 2014, 127049 Search PubMed.
- X. Guo, Q. Zhang, X. Ding, Q. Shen, C. Wu, L. Zhang and H. Yang, J. Sol-Gel Sci. Technol., 2016, 79, 328–358 CrossRef CAS.
- P. Wagh, R. Begag, G. Pajonk, A. V. Rao and D. Haranath, Mater. Chem. Phys., 1999, 57, 214–218 CrossRef CAS.
- A. V. Rao and M. M. Kulkarni, Mater. Res. Bull., 2002, 37, 1667–1677 CrossRef CAS.
- O.-J. Lee, K.-H. Lee, T. J. Yim, S. Y. Kim and K.-P. Yoo, J. Non-Cryst. Solids, 2002, 298, 287–292 CrossRef CAS.
- A. V. Rao, S. D. Bhagat, H. Hirashima and G. Pajonk, J. Colloid Interface Sci., 2006, 300, 279–285 CrossRef CAS.
- S. He, D. Huang, H. Bi, Z. Li, H. Yang and X. Cheng, J. Non-Cryst. Solids, 2015, 410, 58–64 CrossRef CAS.
- S. D. Bhagat, Y.-H. Kim, M.-J. Moon, Y.-S. Ahn and J.-G. Yeo, Solid State Sci., 2007, 9, 628–635 CrossRef CAS.
- A. P. Rao and A. V. Rao, J. Non-Cryst. Solids, 2008, 354, 10–18 CrossRef CAS.
- M. Stolarski, J. Walendziewski, M. Steininger and B. Pniak, Appl. Catal., A, 1999, 177, 139–148 CrossRef CAS.
-
C. J. Brinker and G. Scherer, The Processing and the Chemistry of Sol-Gel Processing, 1990 Search PubMed.
- D. A. Nivens, Y. Zhang and S. M. Angel, Anal. Chim. Acta, 1998, 376, 235–245 CrossRef CAS.
- F. He, H. Zhao, X. Qu, C. Zhang and W. Qiu, J. Mater. Process. Technol., 2009, 209, 1621–1626 CrossRef CAS.
- S. Iswar, W. J. Malfait, S. Balog, F. Winnefeld, M. Lattuada and M. M. Koebel, Microporous Mesoporous Mater., 2017, 241, 293–302 CrossRef CAS.
- H. Omranpour and S. Motahari, J. Non-Cryst. Solids, 2013, 379, 7–11 CrossRef CAS.
- S. Hæreid, E. Nilsen and M.-A. Einarsrud, J. Non-Cryst. Solids, 1996, 204, 228–234 CrossRef.
- S. Smitha, P. Shajesh, P. Aravind, S. R. Kumar, P. K. Pillai and K. Warrier, Microporous Mesoporous Mater., 2006, 91, 286–292 CrossRef CAS.
- G. Reichenauer, J. Non-Cryst. Solids, 2004, 350, 189–195 CrossRef CAS.
- T. Y. Wei, T. F. Chang, S. Y. Lu and Y. C. Chang, J. Am. Ceram. Soc., 2007, 90, 2003–2007 CrossRef CAS.
- C. Lei, J. Li, C. Sun, H. Yang, T. Xia, Z. Hu and Y. Zhang, Microporous Mesoporous Mater., 2018, 267, 107–114 CrossRef CAS.
- M. Mukhopadhyay and B. S. Rao, J. Chem. Technol. Biotechnol., 2008, 83, 1101–1109 CrossRef CAS.
- H. Zhang, F. Yang, R. Bai, Z. Zhao, J. Li, X. Zeng and X. Zhang, Materials, 2019, 12, 3459 CrossRef CAS.
- P. H. Tewari, A. J. Hunt and K. D. Lofftus, Mater. Lett., 1985, 3, 363–367 CrossRef CAS.
- C. García-González, M. Camino-Rey, M. Alnaief, C. Zetzl and I. Smirnova, J. Supercrit. Fluids, 2012, 66, 297–306 CrossRef.
- Y. K. Lee, V. Parale, H. H. Cho, D. Mahadik and H.-H. Park, J. Sol-Gel Sci. Technol., 2017, 83, 692–697 CrossRef.
- A. P. Rao, A. V. Rao and G. Pajonk, Appl. Surf. Sci., 2007, 253, 6032–6040 CrossRef CAS.
- F. Schwertfeger, W. Glaubitt and U. Schubert, J. Non-Cryst. Solids, 1992, 145, 85–89 CrossRef CAS.
- L.-J. Wang, S.-Y. Zhao and M. Yang, Mater. Chem. Phys., 2009, 113, 485–490 CrossRef CAS.
- S. S. Prakash, C. J. Brinker and A. J. Hurd, J. Non-Cryst. Solids, 1995, 190, 264–275 CrossRef CAS.
- S.-K. Kang and S.-Y. Choi, J. Mater. Sci., 2000, 35, 4971–4976 CrossRef CAS.
- P. B. Sarawade, J.-K. Kim, H.-K. Kim and H.-T. Kim, Appl. Surf. Sci., 2007, 254, 574–579 CrossRef CAS.
- A. P. Rao, G. Pajonk and A. V. Rao, J. Mater. Sci., 2005, 40, 3481–3489 CrossRef CAS.
- P. M. Shewale, A. V. Rao and A. P. Rao, Appl. Surf. Sci., 2008, 254, 6902–6907 CrossRef CAS.
- S. Hyun, T. Kim, G. Kim and H.-H. Park, J. Mater. Sci. Lett., 2000, 19, 1863–1866 CrossRef CAS.
- H. Tamon, H. Ishizaka, T. Yamamoto and T. Suzuki, Carbon, 2000, 38, 1099–1105 CrossRef CAS.
- G. Pajonk, J. Non-Cryst. Solids, 1998, 225, 307–314 CrossRef CAS.
- C. Mandal, S. Donthula, R. Soni, M. Bertino, C. Sotiriou-Leventis and N. Leventis, J. Sol-Gel Sci. Technol., 2019, 90, 127–139 CrossRef CAS.
- A. V. Rao and G. Pajonk, J. Non-Cryst. Solids, 2001, 285, 202–209 CrossRef.
- G. Pajonk, E. Elaloui, B. Chevalier and R. Begag, J. Non-Cryst. Solids, 1997, 210, 224–231 CrossRef CAS.
- M. Tabata, I. Adachi, H. Kawai, M. Kubo and T. Sato, Phys. Procedia, 2012, 37, 642–649 CrossRef CAS.
- T. Bellunato, M. Calvi, C. Matteuzzi, M. Musy, D. Perego and B. Storaci, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 595, 183–186 CrossRef CAS.
- P. Wang, A. Beck, W. Korner, H. Scheller and J. Fricke, J. Phys. D: Appl. Phys., 1994, 27, 414 CrossRef CAS.
- M. Tabata, I. Adachi, H. Kawai, T. Sumiyoshi and H. Yokogawa, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 668, 64–70 CrossRef CAS.
- A. Emmerling, R. Petricevic, A. Beck, P. Wang, H. Scheller and J. Fricke, J. Non-Cryst. Solids, 1995, 185, 240–248 CrossRef CAS.
- L. Zhao, S. Yang, B. Bhatia, E. Strobach and E. N. Wang, AIP Adv., 2016, 6, 025123 CrossRef.
- L. Zhao, E. Strobach, B. Bhatia, S. Yang, A. Leroy, L. Zhang and E. N. Wang, Opt. Express, 2019, 27, A39–A50 CrossRef CAS.
- A. V. Rao, A. P. Rao and M. Kulkarni, J. Non-Cryst. Solids, 2004, 350, 224–229 CrossRef CAS.
- M. V. Khedkar, S. A. Jadhav, S. B. Somvanshi, P. B. Kharat and K. Jadhav, SN Appl. Sci., 2020, 2, 1–10 Search PubMed.
- M. Tabata, I. Adachi, Y. Hatakeyama, H. Kawai, T. Morita and T. Sumiyoshi, J. Supercrit. Fluids, 2016, 110, 183–192 CrossRef CAS.
- G. Liu, B. Zhou, A. Du, J. Shen and Q. Yu, SN Appl. Sci., 2013, 20, 1163–1170 CAS.
- P. B. Sarawade, J.-K. Kim, J.-K. Park and H.-K. Kim, Aerosol Air Qual. Res., 2016, 6, 93–105 CrossRef.
- C. Buratti, E. Moretti, E. Belloni and F. Agosti, Sustainability, 2014, 6, 5839–5852 CrossRef.
- T. Linhares, M. T. P. de Amorim and L. Durães, J. Mater. Chem. A, 2019, 7, 22768–22802 RSC.
- F. Hu, S. Wu and Y. Sun, Adv. Mater., 2019, 31, 1801001 CrossRef.
- G. Lu, X.-D. Wang, Y.-Y. Duan and X.-W. Li, J. Non-Cryst. Solids, 2011, 357, 3822–3829 CrossRef CAS.
-
M. Modest, Radiative Heat Transfer, Academic Press, San Diego, CA, 2003, pp. 465–492 Search PubMed.
- Y.-G. Kwon, S.-Y. Choi, E.-S. Kang and S.-S. Baek, J. Mater. Sci., 2000, 35, 6075–6079 CrossRef CAS.
- I. F. Al-sharuee, Baghdad Sci. J., 2019, 16, 0770 CrossRef.
- A. A. Pisal and A. V. Rao, SN Appl. Sci., 2016, 23, 1547–1556 CAS.
- D. Y. Nadargi, S. S. Latthe and A. V. Rao, J. Sol-Gel Sci. Technol., 2009, 49, 53–59 CrossRef CAS.
- J. C. Wong, H. Kaymak, S. Brunner and M. M. Koebel, Microporous Mesoporous Mater., 2014, 183, 23–29 CrossRef CAS.
- D. Ge, L. Yang, Y. Li and J. Zhao, J. Non-Cryst. Solids, 2009, 355, 2610–2615 CrossRef CAS.
- T. Woignier and J. Phalippou, J. Non-Cryst. Solids, 1988, 100, 404–408 CrossRef CAS.
- L. Kocon, F. Despetis and J. Phalippou, J. Non-Cryst. Solids, 1998, 225, 96–100 CrossRef CAS.
- S. Hæreid, J. Anderson, M. Einarsrud, D. Hua and D. Smith, J. Non-Cryst. Solids, 1995, 185, 221–226 CrossRef.
- V. Gibiat, O. Lefeuvre, T. Woignier, J. Pelous and J. Phalippou, J. Non-Cryst. Solids, 1995, 186, 244–255 CrossRef CAS.
- L. Cao, Y. Si, Y. Wu, X. Wang, J. Yu and B. Ding, Nanoscale, 2019, 11, 2289–2298 RSC.
- D. Li, C. Zhang, Q. Li, C. Liu, M. Arıcı and Y. Wu, Appl. Therm. Eng., 2020, 165, 114547 CrossRef CAS.
- M. M. H. Bhuiya, A. M. Anderson, M. K. Carroll, B. A. Bruno, J. L. Ventrella, B. Silberman and B. Keramati, Ind. Eng. Chem. Res., 2016, 55, 6971–6981 CrossRef CAS.
- M. Zinzi, G. Rossi, A. M. Anderson, M. K. Carroll, E. Moretti and C. Buratti, Sol. Energy, 2019, 183, 30–39 CrossRef CAS.
- C. Buratti, E. Moretti, E. Belloni and M. Zinzi, Appl. Sci., 2019, 9, 5473 CrossRef CAS.
- F. Cotana, A. L. Pisello, E. Moretti and C. Buratti, Build. Environ., 2014, 81, 92–102 CrossRef.
- U. Berardi, Appl. Energy, 2015, 154, 603–615 CrossRef.
- C. Garnier, T. Muneer and L. McCauley, Build Environ., 2015, 94, 231–238 CrossRef.
- E. Strobach, B. Bhatia, S. Yang, L. Zhao and E. N. Wang, J. Non-Cryst. Solids, 2017, 462, 72–77 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2020 |
 Open Access Article
Open Access Article *abc
*abc

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent
solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water
water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH
EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1
H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1
H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH
EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1
H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH 1
EtOH 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–(OH) + Si–(OH)
Si–(OH) + Si–(OH)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ⇌
⇌ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si
Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) + H2O
+ H2O![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–(OH) + Si–(OR)
Si–(OH) + Si–(OR)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ⇌
⇌ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si
Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) + ROH
+ ROH
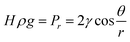


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (A is the normal-hemispherical transmittance, B is the normal-diffuse transmittance and C is the normal-direct transmittance). (e) Plot showing the refractive index of the silica aerogel achieved in 2001, 2005 and 2008. (f) The prism method for the measurement of the silica aerogel refractive index, n. (g) A plot showing the refractive index n as a first-order function of silica aerogel density ρ. Reproduced from ref. 4, 61, 64, 66 and 68 with the permission of Degruyter and Elsevier.
1 ratio (A is the normal-hemispherical transmittance, B is the normal-diffuse transmittance and C is the normal-direct transmittance). (e) Plot showing the refractive index of the silica aerogel achieved in 2001, 2005 and 2008. (f) The prism method for the measurement of the silica aerogel refractive index, n. (g) A plot showing the refractive index n as a first-order function of silica aerogel density ρ. Reproduced from ref. 4, 61, 64, 66 and 68 with the permission of Degruyter and Elsevier.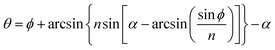
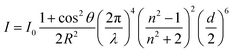
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH
EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acidic H2O
acidic H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) basic H2O
basic H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oxalic acid
oxalic acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH4OH
NH4OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HMDZ (surface modification agent) is kept at 1
HMDZ (surface modification agent) is kept at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.75
3.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.25
2.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.23 × 10−5
6.23 × 10−5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04
0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.36, TEOS-based transparent aerogels (transmittance > 90%) can be obtained.56
0.36, TEOS-based transparent aerogels (transmittance > 90%) can be obtained.56





