Enhancing FRET biosensing beyond 10 nm with photon avalanche nanoparticles

Abstract

Förster Resonance Energy Transfer (FRET) between donor (D) and acceptor (A) molecules is a phenomenon commonly exploited to study or visualize biological interactions at the molecular level. However, commonly used organic D and A molecules often suffer from photobleaching and spectral bleed-through, and their spectral properties hinder quantitative analysis. Lanthanide-doped upconverting nanoparticles (UCNPs) as alternative D species offer significant improvements in terms of photostability, spectral purity and background-free luminescence detection, but they bring new challenges related to multiple donor ions existing in a single large size UCNP and the need for nanoparticle biofunctionalization. Considering the relatively short Förster distance (typically below 5–7 nm), it becomes a non-trivial task to assure sufficiently strong D–A interaction, which translates directly to the sensitivity of such bio-sensors. In this work we propose a solution to these issues, which employs the photon avalanche (PA) phenomenon in lanthanide-doped materials. Using theoretical modelling, we predict that these PA systems would be highly susceptible to the presence of A and that the estimated sensitivity range extends to distances 2 to 4 times longer (i.e. 10–25 nm) than those typically found in conventional FRET systems. This promises high sensitivity, low background and spectral or temporal biosensing, and provides the basis for a radically novel approach to combine luminescence imaging and self-normalized bio-molecular interaction sensing.

---

Introduction

Förster Resonance Energy Transfer (FRET) is a photophysical phenomenon that enables the measurement of the colocalization and the distance between two emitting species. In biology, FRET constructs are routinely used to probe the conformation of proteins or nucleic acids, DNA hybridization, cellular membrane potential, and ligand–receptor or antibody–antigen interactions.^1–4 FRET relies on resonant dipole–dipole energy transfer (ET) between a photo-excited donor (D) and a ground-state acceptor (A) molecule. For efficient ET, the donors must lie in close proximity to acceptors and overlap spectrally, i.e., the donor emission must overlap with the acceptor absorption. Various FRET detection methodologies^1,5–8 and numerous D and A molecules have been exploited (e.g. fluorescent proteins, organic dyes, and fluorescent nanoparticles (NPs))^1,5,9–12 so far. However, exploiting FRET between donor and acceptor molecules separated by distances larger than twice the typical Förster distance (i.e. more than 8–10 nm) remains a serious challenge. Various approaches have been proposed to address this issue, such as using triplet states of acceptors,¹³ localized surface plasmon Au nanoparticles as an intermediate layer between D and A,^14–16 plasmonic nano-antennae,¹⁷ photonic wires^18,19 and plasmonic AuNP acceptors,^15,16,20 or using multiple acceptors to promote the energy transfer.^21–24 Alternatively, more complex nanophotonic devices have been designed based on waveguides,²⁵ which aim to tailor the electromagnetic field around D–A FRET constructs to enhance energy transfer and/or emission rates. The advantage of such approaches is the ability to use standard D–A fluorophore pairs; however, numerous corrections and control experiments are still required to extract quantitative and exact information, such as the D–A distance or the concentration of A, from FRET experiments.^26–28 These corrections are required for reasons including the photobleaching of D or A molecules, spectral bleed-through, photoconversion or photochromism of D or A molecules, susceptibility of D and A to the local chemical environment (pH, concentration, viscosity, and aggregation) and finally sample autofluorescence, which complicates reliable and quantitative data analysis.^29,30

FRET donors based on lanthanide doped nanoparticles (LnNPs) offer a promising alternative to conventional donors such as fluorescent dyes, fluorescent proteins, nitrogen vacancies and quantum dots.^31–33 LnNPs are used in bio-medical applications as multi-modal (e.g. fluorescence/MRI/CT contrast agents) and background free multicolour/temporal imaging labels,^34–37 FRET donors in biosensors,^38–41 remote optical nano-heaters⁴² and nano-thermometers,^43,44 deep tissue NIR activatable photodynamic agents,^45,46 and labels in super-resolution imaging.^47,48 LnNPs show exceptional photo-stability, limited toxicity,⁴⁹ long luminescence lifetimes (10¹ to 10⁴ μs range), narrow-band absorption and emission at various wavelengths in the visible and near infrared regions.^50–52 Moreover, the background-free detection (i.e. rejection of tissue autofluorescence) with LnNPs is of critical importance for most bio-detection/bio-imaging applications and may be achieved by time-gated and/or anti-Stokes emission.^53,54 The latter method originates from the capability of lanthanide-doped upconverting nanoparticles (UCNPs) to effectively convert long wavelength photons to shorter wavelength photons (so called upconversion or UC). Although the absolute quantum efficiency of emission in such upconverting nanoparticles does not typically exceed 3%, the anti-Stokes processes in UCNPs are significantly more efficient than two-photon absorption or harmonic generation in non-linear materials.⁵⁵

LnNPs have been demonstrated to be suitable for FRET antibody–antigen reaction or DNA hybridization sensing.^56–58 Lanthanide based Resonance Energy Transfer (RET) with lanthanide ion donor doped inorganic nanoparticles has been demonstrated with a wide range of acceptors, such as organic dyes (e.g. rose bengal,^59,60 cyanine Cy3.5,⁶¹ rhodamine B,⁶² a DBD-6 small organic dye⁶³ and others⁶⁴) and also with inorganic nanoparticle acceptors, such as quantum dots,^9,10,65–73 gold nanoparticles⁷⁴ or even lanthanides themselves.⁷⁵ For the sake of clarity we will use the term FRET to denote resonant energy transfer between molecules, while RET acronyms will be used to discuss cases in which Ln³⁺ ions are donors. RET from LnNPs is potentially advantageous over conventional FRET because lanthanide emission produces large emission (anti)Stokes shifts and narrower emission bandwidths, which reduces background and the probability of direct photoexcitation of acceptors.

Despite these benefits, RET with LnNPs currently still suffers from insufficient sensitivity and requires further optimization. Additionally, utilizing UCNPs as RET donors is more complicated than with conventional single molecule fluorophores.^76,77 Unlike for molecular FRET between two molecules, lanthanide donors D_i (i.e. D_i = Ln³⁺ ions) within a single dielectric donor nanoparticle (D_NP) are capable of transferring their energy to multiple acceptors (A_j) at the NP surface in an uncorrelated manner. Moreover, this D_i network is distributed randomly throughout the nanoparticle, resulting in a large distribution of D_i–A_j distances. The bio-functionalization of biologically non-specific dielectric NPs with appropriate ligands as needed, e.g., antibodies attached to their surface, shifts acceptors further away from the surface of a D_NP and thus donor ions become available for RET at distances larger than typical Förster distances (i.e. R₀ = 6–12 nm) (Fig. 1a). Following eqn (S1),† it becomes obvious that increasing the actual D–A distance r_D–A to twice the Förster distance r_D–A = 2R₀ reduces RET efficiency to a value as small as 1.5% of the maximum possible value (Fig. 1c), which obviously is highly disadvantageous.

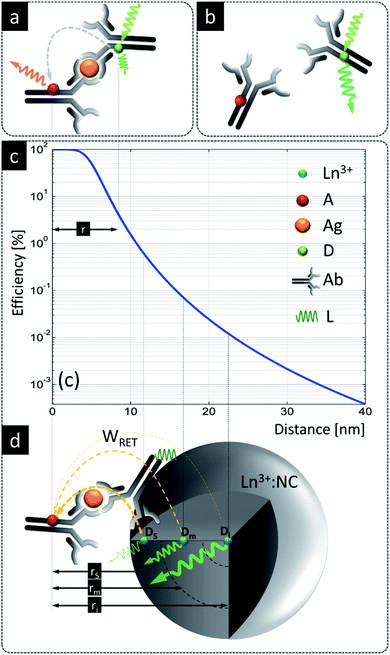Fig. 1 A comparison of LnNPs and conventional LRET based sensing. (a) Molecular FRET between donor () and acceptor () in the presence of antigen (); (b) lack of FRET due to missing antigen; (c) distance dependence of RET efficiency (based on eqn (S1)† for R₀ = 4 nm); (d) LnNP as a RET donor contains ca. 3 zones of lanthanide donor ions, i.e. superficial (s), intermediate (m) and internal (i) donor ions (, D_x, x = s, m, i) positioned, respectively, at r_s, r_m and r_i distances from the acceptor anchored to the surface of NPs through the Ag–Ag reaction. Ln³⁺ – lanthanide as the donor, D – donor, Ag – antigen, A – acceptor, Ab – antibody, L – ligand; bound (b) and unbound (d) Ag–Ab pairs using organic D and A molecules. All elements are in the scale of the X axis in (c).

One complicating issue when using RET from LnNPs is that, due to the large number of Ln³⁺ dopants in a D_NP and due to the large number of acceptor molecules on its surface, there are many D_i–A_j pairs at variable r_ij distances, resulting in a wide variation of RET efficiencies (Fig. 1d). RET-active donor ions are located close to the surface (D_s), while donors located in the center of the NP (D_i) do not participate in RET. Intermediate zone donors (D_m) have intermediate RET efficiencies. All three classes contribute to the total rate of energy transfer, but the presence of the latter two classes of donors (D_m, D_i) reduces the sensitivity of RET-based sensors because these donors emit photons but are less susceptible to the presence of acceptors. Proposed solutions to these issues, such as decreasing the UCNP size, utilizing undoped-core/doped-shell upconverting nanoparticles^59,61,66,78 or utilizing energy migration in a Gd³⁺ network,⁷⁹ have not yet realized radical improvements in RET efficiency for ultrasensitive biosensing. Thus, there is a strong demand to better understand how the composition and architecture of a D_NP affect the spectral properties and RET sensitivity of such donors. Moreover, it is important to identify alternative energy transfer mechanisms that may contribute to enhanced RET sensitivity.

In this work we theoretically predict and show that donors that host photon avalanche (PA) upconversion can enhance the interaction range over which RET can be detected, compared to conventional FRET length scales. The PA phenomenon is a highly non-linear optical process in which minute changes in excitation intensity result in many orders of magnitude changes in emission intensity critically slowing down emission risetimes.^80,81 We hypothesize and confirm via modeling that the PA phenomenon should be exceptionally susceptible to any kind of perturbation such as the presence of acceptor molecules on the surface of such photon avalanche nanoparticles (ANPs). Such a sensitivity would allow ANP–acceptor pairs to operate at long distances, which would provide new opportunities for biological FRET studies.

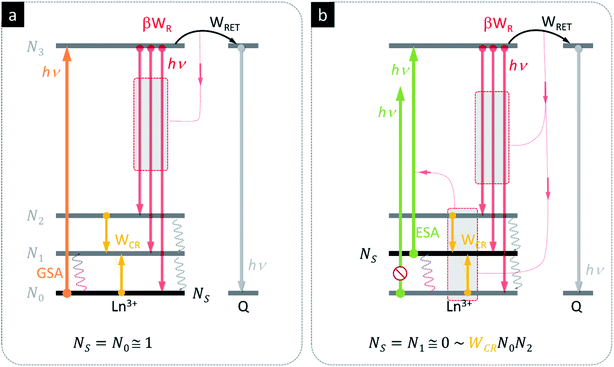
The basic photon avalanche mechanism is schematically presented in Fig. 2, where the energy levels of the same donor ion and the same acceptor are presented under two photoexcitation scenarios – ground state absorption (Fig. 2a, GSA) and excited state absorption (Fig. 2b, ESA). In both cases, the donors may either emit photons (red arrows), cross-relax (yellow arrows) or transfer energy to quencher Q (black arrows). In conventional Stokes luminescence (Fig. 2a), the absorption occurs from the ground state, whose population is close to N_o ≅ 1. The presence of the quencher is therefore competing only with the emission from the N₃ level and ultimately, for rising Q concentration, donor emission becomes quenched, while in principle, the acceptor emission intensity rises up. The phenomena proceeding photon avalanche emission are very different (Fig. 2b), because the absorption predominantly occurs via excited state absorption (ESA). In this case, the initial population of the starting level is therefore almost empty (N₁ ≅ 0); to achieve PA emission, the N₁ level population must be first established. In the course of initial thermal balance with the ground state, as well as radiative (W_R) or non-radiative (W_CR) processes (W denotes the rate constants), this level becomes populated more and more in a non-linear way. For example, the cross-relaxation between one excited (N₂) and one ground state (N₀) ion doubles the population of the ESA starting level. In consequence, these phenomena result in a very steep S-shape power dependence I_EMI = (I_EXC)^N of photon avalanche emission, with power N = 1–2 below and above the PA region, and power N = 10 (and up) above the PA threshold.

Fig. 2 Comparison of simplified schemes for conventional luminescence (a) and photon avalanche upconversion (b) with the same donor and the same acceptor. For conventional luminescence, Q reduces the emission output proportionally to Q distance and concentration. For the avalanche process, the presence of Q affects the absorption and gain coefficients of the PA donor. The colour arrows indicate GSA (orange) and ESA (green) excitation, gain by looping (yellowish), emission (red), D–A RET (black) and A emission (grey). The starting level (N_s) differs between the two schemes. The thermal population of the N₁ level and non-radiative quenching of N_1,2 levels are indicated by red-blue and grey dotted-wave-arrows, respectively.

We therefore hypothesized that the strongly non-linear photophysics of PA could be exploited for efficient RET sensors, since small changes in population driven by RET would drive disproportionately larger changes in the LnNP luminescence. Bringing an acceptor molecule near a lanthanide ion donor would depopulate the first excited state (the starting level of ESA absorption) via RET, inhibiting the absorption coefficient (Fig. 2b) and disrupting the otherwise positive gain of energy looping (CR), which shall ultimately reduce the PA emission itself (Fig. 2b). We reasoned that even at large D–A distances (η_FRET < 1.5% at e.g. r_DA = 2R_o), the RET might still be competitive to the recurrent population of the starting ESA level and impede PA emission. In other words, the PA based RET should not only reduce emission intensity (the result of absorbed photons), but also more importantly disrupt the positive feedback of looping and hinder the photoexcitation itself, which ultimately becomes a self-limiting phenomenon. The emission threshold of PA systems should thus be extremely sensitive to the presence of RET, because they require much higher excitation intensity to overcome losses as conventional FRET probes with linear responses.

Although photon avalanche has been successfully demonstrated in numerous lanthanide doped bulk materials,⁸¹ it is not trivial to achieve PA at room temperature or in nanomaterials intended for bio-medical purposes. Above cryogenic temperatures, the high non-linearity of PA⁸² is reduced due to phonon-assisted GSA and due to faster non-radiative relaxation of excited states. In nanomaterials, a proper balance must be achieved between counteracting phenomena such as cross-relaxation and energy migration (responsible for spreading the excitation over a NP). This balance is particularly challenging to maintain in small nanoparticles suspended in aqueous solutions, since energy migration also facilitates quenching of excited states at surface defects and via high energy phonons of ligands and solvents. Surface passivation with an un-doped shell can prevent surface quenching, but thick shells reduce RET efficiency by increasing the distance between the D and A. Therefore, the host composition, dopants and their concentrations as well as the architecture of NPs must be optimized⁸³ before actual ANP nanoparticles are ready for real-world applications.

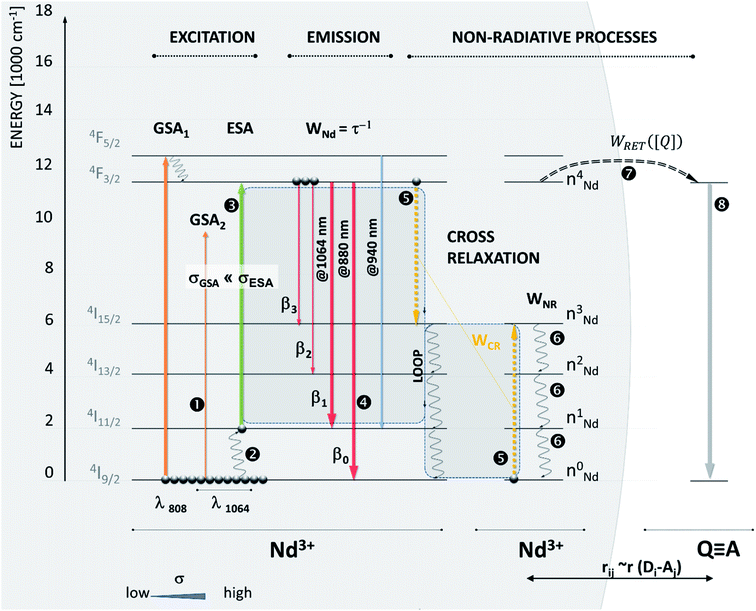
To demonstrate our Photon Avalanche Resonance Energy Transfer (PARET) approach, we computationally investigated the photophysical dynamics in the excited states of Nd³⁺ ions in the presence of a RET acceptor. In our model system, luminescence in these Nd³⁺ ions is excited by 1064 nm photoexcitation, which lies in the second NIR imaging window.⁸⁴ Nd³⁺ doped materials are thought to exhibit PA under 1064 nm excitation since such photons, to a first approximation, are not absorbed by Nd³⁺ ions from the ground state due to significant, ∼2000 cm⁻¹, energy mismatch between the incident photon energy and the gap between the excited state/ground state manifolds (Fig. 3, ➊). At physiologically relevant temperatures, the ⁴I_11/2 level becomes thermally populated (Fig. 3, ➋) to facilitate the ESA photoexcitation of the ⁴F_3/2 level at ∼1064 nm.

Fig. 3 Explanation of the fundamental features of photon avalanche based on the energy diagram in Nd³⁺ ion doped nanomaterials. Energy diagram showing resonant (808 nm, ➊) and non-GSA-resonant (1064 nm, ➌) photoexcitation, radiative emission W_Nd from the ⁴F_3/2 level with its typical branching-ratios (β_{0, …, 3}, ➍), cross-relaxation (W_CR, ➎) leading to recurrent population of the ⁴I_11/2 level, initial thermal population of the ⁴I_11/2 level (➋) and the presence of acceptor species A (➐). Due to a relatively small energy gap, non-radiative depopulation (❻) takes place, feeding among others the ⁴I_11/2 level. The A dissipates the energy either as luminescence (❽) or in other non-radiative ways.

Because the acceptor depopulates the Nd³⁺:⁴F_3/2 multiplet (Fig. 3, ➐), which feeds the intermediate Nd³⁺:⁴I_11/2 level, the presence of the acceptor in close vicinity to ANPs and the consequent D–A RET become a competitive process to the ‘looping’ phenomenon, which is known to be a prerequisite for photon avalanche to occur. In the absence of PA, the ⁴F_3/2 excited state population would be reduced leading to a decrease in emission intensity and luminescence lifetime shortening. However, when PA dominates the photophysics, the ⁴F_3/2 excited state population is critically important to feed the looping phenomenon and double the population of the intermediate ⁴I_11/2 level (Fig. 3, ➎): (⁴F_3/2; ⁴I_9/2) → (⁴I_11/2; ⁴I_11/2).

Therefore, at the PA threshold, where highly non-linear behavior is observed, changing the intermediate level population (⁴I_11/2) a tiny bit has a disproportionately larger impact on the emission than in normal FRET systems. The presence of a quencher is thus responsible not only for quenching the ⁴F_3/2 level population and its emission, but also for reducing the absorption coefficient (Fig. 3, ➌) and looping phenomenon (Fig. 3, ➎), which ultimately reduce the optical gain and affect the non-linear performance of ANP reporters. Hence RET sensitivity over longer distances would be expected from PA systems compared to typical fluorescence.

Because the distance- and concentration-dependent RET phenomenon, described by the term

competes with the energy looping, the presence of a quencher should therefore effectively disrupt the PA phenomenon even at large D–A distances (r_D–A > 2R₀), where the RET efficiency is below 1.5%. In eqn (1), r and [A] denote the D–A distance and A concentration, and n₄ is the population of the metastable ⁴F_3/2 level. Because η(r) is Förster efficiency that describes single-D–single-A interaction and does not take into account specific situation of multiple D and multiple A species in our RET system, we proposed to include the W_DA term, which denotes A concentration dependent average D–A energy transfer rate. The impacts of distance and A concentration on the output RET sensor behavior were numerically studied (Fig. 4 and S3†) by providing the ratio of W_RET to W_CR in a wide variability range (i.e. [A] = (W_RET(r,[Q])/W_CR); [A] ∊ 0.001, …, 10). In this way, the competition of D–A RET in relation to the gain of the system (proportional to W_CR) could be evaluated. Such a relative approach should simplify the analysis and understanding of the obtained theoretical data. Intuitively, these processes should shift the balance between excited state absorption (⁴I_11/2 → ⁴F_5/2) and emission (⁴F_3/2 → ⁴I_J, J = 15/2, 13/2, 11/2 and 9/2), and in consequence, should lead to strong variations of PA emission intensity in response to minute amounts of quenching molecules at relatively large distances. To model the RET process for the actual energy level scheme of Nd³⁺ ions, we constructed rate equations for PA in Nd with dipole–dipole energy transfer from the ⁴F_3/2 (n₄) level to an acceptor site, with the behaviour of D–A energy transfer governed by Förster formalism (eqn (S1)†).

Fig. 4 Photon avalanche enhanced RET (PARET). (a) Susceptibility of PA assisted RET (steady-state ) to D–A distance at different concentrations of acceptor (quantified as a relation of W_RET to the W_CR looping rate, W_RET/W_CR = 〈0.001, …, 10.000〉 pink to blue, the parameters used for simulation: R₀ = 5 nm, W_CR = 1 × 10⁵, W_NR = 1 × 10⁵, T = 32 °C). The black curve is the for conventional FRET with R₀ = 5 nm. (b) Susceptibility of PA assisted RET (steady-state ) to different concentrations of acceptor at variable D–A distance (red to yellow). The arrow in (b) indicates the theoretical dose–response curve of a PARET sensor for r_D–A = 12 nm, demonstrating how W_FRET, being a fraction of W_CR, quenches PA emission intensity.

To calculate the rates of the optical transitions and energy transfer processes in Nd³⁺ ions, we numerically solved a set of phenomenological rate equations (see the ESI, eqn (S3)–(S8)†),⁸² and we evaluated them across a range of acceptor concentrations. Our PA modelling produced kinetic profiles for the populations of all Nd³⁺ excited states (e.g., n_i from i = 0 to 4; for a detailed explanation, see Section S3†). We found that the ⁴F_3/2 (n₄) level was of critical importance since it is effectively proportional to the emission intensity at 880 nm. We quantified the steady-state intensity at a sufficiently long excitation pulse (I_SS) as well as the half risetime of the emission intensity (t_1/2) (as defined in Section S4, Fig. S1 and S2†). The I_SS and t_1/2 values were calculated as a function of D–A distance (r_D–A) and as a function of the concentration of acceptor molecules (representative examples in Fig. S3†). It is intuitive that increasing the concentration of the acceptor affects the delicate balance required for PA to occur, which is evidenced (Fig. S3†) as the PA threshold and t_1/2 shift as well as shifting and reducing the non-linearity of the PA phenomenon. Further, to facilitate comparisons, we defined the figure of merit as (Fig. 4), which normalizes the steady-state I_SS PA donor emission in the presence of an acceptor (quencher) (I_DA) with the luminescence intensity of the donor in the absence of an acceptor (I_D). For the t_1/2 half-rise times, we defined a similar figure of merit as 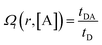(Fig. S4d–f†).

The figure of merit for luminescence intensity (Ω_SS) was evaluated versus the distance r_D–A between the D ion and A species (Fig. 4a) and at various concentrations of the acceptor [A] (Fig. 4b). Similar relationships are shown for D lifetimes (Fig. S4d–f†). Fig. 4a shows how the D emission intensity changes upon A binding at various distances. For very weak interactions (i.e. [A] = W_LRET(r,[Q])/W_CR = 0.001) the presence of an acceptor does not affect PA at all (Ω_SS ≅ 1, pink curve). As the interaction becomes stronger, the presence of the acceptor quenches PA emission more efficiently (Ω_SS ≅ 0, blue curve) at short D–A distances. In agreement with intuition, the PA luminescence intensity ‘recovers’ (i.e. Ω_SS(r,[A]) approaches 1) as the A molecule is moved away from the D to distances larger than 20–30 nm (Fig. 4). The region of high slope visible in Fig. 4a is a consequence of the FRET process competing with the PA photoexcitation process. The transition region shifts to larger r_D–A as the disruption of the looping (introduced by the presence and concentration of A molecules) becomes stronger. Interestingly, this means that the effective Förster distance becomes 2–6 fold larger than the original R₀ Förster distance (Fig. 4a, black curve calculated for R₀ = 5 nm).

This increased 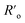suggests that ANPs may be used to overcome the current limitations of LnNP RET donors. Specifically, ANPs can be synthesized with thicker surface passivating shells and longer linkers for bio-functionalization, while maintaining sensitivity to acceptors following the ‘spectroscopic ruler’ principle with neither additional experimental nor analytical complexity or costs. As an illustrative example, let us consider an 8 nm diameter ANP covered with a 4 nm thick un-doped shell and acceptors present 4 nm away from the surface of this donor nanoparticle. The distance between the acceptor and the center of the donor nanoparticle is thus r_DA = 12 nm which conventionally would result in a very low RET efficiency (η_RET < 1%). In the PA regime, however, the W_FRET being only a fraction of W_CR (r_DA = 12 nm, the curve indicated by the arrow in Fig. 4b) is still sufficient to make Ω_SS responsive to the presence of the acceptor. This means that a single acceptor molecule could potentially ‘quench’ all dopants in an entire ANP, which is promising for biosensing. Even larger D–A distances (e.g. due to surface passivation or larger sizes of ligands and bio-recognition molecules) will impede the PA phenomenon, but then larger acceptor coverage of the ANP surface is required. We conclude that the PA system should therefore be particularly susceptible to the presence and concentration of a quencher at the surface of a PA nanoparticle.

In conventional short range FRET in NPs, only superficial lanthanides show sufficiently strong RET to acceptors at the surface, while all other non-RET ions (i.e. the ones in the center of a NP) contribute to the overall emission and thus increase the background signal, reduce the sensitivity and increase the limit of detection. Conversely, all photon avalanche lanthanide emitters being present within the whole volume of the NPs should be capable of responding to the D–A interaction, by being quenched. Based on the results presented in Fig. 4 and S4,† we can conclude that already minute disturbances to the looping process ([A] ∼ 0.1) can change the Ω_SS(r,[A]) more significantly than in conventional FRET. This is evidenced in the complete quenching of Ω_SS(r,[A]) at r = 12 nm. Therefore, the monotonic responsivity of ANPs to an acceptor present at distances 2–4 fold longer than the Förster distance indicates that the PARET solves many of the currently existing drawbacks of lanthanide doped nanoparticles in bio-sensing applications.

The sensitivity of PARET systems to dedicated acceptors over long distances allows the realization of significantly brighter assays with simple technical detection setups and further miniaturization. The brightest UCNPs have passivating shells of ∼4 nm thickness, which increase the UC quantum yield by over 3 orders of magnitude.^85,86 Moreover, the use of passivating shells will minimize the impact of the local chemical microenvironment⁸⁷ or energy migration to surface unspecific quenchers.⁸⁸ Finally, such a long-range sensitivity is also beneficial for biosensors based on LnNPs due to the finite length of ligands and linker molecules that must be attached to the surface of biologically inert LnNPs to make them biocompatible and bio-specific.

The presented example of Nd³⁺ ions acting as donors requires acceptors whose absorption spectra overlap with Nd³⁺ emission at 880 nm. Only a few NIR dyes absorb at this wavelength, but actually, the A does not need to be luminescent – gold NPs, silver NPs, or some quantum dots (e.g. Ag₂S and CuInS₂) with absorption bands in the NIR region should be sufficient as acceptors (or quenchers) at the required NIR spectral range. Although we use Nd³⁺ donors as an exemplary system, our approach of pairing PA systems with RET is general in nature, and any other PA systems at any other PA photoexcitation and PA emission wavelengths should behave in a similar manner.

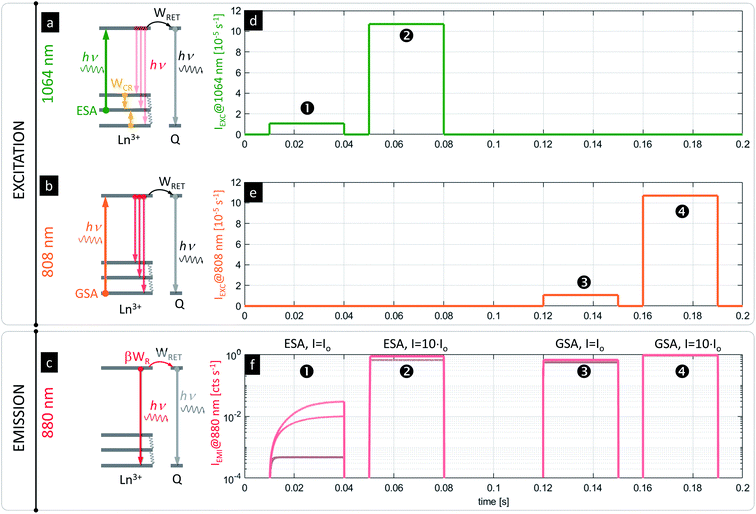
One possible concern when imaging PA nanoparticles in vitro is that the quenching of the PA emission in the presence of strong D–A interaction would make the visualization or detection of PA nanoparticles impossible. Fortunately, the advantage of the presented system is the fact that PA nanoparticles (typically meant to operate according to the scheme in Fig. 5a under 1064 nm photoexcitation pulses, Fig. 5d) can be independently excited with photons matching the GSA (e.g. at 808 nm, Fig. 5b scheme with Fig. 5e pulses) to achieve conventional luminescence (e.g. at 880 or 1064 nm, Fig. 5c and f, ➌ and ➍), which would be more efficient than ESA and PA. Because the PA phenomenon experiences saturation at certain excitation intensities above the PA threshold (Fig. 5f, ➋), the sufficiently strong (I_EXC > I_o) excitation at ESA wavelengths (e.g. at 1064 nm, Fig. 5d, ➋) can be concurrently used for in situ sensing (Fig. 5f, ➊) or visualization of ANPs as well (Fig. 5f, ➋) independently from RET. In fact, it could be an internal standard or a method for estimating the power absorbed by the NP, since the response would be more linear. In consequence, these features should limit the required number of negative control experiments and should simplify the data analysis or correction.

Fig. 5 Simulations of PA sensing and luminescent labeling dual functionality of PA nanoparticles. Schematic presentation of energy transitions for (a) ESA photoexcitation (λ_EXC = 1064 nm) and (b) conventional GSA photoexcitation (λ_EXC = 808 nm) regimes and (c) outcoming emission from the ⁴F_3/2 level (red arrows in (a–c); λ_EMI = 880 nm). The time resolved excitation traces of (d) ESA at 1064 nm and (e) GSA @ 808 nm photoexcitation, and (f) the corresponding kinetics of the same ANPs luminescence (λ_EMI = 880 nm) intensity under ➊, ➋ ESA and ➌, ➍ GSA photoexcitation at variable concentrations of the acceptor ((f), brown to red). The concentration of the acceptor was fixed to A_RET = 1 × 10⁻⁵ (brown), 1 × 10⁻⁴ (dark red), 1 × 10⁻³ (red); the parameters R₀ = 5 nm, T = 32 °C, I_o = 1.07 × 10⁵, and W_CR = 1 × 10⁵ were used for simulations.

The presented modelling (Fig. 5) indicates that the same PA nanoparticles may therefore play a dual role. First, they may act as RET sensors under the PA photoexcitation regime as discussed above. At carefully adjusted excitation intensity (i.e. λ_EXC = 1064 nm, I_EXC ∼ I_o, λ_LUM = 880 nm for Nd³⁺, Fig. 5a and d), the luminescence risetimes or steady-state intensities are proportional to the concentration of acceptors (Fig. 5f, ➊ and S5†). The PA nanoparticles can additionally behave as luminescent labels, whose luminescence intensity is barely dependent on A concentration (Fig. 5f, ➋, ➌ and ➍) and is significantly stronger than in the PA sensing regime. The latter luminescence (λ_LUM = 880 nm) can be achieved either under “above the PA threshold” ESA photoexcitation (λ_EXC = 1064 nm @ e.g. I_EXC > 10 × I_o) (Fig. 5d, ➋) or alternatively under GSA absorption (λ_EXC = 808 nm) (Fig. 5b and e, ➌ and ➍). Either approach will reveal the presence of PA nanoparticles as a reference signal (in homogeneous assays or imaging in vitro) independently from bio-sensing features. Such a two-fold functionality satisfies the requirements imposed by functional FRET imaging, where D and A emission intensity images are mathematically integrated and transformed to quantify RET efficiency in order to derive the D–A interaction. This is a known issue in conventional fluorescent FRET species, which spectrally overlap with high auto-fluorescence background and light scattering in a short wavelength region (Fig. S8†). Moreover, because the emission at two different spectral bands has to be quantified (separately D and A emission), the excitation source should selectively photostimulate only donors but not acceptors, otherwise cumbersome corrections are required.^1,27,89 Using the PA approach proposed here, not only a large (anti)Stokes shift is achieved, but also the same emission band is observed under two electronically switched 808 and 1064 lasers (Fig. 5a and b), or for a single 1064 nm beam with the excitation adjusted to I_o and to e.g. 10 × I_o (Fig. 5d, ➊ and ➋, respectively). Both wavelengths undergo low scattering and show high penetration depths into tissue (Fig. S6†), and thus are beneficial for biomedical applications. These features should possibly outperform current methods with improved sensitivity.

Further biomedical advantages of the PA nanoparticles compared to conventional organic FRET dyes or fluorescent proteins are their long, micro-to millisecond risetimes and photostable emission, which may only weakly be susceptible to the environment (e.g. viscosity and pH). These long risetimes should facilitate the rejection of any remaining, short-lived background autofluorescence, and in consequence, should significantly increase the signal-to-background ratio. Additionally, the technical convenience in recording or imaging luminescent labels with micro-to millisecond risetimes may enable PARET imaging with simple and affordable instrumentation, in contrast to the fs–ps lasers and slow TCSPC scanning lifetime imaging techniques used for organic fluorophores. Finally, we note that we have predicted⁸² and experimentally demonstrated that the highly non-linear behavior of the discussed ANPs enables them to be used as luminescent labels for single beam super-resolution optical imaging below the diffraction limit of light,^82,83 which ultimately, all together, may enable sensing and visualization of molecular interactions at the nanoscale.

Conclusions

Retaining the photostability and NIR spectral region of operation of Nd³⁺ ions, the photon avalanche assisted RET (PARET) sensing modeled here should solve many drawbacks of, otherwise advantageous, LnNP donors. First, our modelling shows that depending on the concentration of acceptors on the surface of a D_NP RET system, the photon avalanche emission can be quenched completely at exceptionally long D–A interaction ranges exceeding the Förster distance by a few-fold. Similar conclusions can be drawn from either steady state intensity or from luminescence risetime kinetics. There are two important consequences of this observation: (i) the surface of a D_NP can be passivated with an undoped shell in order to increase its brightness and (ii) the D_NP surface bio-functionalization, which typically separates acceptor molecules from donors beyond the Förster radius, would not impair its sensitivity. Additionally, the ability to photoexcite the D_NPs with either GSA for conventional luminescence or with ESA for photon avalanche emission can potentially enable combining the localization of luminescent labels with their sensing capability by (a) switching between two excitation wavelengths (λ_GSA ∼ 808 nm, λ_ESA ∼ 1064 nm), (b) switching the excitation intensity, or (c) switching the detection method (continuous or time-resolved decay for conventional emission vs. continuous or pulsed risetime for the photon avalanche case). These dyadic features should facilitate bio-detection and bio-functional imaging of PA probes in vitro, and thus should simplify long-term studies of biomolecular interactions and biosensing at the nanoscale.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. B. acknowledges financial support from NCN, Poland, grant number UMO-2018/31/B/ST5/01827, and K. P. acknowledges financial support from NCN, Poland, grant number 2018/31/D/ST5/01328. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, U.S. Department of Energy, under Contract No. DE-AC02-05CH11231. Part of the conceptual work was performed by A. B. in Łukasiewicz Research Network – Port Polish Center For Technology Development.

References

1. D. W. Piston and G. J. Kremers, Trends Biochem. Sci., 2007, 32, 407–414.
2. J. R. Lakowicz, Principles of Fluorescence Spectroscopy Principles of Fluorescence Spectroscopy, 2006.
3. W. R. Algar, N. Hildebrandt, S. S. Vogel and I. L. Medintz, Nat. Methods, 2019, 16, 815–829.
4. X. Qiu and N. Hildebrandt, Expert Rev. Mol. Diagn., 2019, 19, 767–771.
5. B. T. Bajar, E. S. Wang, S. Zhang, M. Z. Lin and J. Chu, Sensors, 2016, 16(9), 1488.
6. T. Zal and N. R. J. Gascoigne, Biophys. J., 2004, 86, 3923–3939.
7. I. Medintz and N. Hildebrandt, FRET - Förster Resonance Energy Transfer: From Theory to Applications, Wiley-VCH Verlag, 2013.
8. A. Govorov, P. L. H. Martínez and H. V. Demir, Understanding and Modeling FRETFörster-type Resonance Energy Transfer: Introduction to Förster-type Resonance Energy Transfer (FRET) FRET Series, 2016.
9. W. R. Algar, H. Kim, I. L. Medintz and N. Hildebrandt, Coord. Chem. Rev., 2014, 263–264, 65–85.
10. D. Geißler, S. Linden, K. Liermann, K. D. Wegner, L. J. Charbonnière and N. Hildebrandt, Inorg. Chem., 2014, 53, 1824–1838.
11. M. Cardoso Dos Santos and N. Hildebrandt, TrAC, Trends Anal. Chem., 2016, 84, 60–71.
12. N. Hildebrandt, K. D. Wegner and W. R. Algar, Coord. Chem. Rev., 2014, 273–274, 125–138.
13. H. Hevekerl, T. Spielmann, A. Chmyrov and J. Widengren, J. Phys. Chem. B, 2011, 115, 13360–13370.
14. X. Zhang, C. A. Marocico, M. Lunz, V. A. Gerard, Y. K. Gun’Ko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, ACS Nano, 2014, 8, 1273–1283.
15. A. Samanta, Y. Zhou, S. Zou, H. Yan and Y. Liu, Nano Lett., 2014, 14, 5052–5057.
16. C. S. Yun, A. Javier, T. Jennings, M. Fisher, S. Hira, S. Peterson, B. Hopkins, N. O. Reich and G. F. Strouse, J. Am. Chem. Soc., 2005, 127, 3115–3119.
17. J. De Torres, M. Mivelle, S. B. Moparthi, H. Rigneault, N. F. Van Hulst, M. F. García-Parajó, E. Margeat and J. Wenger, Nano Lett., 2016, 16, 6222–6230.
18. C. M. Spillmann, S. Buckhout-White, E. Oh, E. R. Goldman, M. G. Ancon and I. L. Medintz, Chem. Commun., 2014, 50, 7246–7249.
19. J. K. Hannestad, P. Sandin and B. Albinsson, J. Am. Chem. Soc., 2008, 130, 15889–15895.
20. C. Chen and N. Hildebrandt, TrAC, Trends Anal. Chem., 2020, 123, 115748.
21. Á. I. Fábián, T. Rente, J. SzölloSi, L. Matyus and A. Jenei, ChemPhysChem, 2010, 11, 3713–3721.
22. B. P. Maliwal, S. Raut, R. Fudala, S. D'Auria, V. M. Marzullo, A. Luini, I. Gryczynski and Z. Gryczynski, J. Biomed. Opt., 2012, 17, 011006.
23. G. Krainer, A. Hartmann and M. Schlierf, Nano Lett., 2015, 15, 5826–5829.
24. V. Raicu, J. Biol. Phys., 2007, 33, 109–127.
25. M. Baibakov, S. Patra, J. B. Claude, A. Moreau, J. Lumeau and J. Wenger, ACS Nano, 2019, 13, 8469–8480.
26. C. Berney and G. Danuser, Biophys. J., 2003, 84, 3992–4010.
27. A. Pietraszewska-Bogiel and T. W. J. Gadella, J. Microsc., 2011, 241, 111–118.
28. E. Deplazes, D. Jayatilaka and B. Corry, J. Biomed. Opt., 2012, 17, 011005.
29. E. A. Jares-Erijman and T. M. Jovin, Nat. Biotechnol., 2003, 21, 1387–1395.
30. J. Zhang, H. Li, L. Chai, L. Zhang, J. Qu and T. Chen, J. Microsc., 2015, 257, 104–116.
31. H. H. Chen, Y.-P. Ho, X. Jiang, H.-Q. Mao, T.-H. Wang and K. W. Leong, Nano Today, 2009, 4, 125–134.
32. H. Wallrabe and A. Periasamy, Curr. Opin. Biotechnol., 2005, 16, 19–27.
33. J. Tisler, R. Reuter, A. Lämmle, F. Jelezko, G. Balasubramanian, P. R. Hemmer, F. Reinhard and J. Wrachtrup, ACS Nano, 2011, 5, 7893–7898.
34. M. E. Materia, M. Pernia Leal, M. Scotto, P. B. Balakrishnan, S. Kumar Avugadda, M. L. García-Martín, B. E. Cohen, E. M. Chan and T. Pellegrino, Bioconjugate Chem., 2017, 28, 2707–2714.
35. Y. Dai, D. Yang, D. Yu, C. Cao, Q. Wang, S. Xie, L. Shen, W. Feng and F. Li, ACS Appl. Mater. Interfaces, 2017, 9, 26674–26683.
36. M. Cardoso Dos Santos, J. Goetz, H. Bartenlian, K. L. Wong, L. J. Charbonnière and N. Hildebrandt, Bioconjugate Chem., 2018, 29, 1327–1334.
37. M. Cardoso Dos Santos, A. Runser, H. Bartenlian, A. M. Nonat, L. J. Charbonnière, A. S. Klymchenko, N. Hildebrandt and A. Reisch, Chem. Mater., 2019, 31, 4034–4041.
38. P. Alonso-Cristobal, P. Vilela, A. El-Sagheer, E. Lopez-Cabarcos, T. Brown, O. L. Muskens, J. Rubio-Retama and A. G. Kanaras, ACS Appl. Mater. Interfaces, 2015, 7, 12422–12429.
39. X. Chen, J. Wang, C. Yang, Z. Ge and H. Yang, Sens. Actuators, B, 2018, 255, 1316–1324.
40. X. Wang, S. Niazi, H. Yukun, W. Sun, S. Wu, N. Duan, X. Hun and Z. Wang, Microchim. Acta, 2017, 184, 4021–4027.
41. L. J. Charbonnière, C. Charpentier, V. Cifliku, J. Goetz, A. Nonat, C. Cheignon, M. C. Dos Santos, L. Francés-Soriano, K.-L. Wong and N. Hildebrandt, Chem.–Eur. J. DOI:10.1002/chem.202002007.
42. L. Marciniak, A. Pilch, S. Arabasz, D. Jin and A. Bednarkiewicz, Nanoscale, 2017, 9, 8288–8297.
43. M. D. Dramićanin, Methods Appl. Fluoresc., 2016, 4, 042001.
44. C. D. S. D. S. Brites, A. Millán and L. D. D. Carlos, Handb. Phys. Chem. Rare Earths, 2016, 49, 339–427.
45. T. M. Liu, J. Conde, T. Lipiński, A. Bednarkiewicz and C. C. Huang, Prog. Mater. Sci., 2017, 88, 89–135.
46. N. M. Idris, M. K. G. Jayakumar, A. Bansal and Y. Zhang, Chem. Soc. Rev., 2015, 44, 1449–1478.
47. Y. Liu, Y. Lu, X. Yang, X. Zheng, S. Wen, F. Wang, X. Vidal, J. Zhao, D. Liu, Z. Zhou, C. Ma, J. Zhou, J. A. Piper, P. Xi and D. Jin, Nature, 2017, 543, 229–233.
48. Q. Zhan, H. Liu, B. Wang, Q. Wu, R. Pu, C. Zhou, B. Huang, X. Peng, H. Ågren and S. He, Nat. Commun., 2017, 8, 1058.
49. A. Gnach, T. Lipinski, A. Bednarkiewicz, J. Rybka and J. A. Capobianco, Chem. Soc. Rev., 2015, 44, 1561–1584.
50. D. J. Naczynski, M. C. Tan, M. Zevon, B. Wall, J. Kohl, A. Kulesa, S. Chen, C. M. Roth, R. E. Riman and P. V. Moghe, Nat. Commun., 2013, 4, 2199.
51. H. Dong, S.-R. R. Du, X.-Y. Y. Zheng, G.-M. M. Lyu, L.-D. D. Sun, L.-D. D. Li, P.-Z. Z. Zhang, C. Zhang and C.-H. H. Yan, Chem. Rev., 2015, 115, 10725–10815.
52. G. Chen, H. Qiu, P. N. Prasad and X. Chen, Chem. Rev., 2014, 114, 5161–5214.
53. D. Casanova, D. Giaume, T. Gacoin, J. P. Boilot and A. Alexandrou, J. Phys. Chem. B, 2006, 110, 19264–19270.
54. J. M. Zwier and N. Hildebrandt, Time-gated FRET detection for multiplexed biosensing, in Reviews in Fluorescence 2016, ed. C. D. Geddes, Springer, Cham, 2017, pp. 17–43.
55. D. J. Gargas, E. M. Chan, A. D. Ostrowski, S. Aloni, M. V. P. Altoe, E. S. Barnard, B. Sanii, J. J. Urban, D. J. Milliron, B. E. Cohen and P. J. Schuck, Nat. Nanotechnol., 2014, 9, 300–305.
56. K. Kuningas, T. Ukonaho, H. Pakkila, T. Rantanen, J. Rosenberg, T. Lovgren and T. Soukka, Anal. Chem., 2006, 78, 4690–4696.
57. T. Soukka, T. Rantanen and K. Kuningas, Ann. N. Y. Acad. Sci., 2008, 1130, 188–200.
58. Y. H. Wang, P. Shen, C. Li, Y. H. Wang, Z. H. Liu, Z. J. Wu and Z. H. Liu, Anal. Chem., 2013, 85, 258–264.
59. Y. Wang, K. Liu, X. Liu, K. Dohnalová, T. Gregorkiewicz, X. Kong, M. C. G. Aalders, W. J. Buma and H. Zhang, J. Phys. Chem. Lett., 2011, 2, 2083–2088.
60. C. D. Laboda and C. L. Dwyer, Adv. Funct. Mater., 2016, 26, 2866–2874.
61. S. Bhuckory, E. Hemmer, Y.-T. Wu, A. Yahia-Ammar, F. Vetrone and N. Hildebrandt, Eur. J. Inorg. Chem., 2017, 2017, 5186–5195.
62. Y. Ding, F. Wu, Y. Zhang, X. Liu, E. M. L. D. de Jong, T. Gregorkiewicz, X. Hong, Y. Liu, M. C. G. Aalders, W. J. Buma and H. Zhang, J. Phys. Chem. Lett., 2015, 6, 2518–2523.
63. A. L. De Guereñu, P. Bastian, P. Wessig, L. John and M. U. Kumke, Biosensors, 2019, 9, 9.
64. L. Francés-Soriano, N. Peruffo, M. M. Natile and N. Hildebrandt, Analyst, 2020, 145, 2543–2553.
65. H. Liu, J. Han, C. McBean, C. S. Lewis, P. Kumar Routh, M. Cotlet and S. S. Wong, Phys. Chem. Chem. Phys., 2017, 19, 2153–2167.
66. S. Melle, O. G. Calderón, M. Laurenti, D. Mendez-Gonzalez, A. Egatz-Gomez, E. Lopez-Cabarcos, E. Cabrera-Granado, E. Diaz and J. Rubio-Retama, J. Phys. Chem. C, 2018, 122(32), 18751–18758.
67. T. Cheng, R. Marin, A. Skripka and F. Vetrone, J. Am. Chem. Soc., 2018, 140, 12890–12899.
68. A. P. Litvin, P. S. Parfenov, E. V. Ushakova, T. A. Vorsina, A. L. Simões Gamboa, A. V. Fedorov and A. V. Baranov, J. Phys. Chem. C, 2015, 119, 17016–17022.
69. S. Cui, S. Xu, H. Song, W. Xu, X. Chen, D. Zhou, Z. Yin and W. Han, RSC Adv., 2015, 5, 99099–99106.
70. L. Mattsson, K. D. Wegner, N. Hildebrandt and T. Soukka, RSC Adv., 2015, 5, 13270–13277.
71. Y.-W. Li, L. Dong, C.-X. Huang, Y.-C. Guo, X.-Z. Yang, Y.-J. Xu and H.-S. Qian, RSC Adv., 2016, 6, 54241–54248.
72. F. Zhang, C.-L. Zhang, W.-N. Wang, H.-P. Cong and H.-S. Qian, ChemSusChem, 2016, 9, 1449–1454.
73. Y. Wang, B. Si, S. Lu, E. Liu, X. Hu and J. Fan, Sens. Actuators, B, 2017, 246, 127–135.
74. Y. Zhang, G. Wang, L. Yang, F. Wang and A. Liu, Coord. Chem. Rev., 2018, 370, 1–21.
75. L. Labrador-Páez, D. J. Jovanović, M. I. Marqués, K. Smits, S. D. Dolić, F. Jaque, H. E. Stanley, M. D. Dramićanin, J. García-Solé, P. Haro-González and D. Jaque, Small, 2017, 13, 1700968.
76. T. Forster, Naturwissenschaften, 1946, 33, 166–175.
77. T. Förster, Ann. Phys., 1948, 437, 55–75.
78. D. Wawrzynczyk, M. Nyk, A. Bednarkiewicz, W. Strek and M. Samoc, J. Lumin., 2013, 133, 138–144.
79. R. Deng, J. Wang, R. Chen, W. Huang and X. Liu, J. Am. Chem. Soc., 2016, 138, 15972–15979.
80. M. F. Joubert, S. Guy and B. Jacquier, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10031–10037.
81. M.-F. Joubert, Opt. Mater., 1999, 11, 181–203.
82. A. Bednarkiewicz, E. M.-Y. Chan, A. M. Kotulska, L. Marciniak and K. Prorok, Nanoscale Horiz., 2019, 4, 881–889.
83. C. Lee, E. Xu, Y. Liu, A. Teitelboim, K. Yao, A. Fernandez-Bravo, A. Kotulska, S. H. Nam, Y. D. Suh, A. Bednarkiewicz, B. E. Cohen, E. M. Chan and P. J. Schuck, arxiv:2007.10551.
84. E. S. Levy, C. A. Tajon, T. S. Bischof, J. Iafrati, A. Fernandez-Bravo, D. J. Garfield, M. Chamanzar, M. M. Maharbiz, V. S. Sohal, P. J. Schuck, B. E. Cohen and E. M. Chan, ACS Nano, 2016, 10, 8423–8433.
85. C. Würth, S. Fischer, B. Grauel, A. P. Alivisatos and U. Resch-Genger, J. Am. Chem. Soc., 2018, 140, 4922–4928.
86. X. Xu, Z. Zhou, Y. Liu, S. Wen, Z. Guo, L. Gao and F. Wang, APL Photonics, 2019, 4, 026104.
87. S. Fischer, N. D. Bronstein, J. K. Swabeck, E. M. Chan and A. P. Alivisatos, Nano Lett., 2016, 16, 7241–7247.
88. N. J. J. J. Johnson, S. He, S. Diao, E. M. Chan, H. Dai and A. Almutairi, J. Am. Chem. Soc., 2017, 139, 3275–3282.
89. R. Roy, S. Hohng and T. Ha, Nat. Methods, 2008, 5, 507–516.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00404a

---