Open Access Article
Open Access ArticleQuenching of nonlinear photoacoustic signal generation in gold nanoparticles through coating†
Genny A.
Pang
 *a,
Christoph
Haisch
*a,
Christoph
Haisch
 a and
Jan
Laufer
b
a and
Jan
Laufer
b
aChair for Analytical Chemistry and Institute of Hydrochemistry, Technical University of Munich, Marchioninistr. 17, Munich, 81377, Germany. E-mail: genny.pang@tum.de
bInstitut für Physik, Martin-Luther-Universität Halle-Wittenberg, Von-Danckelmann-Platz 3, Halle (Saale), 06120, Germany
First published on 18th June 2020
Abstract
The photoacoustic signal generated from specific gold nanoparticles increases nonlinearly with respect to fluence. We demonstrate experimentally that this nonlinear behavior can be quenched with a particle coating, and present a theoretical analysis to explain this behavior. This effect has the potential to be developed into a photoacoustic-based biochemical sensor.
Photoacoustic (PA) imaging is an emerging biomedical imaging modality that combines the spectroscopic-based contrast of optical imaging with the deep penetration depth capability of ultrasonic imaging.1,2 A PA pressure pulse is generated when intensity-modulated light is absorbed by the biological target, inducing minor temperature fluctuations that create acoustic waves. For contrast enhancement in PA imaging, materials with high absorption coefficients such as nanoparticles can be employed.3,4 Gold nanoparticles (GNPs), for example, exhibit a high surface-plasmon-resonance-based absorption cross section, and provide strong PA contrast. GNPs also enable targeted specificity because they distribute themselves at certain cell sites,3 and can be functionalized to target key molecular sites of interest.4 When a PA signal is generated from light absorption by a GNP, the absorbed energy rapidly diffuses to the surrounding biological fluid, where the majority of the PA signal generation occurs.5–7 Certain GNP colloids, such as nanospheres of 100 nm in diameter and larger in water, exhibit a nonlinear PA signal strength with respect to excitation fluence, which is attributed to extreme heating of nano-scale fluid volumes surrounding the GNPs, leading to variations in the thermal expansion coefficient of the surroundings.7,8 This causes the nonlinear PA signal generation phenomenon, because the PA signal is proportional to the thermal expansion coefficient.1
Common coatings for nanoparticle-based PA contrast agents include polyethylene glycol and silica.4 Coating of GNPs has certain advantages, including increasing colloidal and thermal stability, and adding functionalization.9,10 A nanoparticle coating can affect the PA signal because the heat transfer between the particle and the surrounding medium is influenced.11 Recent reports indicate that a coating with finite heat conductance and capacity may broaden the PA pulse and deteriorate the PA signal amplitude if interfacial thermal resistance is negligible.12 We have recently shown that this is the case with silica coating of small-diameter GNPs, whose PA signal strength is linear with respect to fluence.13 Other theoretical models confirm that for the nanosecond pulses employed in PA imaging, interfacial thermal resistance has no significant effect on the heat transfer process between the GNP and fluid.14 While experimental studies have previously investigated the effect of silica coating on the PA signal from GNPs, all studies in the literature have focused on small diameter GNPs that exhibit a linear PA signal with respect to fluence.5,13
The present study investigates the effect of a particle coating on the linearity of the PA signal strength with respect to fluence. The theoretical PA-induced temperature field around a single silica-coated GNP is analyzed. We then examine experimentally measured PA signals as a function of fluence for GNPs exhibiting nonlinear signal generation, and investigate the effect of a particle coating on this nonlinearity. To close, we discuss how these results may be of importance for developing new PA-based biochemical sensors if certain conditions are met for the particle and coating properties.
Results
We recently presented a theoretical model to solve the spatial and temporal temperature field during PA excitation of a silica-coated GNP in water to explain the reduction in PA signal amplitude due to silica coating for small-diameter GNPs.13 This model solves the heat equation for the spatial and temporal temperature field that arises after PA excitation from a nanosecond pulse. Fig. 1 shows the model prediction of the temperature field resulting from PA excitation of a 100 nm diameter spherical GNP, and the effect of a 15 nm silica coating thickness on the temperature field, assuming an initial temperature of 20 °C and excitation fluence of 1 mJ cm−2 with a 5 ns pulse at a wavelength of 532 nm. Fig. 1a shows that the peak temperature rise in the surrounding water (which is reached at the particle–water interface) is 40% lower in the case of the coated GNP as compared to the uncoated GNP. Fig. 1b and c show the spatial distribution of the peak temperature reached for the uncoated and coated GNP, respectively, within the GNP, in the silica shell, and in the surrounding water for a cross section through the center of the GNP.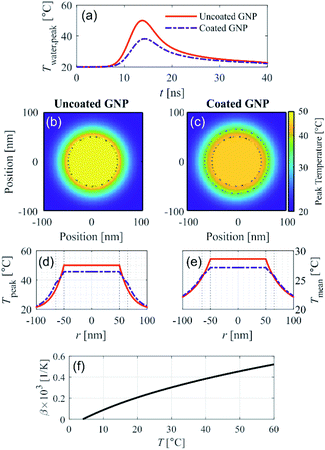 | ||
| Fig. 1 Theoretical modeling of the temperature field after PA excitation of an uncoated and coated gold nanoparticle (GNP) in water assuming an excitation fluence 1 mJ cm−2, pulse width 5 ns, wavelength 532 nm, and initial temperature 20 °C. (a) Temporal evolution of the peak water temperature. 2D spatial distribution of the peak temperature reached for the (b) uncoated GNP and (c) coated GNP. (d) Analogous 1D representation of the peak temperature, and (e) 1D spatial distribution of mean temperature over the first 40 ns after excitation for the uncoated and coated GNP, shown with legend reported in (a). Dotted black lines in (b)–(e) illustrate the GNP core and coating boundaries. (f) Thermal expansion coefficient of water as a function of temperature.15 | ||
It can be seen that with the silica coating, the peak temperature reached within the particle is lower than in the uncoated GNP case (Fig. 1c), and that the temperature rise is distributed over a larger volume that includes the silica coating. Fig. 1d represents the information shown in Fig. 1b and c, respectively, in the radial dimension. The spatial distribution of the temperature averaged over the first 40 ns after PA excitation shown in Fig. 1e for the uncoated and coated GNP. The time-averaged temperature at the particle–water interface is also clearly lower in the case of the coated GNP (25.7 °C) as compared to the uncoated GNP (28.6 °C) because of the finite heat conductance and capacity of the silica coating, which affects the average specific heat capacity of the entire particle. Fig. S1† shows that the reduction in the temperature of the water increases with the coating thickness. The theoretical model accounts for the differences in thermal properties of the gold and silica as described in ref. 13. The results in Fig. 1 suggest that the increase in the thermal expansion coefficient in the nano-scale fluid volume of high temperature surrounding the GNP will be lower in the case of PA excitation of a coated GNP as compared to an uncoated GNP. The temperature dependence of the thermal expansion coefficient of water is shown in Fig. 1f.15 At higher excitation fluence levels, the temperature rise in the nano-sized volume surrounding the GNP is further increased, leading to a higher thermal expansion coefficient, but the temperature rise for the uncoated GNP is always greater than for the coated GNP under the same excitation fluence. Because the PA signal generation nonlinearity is related to the magnitude of the temperature rise in the nano-scale fluid volume surrounding the GNP, these theoretical results suggest that the nonlinear effect seen in PA signal generation should be reduced with a particle coating with sufficient thickness.
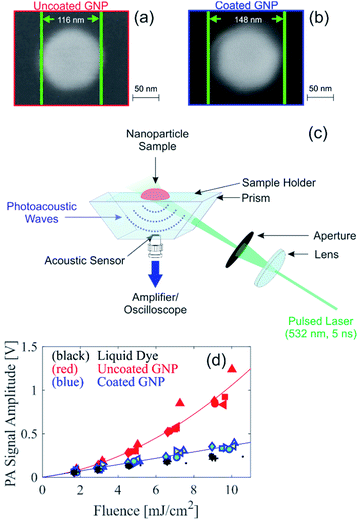
To experimentally assess the theoretical prediction, samples of uncoated and coated GNP suspensions were produced for PA experiments. Citrate-stabilized gold nanospheres of 100 nm in diameter (BBI Solutions) were coated in house with silica using a modified Stöber method.16 Due to the limited electron transparency of the large coated GNPs (overall diameter >100 nm), scanning electron microscopy (SEM) was used for initial characterization of the GNPs. Comparison of SEM images of the uncoated and coated GNPs, shown in Fig. 2a and b, respectively, indicate that the coated GNP has a coating thickness of approximately 16 nm. Based on the resolution of the SEM images and the reproducibility of the coating thickness, we estimate an uncertainty of ±3 nm for the thickness of the silica coating. Fig. S2† presents SEM images of a larger area showing that small deviations in the core particle diameter are possible. Analysis of SEM images of multiple particles reveal a nominal particle diameter of 105 nm with a standard deviation of 10 nm. Dynamic light scattering (DLS) measurements reveal that the coated GNPs have a hydrodynamic diameter 27 nm larger than the uncoated GNP, supporting the silica coating thickness determined from the SEM images, and some degree of deviation in the particle distribution is also seen (Fig. S3†). The larger hydrodynamic diameter from the DLS size determination as compared to with the SEM imaging is expected due to the differences in the characterization methods.17 Energy-dispersive X-ray spectroscopy (EDX) measurements of the coated GNPs (Fig. S4†) confirm that the elements of the silica coating are present in the GNPs. For the PA experiments, the uncoated and coated GNP suspensions were diluted to an identical optical density (OD) of 1.4 at 532 nm. The OD spectra of the GNP suspensions is shown in Fig. S5,† illustrating that the peak absorption of the coated GNP suspension is slightly red shifted from that of the uncoated GNP suspension, as expected from the silica coating.12 For comparison of the PA signals, a homogeneous absorbing liquid dye sample was also prepared with an identical absorption coefficient of the GNP suspensions. The absorption coefficient of the GNP suspensions was determined by multiplying the OD with the percent of the optical extinction due to absorption; this latter quantity was measured using an integrating sphere setup as described previously,7 and the results were consistent to the expected value from Mie theory.18,19
PA signals were measured using the in-house custom-built PA backward mode sensor shown in Fig. 2c. Representative time-resolved PA signals are shown in Fig. S6.† The PA signal amplitude measured in suspensions of uncoated and coated GNP suspensions and the liquid dye sample is shown in Fig. 2d. Multiple measurement repetitions were performed, indicated in Fig. 2d by different symbols shapes. For the coated GNP suspension, the PA signal measurements were performed on two independently synthesized samples, indicated in Fig. 2d by different symbol color. The results show repeatability among measurement repetitions and among independently synthesized samples. More importantly, our results show that the PA signal amplitude measured from the coated GNP suspension is linear with respect to fluence. This is in contrast to the quadratic dependence of the PA signal amplitude with respect to fluence (Fig. 2d), consistent with results in the literature that have been shown to be independent of PA imaging setup.7,20,21 The PA signal amplitude from the coated GNP suspension behaves similarly to that from a homogenous absorber (i.e. liquid dye) that absorbs an identical amount of light. The ratio of the PA signal amplitude to the respective fluence is shown in Fig. S7a,† where the coated GNPs show a fluence-independent ratio, confirming the linear relationship between PA signal amplitude and fluence, and the uncoated GNPs show a linearly increasing ratio with respect to fluence, confirming the quadratic relationship between PA signal amplitude and fluence. From our experimental results, we can conclude that the addition of the 16 nm silica coating to the particles not only reduces the nonlinear effect as predicted from our theoretical analysis, but the coating effectively quenches the nonlinear PA signal generation shown by large GNPs.
In our experiments, all samples had the same absorption coefficient, and the PA signal is primarily generated in the water surrounding the GNPs, indicating that changes in the thermal expansion coefficient is the main cause of differences in the fluence dependence of the PA signal. Fig. S7b† shows the thermal expansion coefficient of water at the model-predicted time- and volume-averaged temperature over the first 40 ns after the PA excitation in the volume surrounding the GNP extending a distance 100 nm from the particle surface (recent reports have indicated that the PA signal generating volume has a thickness greater than the particle diameter22). Through comparison of Fig. S7a,† the experimental ratio of the PA signal amplitude to the respective fluence, and Fig. S7b,† the thermal expansion coefficient at the model-predicted average temperature, the addition of the coating is expected to reduce the PA nonlinearly with respect to fluence according to the model-predicted temperature field. However, the complete quenching of the nonlinearity as a result of the coating (which would be exhibited by a constant thermal expansion coefficient as a function of fluence) is not predicted by the model. We note that our previous experimental study had also found discrepancies between experimental results and theoretical modeling in regard to the extent of the nonlinearity predicted.7 Therefore, while the theoretical model may provide an indication of when a nonlinear PA signal is expected, an experimental confirmation remains necessary to confirm the extent of PA nonlinearity with respect to fluence exhibited by different samples.
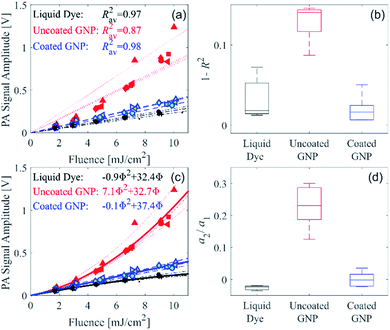
We recently developed a serial PA tomography imaging methodology with the potential to be applied in real time for selective detection in 3D of GNPs exhibiting nonlinear PA signal generation.21 This method can be used to differentiate the PA signal arising from a large-diameter uncoated GNP from another absorber that generates a linear PA signal strength with respect to fluence. To quantify the nonlinearity and demonstrate that our recently reported serial PA tomographic imaging methodology can be used for unambiguous distinction of the uncoated and coated GNP suspensions, the measured PA signal amplitude as a function of fluence was assessed with linear and quadratic functions for each of the measurement repetitions, as described in the ESI.† A linear fit was applied to the data from each of the measurement repetitions for the three different sample types, as shown in Fig. 3a. The deviation of the coefficient of determination (R2) from unity for each sample type is shown in Fig. 3b. For the coated GNP and liquid dye, R2 does not deviate far from unity, as expected as these samples display a linear PA signal amplitude with respect to fluence. However, for the uncoated GNP, R2 deviates further from unity as shown in Fig. 3b, and is statistically different from the R2 for the coated GNP (p = 1 × 10−5). Therefore, R2 can be used to distinguish the uncoated GNP from the coated GNP using serial PA tomographic imaging. Alternatively, the distinction between linear and nonlinear PA signal generation can be determined using a quadratic fit. Fig. 3c shows quadratic fits to all the measurement repetitions, and a boxplot showing the second-order coefficient of the quadratic fit normalized by the respective first-order coefficient (a2/a1) for each of the measurement repetitions is shown in Fig. 3d. The normalized second-order coefficient is approximately zero for the coated GNP and the liquid dye, whereas it is finite and highest the uncoated GNP. The normalized second-order coefficient for the uncoated GNP is statistically different from that of the coated GNP (p = 3 × 10−4).
Interpreting the statistical analysis performed on our data analogously to our demonstrated serial PA tomographic imaging methodology, our results suggest that a process that removes the coating from GNPs could be visualized and detected in vivo, implying the potential of a PA-based biosensor for markers that react with and remove the particle coating. Molecular regions targeted by coated GNPs are typically detected by comparison of the PA image before GNP injection with the PA image after injection. While subsequent changes in the PA image after injection could be attributed to either changes in particle distribution or changes in the PA signal generation properties of the GNP, detecting the formation of nonlinear PA signal behavior due to a coating removal process would unambiguously indicate that the PA signal changes are not arising simply due to GNP redistribution, and instead indicating a biochemical reaction involving the removing of particle coating.
The silica coating used in the current study is not known to be removable through biochemical reactions in vivo. However, the biodegradability of silica can be increased if synthesized as mesoporous silica.23 Moreover, our theoretical modeling results suggest that coatings other than silica with finite heat conductance and capacity can be expected to have a similar effect on the PA signal nonlinearity. Examples of removable coatings include biodegradable polymers presented in the literature. An enteric polymer material based on methacrylate (Eudragit S 100) has been shown to dissolute through the catalytic action of the enzyme urease; through this process, polymer coatings on electrodes have been demonstrated to be capable of urea measurement in serum and whole blood.24 Enzyme-catalyzed dissolution has also been shown to occur for thin films of biodegradable polymers including a poly(ester amide), a dextran hydrogel, and poly(trimethylene) succinate.25 While the two aforementioned studies were based on coatings on electrodes and thin films, respectively, future work needs to be done to determine if these biodegradable polymer coatings are suitable for nanoparticles. Examples of removable polymer coatings on nanoparticles that have been identified in the literature include coatings of the amphiphilic polymer poly(isobutylene-alt-maleic anhydride)-graft-dodecyl on a gold nanoparticle which has been shown to degrade in vivo through proteolytic enzymes in the liver.26 Another removable nanoparticle coating, presented by Harris et al.,27,28 is based on a linear poly(ethylene glycol) tethered by a protease cleavable substrate that can veil and unveil bioactive ligands on a nanoparticle surface. These protease-cleavable polymer nanoparticle coatings were shown to be removed by cancer-associated proteases in a tumor microenvironment, detected through fluorescent and magnetic-resonance imaging.28 The polymer coating presented by Harris et al. increased the hydrodynamic diameter of the nanoparticle by 22 nm, yielding an effective coating thickness of 11 nm. According to our theoretical predictions, this additional volume of the finite-width coating is expected to lower the peak temperature reached in the surrounding fluid in the system after PA excitation, and could also lead to a reduction in or quenching of the nonlinear PA signal generation. However, thinner coatings will lead to a smaller reduction in temperature of the surrounding fluid (as shown in Fig. S1†), and further studies are needed to determine whether there is a minimum coating thickness that is required for nonlinearity quenching to occur. Future work is also needed to determine if the aforementioned coatings would be applicable to nanoparticles that exhibit nonlinear PA signal generation, and if so, whether the coating also leads to complete quenching of the nonlinear PA signal generation behavior as in the case with the silica coating presented in this study.
To our knowledge, the only GNPs known to exhibit a nonlinear PA signal with respect to fluence are large gold nanospheres of 100 nm in diameter or larger. For the development of a PA-based biosensor based on the quenching of the nonlinear PA signal generation behavior, additional studies to determine whether other nanoparticle types exhibit similar nonlinear behavior is recommended to expand the possible materials that can be used for such a sensor. This would involve a comprehensive investigation of other nanoparticle shapes using PA excitation wavelengths near the localized surface plasmon resonance, which is outside the scope of the current work.
Conclusions
We present the first experimental study to show that the nonlinear PA signal generation from large-diameter GNPs can be quenched through the application of a particle coating. We demonstrate this effect experimentally with gold nanospheres of 100 nm diameter suspended in water and a silica coating of 15 nm. Our theoretical analysis attributes the quenching of the nonlinear signal generation to the reduction in the temperature change in the nano-sized volume of fluid surrounding the GNP where the majority of the PA signal generation occurs. The reduction of temperature is due to the finite heat conductance and capacity of the coating that creates a larger volume in which the absorbed energy is distributed. While silica was used in this work to demonstrate PA signal nonlinearily can be quenched with a coating, the theoretical analysis implies the addition of any coating with a finite conductance and capacity will quench the nonlinear PA signal generation at least somewhat if not completely. Furthermore, the theoretical reasoning also suggests also that the removal of a coating on a particle that exhibits nonlinear PA signal generation will cause the PA signal to become nonlinear once again. These findings suggest that PA-based biochemical sensors can be developed if suitable coatings are found that react with and remove the particle coating. We suggest several types of removable polymer coatings that can be further investigated for the purpose of creating a PA-based biochemical sensor. Alternatively, a PA-based biochemical sensor would also be possible if certain biomarkers were found to bind to nanoparticles to cause nonlinear PA signal generation behavior. Future work is needed to determine the minimum coating thickness required for the reported quenching effect to occur, and whether other nanoparticle and coating pairs experimentally exhibit the same quenching effect of the nonlinear PA signal generation as theoretical predicted.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Assistance in the silica-coating synthesis from L. Qiu is gratefully acknowledged. The SEM imaging was performed by C. Benning, and the DLS measurements were performed by J. Hoffmann. We thank W. Lebek for helpful discussions.Notes and references
- P. Beard, Interface Focus, 2011, 1, 602–631 CrossRef PubMed.
- M. Xu and L. V. Wang, Rev. Sci. Instrum., 2006, 77, 041101 CrossRef.
- X. Yang, E. W. Stein, S. Ashkenazi and L. V. Wang, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2009, 1, 360–368 CAS.
- J. E. Lemaster and J. V. Jokerst, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, e1404 CrossRef.
- Y. S. Chen, W. Frey, S. Aglyamov and S. Emelianov, Small, 2012, 8, 47–52 CrossRef CAS.
- A. Prost, F. Poisson and E. Bossy, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 11540 CrossRef.
- G. A. Pang, J. Laufer, R. Niessner and C. Haisch, J. Phys. Chem. C, 2016, 120, 27646–27656 CrossRef CAS.
- O. Simandoux, A. Prost, J. Gateau and E. Bossy, Photoacoustics, 2015, 3, 20–25 CrossRef PubMed.
- X. Hu and X. Gao, Phys. Chem. Chem. Phys., 2011, 13, 10028–10035 RSC.
- P. Botella, A. Corma and M. T. Navarro, Chem. Mater., 2007, 19, 1979–1983 CrossRef CAS.
- A. Alkurdi, J. Lombard, F. Detcheverry and S. Merabia, Phys. Rev. Appl., 2020, 13, 034036 CrossRef CAS.
- Y.-S. Chen, W. Frey, S. Kim, P. Kruizinga, K. Homan and S. Emelianov, Nano Lett., 2011, 11, 348–354 CrossRef CAS PubMed.
- G. A. Pang, F. Poisson, J. Laufer, C. Haisch and E. Bossy, J. Phys. Chem. C, 2020, 124, 1088–1098 CrossRef CAS.
- K. Metwally, S. Mensah and G. Baffou, J. Phys. Chem. C, 2015, 119, 28586–28596 CrossRef CAS.
- D. R. Lide. CRC Handbook of Chemistry and Physics. CRC Press, Boca Raton, FL, 88th edn, 2007 Search PubMed.
- C. Graf, D. L. Vossen, A. Imhof and A. van Blaaderen, Langmuir, 2003, 19, 6693–6700 CrossRef CAS.
- R. F. Domingos, M. A. Baalousha, Y. Ju-Nam, M. M. Reid, N. Tufenkji, J. R. Lead, G. G. Leppard and K. J. Wilkinson, Environ. Sci. Technol., 2009, 43, 7277–7284 CrossRef CAS PubMed.
- C. F. Bohren and D. R. Huffman. Absorption and scattering of light by small particles. John Wiley & Sons: 2008 Search PubMed.
- P. K. Jain, K. S. Lee, I. H. El-Sayed and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 7238–7248 CrossRef CAS PubMed.
- S. V. Egerev and A. A. Oraevsky, Int. J. Thermophys., 2008, 29, 2116–2125 CrossRef CAS.
- S. Schrof, G. Pang, J. Buchmann and J. Laufer, Journal of Imaging, 2018, 4, 146 CrossRef.
- K. Shahbazi, W. Frey, Y.-S. Chen, S. Aglyamov and S. Emelianov, Commun. Phys., 2019, 2, 119 CrossRef.
- P. J. Kempen, S. Greasley, K. A. Parker, J. L. Campbell, H. Y. Chang, J. R. Jones, R. Sinclair, S. S. Gambhir and J. V. Jokerst, Theranostics, 2015, 5, 631–642 CrossRef CAS PubMed.
- C. J. McNeil, D. Athey, M. Ball, W. O. Ho, S. Krause, R. D. Armstrong, J. Des Wright and K. Rawson, Anal. Chem., 1995, 67, 3928–3935 CrossRef CAS.
- C. Sumner, A. Sabot, K. Turner and S. Krause, Anal. Chem., 2000, 72, 5225–5232 CrossRef CAS PubMed.
- W. G. Kreyling, A. M. Abdelmonem, Z. Ali, F. Alves, M. Geiser, N. Haberl, R. Hartmann, S. Hirn, D. J. de Aberasturi, K. Kantner, G. Khadem-Saba, J. M. Montenegro, J. Rejman, T. Rojo, I. R. de Larramendi, R. Ufartes, A. Wenk and W. J. Parak, Nat. Nanotechnol., 2015, 10, 619–623 CrossRef CAS PubMed.
- T. J. Harris, G. von Maltzahn, A. M. Derfus, E. Ruoslahti and S. N. Bhatia, Angew. Chem., Int. Ed., 2006, 45, 3161–3165 CrossRef CAS PubMed.
- T. J. Harris, G. von Maltzahn, M. E. Lord, J. H. Park, A. Agrawal, D. H. Min, M. J. Sailor and S. N. Bhatia, Small, 2008, 4, 1307–1312 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed description of experimental methods, description of linearity assessment, and supporting figures. See DOI: 10.1039/d0na00205d |
| This journal is © The Royal Society of Chemistry 2020 |